Long-term CT surveillance after primary lung cancer treatment captures events in all risk groups

In the article “Risk Stratification for Second Primary Lung Cancer” by Han et al. (1), the authors address the problem of selective screening of lung cancer survivors by creating a competing-risk prognostic model to determine the probability of a secondary primary lung cancer (SPLC). Patients, registered to the US National Cancer Institute’s (NCI) Surveillance, Epidemiology, End Results (SEER) database, were alive at least 5 years after diagnosis of their initial primary lung cancer (IPLC), with a median follow-up of 8 years and maximum follow-up of 16 years. Based on their model, after surviving IPLC for 5 years, the 10-year median risk of SPLC is 8.35%. The authors developed stratifications based on age, histology, and extent of IPLC that ranged from 2.9% in the lowest risk group (1^st decile) up to 12.5% in the highest risk group (10^th decile). Importantly, the results for SPLC rates per year do not suggest that these rates have plateaued at 10 years. Additionally, the median 10-year risk is over twice the incidence of IPLC (3.7%) in the high risk patients enrolled in the National Lung Cancer Screening trial (NLST) (2).

Notably, the patients who develop a SPLC ≥5 years after an IPLC have different clinic-pathologic characteristics than the general population of lung cancer patients. The presenting stage of lung cancer is typically distant 50%, regional 30%, and local 20%, whereas in the select group of patients who develop SPLC, the extent of disease at time of IPLC is reversed: local 70%, regional 25%, and distant is 5%, reflecting the fact that these patients lived at least 5 years after their IPLC diagnosis. Among the study population, twice as many patients died from other causes (23.9%) than from lung cancer (12.7%). Thus, the authors have selected a good patient population to study potential benefit from screening.

The authors used decision curve analysis, which was developed to create a more clinically useful model by making taking into account the relative value of false positives and false negatives (3). This is an alternative to model selection using the more commonly used “area under the curve (AUC)” for the receiver operating characteristic (ROC), also known as the C-index or C-statistic. As mentioned by the authors, a significant clinical shortcoming of using the area under the ROC curve (i.e., AUC) is that it integrates over a continuous number of model parameterizations to create an overall impression of performance, but treats false positives and false negatives with equal weight. As such, a higher AUC does not necessarily mean that a model is superior to one with a lower AUC. In this study, the authors use decision curve analysis to predict how clinicians or patients may value a screen for SPLC by how they weight false positives against true positives.

While many other studies have also looked at secondary lung cancer, Han et al. use the largest yet dataset (to our knowledge) to study the unique issue of incidence of SPLC after survival from IPLC.

We do note a few limitations in methodology and clinical applicability that we address below.

Methodology

Multicollinearity

To perform variable selection, the authors first used a pool of 11 variables: sex, race, age at IPLC diagnosis, stage, histology, disease extent, tumor size, node involvement, the number of positive nodes, radiation therapy or not, and first course of treatment. The authors state that they incorporate interactions of all possible pairs of variables, but subsequently describe using the stepwise methods of forward selection and backward elimination. These methods typically add or remove variables consecutively but certainly do not exhaustively consider all variable-variable interactions (4). Therefore, based on the manuscript as written, it is not clear how they handled interactions in their model selection algorithm. This is particularly important because given the nature of these variables, they would be very highly correlated. For example, stage, tumor size, node involvement and the number of positive nodes would show strong correlation. Particularly, node involvement (none, regional, distant) and extent of disease (local, regional, distant) should have nearly perfect collinearity. There are methods that are better at taking multicollinearity into account. Thus, it is not surprising that the largely independent variables such as age and histology rose to the top while variables with significant overlapping information were not selected, as a stepwise selection method would favor variables that added more significant information. If the authors had combined the collinear staging variables into one variable, this engineered feature may indeed have become significant. For example, perhaps one might see more SPLC with more advanced IPLC stage due to either subclinical disease manifesting or more extensive radiation fields.

Missing data

The authors excluded patients with missing variables but do not report the missingness rate of each of these variables, which makes it difficult to assess the extent to which excluding these patients may bias and limit the generalizability of their results (5). A better approach would be to use multiple imputation, or another principled missing data method that is valid under looser assumptions.

Bootstrap cross-validation

The authors refer to their validation method as a “bootstrap cross-validation” method for which we could not find an authoritative reference. However, their described method uses bootstrap samples for cross-validation, which is similar to bootstrap aggregating or “bagging” (6). The original bootstrap method was developed to measure uncertainty in a population through re-sampling (7). The bootstrap method is best applied to smaller datasets where re-sampling of the same data can be used to make these estimations (8). Cross-validation is a method based on splitting data to assess for performance to assist in selecting models that are mostly likely to generalize to independent data. While cross-validation and the bootstrap are effective in many contexts, the authors used the entire dataset for variable selection, and then used a bootstrap cross-validation method on the same dataset for evaluating the model’s performance. This can create a biased model that is too optimistic (i.e., performs better than if it was assessed on new data) since the data were analyzed twice. In lieu of an independent dataset to externally validate their model, the authors could have parsed out a subset (i.e., 20% of the ~20,000 patients) to provide an independent test set.

Decision curve analysis

The authors use a prediction model called decision curve analysis to weigh the “net benefit” of screening compared to the SPLC risk threshold at which one would offer screening (3). In this study, the authors define net benefit as “the weighted sum of true positives subtracted by the number of false positives.” However, it is unclear how they determine what a false positive is. For example, they do not report data on imaging findings or biopsy results. The advantage of decision curve analysis is that it encapsulates the intrinsic value that physicians or patients put into a true positive compared to a false positive, but this is neither discussed nor are data presented for sensitivity/specificity of imaging and pathology. This is particularly important given that in the NLST, approximately 95% of lesions detected by both chest X-ray and low dose CT-scan were false positives. Given the absence of this information and the marginal separation of curves between Han et al.’s risk-based approach and a “screen all” approach (seen in their Figure 4), it is not clear that a risk-based approach provides significant benefit over a “screen-all approach.” We discuss this later in the “Screen all approach is valid” section.

Clinical applicability

Overlap with surveillance for recurrence of IPLC

Generally, the risk of recurrent lung cancer far outweighs the risk of SPCL within the first 5 years after definitive lung cancer treatment. Even with stage I non-small cell lung cancer, recurrence rates approach 40–50% with the predominant pattern of recurrence being distant at 50–70% (9). It is conceivable that a significant proportion of patients with primary lung cancer may be living with metastatic disease; in those patients a SPLC would not likely be detected (as opposed to being attributed to metastatic progression). Compared to the population studied by Han et al. from 1998–2003, current patients have access to much improved systemic therapies, such as tyrosine kinase inhibitors and immunotherapy, which have increased 5-year survival. Thus, risks of SPCL in those free of disease after 5 years may actually be quite higher that reported by Han et al.

Whether the findings of Han et al. would change management remains unknown. Current guidelines for lung cancer follow-up after definitive therapy from the National Comprehensive Care Network (NCCN), European Society for Medical Oncology (ESMO), and the American College of Chest Physicians (ACCP) recommend interval computed tomography imaging annually starting at 2 years for an indefinite period of time (10). While these guidelines were intended to catch recurrences of IPLC, a coincidental benefit would be in surveilling for SPLC.

Stage of SPLC

Surprisingly, the authors did not describe or account for the stage or extent of disease of the SPLC. Conceivably, screening would be more impactful if it was more apt to detect early stage lung cancers. Had separate analyses been performed, grouped by stage of SPCL, perhaps a different time course of detection would have been observed (i.e., earlier stage cancers detected sooner than late stage cancers). Also confounding the analyses are that the study patients may or may not have been screened, which could not be assessed. It is conceivable that more of these with distant and regional SPLC were diagnosed after clinical symptoms, while those with localized SPCL diagnosed after CT. While the authors describe clinical benefit in terms of cancer detection, clinical benefit would more practically imply cancer detection resulting in early detection and/or improved survival outcomes, for which population-based registry studies cannot readily assess.

Smoking effect

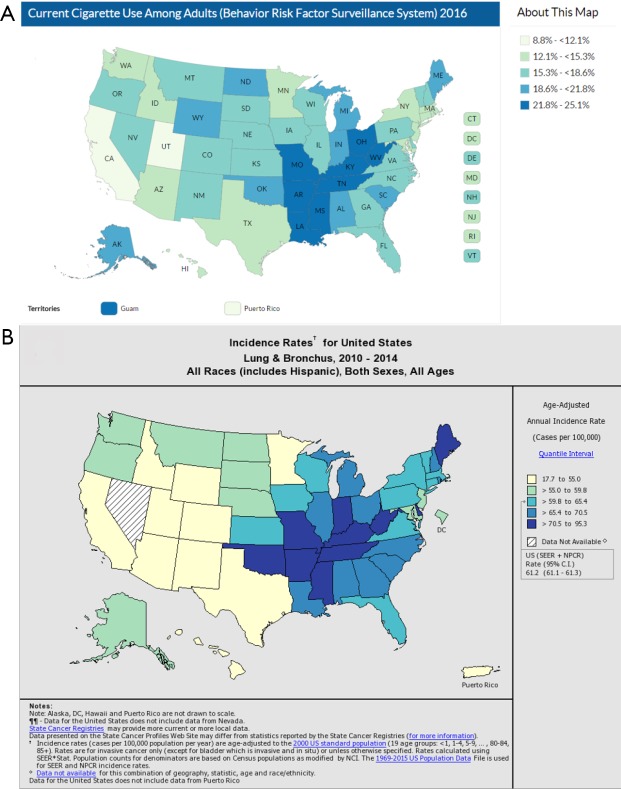
Han et al. readily acknowledge that they do not model smoking history. While patient-specific information on smoking history is lacking in the SEER registries, one approach to capture this information would have been to use the state-specific smoking rates as a surrogate in their model. Overlaying population-based cigarette use and lung cancer incidence heat maps shows almost perfect overlap (Figure 1). Non-smokers may or may not derive as much benefit from screening as current for former smokers. The authors could have created separate models for states (or counties) that are high or low in smoking incidence to determine whether smoking cessation is a confounding factor.

Figure 1.

Heat maps for contemporary cigarette use and lung cancer. Darker colors indicate higher percentile. (A) Current cigarette use among adults based on 2011–2016 data from Centers for Disease Control and Prevention (CDC) (11); (B) age-adjusted annual incidence rate based on 2010–2014 data from NCI SEER and the CDC National Program of Cancer Registries (NPCR) (12). County-level data is also available. NCI, National Cancer Institute; SEER, Surveillance, Epidemiology, End Results.

Screen all approach is valid

Han et al. note that if a 1.5% risk threshold (chosen to represent the 65% risk percentile from the NLST trial) were used, then 99% of the patients in their SEER dataset would qualify for screening. They conclude then that better discriminatory power is needed to select the subset that would benefit most from screening. However, we suggest that a reasonable conclusion is that all patients should be screened. Screening for cancer is a contentious topic given that there is risk for iatrogenic morbidity and mortality for workup of false positives. One important factor to keep in mind is the “number needed to screen” (NNS) to prevent 1 death from cancer (13). In breast cancer and prostate cancer, the NNS has been estimated to be nearly 2,000 (14) and 800 (15), respectively. During the 7-year follow-up period for the NLST trial, the overall incidence of lung cancer was approximately 3.7%, the cancer-specific mortality was 1.5%, and NNS was estimated to be 1:320 (the NNS with low dose CT to prevent 1 death from cancer). In the study by Han et al., the median 10-year incidence of SPLC was 8.4% with the lowest decile having an incidence of 2.9%. Even when choosing the most favorable low risk category, this 2.9% incidence of SPLC is comparable to ~3.7% overall incidence of IPLC in the high-risk patients enrolled in the NLST, which were intended to be high risk due to their virtue of being 55–74 years old with 30+ pack-year history and having quit <15 years ago or actively smoking. Thus, we see that even the lowest risk category has an incidence of cancer comparable to the primary lung cancer patients in the NLST.

Conclusions

In conclusion, while the study by Han et al. has some methodologic and clinical application limitations, the authors present a convincing case for screening for SPLC after surviving IPLC for 5+ years. We are unconvinced that stratification into deciles would be impactful given a 10-year median cumulative SPLC incidence of 8.5% and with the lowest risk decile still having an incidence of 2.9%. Not presenting the stage of SPLC limits the cost-benefit analysis somewhat, as screening would be more beneficial if SPLC tended to be early stage rather than metastatic. Additionally, it still remains unknown how often or what dosage (i.e., low dose CT or not) to use for screening.