Mathematical models of human cerebellar development in the fetal period

Abstract

The evaluation of cerebellar growth in the fetal period forms a part of a widely used examination to identify any features of abnormalities in early stages of human development. It is well known that the development of anatomical structures, including the cerebellum, does not always follow a linear model of growth. The aim of the study was to analyse a variety of mathematical models of human cerebellar development in fetal life to determine their adequacy. The study comprised 101 fetuses (48 males and 53 females) between the 15th and 28th weeks of fetal life. The cerebellum was exposed and measurements of the vermis and hemispheres were performed, together with statistical analyses. The mathematical model parameters of fetal growth were assessed for crown–rump length (CRL) increases, transverse cerebellar diameter and ventrodorsal dimensions of the cerebellar vermis in the transverse plane, and rostrocaudal dimensions of the cerebellar vermis and hemispheres in the frontal plane. A variety of mathematical models were applied, including linear and non‐linear functions. Taking into consideration the variance between models and measurements, as well as correlation parameters, the exponential and Gompertz models proved to be the most suitable for modelling cerebellar growth in the second and third trimesters of pregnancy. However, the linear model gave a satisfactory approximation of cerebellar growth, especially in older fetuses. The proposed models of fetal cerebellar growth constructed on the basis of anatomical examination and objective mathematical calculations could be useful in the estimation of fetal development.

Introduction

The cerebellum develops with some delay in relation to the cerebrum, especially until the 5th month of gestation. Later, the mass of the cerebellum doubles between the 19th and 35–37th weeks of fetal life, reaching 1 : 25 of the cerebrum mass at the moment of birth (Guihard‐Costa & Larroche, 1990, 1992; Co et al. 1991; Triulzi et al. 2006). The cerebellum development rate in the fetal period is mainly determined by the proliferation rates of the cells. The external granular layer (EGL), which appears as a distinct layer at 10–11 weeks of gestation, has a relatively stable thickness until the second postnatal month, after which it gradually decreases, disappearing by 12–18 months of life (Rakic & Sidman,1970; Friede, 1973; Gadson & Emery, 1976; Milosevic & Zecevic,1998). Other cerebellar cells, such as those belonging to molecular layer Purkinje cells, have the highest growth rate after the 38th week of gestation and the first postnatal year (Friede, 1973; Tsekhmistrenko, 1999). The second factor influencing the growth rate of the cerebellum is the migration pattern of the cells, as it can be assumed that Purkinje cells, by changing their orientation in early gestation and spreading primarily in the anteroposterior plane, could differentiate the growth rates of particular lobes (Dastjerdi et al. 2012). Granule cells influence the shape of the cerebellum; they preferentially migrate first to anterior folia and with some delay to the inferior regions of the cerebellum (Altman & Bayer, 1985). In mathematical models of EGL thickness changes during mouse cerebellum development, three factors have been considered: proliferation giving early increases in the volume of the EGL; transition from proliferation to differentiation, which is responsible for slowing the growth; and the migration of the differentiated granule cells, resulting in the gradual disappearance of the EGL (Leffler et al. 2016). The complexity of the description of just one cerebellar layer in one lobule shows the level of the challenge faced by attempts at the description of cerebellum development. Based on histological observations (Leffler et al. 2016), morphological analyses (Nowakowska‐Kotas et al. 2014) and magnetic resonance imaging (MRI) studies (Szulc et al. 2015), it has been stated that not only lobes but also lobules have various growth characteristics.

In addition to the complex process of cerebellar development, one must also consider restrictions with regard to the accessibility of human fetuses both at very early stages and in the third trimester. A good mathematical model of cerebellar development should clearly describe this process in the whole observed period, from the 1st until the 42nd week of fetal life, and this should done in such a manner that the predicted dimensions at the 1st week of gestation should be close to zero. A model that meets those requirements would enable comparison of many surveys focusing on fetal cerebellar development during various time intervals of pregnancy. In the case of restrictions relating mainly to older fetuses, the construction of mathematical models that may be extrapolated outside of the observation period is needed.

Here, we investigate, by means of anatomical and computer – enhanced methods and the development of algorithms and a variety of models of the development of the external dimensions of the cerebellum in the fetal period, and provide a subsequent analysis of their adequacy.

Materials and methods

In all, 101 fetuses (48 male, 53 female), with a crown–rump length (CRL) ranging from 89 to 229 mm, which corresponded to 15–28 weeks of gestation according to the Scammon and Calkins scales (Scammon & Calkins, 1929), were included into the study. The selected fetuses, derived from the Normal Anatomy Department of Wrocław Medical University, did not reveal any morphological anomalies, and an examination of fetus karyotype was not conducted. The sizes of the groups in particular weeks of fetal life, organized according to sex, are presented in Table 1. The subgroups of male and female fetuses did not differ significantly as to the numbers in certain age groups (Fig. 1).

Table 1.

Fetus numbers in particular weeks of fetal life

Fetal life (weeks)	Total Total n = 101		Female Total n = 52		Male Total n = 49
	n	%	n	%	n	%
15	3	3.0	2	3.8	1	2.0
16	7	6.9	5	9.6	2	4.1
17	9	8.9	2	3.8	7	14.3
18	11	10.9	8	15.4	3	6.1
19	7	6.9	3	5.8	4	8.2
20	12	11.9	6	11.5	6	12.2
21	12	11.9	5	9.6	7	14.3
22	7	6.9	5	9.6	2	4.1
23	5	5.0	2	3.8	3	6.1
24	5	5.0	4	7.7	1	2.0
25	9	8.9	5	9.6	4	8.2
26	9	8.9	3	5.8	6	12.2
27	4	4.0	2	3.8	2	4.1
28	1	1.0	0	0.0	1	2.0

Figure 1.

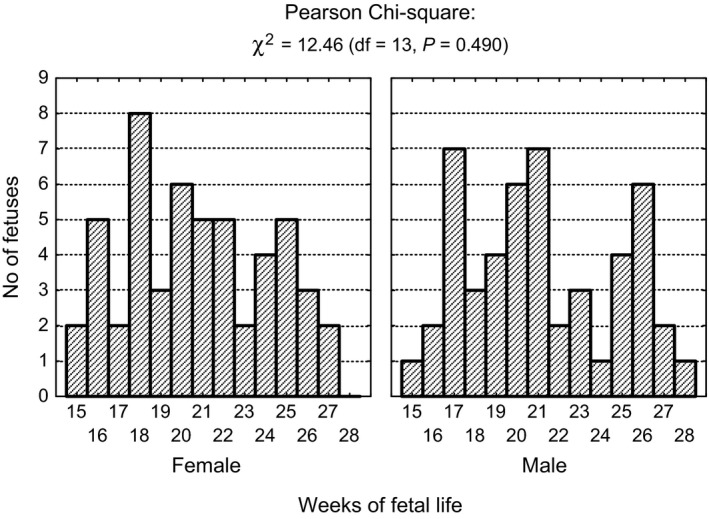
Number of fetuses in sex and age subgroups with results of chi‐square tests of independence.

The Bioethical Committee of Wroclaw Medical University approved the study (agreement No. 466/2011).

The following methods were used in the study: anthropological and dissection methods with measurements of CRL and exposition of the external surfaces of the cerebellum, and digital image acquisition (Sony α100–10 MP with a 70–300 macro lens), followed by measurements made with scion image for windows (National Institute of Mental Health – NIMH – http://rsb.info.nih.gov/nih-image/download.html) and statistical methods performed with the statistica v.12 computer package (StatSoft, Inc., Tulsa, OK, USA).

The following measurements were conducted (Fig. 2):

Figure 2.

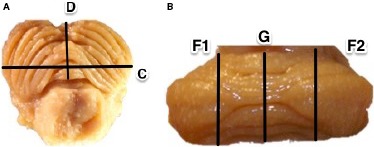
Schematic presentation of measurements performed in transverse plane (A) and frontal plane (B), where; C = transverse cerebellar diameter, D = ventrodorsal dimension of cerebellar vermis, F1 = rostrocaudal dimension of left cerebellar hemisphere, F2 = rostrocaudal dimension of right cerebellar hemisphere and G = rostrocaudal dimension of cerebellar vermis.

• C – transverse cerebellar diameter in transverse plane (mm),

• D – ventrodorsal dimension of cerebellar vermis measured in transverse plane (mm),

• F1 – rostrocaudal dimension of left cerebellar hemisphere in frontal plane (mm),

• F2 – rostrocaudal dimension of right cerebellar hemisphere in frontal plane (mm),

• G – rostrocaudal dimension of cerebellar vermis in frontal plane (mm).

Each measurement was delineated visually according to the anatomical boundaries and was manually measured three times by one researcher (M.N.K.). In data analyses, the average value of repeated measurements was considered.

Intra‐observer agreement was satisfactory, as the error estimated by the coefficient of variation was equal to or less than 1.3% (Table 2).

Table 2.

Coefficient of variation with intra‐individual variability measurements (mm) at the 21st and the 22nd weeks of gestation

Diameter (mm)	Measurement (mean)			Mean ± SD	Coefficient of variation (%)
	1	2	3
C	16.6	16.7	16.6	16.63 ± 0.06	0.3
D	5.5	5.6	5.6	5.57 ± 0.06	1.0
F1	7.9	7.8	7.7	7.80 ± 0.10	1.3
F2	7.8	7.7	7.8	7.77 ± 0.06	0.7
G	6.8	6.7	6.7	6.73 ± 0.06	0.9

Statistical methods

The criterion for the best fit regression function of the empirical distribution is the adopted minimum variance of the residuals (the difference between the measurement results and the theoretical values resulting from the adopted model).

Statistical analysis of the collected material was based on the numerical confirmation of the presence of correlations (interdependence) between the observed variables, mainly by assessing the statistical significance of the relationships between dependent variable Y (dimensions of the cerebellum) and explanatory X (age of the fetus). Where a significant correlation was found, the strength of the correlation of the observed variables (Pearson's correlation coefficient r or coefficient of determination R ²) was determined, as well as its direction (positive or negative) and shape (linear or non‐linear). The null hypothesis of no interdependence observed between random variables was rejected at the significance level of α ≤ 0.05.

Results

All analysed cerebellar dimensions increased 1.9‐ to 3.5‐fold from the 15th to 28th weeks of gestation (Table 3). There was no influence of sex on cerebellar growth during the analysed period (Supporting Information Table S1).

Table 3.

Descriptive statistics (mean ± standard deviation) for each analysed dimension of the cerebellum for each age group

Fetal life (weeks)	Dimensions (mm)
	C	D	F1	G	F2
15	11.3 ± 0.6	2.4 ± 0.8	4.3 ± 0.4	2.6 ± 0.5	4.4 ± 0.4
16	11.9 ± 0.8	2.8 ± 1.0	5.5 ± 0.6	3.8 ± 0.5	5.5 ± 0.6
17	13.4 ± 2.4	3.6 ± 1.1	6.5 ± 1.4	4.8 ± 1.5	6.6 ± 1.3
18	13.9 ± 1.4	4.1 ± 0.7	6.2 ± 0.8	4.8 ± 0.8	6.2 ± 0.9
19	13.7 ± 1.1	4.0 ± 0.7	6.7 ± 1.0	5.4 ± 0.8	6.2 ± 0.5
20	14.7 ± 1.4	4.7 ± 0.7	6.9 ± 1.1	6.0 ± 0.9	6.9 ± 1.1
21	17.2 ± 1.9	6.6 ± 1.5	7.5 ± 1.9	6.7 ± 1.5	7.5 ± 2.0
22	17.6 ± 1.3	6.8 ± 1.4	8.1 ± 1.3	7.7 ± 1.5	8.2 ± 1.3
23	17.4 ± 1.5	6.0 ± 1.0	8.1 ± 0.9	7.6 ± 1.6	7.8 ± 0.9
24	20.4 ± 1.5	7.1 ± 1.7	9.7 ± 1.4	9.3 ± 1.2	9.7 ± 1.1
25	20.4 ± 1.5	7.9 ± 1.5	10.0 ± 1.4	8.8 ± 1.3	9.9 ± 1.3
26	22.9 ± 2.3	7.8 ± 1.4	10.9 ± 1.4	9.7 ± 1.4	10.8 ± 1.3
27	22.5 ± 2.5	8.3 ± 2.0	11.7 ± 2.0	11.2 ± 2.4	11.8 ± 2.0
28	21.8 ± 0.1	8.4 ± 0.4	12.1 ± 0.2	8.4 ± 0.4	12.9 ± 0.4

The linear model was sufficient for the fetal age range examined in this study (from 15 to 28 weeks). Pearson r correlation coefficients are significantly different from zero and the R ² values indicate that these models explain more than 65% of the variation. Interpretation of the regression coefficients (b ₀ and b ₁) is intuitive. The coefficient b ₁ (mm per week) provides information about the average weekly increase in the analysed dimension over the whole analysed period. This model is suitable, provided that the actual course of change is indeed linear in nature.

In addition, it is known that the development of anatomical structures is not always linear during gestation. In the initial period (up to 10 weeks), the growth rate is lower than in the later period. These observations are found in, among others, Scammon and Calkins’ tables which describe the length of the body of the v‐tub fetus as a function of age (Scammon & Calkins, 1929). For this reason, when analysing the current findings, different mathematical models were considered (Table 4).

Table 4.

The considered mathematical models

No	Model name	Formula
(1)	Linear	$Y=b_0+b_1·X$
(2)	Hyperbolic	$Y=b_0-b_1/X$
(3)	Logarithmic	$Y=b_0+b_1·{log}_{10}X$
(4)	Exponential	$Y=exp\left(b_0-\frac{b_1}{X}\right)$
(5)	Parabolic	$Y=b_0+b_1·X+b_2·X^2$
(6)	Gompertz	$Y=b_0·exp\left(-\frac{b_1}{b_2}\right)·exp\left[-\frac{b_1}{b_2}·exp\left(-b_2·X\right)\right]$
(7)	Power	$Y=b_0·\left[1-\frac{1}{{\left(\frac{X}{b_1}\right)}^{b_2}+1}\right]$
(8)	Power‐exponential	$Y=b_0·X^{b_1}·\text{exp}(b_2·X)$
(9)	Log‐logistic	$Y=\frac{b_0·ln\left(X\right)}{1+exp\left(b_1+b_2·X\right)}$
(10)	Von Bertalanffy	$Y=b_0·\left\{1-exp\left[-b_1·\left(X-b_2\right)\right]\right\}$
(11)	Three‐equation linear	$\begin{array}{cc}& Y=b_{\mathrm{o}\mathit{I}}+b_{1\mathit{I}}·XX\le x_{\mathit{I}};\hfill \\ & Y=b_{\mathrm{o}\mathit{II}}+b_{1\mathit{II}}·X{x}_{\mathit{I}}<X\le x_{\mathit{II}};\hfill \\ & Y=b_{\mathrm{o}\mathit{III}}+b_{1\mathit{III}}·XX>x_{\mathit{II}}\hfill \end{array}$

The dependent variable (described) Y in these equations is the dimension characterising the morphology of the cerebellum, and the independent variable (describing) X is the age of the fetus. Models arranged in order of increasing complexity are included in Table 4: (1) – linear with two parameters; (2–4) – curvilinear with two parameters; (5–10) – curvilinear with three parameters; and (11) – a straight line consisting of three segments. With the curvilinear function, models that can be transformed into the form of a straight line regression function are of interest. These include equations 2, 3 and 4.

When describing the dimensional change, single equation models were used monotonically increasing non‐linearly, and these had a sigmoid shape, because they were characterised by high ease of use at the maximum permissible level of model simplification. In addition, they enabled extrapolation of the results to younger specimens not reaching values smaller than zero (Merz, 1989). Although for all models, b ₀, b ₁ and b ₂, as well as the coefficient of determination R ² were estimated; only those with the highest R ² are presented in graphic form. Figures 3 and 4 show diagrams illustrating the dimensions of the cerebellar vermis as a function of the age of the fetus using linear (1) or exponential models (4). Table 5 shows the parameters of the selected models for the development of the cerebellum. None of the differences between the coefficients of correlation (R) for the two models for any considered dimension of the cerebellum was statistically significant (P > 0.05), as verified by Student's t‐test between the correlation coefficients. The goodness of fit for all analysed models was verified using the Kolmogorov–Smirnov normality test of standardised residuals. The exponential model (exponential function of the natural logarithm base) and the Gompertz model proved to be best matched to the results of the measurement models. As individual variability in prenatal development increases with gestational age due to genetic and environmental factors influencing the dimensions of cerebellum, we estimated that our models may explain 65–79% of the variability in cerebellar measurements.

Figure 3.

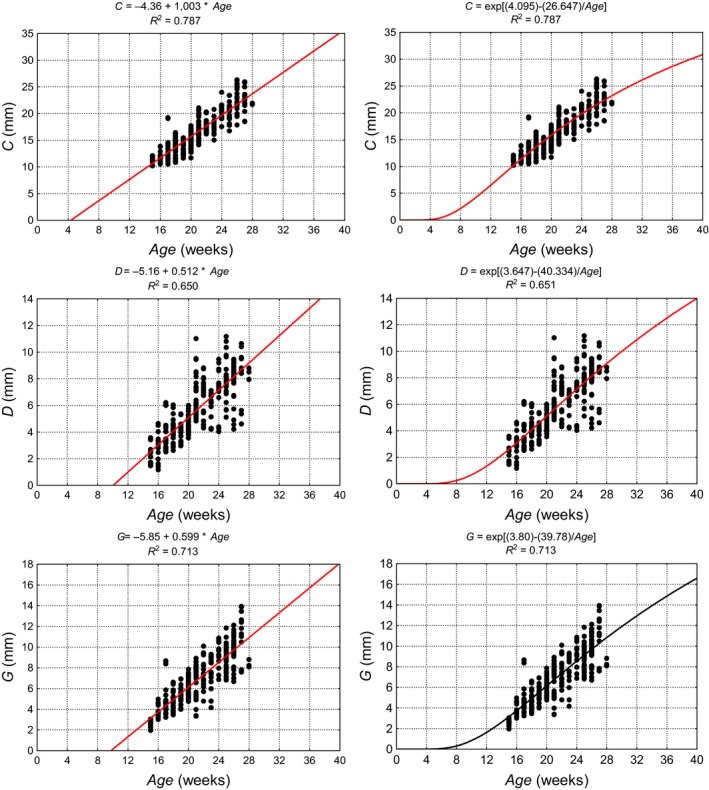
Linear (left) and exponential models (right) showing growth parameters of the cerebellum and cerebellar vermis on the basis of the measured results, their equations and determination of coefficients (R ²). C, transverse cerebellar diameter in transverse plane; D, ventrodorsal dimension of cerebellar vermis measured in transverse plane; G, rostrocaudal dimension of cerebellar vermis in frontal plane.

Figure 4.

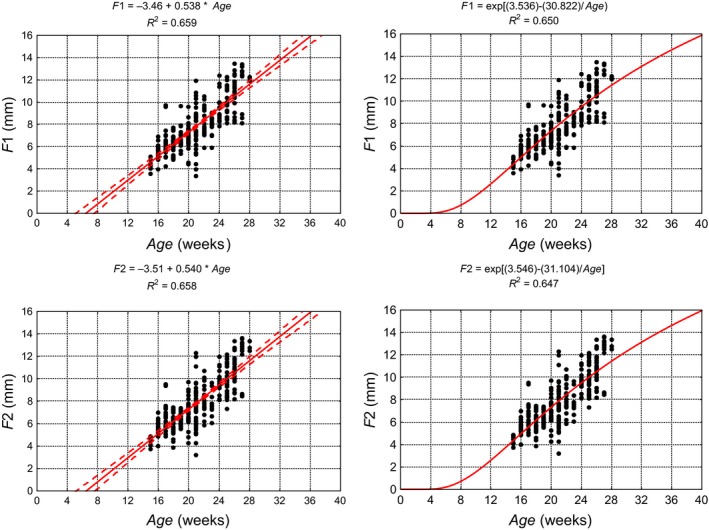
Linear (left) and exponential models (right) showing growth parameters of the cerebellum and cerebellar vermis on the basis of the measured results, their equations and determination of coefficients (R ²). F1, rostrocaudal dimension of left cerebellar hemisphere in frontal plane; F2, rostrocaudal dimension of right cerebellar hemisphere in frontal plane.

Table 5.

Parameters of linear and exponential models describing growth of the cerebellar hemispheres and vermis

Model and its structural parameters	Dimensions (mm)
	C	F1	F2	G	D
Linear
b 0	−4.36	−3.46	−3.51	−5.85	−5.16
b 1	1.003	0.538	0.540	0.599	0.512
R 2	0.787	0.659	0.658	0.713	0.650
Exponential
b 0	4.095	3.536	3.546	3.803	3.647
b 1	26.647	30.822	31.104	39.780	40.334
R 2	0.787	0.650	0.647	0.713	0.651

Discussion

The most common methods for the evaluation of cerebellar development are neuroimaging studies such as magnetic resonance imaging (MRI), computed tomorgraphy (CT) and fetal ultrasonography (Nakamura et al. 1986; Goldstein et al. 1987; Triulzi et al. 2006; Sherer et al. 2007). With regard to the morphometric method, only a few pathological studies have been published (Guihard‐Costa & Larroche, 1990; Murakami et al. 2016) where fetuses without overt abnormalities in the central nervous system were focused on. Both of these papers focused on changes in the weight of the cerebellum in relationship to either cerebral and body weight or the gestational age. Guihard‐Costa and Larroche (1990) described the non‐linear relationship between the weight of the infratentorial part of the brain and age. Murakami et al. (2016) described the exponential regression models of cerebellar weight gain. In our previous (Nowakowska‐Kotas et al. 2014) and present survey, the linear models were the simplest to apply. Using such models for the cerebellar measurements conducted in our study, we have been able to find close agreement between the linear and exponential curves, especially between 16 and 24 weeks of gestation; thus, the choice of the linear model is well justified. This is also the period of fetal life when most ultrasonographic measurements in clinical practice are performed. Most of the proposed models are linear, and reference tables produced using this technique are reliable during the standard sonographic screening weeks (that is, between the 19th and 24th weeks of gestation) (Goldstein et al. 1987; Co et al. 1991; Zalel et al. 2002; Paladini & Volpe, 2006; Sherer et al. 2007; Lei et al. 2015). However, comparison of these results with the results from other centres does not show an overlap of fetal age ranges, and there is sometimes a need for extrapolation models beyond the scope of the surveyed age ranges. In the case of linear models, there is the concern that extrapolation of results may lead to errors. In addition, ultrasonographic data become scarce in later gestational weeks, and it is more advisable to rely on non‐linear models, which have only been proposed in a few papers describing human cerebellar development (Chavez et al. 2004; Cignini et al. 2016). Based on voxel measurements of mouse cerebellum in MRI, Szulc et al. (2015) stated that the non‐linear model (polynomial of degree three) was the best fit. To build a model able to predict cerebellar dimensions beyond the age range of our survey, we also stated that the non‐linear model allowed a more accurate extrapolation. New methods for the assessment of the cerebellum are based on the age‐independent biometric parameters of the cerebellar vermis (Lei et al. 2015).

The comparison of parameters C, D and G with measurements obtained in ultrasonographical studies revealed that regression coefficients calculated for morphological surveys were lower than those measured in ultrasonography. The value of coefficient b ₁ for parameter C, which can be compared to the transcerebellar diameter (TCD) commonly measured in ultrasonography, was statistically significantly lower in our group that in the linear models of Goldstein et al. (1987) or Co et al. (1991). This disparity may be due to methodological differences, mainly because TCD is measured on the midsagittal plane of the brain and not on the subtentorial surface as in our method. The lack of older fetuses in our material prevented us from making a comparison with the non‐linear model proposed by Chavez et al. (2004). The value of the regression coefficient for the ventrodorsal dimension of the cerebellar vermis (D) was statistically insignificantly lower than those calculated by Malinger et al. (2001), Vinals et al. (2005) and Scott et al. (2012). The b ₁ coefficient of the rostrocaudal dimension of the cerebellar vermis in the frontal plane (G) was significantly lower in comparison with results from ultrasonographical surveys (Vinals et al. 2005; Scott et al. 2012).

The strength of a morphological study is the possibility to calculate the regression coefficients and the formulation of mathematical models for various measurements in different planes concomitantly. Any limitations are linked to the low number of fetuses from the third trimester, due to ethical limitations and legal constraints.

Conclusion

The evaluation of cerebellar growth in the fetal period has been part of an extensive research project to identify any features of abnormalities in early human development. The proposed mathematical models of cerebellar development could be useful in the diagnosis of fetal hypotrophy.

The advantage of linear models is their ease of interpretation; a disadvantage is that extrapolation outside the tested range, particularly in younger fetuses, can cause the dimensions to be negative. Exponential models allow safer extrapolation beyond the age range tested, which allows for comparisons with the results obtained from other centres.

Nevertheless, the preparation of coefficients based on the ratios of cerebellar parameters to other fetal growth parameters, such as head circumference, biparietal diameter, abdominal circumference or femoral length, could improve the accuracy of mathematical models. Analysis of such ratios could contribute to a more precise and age‐independent assessment of the cerebellum.

Contributions

Krzysztof Dudek – data analysis and interpretation, drafting of the manuscript, critical revision of the manuscript. Marta Nowakowska‐Kotas – concept of the manuscript, acquisition of data, data interpretation, drafting of the manuscript. Alicja Kędzia – concept of the manuscript, critical revision of the manuscript, approval of the article.

Supporting information

Table S1. Covariance analysis results of analysed dimensions of the cerebellum.