Abstract
Large genomic data sets generated with restriction site-associated DNA sequencing (RADseq), in combination with demographic inference methods, are improving our ability to gain insights into the population history of species. We used a simulation approach to examine the potential for RADseq data sets to accurately estimate effective population size (N e) over the course of stable and declining population trends, and we compare the ability of two methods of analysis to accurately distinguish stable from steadily declining populations over a contemporary time scale (20 generations). Using a linkage disequilibrium-based analysis, individual sampling (i.e., n ≥ 30) had the greatest effect on N e estimation and the detection of population size declines, with declines reliably detected across scenarios ~10 generations after they began. Coalescent-based inference required fewer sampled individuals (i.e., n = 15), and instead was most influenced by the size of the SNP data set, with 25,000–50,000 SNPs required for accurate detection of population trends and at least 20 generations after decline began. The number of samples available and targeted number of RADseq loci are important criteria when choosing between these methods. Neither method suffered any apparent bias due to the effects of allele dropout typical of RAD data. With an understanding of the limitations and biases of these approaches, researchers can make more informed decisions when designing their sampling and analyses. Overall, our results reveal that demographic inference using RADseq data can be successfully applied to infer recent population size change and may be an important tool for population monitoring and conservation biology.
Introduction
One of the most important parameters in wildlife management and conservation biology is effective population size (N e), with estimates providing insight into the demographic history and extinction risk of populations. Although N e is informative about population viability and broadly applicable in ecology, conservation, and evolution, it is notoriously difficult to estimate (Luikart et al. 2010). Rarely is enough demographic information available from natural populations to directly estimate N e, making indirect genetic estimates of considerable use, especially given their ease of generation relative to direct demographic methods (Schwartz et al. 2007; Luikart et al. 2010; Dudgeon and Ovenden 2015; Andreotti et al. 2016). It is now possible to generate population genomic data for almost any species for the investigation of population and evolutionary history (Narum et al. 2013; Andrews et al. 2016; Nunziata et al. 2017). The increase in power and precision offered by a genomic approach is poised to greatly improve estimates of demographic history, including N e, the timing of demographic events, and migration. Genomic-based demographic inference has yielded insight into invasion dynamics (Trucchi et al. 2016), climate-driven population shifts (Prates et al. 2016), and glacial refugium dynamics (Kopuchian et al. 2016) at historical timescales. However, as emphasized in a recent review, the application of genomic techniques in conservation studies has been rare (Shafer et al. 2015a). One obvious, but unanswered, question is whether genomic-based demographic inference methods have the ability to accurately characterize population history over a contemporary time scale (e.g., tens of generations), and whether there is a time lag between decline in census size and decline in N e.
Previous work has begun to hint at the ability for genetic data to uncover recent population history. Simulation studies have suggested that microsatellite markers have the ability to detect bottlenecks and population size trends at a contemporary scale, but require sample sizes of 60 or more individuals and are not accurate with large (≥1000) population sizes (Tallmon et al. 2010; Antao et al. 2011). While increasing the number of microsatellite markers employed can increase the power to detect population size change (Hoban et al. 2013), in many cases researchers will not have access to, or resources to generate, ≥100 microsatellite markers. These studies either did not use single-nucleotide polymorphism (SNP) data which would be common in contemporary population genomic studies, or they simulated a small number (100–1000) of SNP markers (Antao et al. 2011; Hollenbeck et al. 2016). It is possible that the increased power offered by large genomic data sets can result in accurate estimates of population size trends over short timescales while using smaller numbers of sampled individuals.
Recent empirical studies have shown that coalescent-based demographic inference can accurately date documented introductions of populations occurring in the past few decades (McCoy et al. 2013; Fraser et al. 2015). Coalescence theory states that the probability of coalescence t generations ago is (1−(1/2N e))t−1(1/2N e), with the coalescent Ne estimated as the expected time of coalescence in generations, T, or T = 2N e (Nordborg and Krone 2002; Wakeley and Sargsyan 2009). Given these equations, when N e is small enough, as is often the case in species of conservation concern, large sample sizes (individuals and/or loci) may be effective in estimating coalescent N e at a contemporary scale as coalescent events will be clustered in the recent past. Consistent with this theory, a simulation study found that although large sample sizes are generally not needed for accurate demographic inference of ancient events, increased sampling of individuals increases accuracy of parameter estimates for more recent events (Robinson et al. 2014). Before these methods can be applied to real-world conservation biology, vigorous exploration is needed to estimate their accuracy with realistic sampling conditions to gain an understanding of implicit limitations and biases (Shafer et al. 2015a).
Restriction site-associated DNA sequencing (RADseq) is arguably the most popular method for generating genome-wide population genetic data from a reduced subset of the genome (Davey et al. 2011; Andrews et al. 2016). While RADseq can yield many thousands or tens of thousands of shared orthologous loci across individuals and populations, it also has inherent properties that lead to allele dropout, and consequently, missing data that may create biases in population genetic results. Allele dropout via mutations in restriction cut sites and the shotgun nature of Illumina sequencing, which under-sequences loci or alleles can randomly lead to either missing genotypes for loci, or the misinterpretation of null alleles as homozygous at heterozygous loci. Both of these scenarios can result in skewed estimation of allele frequencies (Arnold et al. 2013), and a misrepresentation of the site frequency spectrum (Shafer et al. 2017). Simulation studies have highlighted the downstream effects of these biases in commonly estimated population genetic summary statistics (Gautier et al. 2013; Arnold et al. 2013) and in phylogenetic inferences (Huang and Knowles 2014). However, the effect of allele dropout in RADseq-based studies of N e and contemporary population size trends has not been investigated.
Here we use an approach similar to Tallmon et al. (2010) and assess the ability of RADseq-generated SNP data and different N e estimators to infer population abundance and population size trends (λ) over a contemporary time scale. We simulated ideal Wright–Fisher (W–F) populations over a range of known census sizes (N C) and with either stable population size, or a steadily declining population. In ideal W–F populations N C = N e, so that estimates of N e can be directly compared to the simulated N C. Using both linkage disequilibrium-based analysis, and a coalescent-based analysis, we assess the estimation of N e and population size trends. In doing so, we also evaluate the impacts of the various aspects of the population model (initial population size and the number of generations since λ began) on estimation, as well as the impacts of sampling, number of SNPs sampled, allele dropout, and data filtering.
Methods
Data simulation
We conducted simulations of RADseq data for populations with both stable and declining population sizes using the Python program simuPOP v1.1.4 (Peng and Kimmel 2005), a forward-time and individual-based population genetic modeling program. Prior to simuPOP simulations, initial haploid allele frequencies were generated with the coalescent simulator fastsimcoal2 v2.5.2.21 (fsc2; Excoffier et al. 2013) for 20,000 150 base pair (bp) loci using a diploid N e of 1000. A mutation rate (µ) was randomly assigned to each locus from a log-normal distribution with a mean µ of 2.5E−8 and a log standard deviation of 1.3. This mutation rate has been robustly estimated in humans (Nachman and Crowell 2000) and similarly used in other RADseq simulation studies (Huang and Knowles 2014). We used this log-normal distribution of mutation rates among loci to account for variance in the mutation rate across the genome, and to generate a large number of highly diverse loci. Our rational was to generate a large number of SNPs typical of empirical RAD studies, while balancing computational demand of simulating even greater numbers of individual RAD loci variable in one or a few SNPs. This created a larger proportion of allele dropout than would be typical of empirical studies, but the loci retained to assess impacts of allele dropout should be comparable to those typical of empirical studies. Loci were generated as Arlequin-formatted files and were subsequently converted to Phylip format using the program PGDSpider v2.0.5.1 (Lischer and Excoffier 2012). Initial diploid genotypes for individuals in the simuPOP population were generated by pairing the fsc2-simulated alleles for each locus using random sampling with replacement, which approximated random mating and W–F populations. Diploid populations were constructed with initial population sizes of n = 250, 500, and 1000, with 100 replicates constructed for each initial population size. Throughout the subsequent simulations, populations maintained an average sex ratio of 1 with random mating, non-overlapping generations, a fixed µ = 2.5E−8 across all loci, and with no assignment to chromosomes. Under these conditions N C should be approximately equal to N e. All simulated populations went through an equilibrium phase of 10 generations to reach Hardy–Weinberg equilibrium (Waples 2006; Tallmon et al. 2010; Antao et al. 2011), after which each replicate diploid population evolved for one generation (t − 1) according to two separate deterministic growth rates that approximated a stable population (λ = 1.0) and a declining population (λ = 0.9). Data collection began at generation t 0 as the population evolved at the same λ for 20 generations as in Tallmon et al. (2010). In each simulation, genotypes from all loci were recorded after 0, 5, 10, 15, and 20 generations. Sample collection began with one generation after the initiation of the deterministic growth rate because inbreeding N e estimates are reflective of the number of parents in the parental generation (Waples 2005). To assess the effect of the sample size of individuals, we sampled 15, 30, and 60 individuals from each of the specified generations.
In silico RADseq mutations and data filtering
Using custom Python scripts, we filtered RADseq loci from sampled individuals to mimic empirical RADseq data recovery and filtering conditions typically used in population genomic studies. To simulate allelic dropout as a result of a mutation in the restriction enzyme cutting site, all individual sequences were deleted containing a mutation in the first 8 bp, which represents our restriction cut site. To simulate missing data as a result of variation in sequencing coverage, we simulated the number of reads for each individual allele by drawing randomly from a Poisson distribution with a mean of 10 (Huang and Knowles 2014). We imposed a sequencing coverage cutoff of 10, which is considered an efficient sequencing coverage cutoff for diploids. To be genotyped as heterozygous, individuals were required to have a coverage ≥5 reads per allele for a given locus. If one allele had a coverage ≥10 reads and the other had <5, the locus was recorded as homozygous for the higher-coverage allele due to allele dropout. Loci below these coverage cutoffs were recorded as missing data. All other sources of missing data and biases from sequencing errors, coverage cutoffs, and alignment errors were ignored here as they are not the focus of our study. These have been thoroughly reviewed in other studies, and are expected to cause general biases in all sequencing projects (Rokas and Abbot 2009, Pool et al. 2010, Huang and Knowles 2014).
We next filtered our simulated RADseq data using the criteria specific to the two analytical programs used in demographic estimation.
Linkage disequilibrium-based estimation
Linkage disequilibrium (LD) methods for N e estimation assume unlinked loci. To remove the inclusion of linked sites within a RADseq locus, we used only the first SNP in a locus in all LD-based data sets. To examine whether the LD-based method produced unbiased N e estimates with perfect detection of allele dropout, we analyzed data sets that removed all loci with missing data exclusively due to RADseq cut site mutations, hereafter referred to as the LD RAD mutation data set. We further examined how LD-based N e estimation would be affected by the combined impacts of missing data from allele dropout due to RADseq cut site mutation and low sequencing coverage. For these analyses, we generated two filtered data sets that removed loci with ≥10% and ≥50% missing data; hereafter referred to as the 10% missing and 50% missing data sets, respectively.
Fastsimcoal2
In fsc2, the use of linked SNPs should not bias parameter estimation, so all data sets analyzed in this study used all SNPs in a locus. However, the inclusion of loci with missing data is expected to lead to a biased site frequency spectrum (SFS) and result in inaccurate parameter estimates (Excoffier et al. 2013). Therefore, we included only loci with no missing data across all sampled individuals. Only variable sites were included in the SFS. To examine the potential effects of allele dropout on N e estimation in the program fsc2, we analyzed our simulated RADseq data under a range of filtering strategies that accounted for allele dropout due to mutations in restriction cut sites and insufficient sequencing coverage. First, we analyzed an unfiltered data matrix with no allele dropout. Here the SFS was constructed using the complete 20,000 locus (3,000,000 bp) simulated data set, and is hereafter referred to as the fsc2 complete data set. Next, we examined the performance of N e estimation in fsc2 when accounting for the perfect detection of allele dropout due to restriction cut site mutations. Here the SFS was constructed after removal of all loci with a restriction cut site mutation, hereafter referred to as the fsc2 RAD mutation data set. We examined the performance of N e estimation in fsc2 when allowing for allele dropout due to both cut site mutation and low sequencing coverage, hereafter referred to as the fsc2 RAD mutation and coverage data set. Finally, to examine the impact of number of SNPs included in the joint SFS, we subsampled the fsc2 complete data set for 5000, 15,000, 25,000, 50,000, 100,000, and 150,000 SNPs.
Ne estimation and demographic inference
We used the program NeEstimator v2.01 (Do et al. 2014) to estimate N e using the linkage disequilibrium method (Hill 1981). With finite population size and a limited number of parents, nonrandom associations of alleles at different genetic markers occur (i.e., linkage disequilibrium), even without any physical linkage on a chromosome (Waples and Do 2010). We estimated N e from all sampled generations of our temporally simulated populations, employing all three LD-based data-filtering scenarios described above. In addition, we assessed the effect of excluding rare alleles using P crit cutoffs, which is important in LD-based N e estimation. For all data sets, we separately applied a P crit of 0.01, 0.02, and 0.05. A P crit of 0.02 has been recommended to balance precision and bias (Waples and Do 2010), although 0.05 is a common value used in SNP-based studies.
We used fsc2 to perform demographic inference using the joint SFS generated from serial samples taken at generations 0 (t 0) and 20 (t 20) in our temporally simulated populations. For all fsc2 analyses, we used a simple model of a single population with N e at t 0 fixed at the known starting value and N e in subsequent generations allowed to vary according to the model. Fixing N e at t 0 allowed us to reduce the number of parameters estimated from the model, scale N e estimation without a mutation rate, and ignore invariant sites in the SFS. Defined parameter ranges were uniformly distributed with N e ranging from 1 to 10,000. A total of 100,000 simulations were performed to estimate the SFS, with a minimum and maximum of 10 and 100 loops (ECM cycles), respectively. The stopping criterion was defined as the minimum relative difference in parameters between two iterations, and was set to 0.001. A total of 50 replicate fsc2 runs were performed for each replicate simulation of a demographic scenario, and for each of the three fsc2 filtering options described above. The overall maximum likelihood run across all 50 fsc2 replicates was retained as a point estimate for N e t20. Due to computational limitations, for each combination of initial population size and population growth rate, only the first 40 temporally simulated replicates (out of 100) were analyzed with fsc2.
Accuracy assessments
The performance of each N e estimation method was evaluated for the overall accuracy of N e estimates. To characterize the accuracy of N e estimates across simulation replicates, we measured the root mean squared error (RMSE) calculated after removing infinitely large estimates by
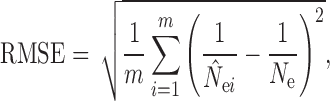 |
where 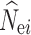 is the estimated N
e in the ith (i = 1–100) replicate, and N
e is the simulated N
e. The RMSE was not calculated if over 50% of the estimates of
is the estimated N
e in the ith (i = 1–100) replicate, and N
e is the simulated N
e. The RMSE was not calculated if over 50% of the estimates of 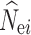 reached infinity.
reached infinity.
Detection of population size change
To estimate population size trends, we calculated 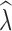 as the slope of a linear regression of the log transformation of N
e estimates from current and historical samples within a simulated replicate and we compared these to known λ. We performed these calculations for results generated from both NeEstimator and fsc2 using all simulated demographic scenarios, data-filtering scenarios, and P
crit levels. Following Tallmon et al. (2010), we recorded the proportion of times
as the slope of a linear regression of the log transformation of N
e estimates from current and historical samples within a simulated replicate and we compared these to known λ. We performed these calculations for results generated from both NeEstimator and fsc2 using all simulated demographic scenarios, data-filtering scenarios, and P
crit levels. Following Tallmon et al. (2010), we recorded the proportion of times 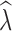 < 0.95 when true λ = 0.9. This is a practical conservation scenario to identify populations that are declining by at least 5% per generation. We also assessed how often a stable population was incorrectly identified as declining as the proportion of times
< 0.95 when true λ = 0.9. This is a practical conservation scenario to identify populations that are declining by at least 5% per generation. We also assessed how often a stable population was incorrectly identified as declining as the proportion of times 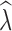 < 0.95 when true λ = 1.0 (false positive rate).
< 0.95 when true λ = 1.0 (false positive rate).
Results
The number of SNPs generated in the simulation depended on the initial population size, imposed lambda, and the post-simulation filtering scenario used (LD-based data: Table 1; fsc2 data: Table S1). Consistent with theoretical expectations, in the LD-based SNP data sets, larger populations generally had more SNPs and lost genetic diversity less rapidly due to drift, and declining populations lost genetic diversity more rapidly than stable populations. The mean number of SNPs in the joint SFS was highly dependent on data-filtering method, with the number of shared SNPs between t 0 and t 20 declining with allele dropout from both RADseq mutation and insufficient sequencing coverage. Although the number of SNPs will vary with study design, such as the number of individuals multiplexed in an Illumina sequencing lane, and coverage cutoffs, the number of SNPs we recovered in our simulations is comparable to empirical RADseq studies.
Table 1.
Number of SNPs used for LD-based analysis resulting from simulations in simuPop
| Initial variation at t 0 | Final variation at t 20 | ||||||
|---|---|---|---|---|---|---|---|
| RAD mutation | 10% | 50% | RAD mutation | 10% | 50% | ||
| N | λ | # SNPs | # SNPs | # SNPs | # SNPs | # SNPs | # SNPs |
| 250 | 1.0 | 3660 | 3938 | 4527 | 3521 | 3695 | 4223 |
| 500 | 1.0 | 3718 | 4054 | 4657 | 3629 | 3876 | 4451 |
| 1000 | 1.0 | 3756 | 4130 | 4742 | 3703 | 4013 | 4611 |
| 250 | 0.9 | 3915 | 3941 | 4676 | 3099 | 2965 | 3457 |
| 500 | 0.9 | 3719 | 4053 | 4661 | 3392 | 3493 | 3975 |
| 1000 | 0.9 | 3756 | 4128 | 4739 | 3570 | 3773 | 4327 |
SNPs were calculated as average across the 100 replicates for each simulated scenario and are presented for the initial generation (t 0) after the 10-generation equilibrium phase and from the final generation (t 20). SNP levels are broken down across the different initial population sizes (N), population growth rates (λ), and data-filtering methods (LD RAD mutation, 10% missing, and 50% missing data sets).
Stable population size estimation
LD-based estimation
Here we focus on results from estimation of 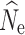 at t
20 under a λ = 1.0, where the accuracy of
at t
20 under a λ = 1.0, where the accuracy of 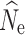 estimation was most influenced by the number of individuals sampled and the P
crit employed (Fig. 1; Fig. S1). Estimates of
estimation was most influenced by the number of individuals sampled and the P
crit employed (Fig. 1; Fig. S1). Estimates of 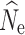 at time points t
0 through t
15 were nearly identical to
at time points t
0 through t
15 were nearly identical to 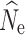 at t
20, and are not presented here. RMSE calculations yielding the lowest measures of error for all simulated demographic and filtering scenarios are presented in Table 2. The lowest individual sample size (n = 15) only produced meaningful results at a simulated population size of n = 250 and a P
crit = 0.05, with the majority of replicates at higher simulated population sizes and/or different filtering methods yielding either infinite
at t
20, and are not presented here. RMSE calculations yielding the lowest measures of error for all simulated demographic and filtering scenarios are presented in Table 2. The lowest individual sample size (n = 15) only produced meaningful results at a simulated population size of n = 250 and a P
crit = 0.05, with the majority of replicates at higher simulated population sizes and/or different filtering methods yielding either infinite 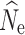 or very wide ranges of parameter estimates. A full summary of the proportion of replicate estimates that reached infinity can be found in Tables S2–S4. In contrast, increased individual sampling (n = 30 and n = 60) produced more accurate estimates of
or very wide ranges of parameter estimates. A full summary of the proportion of replicate estimates that reached infinity can be found in Tables S2–S4. In contrast, increased individual sampling (n = 30 and n = 60) produced more accurate estimates of 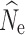 over most demographic and data-filtering scenarios. Analyses of the LD RAD mutation data set generated
over most demographic and data-filtering scenarios. Analyses of the LD RAD mutation data set generated 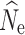 estimates with the greatest accuracy and least variance; however, data sets with 10 and 50% missing data due to both cut site mutations and insufficient read coverage also generated similarly accurate
estimates with the greatest accuracy and least variance; however, data sets with 10 and 50% missing data due to both cut site mutations and insufficient read coverage also generated similarly accurate 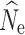 estimates under many simulated population sizes and P
crit levels. The P
crit level yielding the most accurate results varied with the number of individuals sampled and simulated population size. Generally, including low frequency alleles with an P
crit = 0.01 appeared to have the largest effect by upwardly biasing
estimates under many simulated population sizes and P
crit levels. The P
crit level yielding the most accurate results varied with the number of individuals sampled and simulated population size. Generally, including low frequency alleles with an P
crit = 0.01 appeared to have the largest effect by upwardly biasing 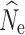 and yielding the greatest variance (Fig. S1).
and yielding the greatest variance (Fig. S1).
Fig. 1.
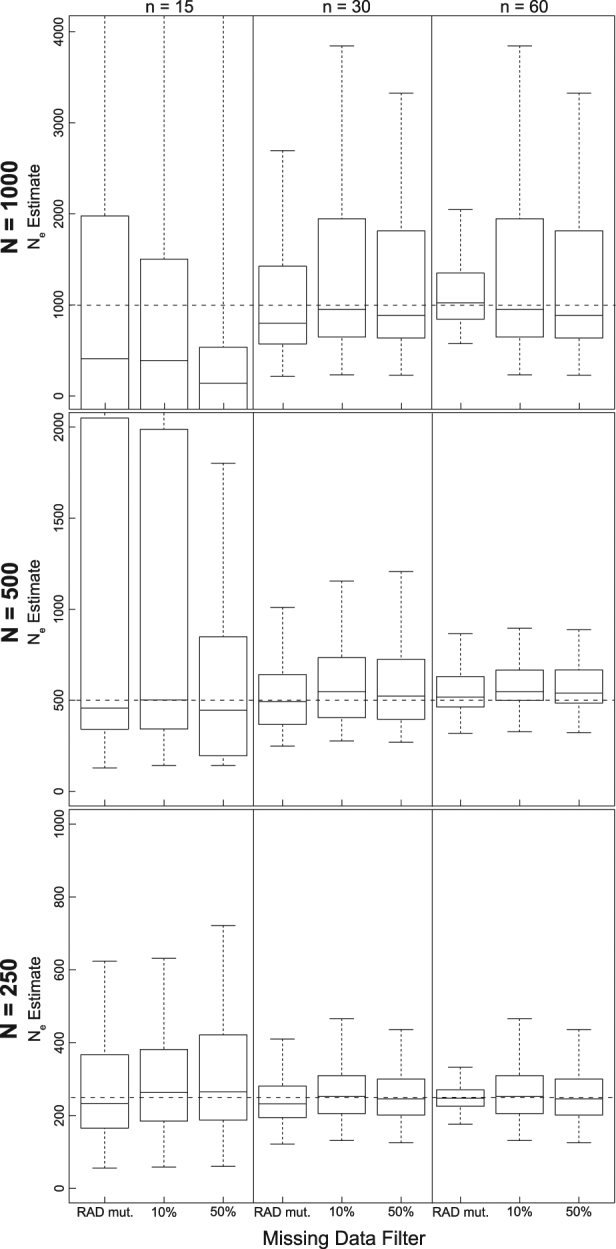
Boxplots of the distribution of 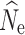 estimates from 100 replicate simulations for LD-based estimation at generation 20 from temporal simulations under stable population sizes (λ = 1.0) with a P
crit = 0.05. Dashed lines represent true N
e for the three population size models (1000, 500, and 250). Different missing data-filtering strategies are shown at the bottom of the figure. The number of individuals sampled is shown at the top
estimates from 100 replicate simulations for LD-based estimation at generation 20 from temporal simulations under stable population sizes (λ = 1.0) with a P
crit = 0.05. Dashed lines represent true N
e for the three population size models (1000, 500, and 250). Different missing data-filtering strategies are shown at the bottom of the figure. The number of individuals sampled is shown at the top
Table 2.
RMSE values for all filtering scenarios for LD-based analysis in NeEstimator under a stable population (λ = 1.0)
| LD RAD mutation | 10% missing data | 50% missing data | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (&P crit level) | (&P crit level) | (&P crit level) | ||||||||
| 0.01 | 0.02 | 0.05 | 0.01 | 0.02 | 0.05 | 0.01 | 0.02 | 0.05 | ||
| N = 250 | n = 15 | 2.73E−03 | 2.73E−03 | 2.95E−03 | 3.41E−03 | 3.41E−03 | 2.73E−03 | 3.68E−03 | 3.68E−03 | 2.70E−03 |
| n = 30 | 1.41E−03 | 1.10E−03 | 1.25E−03 | 1.55E−03 | 1.11E−03 | 1.18E−03 | 1.532E−03 | 1.11E−03 | 1.23E−03 | |
| n = 60 | 6.88E−04 | 6.17E−04 | 6.10E−04 | 1.55E−03 | 1.11E−03 | 1.18E−03 | 1.53E−03 | 1.11E−03 | 1.23E−03 | |
| N = 500 | n = 15 | Inf. | Inf. | 1.60E−03 | Inf. | Inf. | 1.54E−03 | Inf. | Inf. | 1.62E−03 |
| n = 30 | 9.65E−04 | 7.98E−04 | 8.41E−04 | 1.16E−03 | 7.79E−04 | 8.06E−04 | 1.16E−03 | 7.79E−04 | 8.15E−04 | |
| n = 60 | 4.59E−04 | 4.63E−04 | 4.40E−04 | 4.99E−04 | 4.56E−04 | 4.54E−04 | 5.02E−04 | 4.47E−04 | 4.43E−04 | |
| N = 1000 | n = 15 | Inf. | Inf. | 1.99E−03 | Inf. | Inf. | 1.84E− 03 | Inf. | Inf. | 1.87E−03 |
| n = 30 | 6.65E−04 | 7.76E−04 | 8.90E−04 | 8.03E−04 | 7.44E−04 | 7.87E−04 | 8.23E−04 | 7.32E−04 | 8.14E−04 | |
| n = 60 | 3.01E−04 | 3.14E−04 | 3.04E−04 | 8.03E−04 | 7.44E−04 | 7.87E−04 | 8.23E−04 | 7.32E−04 | 8.14E−04 | |
Bold values identify the lowest RMSE for a particular combination of population size (N), individual sampling level (n), and minor allele frequency cutoff (P
crit). Bold and italicized values identify the lowest RMSE for a particular population size. RMSE was not estimated if over 50% of the estimates of 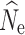 reached infinity for a particular parameter combination (Inf.)
reached infinity for a particular parameter combination (Inf.)
Fastsimcoal2
Estimation of 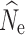 at t
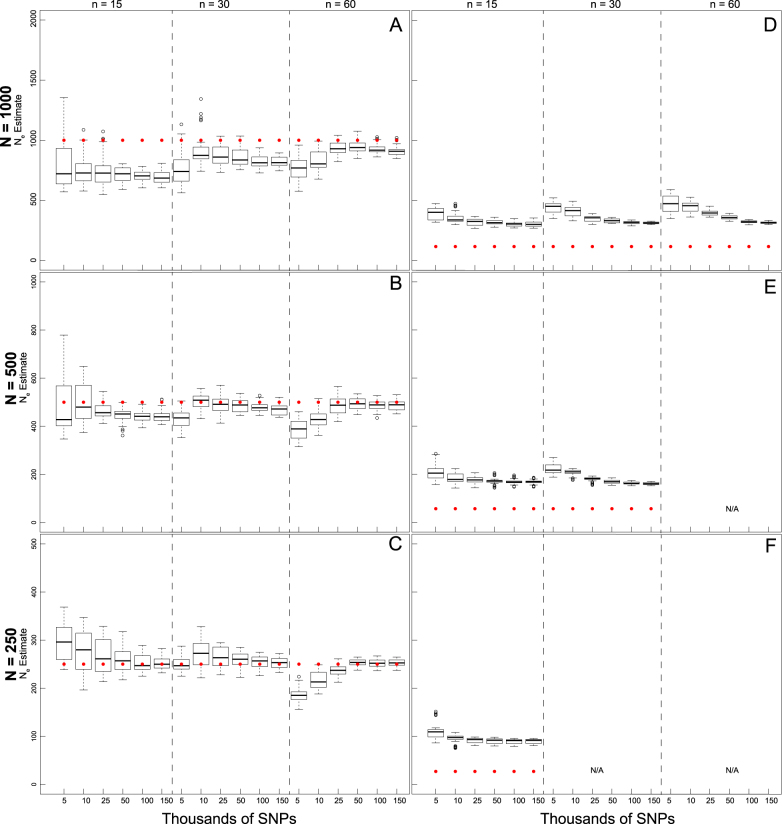
20 under a λ = 1.0 population model was most influenced by the number of SNPs included in the SFS (Fig. 2a, b, c) and, therefore, the allele dropout filtering scenario was used (Fig. 2S A–C). Overall, the fsc2 RAD mutation and fsc2 RAD mutation and coverage data sets yielded similar precision and accuracy compared to data sets using a similar number of randomly chosen SNPs from the fsc2 complete data set. Increased individual sampling had a slight improvement on accuracy and/or precision under all three population size models. However, analysis of 60-individual data sets in combination with lower numbers of SNPs (5000 and 10,0000), including the fsc2 RAD mutation and coverage data sets, yielded a very wide range of estimates under all three population size models, with highly inaccurate and negatively biased estimates under a n = 250 model. In general, accuracy and precision in all scenarios proportionally decreased with the number of SNPs in the data set.
at t
20 under a λ = 1.0 population model was most influenced by the number of SNPs included in the SFS (Fig. 2a, b, c) and, therefore, the allele dropout filtering scenario was used (Fig. 2S A–C). Overall, the fsc2 RAD mutation and fsc2 RAD mutation and coverage data sets yielded similar precision and accuracy compared to data sets using a similar number of randomly chosen SNPs from the fsc2 complete data set. Increased individual sampling had a slight improvement on accuracy and/or precision under all three population size models. However, analysis of 60-individual data sets in combination with lower numbers of SNPs (5000 and 10,0000), including the fsc2 RAD mutation and coverage data sets, yielded a very wide range of estimates under all three population size models, with highly inaccurate and negatively biased estimates under a n = 250 model. In general, accuracy and precision in all scenarios proportionally decreased with the number of SNPs in the data set.
Fig. 2.
Boxplots of the distribution of fastsimcoal2 estimates of 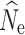 at t
20 from 40 replicate temporal simulations. a–c
at t
20 from 40 replicate temporal simulations. a–c
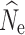 estimates under a stable population size (λ = 1.0) for population sizes of (a) 1000, (b) 500, and (c) 250. d–f
estimates under a stable population size (λ = 1.0) for population sizes of (a) 1000, (b) 500, and (c) 250. d–f
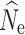 estimates under declining population size (λ = 0.9), for initial population size of (d) 1000, (e) 500, and (f) 250. Red dots represent the true N
e at t
20. Results are broken down across the number of individuals sampled (identified at the top of each panel) and the different numbers of SNPs used in analysis (identified at the bottom of each panel). For some parameter combinations, there were insufficient numbers of individuals for target n
estimates under declining population size (λ = 0.9), for initial population size of (d) 1000, (e) 500, and (f) 250. Red dots represent the true N
e at t
20. Results are broken down across the number of individuals sampled (identified at the top of each panel) and the different numbers of SNPs used in analysis (identified at the bottom of each panel). For some parameter combinations, there were insufficient numbers of individuals for target n
The 150,000 SNP data set yielded the lowest RMSE values for the n = 250 and n = 500 population models, and when sampling 60 individuals in the n = 1000 model (Table 3). Subsampled SNP data sets with 25,000 or more SNPs yielded only small decreases in RMSE with increasing numbers of SNPs. In the allele dropout data sets, the fsc2 complete data set yielded the lowest RMSE values for the n = 250 and n = 500 population models, and when sampling 60 individuals in the n = 1000 model (Table S5). Overall, fsc2 RAD mutation and fsc2 RAD mutation and coverage data sets had similar RMSE values.
Table 3.
RMSE values for increasing number of SNPs using fastsimcoal2 under a stable population (λ = 1.0)
| 5000 | 10,000 | 25,000 | 50,000 | 100,000 | 150,000 | ||
|---|---|---|---|---|---|---|---|
| N = 250 | n = 15 | 0.000357 | 0.000357 | 0.000267 | 0.000201 | 0.000136 | 0.000101 |
| n = 30 | 0.000118 | 0.000234 | 0.000178 | 0.00014 | 0.000103 | 8.58E−05 | |
| n = 60 | 0.000738 | 0.000367 | 0.000153 | 6.30E−05 | 6.14E−05 | 5.73E−05 | |
| N = 500 | n = 15 | 0.000233 | 0.00017 | 0.000105 | 0.000153 | 0.000152 | 0.000147 |
| n = 30 | 0.00019 | 6.69E−05 | 8.29E−05 | 6.43E−05 | 6.10E−05 | 8.13E−05 | |
| n = 60 | 0.000352 | 0.000191 | 8.78E−05 | 5.30E−05 | 5.33E-05 | 5.28E-05 | |
| N = 1000 | n = 15 | 0.000217 | 0.000208 | 0.000217 | 0.000208 | 0.00022 | 0.000234 |
| n = 30 | 0.000205 | 8.59E−05 | 9.19E−05 | 9.73E−05 | 0.000115 | 0.000113 | |
| n = 60 | 0.000188 | 1.18E−04 | 4.66E−05 | 4.04E-05 | 4.52E−05 | 5.50E−05 |
Bold values identify the lowest RMSE for a particular combination of population size (N) and individual sampling level (n). Bold and italicized values identify the lowest RMSE for a particular population size
Declining population size estimation
LD-based estimation
The number of generations since the beginning of a population decline was the biggest factor affecting the accuracy and precision of 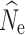 estimation (Fig. 3, Figs. S3–S5), with the variance in estimates decreasing over time as population size declined. Individual sampling also affected results, with an n = 15 yielding a greater estimation variance, particularly in earlier generations of the decline. Estimation using an n = 30 or 60 produced highly accurate estimates of
estimation (Fig. 3, Figs. S3–S5), with the variance in estimates decreasing over time as population size declined. Individual sampling also affected results, with an n = 15 yielding a greater estimation variance, particularly in earlier generations of the decline. Estimation using an n = 30 or 60 produced highly accurate estimates of 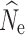 in t
10 through t
20. In general,
in t
10 through t
20. In general, 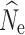 estimation over time was only minimally affected by the initial population size, the missing data filter used, or the P
crit used. However, with individual samples size of n = 15 a P
crit of 0.05 lead to a greater proportion of finite
estimation over time was only minimally affected by the initial population size, the missing data filter used, or the P
crit used. However, with individual samples size of n = 15 a P
crit of 0.05 lead to a greater proportion of finite 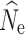 (Table S8–S10).
(Table S8–S10).
Fig. 3.
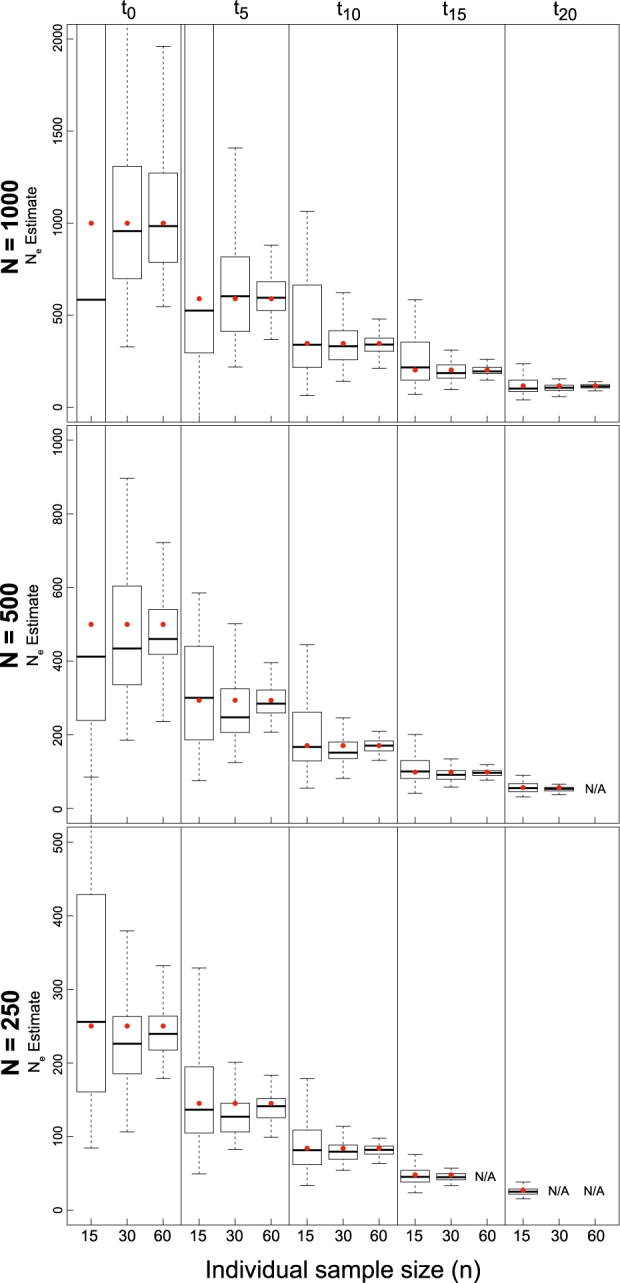
Boxplots of the distribution of point estimates from 100 replicate simulations for LD-based N e estimation from five temporal sampling points (t 0–t 20) under declining population growth model (λ = 0.9) using the 10% missing data set and a P crit = 0.05. Red dots represent true N e over time, starting from an initial N of 1000 (top), 500 (middle), or 250 (bottom). Results are also broken down across different levels of individual sample size (n = 15, 30, or 60). For some parameter combinations, there were insufficient numbers of individuals for target n
Similarly, estimation of 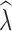 over different time intervals was most influenced by the number of generations passing between sampling events. The data filter used had minimal impact on the accuracy of
over different time intervals was most influenced by the number of generations passing between sampling events. The data filter used had minimal impact on the accuracy of 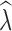 estimation and we present results from analyses of the 10% missing data here (Table 4) with results from analysis of additional allele dropout data sets presented in Tables S6–S7. When sampling 30–60 individuals, the P
crit did not have a large impact on population trend detection, but with an individual samples size of 15, a P
crit of 0.05 improved population trend detection. For example, when sampling 15 individuals, population declines with an initial n ≤ 500 were detected 67% of the time when at least ten generations passed, and increased to 85% of the time when 20 generations passed. With n = 15 and an initial n = 1000, at least 20 generations must pass for population declines to be detected 64% of the time. However, with n = 15 using a P
crit of 0.05 also increased the false positive rate, where stable populations were incorrectly identified as declining with
estimation and we present results from analyses of the 10% missing data here (Table 4) with results from analysis of additional allele dropout data sets presented in Tables S6–S7. When sampling 30–60 individuals, the P
crit did not have a large impact on population trend detection, but with an individual samples size of 15, a P
crit of 0.05 improved population trend detection. For example, when sampling 15 individuals, population declines with an initial n ≤ 500 were detected 67% of the time when at least ten generations passed, and increased to 85% of the time when 20 generations passed. With n = 15 and an initial n = 1000, at least 20 generations must pass for population declines to be detected 64% of the time. However, with n = 15 using a P
crit of 0.05 also increased the false positive rate, where stable populations were incorrectly identified as declining with 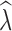 estimates of <0.95 across many replicates (Table 5, Tables S11–S12). Increased individual sampling greatly improved the correct identification of a declining population. For example, under an n = 1000 model, sampling 60 individuals resulted in the correct identification of a population decline >95% of the time when 10 generations passed and correct identification >71% of the time after just five generations.
estimates of <0.95 across many replicates (Table 5, Tables S11–S12). Increased individual sampling greatly improved the correct identification of a declining population. For example, under an n = 1000 model, sampling 60 individuals resulted in the correct identification of a population decline >95% of the time when 10 generations passed and correct identification >71% of the time after just five generations.
Table 4.
Number of times that a declining population trend was correctly identified out of 100 replicate runs for LD-based analysis in NeEstimator under a declining population model (λ = 0.9)
| t 0–t 5 | t 0–t 10 | t 0–t 15 | t 0–t 20 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (&P crit level) | (&P crit level) | (&P crit level) | (&P crit level) | ||||||||||
| 0.01 | 0.02 | 0.05 | 0.01 | 0.02 | 0.05 | 0.01 | 0.02 | 0.05 | 0.01 | 0.02 | 0.05 | ||
| N = 250 | n = 15 | 49 | 49 | 68 | 63 | 63 | 83 | 71 | 71 | 95 | 72 | 72 | 99 |
| n = 30 | 86 | 79 | 79 | 99 | 94 | 93 | 100 | 100 | 100 | — | — | — | |
| n = 60 | 94 | 94 | 94 | 100 | 100 | 100 | — | — | — | — | — | — | |
| N = 500 | n = 15 | 8 | 8 | 48 | 18 | 18 | 67 | 25 | 25 | 79 | 29 | 29 | 85 |
| n = 30 | 79 | 73 | 72 | 94 | 84 | 86 | 100 | 99 | 98 | 100 | 99 | 99 | |
| n = 60 | 80 | 81 | 84 | 97 | 98 | 98 | 100 | 100 | 100 | — | — | — | |
| N = 1000 | n = 15 | 0 | 0 | 35 | 0 | 0 | 40 | 2 | 2 | 53 | 2 | 2 | 64 |
| n = 30 | 57 | 65 | 66 | 70 | 80 | 79 | 76 | 91 | 91 | 78 | 97 | 97 | |
| n = 60 | 71 | 73 | 74 | 96 | 95 | 96 | 100 | 100 | 100 | 100 | 100 | 100 | |
Results are presented for increasing intervals of time and by the combination of population size (N), individual sampling level (n), and minor allele frequency cutoff (P crit). Results are based on the analysis of data sets with 10% missing data.
For some parameter combinations, there were insufficient numbers of individuals for target n (—)
Table 5.
Number of times that a population trend was incorrectly identified as declining out of 100 replicate runs for LD-based analysis in NeEstimator under a stable population model (λ = 1.0)
| t 0–t 5 | t 0–t 10 | t 0–t 15 | t 0–t 20 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (&P crit level) | (&P crit level) | (&P crit level) | (&P crit level) | ||||||||||
| 0.01 | 0.02 | 0.05 | 0.01 | 0.02 | 0.05 | 0.01 | 0.02 | 0.05 | 0.01 | 0.02 | 0.05 | ||
| N = 250 | n = 15 | 26 | 26 | 38 | 24 | 24 | 29 | 24 | 24 | 24 | 20 | 20 | 10 |
| n = 30 | 29 | 27 | 25 | 20 | 13 | 12 | 15 | 9 | 8 | 3 | 1 | 1 | |
| n = 60 | 8 | 9 | 8 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |
| N = 500 | n = 15 | 1 | 1 | 38 | 0 | 0 | 32 | 2 | 2 | 29 | 3 | 3 | 23 |
| n = 30 | 47 | 41 | 43 | 36 | 21 | 22 | 29 | 16 | 15 | 20 | 8 | 8 | |
| n = 60 | 26 | 24 | 27 | 6 | 6 | 6 | 1 | 1 | 1 | 0 | 0 | 0 | |
| N = 1000 | n = 15 | 1 | 1 | 20 | 0 | 0 | 12 | 0 | 0 | 10 | 0 | 0 | 9 |
| n = 30 | 16 | 36 | 37 | 11 | 30 | 28 | 16 | 27 | 27 | 7 | 18 | 18 | |
| n = 60 | 21 | 18 | 25 | 14 | 13 | 12 | 4 | 4 | 4 | 1 | 1 | 0 | |
Results are presented for increasing intervals of time and by combination of population size (N), individual sampling level (n), and minor allele frequency cutoff (Pcrit). Results are based on the analysis of data sets with 10% missing data.
Fastsimcoal2
The accuracy of 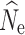 at t20 was most influenced by the number of SNPs included in the joint SFS (Figs. 2d, e, f), and therefore also the allele dropout filter used (Fig. S2 D-F). Estimates of
at t20 was most influenced by the number of SNPs included in the joint SFS (Figs. 2d, e, f), and therefore also the allele dropout filter used (Fig. S2 D-F). Estimates of 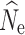 at t
20 were positively biased across all data sets, with greater bias in data sets with fewer numbers of SNPs. Similarly, estimation of
at t
20 were positively biased across all data sets, with greater bias in data sets with fewer numbers of SNPs. Similarly, estimation of 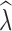 was most influenced by the number of SNPs included in the joint SFS. When sampling 5000–10,000 SNPs, population declines were detected <50% of the time across most scenarios (Table S13). With samples of 50,000–150,000 SNPs, population declines were detected across most replicates for an initial N of 500 and 1000. Population declines were not reliably detected for an initial N of 250 for any sampling scenario. For the allele dropout data sets, population declines of
was most influenced by the number of SNPs included in the joint SFS. When sampling 5000–10,000 SNPs, population declines were detected <50% of the time across most scenarios (Table S13). With samples of 50,000–150,000 SNPs, population declines were detected across most replicates for an initial N of 500 and 1000. Population declines were not reliably detected for an initial N of 250 for any sampling scenario. For the allele dropout data sets, population declines of 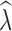 < 0.95 were detected across all 40 analyzed replicates using the fsc2 complete data set (Fig. S2 D–F). In contrast, none of the replicates for either fsc2 RAD mutation, or fsc2 RAD mutation and coverage data sets meet our criteria of
< 0.95 were detected across all 40 analyzed replicates using the fsc2 complete data set (Fig. S2 D–F). In contrast, none of the replicates for either fsc2 RAD mutation, or fsc2 RAD mutation and coverage data sets meet our criteria of 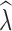 < 0.95, although most qualitatively indicated decline relative to N
e at t
0. Stable populations were never identified as declining in any data set examined.
< 0.95, although most qualitatively indicated decline relative to N
e at t
0. Stable populations were never identified as declining in any data set examined.
Discussion
Our results demonstrate that RADseq data have the potential to improve the inference of population demography and the detection of population declines on a very recent time scale. The linkage disequilibrium and coalescent methods we applied to estimate Ne use largely different sources of information from genomic data sets. The relative performance of these methods was influenced by different factors related to the study design, such as the number of individuals sampled (important for LD-based estimation) and the amount of variable data generated (important for coalescent estimation). Given that the accuracy and precision of N e estimators hinge on aspects of the study design and the underlying population history, we further discuss these influences and provide guidelines for inferring N e and population size trends. While we compare and contrast the performance of both estimators, combining results from both methods in empirical studies may be the best approach to develop an encompassing view of overall population demographic history, as suggested by Waples (2016).
Performance of estimators
In our analysis of RADseq data, LD-based demographic inference generally outperformed coalescent-based inference for N e estimation and the detection of population declines. However, there were limitations with LD-based inference, most notably with the number of sampled individuals required to provide both accurate and precise results. Sampling of 15 individuals led to large variance in estimates. This was most evident under a stable population size and in early generations of a population decline, particularly when population size was large (e.g., N = 1000). In contrast, increasing sampling to 30 individuals greatly increased the accuracy and precision of N e estimates. This may be discouraging from the perspective of sampling, as many-population genetic studies sample far fewer than 30 individuals per population. However, in light of microsatellite-based simulations showing that 30 individuals resulted in largely biased Ne estimation (Tallmon et al. 2010), LD-based analysis of RADseq appears to provide new opportunities for accurate demographic inference.
In contrast, coalescent-based N e estimation (using fsc2) was not greatly affected by the number of individuals sampled, with highly precise N e estimates produced using as few as 15 individuals. This result is similar to those obtained with ABC estimates based on large genomic data sets (Robinson et al. 2014). The most significant limitation for the coalescent approach was the number of SNPs in the joint SFS, and therefore the data filter used. We found that sampling 25,000 SNPs, and in some cases as many as 50,000 SNPs, were required to obtain accurate estimates of N e under a stable population model, with minimal increases in accuracy with greater number of SNPs. Previous simulation studies using coalescent-based ABC approaches found similar limitations with population size difficult to estimate even with 50,000 loci in some cases (Shafer et al. 2015b). All data sets yielded a consistent upward bias in N e estimation in the declining populations (Figs. 2d, e, f), and we are not sure what drives this estimation bias, but it was most pronounced in the data sets with fewer SNPs. Despite this positive bias, population declines were obvious using ≥50,000 SNPs at 20 generations from initiating declines. Due to the intense computational needs inherent to fsc2, N e was not estimated at earlier time points. Interestingly, detection of population declines were more difficult when initial population size was smaller (i.e., N = 250). While complete data sets similar to the ones used here are not attainable in empirical research, the positive correlation between numbers of SNPs and accurate coalescent-based N e estimation is encouraging. Technological improvements and sequencing costs continue to increase our ability to generate more complete genome-wide SNP data, even when factoring in allele dropout. In contrast, increasing sample size, especially temporally, will remain difficult for many species. Our use of true N e as a prior for one of our sampled years is also unlikely to be available in most study systems, which would further model complexity and add analytical time to an already computationally challenging set of analyses. Ultimately, coalescent-based demographic inference using a joint SFS-based method may be a great option for a more limited set of studies with access to large SNP data sets, and prior population information, as has been illustrated in a number of empirical studies (McCoy et al. 2013; Fraser et al. 2015; Nunziata et al. 2017).
Allele dropout and data filtering
Missing data via allele dropout in RADseq studies has been shown to affect a number of population genetic summary statistics, including measures of genetic diversity and population structure (Arnold et al. 2013; Gautier et al. 2013). Our results from parameter estimators for N
e are therefore encouraging, as increasing levels of missing data via allele dropout had little impact on LD-based N
e estimation and were generally comparable to the data set with no null alleles. Interestingly, while LD-based estimation was robust to the effects of allele dropout and missing data, the P
crit influenced 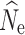 accuracy and precision, particularly under a model of stable population size. These results are consistent with other studies (Waples and Do 2010), where the inclusion of low frequency alleles created a positive bias, while the exclusion of these alleles created a slightly negative bias, particularly at the lowest sample size (Waples and Do 2010). Also consistent with the guidelines outlined in Waples and Do (2010), when low individual samples sizes were used (n = 15) a P
crit of 0.05 yielded the most finite and accurate estimates, as it is the only P
crit that screened out singletons, which can bias
accuracy and precision, particularly under a model of stable population size. These results are consistent with other studies (Waples and Do 2010), where the inclusion of low frequency alleles created a positive bias, while the exclusion of these alleles created a slightly negative bias, particularly at the lowest sample size (Waples and Do 2010). Also consistent with the guidelines outlined in Waples and Do (2010), when low individual samples sizes were used (n = 15) a P
crit of 0.05 yielded the most finite and accurate estimates, as it is the only P
crit that screened out singletons, which can bias 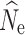 .
.
In contrast to the LD-based analyses, the allele dropout filter used in the fsc2 analyses did affect the results. However, allele dropout data sets did not appear to create any systematic bias compared to data sets using a similar number of randomly chosen SNPs from the fsc2 complete data set. Because these analyses preclude the use of loci with missing data, the direct impact of filtering loci by allele dropout was a major reduction of the number of SNPs included in the joint SFS. Contemporary population declines purge rare alleles, creating a predictable signature in the SFS (Nei et al. 1975; Gattepaille et al. 2013), with the likelihood of detecting this signature increasing with the number of SNPs included in the data set. We found that N
e estimation was accurate, and declines were reliably detected, using our data set containing ≥50,000 SNPS. The generation of empirical data sets robust enough to detect population declines may, therefore, require increased sequencing efforts to offset the effects of allele dropout by increasing the number of loci sampled and their coverage. Maybe counter intuitively, increased individual sampling does not solve this problem as adding individuals increases the probability of allele dropout through a cut site mutation or insufficient sequencing coverage, creating a smaller SNP matrix and decreasing precision in 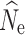 (Fig. 2S). Potentially, this result can be overcome by subsampling individuals for non-missing data (e.g., Papadopoulou and Knowles 2015).
(Fig. 2S). Potentially, this result can be overcome by subsampling individuals for non-missing data (e.g., Papadopoulou and Knowles 2015).
Allele dropout often goes undetected in many studies, and our preliminary exploration suggests that the underlying population history of either stable or declining populations were recovered and point estimates were almost always within an order of magnitude of real N e. Previous simulation work has revealed that non-equilibrium demography, such as a population decline, can cause low N e and result in fewer loci with missing data and more accurate allele frequency estimation (Arnold et al. 2013). Therefore, our findings should not be interpreted as applicable across systems, since we may have modeled scenarios (i.e., low N e, steadily declining) that create evident signatures in the SFS at a contemporary time scale.
Practical considerations
Many additional factors influence N
e that we have not modeled here, including selection, migration, and overlapping generations (Slatkin 2008). In real populations, N
e rarely equals N
C, and changes in N
e could track any number of demographic changes, not exclusively N
C (Palstra and Ruzzante 2008). Further simulations are needed under more realistic scenarios to determine the application of evaluated methods across systems. One factor that must be considered with RADseq data sets and the LD-based approach is that although pairwise r
2 values (correlation of genes within individuals) increase with number of loci, SNPs on the same chromosome are not independent and will reduce the precision of 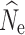 because LD will be the result of physical linkage and not drift (Waples et al. 2016). The use of linked SNPs could be corrected for by using known genomic architecture (Waples et al. 2016); and is an important consideration in the application of LD-based N
e estimation to RADseq data.
because LD will be the result of physical linkage and not drift (Waples et al. 2016). The use of linked SNPs could be corrected for by using known genomic architecture (Waples et al. 2016); and is an important consideration in the application of LD-based N
e estimation to RADseq data.
Both LD and coalescent methods produced a time lag between census size declines and corresponding decline in Ne. The LD-based method has potential for accurate detection of population declines, generally after only 10 generations from initiation of a decline. However, if working with long-lived species with long-generation times, these 10 generations could equate to several decades within which populations could decline rapidly toward extinction with a little change in N e. Given these findings, we emphasize that genomic monitoring is not a replacement for traditional census size monitoring in many cases, but may serve as an informative complement.
When inferring 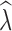 from
from 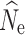 for conservation purposes, false positives can lead to a waste of management resources when stable populations are misidentified as declining (Schwartz et al. 2007). The absence of any false positives in the fsc2-based λ estimation, and the lower number of individuals required, is promising for its application in conservation studies. However, the failure to detect declines in most replicates with <25,000 SNPs highlights the need for very large SNP data sets, as well as temporal sampling, especially if quick detection of population declines is a goal. False positives for LD-based λ estimates were also low, although this typically required larger sample sizes of at least 30 individuals. With large resources available to researchers, the application of both methods for demographic inference will be the ideal approach to take, but given constraints on sampling or sequencing, the results here can be useful for guiding decisions about how to design a conservation genetic study aimed at detecting recent population declines. Finally, even when temporal sampling is unavailable, N
e is itself an important indicator of population viability and evolutionary potential and RADseq data can serve as a valuable source of information for this parameter.
for conservation purposes, false positives can lead to a waste of management resources when stable populations are misidentified as declining (Schwartz et al. 2007). The absence of any false positives in the fsc2-based λ estimation, and the lower number of individuals required, is promising for its application in conservation studies. However, the failure to detect declines in most replicates with <25,000 SNPs highlights the need for very large SNP data sets, as well as temporal sampling, especially if quick detection of population declines is a goal. False positives for LD-based λ estimates were also low, although this typically required larger sample sizes of at least 30 individuals. With large resources available to researchers, the application of both methods for demographic inference will be the ideal approach to take, but given constraints on sampling or sequencing, the results here can be useful for guiding decisions about how to design a conservation genetic study aimed at detecting recent population declines. Finally, even when temporal sampling is unavailable, N
e is itself an important indicator of population viability and evolutionary potential and RADseq data can serve as a valuable source of information for this parameter.
Data archiving
All simulation scripts Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.6d925.
Electronic supplementary material
Acknowledgements
We thank D. Herring and three anonymous reviewers for constructive comments on this manuscript. We thank the University of Kentucky Center for Computational Sciences and the Lipscomb High-Performance Computing Cluster for access to computing resources, and Vikram Gazula for help with script optimization. This research was supported by the National Science Foundation through a DDIG award (DEB-1601470 to S.O.N.), and by awards DEB-0949532 and DEB-1355000 (to D.W.W.).
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
Electronic supplementary material
The online version of this article (10.1038/s41437-017-0037-y) contains supplementary material, which is available to authorized users.
References
- Andreotti S, Rutzen M, Van der Walt S, von der Heyden S, Henriques R, Meÿer M, Oosthuizen H, Matthee CA. An integrated mark-recapture and genetic approach to estimate the population size of white shark in South Africa. Mar Ecol Progress Ser. 2016;552:241–253. doi: 10.3354/meps11744. [DOI] [Google Scholar]
- Andrews KR, Good JM, Miller MR, Luikart G, Hohenlohe PA. Harnessing the power of RADseq for ecological and evolutionary genomics. Nat Rev Genet. 2016;17:81–92. doi: 10.1038/nrg.2015.28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antao T, Pérez-Figueroa A, Luikart G. Early detection of population declines: high power of genetic monitoring using effective population size estimators. Evol Appl. 2011;4:144–154. doi: 10.1111/j.1752-4571.2010.00150.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold B, Corbet-Detig RB, Hartl D, Bomblies K. RAD-seq underestimates diversity and introduces genealogical biases due to nonrandom haplotype sampling. Mol Ecol. 2013;22:3179–3190. doi: 10.1111/mec.12276. [DOI] [PubMed] [Google Scholar]
- Davey JW, Hohenlohe PA, Etter PD, Boone JQ, Catchen JM, Blaxter ML. Genome-wide genetic marker discovery and genotyping using next-generation sequencing. Nat Rev Genet. 2011;12:499–510. doi: 10.1038/nrg3012. [DOI] [PubMed] [Google Scholar]
- Do C, Waples RS, Peel D, et al. NeEstimator V2: re-implementation of software for the estimation of contemporary effective population size (Ne) from genetic data. Mol Ecol Resour. 2014;14:209–214. doi: 10.1111/1755-0998.12157. [DOI] [PubMed] [Google Scholar]
- Dudgeon CL, Ovenden JR. The relationship between abundance and genetic effective population size in elasmobranchs: an example from the globally threatened zebra shark Stegostoma fasciatum within its protected range. Conserv Genet. 2015;16:1443–1454. doi: 10.1007/s10592-015-0752-y. [DOI] [Google Scholar]
- Excoffier L, Dupanloup I, Huerta-Sanchez E, Sousa VC, Foll M (2013) Robust demographic inference from genomic and SNP data. PLoS Genet 9:e1003905 [DOI] [PMC free article] [PubMed]
- Fraser BA, Kunstner A, Reznick DN, Dreyer C, Weigel D. Population genomics of natural and experimental populations of guppies (Poecilia reticulata) Mol Ecol. 2015;24:389–408. doi: 10.1111/mec.13022. [DOI] [PubMed] [Google Scholar]
- Gautier M, Gharbi K, Cezard T, et al. The effect of RAD allele dropout on the estimation of genetic variation within and between populations. Mol Ecol. 2013;22:3165–3178. doi: 10.1111/mec.12089. [DOI] [PubMed] [Google Scholar]
- Gattepaille LM, Jakobsson M, Blum MGB. Inferring population size changes with sequence and SNP data: lessons from human bottlenecks. Heredity. 2013;110:409–419. doi: 10.1038/hdy.2012.120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutenkunst RN, Hernandez RD, Williamson SH, Bustamante CD. Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet. 2009;5:1–11. doi: 10.1371/journal.pgen.1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG. Estimation of effective population size from data on linkage disequilibrium. Genet Res. 1981;38:209–216. doi: 10.1017/S0016672300020553. [DOI] [Google Scholar]
- Hoban SM, Gaggiotti OE, Bertorelle G. The number of markers and samples needed for detecting bottlenecks under realistic scenarios, with and without recovery: a simulation-based study. Mol Ecol. 2013;22:3444–3450. doi: 10.1111/mec.12258. [DOI] [PubMed] [Google Scholar]
- Hollenbeck CM, Portnoy DS, Gold JR. A method for detecting recent changes in contemporary effective population size from linkage disequilibrium at linked and unlinked loci. Heredity. 2016;117:207–216. doi: 10.1038/hdy.2016.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang H, Knowles LL (2014) Unforeseen consequences of excluding missing data from next-generation sequences: simulation Study of RAD Sequences. Syst Biol 65:357–365 [DOI] [PubMed]
- Kopuchian C, Campagna L, Di Giacomo AS, et al. Demographic history inferred from genome-wide data reveals two lineages of sheldgeese endemic to a glacial refugium in the southern Atlantic. J Biogeogr. 2016;43:1979–1989. doi: 10.1111/jbi.12767. [DOI] [Google Scholar]
- Lischer HEL, Excoffier L. PGDSpider: an automated data conversion tool for connecting population genetics and genomics programs. Bioinformatics. 2012;28:298–299. doi: 10.1093/bioinformatics/btr642. [DOI] [PubMed] [Google Scholar]
- Luikart G, Ryman N, Tallmon DA, Schwartz MK, Allendorf FW. Estimation of census and effective population sizes: the increasing usefulness of DNA-based approaches. Conserv Genet. 2010;11:255–373. doi: 10.1007/s10592-010-0050-7. [DOI] [Google Scholar]
- McCoy RC, Garud NR, Kelley JL, Boggs CL, Petrov D. Genomic inference accurately predicts the timing and severity of a recent bottleneck in a nonmodel insect population. Mol Ecol. 2013;23:136–150. doi: 10.1111/mec.12591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nachman MW, Crowell SL. Estimate of the mutation rate per nucleotide in humans. Genetics. 2000;156:297–304. doi: 10.1093/genetics/156.1.297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narum SR, Buerkle CA, Davey JW, Miller MR, Hohenlohe PA. Genotyping-by-sequencing in ecological and conservation genomics. Mol Ecol. 2013;22:2841–2847. doi: 10.1111/mec.12350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei M, Maruyama T, Chakraborty R. The bottleneck effect and genetic variability in populations. Evolution. 1975;29:1–10. doi: 10.1111/j.1558-5646.1975.tb00807.x. [DOI] [PubMed] [Google Scholar]
- Nordborg M, Krone SM. Separation of time scales and convergence to the coalescent in structured populations. In: Slatkin M, Veuille M, editors. Modern developments in theoretical population genetics. Oxford: Oxford University Press; 2002. pp. 130–164. [Google Scholar]
- Nunziata SO, Lance SL, Scott DE, Lemmon EM, Weisrock DW. Genomic data detect corresponding signatures of population size change on an ecological time scale in two salamander species. Mol Ecol. 2017;26:1060–1074. doi: 10.1111/mec.13988. [DOI] [PubMed] [Google Scholar]
- Palstra FP, Ruzzante DE. Genetic estimates of contemporary effective population size: what can they tell us about the importance of genetic stochasticity for wild population persistence? Mol Ecol. 2008;17:3428–3447. doi: 10.1111/j.1365-294X.2008.03842.x. [DOI] [PubMed] [Google Scholar]
- Papadopoulou A, Knowles LL. Genomic tests of the species-pump hypothesis: recent island connectivity cycles drive population divergence but not speciation in Caribbean crickets across the Virgin Islands. Evolution. 2015;69:1501–1517. doi: 10.1111/evo.12667. [DOI] [PubMed] [Google Scholar]
- Peng B, Kimmel M. simuPOP: a forward-time population genetics simulation environment. Bioinformatics. 2005;21:3686–3687. doi: 10.1093/bioinformatics/bti584. [DOI] [PubMed] [Google Scholar]
- Pool JE, Hellmann I, Jensen JD, Nielsen R. Population genetic inference from genomic sequence variation. Genome Res. 2010;20:291–300. doi: 10.1101/gr.079509.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prates I, Xue AT, Brown JL, Alvarado-Serrano DF, Rodrigues MT, Hickerson MJ, Carnaval AC. Inferring responses to climate dynamics from historical demography in neotropical forest lizards. Proc Natl Acad Sci USA. 2016;113:7978–7985. doi: 10.1073/pnas.1601063113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson JD, Coffman AJ, Hickerson MJ, Gutenkunst RN. Sampling strategies for frequency spectrum-based population genomic inference. BMC Evol Biol. 2014;14:254. doi: 10.1186/s12862-014-0254-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rokas A, Abbot P. Harnessing genomics for evolutionary insights. Trends Ecol Evol. 2009;24:192–200. doi: 10.1016/j.tree.2008.11.004. [DOI] [PubMed] [Google Scholar]
- Schwartz MK, Luikart G, Waples RS. Genetic monitoring as a promising tool for conservation and management. Trends Ecol Evol. 2007;22:25–33. doi: 10.1016/j.tree.2006.08.009. [DOI] [PubMed] [Google Scholar]
- Shafer ABA, Wolf JBW, Alves PC, et al. Genomics and the challenging translation into conservation practice. Trends Ecol Evol. 2015;30:78–87. doi: 10.1016/j.tree.2014.11.009. [DOI] [PubMed] [Google Scholar]
- Shafer ABA, Gattepaille LM, Stewart RE, Wolf JB. Demographic inferences using short-read genomic data in an approximate Bayesian computation framework: in silico evaluation of power, biases and proof of concept in Atlantic walrus. Mol Ecol. 2015;24:328–345. doi: 10.1111/mec.13034. [DOI] [PubMed] [Google Scholar]
- Shafer ABA, Peart CR, Tusso S, Maayan I, Brelsford A, Wheat CW, Wolf JBW. Bioinformatic processing of RAD-seq data dramatically impacts downstream population genetic inference. Methods Ecol Evol. 2017;8:907–917. doi: 10.1111/2041-210X.12700. [DOI] [Google Scholar]
- Slatkin M. Linkage disequilibrium – understanding the evolutionary past and mapping the medical future. Nat Rev Genet. 2008;9:477–485. doi: 10.1038/nrg2361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tallmon DA, Gregovich D, Waples RS, et al. When are genetic methods useful for estimating contemporary abundance and detecting population trends? Mol Ecol Resour. 2010;10:684–692. doi: 10.1111/j.1755-0998.2010.02831.x. [DOI] [PubMed] [Google Scholar]
- Trucchi E, Facon B, Gratton P, Mori E, Stenseth NC, Jentoft S. Long live the alien: is high genetic diversity a pivotal aspect of crested porcupine (Hystrix cristata) long-lasting and successful invasion? Mol Ecol. 2016;25:3527–3539. doi: 10.1111/mec.13698. [DOI] [PubMed] [Google Scholar]
- Wakeley J, Sargsyan O. Extensions of the coalescent effective population size. Genetics. 2009;181:341–345. doi: 10.1534/genetics.108.092460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waples RS. Genetic estimates of contemporary effective population size: to what time periods to estimates apply? Mol Ecol. 2005;14:3335–3352. doi: 10.1111/j.1365-294X.2005.02673.x. [DOI] [PubMed] [Google Scholar]
- Waples RS. A bias correction for estimates of effective population size based on linkage disequilibrium at unlinked gene loci. Conserv Genet. 2006;7:167–184. doi: 10.1007/s10592-005-9100-y. [DOI] [Google Scholar]
- Waples RS, Do C. Linkage disequilibrium estimates of contemporary Ne using highly variable genetic markers: a largely untapped resource for applied conservation and evolution. Evol Appl. 2010;3:244–262. doi: 10.1111/j.1752-4571.2009.00104.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waples RK, Larson WA, Waples RS. Estimating contemporary effective population size in non-model species using linkage disequilibrium across thousands of loci. Heredity. 2016;117:233–240. doi: 10.1038/hdy.2016.60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waples RS. Making sense of genetic estimates of effective population size. Mol Ecol. 2016;25:4689–4691. doi: 10.1111/mec.13814. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.