How input fluctuations reshape the dynamics of a biological switching system

Abstract

An important task in quantitative biology is to understand the role of stochasticity in biochemical regulation. Here, as an extension of our recent work [Phys. Rev. Lett. 107, 148101 (2011)], we study how input fluctuations affect the stochastic dynamics of a simple biological switch. In our model, the on transition rate of the switch is directly regulated by a noisy input signal, which is described as a non-negative mean-reverting diffusion process. This continuous process can be a good approximation of the discrete birth-death process and is much more analytically tractable. Within this setup, we apply the Feynman-Kac theorem to investigate the statistical features of the output switching dynamics. Consistent with our previous findings, the input noise is found to effectively suppress the input-dependent transitions. We show analytically that this effect becomes significant when the input signal fluctuates greatly in amplitude and reverts slowly to its mean.

I. INTRODUCTION

Stochasticity appears to be a hallmark of many biological processes involved in signal transduction and gene regulation [1–11]. Over the past decade, there have been numerous experimental and theoretical efforts to understand the functional roles of noise in various living systems [2–41]. Remarkably, the building block of different regulatory programs is often a simple two-state switch under the regulation of some noisy input signal. For example, a gene network is composed of many interacting genes, each of which is a single switch regulated by specific transcription factors. At a synapse, switching of ligand-gated ion channels is responsible for converting the presynaptic chemical message into postsynaptic electrical signals, while the opening and closing of each channel depends on the binding of certain ligands (such as a neurotransmitter). In bacterial chemotaxis, the cellular motion is powered by multiple flagellar motors, and each motor rotates clockwise or counterclockwise depending on the level of some specific response regulator (e.g., CheY-P in E. coli). Irrespective of the context, the input signal, i.e., the number of regulatory molecules, is usually stochastic due to discreteness, diffusion, random birth, and death. How does a biological switching system work in a noisy environment? This is the central question we attempt to address in this paper.

Previous studies on this topic have usually focused on the approximate, static relationship between input and output variations (e.g., the additive noise rule) [12–19], while the dynamic details (e.g., dwell time statistics) of the switching system have often been ignored. Our recent work suggests that there is more to comprehend even in the simplest switching system [22]. For example, we showed that increasing input noise does not always lead to an increase in the output variation, disagreeing with the additive noise rule as derived from the coarse-grained Langevin approach. Traditional methods often use a single Langevin equation to approximate the joint input-output process (which is only applicable for an ensemble of switches), and they rely on the assumption that the input noise is small enough such that one can linearize input-dependent nonlinear reaction rates. Our approach to this problem is quite different as we explicitly model how the input stochastic process drives a single output switch, without making any small noise assumption.

In our previous paper [22], the input signal was generated from a discrete birth-death process and regulated the on transition of a downstream switch. By explicitly solving the joint master equation of the system, we found that input fluctuations can effectively reduce the on rate of the switch. In this paper, this problem is revisited in a continuous noise formulation. We propose to model the input signal as a general diffusion process, which is mean-reverting, non-negative, and tunable in Fano factor (the ratio of variance to mean). We employ the Feynman-Kac theorem to calculate the input-dependent dwell time distribution and examine its asymptotic behavior in different scenarios. Within this framework, we recover several findings reported in [22], and we also demonstrate how the noise-induced suppression depends on the noise intensity as well as the relative time scales of the input and output dynamics. Finally, we elaborate on how the diffusion process introduced in this paper can be a reasonable approximation of the discrete birth-death process.

II. MODEL

The input of our model, denoted by X(t), represents a specific chemical concentration at time t and directly governs the transition rates of a downstream switch. The binary on-off states of the switch in continuous time constitute the output process, Y(t). A popular choice for X(t) is the Ornstein-Uhlenbeck (OU) process due to its analytical simplicity and mean-reverting property [42–44]. However, this process does not rule out negative values, an unphysical feature for modeling chemical concentrations. For both mathematical convenience and biophysical constraints (see Sec. IV for more details), we model X(t) by a square-root diffusion process [45–48]:

$$dX(t)=\lambda [\mu -X(t)]dt+\sigma \sqrt{X(t)}d{W}_t,$$ (1)

where λ represents the rate at which X(t) reverts to its mean level μ, σ controls the noise intensity, and W_t denotes the standard Brownian motion. This simple process is known as the Cox-Ingersoll-Ross (CIR) model of interest rates [45]. The square-root noise term not only ensures that the process never goes negative but also captures a common statistical feature underlying many biochemical processes, that is, the standard deviation of the copy number of molecules scales as the square root of the copy number, as dictated by the central limit theorem. Solving the Fokker-Planck equation for Eq. (1), we obtain the steady-state distribution of the input signal:

$$P_s(X=x)=\frac{{\beta }^{\alpha }{x}^{\alpha -1}{e}^{-\beta x}}{\mathrm{\Gamma }(\alpha )},\alpha \equiv \frac{2\mu \lambda }{{\sigma }^2},\beta \equiv \frac{2\lambda }{{\sigma }^2},$$ (2)

which is a Gamma distribution with stationary variance ${\sigma }_X^2=\mu {\sigma }^2/(2\lambda )$. This is another attractive aspect of this model, since the protein abundance from gene expression experiments can often be fitted by a Gamma distribution [8–10]. The parameter α in Eq. (2) can be interpreted as the signal-to-noise ratio, since $\alpha ={\mu }^2/{\sigma }_X^2$. For α ≥ 1, the zero point is guaranteed to be inaccessible for X(t). The other shape parameter β sets the Fano factor as we have $1/\beta ={\sigma }_X^2/\mu$. Using the Itó calculus [44], one can also find the steady-state covariance: ${lim}_{t\to \infty }cov[X(t),X(t+s)]={\sigma }_X^2{e}^{-\lambda \mid s\mid }$. Thus X(t) is a stationary process with correlation time λ⁻¹.

In reality, the output switching rates may depend on the input X(t) in complicated ways, depending on the detailed molecular mechanism. For analytical convenience, we assume that the on and off transition rates of the switch are k_onX(t) and k_off, respectively (Fig. 1). As a result, the input fluctuations should only affect the chance of the switch exiting the off state; the on-state dwell time distribution is always exponential with rate parameter k_off. If we mute the input noise, then Y(t) reduces to a two-state Markov process with transition rates k_onμ and k_off. However, the presence of input noise will generally make Y(t) a non-Markovian process, because the off-state time intervals may exhibit a nonexponential distribution. To illustrate this point more rigorously, we consider the following first passage time problem [44]. Suppose the switch starts in the off state at t = 0 with the initial input X(0) = x. Let τ̃ be the first time of the switch turning on (Fig. 1). Then the survival probability f(x,t) for the switch staying off up to time t is given by

FIG. 1.

Illustration of our model: X(t) represents the input signal which fluctuates around a mean level over time; Y(t) records the switch process which flips between the off (Y = 0) and on (Y = 1) states with transition rates k_onX(t) and k_off. τ̃ is the dwell time in the off state.

$$f(x,t)\equiv P[\stackrel{\sim }{\tau }>t\mid X(0)=x]=E^x\left[e^{-{\int }_0^t{k}_{\text{on}}X(s)ds}\right],$$ (3)

where E^x[⋯] denotes expectation over all possible sample paths of X(s) for 0 ≤ s ≤ t, conditioned on X(0) = x. In probability theory, Jensen’s inequality is generally stated in the following form: if X is a random variable and φ is a convex function, then E[φ(X)] ≥ φ(E[X]). Applying Jensen’s inequality to Eq. (3) leads to f (x,t) ≥ exp(−k_onμt), where the equality holds if the input is noise-free. This inequality suggests that the input noise will elongate the mean waiting time for the off-to-on transitions, regardless of the noise intensity or the correlation time. We will elaborate on this noise effect in a more analytical way. The Feynman-Kac formula [44] asserts that f (x,t) solves the following partial differential equation:

$$\frac{\partial f}{\partial t}=\lambda (\mu -x)\frac{\partial f}{\partial x}+\frac{1}{2}{\sigma }^{2}x\frac{{\partial }^{2}f}{\partial x^2}-k_{\text{on}}xf,$$ (4)

with the initial condition f (x,0) = 1. As we will show in the next section, the off-state dwell time distribution is not exactly exponential, though it is asymptotically exponential when t is large.

III. RESULTS

A similar partial differential equation to Eq. (4) has been solved in Ref. [45] to price zero-coupon bonds under the CIR interest rate model. The closed-form solution for our problem is similar and is found to be

$$f(x,t)={\left[\frac{\stackrel{\sim }{\lambda }{e}^{\lambda t/2}/sinh(\stackrel{\sim }{\lambda }t/2)}{\lambda +\stackrel{\sim }{\lambda }coth(\stackrel{\sim }{\lambda }t/2)}\right]}^{\alpha }exp\left[\frac{-2k_{\text{on}}x}{\lambda +\stackrel{\sim }{\lambda }coth(\stackrel{\sim }{\lambda }t/2)}\right],$$ (5)

where

$$\stackrel{\sim }{\lambda }\equiv \sqrt{{\lambda }^2+2k_{\text{on}}{\sigma }^2}=\lambda \sqrt{1+2k_{\text{on}}{\sigma }^2/{\lambda }^2}.$$ (6)

Evidently, f (x,t) remembers the initial input x and decays with t in a manner which is not exactly exponential. For t ≫ λ̃⁻¹, Eq. (5) takes the following form:

$$f(x,t)\simeq {\left(\frac{2\stackrel{\sim }{\lambda }}{\lambda +\stackrel{\sim }{\lambda }}\right)}^{\alpha }exp\left(-\frac{{\stackrel{\sim }{k}}_{\text{on}}x}{\lambda }-{\stackrel{\sim }{k}}_{\text{on}}\mu t\right).$$ (7)

In deriving Eq. (7), we have used the following relationship, which defines the parameter k̃_on as below:

$${\stackrel{\sim }{k}}_{\text{on}}\equiv \frac{\alpha (\stackrel{\sim }{\lambda }-\lambda )}{2\mu }=\frac{\lambda }{{\sigma }^2}(\stackrel{\sim }{\lambda }-\lambda )=\frac{2\lambda }{\stackrel{\sim }{\lambda }+\lambda }{k}_{\text{on}}<k_{\text{on}}.$$ (8)

Thus, asymptotically speaking, f(x,t) decays with t in an exponential manner at the rate k̃_onμ. It can be easily verified that Eq. (7) is a particular solution to Eq. (4).

To gain further insight into how the input noise affects the switching dynamics, we first study the “slow switch” limit where X(t) fluctuates so rapidly that λ⁻¹ ≪ 𝒯_Y. Here, 𝒯_Y ≡ (k_onμ + k_off)⁻¹ is the output correlation time for the noiseless input model. In this limit, the initial input x in f (x,t) at the start of each off period is effectively drawn from the Gamma distribution P_s(x) defined in Eq. (2); the successive off-state intervals are almost independent of each other (as the input loses memory quickly) and are distributed as

$$P(\stackrel{\sim }{\tau }\le t)=1-P(\stackrel{\sim }{\tau }>t)=1-{\int }_0^{\infty }f(x,t)P_s(x)dx.$$ (9)

By direct integration over x, we find that

$$\begin{gathered} P(\stackrel{\sim }{\tau }>t)={\left[\frac{\beta \stackrel{\sim }{\lambda }{e}^{\lambda t/2}}{(\beta \lambda +2k_{\text{on}})sinh(\stackrel{\sim }{\lambda }t/2)+\beta \stackrel{\sim }{\lambda }cosh(\stackrel{\sim }{\lambda }t/2)}\right]}^{\alpha } \\ \simeq {\left[\frac{2\beta \stackrel{\sim }{\lambda }{e}^{-(\stackrel{\sim }{\lambda }-\lambda )t/2}}{\beta (\lambda +\stackrel{\sim }{\lambda })+2k_{\text{on}}}\right]}^{\alpha }\simeq exp(-{\stackrel{\sim }{k}}_{\text{on}}\mu t). \end{gathered}$$ (10)

In the last step above, we have used Eq. (8) as well as the following observation: By introducing θ ≡ k_onσ²/λ², which reflects the deviation of λ̃ from λ, one can check that as long as λ ≫ k_onμ (as ensured by λ⁻¹ ≪ 𝒯_Y) the following holds, regardless of the values of θ:

$${\left[\frac{2\beta \stackrel{\sim }{\lambda }}{\beta (\lambda +\stackrel{\sim }{\lambda })+2k_{\text{on}}}\right]}^{\alpha }={\left(\frac{1}{2}+\frac{1+\theta }{2\sqrt{1+2\theta }}\right)}^{-\frac{2}{\theta }\frac{k_{\text{on}}\mu }{\lambda }}\simeq 1.$$

Our simulations show that the approximate result, P(τ̃ > t) ≃ e^−k̃_onμt, is excellent [Fig. 2(a)], independent of the values of θ. Thus, the average waiting time for the switch to turn on is (k̃_onμ)⁻¹, longer than the corresponding average time (k_onμ)⁻¹ for the noiseless input model. This is similar to our previous result [22], and suggests that the input noise will effectively suppress the on state by increasing the average waiting time to exit the off state. Consequently, the probability, P_on, to find the switch on (Y = 1) is less than that in the noiseless input model:

$$P_{\text{on}}\simeq \frac{\mu }{\mu +{\stackrel{\sim }{K}}_d}<\frac{\mu }{\mu +K_d}=\underset{\sigma \to 0}{lim}{P}_{\text{on}},$$ (11)

where K̃_d ≡ k_off/k̃_on, the effective equilibrium constant, is larger than the original K_d ≡ k_off/k_on as per Eq. (8).

FIG. 2.

The slow switch case. Here we use λ = 10, k_on = 0.02, and k_off = 0.1 (thus K_d = 5). (a) P (τ̃ > t) vs t for μ = 3 and θ = 0.005, 0.5, and 2.0, which are achieved by choosing σ = 5, 50, and 100. Symbols represent simulation results, while lines denote exp(−k̃_onμt). (b) ${\stackrel{\sim }{\sigma }}_Y^2-{\sigma }_Y^2$ vs ${\sigma }_X^2$, where different values of ${\sigma }_X^2$ are obtained by tuning σ. (c) ${\stackrel{\sim }{\sigma }}_Y^2$ and ${\sigma }_Y^2$ vs μ/K_d with fixed θ = 0.50. (d) 𝒯̃_Y − 𝒯_Y vs ${\sigma }_X^2$.

Therefore, in the slow switch limit (𝒯_Y ≫ λ⁻¹), the output Y(t) is approximately a two-state Markov process with transition rates k̃ _onμ and k_off. If we further assume that the noise is modest (i.e., σ_X ≤ μ), then

$$\theta \equiv k_{\text{on}}\frac{{\sigma }^2}{{\lambda }^2}=\frac{2k_{\text{on}}\mu }{\alpha \lambda }=\frac{2k_{\text{on}}\mu }{\lambda }\left(\frac{{\sigma }_X^2}{{\mu }^2}\right)\ll 1.$$ (12)

The equality above shows that θ is a characteristic parameter determined by the ratio of the input to output time scales and the relative noise strength. For θ ≪ 1, we have $\stackrel{\sim }{\lambda }=\lambda \sqrt{1+2\theta }\simeq \lambda (1+\theta )$ by Eq. (6), and the effective on rate defined in Eq. (8) becomes

$${\stackrel{\sim }{k}}_{\text{on}}=\frac{2k_{\text{on}}}{1+\sqrt{1+2\theta }}\simeq \frac{k_{\text{on}}}{1+\frac{\theta }{2}}=k_{\text{on}}{\left(1+\frac{k_{\text{on}}}{\lambda }\frac{{\sigma }_X^2}{\mu }\right)}^{-1}.$$ (13)

In [22], the input signal was taken to be a Poisson birth-death process for which the variance is equal to the mean ( ${\sigma }_X^2=\mu$), and the time scale has been normalized by putting the death rate equal to 1 (which amounts to setting λ = 1 here). These two constraints reduce Eq. (13) to k̃_on ≃ k_on/(1 + k_on), recovering the result we derived in [22]. The consistency indicates that our key findings are general and independent of the specific model we choose. The continuous diffusion model here, however, is more flexible as it allows the Fano factor to differ from 1, that is, ${\sigma }_X^2\ne \mu$.

For small θ, the stationary variance of Y(t) can be expanded as follows:

$$\begin{gathered} {\stackrel{\sim }{\sigma }}_Y^2=P_{\text{on}}(1-P_{\text{on}})\simeq {\sigma }_Y^2+\frac{\mu K_d(\mu -K_d)}{2{(\mu +K_d)}^3}\theta +O({\theta }^2), \\ ={\sigma }_Y^2+\frac{\mu -K_d}{{(\mu +K_d)}^3}\frac{k_{\text{off}}}{\lambda }{\sigma }_X^2+O\left({\sigma }_X^4\right), \end{gathered}$$ (14)

where ${\sigma }_Y^2\equiv \mu K_d/{(\mu +K_d)}^2$ is the output variance of the noiseless input model. Equation (14) indicates that the input noise ${\sigma }_X^2$ does not always contribute positively to the output variance ${\stackrel{\sim }{\sigma }}_Y^2$. In fact, the contribution is negligible when μ is near K_d and even negative for μ < K_d [Fig. 2(b)]. The explanation is that the input noise will effectively suppress the on transition rate and thus defines an effective equilibrium constant K̃_d which, as implied by Eq. (11) and shown in Fig. 2(c), is larger than the original dissociation constant K_d. Finally, with the effective on rate k̃_on, the correlation time of Y(t) becomes 𝒯̃_Y = (k̃_onμ + k_off)⁻¹, and can likewise be expanded as

$${\stackrel{\sim }{\mathcal{T}}}_Y={\mathcal{T}}_Y{\left(1+\frac{\stackrel{\sim }{\lambda }-\lambda }{\stackrel{\sim }{\lambda }+\lambda }\frac{\mu }{\mu +K_d}\right)}^{-1}\simeq {\mathcal{T}}_Y+\frac{1}{\lambda }\frac{{\sigma }_X^2}{{(\mu +K_d)}^2}.$$ (15)

Thus, 𝒯̃_Y increases almost linearly with the input noise in this small noise limit [Fig. 2(d)].

We now examine the “fast switch” limit where the switch flips much faster than the input reverts to its mean (𝒯_Y ≪ λ⁻¹). In this scenario, the initial input values {x_i,i = 1,2, …} for successive first-passage time intervals {τ̃_i,i = 1,2, …} are correlated due to the slow relaxation of X(t). This memory makes the sequence {τ̃_i,i = 1,2, …} correlated as well, as confirmed by our Monte Carlo simulations [Fig. 3(a)]. For the same reason, the autocorrelation function (ACF) of the output Y(t) exhibits two exponential regimes [Fig. 3(b)]: over short time scales, it is dominated by the intrinsic time 𝒯_Y of the switch; over long time scales, however, it decays exponentially at the input relaxation rate λ. This demonstrates that the long-term memory in X(t) is inherited by the output process Y(t). For a fast switch, the distribution P(τ̃ > t) is not fully exponential [Fig. 3(c)], though it decays exponentially at the rate k̃_onμ for large t, as predicted by the asymptotic Eq. (7). We can still use the closed-form solution of f (x,t) in Eq. (5) to fit the simulation data. Specifically, we calculate $P(\stackrel{\sim }{\tau }>t)={\int }_0^{\infty }f(x,t)P_{\stackrel{\sim }{\tau }}(x)dx$, where P_τ̃(x) is the distribution of the initial x for each switching event (defining the “first-passage” time τ̃) and can be obtained from the same Monte Carlo simulations. Clearly, this semianalytical approach [solid blue line in Fig. 3(c)] provides a nice fit to the simulation results (open circles).

FIG. 3.

The fast switch case. Here we choose λ = 0.0125, μ = 5, k_off = 0.1, k_on = 0.02, and θ = 10 (such that σ ≃ 0.28). (a) Sample autocorrelation function (ACF) of successive off-state time intervals. (b) Sample ACF of a simulated sample path of Y(t) in the semilogarithmic scale. (c) Distribution of the off-state intervals, P(τ̃ > t). Symbols are from Monte Carlo simulations and the solid blue line is the semianalytical prediction described in the main text. (d) Input distributions conditioned on the output.

Note that P_τ̃(x) ≠ P_s(x) due to memory effects in the fast switch limit. To show this, we illustrate the input-output interdependence by plotting the input distributions conditioned on the output state in Fig. 3(d). In fact, we have P(X = x|Y = 1) = P_τ̃(x). This is because x in P_τ̃(x) denotes $x=X(t_0^{+})$, where t₀ is the last time of off-transition; $X(t_0^{+})=X(t_0^{-})$ due to continuity and $Y(t_0^{-})=1$ by definition; and finally, all the on-state intervals are memoryless with the same Poisson rate k_off. This simple relation P (X = x|Y = 1) = P_τ̃(x) has been confirmed by our simulations (results not shown). It is also obvious from Fig. 3(d) that the expectation value of the input conditioned on Y = 1 is larger than when conditioned on Y = 0. Thus the mean of X(t) should lie in between, i.e., E[X|Y = 1] > E[X] > E[X|Y = 0], an interesting feature of the fast switch limit [22]. Since f (x,t) is a decreasing function of x and the initial input x is likely to be larger under P_τ̃(x) = P (X = x|Y = 1) than under the measure P_s(X = x), we should have

$$\begin{gathered} P(\stackrel{\sim }{\tau }>t)={\int }_0^{\infty }f(x,t)P_{\stackrel{\sim }{\tau }}(x)dx \\ <{\int }_0^{\infty }f(x,t)P_s(x)dx\simeq e^{-{\stackrel{\sim }{k}}_{\text{on}}\mu t}. \end{gathered}$$ (16)

The above inequality explains why the distribution of τ̃ is below the single exponential e^−k̃_onμt (dashed black line) in Fig. 3(c). All the above results [Figs. 3(a)–3(d)] indicate that the output process Y(t) is non-Markovian in the fast switch limit and, again, confirm the more general applicability of our findings reported in [22].

IV. DIFFUSION APPROXIMATION

In this paper, we have used the square-root diffusion (or CIR) process to model biochemical fluctuations. Here, we will show that the CIR process is well motivated and gives an excellent approximation to the birth-death process adopted in our earlier work [22]. We will also demonstrate that the non-negativity of the CIR process is advantageous as it avoids unphysical results.

We first argue that the CIR process is inspired by the fundamental nature of general biochemical processes. Many biochemical signals are subject to counteracting effects: synthesis and degradation, activation and deactivation, transport in and out of a cellular compartment, etc. As a result, these signals tend to fluctuate around their equilibrium values. A simple yet realistic model to capture these phenomena is the birth-death process, which we adopted to model biochemical noise in [22]. Remarkably, a birth-death process can be approximated by a Markov diffusion process [42]. The standard procedure is to employ the Kramers-Moyal expansion to convert the master equation into a Fokker-Planck equation (terminating after the second term). This connection allows the use of a Langevin equation to approximate the birth-death process. We will explain this in a more intuitive way.

Assume that the birth and death rates for the input signal X(t) are ν and λX(t). Then the stationary distribution of X(t) is a Poisson distribution, with its mean, variance, and skewness given by μ ≡ ν/λ, ${\sigma }_X^2=\mu$, and μ^−1/2, respectively. The corresponding Langevin equation that approximates this birth-death process is

$$\frac{dX(t)}{dt}=\nu -\lambda X(t)+\eta (t),$$ (17)

where the stochastic term η(t) represents a white noise with 〈η(t)〉 = 0 and δ correlation,

$$\langle \eta (t)\eta (t^{\prime })\rangle =(\nu +\lambda X)\delta (t-t^{\prime })=\lambda (\mu +X)\delta (t-t^{\prime }).$$ (18)

Physically, the Langevin approximation Eq. (17) holds when the copy number of molecules is large and the time scale of interest is longer than the characteristic time (λ⁻¹) of the birth-death process. Equation (18) indicates that the instantaneous variance of the noise term η(t) equals the sum of the birth rate ν and the death rate λX(t). An intuitive interpretation is that since both the birth and death events follow independent Poisson processes, the total variance of the increment X(t + Δt) − X(t) over a short time Δt must be equal to νΔt + λX(t)Δt. As μ ≡ ν/λ, we can rewrite the Langevin Eq. (17) as the following Itó-type stochastic differential equation (SDE):

$$dX(t)=\lambda [\mu -X(t)]dt+\sqrt{\lambda \mu +\lambda X(t)}d{W}_t,$$ (19)

which is similar to Eq. (1) introduced at the beginning. A transformation X′(t) ≡ X(t) + μ is convenient for exploiting our existing results, as the SDE for X′(t) is

$$d{X}^{\prime }=\lambda (2\mu -X^{\prime })dt+\sqrt{\lambda X^{\prime }}d{W}_t,$$ (20)

which is a particular CIR process. It is easy to check that the stationary variance of X′(t) equals μ, and so does the variance of X(t). In other words, we still have ${\sigma }_X^2=\mu$ for X(t) under Eq. (19). As a CIR process, X′ in equilibrium follows a Gamma distribution, the skewness of which is found to be μ^−1/2. Therefore, X = X′ − μ follows a “shifted” Gamma distribution with its mean, variance, and skewness given by μ, μ, and μ^−1/2, respectively, equal to those of the Poisson distribution. This matching of moments suggests that Eq. (19) is indeed a good approximation to the original birth-death process. However, X(t) in Eq. (19) can take negative values, because X = X′ − μ is bounded below by −μ due to its “shift” in distribution. This becomes a limitation of the Langevin approximation Eq. (17), which could fail if the noise is large (i.e., the number of molecules is small).

Under Eq. (19) for the input X(t), we can still evaluate the analog of Eq. (3):

$$f(x,t)=E^x\left[e^{-{\int }_0^t{k}_{\text{on}}X(s)ds}\right]=E^{x+\mu }\left[e^{-{\int }_0^t{k}_{\text{on}}{X}^{\prime }(s)ds}\right]e^{k_{\text{on}}\mu t},$$ (21)

where E^x+μ[⋯] denotes expectation over all possible sample paths of X′ over [0,t], conditioned on X′ (0) = x + μ. Since X′ follows the CIR process Eq. (20), the expectation E^x+μ[⋯] has an expression similar to Eq. (5). In fact, the survival probability f (x,t) in Eq. (21) equals

$${\left[\frac{\stackrel{\sim }{\lambda }{e}^{\lambda t/2}/sinh(\stackrel{\sim }{\lambda }t/2)}{\lambda +\stackrel{\sim }{\lambda }coth(\stackrel{\sim }{\lambda }t/2)}\right]}^{\alpha }exp\left[\frac{-2k_{\text{on}}(x+\mu )}{\lambda +\stackrel{\sim }{\lambda }coth(\stackrel{\sim }{\lambda }t/2)}+k_{\text{on}}\mu t\right],$$

with $\stackrel{\sim }{\lambda }\equiv \sqrt{{\lambda }^2+2k_{\text{on}}\lambda }$ and α= 4μ. At large t, this is

$$f(x,t)~exp\left[-\frac{k_{\text{on}}^{\prime }(x+\mu )}{\lambda }-(2k_{\text{on}}^{\prime }-k_{\text{on}})\mu t\right],$$ (22)

where $k_{\text{on}}^{\prime }\equiv 2k_{\text{on}}/(1+\sqrt{1+2{\theta }^{\prime }})$ and θ′ ≡ k_on/λ. Thus, the dwell time distribution behaves asymptotically as

$$P(\stackrel{\sim }{\tau }>t)~e^{-{\stackrel{\sim }{k}}_{\text{on}}\mu t},\text{where}{\stackrel{\sim }{k}}_{\text{on}}=2k_{\text{on}}^{\prime }-k_{\text{on}}.$$ (23)

For θ′ ≪ 1, the asymptotic rate above becomes

$${\stackrel{\sim }{k}}_{\text{on}}=\left(\frac{3-\sqrt{1+2{\theta }^{\prime }}}{1+\sqrt{1+2{\theta }^{\prime }}}\right)k_{\text{on}}\simeq \left(\frac{2-k_{\text{on}}/\lambda }{2+k_{\text{on}}/\lambda }\right)k_{\text{on}}.$$ (24)

The first equality above shows that k̃_on can be negative when θ′ > 4 or k_on > 4λ. This is a consequence of the possibility that X(t) becomes negative under Eq. (19).

When dealing with the Langevin approximation Eq. (17), one usually assumes that the input noise is small enough (given a large copy number) such that the random variable X could be replaced by its mean μ in Eq. (18). This results in an OU approximation:

$$dX(t)=\lambda [\mu -X(t)]dt+\sqrt{2v}d{W}_t,$$ (25)

which takes a Gaussian distribution in steady state with ${\sigma }_X^2=\mu$. Compared to the shifted Gamma distribution derived from Eq. (19), the Gaussian model of X(t) has zero skewness and is unbounded below. Thus, when μ is small, the OU approximation becomes an inappropriate choice. By the Feynman-Kac theorem, the survival probability f (x,t) under Eq. (25) satisfies

$$\frac{\partial f}{\partial t}=(\nu -\lambda x)\frac{\partial f}{\partial x}+\nu \frac{{\partial }^{2}f}{\partial x^2}-k_{\text{on}}xf,$$ (26)

which can also be exactly solved. We omit the solution here, but later will show that P[X(t) < 0] > 0 for the OU process will lead to k̃_on < 0 in certain regimes.

We can propose an alternative fix for the Langevin approximation, replacing the mean μ by its random counterpart X(t) in Eq. (18). This yields a CIR process:

$$dX(t)=\lambda [\mu -X(t)]dt+\sqrt{2\lambda X(t)}d{W}_t,$$ (27)

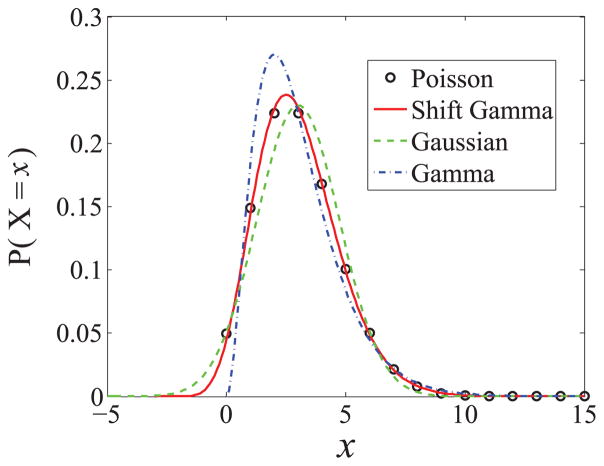
under which X(t) follows a Gamma distribution in steady state, with ${\sigma }_X^2=\mu$ as in all the previous diffusion approximations. The skewness in this model is found to be 2μ^−1/2, which is twice the skewness in the (birth-death) Poisson distribution. However, it is better than the OU model, which gives zero skewness. Figure 4 plots a comparison of the Poisson, Gamma, shifted Gamma, and Gaussian distributions, all satisfying ${\sigma }_X^2=\mu$. One can see that the shifted Gamma distribution, which follows from Eq. (19), gives the closest approximation to the (birth-death) Poisson distribution, while the Gamma and Gaussian distributions are both good enough to approximate the Poisson. Nonetheless, only the Gamma density from the CIR model is non-negative, like the original Poisson distribution.

FIG. 4.

Comparison of the Poisson, “shifted” Gamma, Gaussian, and Gamma distributions, all of which have the same mean μ = 3 and the same variance ${\sigma }_X^2=\mu$.

The diffusion approximations we have discussed so far, including Eqs. (1), (19), (25), and (27), are all special cases of the following general Itó SDE:

$$dX(t)=\lambda [\mu -X(t)]dt+\sqrt{{\sigma }_0^2+{\sigma }_1^{2}X(t)}d{W}_t.$$ (28)

Under Eq. (28), the survival probability f (x,t) satisfies

$$\frac{\partial f}{\partial t}=\lambda (\mu -x)\frac{\partial f}{\partial x}+\frac{1}{2}\left({\sigma }_0^2+{\sigma }_1^{2}x\right)\frac{{\partial }^{2}f}{\partial x^2}-k_{\text{on}}xf.$$ (29)

Again, a shortcut for solving Eq. (29) is to introduce $X^{\prime }\equiv X+{\sigma }_0^2/{\sigma }_1^2$, which will evolve as a CIR process. This will allow us to make use of the existing results and obtain a similar expression for f (x,t) as before. However, our main interest is the effective rate k̃_on in the asymptotic behavior of P(τ̃ > t) ≃ Ω exp(−k̃_onμt), where Ω is some constant. Inspired by Eqs. (7) and (22), we guess that when t is sufficiently large, f (x,t) ~ exp(−Ax − k̃_onμt), for some constant coefficients A and k̃_on (to be determined). Plugging this expression into Eq. (29) yields

$$-{\stackrel{\sim }{k}}_{\text{on}}\mu f=-A\lambda (\mu -x)f+\frac{1}{2}{A}^2\left({\sigma }_0^2+{\sigma }_1^{2}x\right)f-k_{\text{on}}xf,$$ (30)

which holds only when A and k̃_on jointly solve the following two algebraic equations:

$$A\lambda \mu -\frac{1}{2}{A}^2{\sigma }_0^2={\stackrel{\sim }{k}}_{\text{on}}\mu ,$$ (31)

$$A\lambda +\frac{1}{2}{A}^2{\sigma }_1^2=k_{\text{on}}.$$ (32)

Given ${\sigma }_1^2>0$, the solution of Eq. (32) is

$$A=\frac{-\lambda +\sqrt{{\lambda }^2+2k_{\text{on}}{\sigma }_1^2}}{{\sigma }_1^2}=\frac{2k_{\text{on}}}{\lambda +\sqrt{{\lambda }^2+2k_{\text{on}}{\sigma }_1^2}}.$$ (33)

Thus, by defining ${\theta }^{\prime }\equiv k_{\text{on}}{\sigma }_1^2/{\lambda }^2$, Eq. (33) becomes

$$A\lambda =\frac{2k_{\text{on}}}{1+\sqrt{1+2{\theta }^{\prime }}}\equiv k_{\text{on}}^{\prime }.$$ (34)

Eliminating A² in Eqs. (31) and (32), we find that

$${\stackrel{\sim }{k}}_{\text{on}}=k_{\text{on}}^{\prime }\frac{{\sigma }_0^2+\mu {\sigma }_1^2}{\mu {\sigma }_1^2}-k_{\text{on}}\frac{{\sigma }_0^2}{\mu {\sigma }_1^2}.$$ (35)

Clearly, when ${\sigma }_0^2=0$, Eq. (28) becomes a CIR process and Eq. (35) reduces to ${\stackrel{\sim }{k}}_{\text{on}}=k_{\text{on}}^{\prime }=2k_{\text{on}}/(1+\sqrt{1+2{\theta }^{\prime }})$, recovering our result in Sec. III. When ${\sigma }_0^2/{\sigma }_1^2=\mu$, Eq. (35) is ${\stackrel{\sim }{k}}_{\text{on}}=2k_{\text{on}}^{\prime }-k_{\text{on}}$, coinciding with Eq. (23).

Finally, if ${\sigma }_1^2=0$, the diffusion Eq. (28) becomes an OU process and A = k_on/λ by Eq. (32). In this case,

$${\stackrel{\sim }{k}}_{\text{on}}=k_{\text{on}}\left(1-\frac{k_{\text{on}}{\sigma }_0^2}{2\mu {\lambda }^2}\right)=k_{\text{on}}\left[1-\frac{k_{\text{on}}\mu }{\lambda }\left(\frac{{\sigma }_X^2}{{\mu }^2}\right)\right],$$ (36)

where ${\sigma }_X^2\equiv {\sigma }_0^2/(2\lambda )$ is the variance of the OU process. We can define θ in the same way as in Eq. (12), such that k̃_on = k_on(1 − θ/2) in Eq. (36). This becomes negative if θ > 2. It is again a consequence of the finite probability that X(t) takes negative values. Note that the OU approximation Eq. (25) is a particular OU process with ${\sigma }_X^2=\mu$. This leads to k̃_on = k_on(1 − k_on/λ) in Eq. (36). So for small θ or λ ≫ k_on, we have k̃_on ≃ k_on/(1 + k_on/λ), consistent with our result in [22].

In sum, the general diffusion process defined by Eq. (28) may take negative values with finite probability unless ${\sigma }_0^2=0$, which corresponds to the CIR process. Negative biochemical input is unrealistic and may lead to unphysical results (such as k̃_on < 0) if the input noise is large. For this reason, we conclude that the CIR process Eq. (1) is more suitable for modeling biochemical noise in the continuous framework. As shown, it is analytically tractable and possesses desirable statistical features, including stationarity, mean reversion, Gamma distribution, and a tunable Fano factor.

V. CONCLUSION

In this paper, we have extended our previous work on the role of noise in biological switching systems. We propose that a square-root diffusion process can be a more reasonable model for biochemical fluctuations than the commonly used OU process. We employ standard tools in stochastic processes to solve a well-defined fundamental biophysical problem. Consistent with our earlier results, we find that the input noise acts to suppress the input-dependent transitions of the switch. Our analytical results in this paper indicate that this suppression increases with the input noise level as well as the input correlation time. The statistical features uncovered in this basic problem can provide us with insights to understand various experimental observations in gene regulation and signal transduction systems. The current modeling framework may also be generalized to incorporate other biological features such as ultrasensitivity and feedbacks. Work along these lines is underway.