Avian photoreceptor patterns represent a disordered hyperuniform solution to a multiscale packing problem

Abstract

Optimal spatial sampling of light rigorously requires that identical photoreceptors be arranged in perfectly regular arrays in two dimensions. Examples of such perfect arrays in nature include the compound eyes of insects and the nearly crystalline photoreceptor patterns of some fish and reptiles. Birds are highly visual animals with five different cone photoreceptor subtypes, yet their photoreceptor patterns are not perfectly regular. By analyzing the chicken cone photoreceptor system consisting of five different cell types using a variety of sensitive microstructural descriptors, we find that the disordered photoreceptor patterns are “hyperuniform” (exhibiting vanishing infinite-wavelength density fluctuations), a property that had heretofore been identified in a unique subset of physical systems, but had never been observed in any living organism. Remarkably, the patterns of both the total population and the individual cell types are simultaneously hyperuniform. We term such patterns “multihyperuniform” because multiple distinct subsets of the overall point pattern are themselves hyperuniform. We have devised a unique multiscale cell packing model in two dimensions that suggests that photoreceptor types interact with both short- and long-ranged repulsive forces and that the resultant competition between the types gives rise to the aforementioned singular spatial features characterizing the system, including multihyperuniformity. These findings suggest that a disordered hyperuniform pattern may represent the most uniform sampling arrangement attainable in the avian system, given intrinsic packing constraints within the photoreceptor epithelium. In addition, they show how fundamental physical constraints can change the course of a biological optimization process. Our results suggest that multihyperuniform disordered structures have implications for the design of materials with novel physical properties and therefore may represent a fruitful area for future research.

I. INTRODUCTION

The purpose of a visual system is to sample light in such a way as to provide an animal with actionable knowledge of its surroundings that will permit it to survive and reproduce [1]. In most cases, this goal is achieved most effectively by a highly regular two-dimensional (2D) array of photoreceptors that evenly sample incoming light to produce an accurate representation of the visual scene. Classical sampling theory [2,3] as well as more recent studies [4–6] have demonstrated that the optimal arrangement of a 2D array of detectors is a triangular lattice (i.e., a hexagonal array). Indeed, modeling studies suggest that any deviation from a perfectly regular arrangement of photoreceptors will cause deterioration in the quality of the image produced by a retina [7]. Accordingly, many species have evolved an optimal sampling arrangement of their photoreceptors. For example, the insect compound eye consists of a perfect hexagonal array of photoreceptive ommatidia [8,9]. In addition, many teleost fish [10–12] and some reptiles [13] possess nearly crystalline arrangements of photoreceptors. These and other examples attest that a perfect or nearly perfectly ordered arrangement of photoreceptors can be realized in a biological system.

Diurnal birds have one of the most sophisticated cone visual systems of any vertebrate, consisting of four types of single cone (violet, blue, green, and red) which mediate color vision and double cones involved in luminance detection [14–16] (see Fig. 1). Despite the presence of numerous evolutionary specializations in the avian eye, the overall arrangement of bird cone photoreceptors is not perfectly ordered but rather is irregular [17,18]. The five avian cone types exist as five independent, spatial patterns, all embedded within a single monolayered epithelium. The individual cone patterns in the bird’s retina are arranged such that cones of one type almost never occur in the near vicinity of other cones of the same type [18]. In this way, the bird achieves a much more uniform arrangement of each of the cone types than would exist in a random (Poisson) pattern of points.

FIG. 1.

(Color online) Spatial arrangements of chicken cone photoreceptors. The leftmost panel shows a flatmount preparation of a post-hatch day 15 chicken retina with colored oil droplets within the inner segments of the five cone photoreceptor types. Size bar = 10 µm. The additional panels (from left to right) depict the same field of view under illumination with ultraviolet, blue, and green light, respectively. Oil droplet autofluorescence permits subtype classification of the individual photoreceptor cells and determination of their spatial coordinates. These figures derive from Ref. [18].

Given the utility of the perfect triangular-lattice arrangement of photoreceptors for vision [7], the presence of disorder in the spatial arrangement of avian cone patterns is puzzling. It is crucial to ascertain whether the apparent “disordered” photoreceptor arrangements correspond to a different optimal solution because of constraints, such as cell size polydispersity, that are not present in the aforementioned insect retinas. By analyzing the chicken cone photoreceptor system using a variety of sensitive microstructural descriptors that arise in statistical mechanics and particle-packing theory [19], we show here that the avian system possesses a remarkable type of correlated disorder at large length scales known as hyperuniformity [20], which has heretofore not been observed in a living organism. A disordered hyperuniform many-body system is an exotic state of matter that behaves like a perfect crystal or quasicrystal in the manner in which it suppresses large-scale density fluctuations and yet, like a liquid or glass, is statistically isotropic with no Bragg peaks. Moreover, in a departure from any known physical system, the photoreceptor patterns of both the total population and the individual cell types are simultaneously hyperuniform, which we term multihyperuniformity. We subsequently determine effective interactions between the photoreceptors on multiple length scales that could possibly explain their unusual disordered hyperuniform state. Specifically, we consider two types of interactions that have competing effects in determining the degree of order in the system. Indeed, we show via computer simulations that the local-energy minimizing configurations of such a many-particle interacting system quantitatively capture, with high accuracy, the unique spatial characteristics, including multihyperuniformity. The fact that the aforementioned competing interactions lead to disordered hyperuniform systems suggests that the photoreceptor patterns may represent the most uniform sampling arrangement attainable in the avian system due to intrinsic packing constraints associated with the photoreceptor cells.

The rest of the paper is organized as follows: In Sec. II, we provide definitions of fundamental concepts used in our analysis including various statistical microstructural descriptors, order metrics, as well as the concept of hyperuniformity. In Sec. III, we quantitatively investigate structural characteristics of avian photoreceptor patterns containing multiple cell species and show that both the overall pattern and the arrangements of individual species are hyperuniform. In Sec. IV, we determine the effective interactions between the photoreceptors and devise a unique multiscale packing model incorporating such interactions. We show that our multiscale packing model can lead to point configurations that are virtually indistinguishable from the actual photoreceptor arrangements. In Sec. V, we provide concluding remarks.

II. DEFINITIONS AND FUNDAMENTAL CONCEPTS

Before presenting our analysis of the avian photoreceptor system, we first briefly review the “hyperuniformity” concept and its quantification, which plays a central role in this paper. In addition, we introduce the order metrics that will be employed to characterize the avian patterns.

A. Hyperuniform systems

The ensemble-averaged structure factor of infinite point configurations in d-dimensional Euclidean space at number density ρ is defined via

$$S(\mathbf{k})=1+\rho \stackrel{\sim }{h}(\mathbf{k}),$$ (1)

where h̃(k) is the Fourier transform of the total correlation function h(r) = g₂(r) − 1 and g₂(r) is the pair-correlation function of the system. Note that definition (1) implies that the forward scattering contribution to the diffraction pattern is omitted. For statistically homogeneous and isotropic systems, the focus of this paper, g₂ depends on the radial distance r ≡ |r| between the points (cell centers) as well as the number density ρ. In two dimensions, the quantity ρg₂(r)2πr dr is proportional to the conditional probability of finding a cell center at a distance between r and r + dr given that a cell center is at the origin, where ρ is the number of cell centers per unit area.

The small-k behavior of the structure factor S(k) encodes information about large-scale spatial correlations in the system and in the limit k → 0 determines whether the system is hyperuniform. Specifically, an infinite point configuration in d-dimensional Euclidean space is hyperuniform if

$$\underset{k\to 0}{\text{lim}}S(k)=0,$$ (2)

which implies that the infinite-wavelength density fluctuations of the system (when appropriately scaled) vanish [20].

For computational purposes, the structure factor S(k) for a given finite point configuration can be obtained directly from the positions of the points r_j [21], i.e.,

$$S(\mathbf{k})=\frac{1}{N}{|\sum _{j=1}^N\text{exp}(i\mathbf{k}·{\mathbf{r}}_j)|}^2(\mathbf{k}\ne \mathbf{0}),$$ (3)

where N is the total number of points in the system (under periodic boundary conditions) and k is the wave vector. Note that the forward scattering contribution (k = 0) in (3) is omitted, which makes relation (3) completely consistent with the definition (1) in the ergodic infinite-system limit. For statistically homogeneous and isotropic systems, the focus of this paper, the structure factor S(k) only depends on the magnitude of the scalar wave number k = |k| = 2πn/L, where n = 0, 1, 2 … and L is the linear size of the system.

A hyperuniform point configuration has the property that the variance in the number of points in an observation window Ω grows more slowly than the volume of that window [20]. In the case of a spherical observation window of radius R, this definition implies that the local number variance σ²(R) grows more slowly than R^d in d dimensions. The expression for the local number variance of a statistically homogeneous point configuration in a spherical observation window is given exactly by

$${\sigma }^2(R)=\rho \upsilon (R)[1+\rho {\int }_{{ℝ}^d}h(\mathbf{r})\alpha (\mathbf{r};R)d\mathbf{r}],$$ (4)

where υ(R) is the volume of a spherical window of radius R and α(r; R) is the scaled intersection volume, i.e., the intersection volume of two spheres of radius R separated by a distance r divided by the volume of a sphere υ(R). We remark that the average number of points in an observation window is 〈N(R)〉 = ρυ(R) for any statistically homogeneous point configuration.

It has been shown that the number variance (4), under certain conditions, admits the following asymptotic scaling [20]:

$${\sigma }^2(R)=2^d\varphi \{A{\left(\frac{R}{D}\right)}^d+B{\left(\frac{R}{D}\right)}^{d-1}+𝒪[{\left(\frac{R}{D}\right)}^{d-3}\left]\right\},$$ (5)

where

$$A=1+\rho {\int }_{{ℝ}^d}h(\mathbf{r})d\mathbf{r}=\underset{\Vert \mathbf{k}\Vert \to 0}{\text{lim}}S(\mathbf{k}),$$ (6)

and D is a characteristic microscopic length associated with the point configuration (e.g., the average nearest-neighbor distance between the points). Clearly, when the coefficient A = 0, i.e., lim_k→0 S(k) = 0 satisfies the requirements for hyperuniformity. The relation in (6) then implies that hyperuniform point patterns do not possess infinite-wavelength density fluctuations (when appropriately scaled) and hence from (5) the number variance scales as the surface area of the window for large R, i.e., σ²(R) ~ R^d−1 in the large-R limit. This result is valid for all periodic point patterns (including perfect crystals), quasicrystals, and disordered systems in which the pair-correlation function g₂ decays to unity exponentially fast [20]. The degree to which large-scale density fluctuations are suppressed enables one to rank order crystals, quasicrystals, and special disordered systems [20,21]. Disordered hyperuniform structures can be regarded as new states of disordered matter in that they behave more like perfect crystals or quasicrystals in the manner in which they suppress density fluctuations on large length scales, and yet are also like liquids and glasses in that they are statistically isotropic structures with no Bragg peaks. Thus, hyperuniform disordered materials possess a “hidden order” that is not apparent on short length scales.

For disordered hyperuniform systems with a total correlation function h(r) that does not decay to zero exponentially fast, other dependencies of the number variance on R may be observed. For example, it is known that if S(k) for k → 0 or, equivalently, if the total correlation function h ~ −r^−(d+1) for large r, then σ²(R) ~ (a₀ ln R + a₁)R^d−1. More generally, for any reciprocal power law,

$$S(k)~k^{\alpha }(k\to 0)$$ (7)

or, equivalently,

$$h(r)~-\frac{1}{r^{d+\alpha }}(r\to +\infty ),$$ (8)

one can observe a number of different kinds of dependencies of the asymptotic number variance σ² on the window radius R for R → ∞ [20–22]:

$${\sigma }^2(R)~\{\begin{array}{cc}\hfill R^{d-1}\text{ ln }R,\hfill & \hfill \alpha =1\hfill \\ \hfill R^{d-\alpha },\hfill & \hfill \alpha <1\hfill \\ \hfill R^{d-1},\hfill & \hfill \alpha >1.\hfill \end{array}$$ (9)

Note that in all cases, the number variance of a hyperuniform point pattern grows more slowly than R^d.

B. Order metrics

The local bond-orientational-order metric q₆ is defined as [23]

$$q_6=|\frac{1}{N_b}\sum _j\sum _k\text{exp}(6i{\theta }_{\mathit{\text{jk}}})|,$$ (10)

where j runs over all cells in the system, k runs over all neighbors of cell j, θ_jk is the angle between some fixed reference axis in the system and the bond connecting the centers of cells j and k, and N_b is the total number of such bonds in the system. This quantity indicates the degree of orientational order in the local arrangement of the immediate neighbors of a cell and it is maximized (i.e., q₆ = 1) for the perfect hexagonal arrangement.

To characterize translational order of a configuration, we use the following translation order metric T introduced in Ref. [24] and further applied in Ref. [25]:

$$T=\frac{1}{{\eta }_c}{\int }_0^{{\eta }_c}|g_2(r)-1|\mathit{\text{dr}}=\frac{1}{{\eta }_c}{\int }_0^{{\eta }_c}|h(r)|\mathit{\text{dr}},$$ (11)

where g₂(r) is the pair-correlation function, h(r) = g₂(r) − 1 is the total correlation function, and η_c is a numerical cutoff determined by the linear size of the system. The translational order metric measures the deviation of the spatial arrangement of cell centers in a pattern from that of a totally disordered system (i.e., a Poisson distribution of points). The greater the deviation from zero, the more ordered is the point configuration.

III. STRUCTURAL PROPERTIES OF EXPERIMENTALLY OBTAINED PHOTORECEPTOR PATTERNS

The chicken retina contains five different cone cell types of different sizes: violet, blue, green, red, and double. Each cell type of this multicomponent system is maximally sensitive to visible light of a different wavelength. The spatial coordinates of each cell can be determined by the presence of a colored oil droplet in the cell’s inner segment (Fig. 1). Since the oil droplets used to identify the locations of individual photoreceptors are not always in exactly the same plane [18], pairs of real photoreceptors sometimes appear to be closer to one another than they are in actuality and in the simulations. In addition, the original slightly curved retina epithelium was flattened for imaging purposes [18]. These effects introduce small errors in the intercell small-distance behavior but do not affect the overall statistics, especially on large length scales. The spatial coordinate data sets of post-hatch day 15 chicken (Gallus gallus) cone photoreceptors were obtained from a published study [18]. Each data set contains approximately 4430 photoreceptors, and the average number of violet, blue, green, red, and double species are, respectively, 350, 590, 880, 670, and 1840. To clearly illustrate the photoreceptor patterns of different species, only a portion of the entire system is shown in Fig. 2. We compute a variety of the associated statistical structural descriptors and order metrics to quantify the degree of spatial regularity (or disorder) of the cell arrangements.

FIG. 2.

(Color online) Experimentally obtained configurations representing the spatial arrangements of chicken cone photoreceptors. Upper panels: The configurations shown from left to right, respectively, correspond to violet, blue, green species. Lower panels: The configurations shown from left to right, respectively, correspond to red, double species, and the overall pattern.

A. Disordered hyperuniformity

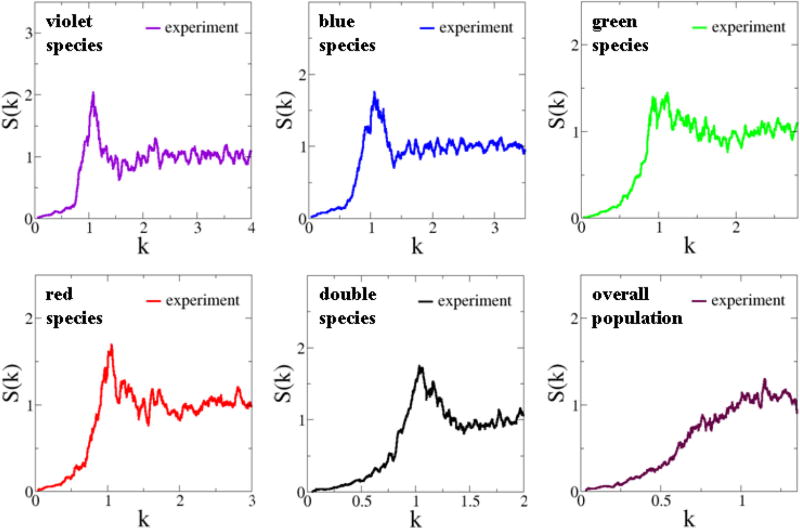
As discussed in Sec. II B, a point pattern is hyperuniform if the number variance σ²(R) within a spherical sampling window of radius R (in d dimensions) grows more slowly than the window volume for large R, i.e., more slowly than R^d [20]. The property of hyperuniformity can also be ascertained from the small wave number behavior of the structure factor, i.e., S(k = 0) = 0 of the pattern [20], which encodes information about large-scale spatial correlations (see Sec. II B for details). We find that S(k) for the cell configurations associated with both the total population and the individual photoreceptor species are hyperuniform and each of these structure factors vanishes linearly with k as k tends to zero, i.e., S(k) ~ k (k → 0) (see Fig. 3). As discussed in Sec. II B [cf. Eq. (9)], such a linear behavior indicates a power-law decay for large-r values in the pair-correlation function [i.e., g₂(r) − 1 ~ − 1/r³] instead of an exponential decay and therefore quasi-long-range correlations in the system. We will elaborate on this point in the ensuing discussion.

FIG. 3.

(Color online) Structure factors S(k) of the experimentally obtained point configurations representing the spatial arrangements of chicken cone photoreceptors. The experimental data were obtained by averaging 14 independent patterns. The estimated values of S(k = 0) by extrapolation for violet, blue, green, red, double, and the overall population in the actual pattern are respectively given by 2.11 × 10⁻³, 6.10 × 10⁻⁴, 1.06 × 10⁻³, 5.72 × 10⁻⁴, 1.38 × 10⁻⁴, and 1.13 × 10⁻³.

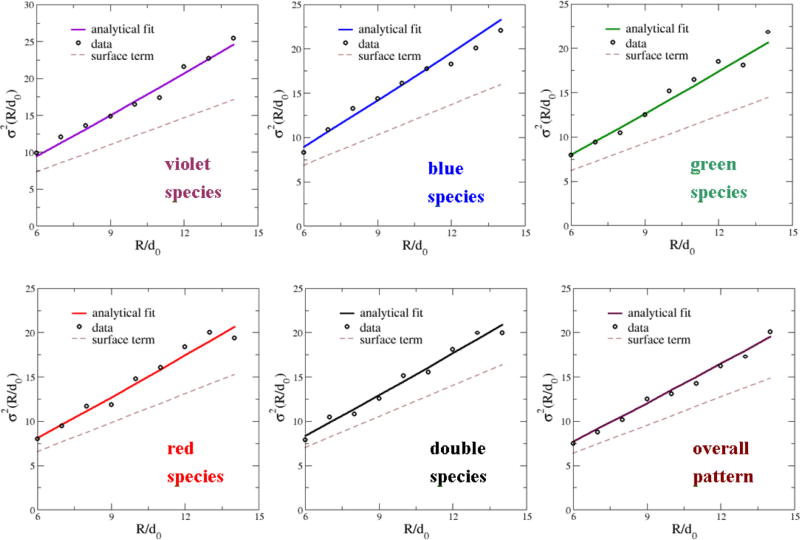
We have directly computed the number variance σ²(R) for the individual and overall patterns and verified that they are also consistent with hyperuniformity, i.e., the “volume term” in σ²(R) is several orders of magnitude smaller than the other terms [cf. Eq. (5)]. Specifically, for each R value, 2500 windows are randomly placed in the system without overlapping the system boundary. The finite system size L imposes an upper limit on the largest window size, which is chosen to be R_max = L/2 here. Figure 4 shows the experimental data as well as the associated fitting functions of the form

$${\sigma }^2(R)={\mathit{\text{A R}}}^2+\mathit{\text{B R}}\text{ln}(R)+\mathit{\text{C R}},$$ (12)

where A = S(k = 0) and B, C > 0. Note that in the plots, the window size R is normalized by the corresponding nearest-neighbor distance d₀ for each species. Also shown in each plot is the corresponding “surface term” C R for purposes of comparison. The numerical values of the fitting parameters for both the overall pattern and the individual species are given in Table I. It can be clearly seen that the values of the parameter A are several orders of magnitude smaller than the other two parameters, indicating that the associated patterns are effectively hyperuniform. These values are also consistent with the numerical values of S(k = 0) obtained by directly fitting S(k) for small-k values [26].

FIG. 4.

(Color online) The number variance σ²(R) associated with the photoreceptor patterns in chicken retina as well as the associated fitting function of the form σ²(R) = A R² + B R ln(R) + C R. We found that the values of the parameter A are several orders of magnitude smaller than the other two parameters, indicating that the associated patterns are effectively hyperuniform. Also shown in each plot is the “surface term” C R for purposes of comparison. The window radius R is normalized with respect to the mean nearest-neighbor distance d₀ of the corresponding point configurations.

TABLE I.

The numerical values of the fitting parameters for both the overall pattern and the individual species.

	Violet	Blue	Green	Red	Double	Overall
A	2.53 × 10−4	9.24 × 10−4	1.07 × 10−3	1.77 × 10−3	4.46 × 10−3	1.93 × 10−3
B	0.203	0.198	0.169	0.146	0.122	0.127
C	1.22	1.14	1.03	1.09	1.17	1.06

The fact that the photoreceptor patterns display both overall hyperuniformity and homotypic hyperuniformity implies that if any subpopulation of the individual species is removed from the overall population, the remaining pattern is still hyperuniform. We term such patterns multihyperuniform because distinct multiple subsets of the overall point pattern are themselves hyperuniform. These are highly unusual and unique structural attributes. Until now, the property of overall hyperuniformity was identified only in a special subset of disordered physical systems [27–38]. The chicken photoreceptor patterns provides the first example of a disordered hyperuniform biological system. In addition, the photoreceptor patterns possess quasi-long-range (QLR) correlations as indicated by the linear small-k behavior in S(k). We will elaborate on these points in Sec. V.

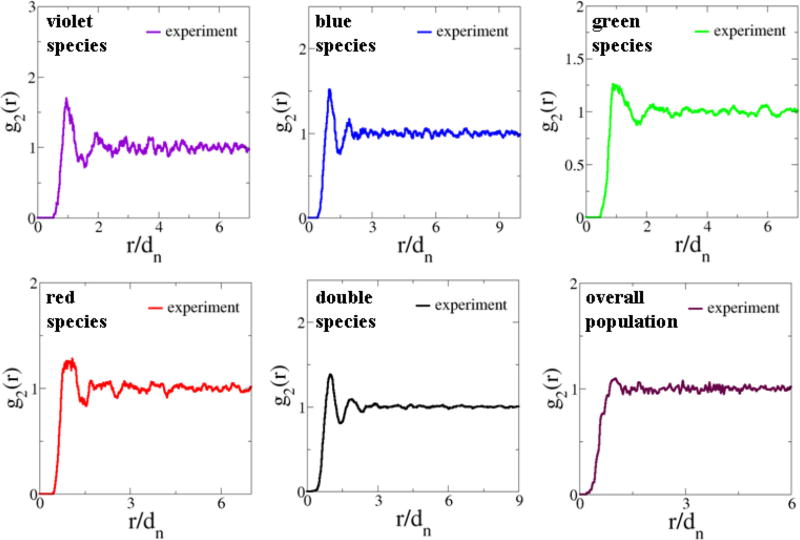
B. Pair-correlation functions

We find that each cell is associated with an effective exclusion region (i.e., an area in 2D) with respect to any other cells, regardless of the cell types. The size of these exclusion regions roughly corresponds to the size of the cells themselves [18]. In addition, cells belonging to the same subtype (i.e., like-cells) are found to be mutually separated from one another almost as far as possible, leading to a larger effective exclusion region associated with like-cells of each species. The exclusion effects are quantitatively captured by the associated pair-correlation functions (Fig. 5). The hard-core exclusion effect is manifested in g₂(r) as an interval of r for which g₂(r) = 0 (i.e., an “exclusion gap”) and g₂(r) approaches its large-r asymptotic value of unity very quickly, indicating the absence of any long-range spatial ordering. This is to be contrasted with ordered systems, such as crystals, whose pair-correlation functions are composed of individual Dirac delta functions at specific r values.

FIG. 5.

(Color online) Pair-correlation functions g₂(r) of the experimentally obtained point configurations representing the spatial arrangements of chicken cone photoreceptors. The experimental data were obtained by averaging 14 independent patterns. The distance is rescaled by the average nearest-neighbor distance d_n in the system.

C. Order metrics

A bond-orientational order metric q₆ [23] and a translational order metric T [25] were used next to quantify the degree of spatial regularity in the photoreceptor patterns (see Table II), each of which are maximized by the triangular lattice and minimized by a spatially uncorrelated point pattern. Interestingly, the q₆ and T values for the total population are close to the corresponding values for polydisperse hard-disk packings we obtained, implying that the local cell exclusion effect plays a primary role in determining the overall pattern. In contrast, the higher-q₆ and -T values for individual cell species suggest that like-cells interact with one another on a length scale larger than the size of a single cell, which tends to increase the degree of order in the arrangements of like-cells.

TABLE II.

Bond-orientational and translational order metrics q₆ and T, respectively, of the chicken photoreceptor patterns. The experimental data were obtained by averaging 14 independent patterns.

Species	q6	T
Violet	0.150	0.304
Blue	0.158	0.411
Green	0.130	0.278
Red	0.147	0.254
Double	0.184	0.390
All	0.058	0.096

From a functional point of view, photoreceptor cells of a given type maximize their sampling efficiency when arranged on an ordered triangular lattice, as in the case of the compound eye of insects [8,9]. Importantly, the triangular lattice has been shown to be the most hyperuniform pattern [20], i.e., it minimizes the large-scale density fluctuations among all 2D patterns. However, this most hyperuniform pattern may not be achieved if other constraints (e.g., cell size polydispersity) are operable. We therefore hypothesize that the disordered hyperuniformity of avian photoreceptor patterns represents a compromise between the tendency of the individual cell types to maximize their spatial regularity and the countervailing effects of packing heterotypic cell types within a single epithelium, which inhibits the spatial regularity of the individual cell types. In other words, the avian photoreceptors are driven to achieve the most “uniform” spatial distribution subject to heterotypic cell packing constraints.

IV. COMPUTATIONAL MODEL THAT YIELDS MULTIHYPERUNIFORM PATTERNS

Our initial attempt to model the avian photoreceptor cell patterns employed classic packing models of polydisperse hard disks that are driven to their “jammed states” [19]. However, these models failed to generate patterns with multihyperuniformity. Such standard jamming models involving interactions on a single length scale are insufficient to represent the two competing effects leading to the photoreceptor patterns and motivated us to develop a unique multiscale packing model as described in the following.

In the experimental data representing the spatial arrangements of chicken cone photoreceptors, each cell is represented by a point. We refer to these points as “cell centers,” although they may not correspond to the actual geometrical centers of the cells.

In order to modify a simple hard-core interaction, we consider two types of effective cell-cell interactions: isotropic short-range hard-core repulsions between any pair of cells and isotropic long-range soft-core repulsions between pairs of like-cells (i.e., cells of the same subtype). The multiscale nature of the model results from the multiple length scales involved in these interactions for different species, as we discuss now. The strength of the hard-core repulsion is characterized by the radius $R_h^i$ of a hard-disk exclusion region associated with a cell type i. This interaction imposes a nonoverlap constraint such that the distance between the cells i and j can not be smaller than $(R_h^i+R_h^j)$, which mimics the physical cell packing constraint. In this regard, $R_h^i$ will also be referred to as the radius of a cell i in the ensuing discussions. The relative magnitudes of $R_h^i$ are estimated from an electron micrograph showing photoreceptor cell packing at the level of the inner segment [17]. The characteristic radius R_s of the soft-core repulsion is associated with the mean nearest-neighbor distance of the cells of the same type. Specifically, the pair potential between two like-cells is given by

$$E(r)=\{\begin{array}{cc}\hfill \frac{\alpha }{\beta +1}{(2R_s-r)}^{\beta +1},\hfill & \hfill r\le 2R_s\hfill \\ \hfill 0,\hfill & \hfill r>2R_s\hfill \end{array}$$ (13)

where the parameters α > 0 and β > 0 set the scale of the interaction energy [39]. In our simulations, we require that the value of R_s be uniquely determined by the associated cell number density ρ, i.e., $R_s=\frac{1}{2}\sqrt{2/[\sqrt{(3)}\rho ]}$. This implies that a system composed of cells of the same type (i.e., a single-component system) interacting via a pair potential given by Eq. (13) at number density ρ (i.e., the number of cells per unit area) possesses the triangular-lattice ground state, i.e., an arrangement associated with a minimal total energy (sum of the total interaction energy between any pairs of like-cells). In other words, when the total energy in a single-component system is reduced to its minimal value (e.g., zero), sufficiently slowly from an arbitrary initial configuration, the cells will reorganize themselves into a triangular-lattice arrangement.

When the system contains multiple species, the hard-and soft-core interactions represent two competing effects in determining the packing arrangement of the cells (see Fig. 6). Specifically, the polydisperse hard-disk exclusion regions induce geometrical frustration in the packing, i.e., in this five-component system, it is not possible for the subset of disks with the same size, surrounded by disks with different sizes to be arranged on a perfect triangular lattice. On the other hand, the long-range soft interaction between like species tends to drive the cells of the same type to arrange themselves on a perfect triangular lattice. Note that although the relative magnitudes of $R_h^i$ for different species (i.e., the ratio between any two $R_h^i$) are fixed, the actual values of $R_h^i$ are variable and used as a tuning parameter in our model. As stated above, the ratios between $R_h^i$ are estimated from a previously published study [17]. Specifically, the relative sizes of the violet, blue, green, red, and double species are 1.00, 1.19, 1.13, 1.06, and 1.50, respectively. Given the number of cells of each species, the values of $R_h^i$ can be uniquely determined from the packing fraction ϕ of the cells (i.e., the fraction of space covered by the cells) and vice versa:

$$\varphi =\frac{1}{A}\sum _i{N}_i\pi {(R_h^i)}^2,$$ (14)

where N_i is the number of cells of species i and A is the area of the system.

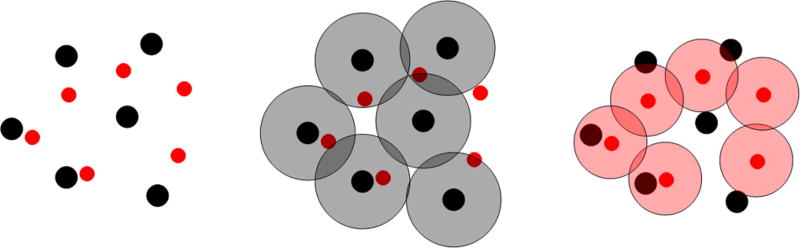
FIG. 6.

(Color online) Illustration of the hard- and soft-core interactions in a two-species system containing black and red (or light gray in the print version) cells. The left panel shows the exclusion regions (circular disks with two distinct sizes) associated with the two types of cells, which are proportional to the actual sizes of the cells. The black cells have a larger exclusion region than the red cells. The middle panel illustrates the soft-core repulsive interaction (large concentric overlapping circles of the solid black disks) between the black cells. Such a repulsive interaction will drive the black cells to arrange themselves in a perfect triangular lattice in the absence of other species. The right panel illustrates the soft-core repulsive interaction (large concentric overlapping circles of the solid red disks) between the red cells.

Our Monte Carlo algorithm, which involves iterating “growth” and “relaxation” steps, works as follows:

1. Initialization. In the beginning of the simulation, cell centers of each species are generated in a simulation box using the random-sequential-addition (RSA) process [19]. Specifically, for each species i, N_i cell centers are randomly generated such that these cell centers are mutually separated by a minimal distance μR_s (0 < μ < 1). In addition, the newly added cell can not overlap any existing cells in the box (determined by the hard-core radius R_s), regardless of cell types. The initial covering fraction ϕ_I associated with the hard-core exclusion regions is determined by $R_h^i$ via Eq. (14), and is about 80% of the RSA saturation density [19].

2. Growth step. At each stage n, the cells are allowed to randomly move a prescribed maximal distance (~0.25 $R_h^i$) and direction such that no pairs of cells overlap. After a certain number (≈1000) of such random movements for each cell, the radius $R_h^i$ of each cell is increased by a small amount such that the size ratios of the cells remain the same. This leads to an increase of the packing fraction ϕ_n at this stage by an amount of about 1%–3%. Note that in this “growth” step, the long-range soft interactions between the like-cells are turned off.

3. Relaxation step. At the end of the “growth” step, the soft interactions are then turned on, and the cells are allowed to relax from their current positions to reduce the total system energy subject to the nonoverlap condition. The steepest descent method is used to drive the system to the closest local energy minimum (i.e., the inherent structure [19]) associated with the starting configuration. This is referred to as the “relaxation” process.

4. Statistics. After the relaxation process, structural statistics of the resulting configuration of cell centers are obtained and compared to the corresponding experimental data. To ensure that the simulations match the data for the pair statistics to the best extent possible, we introduce a deviation metric Δ. Specifically, Δ is the normalized sum of the squared differences between the simulated and experimental S(k) and g₂(r) associated with the simulated and actual patterns, i.e.,

   $$\mathrm{\Delta }=\frac{1}{n_S}\sum _i^{n_S}\sum _r{[g_2^{(i)}(r)-{\overline{g}}_2^{(i)}(r)]}^2+\frac{1}{n_S}\sum _i^{n_S}\sum _k{[S^{(i)}(k)-{\overline{S}}^{(i)}(k)]}^2,$$ (15)

   where n_S = 6 is the total number of species including both the five individual species and the overall pattern, $g_2^{(i)}(r)$ and S⁽ⁱ⁾(k) are the simulated functions associated with species i, and ${\overline{g}}_2^{(i)}(r)$ and S̄⁽ⁱ⁾(k) are the corresponding experimentally measured functions.

5. The growth and relaxation steps described in the bullet items (2) and (3), respectively, are repeated until ϕ_n reaches a prescribed value ϕ_F. Specifically, the configuration obtained by relaxation at stage n is used as the starting point for the growth step at stage n + 1. The best simulated pattern (i.e., that with the smallest deviation metric Δ_min) and the associated ϕ* value are then identified.

At a given packing fraction ϕ (or equivalently a set of $R_h^i$), the polydispersity of the exclusion regions associated with different species and the resulting nonoverlap constraints frustrate the spatial order in the system. For example, the long-range soft interaction drives a single-species system to the triangular-lattice arrangement in the absence of other species. On the other hand, for any ϕ > 0, it is impossible for cells of a particular species, surrounded by cells of other species, to sit on a perfect triangular lattice [18]. Therefore, the disordered point configurations obtained by minimizing the energy associated with the soft repulsive interactions subject to the hard-core packing constraints are the local energy minima (i.e., inherent structures) of the system. The extent to which the structure deviates from that of a perfect triangular lattice (i.e., global energy minimum) is determined by the parameter ϕ (or, equivalently, $R_h^i$). Therefore, by tuning this parameter in our algorithm, one can, in principle, generate a continuous spectrum of configurations of cell centers with varying degrees of spatial order (see Appendix). Note that in the limit $R_h^i\to 0$, triangular-lattice arrangements for individual species are accessible again and the resulting configuration is a superposition of five triangular-lattice arrangements of the cell centers.

We note that the order of the aforementioned growth and relaxation steps can be interchanged without affecting the final configuration. In addition, instead of starting from a disordered RSA arrangement of cell centers as described above, we have also used ordered initial configurations (i.e., superposition of triangular-lattice arrangements), leading to the same configuration at a given number density ρ. However, the initial packing density ϕ_I associated with ordered initial configurations is very low and, thus, it is computationally inefficient to start from such initial configurations. By tuning the “strength” of the hard-core interactions via the packing fraction associated with the exclusion regions, our multiscale packing model enables us to produce disordered point configurations with various degrees of hyperuniformity, examples of which are provided in the Appendix for a three-component system for illustrative purposes.

A. Modeling avian photoreceptor system via multiscale particle packing

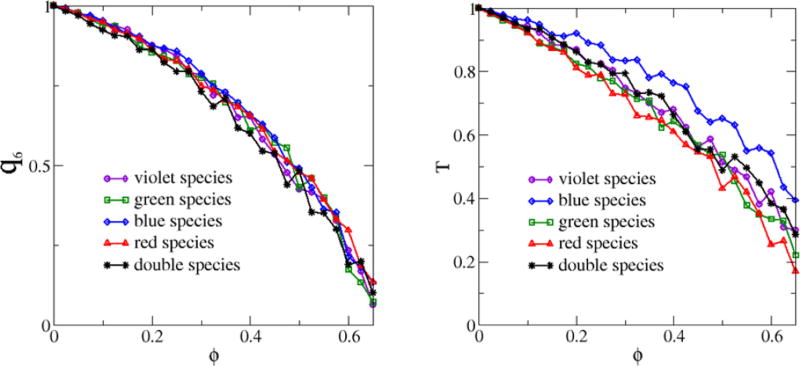
By using the multiscale packing model, we were able to accurately reproduce the unique features of the native avian photoreceptors. We modeled the aforementioned two competing effects as two types of effective interactions between the cells: a long-range soft-core repulsion between the cells of the same type (that would lead to an ordered triangular-lattice arrangement in the absence of packing constraints) and a short-range hard-core repulsion (with polydisperse exclusion regions associated with different cell species) between any pair of cells that frustrates spatial ordering in the system. Given the sizes of the hard-core exclusion regions associated with each cell species (or equivalently the packing fraction ϕ of the exclusion regions), the system is allowed to relax to a state that is a local energy minimum for the long-range soft-core repulsive interactions between like-species. Such long-range interactions would drive each of the five cell species in the multicomponent system to the associated triangular-lattice arrangement (global energy minimum) in the absence of the hard-core repulsions. As we increase the strength of the hard-core repulsions by increasing ϕ, the degree of order in the system, which is quantified by the order metrics q₆ and T, decreases (see Fig. 7). It is important to emphasize that these disordered hyperuniform avian photoreceptor patterns are not simple random perturbations of a triangular-lattice pattern. Statistically equivalent disordered hyperuniform patterns have also been obtained from disordered initial configurations (e.g., RSA packings). Thus, the unique structural features in these patterns are not attributed to particular initial configurations but rather arise from the two competing effects, which are well captured by our multiscale packing model.

FIG. 7.

(Color online) Left panel: The bond-orientational order metric q₆ of the individual species as a function of the packing fraction ϕ associated with the exclusion regions. Right panel: The translational order metric T of the individual species as a function of the packing fraction ϕ associated with the exclusion regions.

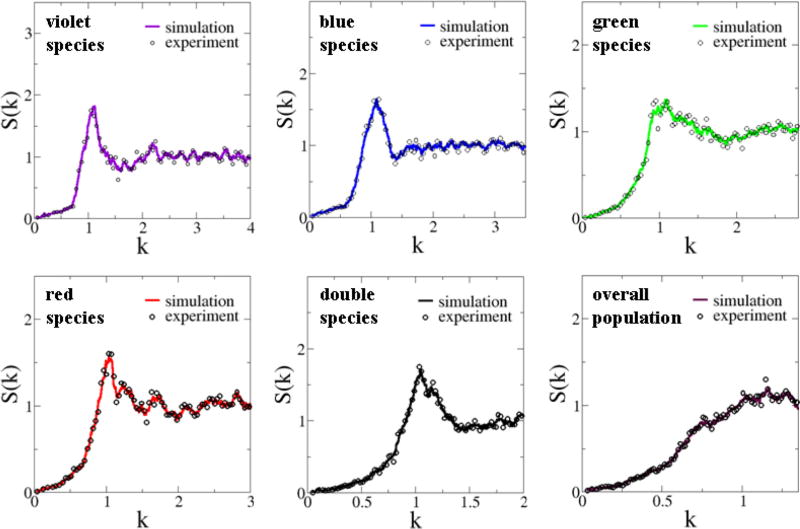
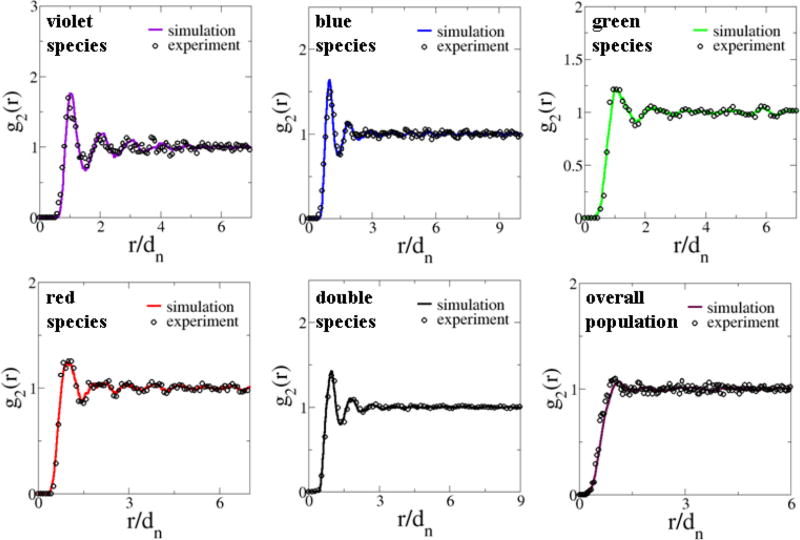
The simulation box contains 2600 cell centers and the numbers of violet, blue, green, red, and double species are, respectively, 210, 355, 530, 405, and 1100. The relative sizes of the violet, blue, green, red, and double species are 1.00, 1.19, 1.13, 1.06, and 1.50, respectively. The initial packing fraction associated with the hard cores is ϕ_I = 0.45 and the simulation stops at ϕ_F = 0.7. At ϕ ≈ 0.58, the resulting configurations (see Fig. 8) are virtually indistinguishable from the actual photoreceptor patterns, as quantified using a variety of descriptors. Specifically, the associated structure factors (see Fig. 9) and pair-correlation functions (see Fig. 10) match the experimental data very well, as quantified by the minimum deviation metric value of Δ_min ≈ 0.4 [cf. Eq. (15)]. We note that the major contributions to Δ_min are the large fluctuations in the experimental data due to a limited number of samples. (The initial value of Δ is roughly 3.16.) The order metrics q₆ and T of the simulated pattern also match those of the experimental data very well (see Table III). This is a stringent test for the simulations to pass. The success of the simulations strongly suggests that the disordered hyperuniform photoreceptor patterns indeed arise from the competition between cell packing constraints and the tendency to maximize the degree of regularity for efficient light sampling, suggesting that the individual photoreceptor types are as uniform as they can be, given the packing constraints within the photoreceptor epithelium.

FIG. 8.

(Color online) Simulated point configurations representing the spatial arrangements of chicken cone photoreceptors. Upper panels: The configurations shown from left to right, respectively, correspond to violet, blue, and green species. Lower panels: The configurations shown from left to right, respectively, correspond to red, double species, and the overall pattern. The simulated patterns for individual photoreceptor species are virtually indistinguishable from the actual patterns obtained from experimental measurements.

FIG. 9.

(Color online) Comparison of the structure factors S(k) of the experimentally obtained and simulated point configurations representing the spatial arrangements of chicken cone photoreceptors. The simulation data were obtained by averaging 50 independent configurations.

FIG. 10.

(Color online) Comparison of the pair-correlation functions g₂(r) of the experimentally obtained and simulated point configurations representing the spatial arrangements of chicken cone photoreceptors. The simulation data were obtained by averaging 50 independent configurations. The distance is rescaled by the average nearest-neighbor distance d_n in the system.

TABLE III.

Comparison of the bond-orientational and translational order metrics q₆ and T of the experimental and simulated point configurations. The simulation data were obtained by averaging 50 independent configurations.

	q6		T
Species	Expt.	Sim.	Expt.	Sim.
Violet	0.150	0.148	0.304	0.327
Blue	0.158	0.164	0.411	0.395
Green	0.130	0.134	0.278	0.266
Red	0.147	0.149	0.254	0.263
Double	0.184	0.189	0.390	0.363
All	0.058	0.063	0.096	0.108

V. CONCLUSIONS AND DISCUSSION

By analyzing the chicken cone photoreceptor patterns using a variety of sensitive microstructural descriptors arising in statistical mechanics and particle-packing theory, we found that these disordered patterns display both overall and homotypic hyperuniformity, i.e., the system is multihyperuniform. This singular property implies that if any subset of the individual species is removed from the overall population, the remaining pattern is still hyperuniform. Importantly, it is highly nontrivial to devise an algorithm that would remove a large fraction of the points from a disordered hyperuniform system while leaving the remaining point pattern hyperuniform, and yet Nature has found such a design.

Until now, the property of overall hyperuniformity was identified only in a special subset of disordered physical systems, including ground-state liquid helium [34], one-component plasmas [35], Harrison-Zeldovich power spectrum of the density fluctuations of the early Universe [36], fermionic ground states [37], classical disordered ground states [38], and maximally random jammed packings of equal-sized hard particles [32,33]. All of these examples involve single-component systems. More recently, disordered multicomponent physical systems such as maximally random jammed (MRJ) hard-particle packings [27–29] have been identified that possess an appropriately generalized hyperuniformity property ascertained from the local volume fraction fluctuations. However, the multicomponent photoreceptor avian system pattern, which represents the first example of a disordered hyperuniform system in a living organism, is singularly different from any of these hyperuniform physical systems in that in the pattern each species and the total population are hyperuniform, i.e., the avian patterns are multihyperuniform. Although it is not very difficult to construct an overall hyperuniform system by superposing subsystems that are individually hyperuniform, the reverse process (i.e., decomposing a hyperuniform system into individually hyperuniform subsets) is highly nontrivial. It will be of interest to identify other disordered hyperuniform biological systems. It is likely that some other epithelial tissues and phyllotactic systems [19] possess such attributes. Interestingly, it has been shown that the large-scale number-density fluctuations associated with the malignant cells in brain tumors are significantly suppressed, although the cell patterns in such brain tumors are not hyperuniform [40].

In addition, the photoreceptor patterns possess quasi-long-range (QLR) correlations as indicated by the linear small-k behavior in S(k). Such QLR correlations are also observed in the ground-state liquid helium [34], the density fluctuations of the early Universe [36], fermionic ground states [37], and MRJ packings of hard particles [27–29]. In the MRJ particle packings, it is believed that the QLR correlations arise from the competition between the requirement of jamming and maximal disorder in the system [27–29]. As we showed employing the unique multiscale packing model, the multicomponent avian system that is both homotypic and overall hyperuniform, i.e., multihyperuniform, can result from two competing interactions between the photoreceptors.

It is noteworthy that while hard-core exclusion and high density in a disordered particle packing are necessary conditions to achieve a hyperuniform state, these are not sufficient conditions. Figure 11 shows a nonequilibrium random-sequential-addition (RSA) packing of hard circular disks in two dimensions with a packing fraction ϕ = 0.54 (left panel), which is generated by randomly and sequentially placing hard disks in a domain without overlapping existing disks, until there is no room for additional disks [41]. The right panel of Fig. 11 shows an equilibrium system of hard disks at ϕ = 0.54 (right panel). The structure factor values at k = 0 for the RSA and equilibrium systems are respectively given by S(0) = 0.059 [41] and S(0) = 0.063 [42–44]. Although hard-core exclusion plays a central role in these two distinct high-density packings, neither packing is hyperuniform, as indicated by the relatively large positive values of the corresponding S(0).

FIG. 11.

(Color online) Left panel: A random-sequential-addition (RSA) packing of hard, identical circular disks in two dimensions with a packing fraction ϕ = 0.54, which is close to the saturation state. Right panel: An equilibrium system of hard, identical disks at ϕ = 0.54. The fact that neither of these systems is hyperuniform, as discussed in the text, indicates that hard-core exclusion effects alone are not sufficient to induce hyperuniformity.

To understand the origin of the unique spatial features of the avian photoreceptor patterns, we have devised a unique multiscale cell packing model that suggests that photoreceptor types interact with both short- and long-ranged repulsive forces and that the resultant competition between the types gives rise to the singular cell patterns. The fact that a disordered hyperuniform pattern corresponds to a local optimum associated with the multiscale packing problem indicates that such a pattern may represent the most uniform sampling arrangement attainable in the avian system, instead of the theoretical optimal solution of a regular hexagonal array. Specifically, our studies show how fundamental physical constraints can change the course of a biological optimization process. Although it is clear that physical cell packing constraints are the likely cause of the short-range hard-core repulsion, the origin of the effective longer-range soft-core repulsion is less obvious. We hypothesize that repulsive forces of this type occur during retinal development and may be secondary to cell-cell interactions during photoreceptor neurogenesis. However, a comprehensive test of this hypothesis is beyond the scope of this investigation, and therefore its resolution represents a fascinating avenue for future research.

Recent studies have shown that disordered hyperuniform materials can be created that possess unique optical properties, such as being “stealthy” (i.e., transparent to incident radiation at certain wavelengths) [38]. Moreover, such disordered hyperuniform point patterns have been employed to design isotropic disordered network materials that possess complete photonic band gaps (blocking all directions and polarizations of light) comparable in size to those in photonic crystals [45,46]. While the physics of these systems is not directly related to the avian photoreceptor patterns, such investigations and our present findings demonstrate that a class of disordered hyperuniform materials are endowed with novel photonic properties.

Aside from capturing the unusual structural features of photoreceptor patterns, our multiscale packing model represents a unique algorithm that allows one to generate multihyperuniform multicomponent systems with varying degrees of order by tuning the packing fraction ϕ of the hard-core exclusion regions (see Appendix for additional examples). This knowledge could now be exploited to produce multihyperuniform disordered structures for applications in condensed matter physics and materials science. For example, it would be of interest to explore whether colloidal systems can be synthesized to have such repulsive interactions in order to self-assemble into the aforementioned unique disordered arrangements and to study the resulting optical properties. It is noteworthy that it has already been demonstrated that three-dimensional disordered hyperuniform polymer networks can be fabricated for photonic applications using direct laser writing [47].

APPENDIX

MULTIHYPERUNIFORM DISORDERED POINT CONFIGURATIONS VIA THE MULTISCALE PACKING MODEL

In this appendix, we provide additional examples of multihyperuniform disordered point configurations obtained via the multiscale packing model for the case of three components (red, blue, and green species). These examples illustrate the versatility and capacity of our model to generate multicomponent systems with varying degrees of hyperuniformity (see discussion below), apart from modeling the avian system. Specifically, we will show that the degree of hyperuniformity of the overall patterns can be controlled by tuning the overall final packing fraction ϕ associated with the hard-core exclusion regions for different species in the system. Note that in our model, in the infinite-dilute limit ϕ → 0, i.e., in the absence of the hard-core exclusion effects, the inherent structures associated with the remaining long-range soft-core repulsion are triangular-lattice arrangements of points, which are in fact the most hyperuniform point configurations in two dimensions [15]. As the hard-core exclusion regions for each species grow in size (i.e., ϕ increases), the degree of spatial order will be gradually reduced due to the aforementioned geometrical frustrations caused by the hard cores, while the system remains hyperuniform and disordered up to some packing fraction ϕ_C. Therefore, our algorithm is robust in producing multihyperuniform systems with a varying degree of disorder over a wide range of packing fractions. However, we emphasize that there exists a threshold packing fraction ϕ_C, above which the system ceases to be hyperuniform.

In our simulations, the numbers of particles for different species are chosen to be the same, i.e., n_R = n_B = n_G = 500, where the subscripts “R,” “B,” “G” indicate the red, blue, and green species, respectively. The three species possess the same number density and thus, the same size R_s for the homotypic repulsion [cf. Eq. (13)]. The relative sizes of the hard core are, respectively, 1.0, 1.5, and 2.0 for red, blue, and green species. Initial configurations with an overall packing fraction ϕ = 0.3 are generated using the random sequential addition process. Then, the growth and relaxation procedure is employed to generate disordered inherent structures associated with the soft interactions at different packing fractions.

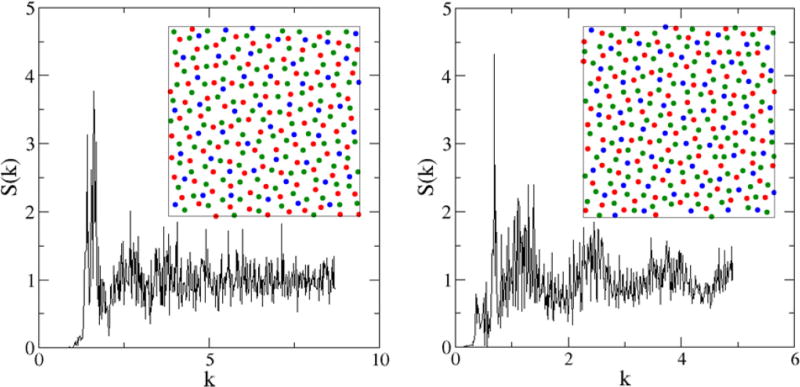
The resulting patterns are multihyperuniform, i.e., both the individual species and the overall patterns are hyperuniform. However, here we will only focus on the degree of hyperuniformity in the overall pattern. Figure 12 shows the configurations and associated S(k) of the overall system for selected ϕ values. At ϕ = 0.35, the structure factor S(k) = 0 for k < K*, indicating that the system is stealthy [38] (i.e., the pattern completely suppresses scattering of the incident radiation associated with wave numbers smaller than K* and, thus, is transparent at the corresponding wavelengths) and yields a higher degree of order. At ϕ = 0.55, the structure factor is quadratic in k, i.e., S(k) ~ k² for small-k values, which indicates that number variance grows with the surface of the observation window, i.e., σ²(R) ~ R for large window sizes (i.e., large-R values). This is to be contrasted with the large-R behavior of σ²(R) for the photoreceptor patterns in chicken retina, i.e., σ²(R) ~ R ln R, which indicates that the number variance grows more rapidly than that in the three-component system associated with ϕ = 0.55. In other words, the three-component system at ϕ = 0.55 possesses smaller local number density fluctuations than those in the chicken retina, indicating that the former is more uniform on large length scales (i.e., displays a higher degree of hyperuniformity) than the latter.

FIG. 12.

(Color online) Configurations and the associated S(k) of a three-component system for selected ϕ values. Left panel: At ϕ = 0.35, the structure factor S(k) = 0 for k < K* which indicates the system is stealthy. Right panel: At ϕ = 0.55, the structure factor S(k) ~ k² for small-k values, which indicates that number variance σ²(R) ~ R for large window sizes. The system possesses different degrees of hyperuniformity that can be ascertained from the small-k behavior of S(k).