Federated learning of predictive models from federated Electronic Health Records

Abstract

Background

In an era of “big data,” computationally efficient and privacy-aware solutions for large-scale machine learning problems become crucial, especially in the healthcare domain, where large amounts of data are stored in different locations and owned by different entities. Past research has been focused on centralized algorithms, which assume the existence of a central data repository (database) which stores and can process the data from all participants. Such an architecture, however, can be impractical when data are not centrally located, it does not scale well to very large datasets, and introduces single-point of failure risks which could compromise the integrity and privacy of the data. Given scores of data widely spread across hospitals/individuals, a decentralized computationally scalable methodology is very much in need.

Objective

We aim at solving a binary supervised classification problem to predict hospitalizations for cardiac events using a distributed algorithm. We seek to develop a general decentralized optimization framework enabling multiple data holders to collaborate and converge to a common predictive model, without explicitly exchanging raw data.

Methods

We focus on the soft-margin l₁-regularized sparse Support Vector Machine (sSVM) classifier. We develop an iterative cluster Primal Dual Splitting (cPDS) algorithm for solving the large-scale sSVM problem in a decentralized fashion. Such a distributed learning scheme is relevant for multi-institutional collaborations or peer-to-peer applications, allowing the data holders to collaborate, while keeping every participant’s data private.

Results

We test cPDS on the problem of predicting hospitalizations due to heart diseases within a calendar year based on information in the patients Electronic Health Records prior to that year. cPDS converges faster than centralized methods at the cost of some communication between agents. It also converges faster and with less communication overhead compared to an alternative distributed algorithm. In both cases, it achieves similar prediction accuracy measured by the Area Under the Receiver Operating Characteristic Curve (AUC) of the classifier. We extract important features discovered by the algorithm that are predictive of future hospitalizations, thus providing a way to interpret the classification results and inform prevention efforts.

INTRODUCTION

Motivation

As the volume, variety, velocity and veracity (the four V’s) of the clinical data grow, there is greater need for efficient computational models to mine these data. Insights from these techniques could help design efficient healthcare policies, detect disease causes, provide medical solutions that are personalized and less costly, and finally, improve the quality of care for the patients. We are motivated by problems in the medical domain that can be formulated as binary supervised classification problems and solved using Support Vector Machines; the applications range from prediction of the onset of diabetes,[1,2] prediction of hospitalizations for cardiac events,[3] prediction of medication adherence in heart failure patients,[4] and cancer diagnosis,[5] to automated recognition of the obstructive sleep apnea syndrome.[6]

Results in the literature suggest that sparse classifiers (i.e., those that rely on few features), have strong predictive power and generalize well out-of-sample,[7,8] providing at the same time interpretability in both models and results. Interpretability is crucial for healthcare practitioners to trust the algorithmic outcomes. Another major concern, especially in the medical domain, is the privacy of the data, attracting recent research efforts.[9–11] Two well-known examples of privacy breaches are the Netflix Prize and the Massachusetts Group Insurance Commission (GIC) medical records database. In both cases, individuals were identified even though the data had been through a de-identification process. This demonstrated that one’s identity and other sensitive information could be compromised once a single center has access and processes all the data. Especially under the Precision Medicine Initiative,[12] in the near future, these data could include individuals’ genome information, which is too sensitive to be shared.

We are particularly interested in addressing three challenges tied to healthcare data: (1) data reside in different locations (e.g., hospitals, doctors’ offices, home-based devices, patients’ smartphones); (2) there is a growing availability of data, which makes scalable frameworks important; and (3) aggregating data in a single database is infeasible or undesirable due to scale and/or data privacy concerns. In particular, even though maintaining all data in a central location enables the implementation of anonymization measures (e.g., k-anonymity [13]), it introduces a single point of attack or failure and makes it possible for a data breach to expose identifiable data for many individuals. Furthermore, establishing a central data repository requires significant infrastructure investments and overcoming information governance hurdles such as obtaining permissions for storing and processing data. Instead, a decentralized computational scheme that treats the available data as part of a federated (virtual) database, avoiding centralized data collection, processing, and raw data exchanges, may address the above challenges.

Aim

The focus of this paper is to develop a distributed (federated) method to predict hospitalizations during a target year for patients with heart diseases, based on their medical history as described in their Electronic Health Records (EHRs). The records of each patient may lie with them in the patient’s smartphone, or may be stored in the EHR systems of different hospitals. In all cases, the collaboration of different parties (agents) is required to develop a global hospitalization prediction model. We will formulate the problem as a binary supervised classification problem and we will develop a distributed soft-margin ℓ₁-regularized (sparse) Support Vector Machines (sSVM) algorithm. We consider SVMs because they are effective classifiers [14] and perform well in predicting hospitalizations.[3] Furthermore, sparse classifiers can reveal relatively few predictive features and, thus, enable interpretation of the predictions.[15]

Health application

We focus on cardiovascular conditions because they comprise a significant portion of morbidity and mortality, as well as, hospitalization in the U.S. and worldwide. In the fact, in the U.S. alone, more than 30% (equal to $9 billion) of hospitalizations deemed preventable are due to cardiovascular conditions.[16] For many decades, the research interest has been focused on understanding the pathophysiology of these conditions and treating them effectively. The efforts have now shifted to the understanding of the disease process and the early prevention. This goal has obvious public health implications, but also socioeconomic significance. It is well known that preventing the progression of the disease process by intensified follow up and treatment can result in long-term stability and improved survival of the patient. Hospitalization is a well-known negative prognostic factor for cardiovascular disease outcome. One critical step in the effort to halt the disease process is the understanding of the etiology and modifiable risk factors of hospitalization.

Main contributions

We summarize our main contributions below:

• We develop a federated optimization scheme (cPDS) for solving the sparse Support Vector Machine problem. Advantages include scalability and the fact that it avoids raw data exchanges, which is important in healthcare. We also demonstrate that cPDS has improved convergence rate and favorable communication cost compared to various centralized and distributed alternatives.

• We apply our new methodology to a dataset of de-identified Electronic Heart Records from the Boston Medical Center, containing patients with heart-related diseases. Each patient is described by a set of features, including demographics, diagnoses, prior admissions, and other relevant medical history.

• We use cPDS to differentiate between patients that are likely and not likely to be hospitalized within a target year and report and discuss the experimental results.

• The proposed cPDS framework is general and can be applied to any learning problem with a “nonsmooth+nonsmooth” loss function objective. Such problems can be found in machine learning, where we aim to minimize functions with non-smooth regularizers, or in distributed model predictive control.

MATERIAL AND METHODS

Objective and background

We consider a dataset extracted from an EHR system, containing patients’ demographic data such as age, gender, and race, physical characteristics such as weight, height, Body Mass Index (BMI), medical history captured by diagnoses, procedures, office visits, and a history of drug prescriptions, all captured by a feature vector ϕ_i ∈ ℝ^d, for each patient i = 1, …, n. We are interested in predicting whether or not a patient will be hospitalized in a given year, for instance in the next calendar year from the time the record is being examined. We denote a hospitalization by a label l_i = +1, and a non-hospitalization by a label l_i = −1. Using machine learning terminology, this is a binary classification problem. Using the popular Support Vector Machine (SVM) classifier,[14] we seek to find a hyperplane that maximizes the margin (“distance”) between the two classes, while allowing a few points to be misclassified (as shown in Figure 1). Further requiring that a few features are used, we end up with a sparse Support Vector Machine (sSVM) problem:

$$\underset{\mathit{\beta },{\beta }_0}{\min }{\displaystyle {\sum }_{i=1}^n{h}_i(\mathit{\beta },{\beta }_0)+0.5\tau {\Vert \mathit{\beta }\Vert }_2^2+\rho {\Vert \mathit{\beta }\Vert }_1,}$$ (1)

where (β, β₀), β ∈ ℝ^d, β₀ ∈ ℝ, identifies the hyperplane/classifier; $h_i(\mathit{\beta },{\beta }_0=\max \{0,1-l_i({\varphi }_i^{\top }\mathit{\beta }+{\beta }_0)\}$ is a hinge loss function for sample i ; τ and ρ are penalty coefficients; ⊤ denotes transpose, and the l₁-norm term ║β║₁ serves to induce sparsity.

Figure 1.

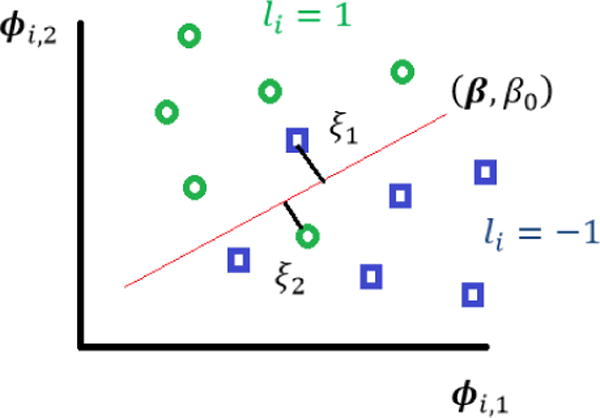
Support Vector Machines.

In the distributed context, we are interested in a setting where each agent¹ holds a part of the data/samples, namely, a subset of {ϕ_i; i = 1 …, n} and {l_i, i = 1, …, n}, and would like to collaborate with others to solve Problem (1) for β and β₀. Due to scalability, regulatory, and privacy reasons, agents are not willing to share their raw data with each other or with a processing center. We will develop a decentralized algorithm that avoids raw data exchanges.

Related literature

Problem (1) involves minimization of the sum of two convex but non-smooth terms, i.e., the loss function and the penalty terms $0.5\tau {\Vert \mathit{\beta }\Vert }_2^2+\rho {\Vert \mathit{\beta }\Vert }_1$. When all the data are stored and computations are executed in a centralized unit, we can solve the problem using the interior point (also referred to as barrier) method or the classical subgradient method (SubGD).[17] Another approach with $0(1/\sqrt{k)}$ convergence rate that can solve the sSVM and allows a decentralized implementation is the incremental subgradient method (IncrSub).[18] However, IncrSub needs to deploy vanishing step size to reach exact convergence and only works over networks with a ring structure. A recent fully decentralized scheme that has made a significant improvement over the IncrSub is the linear time-average consensus optimization algorithm (LAC).[19] The LAC algorithm is an iterative algorithm that takes smalls steps towards the optimal solution at each iteration utilizing a fixed but small step size and is shown to have $0(1/\sqrt{k)}$ convergence rate. A good feature of the LAC is that it improves algorithmic scalability in the size of the network.

The Cluster Primal Dual Splitting

Next, we introduce the general decentralized primal-dual splitting scheme we have designed for solving “nonsmooth+nonsmooth” optimization problems like (1).

Let us assume there is a network of agents, each of which is holding part of the data and they all collectively would like to solve (1) utilizing all data. We consider two scenarios: each agent is holding multiple samples (semi-centralized); or one sample (fully-decentralized). In our healthcare context, agents in the first scenario are hospitals that process the data of their patients only and exchange messages with other hospitals to jointly solve (1). In the second scenario, each patient maintains personal data (e.g.. in a smartphone) and exchanges messages with other patients to jointly solve (1). A combination of these two scenarios is also possible. In either scenario, the m agents are connected through a communication network, which is modeled by an undirected graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$, where $\mathcal{V}=\{1,2,\dots ,m\}$ is the vertex set and $\mathcal{E}$ is the edge set. Throughout the paper, we make the assumption that (A1) the graph $\mathcal{G}$ is connected; and (A2) information exchange happens only between neighbors.

In the decentralized environment, Problem (1) can be reformulated into the following m-cluster splitting formulation:

$$\begin{array}{ll}\underset{\{{\mathbf{x}}_j,{\mathbf{y}}_j\},{\forall }_j}{\min }& {\displaystyle {\sum }_{j=1}^m\{{\mathbf{g}}_j({\mathbf{x}}_j)+{\mathbf{f}}_j({\mathbf{y}}_j)\}}\\ \mathrm{s}.\mathrm{t}.& {\mathbf{\Gamma }}_j({\mathbf{A}}_j{\mathbf{x}}_j-{\mathbf{y}}_j)=0,\forall \text{j,}\\ & {\mathbf{x}}_1={\mathbf{x}}_2=\cdots ={\mathbf{x}}_m,\end{array}$$ (2)

where each agent j holds n_j samples (such that $n={\displaystyle {\sum }_{j=1}^m{n}_j}$) and maintains its own copy of the model parameters to be estimated ${\mathbf{x}}_j=({\mathit{\beta }}_j,{\beta }_{j_0})\in {\mathrm{ℝ}}^{d+1}$. Let us define a vector x = [x₁; … ; x_m] ∈ ℝ^m(d+1) to compactly represent all the local copies; a vector variable y = [y₁; … ; y_m] ∈ ℝⁿ where each block ${\mathbf{y}}_j=[y_{j1};\dots ;y_{j{n}_j}]\in {\mathrm{ℝ}}^{n_j}$ is handled by agent j, and y_ji = l_ji(φ_ji^T β_j + β_j0), with l_ji, φ_ji being the label and features of the i-th sample held by agent j, respectively. This relationship between x_j and y_j is described by the first set of constraints, with Γ_j some locally produced/tuned pre-conditioner to ensure the fast convergence of the cPDS algorithm. The function (f_j) contains all the hinge loss functions at agent j while the function g_j(x_j) includes the regularizers over agent j. The consensus among agents is achieved through the second group of constraints in (2). To solve the cluster sSVM, or its more general form (2), in a decentralized fashion, we propose the following algorithm (cPDS), which finds the separating hyperplane through updates on parameters of both the primal problem (2), i.e., x_j, y_j, and its corresponding dual problem, i.e., q_j, λ_j. The matrices Γ_j and Θ_j serve as algorithmic parameters that accelerate the convergence, and W = [w_ij] is a doubly stochastic weight matrix of the graph (see definition in the Appendix). In the algorithm, the norm ${\Vert \mathit{x}\Vert }_{{\Theta }_j}$ is the Θ_j-weighted norm of x defined as ${\Vert \mathit{x}\Vert }_{{\Theta }_j}=\sqrt{{\mathit{x}}^{\prime }{\mathbf{\Theta }}_j\mathit{x}}$ and denotes the neighboring nodes of node j. We emphasize that the update of the classifier x_j for each agent is implemented using only the local information, which constitutes a salient advantage of cPDS compared to other methods in the literature.

Algorithm 1.

The cluster Primal Dual Splitting Algorithm (cPDS).

Cluster PDS Method
INPUT: ∀j,
Prepare data/objectives fj and gj. Set parameters Γj and Θ j.
INITIALIZE: ∀j,
${\mathbf{x}}_j^0\in {\mathrm{ℝ}}^{d+1}$, ${\mathbf{y}}_j^0\in {\mathrm{ℝ}}^{n_j}$, ${\mathbf{q}}_j^{-1}=\mathit{0}$, ${\mathbf{q}}_j^0={\mathbf{\Gamma }}_j({\mathbf{A}}_j^{\top }{\mathbf{x}}_j^0-{\mathbf{y}}_j^0)$, ${\mathit{\lambda }}_j^{-1}=\mathit{0}$ and ${\mathbf{x}}_j^0={\mathbf{y}}_j^0-{\displaystyle {\sum }_{i\in {\mathcal{N}}_j\cup \left\{j\right\}}{w}_{ji}}{\mathbf{x}}_i^0$.
REPEAT
x – update (locally): ∀j
${\mathbf{x}}_j^{k+1}=\arg \underset{{\mathbf{x}}_j}{\min }\left\{\langle 2{\mathbf{q}}_j^k-{\mathbf{q}}_j^{k-1},{\mathbf{\Gamma }}_j{\mathbf{A}}_j{\mathbf{x}}_j\rangle +{\mathbf{g}}_j({\mathbf{x}}_j)+\langle 2{\mathit{\lambda }}_j^k-{\mathit{\lambda }}_j^{k-1},{\mathbf{x}}_j\rangle +0.5{\Vert {\mathbf{x}}_j-{\mathbf{x}}_j^k\Vert }_{{\mathbf{\Theta }}_j}^2\right\}$
y- update (locally): ∀j
${\mathbf{y}}_j^{k+1}=\arg \underset{{\mathbf{y}}_j}{\mathit{min}}\left\{{\mathbf{f}}_j({\mathbf{y}}_j)+\langle {\mathbf{q}}_j^k,-{\mathbf{\Gamma }}_j{\mathbf{y}}_j\rangle +0.5{\Vert {\mathbf{y}}_j-{\mathbf{A}}_j{\mathbf{x}}_j^{k+1}\Vert }_{{\mathbf{\Gamma }}_j^{\top }{\mathbf{\Gamma }}_j}^2\right\}$
q-update (locally): ∀j
${\mathbf{q}}_j^{k+1}={\mathbf{q}}_j^k+{\mathbf{\Gamma }}_j\left({\mathbf{A}}_j{\mathbf{x}}_j^{k+1}-{\mathbf{y}}_j^{k+1}\right)$
λ-update (requires information exchange): ∀j
${\mathit{\lambda }}_j^{k+1}={\mathit{\lambda }}_j^k+{\mathbf{x}}_j^{k+1}-{\displaystyle {\sum }_{i\in {\mathcal{N}}_j\cup \left\{j\right\}}{w}_{ji}}{\mathbf{x}}_i^{k+1}$.
UNTIL specific criteria are met.

Theoretical comparison of methods

The table below shows comparative results that illustrate the trade-offs between different methods when applied to the sSVM problem. “Per iteration complexity” measures how many scalar multiplications are needed per iteration. “ε-accuracy iterations” measures how many iterations are needed to reach ε-accuracy. The details for applying cPDS to sSVM can be found in the Appendix.

Performance evaluation

We split the patients in our dataset into two sets: a training and a test set. Training patients are used to train the algorithm. In order to evaluate the accuracy of the predictions, we use the trained classifier to predict the label of patients (whether or not will be hospitalized) in the test set. We measure the performance of cPDS in terms of the Area Under the Receiver Operator Characteristic (ROC) curve (AUC), which plots the true positive rate (i.e., out of the hospitalized patients how many were correctly predicted as hospitalized) versus the false positive rate (i.e., out of the non-hospitalized patients how many were wrongly predicted to be hospitalized). The true positive rate is also referred to as sensitivity or recall and specificity is used to refer to one minus the false positive rate. We also report the computation time, i.e., the cumulative time needed at all nodes to train the model, and the communication cost, which is defined as 2 times the product of the number of edges, the dimension of the features, and the number of iterations. (Only the coefficients of the features are exchanged with adjacent nodes.) Note that the number of edges in the graph decides the amount of information exchanged.

DATA-RESULTS-DISCUSSION

Data description and preprocessing

The data used for the experiments come from the Boston Medical Center and consist of Electronic Health Records (EHRs) containing the medical history in the period 2001–2012 of patients with at least one heart-related diagnosis between 2005–2010. The medical history of each patient includes demographics, diagnoses, procedures, vitals, lab tests, tobacco use, emergency room visits, and past admission records. For each patient, we set a specific target year and we predict hospitalization during that year based on the prior medical history. We follow the steps below to preprocess the data:

• Setting the target time interval to a calendar year. Based on preliminary experiments, we observed that there is greater variability in the results when trying to predict hospitalizations in periods of time shorter than a year. Thus, we have designed our experiment to predict hospitalizations in the target time interval of a year (January 1^st – December 31^st). We elected to use a calendar year after observing that hospitalizations occur roughly uniformly within a year.

• Selection of the target year. As a result of the nature of the data, the two classes (hospitalized and non-hospitalized patients) are highly imbalanced. To increase the number of hospitalized patient examples, if a patient had only one hospitalization throughout 2005–2010, the year of hospitalization will be set as the target year. If a patient had multiple hospitalizations, a target year between the first and the last hospitalizations will be randomly selected. 2010 is set as the target year for patients with no hospitalization, so that there is as much available history for them as possible. By this policy, the ratio of hospitalized patients in the data set is 16.97%.

• Summarization of the features in the history of a patient. An effective way to summarize each patient’s medical history is to form four time blocks for each medical factor with all corresponding records summarized over one, two, three years before the target year and a fourth time block containing averages of all earlier records. This produces a 215-dimensional vector of features characterizing each patient.

• Removing patients with no record. Patients who have no records before the target year are removed, since there is nothing on which a prediction can be based. The total number of patients left is 45,579.

• Splitting the data into a training set and a test set randomly. As is common in supervised learning, the population of patients is randomly split into a training and a test set. Since from a statistical point of view, all the data points (patients’ features) are drawn from the same distribution, we do not differentiate between patients whose records appear earlier in time than others with later time stamps. A retrospective/prospective approach appears more often in the medical literature and is more relevant in a clinical trial setting, rather than in our algorithmic approach. What is critical in our setting is that for each patient prediction we make (hospitalization/non-hospitalization in a target year), we only use that patient’s information before the target year.

• Normalization of the features. All predictors are standardized before fed into our algorithm.

• Balancing the training set. During training, we oversample the positive class in order to make the two classes balanced.

Experimental results and discussion

The data are distributed between m hospitals connected through a specific graph topology. The cPDS algorithm is considered to converge if the normalized residual, which is defined as the l₂ norm of the difference between the cPDS and the sSVM parameter estimates, is small enough. Since we do not know the true parameter values, the solution from solving sSVM with a centralized (barrier) method is used as a substitute for the ground truth. We want to investigate the impact of two factors on the convergence of cPDS:

1. The number of hospitals m ∈ {5,10}.

2. The graph topology: (a) random graph generated by the Erdős–Rényi model, where two nodes are connected with a probability p; (b) cyclic graph, where nodes are connected in a closed chain; (c) fully connected graph, where each node is connected with every other node in the graph.

Table 2 shows the comparison between cPDS and the centralized barrier method, the SubGD, the IncrSub descent and the LAC scheme. For SubGD and IncrSub, we use the steplength rule for the diminishing stepsize². We defined in Materials and Methods the various performance metrics we use. AUC for all methods is similar since they solve the same problem. Just to provide a baseline, we note that using a classifier based on a common risk factor used by cardiologists yields less accurate predictions. Specifically, using the 10-year risk factor for cardiovascular disease developed by the Framingham heart study [20], and comparing that risk-factor to a threshold in order to classify, yields an AUC of 0.56.

Table 2.

Experimental comparison for various methods that solve the sSVM problem.

Method	Distributed?	AUC	Number of iterations	Computation cost (sec)	Communication cost
Subgradient Descent	×	0.7667	1500	2055	N/A
Barrier	×	0.7688	32	40,174	N/A
Incremental Subgradient	×	0.7734	554	6.3485	N/A
Linear Average Consensus (LAC)	√	0.7683	200	27,703	1.04e+11
Cluster Primal Dual Splitting (cPDS) (m = 10, random graph)	√	0.7806	100	544	2600

The computation cost reported in Table 2 reflects effort at all nodes (or the single node for centralized schemes), so it depends on both the number of iterations and the number of nodes (hospitals). On one hand, the more hospitals there are, the longer the computation time. On the other hand, the more edges in the graph, the less time needed for convergence because information reaches all nodes faster. The communication cost measures the number of messages exchanged between nodes (each message is a vector in ℝ^d+1) and is mainly impacted by the number of edges in the graph, which also depends on the number of nodes. In the table, LAC is much more costly than cPDS because it uses a fully distributed approach with n nodes, whereas cPDS uses a graph with m ≪ n nodes.

Table 3 considers only cPDS and shows the convergence time and AUC for different combinations of m and graph topology. Fully connected graphs have the most edges, and thus the highest communication cost. But the number of iterations needed for convergence is not significantly smaller than others. In general, the more edges there are, the faster the algorithm converges, since the information exchange becomes faster³. We note that when the number of edges is “large enough,” the number of iterations needed for convergence stays stable, in other words, the convergence speed comes to be saturated. This is incarnated in the random graph topology. When m = 5, 4 edges lead to saturation; and for m = 10, 13 edges are needed.

Table 3.

Performance of cPDS for different number of agents m and different graph topologies.

Graph topology	Number of hospitals	Number of edges	Number of iterations	Computation time (sec)	Communication cost	AUC
Random	5	4	90	906	720	0.7738
Random	10	13	100	544	2600	0.7806
Cyclic	5	5	90	909	900	0.7736
Cyclic	10	10	250	1482	5000	0.7723
Fully connected	5	10	90	917	1800	0.7696
Fully connected	10	45	100	585	9000	0.7747

In Table 4 we summarize the important features identified by the cPDS algorithm. We run cPDS for each of the six settings of Table 3, averaged the coefficients corresponding to the various features (elements of the vector β) over the six runs, and report the features with the largest average coefficients. Note that all features are standardized, and thus it is reasonable to identify important features based on the magnitudes of the average coefficients.

Table 4.

Important features.

	Important features	Average coefficients over 6 runs
	Age	224.03
Factors - 1 year the before target year	Diagnosis of Heart Failure- 1 year before the target year	225.63
	Admission due to Other Circulatory System Diagnoses- 1 year before the target year	204.14
	Admission due to Heart Failure- 1 year before the target year	183.09
	Admission due to a Percutaneous Cardiovascular Procedure- 1 year before the target year	168.53
	Admission for Cardiac Defibrillator Implant with Cardiac Catheterization – 1 year before the target year	145.78
	Admission due to Cardiac Arrest- 1 year before the target year	144.96
	Systolic Blood Pressure Measured -1 year before the target year	136.71
Factors - 2 years before the target year	Diagnosis of Heart Failure- 2 years before the target year	162.20
	Admission due to Other Circulatory System Diagnoses- 2 years before the target year	139.12
	Admission due to Cardiac Arrest- 2 years before the target year	127.59
	Admission due to a Circulatory Disorder Except Acute Myocardial Infarction -2 years before the target year	184.57
	Admission due to Cardiac Valve or Other Major Cardiothoracic Procedure- 2 years before the target year	175.84
	Diagnostic ultrasound of heart - 2 years before the target year	137.40
	Admission for Acute and Subacute endocarditis - 2 years before the target year	129.07
	Admission for Acute Myocardial Infarction - 2 years before the target year	120.73
Factors - 3 years before the target year	Diagnosis of Heart Failure- 3 years before the target year	178.02
	Admission due to Other Circulatory System Diagnoses- 3 years before the target year	158.67
	Admission due to a Percutaneous Cardiovascular Procedure- 3 years before the target year	170.34
	Admission due to Cardiac Arrest-3 years before the target year	155.05
	Admission for Acute and Subacute endocarditis - 3 years before the target year	135.91

It is interesting that the classifier identifies many of the diagnoses and health events that are major public health problems and which constitute common reasons for hospitalization with major economic implications. Hypertension, increasing in parallel with obesity, coronary artery disease, as it is identified indirectly by cardiac catheterization, heart failure – a true epidemic as the population is getting older, as well as, cardiac arrest are some of the most prevalent heart-related diagnoses. It is, therefore, important to establish the ability of these diagnoses to predict hospitalization and use such predictions as a tool to prevent the disease process.

CONCLUSIONS

In this paper, we focused on developing a federated learning model that is able to predict future hospitalizations for patients with heart-related diseases using EHR data spread among various data sources/agents. Our proposed decentralized framework, the cluster Primal Dual Splitting (cPDS) algorithm, can solve the sparse Support Vector Machine problem, which yields classifiers using relatively few features and facilitates the interpretability of the classification decisions. cPDS has improved convergence rate compared to various alternatives we present. The method is applicable to any binary classification problem with distributed data.

A major advantage of our formulation is the flexibility to address a range of settings, from fully-centralized to fully-decentralized. We formulate our motivating healthcare problem as a binary classification problem. Information processing can happen either at the level of the patients, e.g., through their smartphones, or at the level of the hospitals that process data of their own patients. cPDS is a general framework and can be applied to any problem that has the structure of minimizing two non-smooth terms. A possible extension of this work could be the analysis of cPDS when the graph that connects the agents is time-varying.

Research Highlights.

• A new federated learning framework is proposed that can learn predictive models through peer-to-peer collaboration of federated databases without raw data exchanges.

• Using the EHR, it is possible to accurately predict heart-related hospitalizations.

• The predictive model derived improves prediction accuracy over existing risk metrics.

• The predictive model is sparse, identifying the most informative EHR variables for hospitalization prediction.

SUMMARY TABLE.

What was already known	What this study added to our knowledge
Electronic Health Records (EHRs) can potentially be used to assess a person’s health and predict future hospitalizations. Some comprehensive risk metrics exist (Framingham risk factor) to assess the risk of a major heart-related episode.	Using the entirety of the EHR, it is possible to accurately predict an individual’s hospitalization for cardiac events in the following calendar year, improving upon the accuracy of existing risk metrics (such as the Framingham risk factor).
Centralized machine learning methods are typically used to train predictive models (classifiers) from data.	A new distributed learning framework has been developed to solve the learning (classification) problem in a setting where data reside with many agents, no raw data get exchanged, and the agents collaborate to jointly learn the model (classifier). The distributed algorithms is more scalable than centralized algorithms or earlier distributed methods.
	The new learning framework is flexible to accommodate a range of data aggregation levels at the nodes, from each node holding a single data point (e.g., an individual EHR) to a setting where each node maintains many data points (a hospital maintaining all the hospital’s EHRs).
	The sparse classifiers produced by our method automatically concentrate on relatively few features, facilitating the interpretability of the classification results.

APPENDIX

The sparse Support Vector Machine (sSVM) Problem

sSVM finds the classifier (β, β₀), β ∈ ℝ^d, β₀ ∈ ℝ, by solving the following problem:

$$\begin{array}{l}\underset{\beta ,{\beta }_0}{\min }0.5{\Vert \mathit{\beta }\Vert }^2+C{\displaystyle {\sum }_{i=1}^n}{\xi }_i+\kappa {\Vert \mathit{\beta }\Vert }_1\\ s.t{\xi }_i\ge 0,\forall i,l_i\left({\varphi }_i^{\top }\mathit{\beta }+{\beta }_0\right)\ge 1-{\xi }_{i,}\forall i.\end{array}$$ (3)

The ‖ ∙ ‖₁ constraint in the above formulation is forcing the classifier β to be sparse. In the decentralized setting with m agents, problem (3) could be reformulated into the following m-cluster splitting form:

$$\begin{array}{l}\underset{\mathit{\beta },{\beta }_0}{\min }{\displaystyle {\sum }_{j=1}^m\{{\displaystyle {\sum }_{i=1}^{n_j}{[1-y_{ji}]}_{+}+0.5{\tau }_j{\Vert {\mathit{\beta }}_j\Vert }_2^2+{\rho }_j{\Vert {\mathit{\beta }}_j\Vert }_1\}}}\\ \mathrm{s}.\mathrm{t}.{\gamma }_{ji}(l_{ji}({\varphi }_{ji}^{\top }{\mathit{\beta }}_j+{\beta }_{j0})-y_{ji})=0,\forall j,i;{\mathit{\beta }}_1={\mathit{\beta }}_2=\cdots ={\mathit{\beta }}_m;{\beta }_{1,0}={\beta }_{2,0}=\cdots ={\beta }_{m0},\end{array}$$

where each agent (hospital) j holds n_j samples (such that $n={\displaystyle {\sum }_{j=1}^m{n}_j}$), and $y_{ji}=l_{ji}({\varphi }_{ji}^{\top }{\mathit{\beta }}_j+{\beta }_{j0})$. The parameters γ_ji's are arbitrary nonzero scalar constants and serve as algorithmic parameters.

Definition 1

[Doubly stochastic matrix] W = [w_ij] is defined to be a doubly stochastic matrix generated by the following the Metropolis rule on $\mathcal{G}$:

$$w_{ij}=\{\begin{array}{cc}\frac{1}{\max \{\text{degree}(i),\text{degree}(j)\}+1},\hfill & \hfill \text{if}(i,j)\in \epsilon ,\\ 0,\hfill & \hfill \text{if}(i,j)\notin \epsilon \text{and}i\ne j,\\ 1-{\displaystyle \sum _{k\in V}{w}_{ik},}\hfill & \hfill \text{if}i=j.\end{array}$$

Such rule allows each agent i to generate w_ij, ∀j, by only using local information (its own and neighbors' degree information). Note we always have −I_m ≺ W ≼ I_m. Let us also define L ≜ (I_m − W) ⊗ I_d+1 and $\mathit{U}\triangleq \sqrt{\mathit{L}}$. Here, ⊗ denotes the Kronecker product of matrices and I_m the m × m identity matrix. We note U has the same null space as that of L.

Insights on the cPDS Algorithm

To get some insight on how the algorithm works, let us further write (2) into an even more compact form.

$$\begin{array}{l}\underset{\mathbf{x},\mathbf{y}}{\min }\{\mathbf{g}(\mathbf{x})+\mathbf{f}(\mathbf{y})\}\\ \mathrm{s}.\mathrm{t}.\mathbf{\Gamma }(\mathbf{Ax}-\mathbf{y})=0,\mathbf{Ux}=0.\end{array}$$ (4)

We note that Ux = 0 is equivalent to x₁ = x₂ = ⋯ = x_m as long as the graph is connected.

We will make two more assumptions: (A3) The functions g: ℝ^m(d+1) → ℝ and f: ℝⁿ → ℝ are both proper, closed, and convex. (A4) The solution set χ^∗ is nonempty and bounded. Assumption (A3) imposes a minimal requirement on the objectives to conduct convex analysis. Assumption (A4) is obviously satisfied by the sSVM problem.

The augmented Lagrangian function of (4) is as follows

$$\mathcal{L}=\mathbf{g}(\mathbf{x})+\mathbf{f}(\mathbf{y})+\langle \mathbf{r},\mathbf{Ux}\rangle +\langle \mathbf{q},\mathbf{\Gamma }(\mathbf{Ax}-\mathbf{y})\rangle ,$$

where r and q contain the dual variables. The idea behind our proposed algorithm is based on minimizing the Lagrangian function with respect to the primal variables x and y and the dual variables r and q. However, when doing so, the x – update is not implementable in a fully distributed setting. This is the key limitation that cPDS is addressing and contributing to the literature.

Application of cPDS on ℓ₁-Regularized Support Vector Machines

We will show the details of applying the cPDS framework to solve the distributed sSVM problem. Assume that n samples of data are distributed among m agents that want to collectively agree on a global classifier to separate the two classes. Each agent is holding n_j samples and maintains a copy (β_j, β_j0) of the classifier parameters to be estimated. (β_j, β_j0) are updated in each iteration of the method, using data locally stored at the agent j as well as information that the agent receives from its neighbors. Let ϕ_ji ∈ ℝ^d and l_ji ∈ ℝ be the features and the label of sample i in agent j accordingly, and f_ji be the corresponding hinge loss for that sample. g_j contains the regularizers of parameters (β_j, β_j0) for each agent j. Define a_ji = (l_jiϕ_ji, l_ji), which we will use later. In every iteration each agent updates x_j = (β_j, β_j0) ∈ ℝ^d+1, ${\mathit{y}}_j\in {\mathrm{ℝ}}^{n_j}$, ${\mathit{q}}_j\in {\mathrm{ℝ}}^{n_j}$ and λ_j ∈ ℝ^d+1. Let us illustrate below the cPDS updates that each agent is performing. For simplicity, in the implementation, we use Θ_j = θ_jI_d+1 where θ_j is a positive scalar maintained by agent j locally. Next we describe the updates over each agent j.

x – update

$$({\mathit{\beta }}_j^{k+1},{\beta }_{j0}^{k+1})=\underset{{\mathit{\beta }}_j,{\beta }_{0j}}{\arg \min }{\displaystyle {\sum }_{i=1}^{n_j}}{\gamma }_{ji}(2q_{ji}^k-q_{ji}^{k-1}){\mathit{a}}_{ji}^{\top }{(}_{{\beta }_{j0}}^{{\mathit{\beta }}_j})+\frac{\tau }{2}{\Vert {\mathit{\beta }}_j\Vert }^2+\rho {\Vert {\mathit{\beta }}_j\Vert }_1+{(2{\lambda }_j^k-{\lambda }_j^{k-1})}^{\top }{(}_{{\beta }_{j0}}^{{\mathit{\beta }}_j})+0.5{\Vert \left(\begin{array}{c}{\mathit{\beta }}_j\\ {\beta }_{j0}\end{array}\right)-\left(\begin{array}{c}{\mathit{\beta }}_j^k\\ {\beta }_{j_0}^k\end{array}\right)\Vert }^2{\theta }_j.$$ (5)

The simple form of the non-smooth g_j allows us to get a closed form solution for this problem. Problem (5) can be decoupled into two problems, one that finds ${\mathit{\beta }}_j^{k+1}$, whose solution is given by the soft thresholding function, i.e., ∀t = 1, …, d,

$${\beta }_{jt}^{\ast }=\mathrm{sgn}(u_{jt}){(|u_{jt}|-\mu )}_{+}=\{\begin{array}{ll}{u}_{jt}-\mu ,\hfill & \text{if}{u}_{jt}>\mu ,\hfill \\ 0,\hfill & \text{if}|u_{jt}|\le \mu ,\hfill \\ u_{jt}+\mu ,\hfill & \text{if}{u}_{jt}<-\mu ,\hfill \end{array}$$

with = $\frac{2\rho }{\tau +{\theta }_j}$, and ${\mathbf{u}}_j=-\frac{1}{\tau +{\theta }_j}[{\displaystyle {\sum }_{i=1}^{n_j}{\mathit{\gamma }}_{ji}{l}_{ji}(2q_{ji}^k-q_{ji}^{k-1}){\varphi }_{ji}+(2{\mathit{\lambda }}_{j,1:d}^k-{\mathit{\lambda }}_{j,1:d}^{k-1})-{\theta }_j{\mathit{\beta }}_j^k]}$ and one that finds ${\beta }_{j0}^{k+1}$, which has as an optimal solution:

$${\beta }_{j0}^{\ast }=\frac{-{\displaystyle {\sum }_{i=1}^{n_j}{\gamma }_{ji}{l}_{ji}(2q_{ji}^k-q_{ji}^{k-1})-(2{\mathit{\lambda }}_{i,d+1}^k-{\mathit{\lambda }}_{i,d+1}^{k+1})+{\theta }_j{\beta }_{j0}^k}}{{\theta }_j}.$$

y- update

$${\mathbf{y}}_j^{k+1}=\underset{{\mathbf{y}}_j}{\arg \min }{\displaystyle {\sum }_{i=1}^{n_j}}\left\{\max \right\{0,1-y_{ji}\}+\langle {\gamma }_{ji}{q}_{ji}^k,-y_{ji}\rangle +\frac{1}{2}||{\gamma }_{ji}(l_{ji}{\mathit{\varphi }}_{ji}^{\top }{\mathit{\beta }}_j^{k+1}+l_{ji}{\beta }_{j0}^{k+1}-y_{ji})|{|}^2\}.$$

To deal with the second non-smooth term, the hinge loss function, we consider three cases for each term: 1 − y_ji > 0, 1 − y_ji < 0, 1 − y_ji = 0. For each agent j, we can obtain every entry of y_j in parallel, i.e., for all i:

• Solve

  $$\begin{gathered} {\stackrel{\sim }{y}}_{ji}^{k+1}=\underset{{\mathbf{y}}_{ji}}{\arg \min }\{\frac{{\gamma }_{ji}^2}{2}{y}_{ji}^2+(-1-{\gamma }_{ji}{q}_{ji}^k-{\gamma }_{ji}^2{l}_{ji}{\varphi }_{ji}^{\top }{\mathit{\beta }}_j^{k+1}-{\gamma }_{ji}^2{l}_{ji}{\beta }_{j0}^{k+1})\}\Rightarrow {\stackrel{\sim }{y}}_{ji}^{k+1} \\ =\frac{1}{{\gamma }_{ji}^2}(1+{\gamma }_{ji}{q}_{ji}^k+{\gamma }_{ji}^2{l}_{ji}{\varphi }_{ji}^{\top }{\mathit{\beta }}_j^{k+1}+{\gamma }_{ji}^2{l}_{ji}{\beta }_{j0}^{k+1}). \end{gathered}$$

  If $1-{\stackrel{\sim }{y}}_{ji}>0$, then $y_{ji}^{k+1}={\stackrel{\sim }{y}}_{ji}^{k+1}$; otherwise proceed to the next step.

• Solve

  $${\stackrel{\sim }{y}}_{ji}^{k+1}=\arg \underset{{\mathbf{y}}_{ji}}{\mathit{min}}\{{\gamma }_{ji}{q}_{ji}^k,-y_{ji}+\frac{1}{2}{\Vert {\gamma }_{ji}(l_{ji}{\varphi }_{ji}^{\top }{\mathit{\beta }}_j^{k+1}+l_{ji}{\beta }_{j0}^{k+1}-y_{ji})\Vert }^2\}\Rightarrow {\stackrel{\sim }{y}}_{ji}=\frac{1}{{\gamma }_{ji}^2}({\gamma }_{ji}{q}_{ji}^k+{\gamma }_{ji}^2{l}_{ji}{\varphi }_{ji}^{\top }{\mathit{\beta }}_j^{k+1}+{\gamma }_{ji}^2{l}_{ji}{\beta }_{j0}^{k+1}).$$

  If $1-{\stackrel{\sim }{y}}_{ji}^{k+1}<0$, then $y_{ji}^{k+1}={\stackrel{\sim }{y}}_{ji}^{k+1}$; otherwise proceed to the next step.

• $y_{ji}^{k+1}=1$.

q-update: ∀i

$$q_{ji}^{k+1}=q_{ji}^k+{\gamma }_{ji}(l_{ji}{\mathit{\varphi }}_{ji}^{\top }{\mathit{\beta }}_j^{k+1}+l_{ji}{\beta }_{j0}^{k+1}-y_{ji}^{k+1}).$$

λ-update

$${\mathit{\lambda }}_j^{k+1}={\mathit{\lambda }}_j^k+{\displaystyle {\sum }_{i\in {\mathcal{N}}_j\cup \left\{j\right\}}{w}_{ji}{\mathbf{x}}_j^{k+1}}.$$

Last, let us mention that the storage needed to operate cPDS for sSVM following the above updates is O(nd), which is the same as the other methods listed in Table 1.

Table 1.

Theoretical comparison of various methods that solve the sSVM problem.

Method	Decentralized?	Per iteration complexity	ε -accuracy iterations
Subgradient Descent	×	O(nd)	O(1/ε2)
Incremental Subgradient	×	O(d)	O(1/ε2)
Linear Average Consensus (LAC)	√	O(n2 + nd)	O(1/ε2)
Cluster Primal Dual Splitting (cPDS)	√	O((n + m2)d)	o(1/ε)