Interlayer Bond Formation in Black Phosphorus at High Pressure

Abstract

Black phosphorus was compressed at room temperature across the A17, A7 and simple‐cubic phases up to 30 GPa, using a diamond anvil cell and He as pressure transmitting medium. Synchrotron X‐ray diffraction showed the persistence of two previously unreported peaks related to the A7 structure in the pressure range of the simple‐cubic phase. The Rietveld refinement of the data demonstrates the occurrence of a two‐step mechanism for the A7 to simple‐cubic phase transition, indicating the existence of an intermediate pseudo simple‐cubic structure. From a chemical point of view this study represents a deep insight on the mechanism of interlayer bond formation during the transformation from the layered A7 to the non‐layered simple‐cubic phase of phosphorus, opening new perspectives for the design, synthesis and stabilization of phosphorene‐based systems. As superconductivity is concerned, a new experimental evidence to explain the anomalous pressure behavior of T_c in phosphorus below 30 GPa is provided.

The current renaissance1 of black phosphorus (bP), first obtained under high pressure by Bridgman in 1914,2 is intimately related to the recent synthesis of phosphorene,3, 4 a 2D corrugated monoatomic layer of P, where each atom is single‐bonded to 3 nearest neighbors. The advent of phosphorene5, 6, 7, 8, 9, 10 has indeed dramatically raised the interest of the scientific community about bP, whose crystalline structure is actually made by the periodic stacking of phosphorene layers, in a similar way as graphene is related to graphite, and the layered phases of this element currently represent an extremely active research topic11, 12 (see the Supporting Information, SI‐1).

At the moment crystalline bP, which is typically obtained from amorphous red phosphorus at high temperature and/or high pressure,13, 14 is the starting material for the synthesis of phosphorene, either by liquid or mechanical exfoliation. The layered semiconducting orthorhombic bP (A17, Cmce, Z=8)15, 16 is the thermodynamically stable allotrope of the element at ambient conditions (Figure 1).17 By increasing pressure at room temperature bP undergoes a characteristic phase transition at ∼5 GPa to a layered semimetallic rhombohedral phase (A7, R $\bar{3}$ m, Z=2), which is reported to transform to a metallic simple‐cubic phase (sc, Pm $\bar{3}$ m, Z=1) at ∼11 GPa.18, 19, 20 The sc structure, rarely observed in nature (α‐Po and high‐pressure Ca‐III and As‐II),21 is stable up to 103 GPa, where it transforms to an incommensurate modulated structure (P‐IV, IM, Cmmm(00γ)s00).22, 23 At 137 GPa P‐IV converts to a simple‐hexagonal phase (P‐V, sh, P6/mmm, Z=1) observed up to 282 GPa,24, 25 which is also a rarely adopted structure.21 A body‐centered cubic structure (bcc),26, 27 successively identified as a superlattice structure (P‐VI, cI16(I $\bar{4}$ 3d)), has been reported to form above 262 GPa and to be stable up to 340 GPa.28

Figure 1.

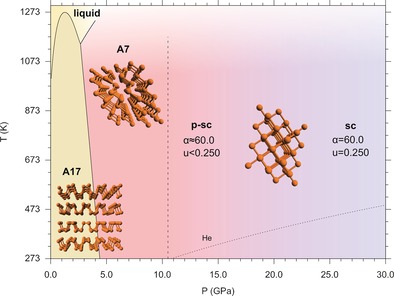
Phase diagram of phosphorus between 0.0 and 30.0 GPa, showing the pressure and temperature ranges where A17 and A7 are reported to be stable.20, 29, 30 The dashed line at 10.5 GPa marks the A7 to sc phase transition according to current literature. Our room T data indicate that the sc phase is not achieved up to 27.6 GPa and that an intermediate pseudo simple‐cubic (p‐sc) structure exists between the A7 and the sc structures (see text). The melting line of He is also displayed (dotted line).31 The snapshots of the structures reported in the phase diagram were generated by Rietveld refinement of our data in the corresponding phases.

However, despite the phase diagram of phosphorus under high pressure being known up to 340 GPa,28 the details of the transformations involving bond breaking and reconstruction in the layered A17 and A7 structures remain experimentally elusive. Indeed, whereas extensive theoretical investigation about the A17 to A7 transition has been carried out by several groups over the years, no experimental data about its mechanism have been reported.32, 33 Similarly, theoretical studies have tried to model the A7 to sc transition, with no experimental confirmation so far.32, 34, 35, 36, 37, 38

In the A17 and A7 layered phases each P atom has three shorter distances, corresponding to the atoms within the layer, and three longer distances, corresponding to the atoms in the adjacent layers. Both phases are structurally related to the sc phase. Particularly, the A7 structure can be derived from the sc one by a distortion and a displacement of the atoms along the space diagonal of the sc cell.39 The last transformation is relevant for two fundamental aspects.

Firstly, from a chemical point of view, the A7 to sc phase transition involves bond formation and reconstruction resulting in the loss of the layers, where each P atoms is single‐bonded to three nearest neighbors, and in the obtainment of a cubic lattice, where P is coordinated to 6 nearest neighbors with equivalent distances. Considering the emerging interest for the intriguing properties of phosphorene, the knowledge of the mechanism underlying the stability of these 2D layered phases of phosphorus with respect to their competing extended 3D allotropes becomes extremely relevant for designing and synthesizing phosphorene‐based materials and heterostructures.

Secondly, superconducting sc‐P is known to exhibit an anomalous pressure evolution of T _c in the pressure range below 30 GPa, where the sc phase connects to the A7 one.40

In this study we report the first experimental data able to disclose the mechanism determining the interlayer bond formation, which leads from the A7 to the sc structure.

We performed room temperature compression of bP using He as hydrostatic pressure transmitting medium, starting from pressure conditions lower than 1 GPa, where phosphorus is in the A17 phase and He is liquid. The XRD patterns acquired during the compression show that the peaks of the A17, A7 and sc phases shift towards higher 2θ values, indicating a decrease of the lattice parameters and a contraction of the unit cell volume (Figure 2). Between 4.6 and 5.0 GPa, the diffraction pattern of the A17 phase changes dramatically, revealing the occurrence of the transition to the A7 phase in agreement with literature data (SI‐2).20 Between 10.2 and 10.8 GPa several changes in the diffraction pattern indicate the occurrence of a further transformation, identified in literature as the A7 to the sc phase transition (SI‐2).

Figure 2.

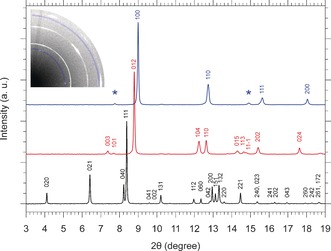
XRD patterns of phosphorus at room temperature in the A17 phase at 0.2 GPa (lower black trace), in the A7 phase at 6.5 GPa (middle red trace) and in the sc phase at 11.2 GPa (upper blue trace) with the corresponding peak indexing. The peaks of the A7 phase have been indexed according to the hexagonal cell (see SI‐3). After background subtraction each pattern has been normalized to its most intense peak. The asterisks mark the two extra peaks not expected in the sc phase, which are highlighted by the blue‐shaded arcs in the image of the diffraction pattern (upper left).

Nevertheless, in contrast to the experimental observation reporting this transition to occur sharply in pressure,19, 20 a more complex transition dynamics emerges from our data. In particular, above 10.2 GPa two peaks, apparently related to the 003_A7‐h and 113_A7‐h reflections of the A7 phase (Figure 2), persist together with the reflections expected for the sc structure and do not vanish on further compression up to the highest investigated pressure. The two peaks were observed also using different pressure transmitting media (SI‐4).

Both A7 and sc structures can be described in terms of a rhombohedral cell (R $\bar{3}$ m), with the sc one as a limit case having the angle α=60.0 degree and the atomic position u=0.250. It turns out that, assuming a sc structure, no extra peaks should be present in the diffraction pattern. In contrast, the two extra peaks naturally emerge, if α=60.0 and the atoms are slightly shifted from the u=0.250 position. To gain insight about this behavior we decided to adopt the rhombohedral cell and follow the A7 to sc phase transitions by continuously monitoring the pressure evolutions of the same parameters across the two phases. A Rietveld refinement of the XRD data was performed to obtain the values of a (lattice parameter), α (angle), u (atomic position) and nn (nearest neighbor distance) at each pressure across the investigated pressure range.

The results, reported in Figure 3, clearly show a discontinuity at 10.5 GPa, where the A7 to sc transition is expected to take place according to literature. Nevertheless, while at this pressure α rapidly approaches the limit value of 60.0 degree, u, except for a small discontinuity, is still far from the 0.250 value expected in the sc phase, which is indeed not yet reached at 27.6 GPa. Correspondingly, a first (d ₁, 3 atoms) and a second (d ₂, 3 atoms) nearest neighbor distance are observed instead of the single nn value (6 atoms) expected in the sc structure. Also in this case d ₁ and d ₂ do not converge at the highest pressure, consistently with the pressure evolution of u. As shown in Figure 3, our experimental pressure evolutions of α, a, u, d ₁ and d ₂ are in remarkable agreement with the values calculated by Chan and co‐authors.38

Figure 3.

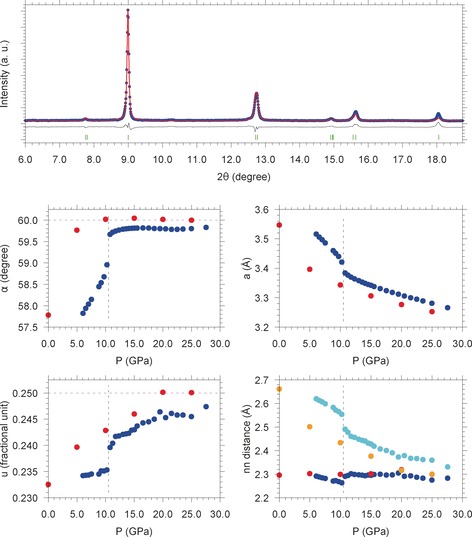
Pressure evolution of the angle α (middle left panel), the fractional atomic position u (lower left panel), the lattice parameter a (middle right panel), and the nearest neighbor distances nn (lower right panel) across the A7 to sc phase transition of phosphorus obtained by Rietveld refinement. The blue points indicate the experimental data of this study, whereas the red points are the calculated values extracted from Ref. 38. In the case of nn the blue and cyan points, respectively indicate the experimental first (d ₁) and second (d ₂) nearest neighbor distances, whereas the red and orange points, respectively indicate the calculated38 first and second nearest neighbor distances. The dashed vertical line at 10.5 GPa represents the A7 to sc phase transition, reported in literature to occur sharply. The two dashed horizontal magenta lines at 60.0 degree (middle left panel) and at 0.250 fractional unit (lower left panel) indicate the limiting values of these quantities once the transition from the A7 to the sc phase is completed. In the upper panel an experimental XRD pattern acquired at 11.2 GPa (blue points), the corresponding Rietveld fit (red trace and green markers) and their difference (black trace) are shown.

The experimental observation of the two additional peaks in our diffraction patterns, together with the pressure evolution of the rhombohedral cell parameters, unambiguously demonstrates the occurrence of a two‐step mechanism for the A7 to sc phase transition, as suggested by Chan and co‐authors.38 According to their calculations, whereas in the first step α rapidly approaches the expected value of 60.0 degree and u is still far from 0.250, in the second step u slowly approaches the expected 0.250 value at 20 GPa. Our experimental data provide a deeper insight on this mechanism indicating that at room T the first step occurs sharply in pressure at 10.5 GPa, and that the second step is not yet completed even at 27.6 GPa.

A further confirmation of this occurrence is obtained by treating the two extra reflections as originating from a distortion of the A7 structure, described by a hexagonal cell with lattice parameters a and c (SI‐5). Within this picture, as the hexagonal cell approaches the sc one, the c/a axial ratio reaches the √6≈2.45 theoretical limit.20 The data clearly show a decrease of the c/a ratio up to 10.5 GPa, where a discontinuity suddenly marks the fulfillment of the c/a≈2.45 condition, approximately corresponding to a sc lattice (Figure 4). Above 10.5 GPa the second step of the transition, involving the displacement of the atoms, dominates the transition mechanism. These observations imply that, in the pressure range from 10.5 up to at least 27.6 GPa, a pseudo simple‐cubic (p‐sc) structure exists.

Figure 4.

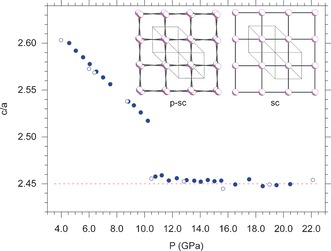
Pressure evolution of the c/a lattice parameter ratio for the A7 phase, indexed according to a hexagonal cell. The data clearly show that c/a continuously decreases up to 10.5 GPa, where the theoretical limit value of √6≈2.45, expected in the sc phase, is reached. The solid and empty circles, respectively correspond to data acquired during compression and decompression. The c/a ratio does not provide information on the atomic positions, but simply and clearly shows the effect of α≈60.0 degree on the lattice structure, which is only slightly distorted with respect to the sc one. In contrast, as indicated by the Rietveld refinement, the atomic positions are different enough to activate the extra peaks. The two insets clearly illustrate the slight distortion of the p‐sc structure (left) compared the sc one (right). The p‐sc structure was generated by the Rietveld refinement of our data at 11.2 GPa (α=59.716 degree, u=0.2404), whereas the sc one was generated imposing α=60.0 degree and u=0.250 constraints.

The abrupt changes in the pressure evolutions of α and u at 10.5 GPa suggest the A7 to p‐sc phase transition to be of the I order, whereas that of the p‐sc to sc one has to be further investigated (SI‐6).

Two major trends emerge from literature in explaining the A7 to sc phase transition in phosphorus. On one side, a Peierls distortion mechanism of the sc structure of phosphorus has been invoked to account for the formation of the A7 phase. Adopting this approach Sasaki and co‐authors35 have found that bonding in sc phosphorus is essentially covalent, due to the dominating electrostatic contribution to the total energy at high pressure with respect to the band structure one at lower pressure. On the other, Seo and Hoffmann36 have performed extended Hückel calculations observing that the Fermi surfaces of the sc phase of phosphorus are not nested, thus excluding the stability of A17 and A7 structures in phosphorus to originate from a Peierls instability of the sc phase. Instead, they have provided an interpretation of it based on a local distortion at the phosphorus atoms related to the s–p orbital mixing, which is stronger in P compared to the other group 15 elements with larger Z, due to the increasing s orbital contraction and to the weaker p orbital interaction, thus also naturally explaining the presence of lone pairs in A7 and A17.

The last interpretation is particularly appealing for explaining our results. In the A7 structure, a strong s–p mixing is responsible for the stabilizing bonding character in the filled parts of the bands, leading to the formation of lone pairs at the phosphorus sites and to shorter intralayer atomic distances with respect to the interlayer ones. At higher pressure the electrostatic contribution increases and the formation of the denser sc structure implies the shortening of the interatomic distances and the participation of the electron lone pairs in the band structure, resulting in the occupation of the p band, which has antibonding character. Depending on the density, a competition may thus exist between the stabilizing effect of the s–p orbital mixing and the formation of interlayer bonds. For sufficiently high pressure the second effect prevails, but for an intermediate pressure range, as far as this condition is not achieved, such occurrence may be responsible for the existence of the p‐sc structure, which is identified by the pressure range where α≈60.0 degree and the atomic position u≠0.250. Within this pressure range the strong s–p orbital mixing prevents the P atoms from occupying the positions expected in the sc structure and from reaching an octahedral coordination. However, with increasing density, the electrostatic contribution becomes more important, up to prevail and stabilize the sc structure at higher pressure. This interpretation is supported also by theoretical calculations about the A7 to sc transition in As, where the s–p mixing is significantly smaller, reporting that the difference in the pressures between which α and u reach the respective sc values is reduced to only 2–5 GPa.41, 42

The presence of three shorter (nearest neighbor) and three longer (next‐nearest neighbor) distances structurally relates p‐sc to A7, significantly rising the pressure limit where the layered phases of P can be stabilized.

A further remarkable outcome of our data concerns phosphorus superconductivity. The correct identification of the P structure in the 5–30 GPa pressure range is indeed extremely relevant for modeling and explaining the long‐debated anomaly in the pressure evolution of T _c. Since the first reports, many experimental and theoretical efforts over the years have tried to address the anomalous trend of T _c across the 10–30 GPa pressure range in sc‐P.40, 43, 44 Even if controversial data have been published, according to the most recent experimental report, T _c in sc‐P increases with pressure, showing a maximum at ≈32 GPa,40 and then decreases at higher pressure (SI‐7). The ab initio calculations by Chan and co‐authors,38 explicitly treating the pressure dependence of the lattice dynamics, have succeeded in reproducing the experimental T _c values at high pressure above the maximum, but have failed in reproducing the pressure evolution of T _c below the maximum. However, following the hypotheses of Chan and co‐authors,38 if the actual structure is p‐sc instead of sc, then the decrease in T _c could be explained by a decrease in N(ϵ _F ), defined as the density of states at the Fermi energy per unit cell and per spin, as the A7 structure converts to the sc one through the p‐sc structure. Such occurrence would affect the λ coupling constant and hence T _c.42, 45 Interestingly, our measurements were performed at room temperature and the complete A7 to sc conversion via the p‐sc structure was not observed up to the highest investigated pressure (27.6 GPa), suggesting this transformation to be even more hindered at low temperature, where superconductivity data have been acquired.

In this paper we have reported a room temperature XRD study of the phosphorus phase transitions in the 0–30 GPa pressure range, using He as pressure transmitting medium. Our data show previously unreported peaks of weak intensity, related to the A7 phase, which persist from 10.5 GPa, where the transition to the sc phase is reported to occur according to literature, up to the highest investigated pressure. The Rietveld refinement of the data allowed to monitor the structural details of a two‐step mechanism ruling the bond reconstruction, which takes place during the transition from the layered A7 to the extended sc phase. The data unveil the existence of an intermediate structure of phosphorus, which we identified as pseudo simple‐cubic. This experimental evidence has two remarkable implications. From a chemical point of view, the existence of the p‐sc structure is responsible for the presence of three shorter and three longer interatomic distances, similarly to the layered A17 and A7 phases and in contrast with the six‐fold coordination typical of the sc structure, thus significantly rising the pressure range where the layered phases of phosphorus can exist. On the other side, as superconductivity in bP is concerned, it provides a new experimental insight for the interpretation of the anomalous pressure evolution of T _c below 30 GPa. A competition between s–p orbital mixing and electrostatic interactions with increasing pressure, is here proposed to account for the existence of the p‐sc phase. Considering the rising interest in phosphorene and related materials, the knowledge of the effects playing a key role in the stabilization of the layers and of the mechanism determining the interlayer bond formation is of fundamental importance for the design, synthesis and stabilization of phosphorene based systems both at ambient pressure and under high density conditions.

Experimental Section

Pressure was generated by means of membrane diamond anvil cells (DAC) equipped with Ia/IIa type standard cut 16‐sided beveled anvils having 350 to 400 μm culet size. The sample was contained sideways by a Re gasket (200 μm) indented to about 70 μm and laser‐drilled to obtain a 150 μm diameter hole. Highly crystalline and pure orthorhombic bP, synthesized from red phosphorus according to Ref. 46, was used for the experiments. The obtained bP crystals were then fragmented and cut by a metallic tip to obtain smaller 20–50 μm chips, which were placed in the sample chamber of the DAC, together with a ruby chip for the measurement of pressure. The DAC was then gas‐loaded with high purity He (5.0) and the bP/He sample studied by means of synchrotron X‐ray diffraction (XRD). Due to the heterogeneity of the sample a micron‐sized beam spot diameter of the synchrotron source was used to select areas of the sample containing bP. This allowed to spot differently oriented bP crystallites and find the reflections necessary for the calculation of the lattice parameters and the unit cell volume. The XRD patterns were acquired at ESRF‐ID27 high pressure dedicated beam line, using a monochromatic radiation (0.3738 Å wavelength) with beam spot size diameter of 5 μm and a MAR CCD165 detector. Typical acquisition time was 20 s with ≈10 degree oscillation. The detector tilt and sample to detector distance were determined by CeO₂ standard. The raw images were processed using DIOPTAS software47 and the lattice parameters, atomic positions and nearest neighbor distances were evaluated by the Rietveld fits of the integrated patterns using GSAS‐II software48 (Table SI‐1).

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

D. Scelta, A. Baldassarre, M. Serrano-Ruiz, K. Dziubek, A. B. Cairns, M. Peruzzini, R. Bini, M. Ceppatelli, Angew. Chem. Int. Ed. 2017, 56, 14135.