Bandit strategies evaluated in the context of clinical trials in rare life-threatening diseases

Abstract

In a rare life-threatening disease setting the number of patients in the trial is a high proportion of all patients with the condition (if not all of them). Further, this number is usually not enough to guarantee the required statistical power to detect a treatment effect of a meaningful size. In such a context, the idea of prioritizing patient benefit over hypothesis testing as the goal of the trial can lead to a trial design that produces useful information to guide treatment, even if it does not do so with the standard levels of statistical confidence. The idealised model to consider such an optimal design of a clinical trial is known as a classic multi-armed bandit problem with a finite patient horizon and a patient benefit objective function. Such a design maximises patient benefit by balancing the learning and earning goals as data accumulates and given the patient horizon. On the other hand, optimally solving such a model has a very high computational cost (many times prohibitive) and more importantly, a cumbersome implementation, even for populations as small as a hundred patients.

Several computationally feasible heuristic rules to address this problem have been proposed over the last 40 years in the literature. In this article we study a novel heuristic approach to solve it based on the reformulation of the problem as a Restless bandit problem and the derivation of its corresponding Whittle index rule. Such rule was recently proposed in the context of a clinical trial in Villar et al (2015). We perform extensive computational studies to compare through both exact value calculations and simulated values the performance of this rule, other index rules and simpler heuristics previously proposed in the literature. Our results suggest that for the two and three-armed case and a patient horizon less or equal than a hundred patients, all index rules are a priori practically identical in terms of the expected proportion of success attained when all arms start with a uniform prior. However, we find that a posteriori, for specific values of the parameters of interest, the index policies outperform the simpler rules in every instance and specially so in the case of many arms and a larger, though still relatively small, total number of patients with the diseases. The very good performance of bandit rules in terms of patient benefit (i.e. expected number of successes and mean number of patients allocated to the best arm, if it exists) makes them very appealing in context of the challenge posed by drug development for rare life threatening diseases.

1. Introduction

Developing specific statistical learning methods for drug development for rare diseases is one of the most pressing modern clinical needs. Answering scientific questions for rare conditions has long been limited mainly by the unavailability of enough patients for running standard clinical trials. The number of patients required to run a trial is strongly influenced by regulatory agencies, such as the FDA in the U.S.A or the EMA in Europe, and ethical standards as those summarised in the Belmont report. The traditional rationale behind this minimum number comes from embracing as the main goal of the trial that of maximising the learning about the treatments under consideration.

The way in which such a learning goal is implemented in practice is as follows: physicians agree on an improvement over the control response rate Δp (or treatment effect) that would be beneficial to establish. Then, given that patients are randomly assigned to treatments in a balanced fashion, the trial’s number of participants is determined as that which ensures controlling for the probabilities rates of both a false positive (Type I error) and a true positive (Power) associated with the chosen treatment effect Δp. These rates typically are (two-sided) 5% and at least 80%, respectively. The logic behind this widespread paradigm is that because a number of patients much larger than those in the trial stands to benefit from the resulting learning provided by the trial, then its design should ensure conclusions drawn by the end of it are carefully controlled.

However, for rare conditions it occurs that the size of the trial that meets these requirements is either larger than the current estimation of the patient population (or patient horizon) or it would only be achieved after an excessively long recruitment period (after which the learning from the trial would most likely be rendered irrelevant for patients with the disease). In other words, the learning goal as a guide to trial design is usually either impossible or absolutely impractical to achieve in rare diseases populations. There is therefore a real and compelling need for a new and more adequate paradigm for generating clinical evidence and making treatment decisions for small populations, particularly when the disease is life-threatening. Such a need is starting to be acknowledged by institutions worldwide, e.g. the European Union has recently funded three international, multidisciplinary research consortia aiming at the development of efficient statistical methods for the assessment of the safety and/or efficacy of a treatment for small population groups. More importantly, this need will become increasingly pressing as genomic approaches continue to advance and disease categories are fragmented into finer and finer entities.

If such a controlled learning goal is not feasible, then a way out of the conundrum is to change the goal. A sensible goal of a trial involving a rare life-threatening condition is, instead of learning in a highly controlled way, to learn enough so as to effectively treat as many patients in the population as possible. In that context, the relevant statistical question is how much learning is necessary to best treat the whole patient population, thus moving the focus of the trial away from that of maximum learning with a controlled confidence level. The resulting paradigm provides an alternative and feasible method to evaluate new therapies for rare and fatal diseases and to balance the need for experimentation with the desire to guide treatment selection towards the best treatment of a population.

Implementing such a dual learning-earning goal into a trial can be done in several ways. In the first place, it depends on the way the learning and earning phases are envisaged. In Cheng et al (2003) it is assumed that the learning and earning are two distinct phases whose sizes are decided a priori of making any observation and that the learning phase takes the form of a balanced randomized trial. Therefore, the optimal design question reduces to determining the size of the experimenting stage n such that mean proportion of successes in the trial and the remaining population is maximised. Assuming equipoise regarding the therapeutic effectiveness of the treatments involved they show that the optimal sample size for a randomized trial has an order of magnitude of $\sqrt{N},$ where N is the patient horizon.

If, however, the size of the learning phase n is not fixed in advance and the question of balancing learning and earning is asked after every patient (i.e., the approach is fully sequential) then the advantages, in terms of patient benefit, are the highest yet treatment allocation, as determined by decision analysis, is deterministic, tedious to implement and computationally intensive. Examples of papers aiming at overcoming these limitations which are relevant to this article, include Cheng and Berry (2007), Villar et al (2015) and Berry (1978). In the first two papers authors aim at introducing randomization to bandit based strategies. In Cheng and Berry (2007) the authors introduce randomization to decision-analytic rules by determining optimal allocation probabilities that deviate from a balanced randomized scheme and have a minimum value of r, with r ≤ 1/K and K being the number of treatments in the trial. In Villar et al (2015) the authors propose a fully randomized, adaptive group allocation procedure based on the optimal solution to the classic infinite horizon bandit problem. In Berry (1978) the computational and implementation difficulties are addressed by proposing a near-optimal heuristic strategy based on the so called Feldman’s rule. For a recent review paper and a discussion of other limitations to the application of these decision-analytic approaches known as bandit models to clinical trial design see Villar et al (2015).

In this paper we focus on overcoming the computational limitations of bandit-based designs and on the performance evaluation of index-based heuristics. We extend the ideas presented in Villar et al (2015) and relate then to the work in Berry (1978). We explain how to derive near optimal heuristics for the finite-horizon Bernoulli Multi-armed Bandit problem based on a Restless bandit reformulation of the problem and on the Whittle and Gittins indices. We illustrate how this approach manages to reduce the suboptimality gap (when compared to that of Feldman’s approach in Berry (1978)), being computationally feasible and relatively simple to interpret and implement. We compare it with other heuristics and we perform various exact and simulated calculations in different contexts to evaluate when their application is more appropriate.

2. The Whittle Index Approach

2.1. Background

Consider a patient population of size N and K experimental treatments and a control treatment (either standard of care or placebo, represented by k = 0) under study. Patients are assigned sequentially to treatments and the outcome of a patient j allocated to some treatment k is observed before making the treatment decision for patient j + 1. Further, for simplicity, suppose that the response to treatment is random and binary, i.e. is either a success (positive) or a failure (negative). Denote the probability of a success using treatment k by p_k.

The optimization problem is to find a treatment allocation rule that specifies which arm, out of the K + 1 possible ones, will be received by each of the N patients so as to achieve a chosen goal. Such a rule can be expressed by means of a deterministic sequence {a_k,j, j = 1,…, N k = 0,…, K}, with a_k,j being a binary indicator variable denoting whether patient j is assigned to treatment k (a_k,j = 1) or not (a_k,j = 0). Naturally, given that only one treatment can be allocated per patient we impose that ${\Sigma }_{k=0}^K{a}_{k,j}=1$ for every patient j. Randomization of the allocation sequence could be considered by allowing for the definition of allocation probabilities as P (a_k,j = 1) but as it turns out that the optimal policy is deterministic we shall not consider randomized policies in this paper.

Suppose that the objective of the problem is to maximize the mean proportion of positive responses in these N patients. If every p_k is known, then all the information to make a decision is available before the start of the trial and the way to maximise the mean proportion of successes is to allocate all patients to the treatment with the highest success rate, in which case the maximum mean expected proportions of successes is p* where p* = max_{k:0,…,K pk}. If the p_k’s are unknown, as patients are treated information about the treatments will be accumulated which may be used to better treat patients appearing later in time. A unified way to handle such accumulating information is to, following a Bayesian approach, quantify the information about every p_k in the form of a probability distribution and then define an optimal treatment allocation design as that which maximizes the proportion of successes over the N patients averaged over p_k .

Let the outcome of every patient j under any treatment arm k be a K + 1-dimensional random sequence {(X_0,j, X_1,j, …, X_K,j j = 1,…, N} out of which only one element can be observed, i.e. that of the allocated treatment arm: $\left\{Z_j\left(\tau \right)={\Sigma }_{k=0}^K{a}_{k,j}^{\tau }{X}_{k,j},j=1,\dots ,N\right\}$ where τ represents the treatment allocation rule. Applying a decision-analytic approach and considering the utility of the design to be the proportion of successes in the N patients, the value of a design τ is,

$$V\left(\tau ,N,\pi ,K\right)=\frac{𝖤\left[\left({\displaystyle {\sum }_{j=1}^N{Z}_j(\tau )}\right)\right]}{N},$$ (1)

where π is the joint prior distribution of (p₀, p₁, …, p_K), which for Bernoulli independent arms is the product of Beta distributions Be(a, b). And naturally, the optimization problem is therefore, to find the design τ* such that

$$V^{*}\left(N,\pi ,K\right)=V\left({\tau }^{*},N,\pi ,K\right)=\underset{\tau \in 𝒯}{\text{max}}\frac{𝖤\left[\left({\displaystyle {\sum }_{j=1}^N{Z}_j(\tau )}\right)\right]}{N},$$ (2)

where $\mathit{𝒯}$ is the family of admissible designs, i.e. all the feasible sequences of treatment actions $\left\{a_{k,j}^{\tau }\right\}$ for all j and k.

Equation (2) defines a finite-horizon “K + 1-armed bandit” problem whose exact optimal solution can only be found by applying a backwards induction algorithm to solve its associated dynamic programming formulation. This optimal procedure is computationally very expensive and its cost explodes as the number of experimental arms K and the population size N grow, being unfeasible for instances as small as K = 2 and N ≥ 100. Moreover, its implementation is highly difficult since it has to specify a treatment to use in all possible population outcome histories, i.e. 2(K + 1)^N situations. This is the main reason why approximate and simpler methods to solve these problems have long been studied and proposed in the literature.

2.2. Index based strategies: the Gittins index

An elegant and computationally tractable solution to a variant of problem (2) that considers an infinite number of patients, i.e. N = ∞, and therefore, for the sake of tractability of the value function, includes a discount factor 0 ≤ d < 1 to weigh the observed successes across patients, was first obtained by Gittins and Jones (1974). This was a significant breakthrough, as the result brings to the realms of computational feasibility instances of the multi-armed problem that were not available before via the traditional approach. The main reason for that is that the solution to each of those K + 1 two-armed problems is significantly computationally cheaper and, as shown in Bellman (1956), it has a simple structure expressible in terms of an index function which depends only on the total observed number of successes s and failures f of the unknown process. Such function is obtained by comparing a known arm with success rate p to the unknown arm with expected success rate s/(s + f) and returning the value of p, denoted by p* that would make the decision maker indifferent between these two arms. This p* value is the index function which can be used for expressing the optimal policy as a threshold policy: allocate patients to the unknown arm as long as s/(s + f) > p*. Gittins and Jones (1974) showed that Bellman’s index function can be used to express the optimal solution to the K + 1-armed infinite discounted bandit problem: simply allocate patient j to the treatment with the highest Gittins index p* (for a given pair of s and f) at time t.

Specifically, the calibration method uses Dynamic Programming to approximate the Gittins index values based on this idea, as explained in Gittins and Jones (1979). This index computation method solves, for a grid of p values (the size of which determines the accuracy of the resulting index values approximations), the following problem

$$V^{*}\left(s,f,p\right)=\text{max}\left\{\frac{p}{1-d},\frac{s}{s+f}\left(1+d{V}^{*}\left(s+1,f,p\right)\right)+\frac{f}{s+f}\left(d{V}^{*}\left(s,f+1,p\right)\right)\right\},$$ (3)

The set of values of (s, f) (i.e. successes and failures observed in the unknown arm) and p for which the two expressions in the maximum in (3) are equal imply that the Gittins index value for an arm with a prior Be(s, f) and discount factor d is p.

Calculations of the Gittins indices have been reported in brief tables as in Gittins (1979). Improvements to the efficiency of this index computing method have since been proposed by Katehakis and Veinott Jr (1985); Katehakis and Derman (1986). Table 1 reports values of the Gittins index for different combinations of (s, f) and d = 0.999.

Table 1.

The (approximate) Gittins index values for an information vector of s successes and f failures where d = 0.999 and N is truncated at N = 1000.

f/s	1	2	3	4	5	6
1	0.9424	0.9596	0.9673	0.9719	0.9751	0.9774
2	0.8246	0.8748	0.8993	0.9145	0.9250	0.9328
3	0.7075	0.7825	0.8226	0.8483	0.8665	0.8803
4	0.6098	0.6986	0.7492	0.7834	0.8082	0.8272
5	0.5310	0.6249	0.6836	0.7236	0.7532	0.7766
6	0.4667	0.5642	0.6252	0.6696	0.7031	0.7293

2.3. The Whittle index

Of course, patient populations in general (not only those in rare diseases) are never of an infinite size, so the infinite-horizon assumption is not a sensible one. For the rare diseases case, we are interested in the case where N is not only finite but relatively small to run a traditional randomised trial to select a best treatment. Thus, the relevant problem for optimal treatment allocation designs is as defined in (2), with a finite value of N. However, the Gittins Theorem does not apply to this case, and thus the index function as defined for the infinite-horizon variant does not exist (see Berry and Fristedt, 1985). Indeed, a solution could in theory be obtained via DP, but, for reasons already stated, this would be impractical even for relatively small-scale scenarios. In the infinite-horizon problem, when making the treatment decision for any patient j there is always an infinite number of possible sample observations to be drawn from any of the treatments. This is no longer the case in a finite-horizon problem, and the value of an outcome history is not the same when the treatment allocation process is about to start than when it is about to end. The finite-horizon problem analysis is thus more complex, because these transient effects must be considered for the characterization of the optimal policy.

Specifically, a cut-off value similar to the Gittins index will depend on the number of patients treated (or equivalently, the number of patients remaining in the population to treat). Therefore, for every patient j we could compute an index value that will now depend not only on the number of observed successes and failures per arm but also on the number of patients treated. Such an index could be computed using the calibration method solving, for a grid of p values, the following DP problems

$$\begin{gathered} V_{N-1}^{*}\left(s,f,p,N\right)=\text{max}\left\{p,\frac{s}{s+f}\right\} \\ {V}_j^{*}\left(s,f,p,N\right)=\text{max}\{p{\displaystyle \sum _{t=j}^N{d}^t}, \\ \frac{s}{s+f}\left(1+d{V}_{(j+1)}^{*}\left(s+1,f,p,N\right)\right)+\frac{f}{s+f}\left(d{V}_{(j+1)}^{*}\left(s,f+1,p,N\right)\right)\},j=0,\dots ,N-2, \end{gathered}$$ (4)

where in this case, the set of values of (s, f) (i.e. successes and failures observed in the unknown arm), N, j and p for which the two expressions defining the maximum value of $V_j^{*}\left(s,f,p,N\right)$ in (4) are equal determine that the finite-horizon index value for an arm with a prior Be(s, f), N − j patients to treat and discount factor d is $p_{\left(N-j\right)}^{*}.$ For instance, for the last patient in the trial, i.e. for j = N − 1, the associated index value would just be $p_{\left(N-1\right)}^{*}=\frac{s}{s+f},$ the treatment’s posterior mean. Note that, if d < 1 then ${\Sigma }_{t=j}^N{d}^t=\frac{1-d^{N-j}}{1-d}$ whereas if d = 1 then ${\Sigma }_{t=j}^N{d}^t=N-j.$

In fact as mentioned in Villar et al (2015), such index policy can also be derived based on an equivalent reformulation of (2) in which the information state of each arm is augmented, adding to the number of observed successes and failures per arm, the number of remaining patients that can be assigned to the K + 1 treatments. Such a reformulation is an infinite-horizon Restless MABP (Nino-Mora, 2005). The restlessness of bandit models refers to the fact that each arm’s information state continues to evolve even when not selected for being active. In this particular case, the fact that the number of remaining patients is part of every arm’s information state and this varies for all arms (allocated or not) over the trial, introduces the restless feature first proposed by the seminal work by Whittle (1988). Index strategies for Restless MABP do not always exist and if they do, they are not necessarily optimal. Whittle (1988) deployed a Lagrangian relaxation and decomposition approach to derive an index function, analogous to Gittins index, which has become known as the Whittle index. Whittle further conjectured that the index policy for the restless variant enjoys a form of asymptotic optimality (in terms of the ETD rewards achieved), a property later established by Weber and Weiss (1990) under certain conditions. Typically, the resulting heuristic has been found to be nearly optimal in various models.

In general, establishing the existence of an index function for a restless MABP (i.e. showing its indexability) and computing it is a tedious task. In some cases, the sufficient indexability conditions (SIC) introduced by Niño-Mora (2001) can be applied for both purposes. Nevertheless, the restless bandit reformulation of (2) is always indexable. Such a property can either be shown by means of the SIC approach or simply using the seminal result in Bellman (1956), by which the monotonicity of the optimal policies can be ensured, allowing to focus attention on a nested family of stopping-times. Moreover, the computation of the Whittle index can be done as a modified version of the Gittins index (See Proposition 3.1 in Niño-Mora, 2011) in which the search of the optimal stopping time is truncated to be less than or equal to the number of remaining patients to be treated (and this is repeated for each patient to be treated).

Table 2, Table 3 and Table 4 include some values of the Whittle indices for different combinations of (s, f) and d = 0.999 when N = 200, and the number of remaining observations is respectively allowed to be N − j = 50, N − j = 100 and N − j = 150.

Table 2.

The Whittle index values for an information vector of s successes and f failures, n ‒ j = 50, d = 1 and where the size of the trial is n = 200

f/s	1	2	3	4	5	6
1	0.8246	0.8792	0.9042	0.9192	0.9294	0.9370
2	0.6378	0.7373	0.7886	0.8210	0.8437	0.8607
3	0.5047	0.6209	0.6871	0.7317	0.7636	0.7882
4	0.4111	0.5292	0.6040	0.6553	0.6933	0.7233
5	0.3435	0.4603	0.5349	0.5907	0.6328	0.6660
6	0.2929	0.4048	0.4800	0.5357	0.5804	0.6162

Table 3.

The Whittle index at n − j = 100

f/s	1	2	3	4	5	6
1	0.8659	0.9071	0.9258	0.9371	0.9448	0.9505
2	0.6949	0.7797	0.8227	0.8497	0.8685	0.8826
3	0.5610	0.6674	0.7261	0.7653	0.7933	0.8146
4	0.4643	0.5754	0.6441	0.6905	0.7252	0.7521
5	0.3914	0.5040	0.5748	0.6264	0.6652	0.6956
6	0.3365	0.4458	0.5174	0.5709	0.6127	0.6460

Table 4.

The Whittle index at n − j = 150

f/s	1	2	3	4	5	6
1	0.8859	0.9207	0.9365	0.9460	0.9525	0.9573
2	0.7252	0.8019	0.8406	0.8648	0.8817	0.8942
3	0.5925	0.6930	0.7476	0.7837	0.8096	0.8291
4	0.4949	0.6018	0.6667	0.7103	0.7431	0.7682
5	0.4196	0.5291	0.5977	0.6468	0.6837	0.7127
6	0.3625	0.4700	0.5391	0.5913	0.6314	0.6633

Again, the Whittle index rule assigns a number from these tables to every treatment, based on the values of s and f and on the number of remaining periods n − j, and then prioritizes sampling the one with highest value.

2.4. Other index strategies

The index strategies described in the previous sections are an example of simple and natural rules that dynamically prioritize resource allocation among different stochastic projects. However, the class of index policies is still overwhelmingly large, and despite all being computationally tractable only in special cases they result in well-performing or even optimal policies. Index strategies, in general, define a priority index for each treatment as a function of its information state (observed successes and failures). The associated priority-index heuristic allocates for each patient the treatment with currently largest index value.

In this paper we shall also consider three alternative priority-index heuristics for the finite horizon multi-armed bandit problem: the Myopic Index (MI), Feldman’s rule (FR) and a Gittins Index heuristic (GI). The MI is perhaps the simplest priority-index rule, which has usually been proposed as a heuristic for addressing several optimization problems. In the context of this problem the MI uses the posterior mean of each treatment after observing the outcome of a patient j to make the decision for patient j + 1.

FR is based on work by Feldman (1962) which showed that the optimal solution to a special case of the two-armed bandit problem in which we know the possible values for the two arms’ success rates are p_A and p_B but we do not know which arm has which success rate admits a simple index rule. In terms of this simple problem both FE and the optimal rule would allocate treatment k whenever the current probability that p_k = max{p_A, p_B} is at least 1/2. This is equivalent to a much simpler rule in which if s₀ − f₀ ≥ s₁ − f₁ then it is optimal to allocate treatment 0 and otherwise it is optimal to allocate treatment 1. Berry (1978) was the first to propose and assess the use of FR as a heuristic solution for the general two-armed bandit problem. In this paper we shall extend FR as a heuristic for the multi-armed case by letting the index per arm be defined as s_k − f_k and then applying the index rule, i.e. allocating the treatment with the highest index, breaking ties at random.

Additionally we will define a GI heuristic by using the Gittins index for a given discount factor value d to make decisions for all patients in the population. This will imply that the same table of values will be used across the population simplifying computations when comparing it with the Whittle index (WI). Notice that an alternative way to define a GI heuristic would be to choose a different discount factor for each patient. The rationale behind the choice of each discount factor of d_j is that if the discount factor d_j is interpreted as the probability that the trial will continue after each patient, then the probability that the remaining patient population is of size N − j (or smaller) can be computed as $\left(1-d_j^{N-j}\right)$ and we would like this probability to be approximately 1. For example, if j = N − 1 (the last patient in the population is to be treated) then d_N−1 = 0 so that $\left(1-d_j^{N-j}\right)=1.$ Alternatively, if j = 0 (the first patient in the population is to be treated) and N = 100 then d_N−1 = 0.9 makes $\left(1-d_j^{N-j}\right)\approx 1$ (or in other words it makes the expected size of the remaining patient population of size $\frac{1}{\left(1-d_j\right)}=100$). However, using this GI heuristic would result in a computational cost very similar to that of the WI as a different index table per patient would be needed.

3. Numerical Results

3.1. Two-armed trials

In Berry (1978) numerical (exact) results were first shown for FR and the optimal rule in context of the two-armed bandit problem in which the joint density of (p₁, p₂) before the start of the trial is the product of two uniform distributions (corresponding to the clinical equipoise principle by which there is genuine uncertainty in the expert medical community over which treatment will be beneficial, if any). The results in Berry (1978) show how this simple rule has a very good performance, as depicted in Table 5, its suboptimality gap for N = 100 is of only 1.5%.

Table 5.

The simulated expected proportion of successes of the different patient allocation rules for the two-armed bandit problem with uniform priors

1. Expected Proportion of Successes When a1 = b1 = a2 = b2 = 1
n	τ *	WI(N)	GI(0.9)	FR	MI
1	0.50000	0.50000	0.50000	0.50000	0.50000
2	0.54167	0.54167	0.54167	0.54167	0.54167
3	0.55556	0.55556	0.55556	0.55556	0.55556
4	0.56944	0.56944	0.56944	0.56944	0.56875
5	0.57778	0.57778	0.57778	0.57611	0.57694
6	0.58472	0.58472	0.58472	0.58403	0.58371
7	0.59028	0.59028	0.59016	0.58812	0.58910
8	0.59494	0.59494	0.59457	0.59346	0.59367
9	0.59866	0.59866	0.59841	0.59625	0.59727
10	0.60218	0.60215	0.60197	0.60017	0.60058
15	0.61410	0.61406	0.61386	0.61049	0.61164
20	0.62156	0.62147	0.62125	0.61746	0.61827
25	0.62679	0.62670	0.62636	0.62162	0.62271
30	0.63066	0.63061	0.63011	0.62515	0.62594
35	0.63371	0.63363	0.63301	0.62743	0.62840
40	0.63617	0.63609	0.63533	0.63410	0.63034
60	0.64271	0.64265	0.64131	0.63460	0.63526
80	0.64657	0.64651	0.64468	0.63757	0.63800
100	0.64918	0.64912	0.64687	0.63943	0.63975

We have extended the exact numerical results included in Berry (1978) in Table 5 by also including the results for the other rules considered in this paper: MI, GI(d = 0.9) and WI. The results indicate that the MI rule and FR are a priori practically equivalent in their performance (although MI appears to slightly outperform FR for N > 4). As well, the GI and WI are also very similar in their performance but WI always outperforms the GI approach. On the other hand, both GI and WI are also almost equivalent to the optimal rule. According to these results, the simplest approaches perform sufficiently well to justify getting into the complexity of applying the index policies, at least for when K = 2 and n ≤ 100. However, as shown in Table 6, once a fixed pair of success rates is assumed there are important differences that are worth pointing out, i.e. in terms of the resulting value function V* (N, π) and the mean proportion of patients allocated to a best arm (when it exists) p*. These differences in performance are explained because the results in Table 5 correspond to averaging over all possible values of p₁, p₂ whereas the results in Table 6 correspond to a particular point in the parameter space of (p₁, p₂).

Table 6.

The expected proportion of patients allocated to the best arm p* and the expected proportion of successes of the different patient allocation rules for the two-armed bandit problem starting with uniform priors when p₁ = 0.3 and p₂ = 0.5.

2. Expected Proportion of patients allocated to the best arm and Expected Proportion of successes when p1 = 0.3 and p2 = 0.5
N	WI(N)		GI(0.9)		FR		MI
	p*	V*(N, πWI)	p*	V*(N, πGI)	p*	V*(N, πFR)	p*	V*(N, πMI)
50	0.7652	0.4604	0.7364	0.4498	0.7389	0.4518	0.7085	0.4414
100	0.8538	0.4723	0.8283	0.4688	0.8094	0.4625	0.7493	0.4528
150	0.8717	0.4769	0.8573	0.4758	0.8432	0.4705	0.7892	0.4619
200	0.9051	0.4821	0.8886	0.4802	0.8584	0.4738	0.7928	0.4592
250	0.9205	0.4851	0.9029	0.4825	0.8770	0.4763	0.8207	0.4654
300	0.9284	0.4868	0.9197	0.4857	0.8877	0.4789	0.8260	0.4650

Table 6 shows the results of applying each of the patients allocation rule when the true (though unknown to the decision maker) vector of parameters is equal to p = (0.3, 0.5) after 10⁴ trial replicas by simulation. The results show that the WI is superior to all other rules in terms of p*. These results also suggest that FR is superior to the MI rule, both in terms of p* and its resulting value function. The table also suggests that while for the WI and GI the differences tend to vanish as N grows, the opposite happens for FR and MI. Note that the relative increase in the mean proportion of patients assigned to best treatment of using the best index based approach (i.e. WI) over the simpler approaches goes from 0.08 and 0.036 (for N = 50) to 0.124 and 0.046 (for N = 300) for the MI and FR respectively.

3.2. Multi-armed trials

Besides the need for designs specifically tailored for small populations, in some therapeutic areas, such as in cancer treatment, there are several possible agents awaiting trials, and thus a major challenge in their development is the considerable time and resources needed for conducting separate randomized clinical trials. Multi-arm trials in which several novel treatments are compared in the same trial have many advantages: they are more efficient and cheaper, since a shared control group is used; more treatments can be simultaneously tested with a limited set of patients; and tend to be more popular with patients as a greater chance of being allocated to a new/superior treatment is perceived by them or their families. Moreover, the benefits of adaptive rules such as the ones considered in this paper should be the greatest as the number of arms included in the trial grows.

In this section we will illustrate this advantage through an exact computation for the case K = 3 and through simulation results of trials involving three and more arms. All of the index rules here considered are deployed as follows: for every patient allocate the treatment with the current highest index value, breaking ties at random.

The results in Table 7 show how the difference in the performance of the simpler heuristics (MI and FR) tends to be further away from the optimal value for a given number of patients (when compared to the two-armed values in Table 5). The suboptimality gap of the MI rule goes from 0.65% when K = 2 and N = 25 to 1.07% when K = 3 and N = 25. On the other hand, for the WI and GI this suboptimality gap also increases but it is still very close to the optimal value for every N . For example, the suboptimality gap of the WI rule goes from 0.01% when K = 2 and N = 25 to 0.03% when K = 3 and N = 25.

Table 7.

Exact computations: the expected proportion of successes of the different patient allocation rules for the three-armed bandit problem with uniform priors

2. Expected Proportion of Successes When a1 = b1 = a2 = b2 = a3 = b3 = 1
n	τ *	W I(N)	GI(0.9)	FR	MI
1	0.50000	0.50000	0.50000	0.50000	0.50000
2	0.54166	0.54166	0.54166	0.54166	0.54166
3	0.56944	0.56944	0.56944	0.56944	0.56944
4	0.58681	0.58681	0.58681	0.58634	0.58634
5	0.60139	0.60139	0.60139	0.60019	0.60019
6	0.61273	0.61273	0.61273	0.61114	0.61114
7	0.62153	0.62153	0.62141	0.61939	0.61965
8	0.62894	0.62894	0.62847	0.62656	0.62685
9	0.63549	0.63549	0.63494	0.63273	0.63310
10	0.64096	0.64096	0.64051	0.63787	0.63831
15	0.66083	0.66062	0.66034	0.65607	0.65653
20	0.67329	0.67322	0.67276	0.66715	0.66744
25	0.68207	0.68190	0.68130	0.67474	0.67480
30	0.68863	0.68854	0.68766	0.68013	0.68031

In Table 8 we show results of simulations for larger number of arms and different populations sizes. The advantage of the WI and GI rules over the myopic approaches becomes larger as the number of arms and the patient horizon grows. For the case N = 300 and K = 7 the absolute difference in the mean proportion of successes between WI and MI is approximately 0.06, which represents 18 patients. It is worth pointing out that FR outperforms the MI rule in every instance though the difference is less than 10⁻³. This difference could be within Montecarlo error if the exact difference is less than 10⁻⁴ as suggested by the results in Table 7.

Table 8.

Computations through simulations: The expected proportion of successes of the different patient allocation rules for the multi-armed bandit problem with uniform priors as the number of arms grows. Number of simulations: 10⁴

2. (Simulated) Expected Proportion of Successes for different K + 1 and ak = bk = 1 ∀k
K + 1	N	WI(N)	GI(0.9)	FR	MI
3	50	0.69998	0.69418	0.69139	0.68764
4	50	0.74251	0.73112	0.71733	0.72062
5	50	0.76086	0.74831	0.73494	0.73406
6	50	0.77699	0.76223	0.74734	0.74392
7	50	0.78765	0.76882	0.76882	0.74756
3	100	0.72044	0.71546	0.70069	0.69746
4	100	0.76041	0.75474	0.73722	0.73211
5	100	0.78468	0.77740	0.75286	0.74976
6	100	0.80564	0.79454	0.76554	0.76360
7	100	0.81610	0.80490	0.77173	0.76763
3	150	0.72887	0.72065	0.71434	0.70098
4	150	0.77154	0.76511	0.74128	0.73770
5	150	0.79607	0.78962	0.76022	0.75361
6	150	0.81826	0.80795	0.77028	0.76826
7	150	0.82904	0.82564	0.77969	0.77623
3	200	0.73038	0.72806	0.70869	0.70422
4	200	0.77938	0.77465	0.74327	0.73923
5	200	0.80376	0.79647	0.76827	0.75880
6	200	0.82344	0.82099	0.77627	0.77205
7	200	0.83853	0.83263	0.83263	0.78078
3	250	0.73209	0.73395	0.70784	0.70852
4	250	0.77532	0.77750	0.75175	0.74114
5	250	0.80925	0.80394	0.76483	0.76463
6	250	0.82318	0.82946	0.77777	0.77369
7	250	0.84381	0.83838	0.78587	0.78430
3	300	0.73459	0.73450	0.71403	0.71251
4	300	0.78174	0.77852	0.74749	0.74218
5	300	0.80761	0.80962	0.77007	0.76422
6	300	0.83119	0.83053	0.78250	0.77814
7	300	0.84643	0.84440	0.78740	0.78656

3.3. Understanding the Whittle Index rule

In this section we look into the situations under which the WI rule fails to recover the optimal action so as to learn about the biases and mistakes than can result from its use in practice. For simplicity we focus on the two-armed bandit case with an initial uniform prior on both arms.

There are instances in which the WI rule makes a deterministic decision while the optimal action is to randomize the treatments. However, these instances do not affect the resulting value function, because both actions are equally optimal. For example, this occurs for N = 8 and 5 patients have been treated with all of them allocated to one of the arms and 3 successes and 2 failures observed. The optimal decision for the patient 6 is to randomise him/her to the two treatments with equal probability The WI rule however, chooses the more explored arm because its index is 0.6049 whereas the unexplored arm has an index of 0.5909.

The instances in which the WI rule makes a allocation that differs from the optimal one and it affects the resulting value function are those that actually introduce a bias or mistake. The first of these instances happens for N = 10. The only difference between the actions selected by the WI and the optimal rule occur for only two instances out of all the possible trial histories (4¹⁰). They correspond to the case in which 7 patients have been treated and six have been allocated to the first arm n₁ = 6, with 2 successes s₁ = 2 and four failures f₁ = 4 and one observation was allocated to the second arm n₂ = 1 with s₁ = 0 and f₁ = 1. The Whittle indices (for d = 1) respectively are 0.4054 and 0.4000. Therefore, the action selected by the Whittle rule is to allocate treatment 1 to patient 8 whereas the optimal action is to allocate treatment 2 (which is less explored). By symmetry the case of the same history for the alternate arms is the same.

Basically, the mistake happens in those instances in which the difference between the indices is small (in the above case of 0.0054), which means that the arms have a very similar posterior mean, but arms have a significant difference in how much they have been explored. In that case, the WI selects the arm with the highest immediate expected effect while the optimal action is to allocate the one with the smaller index but which has been less explored. This indicates that the instances in which the WI makes a wrong decision are caused by the WI being slightly more myopic than than the optimal rule would be. Of course, there are no suboptimality instances for the last patient in the trial (because both the optimal and the WI rules allocate that patient to the treatment with highest posterior mean) and there are no suboptimal instances in the first patients because the arms have not been significantly differently explored if they all start with the same initial priors.

3.4. Trial design, population size and learning/earning stages

The relative merits of using decision theory and a goal to maximize overall health to decide on a trial’s size and its design as opposed to using a traditional approach depend on the patient horizon. In Cheng et al (2003) the authors illustrate this by addressing the problem of determining the optimal size of the initial learning stage (or trial) using a decision analytic approach. The main result is that for a two-armed trial and a learning phase that takes the form of a fixed equal randomized trial, the optimal size of the initial learning phase under initial equipoise depends on the order of magnitude of the square root of the population size N.

Index based rules have a learning phase and an earning phase whose sizes vary according to the particular sample data that is observed in a trial realization and in the case of the WI, according to the patient horizon (or the number of remaining patients to treat). In this section of the paper we compute by simulation the size of the mean learning phases of the GI and WI rules in a two-armed scenario and compare then to the approach suggested in Cheng et al (2003).

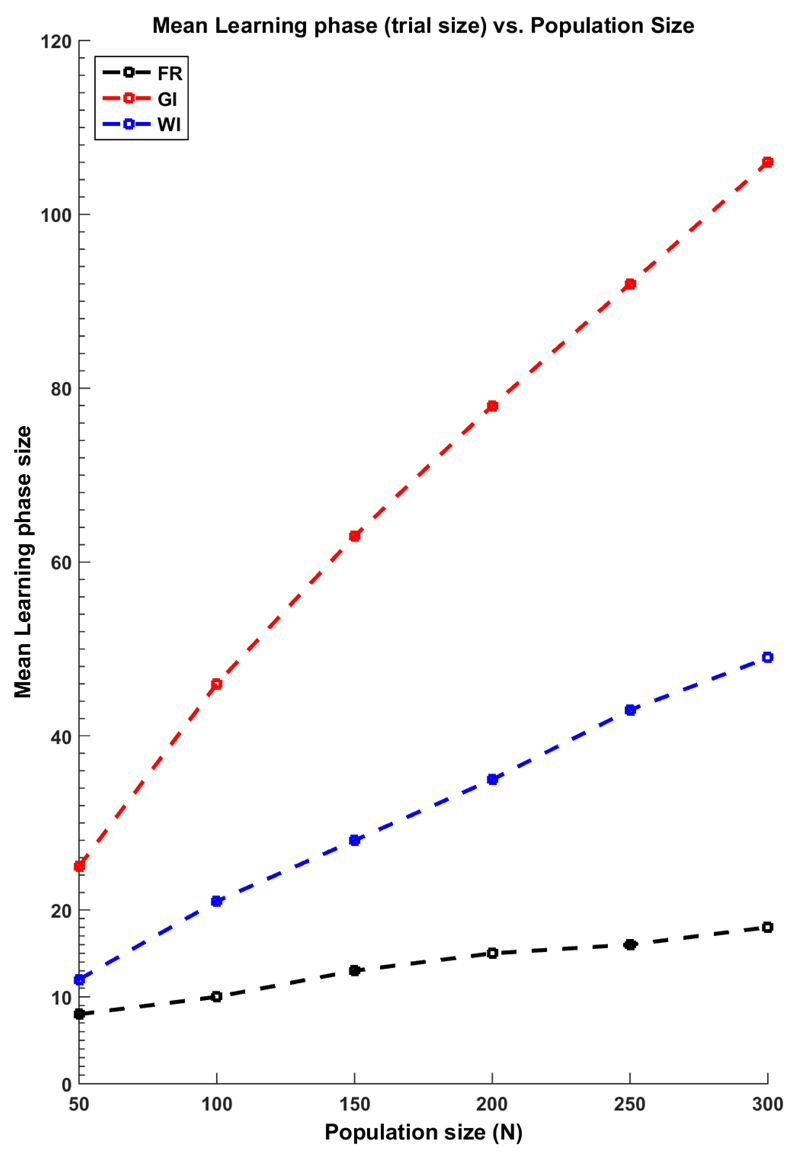
In Figure 1 the simulations results of 10⁴ replicas are depicted. We have defined the mean learning (ML) phase of the WI and GI rules as the mean number of allocations after which the treatment allocations are always to the same treatment (i.e. until the last patient in the population) when using these index rules. For the traditional fixed equal randomised trial (FE) of optimal size as in Cheng et al (2003), the ML has been approximated by $\lceil \sqrt{(}N)\rceil .$ The figure shows that the GI has a larger exploration phase than the other two approaches. The WI has an exploration phase that is larger than the FE approach, and it is only similar to it when N is the smallest. It is important to note that this larger learning phase results in a larger expected proportion of successes not only by being larger in size but also by not being constrained to be balanced, i.e. the WI explores more and it does so in a unbalanced fashion.

Figure 1.

The mean learning phase (or, the size of the trial phase) and the population size for the GI, WI and a the optimal size of a fixed equal randomized learning phase

In Table 9 and Table 10 we illustrate the same idea in different contexts. We assume different values for (p₁, p₂) and we apply the different allocations rules. We then compute the ML phase for the index rules, the mean proportion of patients in the population allocated to the best arm (p*) and the mean number of successes in the population (ENS). We do this for increasing sizes of the population with the disease or patient horizon.

Table 9.

The simulated expected proportion of patients allocated to the best treatment, the mean number of successes and the mean learning phase of the different patient allocation rules for the two-armed bandit problem with p₁ = 0.3 and p₂ = 0.5 for {N = 50, 150}

(p1, p2)	N	Rule	P*	ENSN =50	ML
(0.3, 0.4)	50	GI	0.6246	18.23	41
(0.3, 0.5)	50	GI	0.7323	22.59	37
(0.3, 0.6)	50	GI	0.8166	27.61	31
(0.3, 0.7)	50	GI	0.8692	33.04	24
(0.3, 0.4)	50	WI	0.6584	18.40	24
(0.3, 0.5)	50	WI	0.7608	22.74	19
(0.3, 0.6)	50	WI	0.8411	27.93	13
(0.3, 0.7)	50	WI	0.8883	33.41	8
(0.3, 0.4)	50	FE	0.5427	17.71	8
(0.3, 0.5)	50	FE	0.6381	21.31	8
(0.3, 0.6)	50	FE	0.6917	25.38	8
(0.3, 0.7)	50	FE	0.7712	30.47	8
(p1, p2)	T	Rule	P*	ENSN =150	ML
(0.3, 0.4)	150	GI	0.7308	55.96	112
(0.3, 0.5)	150	GI	0.8635	70.80	90
(0.3, 0.6)	150	GI	0.9210	86.92	72
(0.3, 0.7)	150	GI	0.9468	102.53	58
(0.3, 0.4)	150	WI	0.7522	55.96	59
(0.3, 0.5)	150	WI	0.8831	71.92	41
(0.3, 0.6)	150	WI	0.9363	87.79	28
(0.3, 0.7)	150	WI	0.9558	103.17	18
(0.3, 0.4)	150	FE	0.6270	54.60	13
(0.3, 0.5)	150	FE	0.7388	66.93	13
(0.3, 0.6)	150	FE	0.8245	82.72	13
(0.3, 0.7)	150	FE	0.8847	98.34	13

Table 10.

The expected proportion of patients allocated to the best treatment, the mean number of successes and the mean learning phase of the different patient allocation rules for the two-armed bandit problem with p₁ = 0.3 and p₂ = 0.5 for N = {200, 300}

(p1, p2)	T	Rule	p*	ENS 200	ML
(0.3, 0.4)	200	GI	0.7633	75.41	142
(0.3, 0.5)	200	GI	0.8954	96.21	111
(0.3, 0.6)	200	GI	0.9373	116.99	89
(0.3, 0.7)	200	GI	0.9577	137.43	71
(0.3, 0.4)	200	WI	0.7780	75.49	76
(0.3, 0.5)	200	WI	0.8976	96.33	53
(0.3, 0.6)	200	WI	0.9454	117.26	37
(0.3, 0.7)	200	WI	0.9671	138.30	23
(0.3, 0.4)	200	FE	0.5975	73.10	15
(0.3, 0.5)	200	FE	0.7314	89.39	15
(0.3, 0.6)	200	FE	0.8390	111.33	15
(0.3, 0.7)	200	FE	0.9051	132.08	15
(p1, p2)	T	Rule	p*	ENS 300	ML
(0.3, 0.4)	300	GI	0.8112	114.32	196
(0.3, 0.5)	300	GI	0.9242	145.73	144
(0.3, 0.6)	300	GI	0.9556	176.77	116
(0.3, 0.7)	300	GI	0.9716	207.07	92
(0.3, 0.4)	300	WI	0.8066	114.16	106
(0.3, 0.5)	300	WI	0.9246	145.85	68
(0.3, 0.6)	300	WI	0.9624	176.87	47
(0.3, 0.7)	300	WI	0.9770	208.27	34
(0.3, 0.4)	300	FE	0.6223	109.12	18
(0.3, 0.5)	300	FE	0.7549	135.57	18
(0.3, 0.6)	300	FE	0.8782	167.50	18
(0.3, 0.7)	300	FE	0.9073	198.86	18

The results in the tables show that the WI and GI reduce their learning phases’ size when the difference between p₁ and p₂ is larger. However, the GI will always have a larger average size of a learning phase than the WI. The results also indicate that even when the GI and WI result in practically identical values of ENS, the WI will have an advantage in terms of the proportion of patients allocated to the best treatment. The results also suggest that the larger the difference between the treatments and the smaller the population size, the more important the advantage of the index rules over a FE approach. As well, the bandit results perform as well as the other alternatives under the presence of equal treatments success rates.

4. Discussion

A common definition of a rare disease is that of a disease affecting no more than 5 per 10,000 persons. Yet, rare diseases are not so rare. According to the EU Implementation report on the Commission Communication on Rare Diseases, between 27-36 million people in Europe are affected by a rare diseases. Further, this number is expected to raise with the improvements of diagnosis methods and the advance of genetics partitions diseases into smaller entities. Developing statistical methods specific for drug development for rare diseases is of critical importance and a current health policy priority due to both this expected increase in rare diseases prevalence and the current difficulties that limit running clinical trials for these conditions.

In a rare disease setting, the number of patients available for running a trial is significantly smaller than the number required to run a standard randomized trial. Moreover, randomizing patients to treatments so as to learn the most about them when few or no patients would benefit from that learning is highly questionable. Instead, treatment decisions for the patients recruited in a trial (or with the patients in the whole population, if that would be known) can be guided by the goal of learning about the available treatment options just enough as to maximize effective treatment for the largest number of patients with the disease. This goal can be successfully implemented assuming a decision-analytic approach that would be able to assist physicians both in their learning about treatments efficacy and in their treatment decision making.

Optimal designs, from this effective treatment perspective, have been long studied in the decision-analytic theoretical literature as “bandit ” models. Among other limitations to their use in a clinical settings (See Villar et al, 2015), computational complexity and the difficulty of implementation and interpretation of designs based on their optimal rule is still binding. Developing simple, practical and computational feasible approaches to “bandit ” problems is an open an active area of research in sequential allocation problems in general and beyond clinical trials. In this article we contributed by presenting calculations (both exact and simulated) that suggest that the advantages of the nearly-optimal bandit rules based on non-myopic index policies are increased when the number of arms grows and the disease under study affects a relatively small estimated number of patients. The potential patient benefit gain resulting from treatment decisions based on these ideas suggest that their use in practice could help provide answers to the current challenges faced by drug development for rare conditions.

Further research is needed to overcome other limitations to bandit strategies besides the computational one and also to determine some general conditions under which arms are selected or dropped when using the index rules.