Moving beyond regression techniques in cardiovascular risk prediction: applying machine learning to address analytic challenges

Abstract

Risk prediction plays an important role in clinical cardiology research. Traditionally, most risk models have been based on regression models. While useful and robust, these statistical methods are limited to using a small number of predictors which operate in the same way on everyone, and uniformly throughout their range. The purpose of this review is to illustrate the use of machine-learning methods for development of risk prediction models. Typically presented as black box approaches, most machine-learning methods are aimed at solving particular challenges that arise in data analysis that are not well addressed by typical regression approaches. To illustrate these challenges, as well as how different methods can address them, we consider trying to predicting mortality after diagnosis of acute myocardial infarction. We use data derived from our institution's electronic health record and abstract data on 13 regularly measured laboratory markers. We walk through different challenges that arise in modelling these data and then introduce different machine-learning approaches. Finally, we discuss general issues in the application of machine-learning methods including tuning parameters, loss functions, variable importance, and missing data. Overall, this review serves as an introduction for those working on risk modelling to approach the diffuse field of machine learning.

Introduction

Risk prediction is important in clinical research and patient care. Models for risk of cardiovascular disease are used to identify patients for statin therapy¹ and choose anticoagulation strategies for atrial fibrillation.² Traditional approaches for developing prediction tools have used regression-based models, such as a logistic model to predict 30-day mortality risk for patients with STEMI (TIMI),³ a Weibull model used for the Systematic Coronary Risk Evaluation (SCORE) model,⁴ and a Cox model used for the Framingham Risk Score.⁵ Such models use a small number of variables to predict the probability of an event and are ubiquitous in clinical research because they estimate easy to interpret parameters, e.g. odds ratios, relative risks, and hazard ratios. Such models are useful and often necessary in association analyses; however, this is not necessarily the case in prediction analyses, where the focus is on the outcome instead of the predictors. Therefore, constraints that aid interpretation for association studies—the effect of the predictor on the outcome is linear and homogeneous (i.e. the effect increases uniformly throughout the range of the predictor and the factor operates in the same way in all participants), and relatively few predictors used—serve as limitations in prediction studies.

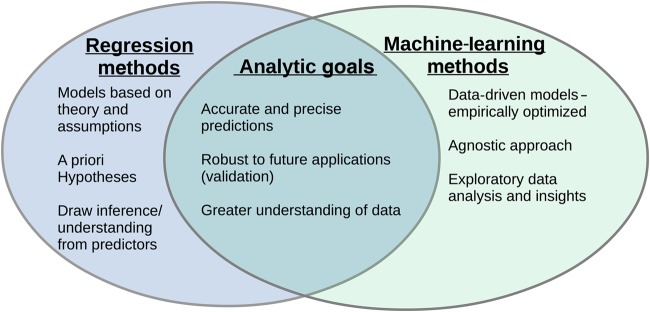
For studies where the goal is to predict the occurrence of an outcome and not measure the association between specific risk factors and an event in a clinically interpretable way, traditional regression models can be modified or abandoned in favour of models that produce a more flexible relationship among the predictor variables and the outcome. These methods—generally referred to as machine learning—have similar goals to regression-based approaches but different motivating philosophies (Figure 1). They do not require pre-specification of a model structure but instead search for the optimal fit within certain constraints (specific to the individual algorithm). This can result in a better final prediction model at the sacrifice of interpretability of how risk factors relate to the outcome of interest.

Figure 1.

One perspective on the intersection of statistical modelling (blue) and machine-learning (green) goals. The figure highlights that while the processes differ the overarching goals are often the same.

Increasing ubiquity of large, multifaceted datasets, such as Electronic Health Records (EHRs)⁶ and −omics data^7,8 (i.e. ‘big data’) for risk prediction, requires researchers and clinicians to rethink risk modelling: for analysts, new statistical techniques may be needed; for clinicians, clinical decision tools may evolve beyond simple scoring algorithms to ones that require computational assistance through computer applications. The European Heart Journal instructs authors to develop their statistical analysis plan to ‘be as simple as possible, but as sophisticated as needed’. But when should more sophisticated techniques, particularly those for model development and validation, be considered as essential? This question is particularly salient when developing prediction or risk models. Recently, Steyerberg and Vergouwe⁹ laid out seven steps for developing prediction models. A natural follow-up is: what is the best prediction model to use? As others have noted that¹⁰ there is no best approach for all data problems. The various techniques differ in their approaches as they aim to solve different data complexities. Therefore, the ‘best’ algorithm will depend on the specific data problem at hand.

Others have reviewed machine-learning methods geared towards technical,¹¹ practitioner,¹² and medical audiences,¹³ to name just a few. Although we recapitulate some of that discussion, the goal of this review is to discuss different complexities that arise in the analysis of clinical cardiology data and illustrate different machine-learning approaches that can address these issues. We consider machine-learning algorithms to be any approach that performs an automated search, either stochastic or deterministic, for the optimal model. While these tools are often presented as ‘black-box’ algorithms that simply take inputs that return an answer, this review will peer under the hood to better understand how they operate. Doing so allows one to understand when certain machine-learning models may be considered, what data challenges each algorithm is trying to resolve, and therefore foretell when a certain approach will be best for one's data problem. We first describe an illustrative data set we will use through the review. We next discuss different challenges that arise in the analysis of clinical data and then present various machine-learning methods and how they address these challenges. We conclude with some additional considerations for using machine-learning methods including some limitations. In the appendices, we provide a glossary of typical terms used as well as additional details on many of the discussed methods.

Illustrative data

We use a sample dataset derived from the EHR system of Duke University Medical Center to illustrate some of the concepts described. Using data from 2007 to 2013, we identified patients that were admitted to the hospital through the emergency department with a primary diagnosis of acute myocardial infarction (AMI). We abstracted information on laboratory tests that were performed in the first 24 h of admission, and included all labs that were present in at least 80% of patients and deemed not redundant (i.e. haematocrit and haemoglobin). Since multiple tests were often performed, we calculated the median, min, and max values. Finally, we abstracted information on patient demographics (age, gender, and race) and comorbidities (combined via the Charlson Comorbidity Index¹⁴).

Overall, we identified 1944 patients who were admitted with a primary diagnosis of AMI. Of these, 101 (5.2%) died during their hospitalization. Among those that died, the median time to death was 6.5 days (IQR: 2.6, 13.5). We identified 13 laboratory tests that were present in at least 80% of the sample (calcium, carbon dioxide, creatinine, creatinine kinase—mb, haemoglobin, glucose, mean corpuscular volume, mean corpuscular haemoglobin concentration, platelet count, potassium, red blood cell distribution width, sodium, white blood cell count). After calculating median, min, and max values, there were 43 predictor variables. We applied various machine-learning algorithms to compare predictive models for in hospital mortality. We used single mean imputation for those without a lab result and as described below, used 10-fold cross-validation to assess predictive performance. Analyses were performed in R 3.1.2.¹⁵

Analytic challenges

We first consider three challenges that are not well handled by typical regression modelling strategies. These challenges may degrade traditional regression model performance, which may result in lower real-world value since they may not account for important relationships in the data.

Non-linearities

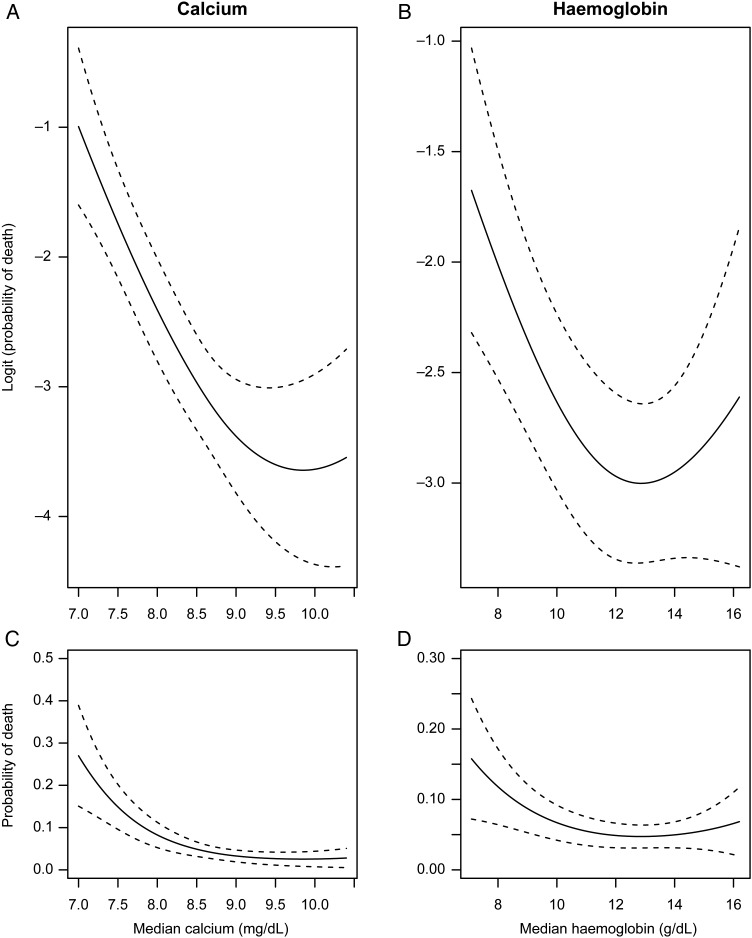
The most basic assumption of regression models is that the relationship between a risk factor and outcome is linear, i.e. the effect increases uniformly throughout the range of the predictor. While this may be plausible, or at least a good approximation, for some risk factors, there are many examples in cardiovascular research that have non-linear relationships. Consider age: the risk of death rises sharply with increasing age. Thus, one's change in risk of death moving from age 40 to 50 years is much lower than increasing age from 70 to 80 years. Other non-linear risk factors include the ‘J’ like relationship of BMI with most diseases—with obese and underweight people being at increased risk;¹⁶ and the many laboratory values that indicate increased risk both above and below the normal ranges (i.e. hypoglycaemia and hyperglycaemia both increasing risk). Even though a regression model may approximate the true non-linear relationship well and provide a more parsimonious interpretation, when developing risk models, we want to ensure that we capture these non-linearities as much as possible. Figure 2 illustrates the non-linear relationship between two of the collected laboratory measures, calcium and haemoglobin, and post-AMI mortality. Calcium and haemoglobin both show decreasing risk as values rise, then level off at moderate and higher values.

Figure 2.

Observed non-linearities in the predicted probabilities of death for calcium (A) and haemoglobin (B) on the logistic (i.e. linear) and probability (C/D) scales. Both show a sharp decreasing relationship with death at lower values, which levels off at more moderate values. Models were estimated using cubic splines and were adjusted for age, sex, and race. 95% confidence bands are shown.

Heterogeneity of effects (interactions)

Related to non-linearities is heterogeneity of effects. Heterogeneity of effects, known as interactions, occurs when a variable's relationship with the outcome depends on the level of some other variable. A typical example of an interaction are gene–environment interactions. For example, researchers have identified that air pollution may have a differential effect on cardiovascular disease risk based on one's genetics.¹⁷ Similarly, interaction effects have been detected with regard to anthropomorphic characteristics and mortality¹⁸ and racial differences in the effects of HDL-C.¹⁹ As with non-linearities, not properly accounting for these interaction effects may degrade the quality of a risk model.

Many predictor variables

A hallmark of large datasets like EHRs is the large amount of potential predictor variables. When working with many predictor variables it is often challenging to know which and how many should be used in a risk model. An oft referred to rule of thumb is to have at least 10 events-per-predictor or degree of freedom used,²⁰ although some have suggested a 20 events-per-predictor rule for prediction studies.²¹ However, with EHRs, it is common to have many potential, often correlated, predictor variables—perhaps even more predictors than events. This particularly becomes a problem when developing risk models for rare events.^22,23 For instance, in our data example, we had 43 predictor variables and only 101 events. Had we included information on vital signs, service utilization history, medications, and other comorbidities, we easily could have had >100 potential predictor variables. The presence of many predictors, relative to the number of events, creates a problem because estimated effects can be unstable with high estimated variability because when one variable is ‘held constant’, there is little remaining variability in the other variables. In these settings, alternative approaches are required. However, even machine-learning methods aimed at handling large numbers of predictors may become unstable.²⁴

Machine-learning methods

How machine-learning models operate: bias-variance trade-off

Machine-learning methods consist of computational algorithms to relate all or some of a set of predictor variables to an outcome. To estimate the model, they search, either stochastically (randomly) or deterministically, for the best fit. This searching process differs across the different algorithms. However, through this search, each algorithm attempts to balance two competing interests: bias and variance. In the machine-learning context, bias is the extent to which the fitted predictions correspond to the true values—i.e. how accurately does the model predict the ‘true’ risk of death in the population? Variance is the sensitivity of the predictions to perturbations in the input data, i.e. how does sampling variability impact the predictions? Even though it is not possible to separately quantify a model's bias and variance, these two values are summarized together by loss functions (see below). While our aim is to reduce both bias and variance, these two goals are often in conflict: decreased bias may increase variance and vice versa. For example, we may create an algorithm that correctly predicts all deaths in our dataset. However, this model may be configured in such a way that it is tied too specifically to the individual intricacies of our dataset, essentially modelling ‘statistical noise.’ The model would then perform poorly when applied in a validation dataset (i.e. have high variance). This is also referred to as an ‘overfit’ model. Different approaches are used to balance bias and variance, but in general the parameters set to control this are called tuning parameters.

Types of machine-learning methods

Many machine-learning methods can be grouped into different families based on their underlying structure. The two largest families are those that amend the traditional regression model and tree-based methods.

Amendments to regression models

A large class of machine-learning methods are those that directly manipulate the traditional regression model in order to improve upon it. These approaches can often be applied to most any regression method, allowing for broad appeal. The most common amendment to regression is stepwise (forwards and backwards) selection. These procedures iteratively search for the best subset of predictors to use and then fit a basic regression model. They are particularly useful when one has a lot of potential predictors and can also be used to search for interactions. Since the final fit is based off of a regression model, they can still be somewhat limited and are prone to overfitting.²⁵

An extension of selection methods are regularized methods which include the common ridge regression²⁶ and LASSO.²⁷ Instead of choosing the optimal subset of variables, one regresses an outcome (e.g. mortality) onto all of the predictors (e.g. laboratory values). To handle many predictor variables, these methods shrink the regression coefficients towards 0. This shrinkage is achieved by placing a penalty on the summation of the estimated coefficients. Although this shrinkage results in biased regression estimates (i.e. the estimated odds ratio is not reflective of the true population odds ratio), and cannot be used for inferences on association, it results in a more stable model that produces a better predictor in particular when applied to external datasets. Regularized methods differ in how the perform this shrinkage: ridge regression results in a relatively equal shrinkage of all regression coefficients; LASSO regression results in a full shrinkage of a subset of variables. This full shrinkage effectively operates as a form of variable selection. The final set of coefficients is determined by choosing the optimal penalty.

Another approach to handling multiply correlated variables is to transform the variables into derived inputs. Algorithms such as principal components regression (PCR) and partial least squares (PLS),¹¹ transform correlated predictor variables into a set of uncorrelated variables to be used in the model. This allows one to fit a regression model using fewer derived inputs while still capturing the variability of the original predictors.

Selection, regularized, and derived methods are useful when one has many variables and/or highly correlated variables. A different approach to amending the regression model when one has non-linear data is generalized additive models (GAMs).²⁸ Generalized additive models start with the basic regression framework (i.e. logistic, linear, etc.), but instead of forcing predictors to have a linear relationship with the outcome, they are allowed to be non-linear. To achieve this non-linearity, GAMs transform the predictor variables via splines. Splines allow for a smooth, flexible, non-linear representation of a continuous variable. The algorithm searches for the optimal degree of flexibility for each predictor. While GAMs are not very efficient with many predictors, they have been combined with regularized methods such as LASSO to perform predictor selection.²⁹ It is also worth noting that these splines are also applicable to regular regression methods and are useful to graphically explore relationships of predictor variables and the outcome.

Classification trees

Another common class of machine-learning approaches for prediction includes the tree-based algorithms. Like regression-based methods, there are many modifications of tree-based models. The most common approach in clinical research is to use classification and regression trees (CART).³⁰ Classification and regression trees was developed with clinical application in mind, with one of the motivating examples triaging a patient in the emergency department with a suspected myocardial infarction. The idea was to mimic the way a doctor may approach a patient with a series of questions guiding the clinician, with subsequent questions based on the answer to the prior. This algorithm is typically able to handle all three challenges of non-linearities, heterogeneous effects, and many predictors.

Classification and regression trees searches among the available predictor variables to find the variable which best separates the outcome into two groups with the most disparate probabilities of event. Since this split is binary, it is able to capture non-linearities in the data, as multiple splits on the same predictor can occur within one tree. Within each group, the algorithm then re-searches the remaining predictors to find the next best split, which may (and often does) vary from one group to the next. This continues until all of the groups (a.k.a. ‘nodes’) are homogeneous. To create a more stable tree, the algorithm then ‘prunes the tree’ (reducing the number of nodes/decision points) to reduce the complexity or over-specification of the model. This separate searching allows for the detection of interactions. For example, if the first split is based on sex, separating males and females into different sides of the tree, than any subsequent split among males that does not also occur among females, is an interaction with gender. Finally, since not all predictors will find their way into the tree, CART can handle the situation of more predictors than observations.

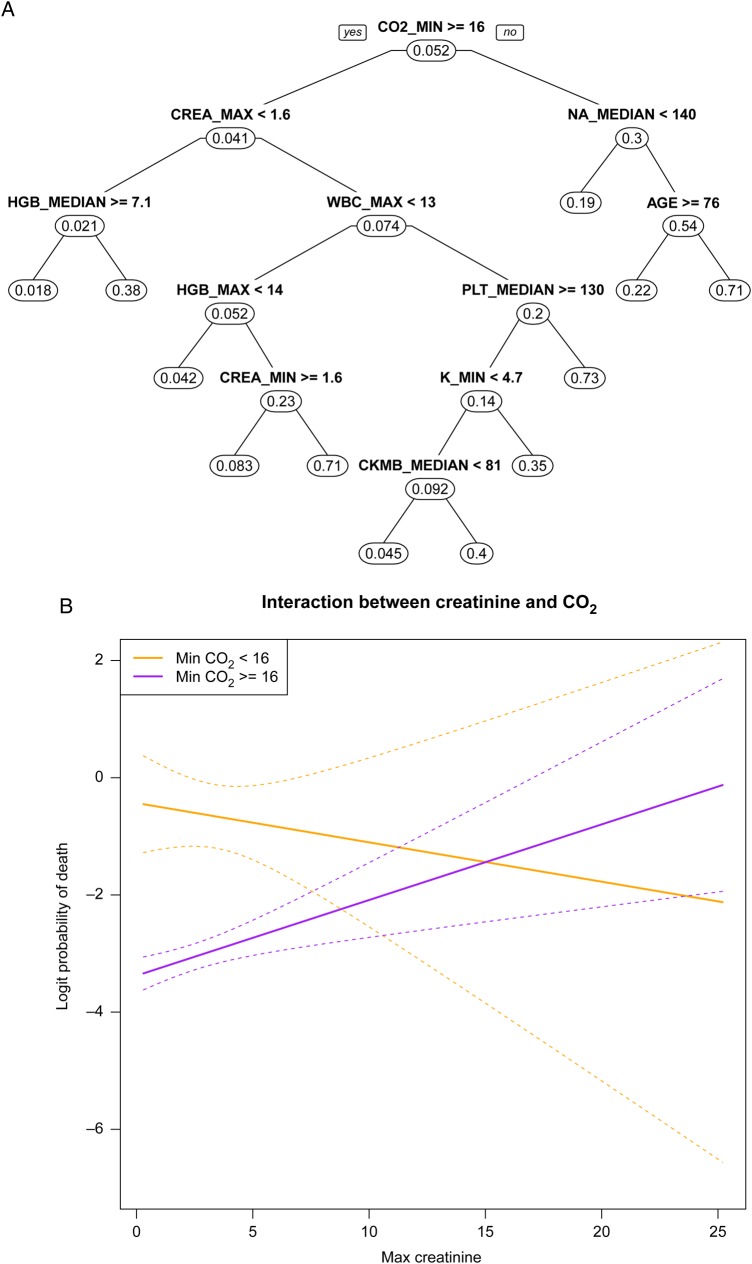
Figure 3A shows the CART tree for predicting mortality among patients with AMI from our dataset. The first split is based on minimum CO₂ with those having a value >16 being at increased risk (4.1% probability of mortality vs. 30%). The fact that creatinine is only on the left-hand side of the tree suggests a potential interaction between CO₂ and creatinine. We explore this in Figure 3B. We fit a logistic regression model, discretizing minimum CO₂ at 16 and keeping maximum creatinine continuous. For those with CO₂ >16, higher creatinine levels increase the probability of mortality. Conversely, for those with CO₂ <16 higher creatinine is not associated with mortality or nominally protective. This lack of effect is reflected by the absence of creatinine on the right-hand side of the tree in Figure 3A. Finally, while the P-value for the interaction is borderline significant (P < 0.075), it is important to note that this is not proper inference since we used the fit from CART to choose our variables and split points.

Figure 3.

Classification and regression trees (A) for predicting acute myocardial infarction. The first split is on minimum CO₂. Splits on different sides of the tree (creatinine on left, sodium on right) indicate potential interactions. Interaction plot (B) between CO₂ and creatinine highlights the differential relationship.

One disadvantage of trees is that they tend to exhibit high variance, limiting their utility as stand-alone prediction models.³¹ However, it is possible to improve the overall predictions by aggregating the results from multiple trees—referred to as ensemble methods. A common ensemble method with trees is the Random Forests algorithm,³² which uses the bagging procedure to combine multiple trees. Another ensemble approach, gradient boosting machines,³³ use the boosting procedure to combine stumps of trees. These ensemble methods can be loosely conceptualized as forming a robust overall prediction by aggregating the predictions of many simpler predictive models. This is similar to the process of deriving a clinical diagnosis for a patient by utilizing consultations from many specialists, each which would that look at the patient in a slightly different way.

Other approaches

There are many other machine-learning algorithms that do not fit into the above groupings. Two common ones are Nearest Neighbours³⁴ and Neural Networks.³⁵ In Nearest Neighbours, one cluster observations with similar predictor variables and predicts an outcome based on that cluster. In the medical context, these can be thought of as predicting a patient's outcome based on previous patients with similar symptoms. While Nearest Neighbours can enforce an intuitive structure to the data, Neural Networks are the canonical ‘black box’ algorithm. They apply a non-linear transformation to the predictor variables and recombine them to derive a prediction. The overall transformation can have multiple layers to achieve what is known as deep learning. Due to these non-linear transformations, one is able to model many non-linear and heterogeneous effects; however, describing this relationship for interpretative purposes can be challenging. Many image recognition algorithms utilize deep learning models to classify image based on data patterns observed in the pixels. Although neural networks and deep learning have gained limited traction in risk prediction, they have seen use in image processing.

Applying machine-learning models

Figure 4 presents a flow chart for applying machine-learning algorithms. Below we outline some of these steps.

Figure 4.

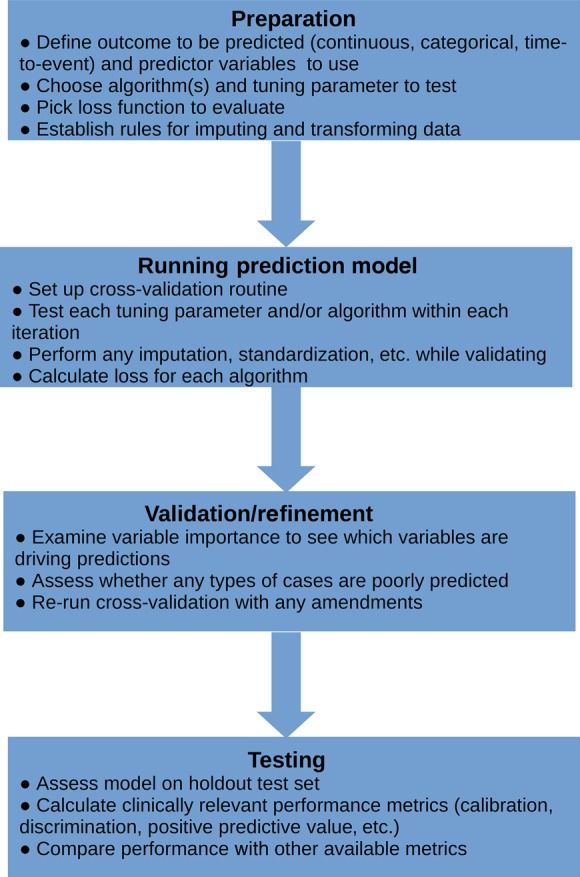
High-level overview of process of applying machine-learning routines to data.

Choosing tuning parameters

As stated above, all machine-learning algorithms require user defined inputs to achieve a balance between accuracy and generalizability (bias and variability), referred to as tuning parameters. These tuning parameters impact the way the algorithm searches for the optimal solution. Through controlling this search, the tuning parameters impact the overall complexity of the final model and the final bias–variance trade-off. For many, the choice of tuning parameters is the most daunting aspect of using a machine-learning algorithm. Fortunately, in our experience, many of these tuning parameters are robust to different settings and many implementations of machine-learning algorithms have default settings. Therefore, one does not need to be concerned with getting the ‘best’ setting rather one that is ‘good enough’. That said, it is important to try different settings to see which works best in a specific data problem. While an in-depth discussion of tuning parameters is beyond the scope of this review, it is usually possible to develop an intuition as to how different setting will impact the model's bias and variance. In the appendix, we detail some of the tuning parameters for the different algorithms.

Need for validation

Implicit in the search for the optimal tuning parameters is the need to check or validate the model. This is a key component of the TRIPOD statement for reporting prognostic models.^36,37 In the traditional regression model framework, internal validation is not necessary because one (ideally) posits an analytic model before fitting it to the data. For instance, the analyst posits that risk of CHD is a function of age, sex, cholesterol, smoking, and blood pressure and the regression model calculates optimal prediction weights for the predictor variables. It does not select the model. Conversely, machine-learning methods involve a ‘search’ for the optimal model. The typical approach is to try a range of settings and use the one with the best performance. However, done naively, this will generally lead to choosing the most complex model resulting in ‘overfitting’.

To avoid over-fitting and provide a means to validate the model, we typically divide the data into training, validation, and testing sets. We fit our model(s) with various tuning parameters using the training data, testing their performance with the validation data. Once we have chosen the ‘best’ model we use the testing data to calculate clinical performance metrics (e.g. calibration, net-benefit,³⁸ etc.) and compare with any other existing approaches. It is typical to combine training and validation together through techniques such as cross-validation and bootstrapping. These approaches involve repeatedly sub-setting the data and fitting the model on one set and testing on the hold out set. These methods are more robust than the split sample validation²¹ (i.e. randomly split a dataset into a training and validation set) since the procedure is repeated many times. An important consideration is the need to test the entire modelling processe.g. variable selection, any imputation—and not just a final model's form.

Choosing the right model: assessing model performance with loss functions

With the wide range of available machine-learning methods and settings, an important step is deciding which approach is best. Even though secondary considerations such as computational time and interpretability may be factors, the most important consideration is model performance. As Steyerberg et al.¹³ discussed in their review, there are multiple metrics to assess the clinical performance of a prediction model. Typically, we apply these metrics during the final testing to assess aspects of model performance. However, for the purposes of choosing the best machine-learning model, we usually focus on metrics that produce an overall assessment of fit, known as loss functions. For binary outcomes, common loss functions include squared-error loss, logistic loss, and miss-classification rate.³⁹ Loss functions aggregate the difference between the observed value and the predicted value and, in doing so, summarize both the model's variance and bias. Typically, we choose the model with the lowest loss (best fit) without regard to the complexity of the model, though there are approaches to assess whether one approach is ‘significantly better’ than another.⁴⁰Table 1 shows model fits for our example based on cross-validation. Since different metrics balance bias and variance differently, they produce different results. While not a standard loss function, we present the familiar c-statistic (area under ROC) as a comparison. Overall, among the best performing algorithms, there is minimal difference in performance and one may choose the approach that meets other subjective criterion (e.g. ease of computation).

Table 1.

Model fits for different algorithms

	c-Statistic	Squared-error loss	Logistic loss	Misclassification ratea
Regression based
Logistic regression	0.702	0.049	0.995	0.23
Forward selection	0.761	0.046	0.995	0.24
LASSO	0.750	0.046	0.995	0.26
Ridge	0.753	0.047	0.996	0.27
PCR	0.546	0.049	0.998	0.41
Generalized additive model	0.708	0.050	0.994	0.22
Tree based
CART	0.623	0.053	0.997	0.12
Random forests	0.741	0.048	0.995	0.32
Boosting	0.763	0.047	0.996	0.20
Other
Nearest Neighbours	0.583	0.050	0.998	0.22
Neural Networks	0.598	0.065	0.996	0.44

The bold value represents the best algorithm for that performance metric.

^aMisclassification rate is discretized at the mean event rate.

Variable importance

Unlike regression models, machine-learning models do not estimate an easily interpretable quantity that relates the predictor variables to the outcome. Since the relationship that machine-learning models fit is more complex than regression models, it is generally not straightforward to summarize the relationship into any single parameter. However, many machine-learning methods attempt to summarize the impact of individual variables into metrics referred to as variable importance. The variable importance metric is specific to the individual algorithm and its value does not generally have a causal or even statistical interpretation. Instead, the measure can often be thought of as a rank ordering of which variables are most ‘important’ to the fitted model.⁴¹ Since each machine-learning algorithm fits a different type of model, one would expect that different methods would come up with different rank orderings. Table 2 shows the variable importance rankings for different algorithms for predicting mortality among AMI patients. As one can see different approaches produce similar but different rankings. Calcium (Ca²⁺) and CO₂ both seem to be consistently important predictors, while potassium (K⁺) and white blood cell count have importance to different models. Although variable importance rankings cannot replace targeted hypothesis tests of specified parameters, they can be hypothesis generating and may help detect which factors are worthy of further study.⁴²

Table 2.

Variable importance rankings

Variable rank	t-Test	GLM	LASSO	GAM	Random forests	Boosting
1	CO2 Min	Ca2+ Max	Ca2+ Median	Ca2+ Min	CO2 Min	CO2 Min
2	CO2 Median	K+ Min	Ca2+ Max	Ca2+ Max	CO2 Median	WBC Max
3	WBC Max	Hgb Median	Hgb Median	CO2 Median	WBC Max	CO2 Median
4	K+ Max	Ca2+ Median	K+ Median	Ca2+ Median	Glucose Max	Ca2+ Median
5	CO2 Max	Hgb Min	K+ Min	RDW Median	WBC Median	K+ Max

Missing data

A common challenge in clinical research is the presence of missing data. Missing data within machine-learning methods present many of the same challenges as in typical regression approaches. In these settings, the focus is usually on the missing data mechanism, specifically whether it is ignorable (the missingness is not related to the unobserved values, i.e. missing at random) or non-ignorable (the missingness is related to the unobserved values).⁴³ Non-ignorable missing data, for example labs not taken because a patient was unconscious, are always challenging to deal with and depending on their extant can undermine one's prediction model. However, if missingness is ignorable, for example a lab not performed due to oversight, it can address be in the same ways as for regression-based approaches, typically imputation. One simplification is that since we often do not care about the variability of the predictions, one can usually use a single imputation strategy to impute the missing value.⁴⁴ Moreover, some machine-learning algorithms—specifically tree-based ones—are able to handle missing values through the modelling process alleviating the need for imputation. The important consideration is that when using techniques such as cross-validation, the imputation process needs to be part of the cross-validation. In our data example, we first split the sample into cross-validation folds, and used the data from each training set to impute into the test set.

Other outcomes: time to event, continuous, and multi-category

While the discussion and data example have focused on binary outcomes, most machine-learning procedures are applicable to many outcome types, including time-to-event outcomes. Such approaches are particularly useful when there is loss to follow-up and censoring, since these are naturally handled. Moreover, such models allow one to derive risk predictions over multiple time points. However, some results suggest that when one cares about risk at a specific time point (e.g. 30-day readmission) binary models may perform better, likely due to non-proportionality in predictor effects.⁴⁵ This is particularly the case when full follow-up is available for all individuals. Similarly, these methods are easily extended to continuous outcomes and multi-category outcomes.⁴⁶ Overall, the above considerations stay the same, though usually the choice of loss functions will change for different outcomes.^39,47

Software implementation

The present analysis was performed in R; however, all of the discussed algorithms are also available in major statistical packages such as SAS and STATA. Additionally, initiatives like WEKA and scientific languages like Python provide advanced quantitative algorithms that excel at model estimation. In the appendix, we provide a list of functions in various software. Implementations of a specific algorithm should involve the choice of the same tuning parameter and provide similar (if not identical) results; however, different algorithms may be coded differently. Moreover, when using stochastic algorithms (e.g. random forests), it is important to use a random number generator ‘seed’ to ensure the results are reproducible. Finally, it is important to note that many of the discussed methods have extensions and derivatives which may provide better performance for a given data problem.

Where machine-learning methods fail

Machine-learning methods are useful in many contexts; however, there are some scenarios where such methods will perform worse. For instance, if the true underlying model is a linear, homogenous relationship (i.e. the regression assumptions are met), then regression-based methods will always be more efficient.⁴⁸ Moreover, extra considerations are needed when observations are correlated.⁴⁹ For example, if one has longitudinal data, most machine-learning methods will not properly utilize the temporal nature of the data. As suggested above, another area where machine-learning methods are limited is if one cares about causality. A risk predictor may be incorporated into a model not because it causes the outcome, but because it is simply a useful maker or directly in the casual pathway. This is not a problem for the purposes of prognostication but does limit causal interpretation. Additionally, even though a machine-learning method may show better performance, presentation of the results may be more complicated. For example, many risk models have been converted into hand calculable scores (e.g. the Framingham risk score). This conversion is usually obtained by rounding regression coefficients into a points-based score for each predictor. However, such a conversion is not obtainable with many machine-learning methods (e.g. any tree-based approach). Finally, machine-learning methods differ in the amount of computational time, which usually depends on data size. Some approaches like LASSO and CART will often be as fast as regression models while ensemble approaches will take longer. For our moderately sized dataset, the longest to fit was boosting which took ∼6-min with cross-validation.

Conclusions

As we enter the age of precision medicine, risk assessment tools are becoming more salient. When one's goal is to generate a model that most accurately predicts an outcome, machine-learning algorithms can be advantageous over traditional regression methods. Such methods can be employed to help confront issues of multiple and correlated predictors, non-linear relationships, and interactions between predictors and endpoints, in large datasets. However, when using machine-learning methods, extra care is needed in the form of model validation. Finally, since each method differs in its utility in addressing individual issues, it is often prudent to compare multiple approaches. This question of how much flexibility to allow for when developing as risk model is what ultimately becomes the art of modelling.

Authors’ contributions

B.A.G. performed statistical analysis, handled funding and supervision, acquired the data, and drafted the manuscript. B.A.G., A.M.N., R.E.C. conceived and designed the research and made critical revision of the manuscript for key intellectual content.

Funding

This work was supported by National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK) career development award K25 DK097279 to B.A.G.

Conflict of interest: none declared.