Free-Breathing Liver Fat Quantification Using a Multiecho 3D Stack-of-Radial Technique

Abstract

Purpose

The diagnostic gold standard for non-alcoholic fatty liver disease is an invasive biopsy. Noninvasive Cartesian MRI fat quantification remains limited to a breath-hold (BH). In this work, a novel free-breathing 3D stack-of-radial (FB radial) liver fat quantification technique is developed and evaluated in a preliminary study.

Methods

Phantoms and healthy subjects (n = 11) were imaged at 3 Tesla. The proton-density fat fraction (PDFF) determined using FB radial (with and without scan acceleration) was compared to BH single-voxel MR spectroscopy (SVS) and BH 3D Cartesian MRI using linear regression (correlation coefficient ρ and concordance coefficient ρ_c) and Bland-Altman analysis.

Results

In phantoms, PDFF showed significant correlation (ρ > 0.998, ρ_c > 0.995) and absolute mean differences < 2.2% between FB radial and BH SVS, as well as significant correlation (ρ > 0.999, ρ_c > 0.998) and absolute mean difference < 0.6% between FB radial and BH Cartesian. In the liver and abdomen, PDFF showed significant correlation (ρ > 0.986, ρ_c > 0.985) and absolute mean differences < 1% between FB radial and BH SVS, as well as significant correlation (ρ > 0.996, ρ_c > 0.995) and absolute mean difference < 0.9% between FB radial and BH Cartesian.

Conclusion

Accurate 3D liver fat quantification can be performed in 1 to 2 min using a novel FB radial technique.

INTRODUCTION

Non-alcoholic fatty liver disease (NAFLD) is the most prevalent chronic liver disease worldwide, affecting up to 45% of the general population (1–3). NAFLD is characterized by steatosis, or intracellular accumulation of triglycerides in the hepatocytes. NAFLD can progress to non-alcoholic steatohepatitis (NASH), which affects about 2% to 5% of the general population and is a leading cause of liver cirrhosis, hepatocellular carcinoma (HCC) and liver failure (1–4). In addition, NAFLD is associated with cardiovascular disease and type 2 diabetes mellitus (1–5). The increased prevalence of NAFLD, due to a rise in the rates of obesity and type 2 diabetes, is expected to make NAFLD a major indication for liver transplantation (2,4). The current gold standard for diagnosing and monitoring NAFLD or NASH is an invasive biopsy to characterize intracellular accumulation of triglycerides in the liver; however, biopsy has associated morbidity and suffers from spatial sampling bias (1–6). Therefore, non-invasive techniques for liver fat quantification have been developed to improve the diagnosis and management of NAFLD.

Historically, MR spectroscopy (MRS) is considered the noninvasive reference standard for liver fat quantification (3); however, MRS is also limited by spatial sampling bias. Non-invasive and spatially resolved fat quantification of the entire liver is possible with chemical-shift-encoded MRI (CSE-MRI) methods (7,8). In CSE-MRI, quantitative proton-density fat fraction (PDFF) is calculated by acquiring multiple echo-time (TE) images and obtaining fat-only and water-only maps by fitting the data to a signal model (9,10). Confounding factors such as T₁ (11) and T₂^* decay (12–15), eddy current effects (16–18), gradient delay errors (16–18), noise (11), and complexities in the spectral model of fat (13,19–21) must be addressed to ensure the accuracy of quantitative PDFF.

Current CSE-MRI methods are mainly based on Cartesian sampling (9–12,14,21–24). A major limitation of Cartesian sampling for abdominal imaging is that it is susceptible to respiratory-motion-induced coherent aliasing artifacts. Thus, scans are performed during a single breath-hold (BH) and face challenges in achieving full volumetric coverage, high spatial resolution, desirable echo times, high signal-to-noise ratio (SNR), and artifact-free images for liver fat quantification. Moreover, breath-holding may not be possible for many patients and the accuracy of fat quantification becomes severely compromised. The development of methods to address motion artifacts is an area of active research, with recent developments investigating respiratory gating or self-navigation for multiecho Cartesian sequences (25,26).

Compared to Cartesian sampling, several non-Cartesian sampling trajectories have greater inherent robustness to motion and may provide a desirable alternative for performing fat quantification in the liver without the need for breath-holding (27,28). In particular, the 3D stack-of-radial trajectory has considerably less obtrusive motion artifacts than 3D Cartesian sampling, even when data is continuously acquired during free-breathing (FB) and all of the data is used for reconstruction (28). Non-Cartesian trajectories such as periodically rotated overlapping parallel lines with enhanced reconstruction (PROPELLER) (29), radial (30), spiral (31,32), and concentric rings (33) have been explored for fat-water separation but have not been evaluated for fat quantification, particularly in the liver. A major challenge for fat quantification using non-Cartesian sampling trajectories is their sensitivity to gradient errors. Therefore, development and evaluation of a gradient calibration and correction method is necessary to ensure accurate PDFF quantification for non-Cartesian imaging.

In this work, a novel FB liver fat quantification technique using a bipolar multiecho non-Cartesian 3D stack-of-radial sequence with golden-angle ordering (FB radial) is developed and evaluated in a preliminary study. Importantly, a technique to characterize and correct the gradient errors in bipolar multiecho radial imaging is developed to ensure accurate PDFF quantification. Various degrees of radial undersampling are investigated to reduce scan time. The fat quantification performance of FB radial is compared to conventional BH Cartesian MRI and reference standard BH single-voxel MR spectroscopy approaches in a fat-water phantom and the pelvis and liver in a pilot cohort of healthy subject.

METHODS

Signal Model

Fat and water content can be quantified using CSE-MRI by fitting the acquired MR signal for each TE (S_q(TE_n) to the signal model (13,34,35)

$${\mathrm{S}}_{\mathrm{q}}({\text{TE}}_{\mathrm{n}})=\left({\mathrm{W}}_{\mathrm{q}}+{\mathrm{F}}_{\mathrm{q}}·\left({\sum }_{\mathrm{j}=1}^{\mathrm{M}}{\mathrm{a}}_{\mathrm{j}}·{\mathrm{e}}^{\mathrm{i}2\mathrm{\pi }{\mathrm{f}}_{\mathrm{j}}{\text{TE}}_{\mathrm{n}}}\right)\right)·{\mathrm{e}}^{-{\mathrm{R}}_{2,\mathrm{q}}^{\ast }{\text{TE}}_{\mathrm{n}}}·{\mathrm{e}}^{\text{i2}\mathrm{\pi }{\mathrm{\phi }}_{\mathrm{q}}{\text{TE}}_{\mathrm{n}}}$$ (1)

to solve for signal contribution from water protons W_q, fat protons F_q, the effective transverse relaxation rate ${\mathrm{R}}_{2,\mathrm{q}}^{\ast }(1/{\mathrm{T}}_{2,\mathrm{q}}^{\ast })$, and the frequency shift due to field inhomogeneity φ_q at each pixel location q. To account for multiple peaks in the fat spectrum, the fat signal is based on an a priori spectral model with relative peak amplitudes a_j and corresponding frequencies f_j for peaks j = 1,…, M, in which M is the number of peaks. In this work, a multipeak fat model with M = 7 fixed frequencies and relative amplitudes (36) is employed. T₁ bias is reduced by using a low flip angle (11). Gradient delay and eddy current effects are corrected using a gradient calibration and correction approach. Liver fat quantification using this signal model in Eq. (1) has been validated in many studies for healthy subjects and patients (7,10,22–24) including concomitant NAFLD and iron overload patients (14). After removing confounding factors, PDFF (0–100%) is calculated using the fat-only (F_q) and water-only (W_q) signals in each pixel by

$${\text{PDFF}}_{\mathrm{q}}=\frac{{\mathrm{F}}_{\mathrm{q}}}{{\mathrm{F}}_{\mathrm{q}}+{\mathrm{W}}_{\mathrm{q}}}\times 100\%.$$ (2)

Multiecho Stack-of-Radial Sequence

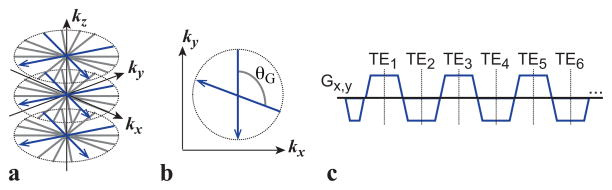
A 3D stack-of-radial image acquisition provides inherent robustness to motion for liver imaging (27,28,37–39). To enable free-breathing fat quantification, a bipolar multiecho radiofrequency-spoiled gradient echo prototype sequence using a golden-angle-ordered (38) 3D stack-of-radial trajectory was developed (Fig. 1). Radial spokes with the same azimuthal angle were acquired for all k_z increments prior to azimuthal angle rotation. For azimuthal angle rotation, golden angle ordering (Fig. 1b) was performed to support flexible reconstruction of an arbitrary number of radial views to balance spatiotemporal resolution, image SNR, and scan time (38). This flexibility is highly favorable for data undersampling to accelerate FB radial imaging (40,41).

Figure 1.

(a) 3D stack-of-radial trajectory. Radial readouts with the same azimuthal angle are acquired for all k_z increments before rotating the azimuthal angle. (b) Radial readouts are rotated continually by the golden angle (θ_G). (c) Six echoes are acquired every repetition time using a bipolar multiecho readout gradient. TE, echo time.

Bipolar multiecho readout gradients (Fig. 1c) were implemented for each spoke because they achieve higher SNR efficiency for improved fitting to the signal model compared to unipolar gradients (16,17,42). However, both bipolar and radial imaging gradients are more sensitive to errors in the k-space trajectory and phase due to uncompensated gradient delays and eddy currents (16,17,43–46), which are a major source of error in PDFF quantification. Therefore, a main requirement for developing a bipolar radial imaging technique for quantitative PDFF is to characterize and compensate for gradient errors (see next subsection).

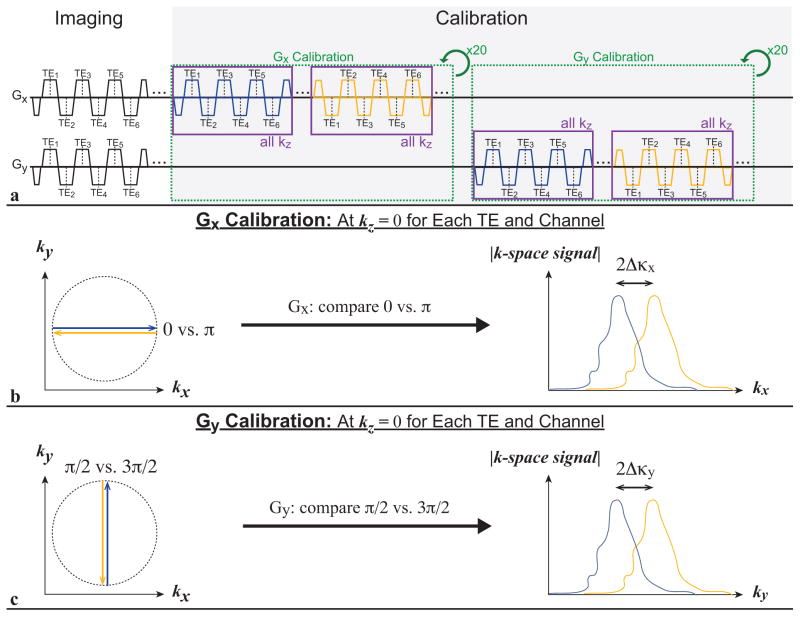
Gradient Calibration and Correction

The main effect of gradient imperfections and deviations, including various delays and eddy current effects, can be modeled as an effective gradient delay and characterized by measuring the corresponding apparent shift of acquired data samples in k-space. Following image data acquisition, deviations in the bipolar and radial gradients were characterized (44) by collecting 80 additional calibration spokes for G_x and G_y in total (20 spokes for each azimuthal angle of 0 vs. π and π/2 vs. 3π/2, respectively) (Fig. 2a). The calibration spokes of the same azimuthal angle were acquired for all k_z increments prior to rotating to the next azimuthal angle to induce similar gradient effects as the image data acquisition. The k-space signals for the azimuthal angles 0 versus π and π/2 versus 3π/2 were compared with cross correlation to determine the apparent k-space sample shifts Δκ_x and Δκ_y, due to effective gradient delays in G_x and G_y, respectively (Fig. 2b–c). The k-space signal was averaged over the 20 calibration spokes for each azimuthal angle, and 4-fold interpolation of the k-space signal was performed prior to cross correlation to achieve 0.25 k-space sample shift accuracy. Apparent k-space sample shifts were estimated for each spoke in the radial k-space trajectory (Δκ_θ),

Figure 2.

(a) Gradient calibration sequence design. As in the imaging module, a bipolar multiecho readout calibration module is repeated for all k_z increments to induce similar gradient effects. (b) The azimuthal angles 0 versus π are compared to calibrate G_x, and (c) π/2 versus 3π/2 are compared to calibrate G_y. The k-space sample shifts Δκ_x and Δκ_y are determined for both G_x and G_y, respectively, and used to correct the k-space trajectory for arbitrary azimuthal angles. TE, echo time.

$$\mathrm{\Delta }{\mathrm{\kappa }}_{\mathrm{\theta }}=\mathrm{\Delta }{\mathrm{\kappa }}_{\mathrm{x}}{(cos\mathrm{\theta })}^2+\mathrm{\Delta }{\mathrm{\kappa }}_{\mathrm{y}}{(sin\mathrm{\theta })}^2$$ (3)

for which θ is the azimuthal angle of the radial spoke and Δκ_x and Δκ_y are obtained from calibration (43,47). The effective gradient delay and apparent k-space sample shift (Δκ_x, Δκ_y) potentially varies for each receiver channel and echo. Therefore, Δκ_x and Δκ_y for each channel and echo were characterized independently. Previous methods (44) have used 15 spokes to calibrate each angle and averaged data from each channel; however, because this proposed strategy for calibration is performed for each individual channel and echo, more calibration spokes are needed to maintain sufficient SNR. Correction of the effective gradient delays was performed using Δκ_θ to shift the radial k-space trajectory for each spoke of each channel and echo during 3D gridding reconstruction. The scan time for acquiring 80 additional spokes for calibration was t_scan = 80 · TR · N_kz (approximately 31 seconds for N_kz = 44).

MRI Experimental Design

This research study was approved by our local institutional review board. All experiments were performed on a 3 Tesla MRI system (MAGNETOM Skyra, Siemens Healthcare GmbH, Erlangen, Germany) using a body array matrix and spine array coil. PDFF (%) was compared for the following techniques: FB bipolar multiecho 3D stack-of-radial prototype sequence with golden angle ordering (FB radial), BH bipolar multiecho 3D Cartesian prototype sequence (BH Cartesian) (24) and BH stimulated-echo acquisition mode (STEAM) single-voxel MR spectroscopy (SVS) prototype sequence (BH SVS) (48). All human subjects gave written informed consent prior to scanning. For radial and Cartesian sequences, a low flip angle of 5° was used to reduce T₁ bias (11); a large bandwidth was chosen to confine fat chemical shift blurring within a single pixel (49); and imaging parameters were matched as much as possible to enable a fair comparison (Table 1). Scan time is reported as minutes: seconds.

Table 1.

Representative sequence parameters for in vivo liver experiments. A slice oversampling factor of 10% was used for all acquisitions.

Imaging Parameters	BH Cartesian	FB Radial	BH Radial
TE (ms)		1.23, 2.46, 3.69, 4.92, 6.15, 7.38
ΔTE (ms)	1.23	1.23	1.23
TR (ms)	8.85	8.85	8.85
Matrix (Nx × Ny × Nz)	256 × 256 × 40	256 × 256 × 40	256 × 256 × 10
FOV (mm × mm × mm)	400 × 400 × 200	400 × 400 × 200	400 × 400 × 50
Slice Thickness (mm)	5	5	5
Radial Spokes	N/A	403 / 210 / 202 / 135	210
Flip Angle (degrees)	5	5	5
Bandwidth (Hz/pixel)	1150	1150	1150
Acceleration Factor (R)	4	1 / 1.92 / 2 / 3	1.92
Scan Time (min:s)	0:27	3:08* / 1:53* / 1:50* / 1:24*	0:27*

^*The radial gradient calibration scan time (31 s for FB radial and 4.25 s for BH radial) is included.

BH, breath-hold; FB, free-breathing; FOV, field of view; N/A, not applicable; TE, echo time; TR, repetition time.

In the phantom and in vivo pelvis experiments, during which there is no breath holding, both fully-sampled Cartesian (R = 1) and fourfold accelerated Cartesian (R = 4) with controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) (twofold acceleration along k_y, twofold acceleration along k_z) (50) were compared to the fully-sampled radial sequence (R = 1). In the liver, BH Cartesian R = 4 was compared to FB radial R = 1. Radial with scan acceleration (R = 2, 3) was emulated during reconstruction (see subsection) for all experiments and included in the comparisons. Imaging parameters for phantom and in vivo pelvis experiments are similar to those for in vivo liver experiments (Table 1).

Phantom Study

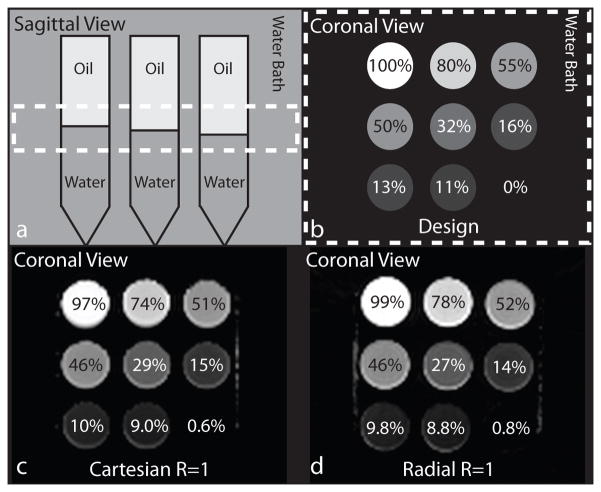
A PDFF phantom was constructed using nine 50-mL test tubes each with different volumes of fat and water, to obtain PDFF varying from 0% to 100%. The water solution was prepared with deionized water, 43mM of NaCl and 0.3mM of gadobenic acid (Gd-BOPTA, MultiHance, Bracco Imaging, Milan, Italy) to reduce the T₁ to approximately 600ms (10). Unrefined peanut oil was selected for fat due to similarities between the peanut oil fat spectrum and the subcutaneous fat spectrum (13).

The phantom was scanned using the SVS, Cartesian R = 1 and R = 4, and radial R = 1 sequences in the coronal plane at a specified position along the anterior-posterior direction, that resulted in a range of PDFF from 0% to 100% when eight coronal slices were combined to form a slab. The design PDFF for each test tube in the coronal slab was obtained by first measuring the filling heights of fat and water on the axial and sagittal MRI images corresponding to the SVS ROIs in OsiriX software version 6.0 (Pixmeo Sarl, Bernex, Switzerland) to calculate the volume fat fraction (VFF). The VFF was then converted to design PDFF by using the molecular weight (MW), density (d) and number of protons (λ) of peanut oil and water. The constants used were: MW_W = 18.015g/mol, MW_F = 283.275g/mol, d_W = 0.998g/mL, d_F = 0.910g/mL, λ_W = 2, and λ_F = 33.926 (10,51).

SVS was performed in each test tube with voxel size 15mm × 15mm × 40mm; five echoes with TE = 12ms, 24ms, 36ms, 48ms, and 72ms; TR = 3,000ms; mixing time = 10ms; vector size = 1,024; and bandwidth = 1,200Hz/pixel. The total acquisition time for the SVS scan was 0:15. Twenty slices were imaged using radial R = 1, Cartesian R = 1, and Cartesian R = 4, with scan times of 2:00, 0:55, and 0:14, respectively.

In Vivo Pelvis Study

In vivo pelvis scans of n = 5 (5 male) healthy subjects were performed to evaluate the agreement of PDFF between the Cartesian, radial, and the SVS scans. Scans in the pelvis have minimal interscan motion, which facilitates the comparison of fat quantification among these techniques. Pelvis scans were acquired in the axial plane using the radial R = 1, Cartesian R = 1 and Cartesian R = 4 techniques, with scan times of 3:08, 1:40, and 0:27, respectively. SVS was performed in selected ROIs, with a 10mm × 10mm × 15mm voxel size in the prostate, muscle, bone marrow and subcutaneous fat. The other parameters for the SVS scan were the same as in the phantom study.

To assess the accuracy of gradient calibration and effectiveness of gradient correction, two additional scans were performed in the pelvis of a healthy subject with the same scan parameters, as shown in Table 1, except that the bulk gradient delay (default 0.65μs, corresponding to Δκ_x,d, Δκ_y,d) was prescribed to be 2.348μs and 4.047μs to induce additional apparent k-space sample shifts of 1- and 2-samples, respectively (i.e., Δκ_x,+1, Δκ_y,+1 and Δκ_x,+2, Δκ_y,+2).

In Vivo Liver Study

In vivo liver scans of n = 11 (7 male) healthy subjects were acquired in the axial plane using the FB radial R = 1 sequence and BH Cartesian R = 4 sequences. The scan time for these acquisitions were 3:08 and 0:27, respectively. BH SVS was performed in six regions of interest (ROIs), with a voxel size of 10mm × 10mm × 15mm in the muscle, bone marrow, subcutaneous fat; and the Couinaud-Bismuth segments II/IV, VII, and VIII in the liver (52,53). These ROIs were selected to avoid major blood vessels and bile ducts. The other parameters for the SVS scan were the same as in the phantom study.

To evaluate the performance of gradient calibration and correction, FB radial R = 1 images were reconstructed with and without gradient error correction in a subset of n = 5 (4 male) subjects. The resulting PDFF maps were randomized and scored by an abdominal radiologist blinded to the reconstruction technique on a quality scale of 1 to 4 (1: definite artifacts that would confound PDFF estimation in a large extent of the liver; 2: definite artifacts that would confound PDFF estimation in some regions of the liver; 3: mild artifacts that would not confound PDFF estimation; and 4: no discernable artifacts and would not confound PDFF estimation.) In the remaining subjects, the gradient bulk delay in the sequence was adjusted to account for the calibrated effective gradient delay and prospectively reduce gradient errors.

To evaluate the robustness of FB radial PDFF in the presence of motion, an additional BH radial R = 1.92 scan was acquired in a subset of n = 5 (4 male) subjects and compared to a FB radial scan that was retrospectively undersampled to R = 1.92 (i.e., only reconstructing the first 53% of readouts).

Reconstruction and PDFF Calculation

The Cartesian and SVS sequences were reconstructed and PDFF maps were determined by the prototype scanner software. The Cartesian PDFF was calculated with mixed fitting using a Levenberg-Marquardt algorithm (24) with the signal model in Eq. (1), a 7-peak fat model with peaks at [0.97, 1.37, 1.66, 2.10, 2.32, 2.84, 5.38] ppm (36), and single effective R₂^* per voxel. SVS PDFF results were calculated by peak integration from 3.6 to 5.8 ppm for water and 0 to 3.6 ppm for fat, and T₂ correction was applied (48). The SVS results were calibrated by measuring PDFF in a test tube containing 100% fat. In this tube, SVS measured a PDFF of 92%; therefore, all results were calibrated by dividing SVS PDFF by 0.92. This compensates for fat peaks that overlap with the water peak (not modeled in the prototype scanner SVS software), corresponding to about 8% to 9% of the total fat fraction (36,48,54).

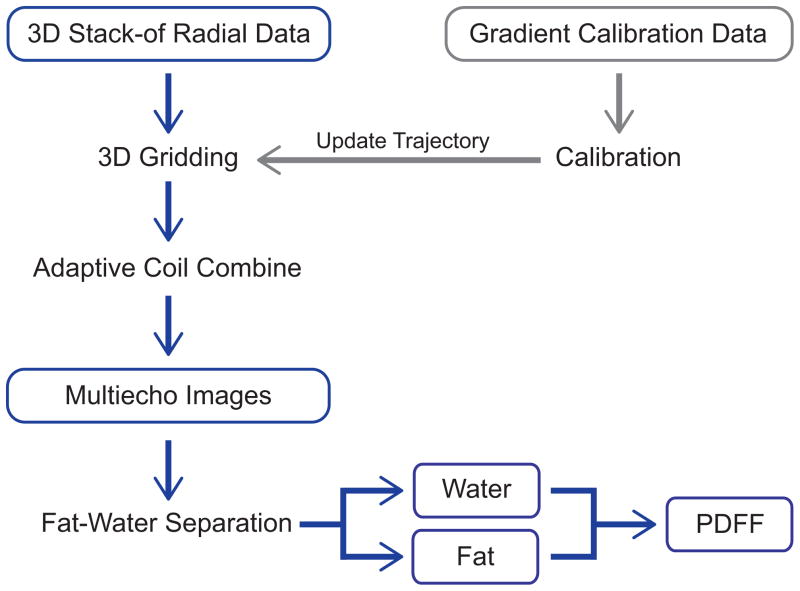
Radial datasets were reconstructed and fat-water separation was performed offline with MatLab R2013b (MathWorks, Natwick, MA, USA). Three-dimensional gridding, a linear density compensation function, and adaptive coil combine (55) were used. Because golden angle ordering supports flexible selection of any contiguous subset of radial readouts for reconstruction, we emulated accelerated scans by retrospectively reconstructing the first 33% of readouts (R = 3), first 50% of readouts (R = 2), and 100% of readouts (R = 1, that is, fully-sampled based on Nyquist criteria with the number of readouts = N_x,y·π/2 where N_x,y is the image size along x or y). Non-Cartesian parallel imaging reconstruction was not employed. Fat-water separation was performed using the signal model in Eq. (1) with complex-fitting using a graph cut algorithm (34,35,56), a 7-peak fat model (36), and a single effective R₂^* per voxel (12–14) (i.e., the same signal model as the prototype scanner-based Cartesian reconstruction). PDFF was calculated according to Eq. (2) with magnitude discrimination to reduce noise bias (11). The offline radial reconstruction pipeline is shown in Figure 3.

Figure 3.

Reconstruction pipeline for the 3D stack-of-radial data. PDFF, proton-density fat fraction.

Image and Statistical Analysis

All images and PDFF maps were converted to DICOM for viewing and analyzing in OsiriX. For quantitative evaluation, ROIs corresponding to the SVS ROIs were drawn on the Cartesian and radial PDFF maps. PDFF for all ROIs are reported as mean ± standard deviation (SD). Statistical analysis was performed in MatLab and Stata version 12.0 (StataCorp LP, College Station, TX). For all statistical comparisons, a P-value of < 0.05 was considered significant.

For the phantom experiments, linear correlation and Bland-Altman analysis were performed between radial R = 1,2,3 and BH Cartesian, BH SVS or design PDFF to evaluate the strength of a linear correlation and mean differences between techniques. For the in vivo pelvis experiments, separate Bland-Altman analyses for low (< 5%) and high (> 80%) PDFF regions were performed to evaluate mean differences between techniques. For the in vivo liver experiments, linear correlation and Bland-Altman analysis were performed to determine the presence of a linear correlation and mean differences between techniques.

Linear correlation analysis yields an equation for the linear regression between two compared methods to determine coefficient estimates of the slope (m) and intercept (b). Pearson’s correlation coefficient (ρ) (57) was determined to evaluate the strength of the linear relationship, and Lin’s concordance coefficient (ρ_c) (58) was determined to evaluate reproducibility and degree of agreement with the line of unity (i.e. y = x). Pearson’s correlation coefficient and Lin’s concordance coefficient were tested for statistical significance. Bland-Altman analysis (59) was used to calculate the mean difference (MD) or bias between two methods, and the 95% limits of agreement (LoA) are reported as the deviation from the mean difference by ± 1.96SD (i.e. [MD − 1.96SD, MD + 1.96SD]).

RESULTS

Gradient Calibration and Correction

Prior to gradient calibration, the radial PDFF maps in the pelvis (Supporting Fig. S1a) show artifacts originating from gradient delays and eddy current effects. The Δκ_x,d, Δκ_y,d (corresponding to the default bulk gradient delay) for different channels from the same echo ranged from 1- to 4.25-sample k-space shifts. This result supports the need to calibrate independently for each channel. Effects of the prescribed additional 1-sample and 2-sample k-space shifts were characterized by gradient calibration, obtaining Δκ_x,+1, Δκ_y,+1 and Δκ_x,+2, Δκ_y,+2, respectively. The incremental differences in apparent k-space sample shifts (δκ_x,+1, δκ_y,+1, δκ_x,+2, δκ_y,+2) were calculated by subtracting the calibrated apparent k-space shifts (Δκ_x,+1, Δκ_y,+1, Δκ_x,+2, Δκ_y,+2) from the default apparent k-space shifts (Δκ_x,d, Δκ_y,d). That is, δκ_x,+1 = Δκ_x,+1 − Δκ_x,d, δκ_x,+2 = Δκ_x,+2 − Δκ_x,d, δκ_y,+1 = Δκ_y,+1 − Δκ_y,d, δκ_y,+2 = Δκ_y,+2 − Δκ_y,d. The average of δκ_x,+1, δκ_y,+1, δκ_x,+2 and δκ_y,+2 over all channels was calculated for each echo. Representative values of δκ_x,+2 for TE₁–TE₆ were: 1.95 ± 0.06, 2.03 ± 0.06, 1.95 ± 0.07, 2.03 ± 0.06, 1.95 ± 0.06, and 2.07 ± 0.08 samples, respectively. A two-tailed Student’s t-test determined that the shifts averaged over all echoes were not statistically different from the prescribed additional 2-sample k-space shifts (P > 0.5 for δκ_x,+2, δκ_y,+2). The same result was obtained for 1-sample k-space shifts (P > 0.9 for δκ_x,+1, δκ_y,+1). The gradient correction strategy successfully removed the artifacts to produce accurate radial PDFF maps (Supporting Fig. S1b).

The mean and SD of the average of all apparent k-space shifts across subjects, the range of the apparent k-space shifts among channels, and the range of the apparent k-space shifts among echoes were evaluated for the phantom, in vivo pelvis and in vivo liver data (Supporting Table S1). For the axial in vivo liver and pelvis scans, the logical G_x and G_y correspond to the physical G_x and G_y, while for the coronal phantom scan, the logical G_x and G_y correspond to the physical G_x and G_z. Similar mean apparent k-space sample shifts were observed for the phantom (Δκ_x = 0.2 samples, Δκ_y = 0.2 samples), in vivo pelvis (Δκ_x = −0.17 ± 0.04 samples, Δκ_y = −0.18 ± 0.05 samples), and in vivo liver experiments (Δκ_x = −0.22 ± 0.04 samples, Δκ_y = −0.21 ± 0.04 samples). Higher mean apparent k-space sample shift values were observed for the n = 5 FB radial scans acquired without prospective bulk gradient delay adjustment (Δκ_x = 0.81 ± 0.08 samples, Δκ_y = 0.86 ± 0.09 samples). In addition, channel and echo variation in Δκ_x and Δκ_y in the in vivo pelvis and liver experiments was observed with a mean range of shifts of 0.71 to 1.56 samples and 0.53 to 0.93 samples, respectively.

Phantom Study

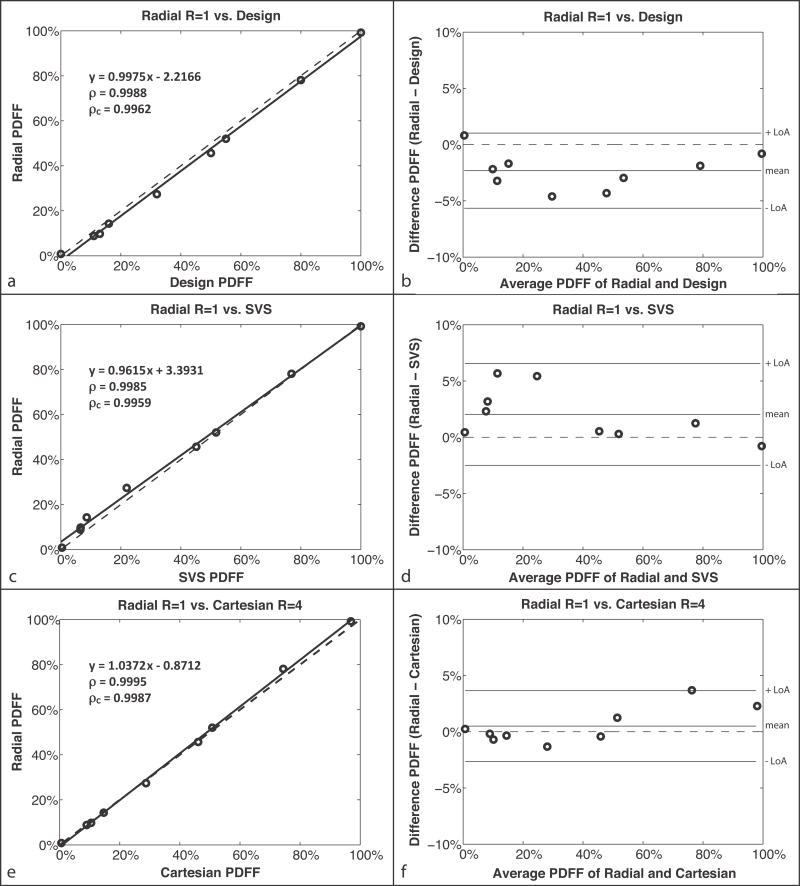
The design PDFF was calculated as 0%, 11%, 13%, 16%, 32%, 50%, 55%, 80%, and 100%. (Fig. 4b) CSE-MRI reconstructed PDFF maps using Cartesian and radial methods are presented in Figure 4c and 4d, respectively. The image quality and PDFF maps were very similar between Cartesian R = 1 and radial R = 1,2,3. Linear correlation and Bland-Altman plots for each comparison with radial R = 1 are shown in Figure 5. Full results from the linear correlation and Bland-Altman analysis are shown in Supporting Table S2 for radial R = 1,2,3.

Figure 4.

(a) Sagittal and (b) coronal views of the PDFF phantom design. A slab defined by the dotted lines (a) is combined to form the PDFF values shown in the coronal view (b). The PDFF maps for (c) Cartesian R = 1 and (d) radial R = 1. PDFF, proton-density fat fraction; SVS, single-voxel MR spectroscopy.

Figure 5.

Phantom study (a,c,e) linear correlation plots and (b,d,f) Bland-Altman plots. For the comparison between (a–b) radial R = 1 and design PDFF (described in the phantom design section of the methods), MD = −2.32% and LoA = MD ± 3.34%; (c–d) radial R = 1 PDFF and SVS PDFF, MD = 2.03% and LoA = MD ± 4.53%; and (e–f) radial R = 1 PDFF and Cartesian R = 4 PDFF, MD = 0.5% and LoA = MD ± 3.15%. The correlation coefficients ρ and ρ_c are statistically significant in all cases (P ≪ 0.01). The dashed lines represent y = x in the linear correlation plots and y = 0 in the Bland-Altman plots. LoA, limits of agreement; MD, mean difference; PDFF, proton-density fat fraction; SVS, single-voxel MR spectroscopy.

For the comparison between the radial R = 1 and design PDFF (Fig. 5a–b), the results showed a significant linear correlation, with ρ = 0.9988 (P ≪ 0.01) and ρ_c = 0.9962 (P ≪ 0.01) for the mean PDFF. There was a mean difference of −2.32% between radial R = 1 and design PDFF. The linear correlation and Bland-Altman analysis show a constant difference that does not depend on PDFF, which is likely due to unmodeled effects in the calculation of design PDFF.

Linear correlation and Bland-Altman plots for the comparison between the proposed radial R = 1 and the noninvasive reference standard SVS (Fig. 5c–d) also showed a significant linear correlation, with ρ = 0.9985 (P ≪ 0.01) and ρ_c = 0.9959 (P ≪ 0.01) for mean PDFF. The mean difference between radial R = 1 and SVS PDFF was 2.03%. This is likely due to a combination of partial-volume effects and the difference in fat models used. The correction for the SVS PDFF may not be sufficient to address all of the differences in the fat models.

The comparison between radial R = 1 and the conventional Cartesian R = 1 showed a significant linear correlation for the mean PDFF. The correlation coefficients ρ and ρ_c were 0.9994 and 0.9987, respectively (P ≪ 0.01). These results were similar to the comparison between radial R = 1 and Cartesian R = 4 (Fig. 5e–f), which also had a significant linear correlation with ρ = 0.9995 (P ≪ 0.01) and ρ_c = 0.9987 (P ≪ 0.01). Comparing radial R = 1 versus Cartesian R = 1 and R = 4, the Bland-Altman plots show absolute mean differences < 0.6% and LoA < mean difference ± 3.3%. Results from radial R = 2,3 are very similar to radial R = 1 for all comparisons. These results show that a radial CSE-MRI technique can provide accurate PDFF results in a phantom.

In Vivo Pelvis Study

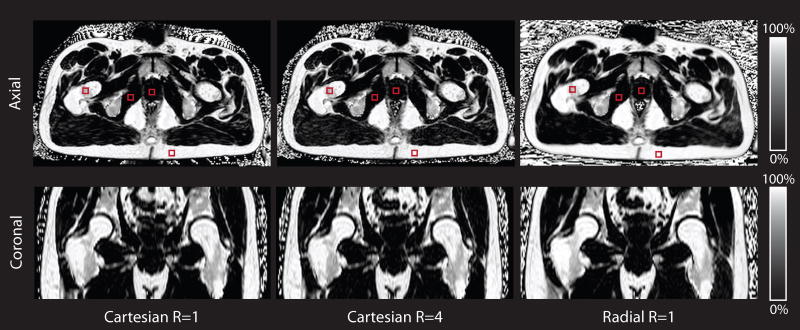
The subject population comprised n = 5 (5 male) healthy subjects with age = 29.20 ± 2.86 years and body mass index (BMI) = 23.75 ± 3.51 kg/m². Representative CSE-MRI reconstructed PDFF maps using Cartesian R = 1, Cartesian R = 4, and radial R = 1 methods are presented in the axial and reformatted coronal orientations. (Fig. 6) In all subjects, these three techniques produce very similar PDFF maps without fat-water swaps. Similar image quality was observed for radial R = 2,3 as was seen for radial R = 1. Bland-Altman plots were constructed separately for the low (< 5%) and high (> 80%) PDFF regions because of the absence of ROIs with intermediate PDFF values. Supporting Table S3 summarizes the Bland-Altman analysis for the low- and high-PDFF regions for radial R = 1,2,3 versus SVS; radial R = 1,2,3 versus Cartesian R = 1; and radial R = 1,2,3 versus Cartesian R = 4.

Figure 6.

Representative in vivo pelvis PDFF maps for Cartesian R = 1, Cartesian R = 4 and radial R = 1 for a representative subject in axial and coronal orientations. The red squares indicate regions of interest in the bone marrow, prostate, muscle, and subcutaneous fat for this subject. BH, breath-hold; FB, free-breathing; PDFF, proton-density fat fraction.

For the low-PDFF regions: radial R = 1 versus Cartesian R = 1 and R = 4 had absolute mean differences < 0.21% and LoA < MD ± 1.76%; radial R = 1 versus SVS had an absolute mean difference < 0.75% and LoA = MD ± 1.65%. For the high-PDFF regions: radial R = 1 versus Cartesian R = 1 and R = 4 had absolute mean differences < 3.7% and LoA < MD ± 3.8%; radial R = 1 versus SVS had absolute mean difference < 4.5% and LoA = MD ± 5.1%. These results illustrate agreement in mean PDFF for in vivo pelvis data between radial R = 1 and the conventional Cartesian R = 4, and radial R = 1 and the reference standard SVS. Similar results were observed for radial R = 2,3 as was seen for R = 1.

In Vivo Liver Study

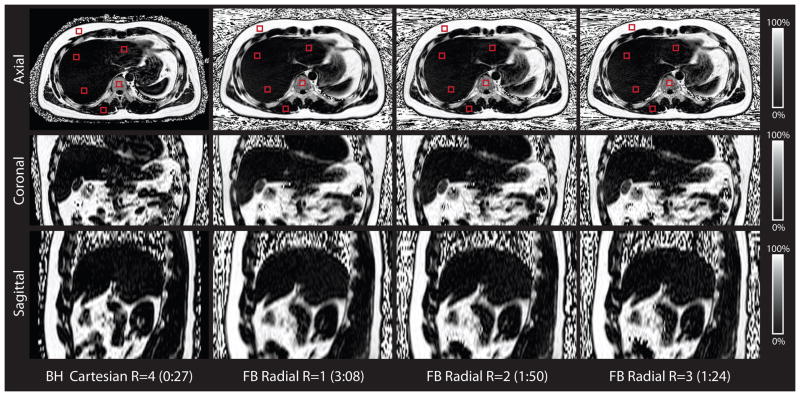
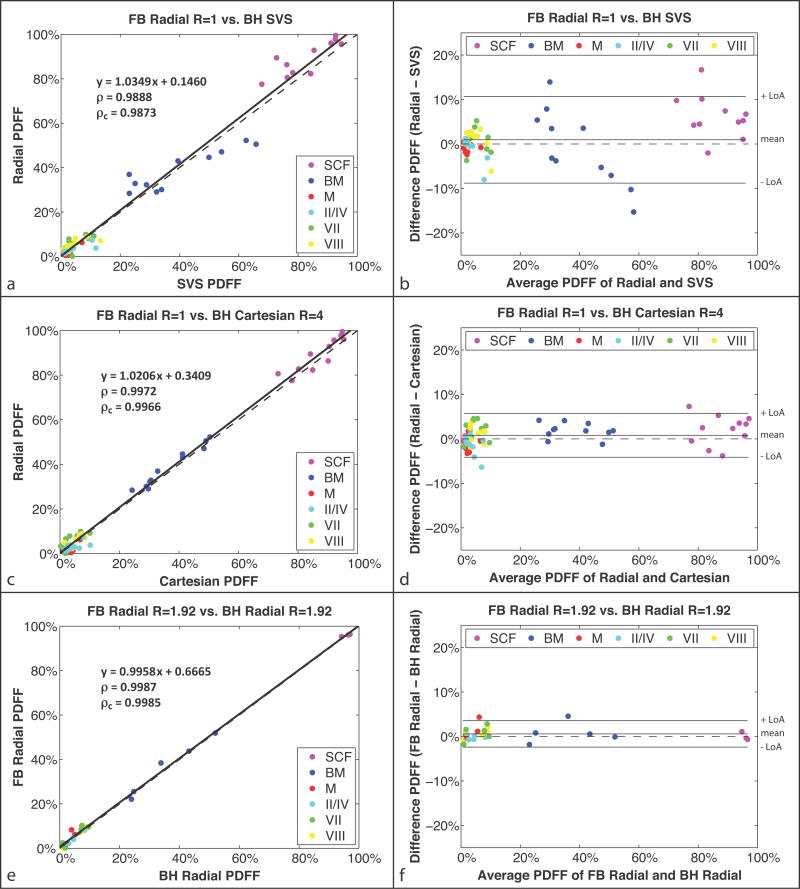
The subject population comprised n = 11 (7 male) healthy subjects with age = 26.09 ± 2.84 years and BMI = 23.17 ± 4.21 kg/m². Representative axial, reformatted coronal and reformatted sagittal PDFF maps from FB radial R = 1,2,3 and BH Cartesian R = 4 are shown in Figure 7. The PDFF maps from FB radial R = 1,2,3 and BH Cartesian R = 4 are very similar but have slight differences in liver position due to breath holding. Radial readouts of the same angle were acquired for all k_z encoding steps (along the superior-inferior direction for axial scans) prior to azimuthal angle rotation. Because the time to acquire all readouts of the same angle is small (≈389ms), there is limited motion along the Cartesian encoding direction k_z prior to each angle rotation. The effects of the motion are therefore distributed predominantly in the in-plane k_x-k_y directions and manifest as radial incoherent motion aliasing artifacts, thereby minimizing Cartesian-encoded through-plane coherent motion artifacts. This is confirmed by inspecting reformatted sagittal and coronal images of the 3D axial dataset (example in Fig. 7). Mean PDFF results from corresponding ROIs using FB radial R = 1, BH Cartesian R = 4 and BH SVS are compared in linear correlation and Bland-Altman analysis (Fig. 8). Full Bland-Altman and linear correlation results for all comparisons in the liver experiments are shown in Table 2.

Figure 7.

Representative in vivo liver PDFF maps for the BH Cartesian and the FB radial scans for a subject in axial, coronal, and sagittal orientations. Representative regions of interest (red squares) for the in vivo liver experiments are shown in the axial orientation. The PDFF maps are similar for FB radial R = 1,2,3 and BH Cartesian R = 4. FB radial and BH Cartesian have slight differences in liver position due to breath-holding. The scan time for each technique is reported as minutes:seconds. BH, breath-hold; FB, free-breathing; PDFF, proton-density fat fraction.

Figure 8.

In vivo liver study (a,c,e) linear correlation plots and (b,d,f) Bland-Altman plots for PDFF of regions of interest in the SCF; BM; M; and Couinaud-Bismuth segments II/IV, VII, and VIII. The comparison of (a–b) radial R = 1 versus SVS had MD = 0.95% and LoA = MD ± 9.74%; (c–d) radial R = 1 versus Cartesian R = 4 had MD = 0.82% and LoA = MD ± 4.9%; and (e–f) FB radial R = 1.92 versus BH radial R = 1.92 had MD = 0.58% and LoA = MD ± 2.97%. The correlation coefficients ρ and ρ_c were significant in all cases with P ≪ 0.01. The dashed lines represent y = x in the linear correlation plots and y = 0 in the Bland-Altman plots. BH, breath-hold; BM, bone marrow; FB, free-breathing; LoA, limits of agreement; M, muscle; MD, mean difference; PDFF, proton-density fat fraction; SCF, subcutaneous fat; SVS, single-voxel MR spectroscopy.

Table 2.

Bland-Altman and linear correlation analysis results for the in vivo liver experiments. The MD, LoA, equation for the linear regression, Pearson’s ρ and Lin’s ρ_c for each comparison are reported. All coefficients ρ and ρ_c are significant with P ≪ 0.01.

In Vivo Liver		LoA (MD ± 1.96SD)	Regression (y = mx + b)	ρ	ρc
FB Radial R = 1 vs.	BH Cartesian R = 4	0.8182% ± 4.9324%	y = 1.0206x + 0.3409	0.9972	0.9966
	BH SVS	0.9474% ± 9.7406%	y = 1.0349x + 0.1460	0.9888	0.9873
FB Radial R = 2 vs.	BH Cartesian R = 4	0.8364% ± 5.3767%	y = 1.0211x + 0.3487	0.9966	0.9960
	BH SVS	0.9656% ± 9.7243%	y = 1.0360x + 0.1382	0.9889	0.9873
FB Radial R = 3 vs.	BH Cartesian R = 4	0.6224% ± 5.6548%	y = 1.0190x + 0.1841	0.9962	0.9958
	BH SVS	0.7517% ± 10.5172%	y = 1.0320x + 0.0158	0.9867	0.9854
FB Radial R = 1.92 vs.	BH Radial R = 1.92	0.5839% ± 2.9721%	y = 0.9958x + 0.6665	0.9987	0.9985

BH, breath-hold; FB, free-breathing; LoA, limits of agreement; MD, mean difference; ρ, correlation coefficient; ρ_c, concordance coefficient; SD, standard deviation; SVS, single-voxel MR spectroscopy.

The results show a significant linear correlation with ρ = 0.9888 and ρ_c = 0.9873 between FB radial R = 1 and BH SVS (Fig. 8a) and with ρ = 0.9972 and ρ_c = 0.9966 between FB radial R = 1 and BH Cartesian R = 4 (Fig. 8c). The Bland-Altman analyses show absolute mean differences < 1% for FB radial R = 1,2,3 versus BH SVS (Fig. 8b, Table 2) and absolute mean differences < 0.9% for FB radial R = 1,2,3 versus BH Cartesian R = 4 (Fig. 8d, Table 2). These results demonstrate that even with motion, accurate fat quantification can be achieved in the liver and abdomen using a FB radial (R = 1,2,3) technique.

In the subset of n = 5 (4 male) healthy subjects with and without gradient error correction in FB radial reconstruction, PDFF maps with gradient error correction successfully suppressed artifacts and demonstrated substantially higher quality (score = 4 ± 0) than without gradient error correction (score = 1.6 ± 0.55). Representative results are shown in Supporting Figure S2.

In the subset of n = 5 (4 male) healthy subjects with both FB radial R = 1.92 and BH radial R = 1.92 acquisitions, the PDFF maps showed similar quality (Supporting Figure S3). The linear correlation analysis between the FB radial R = 1.92 PDFF and BH radial R = 1.92 PDFF showed a significant linear correlation, with ρ = 0.9987, ρ_c = 0.9985, mean difference = 0.58%, and LoA = MD ± 2.97% (Fig. 8e–f).

DISCUSSION

Our results demonstrate that accurate fat quantification can be performed during free-breathing for the entire 3D liver volume using a bipolar multiecho 3D stack-of-radial technique within a fast 1- to 2-min scan. PDFF calculated from FB radial scans, with and without acceleration (R = 1,2,3), had significant linear correlations and < 1% mean differences compared to both conventional BH Cartesian and reference standard BH SVS techniques in the liver and abdomen. BH Cartesian CSE-MRI methods have been previously established for fat quantification, and this is the first study to propose a FB radial technique and evaluate its accuracy with respect to established BH techniques.

For all experiments, when comparing Cartesian PDFF to radial PDFF, imaging parameters were matched as much as possible, including TE, bandwidth, spatial coverage, resolution, and the signal model. Note that echo times for the radial technique were chosen to match the Cartesian technique; however, they may not be the optimal echo times for maximizing the effective number of signal averages (42). The inline scanner reconstruction method for Cartesian data uses a mixed fitting algorithm while radial data is reconstructed offline using complex fitting. It has been shown that CSE-MRI PDFF maps reconstructed from the same dataset with mixed fitting and complex fitting are highly concordant with each other and achieve significant correlation and agreement with SVS PDFF (12,15). In addition, many studies have shown that PDFF from both complex (8–11,13,16,17) and mixed fitting methods (18,24,60) achieve a significant correlation to SVS or known fat fraction phantoms. In this study, all ROIs were drawn by the same individual to correspond to the SVS ROIs, thereby limiting intra- and interobserver variability. Future work will look at the effect of intra- or interobserver variability for PDFF quantification.

Concomitant gradient effects can potentially confound CSE-MRI and the quantification of PDFF. There are two main considerations related to the effects of concomitant gradients for our FB radial fat quantification technique (61,62). The first is the effect of concomitant gradients on radial data acquisition, which could cause blurring in the radial images (61). However, since our sequence design has a short readout window for each radial spoke and we typically have an axial slab with a maximum z position of ± 10cm from isocenter, the extra phase due to concomitant gradients did not cause noticeable blurring in slices toward the edge of the axial slab. The second is the effect of concomitant gradients on CSE-MRI and PDFF. Because we utilize a single bipolar echo train in each TR and the complex fitting algorithm accounts for the field inhomogeneity slice by slice, the extra frequency/phase effects due to concomitant gradients were incorporated as a component of the apparent B₀ field off-resonance term in the signal model and does not create errors in the PDFF calculation (62). Future work can investigate a correction for the effects of concomitant gradients in our FB radial technique.

For NAFLD diagnosis and monitoring, the accuracy of PDFF measurements for low-PDFF regions is important because the reference guideline for defining fatty liver is having liver PDFF > 5.6% (2,63) and clinically relevant liver PDFF usually ranges from 0% to 30% (14,64–67). For low-PDFF regions (< 5%), in vivo pelvis experiments showed absolute mean differences < 0.21% when comparing PDFF between radial R = 1 and Cartesian R = 1,4. Additionally, in vivo liver experiments in healthy subjects showed a significant correlation with absolute mean differences < 0.9% between FB radial R = 1,2,3 and BH Cartesian R = 4. These results provide promising evidence that the proposed FB radial technique can achieve accurate fat quantification in the liver for diagnosis of NAFLD.

For the in vivo liver experiments, the BH Cartesian R = 4 PDFF maps had some minor motion aliasing artifacts depending on the BH ability. Also, in the pelvis and liver, due to Cartesian R = 4 acceleration, there was increased noise compared to Cartesian R = 1 and radial R = 1. The Cartesian aliasing artifacts and increased noise with acceleration can potentially lead to errors in PDFF for low-fat regions, which could be exacerbated for patients who have more problems holding their breath compared to healthy subjects. The proposed FB radial approach may be more favorable to overcome these challenges.

Our study had several limitations. A first limitation is that the prototype SVS inline reconstruction on the scanner does not fully account for the complexities in the fat spectrum: the fat peak in the a priori seven-peak fat spectral model near the water resonance is counted toward the integrated water signal, and not toward the fat signal. This resulted in differences in the PDFF measurements. To account for this, the SVS PDFF was corrected prior to comparison with radial and Cartesian CSE-MRI to reduce differences. However, the correction may not have removed all sources of differences in the fat models. In addition, SVS is subject to errors due to partial-volume effects and motion, which were not corrected. A second limitation is that interscan motion hinders PDFF comparisons between techniques due to changes in tissue ROI position. For example, variability in liver positions between BH and FB scans result in interscan liver positional changes. To account for this, all ROIs were placed in corresponding anatomical locations on the Cartesian and radial PDFF maps. A third limitation is that the scan time for the radial acquisition is increased by 31 seconds due to the addition of calibration spokes. In this study, 20 calibration spokes were averaged to increase SNR for calibration; however, an optimal number of calibration spokes to decrease the calibration scan time has not been determined. Finally, only healthy subjects were included in this study for preliminary evaluation. NAFLD patients have higher liver fat content compared to healthy volunteers and may have more variable breathing patterns. Therefore, the proposed FB radial technique needs to be further evaluated in patient populations for fat quantification.

This work focused on fat quantification using the proposed FB radial technique and did not investigate R₂^* quantification for characterization of iron content in the liver (68). Notably, the proposed FB radial technique already employs the same fat and R₂^* signal model in Eq. (1), which is used by the BH Cartesian technique and has previously been evaluated in concomitant NAFLD and iron overload patients (14). Future work entails specifically evaluating the accuracy of FB radial for R₂^* and iron quantification.

In this work, we leveraged the inherent robustness of radial trajectories to motion, and no data rejection or binning was done prior to reconstruction. Because the radial acquisition was performed throughout free-breathing and without motion gating, image data reflected an average of all respiratory motion states, which may result in slight blurring in the radial PDFF maps; however, this did not affect PDFF quantification. In addition, experiments comparing FB radial versus BH radial demonstrate that fat quantification using the FB radial technique exhibits robustness to motion. Recent research has proposed using a 3D stack-of-radial trajectory with motion correction techniques for additional robustness to motion and removal of motion artifacts (39). It may be advantageous to combine similar motion correction strategies for radial fat quantification. This work has shown that although the radial R = 2 and R = 3 PDFF maps may have increased noise and streaking compared to the radial R = 1 PDFF maps, the fat-water separation quality and PDFF accuracy is maintained. Further work includes combining this technique with non-Cartesian parallel imaging to improve undersampled source image quality by decreasing streaking artifacts, further decreasing scan time, and improving SNR for fat quantification.

The proposed FB radial technique has many potential applications in the chest, abdomen, and pelvis due to its robustness to motion. It can be translated to patient populations that are not capable of breath-holding, such as sick, elderly, mentally impaired, and pediatric patients. The FB radial technique also allows for higher resolution, greater spatial coverage, or higher SNR because there is no BH scan time limitation. Further optimization and evaluation of FB radial fat quantification for these clinical applications will be the topic of future research.

CONCLUSION

We have demonstrated that rapid 1- to 2-min 3D fat quantification of the entire liver can be performed using a new free-breathing bipolar multiecho stack-of-radial technique. This technique demonstrates agreement to the conventional BH Cartesian CSE-MRI technique and reference standard BH single-voxel MR spectroscopy, and may improve patient compliance and fat quantification for management of NAFLD.

Supplementary Material

Supp Tables&Figures

Supporting Figure S1: (a) An in vivo pelvis PDFF map with prescribed additional 2-sample k-space shifts (Δκ_x,+2, Δκ_y,+2) and no gradient error correction. (b) The corresponding in vivo pelvis PDFF map after gradient error correction.

Supporting Figure S2: In vivo liver FB radial PDFF maps reconstructed with and without gradient error calibration and correction. Apparent k-space sample shifts were on average 0.8 samples. Gradient correction substantially improves the quality of the PDFF maps.

Supporting Figure S3: In vivo liver FB radial R = 1.92 and BH radial R = 1.92 PDFF maps. The PDFF maps are very similar with only slight differences in liver positioning due to breath holding.

Supporting Table S1: The apparent k-space sample shifts for the phantom, in vivo pelvis, and in vivo liver experiments reported as mean ± standard deviation (μ ± σ) of the individual means determined from each subject. In (a) the Mean represents the mean (μ_allx, μ_ally) of Δκ_x and Δκ_y over all subjects, channels, and echoes. In (b) and (c) the Mean Range represents the mean of the range (μ_Rx, μ_Ry) of Δκ_x and Δκ_y (b) over all subjects and echoes as a function of channels (i.e. channel variability), and (c) over all subjects and channels as a function of echoes (i.e. echo variability). For the coronal phantom scans, logical G_x and G_y correspond to physical G_x and G_z, respectively. For the axial in vivo scans, logical G_x and G_y correspond to physical G_x and G_y, respectively.

Supporting Table S2: Bland-Altman and linear correlation analysis results for the phantom experiments. The mean difference (MD), limits of agreement (LoA), equation for the linear regression, Pearson’s correlation coefficient (ρ) and Lin’s concordance coefficient (ρ_c) for each comparison are reported. All coefficients ρ and ρ_c are significant with P ≪ 0.01.

Supporting Table S3: Bland-Altman analysis results for the in vivo pelvis experiments. The mean difference (MD) and limits of agreement (LoA) for each comparison are reported.