Strategies for evaluating the assumptions of the regression discontinuity design: a case study using a human papillomavirus vaccination programme

Abstract

Background: The regression discontinuity design (RDD) is a quasi-experimental approach used to avoid confounding bias in the assessment of new policies and interventions. It is applied specifically in situations where individuals are assigned to a policy/intervention based on whether they are above or below a pre-specified cut-off on a continuously measured variable, such as birth date, income or weight. The strength of the design is that, provided individuals do not manipulate the value of this variable, assignment to the policy/intervention is considered as good as random for individuals close to the cut-off. Despite its popularity in fields like economics, the RDD remains relatively unknown in epidemiology where its application could be tremendously useful.

Methods: In this paper, we provide a practical introduction to the RDD for health researchers, describe four empirically testable assumptions of the design and offer strategies that can be used to assess whether these assumptions are met in a given study. For illustrative purposes, we implement these strategies to assess whether the RDD is appropriate for a study of the impact of human papillomavirus vaccination on cervical dysplasia.

Results: We found that, whereas the assumptions of the RDD were generally satisfied in our study context, birth timing had the potential to confound our effect estimate in an unexpected way and therefore needed to be taken into account in the analysis.

Conclusions: Our findings underscore the importance of assessing the validity of the assumptions of this design, testing them when possible and making adjustments as necessary to support valid causal inference.

Key Messages

• We provide a practical introduction to the regression discontinuity design (RDD) for epidemiologists.

• We describe four empirically testable assumptions of the RDD and offer strategies that can be used to assess whether these assumptions are met in a given study.

• Our findings underscore the importance of assessing the validity of the assumptions of this design, testing them when possible and making adjustments as necessary to support valid causal inference.

Introduction

Health researchers often seek to evaluate the effects of a health programme or medical intervention that has been implemented as a result of a change in public policy or practice guidelines. Since these changes occur outside the strictly controlled settings of randomized controlled trials, a major challenge in their evaluation is confounding bias. A recent example of such a policy change was the implementation of population-based human papillomavirus (HPV) vaccination programmes, which are primarily aimed at reducing the burden of cervical cancer in the population.¹ Previously, researchers assessed the effectiveness of HPV vaccination by comparing vaccinated and unvaccinated females.^2–5 Unfortunately, studies comparing vaccinated and unvaccinated groups are notoriously vulnerable to confounding bias since health beliefs and behaviours, which are associated with both the decision to receive a vaccine and the risk of many health outcomes, are difficult to identify and quantify.^6–9 In such cases, alternative strategies are needed.

The regression discontinuity design (RDD) is a quasi-experimental approach that was developed specifically to minimize confounding bias in the assessment of policies, treatments and interventions that are based on a cut-off rule or threshold.¹⁰ This design first appeared in the psychology and education literature and has been used extensively in the field of economics,¹¹ but has only recently been introduced to epidemiology,^12,13 where it may be similarly useful. Given the parallels between the randomized control trial (RCT) and the RDD, the latter is used as a powerful alternative in situations where RCTs are unethical or otherwise unfeasible.¹⁴ For example, it has been used to assess the impact of new age guidelines for breast and colorectal cancer screening,¹⁵ as well as to evaluate the effects of expanded Medicaid coverage on mortality for children born after a certain date.¹⁶ The RDD is an important tool that epidemiologists can use to evaluate the causal effects of health policies and interventions. As with any methodology, however, a thorough investigation of the data and an assessment of whether the design is appropriate for the study question at hand is a critical first step.

In this paper, we provide a practical introduction to the regression discontinuity design, describe the assumptions of the design and offer strategies to assess whether these assumptions are met in a given study. For illustrative purposes, we apply these strategies to our study of the impact of HPV vaccination on cervical dysplasia, the results of which are published elsewhere.¹⁷

Overview of the RDD

The defining feature of the RDD is the method by which exposure is assigned. Specifically, the RDD is used in situations where individuals are assigned to an exposure based on whether they are above or below a pre-specified cut-off on a continuously measured scale. As a result, the probability of being exposed changes discontinuously at the cut-off as a function of the underlying continuous variable. In the RDD literature, this underlying continuous variable is often referred to as the ‘forcing’ or ‘running’ variable. The RDD analysis then measures any corresponding discontinuous change in the probability of the outcome at that same cut-off. The magnitude of this discontinuity is used to estimate the causal effect of the policy change or intervention on those near the cut-off.

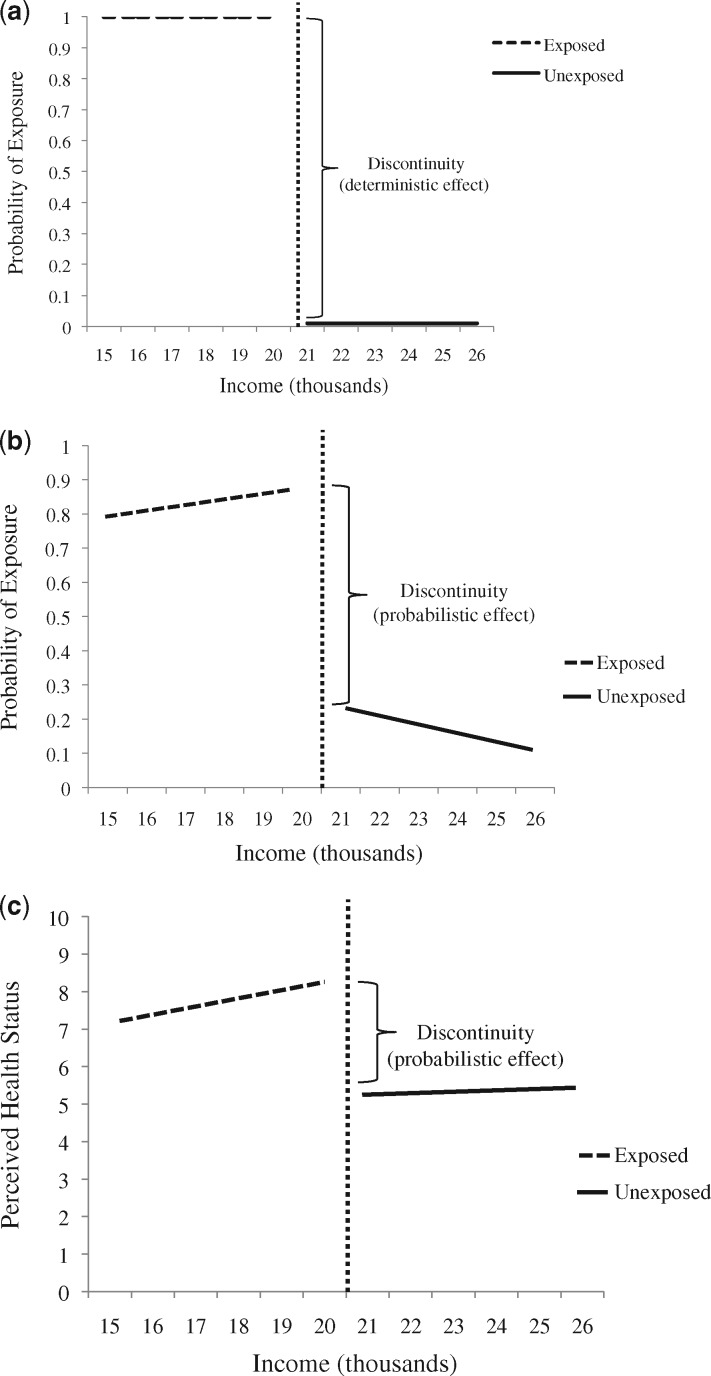
Imagine e.g. a prescription drug programme offered free to those with an annual income of less than $20 000 (Figure 1): the forcing variable would be income, the probability of being insured would be significantly higher among those who make less than $20 000 and the RDD could be used to assess whether there was an improvement in perceived health status 1 year later, as indicated by a discontinuous jump at the cut-off.

Figure 1.

Hypothetical RDD setting. (a) Sharp exposure discontinuity; (b) fuzzy exposure discontinuity; (c) outcome discontinuity.

The RDD is valid when exposure is either completely or partially determined by the assignment rule; the design simply requires that the probability of exposure changes discontinuously between groups at the assignment cut-off. To accommodate both deterministic and probabilistic assignment rules, there are two types of the RDD—the sharp RDD and the fuzzy RDD. The sharp RDD is used when the assignment rule perfectly determines exposure, meaning all individuals on one side of the cut-off are exposed to the policy/intervention/treatment and all individuals on the other side are not, and the proportion exposed changes from 1 to 0 at the cut-off (Figure 1a). Conceptually, this situation may arise in the presence of a population-based policy, such as mandatory vaccination or an environmental exposure, such as fluoridation of the drinking water. In contrast, the fuzzy RDD is applied when the assignment rule affects the probability of exposure, leading to a discontinuous change in the probability of exposure at the cut-off, but by less than 1 (Figure 1b). This scenario may arise when participation in a programme is optional, as is the case with HPV vaccination, or when incentives for participation change at the cut-off, but are not powerful enough to shift everyone from unexposed to exposed. This situation is analogous to non-compliance in an RCT. In the presence of such non-compliance, the RDD estimates the intention-to-treat (ITT) impact of the intervention. As in RCTs, the ITT analysis of the RDD offers a pragmatic assessment of the intervention’s impact.

The strength of the RDD comes from the idea that the exact location of the assignment cut-off is unpredictable because the cut-off is determined by an administrative decision, creating a quasi-experiment in which the precise cut-off value is unrelated to the baseline characteristics of the individuals close to the cut-off. This is analogous to when randomization arbitrarily assigns individuals in an RCT to exposed or control groups. When exposure is unconditionally and randomly assigned, as in RDDs and RCTs, exposed and unexposed individuals are expected to be exchangeable: they are balanced with respect to independent outcome predictors, so their outcome probability would be the same whenever they were subjected to the same exposure history.¹⁸ As a result, the additional assumption of ‘no unobserved confounding’, which is considered the Achilles' heel of non-experimental observational studies,¹⁹ is not required. Indeed, studies show that randomized experiments and the RDD produce similar estimates in regions near the cut-off.²⁰ The RDD has the added advantage over RCTs of being able to estimate local causal effects in a small range near the cut-off, whereas RCTs estimate average causal effects, meaning the RDD can be used to estimate the effect of raising or lowering a cut-off.¹²

In public health as well as medicine, cut-off rules are often used to guide decisions. As a result, the RDD has a broad range of potential applications. As previously mentioned, it has been used to assess the impact of a clinical guideline recommending mammography for all women starting at age 40, where age was the continuous variable and 40 years was the cut-off,¹⁵ as well as Medicaid eligibility, where birth date was the continuous variable and 30 September 1983 was the cut-off.¹⁶ Researchers have also used the RDD to study health outcomes by exploiting discontinuities that arose because of a geographic boundary, a legal age limit, the timing of HIV treatment, insurance eligibility and others.¹³

The RDD is a powerful design, but its ability to estimate causal effects rests on several important assumptions. Some of these are empirically testable and others are not, but all must hold in order to interpret the effect estimates as causal. In this paper, we assess whether the RDD assumptions hold in the context of a study on the effects of a population-based HPV vaccination programme.

Case study

In 2006, Canada was one of several developed countries to approve Gardasil^®, a quadrivalent human papillomavirus (HPV) vaccine designed to protect against four types of HPV that cause 70% of cervical cancers and more than 90% of anogenital warts. Randomized controlled trials of the vaccine showed it to be highly efficacious in preventing pre-cancerous cervical lesions and anogenital warts.^1,21 The following year, Canada’s largest province, Ontario, implemented a publicly funded, school-based HPV vaccination programme that offers optional HPV vaccination to all grade 8 girls.²² Girls who were not eligible for the programme (i.e. those in grade 8 before 2007) were able to obtain the vaccine through a physician or public health unit at a cost of approximately CA$450 for the three-dose immunization series. Similar programmes have been implemented across Canada and around the world, but there is limited real-world information on how effective these programmes have been at reducing HPV-related disease.

To assess whether the RDD was appropriate for evaluating the causal impact of Ontario’s HPV vaccination programme on the risk of cervical dysplasia, an early precursor to cervical cancer, we used data from the Ontario Grade 8 HPV Vaccine Cohort Study. In brief, we used Ontario’s population-based administrative health and immunization databases to identify a cohort of all girls in grade 8 in Ontario in the two years before (2005/06–2006/07) and after (2007/08–2008/09) the programme’s September 2007 implementation date (n = 260 493). Since we did not have information on school grade, we used birth date to determine grade 8 year because more than 95% of Ontario students are 13 years old by 31 December of their grade 8 school year.²³ Additional details on the data and cohort are available in other publications.^17,24

RDD assumptions and variables

There are four assumptions specific to the RDD that are at least partially empirically verifiable and must be assessed prior to analysis. They are as follows:

1. There is a discontinuity in the probability of exposure at the cut-off.

2. Individuals’ value of the forcing variable was not manipulated.

3. Exposure groups are exchangeable around the cut-off.

4. The outcome probability is continuous at the cut-off in the absence of the intervention.

Prior to discussing each of these assumptions, we define the variables needed to test them.

Forcing variable and cut-off

A fundamental component of the RDD is the forcing variable, which is the observed continuous variable that assigns exposure based on whether its value is above or below a fixed cut-off. Assignment to Ontario’s Grade 8 HPV vaccination programme was based on whether a girl was in grade 8 before or after the September 2007 programme implementation date. Since we used birth date to define grade 8 year, it follows that girls born on 31 December 1993 and earlier were ineligible for the programme and girls born on 1 January 1994 and later were eligible for the programme. Accordingly, the forcing variable in this study was based on birth date and the cut-off was 1 January 1994 (Table 1). In operationalizing the forcing variable, it was important to ensure there were sufficient observations for each value of the forcing variable to obtain stable estimates of the mean, as well as enough values of the forcing variable on either side of the cut-off to estimate stable regression lines and predicted values. Given the infrequency of cervical dysplasia in the young age group of our study population, we collapsed birth date into 3-month intervals, henceforth referred to as birth year quarters. For analytic purposes, the data were centred such that ‘0’ represented birthdates at the cut-off (1 January 1994 to 31 March 1994) and the forcing variable ranged from –8 to 7.

Table 1.

Operationalization of forcing variable

	Grade 8 school year	Birth year	Birth year quarter	Value of forcing variable
Ineligible			Mar 1992–Jan 1992	–8
	2005/06	1992	Jun 1992–Apr 1992	–7
			Sept 1992–Jul 1992	–6
			Dec 1992–Oct 1992	–5
			Mar 1993–Jan 1993	–4
	2006/07	1993	Jun 1993–Apr 1993	–3
			Sept 1993–Jul 1993	–2
			Dec 1993–Oct 1993	–1
Eligible			Jan 1994–Mar 1994	0
	2007/08	1994	Apr 1994–Jun 1994	1
			Jul 1994–Sept 1994	2
			Oct 1994–Dec 1994	3
			Jan 1995–Mar 1995	4
	2008/09	1995	Apr 1995–Jun 1995	5
			Jul 1995–Sept 1995	6
			Oct 1995–Dec 1995	7

Exposure

In this study, estimates from both the sharp RDD and the fuzzy RDD were of interest, as each enabled us to answer a different public health question. First, because girls had no control over whether they were eligible for Ontario’s HPV vaccination programme, exposure was defined based on programme eligibility: whether a girl was in grade 8 before or after the September 2007 programme implementation date. Our mapping of birth date to grade created a ‘sharp’ definition of exposure where 100% of girls born on or after 1 January 1994 were eligible and 0% of girls born before that date were eligible. This enabled us to estimate the ITT impact of vaccination for the first time outside of clinical trials and to estimate the impact of the programme on the risk of cervical dysplasia. Second, to determine the effect of vaccination on cervical dysplasia, exposure was defined based on actual HPV vaccination status. We defined HPV vaccine exposure as receipt of all three doses of the vaccine between 1 September of grade 8 and 31 August of grade 9, as these dates corresponded with the programme eligibility period. This second question matches a fuzzy RDD because both eligible and ineligible girls had the option of the receiving the vaccine, but the incentives to do so were very different between groups. Specifically, the vaccination series was free and school-based for eligible girls, whereas it was expensive and required three visits to a physician office or public health unit for ineligible girls.

Outcome

The original RDD was conceived with a continuous forcing variable and a continuous dependent variable. However, recent work in the RDD literature has expanded the design to also include dichotomous outcomes.^12,25–27 This development is particularly important for researchers wishing to apply the design to epidemiologic questions, as outcomes of interest in this field are often dichotomous disease diagnoses. Indeed, the outcome of interest in our study was the detected presence of cervical dysplasia, a precursor to cervical cancer. To ensure temporality between the exposure and outcome, cases of cervical dysplasia were identified in the period immediately following the exposure ascertainment window—i.e. between 1 September of grade 10 and 31 March of grade 12.

Baseline characteristics

To assess the exchangeability/comparability of the groups, we considered a number of potential confounders: baseline characteristics related to socio-demographics, frequency of healthcare use and medical and vaccination histories. Socio-demographics factors considered included age, birth quarter, neighbourhood income quintile and urban/rural residency. Healthcare use was defined in terms of the frequency of emergency department visits, hospitalizations, same-day surgeries and outpatient physician visits in the two years before grade 8, each categorized based on the frequency distribution of the data. Among girls with at least one hospitalization, the mean inpatient length of stay was also determined. We also identified whether a cohort member had been previously diagnosed with cancer, a mental illness, an intellectual disability, a congenital anomaly or Down syndrome, as well as whether she had any diagnosis or procedure related to sexual behaviour in the 2 years before grade 8 (e.g. diagnosis of a sexually transmitted infection, pregnancy, cervical cancer screening). Finally, we created indicators for prior receipt of the measles, mumps and rubella (MMR); diptheria, tetanus and pertussis (DTP); and hepatitis B vaccines.

Assessment of the RDD assumptions

Assumption 1: there is a discontinuity in the probability of exposure at the cut-off

A fundamental assumption of the RDD is that there is a discontinuous change in the probability of exposure at the assignment cut-off. Therefore, we first assessed whether discontinuity of exposure was present in our study. It was also important to assess whether there were discontinuities in exposure at locations other than the cut-off, as these could be indicative of temporal trends, such as other interventions or policy changes that might confound the results. Accordingly, continuity in the probability of exposure across values of the forcing variable with the exception of a single notable discontinuity at the cut-off provides evidence that this first assumption is satisfied.

To evaluate this assumption for each of our exposure definitions, we generated line graphs of the probability of programme eligibility and HPV vaccination according to the forcing variable. Not surprisingly, Figure 2a shows that programme eligibility was a deterministic function of the forcing variable, providing evidence that, conditional on our mapping of birth date to grade, this assumption was satisfied for the sharp RDD. Figure 2b shows that the programme eligibility had an important impact on HPV vaccine exposure, as evidenced by the jump from 0.03 to 0.46 in the proportion of vaccinated girls on either side of the eligibility cut-off. This figure also demonstrates that there was continuity across values of the forcing variable on each side of the cut-off, with the exception of a slight jump between the 1994 and 1995 birth year cohorts (corresponding with the 2007/08 and 2008/09 vaccination programme years). Although the RDD generally requires continuity on either side of the cut-off, this jump is likely attributable to the increase in HPV vaccine acceptance between the first and second years of the programme, rather than to factors external to the programme that increased HPV vaccine acceptance in the 1995 birth cohort and also differentially affected their probability of dysplasia. After further verification of this hypothesis,²⁸ we judged the first assumption to be satisfied for the fuzzy RDD as well. Of note, there is no definition of what is ‘enough’ discontinuity at the cut-off, but smaller discontinuities in exposure at the cut-off reduce the power to detect a difference in the outcome.

Figure 2.

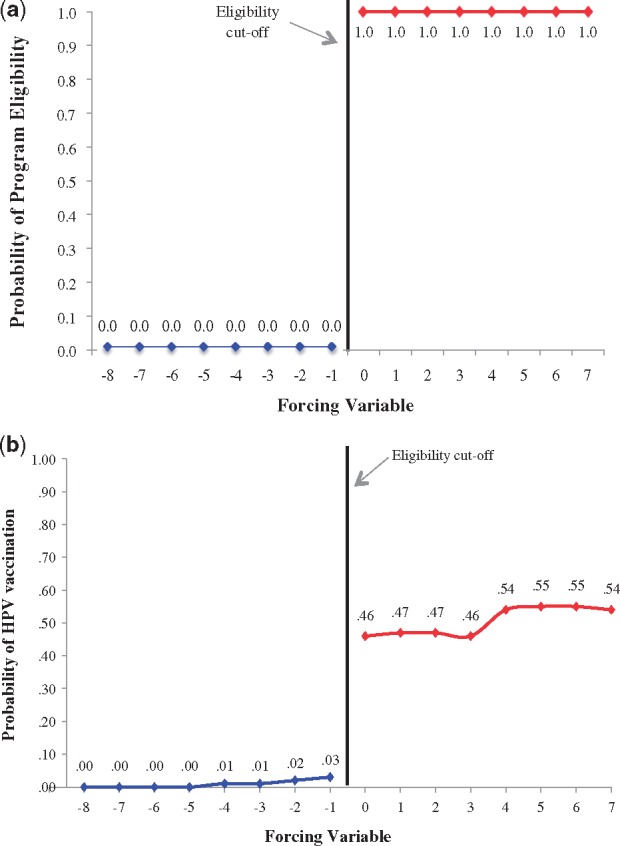
Probability of exposure, by the forcing variable*. (a) Probability of qHPV vaccine programme eligibility; (b) probability of qHPV vaccination. *See Table 1 for how values of the forcing variable were operationalized.

Assumption 2: individuals’ value of the forcing variable was not manipulated

Another important requirement for a causal interpretation of the RDD estimates is that individuals did not exert control over their value of the forcing variable, as this would violate the assumption that groups are assigned to the intervention in a way that is analogous to randomization. Consider e.g. if gastric bypass surgery was offered free to all individuals with a body mass index (BMI) over 40. It is plausible that individuals with BMIs just below 40 might chose to gain the few additional pounds required for them to become eligible. As a result, we would observe a deficit of individuals with BMIs just below the cut-off and an excess with BMIs at or just above, creating a discontinuity in the frequency of observations at the eligibility cut-off. In contrast, if this assumption were satisfied, we would expect continuity in the density of observations across all values of the forcing variable. In principle, continuity of the density is not necessary for valid inference, but discontinuity is suggestive of violations of the non-manipulability assumption. Non-manipulability is advantageous because it supports the exchangeability assumption.

In our study, the forcing variable was based on birth date. Although birth date can theoretically be manipulated to a certain extent through planned date of conception or request for delivery by caesarean section, it is highly unlikely that the reasons for manipulation would be related to the risk of cervical dysplasia or eligibility for an HPV vaccination programme 12 years later. Therefore, manipulation of a girl’s date of birth is unlikely to have introduced confounding in our study. Nevertheless, we tested the continuity of density of observations by determining the percent of cohort members per value of the forcing variable (Table 2) and creating a histogram of the density of the forcing variable (Figure 3). The percentages of cohort members per value of the forcing variable ranged only by 0.7 percentage points, from 5.8% to 6.5%. Moreover, Figure 3 is relatively flat, indicating continuity in the density of the forcing variable. Together, the lack of a plausible manipulation mechanism and the clear continuity observed from our evidence-based assessment provided strong evidence that the forcing variable had not been manipulated and no additional form of testing was needed. However, McCrary’s density test can be applied in more tenuous cases, as it offers a more rigorous assessment of this assumption.²⁹

Table 2.

Distribution of cohort members across birth year quarters (forcing variable)

Forcing variable	Frequency	Percentage (n = 260 493)
–8	16 309	6.26
–7	17 415	6.69
–6	17 126	6.57
–5	15 803	6.07
–4	15 766	6.05
–3	17 035	6.54
–2	16 697	6.41
–1	15 630	6.00
0	15 741	6.04
1	16 860	6.47
2	16 695	6.41
3	15 522	5.96
4	15 419	5.92
5	16 743	6.43
6	16 561	6.36
7	15 171	5.82

Figure 3.

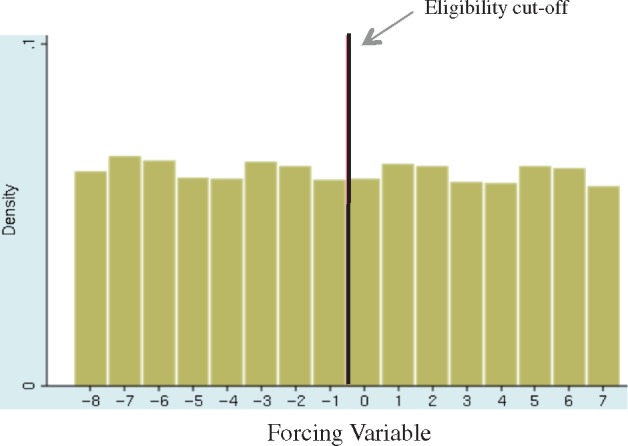
Density of the forcing variable. *See Table 1 for how values of the forcing variable were operationalized.

Assumption 3: exposure groups are exchangeable around the cut-off

The quasi-experimental nature of the RDD implies that groups are similar with respect to all measured and unmeasured factors, with the exception of the exposure and outcome. In classic epidemiological designs, the potential for confounding is assessed by directly comparing exposed and unexposed groups, or cases and controls. In the RDD, the assumption of exchangeability applies to those closest to the cut-off as these are the observations for which the causal effect applies. Therefore, we assume that individuals closest to the cut-off are the most exchangeable with respect to measured and unmeasured confounders, and it is generally accepted that the extent of this exchangeability may decrease with increasing distance from the cut-off. This notion is also incorporated into the RDD analysis, which is often restricted to observations closest to the cut-off (e.g. using local linear regression methods) and/or places the greatest weight on these observations in the analysis, e.g. by triangular kernel weighting.

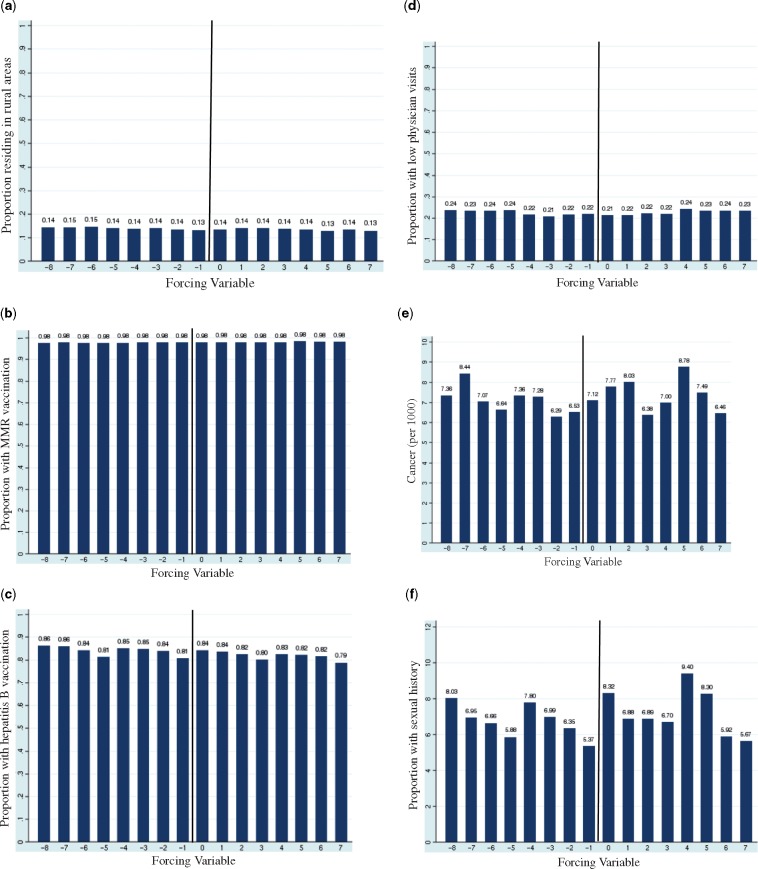
To assess exchangeability around the cut-off, we plotted the distribution of baseline characteristics as a function of the forcing variable. For variables with more than two categories, each category was assessed separately. Figure 4 depicts the distribution of selected baseline characteristics (see Appendix 1, available as Supplementary data at IJE online, for the complete set of graphs). Socio-demographics, vaccination history and frequency of healthcare use were generally balanced across the forcing variable. Not surprisingly, there was greater variability in the distribution of characteristics with low baseline incidence rates, such as cancer. However, there were no discernible patterns in these data and differences at the cut-off were not of greater magnitude than those at locations other than the cut-off, suggesting this variability was attributable to random variation rather than to meaningful differences between exposure groups. In contrast, both hepatitis B vaccination (Figure 4c) and a history of sexual activity (Figure 4f) revealed an important pattern that, independently of birth year, individuals born earlier in the calendar year (January–March) were more likely to have the characteristic than those born later in the year (October–December). These findings suggested that the timing of a girl’s birth relative to that of her grade-matched peers was associated with receipt of optional vaccines and with sexual activity. The relative effect of age has been observed in other areas as well, including sports performance and academic achievement.^30,31

Figure 4.

Distribution of selected baseline characteristics, by forcing variable. (a) Rural residency; (b) Previous MMR vaccination; (c) Previous hepatitis B vaccination; (d) 0–1 outpatient physician visits; (e) Cancer; (f) Sexual history.

Taken together, this assessment provided evidence that cohort members were generally similar with respect to measured potential confounders across levels of the forcing variable, with the exception of birth quarter, which had the potential to confound our association of interest and therefore had to be taken into account in the analysis. Of course, it is not possible to assess exchangeability with respect to unobserved factors. However, the reassuring results with respect to Assumption 2 and the balance demonstrated for observed factors both provided good evidence that the groups being compared were exchangeable.

Assumption 4: the outcome probability is continuous at the cut-off in the absence of the intervention

A fourth fundamental assumption is that the risk of the outcome would have been continuous at the cut-off in the absence of the intervention. This is a logical extension of the exchangeability principle, meaning that any discontinuity in the outcome probability can be attributed to exposure alone. To quantitatively assess this assumption, we would need to observe the counterfactual outcome: rates of cervical dysplasia in the same population over the same time period in the absence of the HPV vaccine programme. Since this is not possible, researchers may assess the outcome in plausibly exchangeable alternative populations or time periods. We took the approach of graphing the risk of the outcome for each value of the forcing variable, where continuity in the risk on either side of the cut-off provided some evidence that this assumption was satisfied; this continuity is especially important near the cut-off. An additional benefit of this assessment is that it allows examination of whether there is a discontinuity in the outcome probability at the cut-off, thereby providing preliminary insight into the results of the causal analysis—a discontinuity would suggest the intervention had a causal effect on the outcome, whereas continuity would suggest little to no causal effect. This graphical analysis also enables the researcher to examine whether there is any discontinuity at locations other than the cut-off, which could suggest the presence of temporal trends, such as other policies/interventions that may have affected the outcome.

Since randomized controlled trials of the HPV vaccine have shown it to be highly efficacious in preventing cervical dysplasia in older girls,^32,33 we expected a drop in the risk of this outcome probability at the programme eligibility cut-off and continuity in the outcome probability on either side of the cut-off. We graphed the risk of cervical dysplasia for each value of the forcing variable (Figure 5a), and our results suggested a pattern similar to what we had observed with hepatitis B vaccination and sexual history: girls born earlier in the calendar year were at higher risk of this outcome than girls born later in the year. To further investigate the potential confounding effect of birth timing, we collapsed the risk of the outcome across birth quarter into birth year. The risk of dysplasia by birth year is displayed in Figure 5b, which suggests rates between ineligible birth years (1992 and 1993) were similar (i.e. continuous), as were rates between eligible birth years (1994 and 1995). These findings confirmed that birth quarter was associated with cervical dysplasia and needed to be conditioned on in the RDD analyses. To control for the effect of birth quarter, we included it as a covariate in the regression models, included all observations in the analysis rather than restricting to observations closest to the cut-off and weighted birth years closest to the cut-off (1993 and 1994) twice as heavily as those further away (1992 and 1995). Additional details on these strategies are described elsewhere.²⁸Figure 5 also demonstrates that, conditional on birth quarter, there is a discontinuous drop in the risk dysplasia between ineligible and eligible girls at the cut-off, thus providing preliminary evidence that the HPV vaccination programme had a significant impact on reducing the risk of cervical dysplasia.

Figure 5.

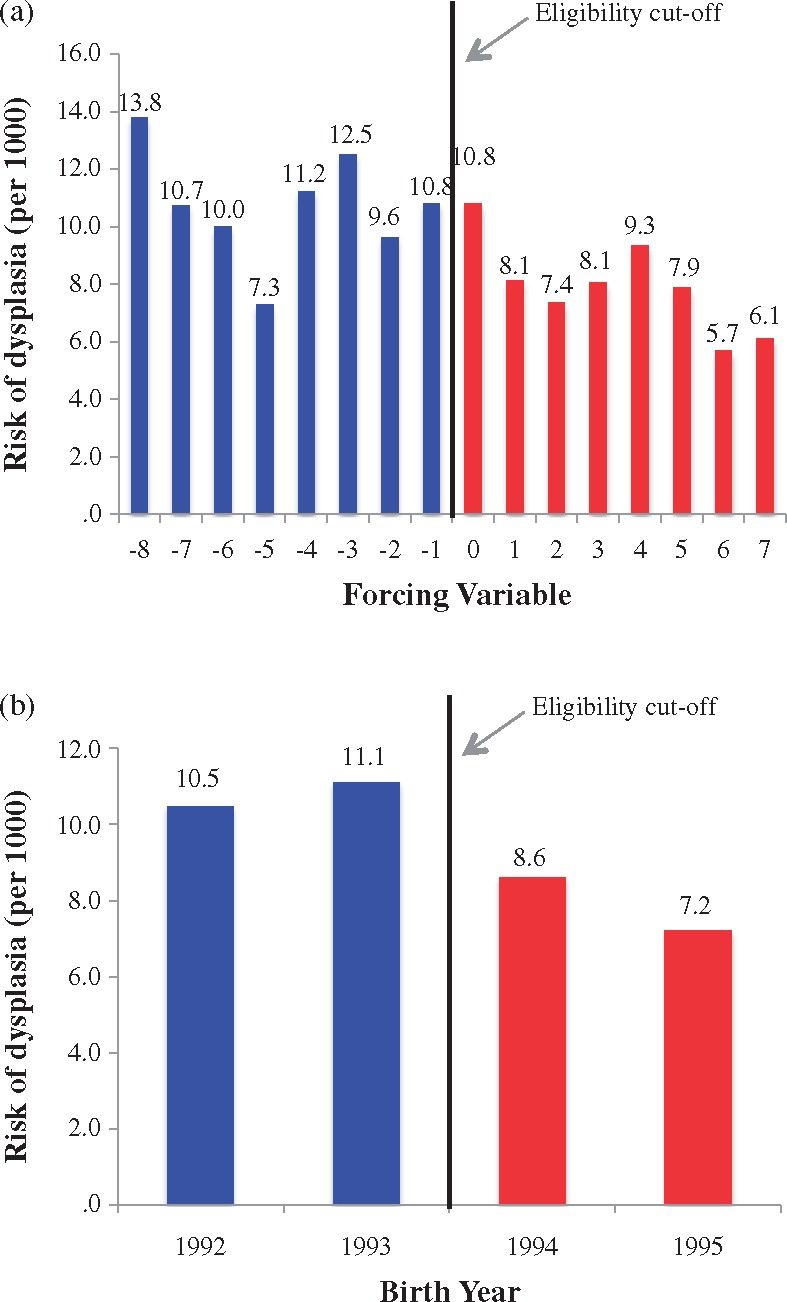
Risk of outcome (cervical dysplasia). (a) Probability of outcome, by forcing variable^*; (b) Probability of outcome, by birth year. *See Table 1 for how values of the forcing variable were operationalized.

Discussion

This tutorial provides one of the first practical introductions to the RDD for epidemiologists. Moreover, it describes four easy strategies researchers can use to assess the assumptions of the RDD and determine whether the design is appropriate for their study question and data. By applying these strategies to our question on the impact of HPV vaccination on cervical dysplasia, we concluded that the four major assumptions of the RDD were sufficiently satisfied, but that we needed to account for birth timing to avoid confounding of our effect estimates.

Conceptually, our research question was well suited to the RDD—there was an observable continuous assignment variable, a clear assignment cut-off and strong incentives to accept the treatment at the cut-off. However, careful checking of the RDD assumptions revealed an important and unexpected effect of birth timing that implied a standard RDD analysis focused only on the observations closest to the cut-off would not have been appropriate. Consequently, we made adjustments to the RDD analysis to account for the confounding effect of birth timing within the school grade.^17,28 This adjustment was critical to circumventing confounding bias in our study, as evidenced by the difference between the adjusted relative risk [0.56; 95% confidence interval (CI) 0.36, 0.87] and unadjusted relative risk (0.84; 95% CI 0.58, 1.23). The adjusted estimate provided clear evidence of a strong protective effect of HPV vaccination on cervical dysplasia, whereas the unadjusted estimate was biased toward the null. As the birth timing effect was not anticipated a priori, our experience highlights the importance of explicitly stating and assessing the RDD assumptions, even when the study question is conceptually well suited to this design. In our case, the results of this assessment led us to revisit and redefine our original statistical approach and instead consider the validity of the assumptions conditional on this covariate. Although it has long been known that conditional RDD analyses are conceptually feasible, prior to our study, there were few published examples.

Until recently, published papers describing the RDD have been largely limited to the economics literature^34,35; it was not until 2014 that this design started to appear in epidemiology journals.^12,13,36 Our paper adds to this new body of literature by providing a practical introduction to the RDD and demonstrating how to assess the RDD assumptions in the context of an applied example. Our case study was not a classic application of the RDD for several reasons. First, it was based on a dichotomous outcome. Given the prominence of categorical outcomes in health research, this paper helps to illustrate that the RDD can be suitable for such study outcomes. Second, we observed a confounding effect of birth timing that meant girls closest to the cut-off were not the most exchangeable, as is generally assumed for the RDD; instead, the exchangeability was present for girls in the same birth quarter. This finding highlights the fact that, in practice, data do not always conform perfectly to the assumptions of the RDD analysis. Understanding and accommodating unique situations is often an important part of the analytic process and careful attention must be given to preserve the conditions necessary for causal inference.

This paper focuses on four important assumptions of the RDD and is intended as an introduction only. Depending on the study question and initial findings, additional strategies may be desired or required. For example, we generally used bar and line graphs to assess the probability of each variable of interest (exposure, outcome, covariate) by the forcing variable since these graphs provided a transparent representation of data patterns. However, scatterplots are another popular tool used to assess these assumptions, especially because adding smoothed regression lines to these plots on each side of the cut-off can improve visual presentation.³⁴ Additional statistical tests may also be applied, such as the previously mentioned McCrary’s density test for determining whether the forcing variable has been manipulated. This manuscript addresses verifications that should be performed prior to undertaking the RDD analysis; however, additional verifications may be required for the analysis.^12,16 Further details on the analytic approach used for our study of the effects of HPV vaccination on cervical dysplasia, including explanation of bandwidth selection and modelling, as well as the substantive results are available elsewhere.^17,28

It has been demonstrated that RDD papers published in the medical, epidemiology and public health literature often do not adequately report these validity checks.¹³ To promote transparency and increase confidence in study validity, Moscoe et al. provide a complete description of the five key elements of the RDD analysis that should be reported when publishing an RDD study. We believe that graphical depictions of the exposure and outcome, in particular, are central to the manuscript and should therefore be contained within the main body, whereas checks on the density of the forcing variable and the distribution of baseline covariates can be referenced in text and included as appendices. We hope this study encourages researchers not only to test the RDD assumptions, but also to share these results in their published work.

Conclusion

The assessment of assumptions is an integral component of any study and our paper demonstrates some of the specific checks necessary in the setting of an RDD while providing an example of the impact this inquiry can have on the validity of findings. Our findings underscore the importance of assessing the validity of the assumptions of this design, testing those that are empirically testable and making adjustments as necessary to support valid causal inference. We hope this paper promotes greater reliance on valid quasi-experimental designs within epidemiology, as well as careful reporting of the assumptions so that readers can critically evaluate the strength of the inference.

Funding

This study was funded by a grant from the Canadian Institutes of Health Research (CIHR; MOP#130339). The funder had no role in the design or conduct of this study; the collection, analysis or interpretation of the data; the preparation, review or approval of the manuscript; nor in the decision to submit the manuscript for publication. This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long-Term Care (MOHLTC). The opinions, results and conclusions reported in this paper are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred. LMS was supported by a CIHR Fredrick Banting and Charles Best Canada Graduate Scholarships Doctoral Award, ECS by a Chercheur boursier Junior 1 from the Fonds de la Recherche du Québec–Santé and the Ministère de la Santé et des Services sociaux du Québec, JSK by the Canada Research Chairs programme and LEL by the Canadian Foundation for Innovation—Leaders Opportunity Fund.

Conflict of interest: The authors have no conflicts of interest to declare.