Estimating glomerular filtration rate for the full age spectrum from serum creatinine and cystatin C

Abstract

Background. We recently published and validated the new serum creatinine (Scr)-based full-age-spectrum equation (FAS_crea) for estimating the glomerular filtration rate (GFR) for healthy and kidney–diseased subjects of all ages. The equation was based on the concept of normalized Scr and shows equivalent to superior prediction performance to the currently recommended equations for children, adolescents, adults and older adults.

Methods. Based on an evaluation of the serum cystatin C (ScysC) distribution, we defined normalization constants for ScysC (Q_cysC=0.82 mg/L for ages <70 years and Q_cysC=0.95 mg/L for ages ≥70 years). By replacing Scr/Q_crea in the FAS_crea equation with ScysC/Q_cysC, or with the average of both normalized biomarkers, we obtained new ScysC-based (FAS_cysC) and combined Scr-/ScysC-based FAS equations (FAS_combi). To validate the new FAS_cysC and FAS_combi we collected data on measured GFR, Scr, ScysC, age, gender, height and weight from 11 different cohorts including n = 6132 unique white subjects (368 children, aged ≤18 years, 4295 adults and 1469 older adults, aged ≥70 years).

Results. In children and adolescents, the new FAS_cysC equation showed significantly better performance [percentage of patients within 30% of mGFR (P30) = 86.1%] than the Caucasian Asian Paediatric Adult Cohort equation (P30 = 76.6%; P < 0.0001), or the ScysC-based Schwartz equation (P30 = 68.8%; P < 0.0001) and the FAS_combi equation outperformed all equations with P30 = 92.1% (P < 0.0001). In adults, the FAS_cysC equation (P30 = 82.6%) performed equally as well as the Chronic Kidney Disease Epidemiology Collaboration equation (CKD-EPI_cysC) (P30 = 80.4%) and the FAS_combi equation (P30 = 89.9%) was also equal to the combined CKD-EPI equation (P30 = 88.2%). In older adults, FAS_cysC was superior (P30 = 88.2%) to CKD-EPI_cysC (P30 = 84.4%; P < 0.0001) and the FAS_combi equation (P30 = 91.2%) showed significantly higher performance than the combined CKD-EPI equation (P30 = 85.6%) (P < 0.0001).

Conclusion. The FAS equation is not only applicable to all ages, but also for all recommended renal biomarkers and their combinations.

INTRODUCTION

Serum creatinine (Scr)-based estimating glomerular filtration rate (eGFR) equations are commonly used and reported when Scr is measured. Despite the worldwide acceptance of isotope dilution mass spectrometry (IDMS)-standardized Scr assays, Scr-based eGFR equations are still relatively imprecise [1]. Also, different equations are proposed for children, adults and older adults as most equations lack continuity and accuracy across the full age spectrum.

We recently published a Scr-based full-age-spectrum (FAS_crea) equation [2] that has been validated in a large number of healthy and kidney–diseased white individuals (n = 6870) including 735 children, 4371 adults and 1764 older adults against measured GFR (mGFR) and using IDMS-equivalent Scr. The FAS_crea equation showed improved validity and continuity across the full age spectrum and was less biased and more accurate than the currently recommended Scr-based eGFR equations.

The FAS equation is based on three fundamental assumptions:

• The average GFR for healthy populations (children, adolescents and young adults) is equal to a value of 107.3 mL/min/1.73 m² after kidney function matures (around 2 years of age) until the age of 40 years. This assumption is also supported by the results of a recent meta-analysis in living kidney donors [3].

• The age decline of GFR begins at around 40 years.

• GFR and population-normalized Scr (Scr/Q_crea) are inversely related (Q_crea being the mean or median Scr concentration of the corresponding age-/sex-matched healthy population).

These three assumptions have led to the construction of the simple age-knotted FAS_crea equation, which takes the form [2]:

$${\mathrm{F}\mathrm{A}\mathrm{S}}_{\mathrm{c}\mathrm{r}\mathrm{e}\mathrm{a}}=\mathrm{ }\frac{107.3}{\frac{\mathrm{S}\mathrm{C}\mathrm{r}}{Q_{\mathrm{c}\mathrm{r}\mathrm{e}\mathrm{a}}}}\times [{0.988}^{\left(\mathrm{A}\mathrm{g}\mathrm{e}-40\right)}\mathrm{ }\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{ }\mathrm{a}\mathrm{g}\mathrm{e}>40\mathrm{ }\mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}].$$

The equation is simple and intuitive and can be easily explained: when Scr/Q_crea deviates from ‘1’, the eGFR will deviate from the average value of 107.3 mL/min/1.73 m². Scr/Q_crea, for every healthy age-/sex-matched population, is normally distributed (Gaussian distribution) around the mean of ‘1’ (a consequence of the definition of Q_crea). It has been shown that the 2.5th percentile (Pct) = 0.67 and the 97.5th Pct = 1.33, or, equivalently, the standard deviation (SD) is 0.1683 [2].

Serum cystatin C (ScysC) is considered to be a potential alternative to Scr for estimating GFR [4], especially since a certified reference cystatin C material became available in 2010, allowing standardization of ScysC assays [5].

In this article, we demonstrate that the last assumption (that GFR is inversely related to the normalized Scr biomarker) also applies to ScysC, if properly normalized. We show that the FAS_crea equation can be transformed into a ScysC-based FAS equation (FAS_cysC) and a combined Scr-/ScysC-based FAS equation (FAS_combi), by simply replacing the normalized Scr (Scr/Q_crea) by ScysC/Q_cysC or by the combination of Scr/Q_crea and ScysC/Q_cysC [i.e. the (weighted) average of Scr/Q_crea and ScysC/Q_cysC], where Q_cysC is the normalization factor for ScysC.

In the first part of this study, we give a rationale for choosing the normalization factor Q_cysC for ScysC. Next, we validate the FAS_cysC and FAS_combi equation against mGFR and compare the performance of these equations with the currently recommended and most used eGFR equations (Schwartz_cysC [6], Chronic Kidney Disease Epidemiology Collaboration equation (CKD-EPI_cysC) [4], Caucasian Asian Paediatric Adult Cohort equation (CAPA) [7], combined CKD-EPI_combi [4] and BIS2 [8]). Finally, we evaluate the performance of all FAS equations (by varying the weighting factors for the normalized biomarkers) in all age groups.

MATERIALS AND METHODS

Overview of study design and participants

We collected data from 11 cohorts, forming a representative sample of the general population and renal disease patients. For the same six cohorts (Saint-Etienne, Tromsø, Rochester and Minnesota for adults; Kent and Berlin for older adults [2]) that were used for the validation of the FAS_crea equation, we additionally collected the ScysC results. The other cohorts used in the previous validation did not have ScysC data available, and, therefore, we collected data of new cohorts. For children, adolescents and young adults (<21 years), one cohort came from the University Hospital in Leuven (n = 114), and one from Lyon (n = 695). Both cohorts contained children and adolescents with established renal pathologies. The data from Leuven contained single-time point measurements per child and the data from Lyon (n = 695) were from 259 children with serial measurements over a period of several years, but we used the first measurement only. We further collected data from a cohort of healthy and renal disease adults from Paris (n = 603), from Lyon (n = 598) and from the Chronic Renal Insufficiency Cohort (CRIC; n = 3939) [9], which we restricted to whites only (n = 1824) and to the first visit where all required variables were available (n = 674). All datasets were centralized by the first author for data analysis. This retrospective non-interventional study was approved by the Institutional Ethical Board of the University Hospital of Leuven, Belgium.

In total, we collected data on mGFR, Scr, ScysC, age, gender, height and weight for n = 6132 participants (n = 368 children aged between 1 and 18 years; n = 4295 adults aged between 18 and 70 years and n = 1469 older adults aged ≥70 years).

We further used a separate cohort (n = 1333) from the Berlin Initiative Study [8] of apparently healthy older subjects to study the age dependency of the ScysC distribution. This cohort was obtained from 2069 subjects (2069 baseline samples and 1693 follow-up samples) aged >70 years (Berlin residents), which we reduced to a subset of 1333 individuals who were defined as apparently healthy; i.e. no history of myocardial infarction, no history of stroke, not on dialysis, not deceased between first and second follow-up study visit, no albuminuria (ACR <30 mg/g), arterial blood pressure <160/90 mmHg.

Methods

The new FAS equation(s)

The form of the FAS_crea equation was maintained, but Scr/Q_crea is replaced by S_cysC/Q_cysC:

$${\mathrm{F}\mathrm{A}\mathrm{S}}_{\mathrm{c}\mathrm{y}\mathrm{s}\mathrm{C}}=\frac{107.3}{\frac{\mathrm{S}\mathrm{c}\mathrm{y}\mathrm{s}\mathrm{C}}{Q_{\mathrm{c}\mathrm{y}\mathrm{s}\mathrm{C}}}}\times [{0.988}^{\left(\mathrm{A}\mathrm{g}\mathrm{e}-40\right)}\mathrm{ }\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{ }\mathrm{a}\mathrm{g}\mathrm{e}>40\mathrm{ }\mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}].$$

By extending the same concept, we used the weighted average of the two normalized biomarkers Scr/Q_crea and ScysC/Q_cysC, leading to the general form of:

$${\mathrm{F}\mathrm{A}\mathrm{S}}_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{b}\mathrm{i}}=\frac{107.3}{\alpha \times \frac{\mathrm{S}\mathrm{c}\mathrm{r}}{Q_{\mathrm{c}\mathrm{r}\mathrm{e}\mathrm{a}}}+\left(1-\alpha \right)\times \frac{\mathrm{S}\mathrm{c}\mathrm{y}\mathrm{s}\mathrm{C}}{Q_{\mathrm{c}\mathrm{y}\mathrm{s}\mathrm{C}}}}\times [{0.988}^{\left(\mathrm{A}\mathrm{g}\mathrm{e}-40\right)}\mathrm{ }\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\mathrm{ }\mathrm{a}\mathrm{g}\mathrm{e}>40\mathrm{ }\mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}].$$

The coefficient ‘α’ in the denominator may be considered as a weighting factor for the normalized renal biomarkers. In case α = 1, the FAS equation depends entirely on Scr/Q_crea and equals the FAS_crea equation; in case α = 0, the FAS equation becomes the ScysC-based FAS_cysC equation. In all other situations for 0 < α < 1, the equation is a combined Scr/ScysC equation. For α = 0.5, the denominator is equal to the average of both normalized biomarkers. We further discuss the influence of α in the ‘Results’ section.

mGFR, Scr and cystatin C assays

A summary of the methods used in the different collaborating centres is given in Tables 1 and 2. Direct GFR measurements were obtained with different reference methods as described previously [2, 10]. Scr was measured with an enzymatic assay, equivalent to IDMS, or directly with IDMS, or recalculated to the enzymatic assay, in all centres. ScysC was measured with the calibrated particle-enhanced nephelometric (PENIA) method of Siemens in Saint-Etienne, Berlin and partially in Lyon. The ScysC measurements for the CRIC Study were done with the non-calibrated PENIA assay of Siemens, but calculated back to the certified reference material, as previously described [4]. The non-calibrated PENIA assay of Siemens was also used in Rochester, Kent, and partially in Lyon, and the results were recalculated to the certified reference standard, using the multiplication factor in Rochester [11] and in Lyon and Kent [12], according to the manufacturer’s specifications. Tromsø used the non-calibrated (with back calculation) and Leuven used the calibrated particle-enhanced turbidimetric (PETIA, Tina quant®) assay of Roche (Tables 1 and 2).

Table 1.

Overview of the methods used in this study for mGFR and Scr

Origin	mGFR	Scr
Leuven, Belgium	51Cr-EDTA (4 points)	Creatinine Plus, Roche enzym.
Lyon, France	Inulina or Iohexol (3 points)	Creatinine Plus, Roche enzym.
Saint-Etienne, France	Iohexol (2 points)	Enzymatic, Orthoclinical Diagn.
Tromsø, Norway	Iohexol (1 point)	Creatinine Plus, Roche enzym.
Rochester, MN, USA	Iothalamatea	Creatinine Plus, Roche enzym.
Berlin, Germany	Iohexol (8 points)	Creatinine Plus, Roche enzym.
Kent, UK	Iohexol (3 points)	IDMS
Paris, France	51Cr-EDTAa	Enzymatic, Siemens, standardized to IDMS
CRIC, USA	125I-Iothalamatea	calculated back to Creatinine Plus, Roche enzym.

For mGFR, ^arenal clearance, all other methods are plasma clearance methods. mGFR is indexed for body surface area using the Dubois formula.

Table 2.

Overview of the methods for ScysC

Origin, time of measurement	ScysC assay	Calibration to reference (ERM®-DA471/IFCC)	Automate	CV (%)
Leuven, 2015	Roche PETIA (Tina quant® Gen2)	Yes	Integra 400 Plus	2.6, 1.2, 1.0 at 0.503, 2.98, 6.11 mg/L
Lyon, 2010–15	Siemens N-Latex® PENIA	No, recalculation by MF = 1.11 before April 2011; yes after April 2011	BN Prospec analyser	3.5 at 2.3 mg/L
Saint-Etienne, 2012	Siemens PENIA [13]	Yes	BN Prospec analyser	2.9, 2.1 at 1.03, 1.93 mg/L
Tromsø, 2007–08	Roche PETIA [14] (Tina quant® Gen1)	No, recalculation using −0.064 + ScysC × 0.998	Gentian reagents, Modular P800 analyser	3.2
Rochester, 2001–11	Siemens PENIA [11]	No, recalculation by MF = 1.14	Dade Behring BN II Nephelometer	3.5
Berlin, 2011	Siemens N-Latex® PENIA [8]	Yes	BN Prospec	1.5, 3.5, 2.4 at 0.8, 2.3, 7.4 mg/L
Kent, 2008–11	Siemens PENIA [12]	No, recalculation by MF = 1.11	BN Prospec analyser	3.5 at 2.3 mg/L
Paris, 2013	Siemens PENIA	Yes	Dimension Vista	≤3.5
CRIC [9], 2003–08	Siemens N-Latex® PENIA [4]	No, recalculation by authors = 1.12 × (0.083 + 0.789 × (0.039 + 1.061 × CRICcysC)	BN Prospec analyser	4.9

MF, multiplication factor; CV, coefficient of variation.

eGFR equations

The new FAS_cysC equation and the FAS_combi equation were compared and validated against mGFR and against the currently available and recommended eGFR equations listed in Table 3.

Table 3.

eGFR equations for the performance comparisons

Scr-based equations
Schwartzcrea [15]	eGFR = 0.413 × Ht/Scr
CKD-EPI [16]	eGFR = 141 × min(Scr/κ)α × max(Scr/κ)−1.209 × 0.993Age × (1.018 if female) κ = 0.7 for females and 0.9 for males; α = −0.329 for females and −0.411 for males
ScysC-based equations
SchwartzcysC [6]	eGFR = 40.6 (1.8/ScysC)0.93
CAPA [7]	eGFR = 130 × ScysC−1.069 × Age−0.117 – 7
CKD-EPIcysc [4]	eGFR = 133 × min(ScysC/0.8,1)−0.499 × max(ScysC/0.8,1)−1.328 × 0.996Age × (0.932 if female)
Combined equations
CKD-EPIcrea,cysc [4]	eGFR = 135 × min(Scr/κ,1)α × max(Scr/κ,1)−0.601 × min(ScysC/0.8,1)−0.375 × max(ScysC/0.8,1)−0.711 × 0.995Age × (0.969 if female) (κ = 0.7 for females, 0.9 for males, α  = −0.248 for females and −0.207 for males)
BIS2 [8]	eGFR = 767 × ScysC−0.61 × Scr−0.40 × Age−0.57 × (0.87 if female)

Scr, serum creatinine (mg/dL); ScysC, serum cystatin C (mg/L); Ht, height in cm.

Statistical analysis

The performance statistics are presented as constant bias (mean of eGFR–mGFR) and proportional bias (mean of eGFR/mGFR), root mean square error (RMSE) of prediction, Lin’s concordance correlation coefficient (Lin’s CCC, which is a measure of both correlation and agreement as it evaluates the degree to which pairs of observations fall on the identity line), P10 and P30 (the percentage of subjects within 10% and 30% of mGFR), for the different age groups, total and in subgroups according to mGFR <60 and ≥60 mL/min/1.73 m². McNemar’s test is used to compare P30 among equations.

RESULTS

Description of the cohorts

Summary statistics for the patient characteristics of the 11 cohorts are given in Tables 4 and 5, and are described in Supplementary data.

Table 4.

Patient characteristics in the different cohorts from young age to old age (mean ± SD) (in years)

Data origin	n	Age	mGFR	Scr	ScysC
Leuven (Belgium)	114	8.8  ± 5.5	89.2 ± 21.5	0.58 ± 0.36	1.00 ± 0.35
Lyon (France)	259	11.1  ± 3.6	88.8 ± 33.5	0.68 ± 0.30	1.22 ± 0.43
Saint-Etienne (France)	203	48.7  ± 10.3	94.7 ± 24.4	0.87 ± 0.19	0.90 ± 0.26
Paris (France)	603	50.3  ± 13.1	67.1 ± 27.2	1.29 ± 0.74	1.41 ± 0.81
Lyon (France)	598	54.6  ± 13.7	74.9 ± 30.9	1.13 ± 0.57	1.24 ± 0.58
CRIC (USA)	674	56.9  ± 12.5	50.7 ± 21.8	1.60 ± 0.50	1.43 ± 0.51
Tromsø (Norway)	1627	58.1  ± 3.8	91.7 ± 14.4	0.76 ± 0.14	0.73 ± 0.12
Rochester CKD (USA)	687	64.8  ± 8.8	80.4 ± 21.3	0.85 ± 0.23	0.87 ± 0.24
Rochester KFC (USA)	406	65.9  ± 9.2	79.5 ± 20.7	0.84 ± 0.18	0.83 ± 0.18
Berlin (Germany)	567	78.5  ± 6.2	60.3 ± 16.4	0.99 ± 0.37	1.14 ± 0.38
Kent (UK)	394	80.4  ± 4.6	51.5 ± 18.8	1.30 ± 0.66	1.45 ± 0.61
Total	6132	58.2  ± 17.6	75.5 ± 26.5	1.01 ± 0.51	1.06 ± 0.52

n, number of patients; mGFR, measured glomerular filtration rate (mL/min/1.73 m²); Scr, serum creatinine (mg/dL); ScysC, serum cystatin C (mg/L).

Table 5.

Patient characteristics in the different age groups (mean ± SD)

Group	n	No. of males	No. of females	mGFR	Scr	ScysC
Children ≤18 years	368	193	175	89.2 ± 30.4	0.65 ± 0.31	1.15 ± 0.42
Adults 18–70 years	4295	2301	1994	80.2 ± 25.6	1.00 ± 0.50	0.99 ± 0.51
Older adults ≥70 years	1469	771	698	58.5 ± 20.0	1.13 ± 0.52	1.24 ± 0.51
Total	6132	3265	2867

n, number of patients; mGFR, measured glomerular filtration rate (mL/min/1.73 m²); Scr, serum creatinine (mg/dL); ScysC, serum cystatin C (mg/L).

Rationale for Q_cysC values for ScysC

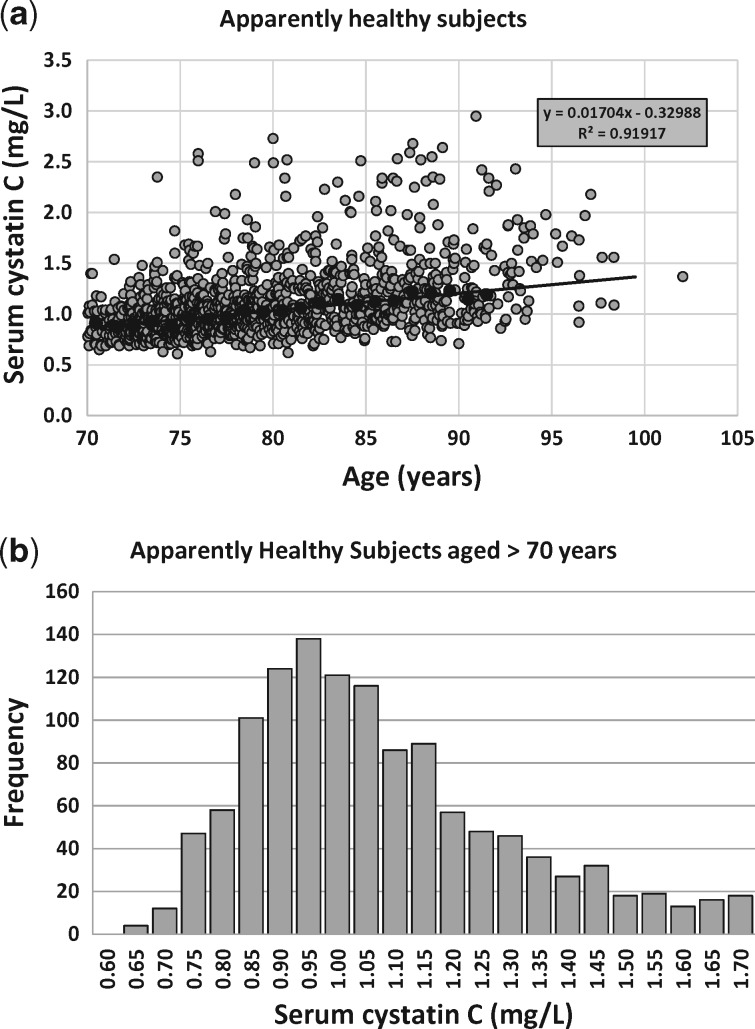
To define normalization factors for ScysC we searched the literature for normal reference ranges and we investigated whether these ranges depend on age or gender differences. We realized that the literature before the year 2010 was based on non-standardized cystatin C assays, but, in general, ScysC is independent of age (up to age 70 years) and gender in children, adolescents and adults [14–16], although there might be small differences between sexes and races [17]. We used the value of 0.82 mg/L as the normalization factor, as it is the middle of the normal reference interval for children, adolescents and adults up to ∼70 years (and in line with the manufacturer’s information on reference ranges) [8, 18]. The ScysC-based CKD-EPI equation normalized ScysC by 0.80 for both males and females [4], a value that is close to the proposed value of 0.82 in this study. The new CAPA equation does not have a gender factor in the equation, suggesting that the same Q_cysC normalization constant can be used for both sexes [7]. For older adults, we could not find normal reference ranges in the literature. In our dataset of 1333 apparently healthy older persons aged >70 years from the Berlin Initiative Study, we modelled Q_cysC as a linear function of age: Q_cysC=0.01704 × Age – 0.3384 = 0.863 + 0.01704 × (Age – 70) (R²=0.919; see Figure 1). At the age of 67.5 years, the corresponding value of Q_cysC=0.82. Therefore, we defined the Q_cysC normalization factor for cystatin C as 0.82 mg/L until the age of 70 years and then Q_cysC gradually (and linearly) increases (Figure 1). The mode of the ScysC distribution (Figure 2) of the n = 1333 apparently healthy subjects was 0.95 mg/L. Based on this analysis, and for the sake of simplicity, we fixed Q_cysC to 0.82 mg/L for all ages <70 years and to 0.95 mg/L for older ages.

FIGURE 1.

(a) The linear relationship between median (solid black circles) ScysC and age for the n = 1333 apparently healthy Berlin Initiative Study participants (grey circles). (b) Histogram for ScysC measurements of n = 1333 apparently healthy older adults.

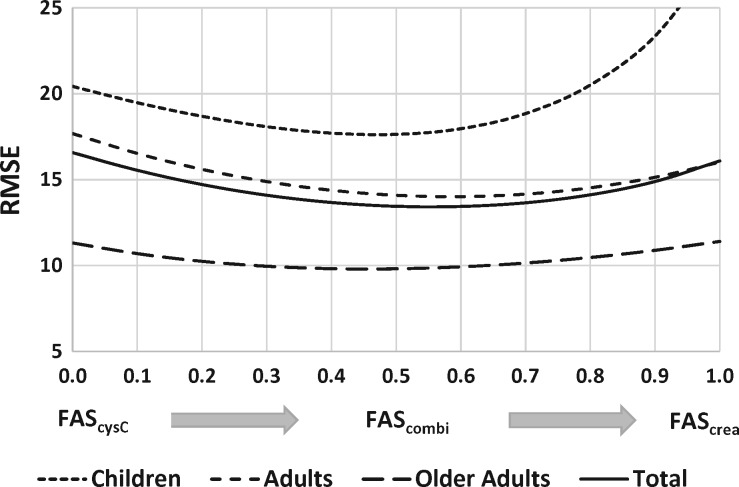
FIGURE 2.

RMSE as a function of the weighting factor α for children [based on Q(height)], adults and older adults. The total RMSE for all n = 6132 measurements is also shown. For children the FAS_cysC equation has smaller RMSE than the FAS_crea equation. For adults there is a slightly smaller RMSE for the single biomarker FAS_crea equation compared with the single marker FAS_cysC equation. For older adults there is no real preference for the value of α. For all age groups the RMSE is minimal for α  ≈ 0.5 (= combined FAS equation).

Performance results of the different equations

The performance statistics for the three FAS equations for the different age groups are presented in Tables 6–8. The FAS_crea equation [for children in two versions, based on Q_crea(age) and Q_crea(height)] is compared with the relevant Scr-based recommended equations (Schwartz for children, CKD-EPI for adults, BIS1 for older adults). The FAS_cysC equation is compared with the ScysC-based Schwartz equation (for children), the CAPA equation (for all ages) and ScysC-based CKD-EPI equation (for adults). Finally, the FAS_combi equation is compared with the combined CKD-EPI equation (for adults and older adults) and the combined BIS2 equation for older adults. To our knowledge, there is no combined equation for children available yet (based on the certified reference material). Tables 6–8 are presented for all subjects within each age group, but also for subgroups according to the mGFR threshold of 60 mL/min/1.73 m².

Table 6.

Children n = 368 (age ≤18 years)

	Scr-based eGFR			ScysC-based eGFR			Combined Scr-/ScysC-based eGFR
mGFR = 89.2 (n = 368)	FAScrea	FAScrea(Ht)*	Schwartzcrea	FAScysC*	CAPA	SchwartzcysC	FAScombi*	FAScombi(Ht)*
eGFR – mGFR	12.3 (7.7; 17.0)	3.8 (0.9; 6.6)	11.1 (8.1; 14.1)	−5.1 (−7.2; −3.1)	0.3 (−2.0; 2.6)	−21.6 (−23.7; −19.6)	0.9 (−0.9; 2.7)	−2.2 (−4.0; −0.4)
eGFR/mGFR	1.17 (1.12; 1.21)	1.06 (1.04; 1.09)	1.15 (1.12; 1.18)	0.98 (0.96; 1.01)	1.03 (1.00; 1.05)	0.79 (0.78; 0.81)	1.05 (1.03; 1.07)	1.01 (0.99; 1.03)
RMSE	47.0 (27.2; 67.6)	28.3 (11.4; 39.2)	31.3 (13.9; 42.9)	20.4 (17.9; 22.5)	22.3 (20.0; 24.3)	29.6 (27.0; 32.1)	17.5 (15.1; 19.7)	17.6 (15.5; 19.7)
Lin’s CCC	0.43 (0.36; 0.49)	0.65 (0.59; 0.70)	0.63 (0.57; 0.68)	0.73 (0.68; 0.77)	0.74 (0.68; 0.78)	0.49 (0.44; 0.54)	0.81 (0.77; 0.84)	0.80 (0.77; 0.84)
P10 (%)	32.3 (27.5; 37.1)	42.7 (37.6; 47.7)	40.5 (35.5; 45.5)	40.5 (35.5; 45.5)	36.4 (31.5; 41.4)	16.0 (12.3; 19.8)	44.6 (39.5; 49.7)	43.2 (38.1; 48.3)
P30 (%)	78.3 (74.0; 82.5)	84.5 (80.8; 88.2)	79.9 (75.8; 84.0)	86.1 (82.6; 89.7)	76.6 (72.3; 81.0)	68.8 (64.4; 73.5)	90.8 (87.8; 93.7)	92.1 (89.4; 94.9)
mGFR <60 mL/min/1.73 m2 (n = 57)
mGFR = 45.2	FAScrea	FAScrea(Ht)*	Schwartzcrea	FAScysC	CAPA	SchwartzcysC*	FAScombi	FAScombi (Ht)*
eGFR – mGFR	12.5 (10.0; 15.1)	5.1 (3.0; 7.2)	8.8 (6.5; 11.0)	6.2 (3.1; 9.3)	3.3 (−0.4; 7.1)	−2.4 (−5.0; 0.2)	8.3 (6.2; 10.5)	5.0 (2.9; 7.1)
eGFR/mGFR	1.31 (1.24; 1.37)	1.14 (1.08; 1.20)	1.22 (1.16; 1.29)	1.17 (1.09; 1.25)	1.10 (1.01; 1.19)	0.98 (0.91; 1.04)	1.21 (1.15; 1.27)	1.14 (1.08; 1.20)
RMSE	15.8 (12.7; 18.4)	9.4 (7.5; 10.9)	12.2 (9.7; 14.2)	13.1 (9.8; 15.7)	14.3 (10.4; 17.3)	10.0 (7.5; 12.0)	11.6 (9.4; 13.5)	9.3 (7.3; 11.0)
Lin’s CCC	0.44 (0.29; 0.56)	0.66 (0.50; 0.77)	0.55 (0.40; 0.68)	0.48 (0.29; 0.64)	0.47 (0.28; 0.63)	0.55 (0.35; 0.71)	0.56 (0.41; 0.69)	0.65 (0.49; 0.77)
P10 (%)	10.5 (2.3; 18.7)	45.6 (32.3; 58.9)	36.8 (23.9; 49.8)	24.6 (13.0; 36.1)	29.8 (17.6; 42.1)	36.8 (23.9; 49.8)	28.1 (16.0; 40.1)	38.6 (25.6; 51.6)
P30 (%)	63.2 (50.2; 76.1)	71.9 (59.9; 84.0)	71.9 (59.9; 84.0)	68.4 (56.0; 80.9)	66.7 (54.0; 79.3)	86.0 (76.7; 95.3)	71.9 (59.9; 84.0)	80.7 (70.1; 91.3)
mGFR ≥60 mL/min/1.73 m2 (n = 311)
mGFR = 97.3	FAScrea	FAScrea(Ht)*	Schwartzcrea	FAScysC*	CAPA	SchwartzcysC	FAScombi*	FAScombi (Ht)*
eGFR – mGFR	12.3 (6.8; 17.8)	3.5 (0.1; 6.9)	11.5 (8.0; 15.1)	−7.2 (−9.5; −5.0)	−0.2 (−2.9; 2.4)	−25.2 (−27.4; −23.0)	−0.5 (−2.5; 1.6)	−3.5 (−5.6; −1.4)
eGFR/mGFR	1.14 (1.09; 1.19)	1.05 (1.02; 1.08)	1.13 (1.10; 1.17)	0.95 (0.93; 0.97)	1.02 (0.99; 1.04)	0.76 (0.74; 0.78)	1.01 (0.99; 1.03)	0.98 (0.96; 1.00)
RMSE	50.7 (10.5; 77.5)	30.5 (10.1; 42.0)	33.7 (12.7; 45.9)	21.5 (18.8; 23.8)	23.5 (21.0; 25.8)	32.0 (29.1; 34.5)	18.4 (13.5; 20.8)	18.8 (16.3; 21.0)
Lin’s CCC	0.29 (0.22; 0.37)	0.50 (0.41; 0.57)	0.48 (0.40; 0.55)	0.59 (0.52; 0.65)	0.60 (0.52; 0.66)	0.33 (0.27; 0.38)	0.71 (0.65; 0.76)	0.69 (0.62; 0.74)
P10 (%)	36.3 (31.0; 41.7)	42.1 (36.6; 47.6)	41.2 (35.7; 46.7)	43.4 (37.9; 48.9)	37.6 (32.2; 43.0)	12.2 (8.6; 15.9)	47.6 (42.0; 53.2)	44.1 (38.5; 49.6)
P30 (%)	81.0 (76.6; 85.4)	86.8 (83.0; 90.6)	81.4 (77.0; 85.7)	89.4 (85.9; 92.8)	78.5 (73.9; 83.1)	65.6 (60.3; 70.9)	94.2 (91.6; 96.8)	94.2 (91.6; 96.8)

Asterisks indicate the best performing equation(s) [13] within the same biomarker category, across all performance statistics. The bold values are the best result(s) for each performance statistic, across all equations. FAS, full-age-spectrum eGFR equation, based on Q(age); FAS(Ht), FAS equation based on Q(height); Schwartz, Schwartz equation for children (Scr-based = 0.413 Ht/Scr; cystatin C-based = 70.1 ScysC ^− 0.93). FAS_combi is calculated for α = 0.5.

Table 7.

Adults n = 4295 (age 18–70 years)

	Scr-based eGFR		ScysC-based eGFR			Combined Scr-/ScysC-based eGFR
mGFR = 80.1 (n = 4295)	FAScrea*	CKD-EPIcrea*	FAScysC*	CKD-EPIcysC	CAPA	FAScombi*	CKD-EPIcombi
eGFR – mGFR	1.4 (0.9; 1.9)	2.4 (1.9; 2.8)	4.2 (3.7; 4.8)	8.0 (7.6; 8.5)	8.9 (8.3; 9.5)	1.9 (1.5; 2.4)	6.2 (5.8; 6.6)
eGFR/mGFR	1.05 (1.04; 1.06)	1.06 (1.05; 1.07)	1.08 (1.07; 1.09)	1.11 (1.10; 1.12)	1.12 (1.11; 1.13)	1.05 (1.04; 1.06)	1.09 (1.08; 1.10)
RMSE	16.0 (15.4; 16.6)	15.1 (14.6; 15.6)	17.7 (17.2; 18.2)	18.1 (17.6; 18.5)	21.3 (20.8; 21.8)	14.1 (13.6; 14.6)	15.3 (14.9; 15.8)
Lin’s CCC	0.80 (0.79; 0.81)	0.82 (0.81; 0.83)	0.78 (0.76; 0.79)	0.78 (0.77; 0.80)	0.73 (0.72; 0.74)	0.84 (0.83; 0.85)	0.83 (0.82; 0.84)
P10 (%)	43.6 (42.1; 45.1)	46.0 (44.5; 47.5)	37.6 (36.2; 39.1)	32.5 (31.1; 34.0)	31.5 (30.1; 32.9)	47.3 (45.8; 48.8)	41.0 (39.6; 42.5)
P30 (%)	87.6 (86.6; 88.6)	88.1 (87.1; 89.0)	82.6 (81.4; 83.7)	80.4 (79.3; 81.6)	75.6 (74.3; 76.9)	89.9 (89.0; 90.8)	88.2 (87.2; 89.1)
mGFR <60 mL/min/1.73 m2 (n = 925)
mGFR = 42.0	FAScrea*	CKD-EPIcrea*	FAScysC	CKD-EPIcysC*	CAPA	FAScombi	CKD-EPIcombi*
eGFR – mGFR	7.0 (6.2; 7.9)	5.9 (5.0; 6.9)	6.9 (6.1; 7.8)	4.9 (3.9; 5.9)	5.3 (4.3; 6.2)	6.3 (5.5; 7.0)	4.2 (3.4; 5.1)
eGFR/mGFR	1.20 (1.18; 1.23)	1.16 (1.13; 1.18)	1.19 (1.17; 1.22)	1.11 (1.09; 1.14)	1.12 (1.10; 1.15)	1.18 (1.16; 1.20)	1.10 (1.08; 1.12)
RMSE	15.4 (14.0; 16.6)	16.1 (14.8; 17.2)	14.8 (13.7; 15.8)	16.2 (14.9; 17.5)	16.0 (14.7; 17.3)	13.2 (12.1; 14.2)	14.4 (13.1; 15.6)
Lin’s CCC	0.54 (0.50; 0.57)	0.55 (0.51; 0.58)	0.56 (0.52; 0.60)	0.57 (0.53; 0.60)	0.57 (0.53; 0.60)	0.61 (0.58; 0.65)	0.62 (0.58; 0.65)
P10 (%)	31.5 (28.5; 34.5)	31.7 (28.7; 34.7)	27.9 (25.0; 30.8)	29.0 (26.0; 31.9)	28.5 (25.6; 31.5)	33.8 (30.8; 36.9)	34.4 (31.3; 37.4)
P30 (%)	70.8 (67.9; 73.7)	72.3 (69.4; 75.2)	68.0 (65.0; 71.0)	70.5 (67.5; 73.4)	70.9 (68.0; 73.9)	75.2 (72.5; 78.0)	79.0 (76.4; 81.7)
mGFR ≥60 mL/min/1.73 m2 (n = 3370)
mGFR = 90.6	FAScrea*	CKD-EPIcrea*	FAScysC*	CKD-EPIcysC	CAPA	FAScombi*	CKD-EPIcombi
eGFR – mGFR	−0.1 (−0.7; 0.4)	1.4 (0.9; 1.9)	3.5 (2.9; 4.1)	8.9 (8.4; 9.5)	9.9 (9.2; 10.6)	0.8 (0.3; 1.2)	6.7 (6.3; 7.2)
eGFR/mGFR	1.01 (1.00; 1.01)	1.03 (1.03; 1.04)	1.05 (1.04; 1.06)	1.11 (1.11; 1.12)	1.12 (1.11; 1.13)	1.02 (1.01; 1.02)	1.09 (1.08; 1.09)
RMSE	16.2 (15.5; 16.8)	14.8 (14.2; 15.3)	18.4 (17.8; 18.9)	18.6 (18.1; 19.0)	22.5 (21.9; 23.1)	14.3 (13.8; 14.9)	15.6 (15.1; 16.0)
Lin’s CCC	0.59 (0.57; 0.61)	0.57 (0.54; 0.59)	0.51 (0.49; 0.54)	0.48 (0.46; 0.50)	0.42 (0.40; 0.45)	0.64 (0.62; 0.66)	0.58 (0.56; 0.60)
P10 (%)	47.0 (45.3; 48.7)	49.9 (48.2; 51.6)	40.3 (38.6; 41.9)	33.5 (31.9; 35.1)	32.3 (30.7; 33.9)	50.9 (49.3; 52.6)	42.9 (41.2; 44.6)
P30 (%)	92.2 (91.3; 93.1)	92.4 (91.5; 93.3)	86.6 (85.4; 87.7)	83.2 (91.9; 84.4)	76.9 (75.4; 78.3)	93.9 (93.1; 94.8)	90.7 (89.7; 91.7)

Asterisks indicate the best performing equation(s) [13] within the same biomarker category, across all performance statistics. The bold values are the best result(s) for each performance statistic, across all equations. FAS, full-age-spectrum eGFR equation (Scr-based with Q = 0.70 mg/dL for females and Q = 0.90 mg/dL for males; SCysC-based with Q′ = 0.82 mg/L). FAS_combi is calculated for α = 0.5.

Table 8.

Older people n = 1469 (age ≥70 years)

	Scr-based eGFR			ScysC-based eGFR			Combined Scr-/ScysC-based eGFR
mGFR = 58.5 (n = 1469)	FAScrea*	CKD-EPIcrea	BIS1*	FAScysC*	CKD-EPIcysC	CAPA	FAScombi*	CKD-EPIcombi	BIS2*
eGFR – mGFR	−2.6 (−3.2; −2.0)	4.6 (4.0; 5.3)	−2.9 (−3.5; −2.4)	0.9 (0.3; 1.4)	3.8 (3.1; 4.4)	5.5 (4.9; 6.2)	−1.4 (−1.9; −0.9)	4.5 (4.0; 5.1)	−1.2 (−1.7; −0.7)
eGFR/mGFR	0.98 (0.97; 1.00)	1.10 (1.09; 1.12)	0.99 (0.98; 1.00)	1.04 (1.03; 1.05)	1.07 (1.05; 1.08)	1.10 (1.09; 1.12)	1.00 (0.99; 1.01)	1.08 (1.07; 1.10)	1.01 (1.00; 1.02)
RMSE	11.4 (10.8; 12.0)	12.8 (12.3; 13.3)	11.3 (10.8; 11.9)	11.3 (10.7; 11.9)	12.9 (12.2; 13.5)	13.8 (13.1; 14.5)	9.8 (9.3; 10.3)	11.8 (11.2; 12.3)	9.6 (9.1; 10.2)
Lin’s CCC	0.82 (0.81; 0.84)	0.81 (0.79; 0.83)	0.81 (0.79; 0.82)	0.84 (0.82; 0.85)	0.83 (0.81; 0.84)	0.81 (0.79; 0.82)	0.87 (0.86; 0.88)	0.85 (0.84; 0.86)	0.87 (0.86; 0.88)
P10 (%)	42.1 (39.5; 44.6)	36.3 (33.8; 38.7)	42.1 (39.5; 44.6)	43.0 (40.5; 45.6)	38.1 (35.6; 40.6)	36.0 (33.6; 38.5)	50.5 (48.0; 53.1)	40.0 (37.5; 42.5)	52.3 (49.8; 54.9)
P30 (%)	88.2 (86.6; 89.9)	80.0 (77.9; 82.0)	89.0 (87.4; 90.6)	88.2 (86.6; 89.9)	84.4 (82.6; 86.3)	82.0 (80.1; 84.0)	91.2 (89.8; 92.7)	85.6 (83.8; 87.4)	92.4 (91.0; 93.7)
mGFR <60 mL/min/1.73 m2 (n = 753)
mGFR = 42.9	FAScrea*	CKD-EPIcrea	BIS1*	FAScysC*	CKD-EPIcysC*	CAPA	FAScombi*	CKD-EPIcombi	BIS2*
eGFR – mGFR	0.7 (0.0; 1.3)	5.9 (5.1; 6.7)	1.7 (1.1; 2.4)	2.9 (2.2; 3.6)	2.7 (1.9; 3.5)	4.9 (4.1; 5.7)	1.4 (0.8; 1.9)	3.9 (3.1; 4.6)	1.8 (1.2; 2.3)
eGFR/mGFR	1.04 (1.02; 1.06)	1.15 (1.12; 1.17)	1.07 (1.05; 1.09)	1.09 (1.07; 1.11)	1.06 (1.04; 1.08)	1.12 (1.10; 1.14)	1.05 (1.03; 1.07)	1.09 (1.07; 1.11)	1.06 (1.05; 1.08)
RMSE	9.2 (8.4; 9.9)	13.0 (12.1; 13.8)	8.7 (8.0; 9.3)	9.8 (8.9; 10.6)	11.4 (10.3; 12.3)	12.1 (11.0; 13.2)	8.1 (7.4; 8.7)	11.0 (10.0; 11.8)	7.9 (7.2; 8.6)
Lin’s CCC	0.75 (0.71; 0.78)	0.65 (0.62; 0.69)	0.75 (0.72; 0.78)	0.73 (0.70; 0.76)	0.72 (0.69; 0.75)	0.69 (0.66; 0.72)	0.80 (0.77; 0.82)	0.73 (0.70; 0.76)	0.80 (0.78; 0.83)
P10 (%)	41.2 (37.6; 44.7)	31.2 (27.9; 34.5)	42.5 (39.0; 46.0)	38.5 (35.0; 42.0)	35.5 (32.0; 38.9)	32.9 (29.6; 36.3)	47.9 (44.4; 51.5)	35.5 (32.0; 38.9)	48.3 (44.8; 51.9)
P30 (%)	84.6 (82.0; 87.2)	69.5 (66.2; 72.8)	85.4 (82.9; 87.9)	83.4 (80.7; 86.1)	81.8 (79.0; 84.6)	78.2 (75.3; 81.2)	87.0 (84.6; 89.4)	79.9 (77.1; 82.8)	89.1 (86.9; 91.3)
mGFR ≥60 mL/min/1.73 m2 (n = 716)
mGFR = 74.8	FAScrea	CKD-EPIcrea*	BIS1	FAScysC*	CKD-EPIcysC*	CAPA	FAScombi*	CKD-EPIcombi	BIS2*
eGFR – mGFR	−6.1 (−6.9; −5.2)	3.3 (2.4; 4.2)	−7.9 (−8.7; −7.1)	−1.3 (−2.2; −0.4)	4.9 (3.9; 5.9)	6.2 (5.1; 7.2)	−4.3 (−5.1; −3.5)	5.2 (4.3; 6.0)	−4.3 (−5.1; −3.6)
eGFR/mGFR	0.93 (0.92; 0.94)	1.06 (1.04; 1.07)	0.90 (0.89; 0.91)	0.99 (0.98; 1.00)	1.07 (1.06; 1.09)	1.09 (1.08; 1.10)	0.95 (0.94; 0.96)	1.08 (1.07; 1.09)	0.95 (0.94; 0.96)
RMSE	13.3 (12.5; 14.1)	12.7 (12.1; 13.3)	13.6 (12.7; 14.4)	12.7 (11.8; 13.6)	14.3 (13.5; 15.0)	15.4 (14.4; 16.3)	11.3 (10.5; 12.1)	12.5 (11.9; 13.2)	11.1 (10.3; 11.9)
Lin’s CCC	0.49 (0.44; 0.54)	0.46 (0.40; 0.51)	0.44 (0.39; 0.49)	0.55 (0.49; 0.60)	0.50 (0.45; 0.55)	0.49 (0.44; 0.54)	0.59 (0.54; 0.63)	0.55 (0.50; 0.59)	0.59 (0.54; 0.63)
P10 (%)	43.0 (39.4; 46.7)	41.6 (38.0; 45.2)	41.6 (38.0; 45.2)	47.8 (44.1; 51.4)	40.9 (37.3; 44.5)	39.2 (35.7; 42.8)	53.2 (49.5; 56.9)	44.7 (41.0; 48.3)	56.6 (52.9; 60.2)
P30 (%)	92.0 (90.0; 94.0)	91.1 (89.0; 93.2)	92.9 (91.0; 94.8)	93.3 (91.5; 95.1)	87.2 (84.7; 89.6)	86.0 (83.5; 88.6)	95.7 (94.2; 97.2)	91.5 (89.4; 93.5)	95.8 (94.3; 97.3)

Asterisks indicate the best performing equation(s) [13] within the same biomarker category, across all performance statistics. The bold values are the best result(s) for each performance statistic, across all equations. FAS, full-age-spectrum eGFR equation (Scr-based with Q = 0.70 mg/dL for females and Q = 0.90 mg/dL for males; SCysC-based with Q′ = 0.95 mg/L). FAS_combi is calculated for α = 0.5.

For children, the FAS_cysC equation performs significantly better than the FAS_crea equation based on Q_crea(age) and slightly better than or, in some cases, equivalent to the FAS_crea equation based on Q_crea(height) (Table 6). We found that n = 7 children [for Q_crea(height)] and n = 20 children [for Q_crea(age)] with Scr/Q_crea<0.67 had FAS_crea predictions that largely overestimate mGFR and were responsible for the large bias, RMSE and worse performance statistics. These children had spina bifida, Duchenne muscular dystrophy and severe growth retardation, explaining the very low Scr values and the poor match between Q_crea and age. The FAS_cysC equation has equivalent Lin’s CCC with CAPA but better RMSE. Also, P10 and P30 performance statistics were superior to CAPA. The Schwartz_cysC equation shows the best performance in the mGFR <60 mL/min/1.73 m² subgroup. However, although all children suffered from some underlying renal pathology, this subgroup was rather small (n = 57, 15%). The FAS_combi equations [based on Q_crea(age) and Q_crea(height)] outperform all other paediatric equations and increase the precision for P10 to ≈45% and P30 to ≈90%, which is significantly higher (P < 0.0001) compared with single biomarker equations, including the single biomarker FAS equations.

For adults, the FAS_cysC equation performs worse than FAS_crea, but better (overall and in the mGFR ≥60 mL/min/1.73 m² subgroup) or equivalent (in the mGFR <60 mL/min/1.73 m² subgroup) than the CKD-EPI_cysC equation. The FAS_cysC equation is significantly better than the CAPA equation. The combined equations show higher precision, but the difference with the FAS_crea equation is small. However, the FAS_combi equation is overall the best prediction equation and performs better than the CKD-EPI combined equation, except for mGFR <60 mL/min/1.73 m², where the performance is statistically equivalent.

In older adults, the FAS_cysC equation (with Q_cysC=0.95) performs better than the CKD-EPI_cysC equation and shows equivalent performance with the FAS_crea equation. If we use the linear function Q_cysC = 0.863 + 0.01704 × (Age – 70) to normalize ScysC in the FAS_cysC and FAS_combi equations, then the performance results (data not shown) are not significantly different than when Q_cysC=0.95 is used to normalize ScysC in the FAS equation. The combined FAS equation is performing equivalent to the BIS2 equation, reaching P10 > 50% and P30 > 90%, and better than the combined CKD-EPI equation.

In Tables 6–8, we highlighted (the equations marked with asterisk) the best performing equation per biomarker category based on the scoring system previously used by Hoste et al. [13], which is based on bias, P10 and P30. We also highlighted (in bold) the best performance statistic.

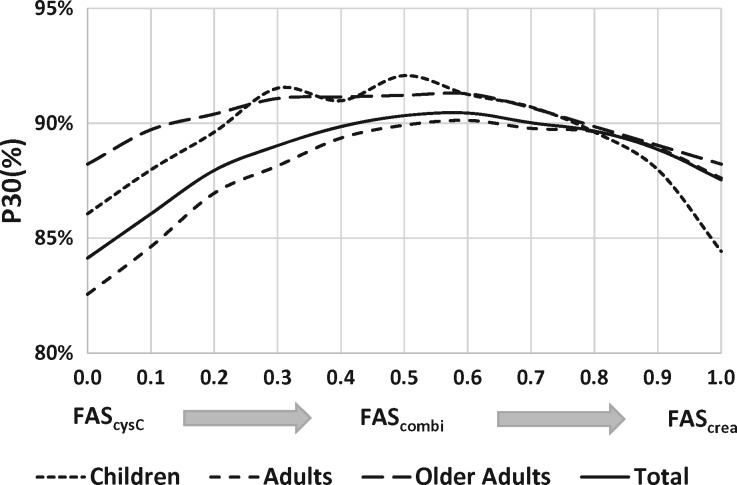
We also calculated the performance statistics (RMSE in Figure 2 and P30 in Figure 3) of the FAS_combi equation as a function of the weighting parameter α. These figures show the performance statistics as a continuous function of α, evolving from the FAS_cysC equation (with α = 0) to the FAS_crea equation (with α = 1), and in-between for the FAS_combi for all values of α.

FIGURE 3.

P30 as a function of the weighting factor α for the different age groups.

DISCUSSION

Through the introduction of the international certified reference material ERM-DA471/IFCC for cystatin C [5] it has become possible to develop ScysC-based as well as combined Scr-/ScysC-based eGFR equations on the basis of normalized biomarkers. Despite the fact that manufacturers still need to improve the accuracy of cystatin C assays [19], we have shown here that the basic concept upon which the FAS_crea equation was built [2] is not only applicable for normalized Scr, but can also be applied to normalized ScysC. By replacing normalized Scr with ScysC, or introducing the (weighted) average of both biomarkers, we can change from a Scr-based FAS equation to a ScysC-based FAS equation or a combined Scr-/ScysC-based FAS equation. These FAS equations show performance values that are equivalent or in some conditions superior to the currently recommended eGFR equations for children, adolescents, adults and older adults. Normalization of the biomarkers is a key in this construction. In the case of Scr, normalization is required to account for the difference in creatinine generation during childhood, the age/gender differences during adolescence and the difference between adult men and women. Normalization of ScysC is required to account for the age effect beyond the age of 70 years. For the healthy population, the normalized biomarkers show equivalent distributions with mean of ‘1’ and 2.5th and 97.5th Pct of 0.67 and 1.33, respectively. These similar characteristics of normalized biomarker concentration distributions lead to an interchangeable usage of both renal markers in the FAS equation(s).

The performance of the new FAS_cysC equation was better than the CAPA equation and better (in adults with mGFR ≥60 mL/min/1.73 m² and in older adults) or equivalent (in adults with mGFR <60 mL/min/1.73 m²) to the CKD-EPI_cysC equation. In children, the RMSE statistic is worst (highest) for the FAS_crea equation due to a fraction of children with Scr/Q_crea<0.67. Therefore, we would recommend not to use FAS_crea (or the combined FAS equations) when Scr/Q_crea<0.67 [2]. For adults, based on the performance statistics (RMSE and P30), there is still a slight preference for the single biomarker FAS_crea equation over the single biomarker FAS_cysC equation. For older adults, both single biomarker FAS equations perform in a similar manner. However, for all age groups, the FAS_combi equation with α ≈ 0.5 (corresponding to the average of both biomarkers) showed the smallest RMSE and the highest P30 and P10. Also the FAS_combi equation outperformed all other combined equations, with the exception of the BIS2 equation, which showed an equivalent performance for older adults (but note that BIS data used to derive the BIS equations are part of the current validation dataset) and the CKD-EPI equation for adults with mGFR <60 mL/min/1.73 m², where FAS showed equivalent performance results.

When the overall performance statistics for specific age groups was calculated, we found that α ≈ 0.5 corresponding to the average of normalized creatinine and cystatin C biomarker concentrations gave the best performance statistics for all age groups and demonstrated the smallest RMSE and highest P10 and P30 values. Although we calculated the average of both biomarkers and entered this into the FAS equation, it approximated the average of both single biomarker FAS equations (Scr and ScysC), a finding that has been observed by Björk et al. [20, 21] in a Swedish cohort, when combining the Scr-based Lund–Malmö and the ScysC-based CAPA equation. The choice to use a single or the mean of two biomarkers should be based on the clinical context, when conditions are disclosed that invalidate either Scr or ScysC as renal biomarker. The use of Scr may be discouraged in case of severe muscle wasting (anorexic patients, patients with muscle disorder, like Duchenne muscle dystrophy), immobile patients, or elderly cachectic patients with reduced muscle mass. Also, abnormal meat consumption, abnormal muscle development in athletes or weight lifters, or medication usage that affects creatinine generation may have an impact on the validity of creatinine as a renal biomarker. The use of ScysC-based equations may be discouraged when patients are treated with (high dose) glucocorticoids or other medication impacting on the biomarker’s serum concentration [22], in obese patients, tobacco users or patients with thyroid dysfunction or inflammation [11, 23–25]. The combination of both biomarkers has the advantage that it may cancel out the non-GFR-related factors influencing creatinine and cystatin C in different directions compared with mGFR [24–26]. The great advantage of our approach is that the same equation can be used, only the appropriate normalized biomarker has to be chosen (either Scr/Q_crea, or ScysC/Q_cysC or the average of both). However, the cost of cystatin C is relatively high and additional studies are needed to prove that measuring cystatin C is cost-effective. In the context of GFR estimation, the additional value of cystatin C could be defined by the clinical condition, knowing that non-GFR determinants influence both creatinine and cystatin C.

We also investigated the impact of the weighting factor α on the performance of the FAS equations by varying α (between 0 = FAS_cysC and 1 = FAS_crea) and calculating the difference ‘FAS – mGFR’, on an individual basis. Due to the way the FAS equations are designed, FAS_crea≈FAS_cysC≈FAS_combi, in the case of the normalized biomarkers Scr/Q_crea≈ScysC/Q_cysC. When Scr/Q_crea strongly deviates from ScysC/Q_cysC, then FAS_crea will strongly deviate from FAS_cysc and FAS_combi will lie in-between both single biomarker FAS predictions. We found that, on an individual basis, in approximately one-third of the subjects, the FAS_crea equation was closest to mGFR, in one-third of the subjects the FAS_cysC equation had the lowest individual bias and in one-third the FAS_combi equation was the best choice for a specific value of α. In the latter, when mGFR lies between FAS_crea and FAS_cysC predictions, there is always a value of α for which FAS_combi=mGFR. We realize that this analysis is mainly speculative as we do not know the optimal value of α in actual clinical situations, but the intention of this analysis was to evaluate in which conditions a preference for single biomarker FAS predictions or for the combined biomarker FAS prediction might exist. Unfortunately, we could not identify specific conditions where one over the other equations was to be preferred (unless the situation where Scr/Q_crea<0.67).

The strength of this study is the large number of subjects (n = 6132) covering the complete age span from 2 to 100 years of age. This study partially used data from our previous study, where n = 6870 subjects were used to validate the FAS_crea equation. Although both studies partially used the same subjects, the ScysC data was not part of the previous evaluation. All ScysC concentrations were analysed with cystatin C assays based on the international certified standard or were back-calculated using calibration curves developed for that purpose. The reference tests used in this study comprise all currently used direct measurement methods: ⁵¹Cr-EDTA (plasma/renal clearance), inulin (renal clearance), iohexol (plasma clearance in its different configurations) and iothalamate (renal clearance), illustrating the diversity of mGFR results and demonstrating the robustness of the FAS construction. Moreover, the cohorts used in this study were from different countries in Europe (Norway, Germany, France, Belgium) and the USA (Rochester, MN and the CRIC cohort), making the sample representative for the general Caucasian population and kidney disease population.

Our study has some limitations. First, we did not incorporate different ancestries, and, therefore, this validation study is limited to Caucasians only. Although it is known that creatinine generation (and thus Scr) is affected by ancestry, it is also known that ScysC is not influenced by differences in ancestry. We always have claimed that using appropriate ancestry-specific normalization factors for Scr may solve this problem and consequently the FAS concept remains applicable. Secondly, our goal was to validate the new FAS equations against mGFR and compare them with the existing and recommended equations, not to predict the risk of mortality. Whether the FAS equations are better predictors of mortality is another topic and requires further studies using a different statistical methodology [27].

CONCLUSIONS

The fundamental concept for the Scr-based FAS equation development, namely that mean GFR for healthy subjects evolves along an age-specific curve, and that deviation from that curve is related to the inverse of normalized Scr/Q_crea, also holds true for normalized ScysC/Q_cysC. The current work shows that the FAS equations display better or equivalent prediction performance than the currently recommended eGFR equations, across the full age spectrum, both in normal and reduced kidney function. The FAS equation is not only applicable to all ages, but also to all currently recommended renal biomarkers. The FAS concept may also be applicable to other renal biomarkers, if appropriately normalized, but this remains to be proven once standardized assays are in place.

SUPPLEMENTARY DATA

Supplementary data are available online at http://ndt.oxfordjournals.org.