Abstract
Most existing measures of distance between phylogenetic trees are based on the geometry or topology of the trees. Instead, we consider distance measures which are based on the underlying probability distributions on genetic sequence data induced by trees. Monte Carlo schemes are necessary to calculate these distances approximately, and we describe efficient sampling procedures. Key features of the distances are the ability to include substitution model parameters and to handle trees with different taxon sets in a principled way. We demonstrate some of the properties of these new distance measures and compare them to existing distances, in particular by applying multidimensional scaling to data sets previously reported as containing phylogenetic islands. [Metric; probability distribution; multidimensional scaling; information geometry.
Many methods for postprocessing phylogenetic trees rely on some measure of distance between pairs of trees. A variety of different distances are used, for example: the Robinson–Foulds metric (Robinson and Foulds 1979, 1981), quartet distance (Estabrook et al. 1985), path-length-difference metric (Penny et al. 1993), Billera–Holmes–Vogtmann (BHV) metric (Billera et al. 2001; Owen and Provan 2011), and matching distance (Lin et al. 2012), among others. These are generally defined by directly comparing the branching pattern (usually called topology) and/or edge lengths in a given pair of trees. For example, the Robinson–Foulds metric is defined by counting the number of splits present in exactly one of a given pair of trees, while the BHV metric is defined in terms of splits and edge lengths. However, phylogenetic trees also represent probability models for genetic sequence data, and for some applications it might be more appropriate to use a distance measure which compares the probability distributions on characters induced by trees, rather than comparing the trees as geometric objects. This article describes methodology and software for calculating such distances and explores their properties. The software is available from http://www.mas.ncl.ac.uk/~ntmwn/probdist.
The following simple example illustrates the difference between the two approaches. Suppose we have two trees  and
and  with a common leaf-set such that the two trees differ only with respect to the position of a single taxon
with a common leaf-set such that the two trees differ only with respect to the position of a single taxon  . In other words, the subtrees of
. In other words, the subtrees of 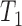 and
and 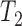 obtained by removing
obtained by removing  are identical. Then, in the limit that the edge leading to
are identical. Then, in the limit that the edge leading to 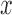 gets increasingly long, distance measures which compare the topology or geometry of the trees will generally view
gets increasingly long, distance measures which compare the topology or geometry of the trees will generally view 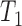 and
and 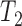 as being bounded away from each other (or getting further apart). However, under the same limit, the genetic sequence of
as being bounded away from each other (or getting further apart). However, under the same limit, the genetic sequence of 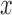 effectively becomes independent of the other taxa. Since the relationships between the other taxa are fixed, the probability distributions on characters induced by
effectively becomes independent of the other taxa. Since the relationships between the other taxa are fixed, the probability distributions on characters induced by 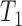 and
and  become identical in the limit, and so the distance tends to zero.
become identical in the limit, and so the distance tends to zero.
This article describes simulation methods which calculate (approximately) the Hellinger distance, Jensen–Shannon distance, and Kullback–Leibler divergence between trees when they are regarded as sequence models. These distance measures also have a natural extension to situations when trees do not share the same set of taxa. Unlike existing distance measures, the distance measures we propose can be defined between pairs 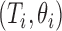 ,
, 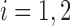 , where
, where 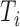 is a tree and
is a tree and 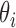 is a vector of DNA substitution model parameters, rather than between trees alone. Phylogenetic trees are usually inferred with an associated substitution model, and so information is lost if comparison is only carried out on inferred trees without the associated substitution models.
is a vector of DNA substitution model parameters, rather than between trees alone. Phylogenetic trees are usually inferred with an associated substitution model, and so information is lost if comparison is only carried out on inferred trees without the associated substitution models.
The idea of identifying trees with points in a space of distributions on characters was first considered by Kim (2000). The space is usually referred to as the space of “hyperdimensional oranges” or “phylogenetic oranges.” Topological and combinatorial aspects of the space were studied by Moulton and Steel (2004). The methods developed in this article enable the computation of metrics on this space, a first step towards more involved geometrical methods such as computation of sample means and variances.
Methods
Probabilistic Distances
A binary character is an assignment of  to each taxon, so there are
to each taxon, so there are 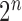 characters in total for a tree with
characters in total for a tree with 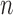 leaves. Likewise, a DNA character is an assignment of
leaves. Likewise, a DNA character is an assignment of  to each taxon, giving
to each taxon, giving 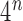 characters in total. We let
characters in total. We let 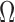 denote the set of states (
denote the set of states (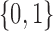 or
or 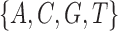 ) and use
) and use 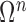 to denote the set of all characters. Evolution over a tree is typically modeled by a Markov substitution process on the edges of the tree (Semple and Steel 2003). Any Markov process substitution model induces a distribution on characters at the leaves, that is, a distribution on
to denote the set of all characters. Evolution over a tree is typically modeled by a Markov substitution process on the edges of the tree (Semple and Steel 2003). Any Markov process substitution model induces a distribution on characters at the leaves, that is, a distribution on 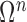 . When
. When  , we assume the Markov substitution process is the unique symmetric process on two states. This Markov process has no parameters. When
, we assume the Markov substitution process is the unique symmetric process on two states. This Markov process has no parameters. When  , we assume a general time-reversible (GTR) model with across-site Gamma rate heterogeneity. The parameters
, we assume a general time-reversible (GTR) model with across-site Gamma rate heterogeneity. The parameters 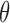 for this model determine the rates of character substitution and the stationary distribution of the process. However, the methodology we develop below can be applied to arbitrary alphabets and substitution models, in particular, to amino acid models.
for this model determine the rates of character substitution and the stationary distribution of the process. However, the methodology we develop below can be applied to arbitrary alphabets and substitution models, in particular, to amino acid models.
We look at distances between probability distributions on characters induced by the tree and substitution model; that is, look at distances
 for trees
for trees 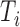 and substitution model parameters
and substitution model parameters 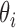 . (Note that
. (Note that 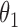 and
and  are empty when the substitution process is the symmetric two-state model). The distance
are empty when the substitution process is the symmetric two-state model). The distance  is either (i) the Hellinger (H) distance, (ii) Kullback–Leibler (KL) divergence, or (iii) Jensen–Shannon (JS) distance, and these are defined below.
is either (i) the Hellinger (H) distance, (ii) Kullback–Leibler (KL) divergence, or (iii) Jensen–Shannon (JS) distance, and these are defined below.
Let 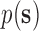 and
and  , where
, where 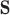 ranges over the set of characters, be probability mass functions for the probability distributions
ranges over the set of characters, be probability mass functions for the probability distributions 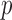 and
and 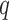 on characters associated with two trees
on characters associated with two trees 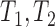 with common leaf-set of size
with common leaf-set of size 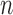 . The Hellinger distance between
. The Hellinger distance between 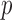 and
and 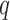 is defined by
is defined by
 |
The Hellinger distance 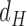 is a metric bounded above by 1 (Gibbs and Su 2002). The Kullback–Leibler divergence of
is a metric bounded above by 1 (Gibbs and Su 2002). The Kullback–Leibler divergence of 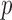 from
from 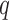 is defined as
is defined as
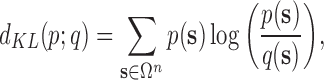 |
where log denotes the natural logarithm. The Kullback–Leibler divergence is not a metric because it is not symmetric and does not satisfy the triangle inequality. It is always non-negative (Gibbs and Su 2002). Finally, the JS distance is defined via the Kullback–Leibler divergence as
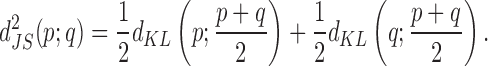 |
(1) |
It is a metric with an upper bound of  .
.
Computing these distance measures exactly for large trees is computationally expensive as there are 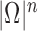 possible values for
possible values for  . However, we can estimate these distances via simulation since each can be expressed in terms of expectations with respect to the distributions
. However, we can estimate these distances via simulation since each can be expressed in terms of expectations with respect to the distributions 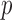 and
and 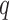 on characters. Suppose that
on characters. Suppose that 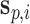 ,
,  are a set of
are a set of 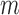 characters simulated on tree
characters simulated on tree 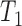 , and
, and 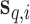 ,
, 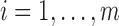 are a set of
are a set of  characters simulated on tree
characters simulated on tree 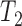 . In other words, the characters
. In other words, the characters 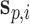 are independent samples from distribution
are independent samples from distribution 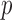 and similarly for the characters
and similarly for the characters  . We can think these samples as each being equivalent to a simulated alignment with
. We can think these samples as each being equivalent to a simulated alignment with 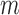 independent columns from the trees
independent columns from the trees 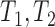 , respectively. Then it can be shown that the Hellinger distance can be estimated via
, respectively. Then it can be shown that the Hellinger distance can be estimated via
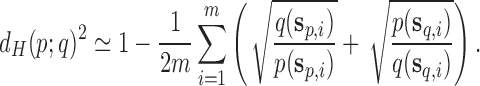 |
A full derivation is given in the Supplementary Appendix available on Dryad at http://dx.doi.org/10.5061/dryad.69bb2. Similarly, the Kullback–Leibler divergence can be estimated using
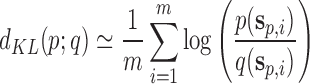 |
and this expression can be used to estimate the Jensen–Shannon metric using Equation (1).
Fixing a choice of distance measure between distributions, and given pairs 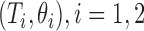 of trees and model parameters, we define the distance
of trees and model parameters, we define the distance 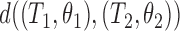 to be the distance between the induced probability distributions on characters
to be the distance between the induced probability distributions on characters 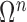 . Since the GTR model is identifiable (Allman et al. 2008), the map from pairs
. Since the GTR model is identifiable (Allman et al. 2008), the map from pairs 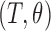 to probability distributions on
to probability distributions on  is injective, that is, one to one, so that distinct trees always induce distinct distributions. This is also the case for the two-state symmetric model and GTR model with across-site Gamma rate heterogeneity. It follows that the Hellinger and JS metrics on distributions induce metrics on pairs
is injective, that is, one to one, so that distinct trees always induce distinct distributions. This is also the case for the two-state symmetric model and GTR model with across-site Gamma rate heterogeneity. It follows that the Hellinger and JS metrics on distributions induce metrics on pairs 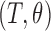 .
.
The total variation metric between distributions is defined by  . We did not explore properties of this metric when preparing this paper, but methods to compute the total variation metric are included in the software.
. We did not explore properties of this metric when preparing this paper, but methods to compute the total variation metric are included in the software.
Sample Size Calculation
When estimating the Hellinger, Kullback–Leibler, and JS distances, it is helpful to determine the smallest size sample needed to be reliably within a given tolerance of the true distance. The estimate
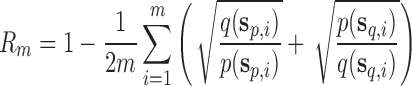 |
is unbiased for the squared Hellinger distance 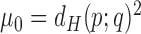 . Also, for large
. Also, for large  ,
,  is approximately normally distributed with variance
is approximately normally distributed with variance  , where
, where 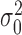 is the variance of
is the variance of 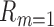 . We can obtain provisional estimates
. We can obtain provisional estimates 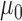 and
and 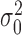 from a pilot run of size
from a pilot run of size  . Each of the
. Each of the 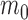 realizations produces an estimate of
realizations produces an estimate of 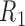 and so their mean and variance are unbiased estimates for
and so their mean and variance are unbiased estimates for 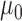 and
and 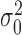 . Absolute or relative error are standard criteria for determining an appropriate sample size
. Absolute or relative error are standard criteria for determining an appropriate sample size 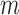 in this situation. For example, to require the estimate
in this situation. For example, to require the estimate  to have an absolute error of
to have an absolute error of 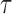 with probability
with probability 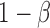 requires
requires
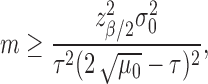 |
(2) |
where 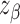 is the upper
is the upper  point of the standard normal distribution (e.g.,
point of the standard normal distribution (e.g., 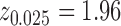 ). If instead we require a relative error of
). If instead we require a relative error of  , this is equivalent to using absolute error
, this is equivalent to using absolute error 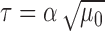 . Estimated values of
. Estimated values of 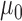 and
and 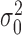 from the pilot run are used in (2) to estimate
from the pilot run are used in (2) to estimate 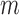 .
.
The estimators described above can be improved using the control variate method (Morgan 1984, Chapter 7, p. 171) to give unbiased estimators which achieve the same precision with fewer samples that is smaller values of 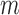 . We have implemented these improved estimators in the software and more information is given in the Supplementary appendix available on Dryad. We found the reduction in
. We have implemented these improved estimators in the software and more information is given in the Supplementary appendix available on Dryad. We found the reduction in 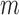 varied very substantially with each data set.
varied very substantially with each data set.
In order to explore the possible values for 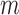 that might be required for experimental data sets, we estimated
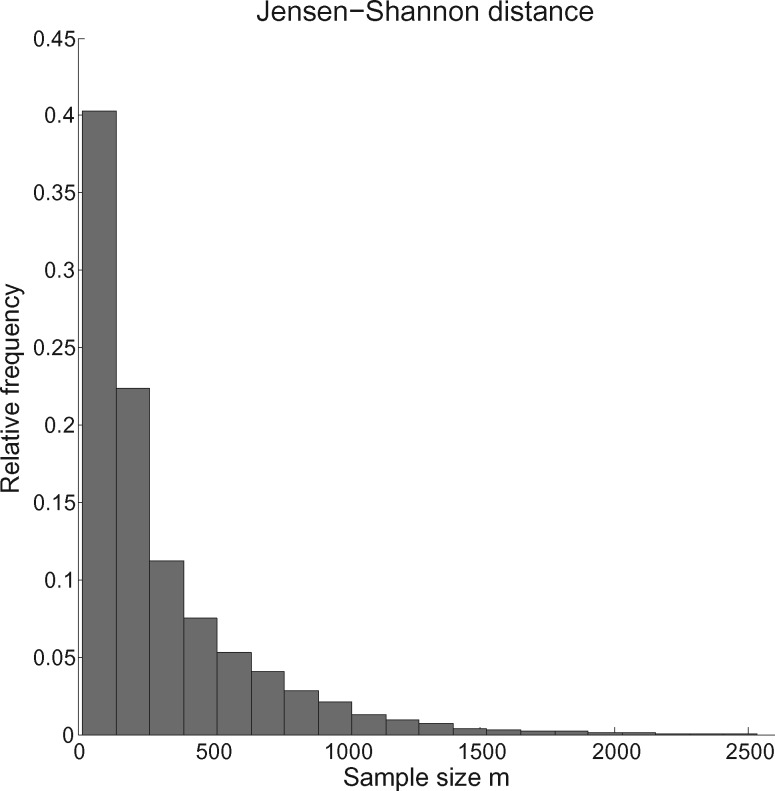
that might be required for experimental data sets, we estimated 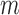 for the JS distance between every pair of gene trees contained in the data set of 106 yeast gene trees on 8 yeast species (Rokas et al. 2003). Figure 1 shows a histogram of estimated values for
for the JS distance between every pair of gene trees contained in the data set of 106 yeast gene trees on 8 yeast species (Rokas et al. 2003). Figure 1 shows a histogram of estimated values for  . Estimation was performed in order to achieve a relative error of
. Estimation was performed in order to achieve a relative error of 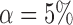 with probability
with probability 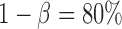 . The figure shows that fairly accurate distances can be obtained using reasonably small sample sizes.
. The figure shows that fairly accurate distances can be obtained using reasonably small sample sizes.
Figure 1.
A histogram of estimated values of 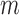 for the comparison of every pair of gene trees in the data set of 106 gene trees due to Rokas et al. 2003, using the two-state symmetric model and JS distance. It can be seen that the distance between most pairs of trees in the data set can be estimated accurately with fewer than 2000 samples. In terms of computational cost, this is similar to the cost of computing the likelihood for an alignment of length 2000 for each pair of trees.
for the comparison of every pair of gene trees in the data set of 106 gene trees due to Rokas et al. 2003, using the two-state symmetric model and JS distance. It can be seen that the distance between most pairs of trees in the data set can be estimated accurately with fewer than 2000 samples. In terms of computational cost, this is similar to the cost of computing the likelihood for an alignment of length 2000 for each pair of trees.
Missing Taxa
Suppose 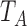 and
and  are trees with taxon sets
are trees with taxon sets 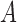 and
and 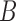 . Let
. Let 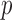 and
and 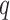 denote probability mass functions on characters induced by
denote probability mass functions on characters induced by  and
and 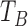 , respectively. Very commonly
, respectively. Very commonly 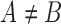 and
and  but many tree-metrics cannot be computed under these assumptions. We consider two approaches for computing distances when taxon sets differ between trees.
but many tree-metrics cannot be computed under these assumptions. We consider two approaches for computing distances when taxon sets differ between trees.
Common taxa method
The analysis is restricted to 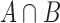 by cropping the trees down to the common taxon set. The resulting reduced trees can then used to obtain the distance measures considered in this article.
by cropping the trees down to the common taxon set. The resulting reduced trees can then used to obtain the distance measures considered in this article.
Augmentation method
This method can only be used for our probabilistic distance measures and does not apply to the BHV metric. The strategy here is that we extend the definition of 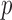 from
from 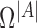 to
to 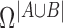 in such a way that the extended distribution is uniform on
in such a way that the extended distribution is uniform on 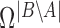 . This is done as follows. Any element
. This is done as follows. Any element 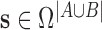 can be decomposed into three parts corresponding to the taxa in each of the sets
can be decomposed into three parts corresponding to the taxa in each of the sets 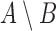 ,
, 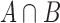 , and
, and 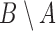 and these parts are denoted
and these parts are denoted 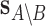 ,
, 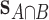 , and
, and 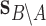 , respectively. Since there are
, respectively. Since there are 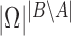 possibilities for
possibilities for  , the uniform assumption implies that the probability of each possibility is
, the uniform assumption implies that the probability of each possibility is 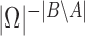 . If the extension of
. If the extension of 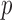 to
to 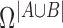 is denoted
is denoted 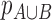 , then we define
, then we define
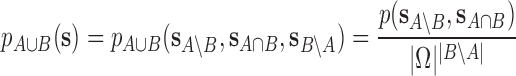 |
for all 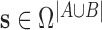 where
where 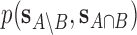 denotes the original distribution on
denotes the original distribution on 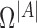 . Probabilistic distances between
. Probabilistic distances between  and
and 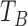 can be computed by extending
can be computed by extending  and
and 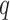 to
to 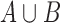 and basing the distance on these extended distributions. The uniform distribution is used as it represents a condition of maximal uncertainty of the position on the trees of the missing taxa.
and basing the distance on these extended distributions. The uniform distribution is used as it represents a condition of maximal uncertainty of the position on the trees of the missing taxa.
Results
We now look at properties of the probabilistic distance measures in several scenarios. The aim is to illustrate possible advantages and disadvantages in comparison to existing metrics, especially the BHV metric.
Scaling Edges
We consider two trees 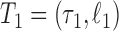 and
and 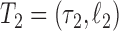 on a shared set of
on a shared set of  taxa, where
taxa, where 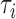 and
and 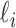 are the topology and vector of edge lengths on the trees respectively. Here the two topologies were sampled from a Yule distribution and the edge lengths were sampled from a Gamma distribution with mean 0.1 and variance 0.005. The edge lengths on both trees were then scaled by a factor
are the topology and vector of edge lengths on the trees respectively. Here the two topologies were sampled from a Yule distribution and the edge lengths were sampled from a Gamma distribution with mean 0.1 and variance 0.005. The edge lengths on both trees were then scaled by a factor 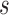 and the quantity
and the quantity
 was computed for different values of
was computed for different values of 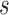 using the probabilistic distances and the BHV metric: here
using the probabilistic distances and the BHV metric: here 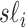 is the vector of edge lengths
is the vector of edge lengths 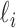 multiplied by
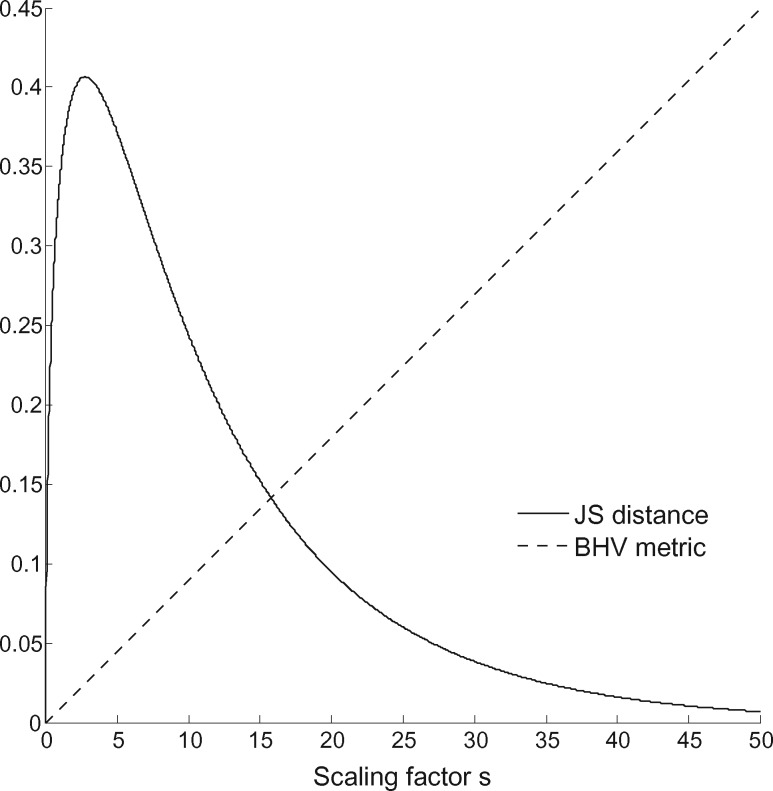
multiplied by 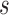 . Distances were calculated using the two-state symmetric substitution model. Figure 2 shows how the Jensen–Shannon (JS) metric does not behave like the BHV metric under this scaling. Note that the absolute values of JS and BHV distances cannot be compared directly (in fact the BHV axis has been rescaled). As we make the edge lengths on both trees increasingly long, the BHV metric increases linearly. However, under the same limit, the distribution of sequence data at each leaf becomes independent of the distribution at any other leaf, and so (due to saturation) both trees give rise to the same distribution on characters under this limit. Therefore, the probabilistic distance between the trees reduces to zero as
. Distances were calculated using the two-state symmetric substitution model. Figure 2 shows how the Jensen–Shannon (JS) metric does not behave like the BHV metric under this scaling. Note that the absolute values of JS and BHV distances cannot be compared directly (in fact the BHV axis has been rescaled). As we make the edge lengths on both trees increasingly long, the BHV metric increases linearly. However, under the same limit, the distribution of sequence data at each leaf becomes independent of the distribution at any other leaf, and so (due to saturation) both trees give rise to the same distribution on characters under this limit. Therefore, the probabilistic distance between the trees reduces to zero as 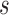 increases whereas BHV increases linearly. For values of
increases whereas BHV increases linearly. For values of 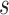 which are more meaningful from a biological perspective (e.g.,
which are more meaningful from a biological perspective (e.g., 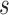 between zero and five) the JS metric also depends non-linearly on
between zero and five) the JS metric also depends non-linearly on 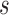 . Hellinger distance and Kullback–Leibler divergence behave similarly to JS distance. This clearly demonstrates the fundamental difference between probabilistic distances and existing distances which use edge-length information.
. Hellinger distance and Kullback–Leibler divergence behave similarly to JS distance. This clearly demonstrates the fundamental difference between probabilistic distances and existing distances which use edge-length information.
Figure 2.
JS distance and BHV metric between two random 16-taxon trees 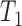 and
and 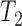 with branch lengths scaled by a factor
with branch lengths scaled by a factor 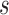 .
.
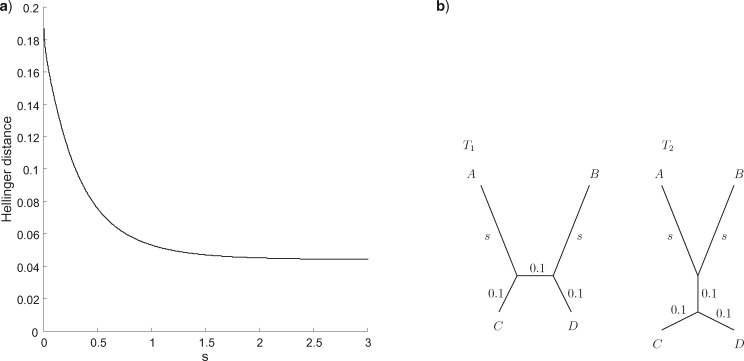
Probabilistic distances behave differently from existing metrics when the trees contain long edges. This is particularly relevant to situations when trees might be subject to long branch attraction artefacts. To illustrate this, we consider trees in the so-called Felsenstein zone and Faris zone (Felsenstein 2008). The trees are shown in Figure 3b. Each represents an alternative hypothesis in the presence of two long edges. As the edge length 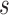 increases, the probabilistic distances between the trees decrease to a constant, as shown in Figure 3a. In contrast, the BHV distance does not vary with
increases, the probabilistic distances between the trees decrease to a constant, as shown in Figure 3a. In contrast, the BHV distance does not vary with 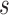 . The probabilistic distances correctly capture the fact that distinguishing one tree from the other as
. The probabilistic distances correctly capture the fact that distinguishing one tree from the other as 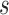 increases is difficult since they induce similar distributions on sequence data.
increases is difficult since they induce similar distributions on sequence data.
Figure 3.
a) Hellinger distance between the two trees shown in b), as a function of  , the length of the long pendant edges. The BHV distance does not vary with
, the length of the long pendant edges. The BHV distance does not vary with 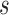 .
.
Missing Taxa
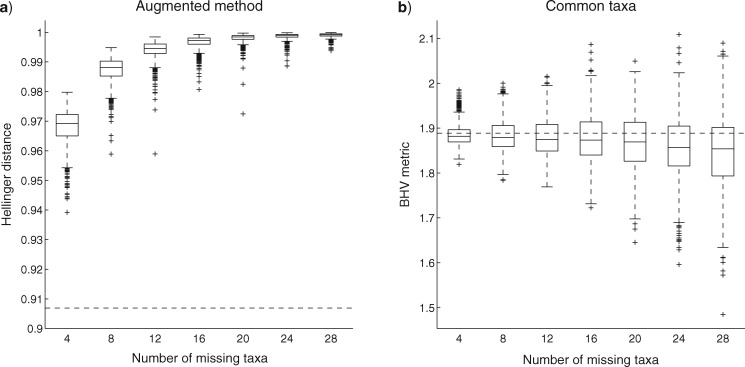
We investigate the effect of missing taxa on tree distances by first considering a tree with 100 taxa, again with topology sampled from a Yule distribution. Two copies of this topology were made and then trees constructed by assigning edge lengths independently to each topology from a Gamma distribution with mean 0.1 and variance 0.005. Each tree was then subjected to random deletions of the same number of taxa. By repeating the random deletion many times on the fixed pair of trees, and computing the distance each time, we obtain a distribution of distances between the two trees for a given proportion of deletion on each tree; see Figure 4. We also looked at the effect of random deletions of the same number of taxa from two trees with different topologies: the first being another tree with 100 taxa and the second being determined by applying 10 random subtree prune and regraft (SPR) operations to the first; see Figure 5. In both figures, we compare the augmentation method using Hellinger distance with the common taxa method using the BHV metric. The augmentation method cannot be applied to the BHV metric, since the method is intrinsically probabilistic.
Figure 4.
Sampling distribution of distance between two trees for different levels of random deletions of taxa using a) augmented method with Hellinger distance, and b) common taxa method with the BHV metric. The initial pair of trees have the same 100 taxa with the same topology but different (random) edge lengths. The dashed horizontal line is the distance/metric between the initial pair of trees (before any deletions).
Figure 5.
Sampling distribution of distance between two trees for different levels of random deletions of taxa using a) augmented method with Hellinger distance, and b) common taxa method with the BHV metric. Both trees have 100 taxa with different (random) edge lengths, with one tree generated at random and the other tree determined using 10 subsequent SPR operations. The dashed horizontal line is the distance/metric between the initial pair of trees (before any deletions).
The figures show that as the number of missing taxa increases, the Hellinger distance increases towards its upper bound of 1 and the BHV metric decreases. The decrease in the BHV metric is more substantial in Figure 4 where both initial trees have the same topology (before deletions). These trends were observed in several replicate experiments and in different sizes of trees; results are given in the Supplementary Appendix available on Dryad. Overall these figures show a desirable property of using the augmentation method over the common taxa method, namely that distances between trees increase as we have more uncertainty about the trees due to missing taxa. The probabilistic distance measures with common taxa method behave similarly to the BHV metric with the same method: results obtained with the Hellinger distance and common taxa method are given in the Supplementary Material available on Dryad.
Incorporating Substitution Model Parameters
We now investigate the distribution of distances calculated over biologically plausible trees and their substitution parameters for an experimental data set of primate DNA data (Huelsenbeck and Ronquist 2001). We analyzed the data set using the PHYML program (Guindon and Gascuel 2003) assuming the GTR model with Gamma rate heterogeneity. This gave us the maximum likelihood (ML) tree and its model parameters 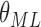 together with a set of 100 bootstrap replicates of trees
together with a set of 100 bootstrap replicates of trees 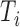 , each with their (ML) model parameters
, each with their (ML) model parameters 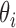 . For each pair of trees in the bootstrap sample, we calculated the Hellinger distance between trees using the same (ML) model parameters,
. For each pair of trees in the bootstrap sample, we calculated the Hellinger distance between trees using the same (ML) model parameters, 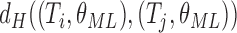 and between trees using the tree-parameter pairs,
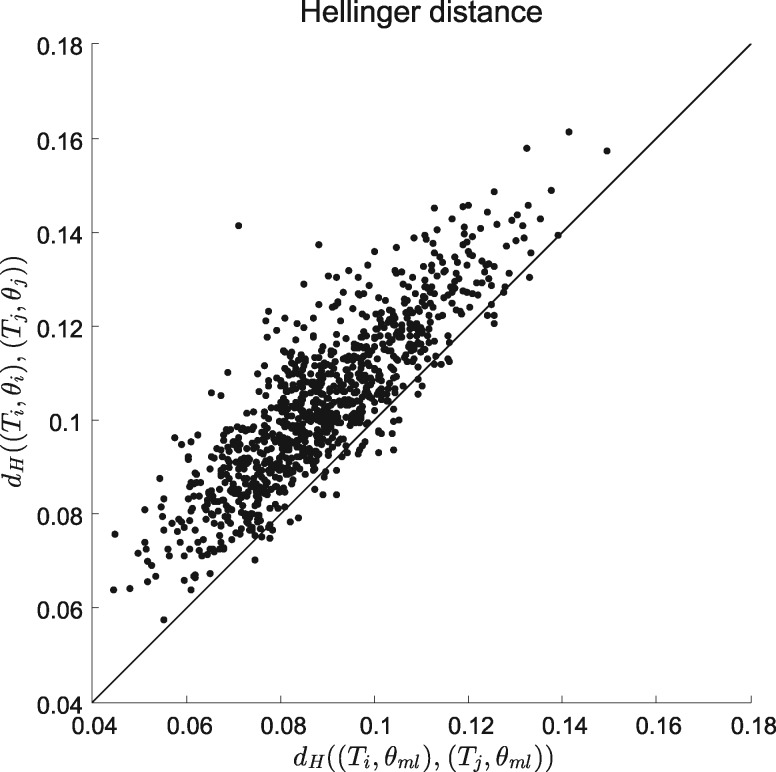
and between trees using the tree-parameter pairs, 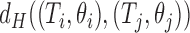 . Pairwise plots of these measures are given in Figure 6. It is clear that the distances are nearly always increased when taking proper account of the substitution parameter values. Similar results were obtained for Kullback–Leibler divergence and Jensen–Shannon distance.
. Pairwise plots of these measures are given in Figure 6. It is clear that the distances are nearly always increased when taking proper account of the substitution parameter values. Similar results were obtained for Kullback–Leibler divergence and Jensen–Shannon distance.
Figure 6.
Comparison of Hellinger distance between pairs of trees 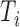 and
and 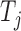 using overall ML substitution parameters
using overall ML substitution parameters 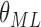 with that using individual ML substitution parameter
with that using individual ML substitution parameter 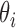 . The trees used are ML trees
. The trees used are ML trees 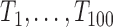 obtained from 100 bootstrap replicates of the primate data set.
obtained from 100 bootstrap replicates of the primate data set.
Phylogenetic Islands
The term phylogenetic island has been used to refer to modes in multimodal posterior distributions, especially when these modes correspond to distinct tree topologies. In this section, we study two data sets for which posterior samples have previously been found to contain distinct clusters of trees when the samples are analyzed with metrics based on topological differences between trees. We compute probabilistic distances between trees in posterior samples and perform multidimensional scaling (MDS) using these distances (Hillis et al. 2005). This leads to contrasting probabilistic interpretations of the results for the two data sets.
The first data set consists of 1949 nucleotides from 27 tetrapod species (Hedges et al. 1990). The alignment was analyzed in MrBayes (Huelsenbeck and Ronquist 2001) using the GTR model with Gamma rate heterogeneity. The analysis used a burn-in of 1 million iterations followed by another 1 million iterations, sampled every 1000 iterations, in order to obtain a posterior sample of 1000 trees  and their associated model parameters
and their associated model parameters 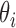 ,
, 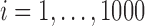 . The Hellinger distance was estimated for each pair
. The Hellinger distance was estimated for each pair 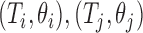 ,
, 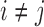 , and these distances were analyzed with MDS. The results are shown in Figure 7a. The second data set consisted of 1485 nucleotides from 17 dengue virus serotype 4 sequences (Drummond and Rambaut 2007). This alignment was analyzed using a GTR model with Gamma rate heterogeneity and invariant sites using an uncorrelated lognormal distributed relaxed molecular clock. The BEAST software was used to perform the analysis (Drummond and Rambaut 2007), using an xml file provided with the software, and 500 pairs
, and these distances were analyzed with MDS. The results are shown in Figure 7a. The second data set consisted of 1485 nucleotides from 17 dengue virus serotype 4 sequences (Drummond and Rambaut 2007). This alignment was analyzed using a GTR model with Gamma rate heterogeneity and invariant sites using an uncorrelated lognormal distributed relaxed molecular clock. The BEAST software was used to perform the analysis (Drummond and Rambaut 2007), using an xml file provided with the software, and 500 pairs 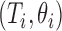 were sampled from the posterior. Figure 7b shows the results of applying MDS to the Hellinger distances between these pairs.
were sampled from the posterior. Figure 7b shows the results of applying MDS to the Hellinger distances between these pairs.
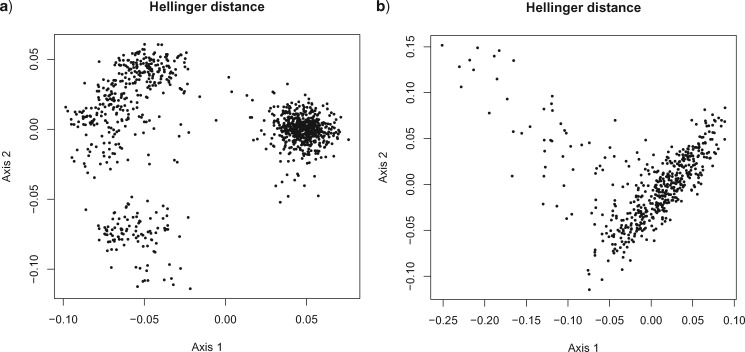
Figure 7.
MDS of the pairwise Hellinger distance between a) posterior sample of 1000 trees from the tetrapod data set under GTR+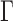 model and b) posterior sample of 500 trees from dengue fever data set under GTR+
model and b) posterior sample of 500 trees from dengue fever data set under GTR+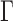 +I substitution model with uncorrelated lognormal-distributed relaxed molecular clock.
+I substitution model with uncorrelated lognormal-distributed relaxed molecular clock.
Previous analyses of these data sets have revealed distinct clusters in posterior samples when distances are measured using topological information alone. Whidden et al. (2015) found clusters in the tetrapod trees using the SPR metric. For the dengue fever sequences, Kendall and Colijn (2015) considered a family of metrics parametrized by 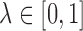 . In the case
. In the case  the metric retains only topological information, and using this metric to perform MDS reveals several distinct clusters in the posterior sample, described by Colijn and Kendall as phylogenetic islands. A figure showing MDS with the Kendall–Colijn metric is contained in the Supplementary Material available on Dryad. MDS with the unweighted Robinson-Foulds metric gives similar results for this data set.
the metric retains only topological information, and using this metric to perform MDS reveals several distinct clusters in the posterior sample, described by Colijn and Kendall as phylogenetic islands. A figure showing MDS with the Kendall–Colijn metric is contained in the Supplementary Material available on Dryad. MDS with the unweighted Robinson-Foulds metric gives similar results for this data set.
The MDS results obtained using the Hellinger distance differ for the two data sets. For the tetrapod data set, the MDS plot shows distinct clusters of trees. The three clusters correspond to distinct topological regions in tree-space. On the other hand, MDS for the probabilistic distances between dengue fever trees did not reveal any clusters in the posterior sample, as shown in Figure 7b. The clusters obtained with the Kendall–Colijn metric do not correspond to separate regions in this plot (see Supplementary Material available on Dryad). As seen in previous examples in this article, two trees with different topologies can induce similar distributions on sequence data for particular choices of edge lengths and substitution model parameters. The same phenomenon is at play for the dengue fever trees: although the posterior sample contains distinct clusters of topologies, trees in different clusters are in fact giving rise to similar distributions of nucleotides. The interpretation of the results is therefore different in the two cases. First, for the tetrapod data, it appears that a single tree together with the GTR model and Gamma rate heterogeneity is not able to explain the information in the sequence alignment. One possibility is that the substitution model is misspecified and a more sophisticated model is required; a second is that the data have arisen from a nontree-like process, such as a mixture of trees. Secondly, for the dengue fever data, it appears that several distinct groupings of topologies are consistent with the data, but regarding the trees as probability models, these groupings lack meaning as trees in different clusters represent similar distributions on characters. If more sequence data were available, and under the assumption that these sequences were generated by the same evolutionary process, we would expect the single cluster in Figure 7b to become tighter, and correspondingly, for the variability in topology in the posterior sample to be reduced.
Computing times
The time taken to estimate distances depends on the sample size and hence on the degree of accuracy required by the user. The time taken to compute all 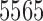 distances for the yeast data in Figure 1 was
distances for the yeast data in Figure 1 was 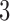 min. Similarly, the time taken to compute all
min. Similarly, the time taken to compute all 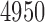 distances between trees in the primate bootstrap sample using the GTR model with Gamma rate heterogeneity was 151 minutes. In both cases, the sample size was estimated to achieve a relative error of
distances between trees in the primate bootstrap sample using the GTR model with Gamma rate heterogeneity was 151 minutes. In both cases, the sample size was estimated to achieve a relative error of 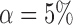 with probability
with probability 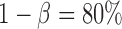 . Calculations were performed using a desktop computer with an Intel(R) Core i7-4790S processor running at 3.20 HGz.
. Calculations were performed using a desktop computer with an Intel(R) Core i7-4790S processor running at 3.20 HGz.
Conclusions
We have provided methods for computing probabilistic distances between phylogenetic trees based on simulation that give qualitatively different result from the BHV metric and other metrics. Unlike other methods that are purely based on topology and/or edge lengths on the trees, these methods are based on the underlying probability distribution on genetic sequence data induced by the trees. The methods have been extended to deal with trees that do not share the same set of taxa. We envisage probabilistic distances being used as an alternative to existing metrics in any postprocessing of phylogenies which involves a metric.
Availability
Open source java software is available from www.mas.ncl.ac.uk/~ntmwn/probdist and the source code is also included in the online supplementary material. The software runs under Mac OSX, Gnu/Linux, and Windows.
Supplementary Material
Data available from the Dryad Digital Respository: http://dx.doi.org/10.5061/dryad.69bb2.
Funding
This work was supported by a Ph.D studentship to M.G. funded by Newcastle University.
References
- Allman E.S.,, Ané C.,, Rhodes J.A. 2008. Identifiability of a Markovian model of molecular evolution with Gamma-distributed rates. Adv. Appl. Probab. 40:229–249. [Google Scholar]
- Billera L.J.,, Holmes S.P.,, Vogtmann K. 2001. Geometry of the space of phylogenetic trees. Adv. Appl. Math. 27:733–767. [Google Scholar]
- Drummond A.J.,, Rambaut A. 2007. BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evol. Biol. 7:214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estabrook G.F.,, McMorris F.R.,, Meacham C.A. 1985. Comparison of undirected phylogenetic trees based on subtrees of four evolutionary units. Syst. Biol. 34:193–200. [Google Scholar]
- Felsenstein J. 2008. Inferring phylogenies. Sunderland, MA: Sinauer Associates, Inc. [Google Scholar]
- Gibbs A.L.,, Su F.E. 2002. On choosing and bounding probability metrics. Int. Stat. Rev. 70:419–435. [Google Scholar]
- Guindon S.,, Gascuel O. 2003. A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Syst. Biol. 52:696–704. [DOI] [PubMed] [Google Scholar]
- Hedges S.B.,, Moberg K.D.,, Maxson L.R. 1990. Tetrapod phylogeny inferred from 18S and 28S ribosomal RNA sequences and a review of the evidence for amniote relationships. Mol. Biol. Evol. 7:607–633. [DOI] [PubMed] [Google Scholar]
- Hillis D.,, Heath T.,, St. John K. 2005. Analysis and visualization of tree space. Syst. Biol. 54:471–482. [DOI] [PubMed] [Google Scholar]
- Huelsenbeck J.P.,, Ronquist F. 2001. MRBAYES: Bayesian inference of phylogenetic trees. Bioinformatics 17:754–755. [DOI] [PubMed] [Google Scholar]
- Kendall M.,, Colijn C. 2015. A tree metric using structure and length to capture distinct phylogenetic signals. Available from: https://arxiv.org/abs/1507.05211. accessed June 1 2017. [Google Scholar]
- Kim J. 2000. Slicing hyperdimensional oranges: the geometry of phylogenetic estimation. Mol. Phylogenet. Evol. 17:58–75. [DOI] [PubMed] [Google Scholar]
- Lin Y.,, Rajan V.,, Moret B.M.E. 2012. A metric for phylogenetic trees based on matching. IEEE/ACM Trans. Comput. Biol. Bioinf. 9:1014–1022. [DOI] [PubMed] [Google Scholar]
- Morgan B.J.T. 1984. Elements of simulation. London: Chapman and Hall. [Google Scholar]
- Moulton V.,, Steel M. 2004. Peeling phylogenetic ‘oranges’. Adv. Appl. Math. 33:710–727. [Google Scholar]
- Owen M.,, Provan J.S. 2011. A fast algorithm for computing geodesic distances in tree space. IEEE/ACM Trans. Comput. Biol. Bioinf. 8:2–13. [DOI] [PubMed] [Google Scholar]
- Penny D.,, Watson E.E.,, Steel M.A. 1993. Trees from languages and genes are very similar. Syst. Biol. 42:382–384. [Google Scholar]
- Robinson D.F.,, Foulds L.R. 1979. Comparison of weighted labelled trees. In: Horadam A.F.,, Wallis W.D. (eds) Combinatorial Mathematics VI. Lecture Notes in Mathematics, Vol 748, 119–126. Springer, Berlin. [Google Scholar]
- Robinson D.F.,, Foulds L.R. 1981. Comparison of phylogenetic trees. Math. Biosci. 53:131–147. [Google Scholar]
- Rokas A.,, Williams B.L.,, King N.,, Carroll S.B. 2003. Genome-scale approaches to resolving incongruence in molecular phylogenies. Nature 425:798–804. [DOI] [PubMed] [Google Scholar]
- Semple C.,, Steel M.A. 2003. Phylogenetics. Oxford: Oxford University Press. [Google Scholar]
- Whidden C.,, Matsen IV, Frederick A. 2015. Quantifying MCMC exploration of phylogenetic tree space. Syst. Biol. 64:472–491. [DOI] [PMC free article] [PubMed] [Google Scholar]