Defining the population attributable fraction for infectious diseases

Abstract

Background: The population attributable fraction (PAF) is used to quantify the contribution of a risk group to disease burden. For infectious diseases, high-risk individuals may increase disease risk for the wider population in addition to themselves; therefore methods are required to estimate the PAF for infectious diseases.

Methods: A mathematical model of disease transmission in a population with a high-risk group was used to compare existing approaches for calculating the PAF. We quantify when existing methods are consistent and when estimates diverge. We introduce a new method, based on the basic reproduction number, for calculating the PAF, which bridges the gap between existing methods and addresses shortcomings. We illustrate the methods with two examples of the contribution of badgers to bovine tuberculosis in cattle and the role of commercial sex in an HIV epidemic.

Results: We demonstrate that current methods result in irreconcilable PAF estimates, depending on how chains of transmission are categorized. Using two novel simple formulae for emerging and endemic diseases, we demonstrate that the largest differences occur when transmission in the general population is not self-sustaining. Crucially, some existing methods are not able to discriminate between multiple risk groups. We show that compared with traditional estimates, assortative mixing leads to a decreased PAF, whereas disassortative mixing increases PAF.

Conclusions: Recent methods for calculating the population attributable fraction (PAF) are not consistent with traditional approaches. Policy makers and users of PAF statistics should be aware of these differences. Our approach offers a straightforward and parsimonious method for calculating the PAF for infectious diseases.

Key Messages

• Recent methods for calculating the population attributable fraction (PAF) for infectious diseases are not consistent with traditional approaches.

• We introduce a parsimonious method for calculating the PAF for infectious diseases.

• Compared with traditional estimates, assortative mixing reduces the PAF, whereas disassortative mixing increases the PAF.

Introduction

The population attributable fraction (PAF) describes the contribution of a risk factor to the burden of disease or death, for example the proportion of lung cancers attributable to smoking^1,2 or the proportion of global deaths attributable to alcohol.³ The PAF combines prevalence of exposure and relative risk. High PAFs can result from high relative risks and low population exposure or from lower relative risks but more widespread exposure,⁴ therefore providing a more balanced measure of the likely impact of public health interventions aimed at particular risk factors than relative risks alone.

Recently, PAFs have been used to quantify the contribution of risk factors to infectious disease burden, for example the contribution of malnutrition to childhood infections,⁵ the contribution of commercial sex work to HIV epidemics⁶ or the contribution of prisons to tuberculosis incidence.⁷ Some approaches have applied methodology developed for non-communicable diseases.^7–9 However, it has been argued that doing this results in an underestimate of PAF, as onward transmission to the general population is not captured ^5,6,10 and the disease risk is not independent across groups.¹¹ Simulation models have been used to estimate the PAF of a risk group by ‘turning down’ the risk factor and observing the relative decrease in incidence^5,12 or cumulative incidence.^6,10,13

In some situations, simulation models result in PAF estimates that are orders of magnitude greater than conventional estimates.^10,14 The differences are ascribed to the fact that simulation models account for onward transmission, whereas conventional estimates do not. However, it is not clear when or whether the different approaches are reconcilable, nor what aspects of the simulation approach lead to the greatly increased values. In this paper, we develop an analytical framework to compare existing methods for calculating the PAF for infectious diseases. Based on shortcomings of existing methods, we propose a new method rooted in population dynamic theory, which bridges the divide between current approaches.

Methods and Results

Comparing existing methods

In order to compare different methods, we formulate each one in terms of the proportion of the population with a risk factor, $p$, the relative risk of disease due to the risk factor, $r$, and—for the simulation model methods—the reproduction number in the general (non-risk) population, $R$.

Traditional method used for non-communicable diseases

The most common formulation of the PAF was introduced by Levin in 1953² as the ratio of excess cases due to a risk factor to the total number of cases, described in terms of the proportion of the population with a risk factor, $p$, and the relative risk of disease due to the risk factor, $r$:

$${PAF}_{trad}=\frac{p(r-1)}{p(r-1)+1}.$$ (1)

As the proportion of the population with a risk factor $p$ tends to 1, the PAF tends to $1-1/r$; therefore only very large relative risks lead to a PAF near 1.

Method of simulated epidemics with and without a risk group

Paynter⁵ and others¹² have estimated PAF as the ratio of excess cases to total cases, where the number of excess cases is estimated by using a mathematical model to simulate disease transmission with and without a risk factor, and taking the difference in incidence.

Given a population in which a risk group experiences a relative risk of disease $r$_, let the incidence rate in the population at time $t$ be $inc(r,t)$. Then the PAF using the difference of incidences method is given by:

$${PAF}_i=\frac{inc(r,t)-inc(1,t)}{inc(r,t)}.$$ (2)

A similar approach is to use a mathematical model to simulate the change in cumulative incidence over time when the effect of the risk factor is `turned down’ by setting the relative risk to one.^6,13 If the cumulative incidence in a population at time $t$ is ${\displaystyle {\int }_0^{t}i}nc(r,s)ds$, then this estimate of PAF is given by:

$${PAF}_c=\frac{tinc(r,t)-{\displaystyle {\int }_0^{t}i}nc(1,s)ds}{tinc(r,t)}.$$ (3)

At the start of the epidemic, $inc(r,0)=(1-p)R+prR$ and $inc(1,0)=R$, therefore after one generation, the methods are equivalent and ${\text{PAF}}_i$ equals ${\text{PAF}}_{trad}$. However, in order to capture the impact of susceptible depletion, ${\text{PAF}}_i$ and ${\text{PAF}}_c$ are estimated by running a transmission model to equilibrium with and without the risk group. In order to compare these methods with the traditional ${\text{PAF}}_{trad}$, we assume that a proportion of individuals are susceptible to infection, $S$, and the rest of the population are infectious, $I$. Assuming homogeneous mixing, the incidence rate at equilibrium is given by $inc(r,t)=\gamma I^{*}/S^{*}=\gamma R_0{I}^{*}$, where $R_0$ is the basic reproduction number, and $S^{*}$ and $I^{*}$ are the equilibrium proportions of susceptible and infectious individuals.

If the risk factor in question only affects susceptibility to disease (as is the case for ${\text{PAF}}_{trad}$), the basic reproduction number is $R_0=prR+(1-p)R$, where $R$ is the basic reproduction number in the non-risk group. Substituting into equation (2) at equilibrium gives a formula for calculating ${\text{PAF}}_i$, which illustrates the difference between the methods when there is homogeneous mixing:

$${PAF}_i=\frac{p(r-1)}{p(r-1)+1-1/R},$$ (4)

valid for $R>1$. If $R<1$ then ${\text{PAF}}_i=1$ as, without the risk group, the prevalence will return to the disease-free equilibrium.

Substituting into equation (3), ${\text{PAF}}_c$ is given by:

$${PAF}_c(t)=\frac{t\gamma R_0{I}_0-{\displaystyle {\int }_0^t\beta }I(s)ds}{t\gamma R_0{I}_0}.$$ (5)

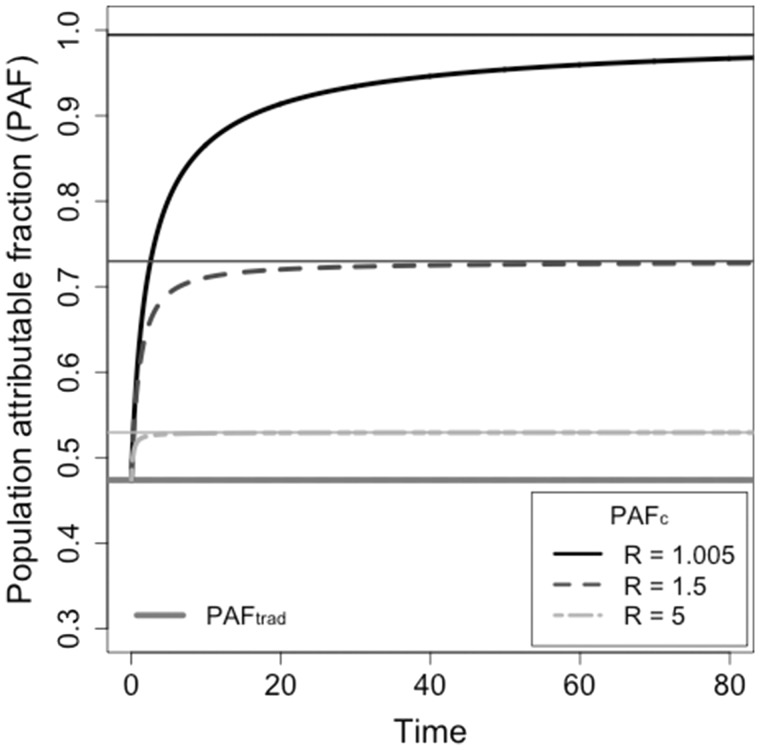
This formulation is not analytically tractable, but it approaches PAF${}_i$ over the time scales at which infectious individuals are removed from the population (Figure 1).

Figure 1.

The relationship between the population attributable fraction (PAF) calculated by simulating epidemics and the basic reproduction number. A risk factor that affects a proportion $p=0.1$ of the population with relative risk of susceptibility of $r=10$ has a traditional PAF estimate of $PA{F}_{trad}=0.47$. Methods for estimating PAF by simulating cumulative incidence with and without a risk factor (PAF${}_c$) result in estimates ranging from $PA{F}_{trad}\le PA{F}_c\le 1$, depending on the basic reproduction number in the general population (the non-risk group). The thick lines illustrate $PA{F}_c$ values when $PA{F}_{trad}=0.47$ for sample reproduction numbers. The thin lines are the asymptotes, given by PAF${}_i$.

The estimates ${\text{PAF}}_i$ and PAF${}_c$ are greater than ${\text{PAF}}_{trad}$ as they involve the reproduction number in the general population, $R$, whereas the original formulation is independent of the biology in the general population. PAF${}_i$ and PAF${}_c$ achieve their maximum value of 1 when $R=1$ and approach the conventional estimate ${\text{PAF}}_{trad}$ when R is large (Figure 1). Therefore the largest discrepancy between PAF${}_i$, PAF${}_c$ and ${\text{PAF}}_{trad}$ occurs when there is low transmission in the general population.

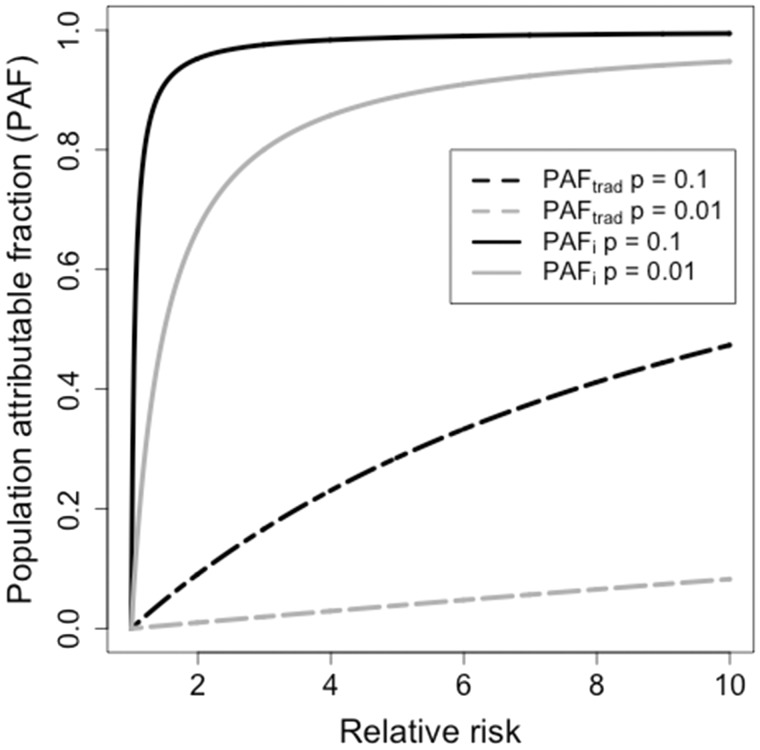
When the reproduction number $R$ in the general population is close to 1, estimates of PAF${}_i$ and PAF${}_c$ are dominated by $R$ and the impact of the relative risk, $r$, and the size of the risk group, $p$, is minimal (Figure 2). For instance, if $p=0.1$ and $R=1.005$, a relative risk of $r=5$ results in a ${\text{PAF}}_i=0.976$; whereas a relative risk of $r=10$ results in a ${\text{PAF}}_i=0.989$ (solid lines in Figure 2). In contrast, the traditional approach would result in ${\text{PAF}}_{trad}=0.17$ and ${\text{PAF}}_{trad}=0.31$ respectively (dashed lines in Figure 2).

Figure 2.

Population attributable fraction (PAF) as a function of relative risk. The solid lines show the estimate produced by model simulation with and without a risk group ($PA{F}_i$) with a basic reproduction number of 1, and the dashed lines give the estimate using the basic reproduction number method ($PA{F}_{R_0}$). Black lines represent a risk group encompassing 10% of the population; grey lines represent a risk group encompassing 1% of the population.

Alternative formulation based on secondary cases

We have demonstrated that traditional, non-communicable disease methods for estimating PAF and methods that involve model simulations give estimates that can be orders of magnitude apart and potentially lead to different prioritization for public health interventions. This leaves a dilemma regarding which method is most appropriate to use.

We will demonstrate that defining PAF as the ratio of the basic reproduction number with and without a risk group, bridges the traditional and simulation estimates of PAF, is robust to changes in the endemic equilibrium prevalence of disease and is sensitive to changes in relative risk in the risk group.

Let the PAF of the risk group be defined as:

$${PAF}_{R_0}=1-\frac{R_0(r=1)}{R_0}.$$ (6)

As before, consider a risk factor that only affects susceptibility to disease so that the basic reproduction number is $R_0=prR+(1-p)R$. In the absence of the risk group, $R_0=R$, therefore:

$${PAF}_{R_0}=1-\frac{R}{(1-p)R+rpR}.$$

which is the same as the traditional formula for ${\text{PAF}}_{trad}$, so the two methods are equivalent when a risk group only affects susceptibility.

Now, say a risk factor affects the probability of onward transmission as well as susceptibility. If the ratio of secondary infections caused by people in the risk group to secondary infections caused by people not in the risk group is denoted $r_t$, then the basic reproduction number is $R_0=pr{r}_{t}R+(1-p)R$ and the PAF will be:

$${PAF}_{R_0}=\frac{p(r{r}_t-1)}{p(r{r}_t-1)+1}.$$

The functional form is the same as the non-infectious disease case, but increased transmission has the potential to vastly increase the risk ratio $r{r}_t$, hence increasing ${\text{PAF}}_{R_0}$.

The advantage to using ${\text{PAF}}_{R_0}$ over ${\text{PAF}}_{static}$ is that any amount of detail about the population and risk group can be incorporated into the calculation of $R_0$. For instance, ${\text{PAF}}_{trad}$ implicitly assumes homogeneous mixing between the risk group and the general population, whereas in some situations people within a high-risk group have a higher contact rate with other high-risk individuals, such as people who inject drugs (PWID), and in other situations people in a high-risk group have more contacts with the general population than within the group itself, such as female sex workers (FSW).

Let $\delta$ be the proportion of contacts that occur within a group. The basic reproduction number is now given by the maximum eigenvalue of the next generation matrix (NGM):

$$NGM=\left(\begin{array}{cc}(1-p)\delta R& rp(1-\delta )R\\ (1-p)(1-\delta )R& rp\delta R\end{array}\right).$$

Using equation (6), the PAF equals:

$${PAF}_{R_0}=1-\frac{\delta +\sqrt{{\delta }^2-4p(1-p)(2\delta -1)}}{\delta (1-p+pr)+\sqrt{{\delta }^2{(1-p+rp)}^2-4(1-p)pr(2\delta -1)}}.$$

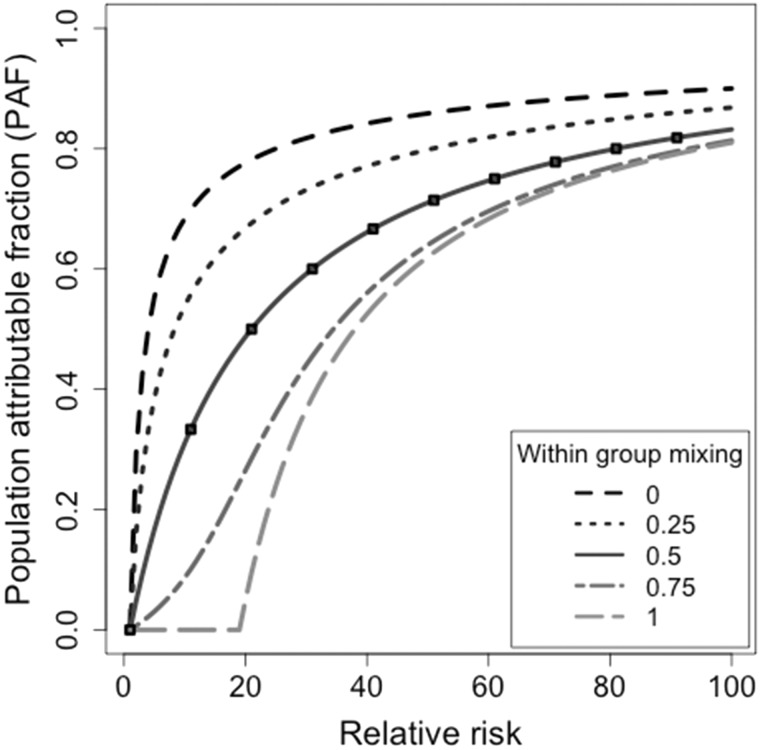
For high-risk groups that tend to mainly mix with themselves, for example PWID, the ${\text{PAF}}_{R_0}$ estimate is less than the traditional estimate (Figure 3). For high-risk groups that mainly transmit to the low-risk population, for example FSW, the ${\text{PAF}}_{R_0}$ is greater than the traditional estimate.

Figure 3.

Population attributable fraction (PAF) as a function of relative risk and inter-group mixing. The relationship between PAF, the relative risk in the high-risk group and the mixing rate between groups where the proportion of people in the high-risk group is $p=0.05$. A within-group mixing rate of 0 represents the situation when high-risk individuals preferentially contact low-risk individuals and vice versa; a within-group mixing rate approaching 1 is when high-risk individuals preferentially contact other high-risk individuals. The black dashed line is produced by the traditional PAF equation, which is equivalent to homogeneous mixing when the within-group mixing rate equals 0.5.

By using a next generation matrix approach, ${\text{PAF}}_{R_0}$ is able to consider the impact of multiple risk factors as well as incorporating behavioural data such as contact patterns, condom usage or needle sharing, and biological data such as transmission probabilities per partnership type. We illustrate the different approaches for estimating PAF with two examples.

Example 1: bovine TB in cattle and badgers

The contribution of badgers to bovine tuberculosis (TB) in cattle in Great Britain is heavily contested. Donnelly et al.^15,16 estimated that pro-active culling of badgers led to a 52% decrease in infection in cattle, but that only 5.2% of cattle infections were due to badger-to-cattle transmission. Based on these data, we estimated that the next generation matrix (NGM) was approximately:¹⁷

$$NGM=\left(\begin{array}{cc}0.94& 0.1\\ 0.1& 0.94\end{array}\right).$$

The reproduction number here is 1.07. Setting transmission within the badger population to zero, results in a reproduction number of 0.94; therefore the PAF due to badgers is 11.5%.

Simulating the transmission model with a removal rate in cattle of 0.9 years⁻¹ and a removal rate in badgers of 2 years⁻¹¹⁷ allows us to estimate PAF using the alternative method. Using the simulation method results in a PAF after 5 years of 3.9%, after 10 years of 20.3%, 52% after 20 years and 99.2% after 100 years. In this scenario, using the simulation method would lead to the conclusion that badgers contribute the majority of cattle infections, whereas the $R_0$ method demonstrates that a more accurate reflection of the contribution from badgers is 11.5%.

Example 2: the role of commercial sex in HIV epidemics

PAF estimates are often used to estimate the contribution of key populations, such as PWID, FSW or men-who-have-sex-with-men (MSM) to HIV epidemics. Using a model and data based on Mishra et al.,¹⁰ we estimate the role of occasional and regular commercial sex in HIV epidemics.

The population is divided into three groups: female sex workers (FSW) who make up 0.4% of the population, male clients (MC) who make up 8.5% of the population, and the remaining population who are defined as low activity (LA). The LA group includes individuals who have multiple partnerships. FSW engage in commercial sex work for 8 years on average, MC for 20 years and individuals in the LA group are sexually active for 34 years. We assume recruitment into each group to maintain constant population sizes.

There are three partnership types: occasional commercial, regular commercial and non-commercial (non-commercial includes casual and main partners in the Mishra et al. model). FSW have 500, 40 and 1/3 partners of each type per year; MC have 24, 2.4 and 1; and the LA group has 1/3 non-commercial partner per year. We assume that non-commercial partners can be in any group. The three contact matrices for each partnership type are:

$$\begin{array}{c}{C}_{occ}=\left(\begin{array}{ccc}0& 500& 0\\ 24& 0& 0\\ 0& 0& 0\end{array}\right)\hspace{1em}{C}_{reg}=\left(\begin{array}{ccc}0& 40& 0\\ 2.4& 0& 0\\ 0& 0& 0\end{array}\right)\\ C_{main}=\left(\begin{array}{ccc}1/0.012& 1/0.255& 1/2.733\\ 1/0.004& 1/0.085& 1/0.911\\ 1/0.012& 1/0.255& 1/2.733\end{array}\right)\end{array}$$

Transmission varies by population group $i$ and partnership type $j$ and is governed by the per-act transmission rate, ${\tau }_{ij}$, condom use, $c_{ij}$, and the number of sex acts per partnership type per year, $s_{ij}$, and is given by ${\beta }_j=1-{\left(1-(1-c_{ij}){\tau }_{ij}\right)}^{s_{ij}}$. The transmission rates for each partnership type are:

$$\begin{array}{cc}{\beta }_{occ}=\left(\begin{array}{c}2.5\times {10}^{-4}\\ 3.9\times {10}^{-4}\\ 3.2\times {10}^{-4}\end{array}\right)& {\beta }_{reg}=\left(\begin{array}{c}6.0\times {10}^{-3}\\ 9.0\times {10}^{-3}\\ 7.5\times {10}^{-3}\end{array}\right)\\ {\beta }_{main}=\left(\begin{array}{c}0.8\times {10}^{-1}\\ 1.2\times {10}^{-1}\\ 1.0\times {10}^{-1}\end{array}\right)\end{array}.$$

The next generation matrix is given by $NGM={\beta }_{occ}{C}_{occ}T+{\beta }_{reg}{C}_{reg}T+{\beta }_{main}{C}_{main}T$ where $T=\left\{8,20,34\right\}$ is the average length of time spent in each group. The basic reproduction number is the largest eigenvalue of the next generation matrix, which for this population is 1.67. Simulating this epidemic results in a stable prevalence in FSW of 54%, in MC of 23% and in the rest of the population of 18%, and an overall population incidence of 0.78%. Based on incidence rate, the relative risk of HIV in FSW compared with LA is $r=10.5$, leading to a conventional PAF estimate of 0.037, or 3.7%.

To estimate the impact of occasional commercial contacts, we consider the next generation matrix without occasional contacts, i.e. $NGM={\beta }_{reg}{C}_{reg}T+{\beta }_{main}{C}_{main}T$. This matrix has a reproduction number of 1.5, leading to a PAF estimate based on the reproduction number of ${\text{PAF}}_{R_0}=0.13$. Simulating the epidemic without occasional contacts leads to an overall population incidence of 0.56%, and a resulting PAF estimate of ${\text{PAF}}_i=0.27$.

Similarly, the impact of regular commercial contacts can be calculated from the next generation matrix without regular contacts, i.e. $NGM={\beta }_{occ}{C}_{occ}T+{\beta }_{main}{C}_{main}T$. This matrix has a reproduction number of 1.4, leading to a PAF estimate based on the reproduction number of ${\text{PAF}}_{R_0}=0.20$. Simulating the epidemic without occasional contacts leads to an overall population incidence of 0.28%, and a resulting PAF estimate of ${\text{PAF}}_i=0.64$.

Discussion

Defining the population attributable fraction (PAF) for infectious diseases is complicated because the increased disease risk due to the presence of a risk factor does not solely affect risk groups, but potentially the entire population. Existing methods for estimating PAF for infectious diseases result in estimates that are orders of magnitude different from each other, and cannot always differentiate between highly variable relative risks. We elucidated the differences between current methods using a simple mathematical framework, and proposed an alternative method that bridges the divide between existing methods and provides a transparent, robust and flexible method for estimating the PAF for infectious diseases.

There are two main previous approaches: the traditional method using a formula developed by Levin² and comparing simulated epidemics with and without a risk group.^5,6,10 The traditional approach is straightforward to calculate and transparent, as it relies on two parameters only: the relative risk of disease and the proportion of the population in the risk group. We demonstrate that in instances where there is homogeneous mixing, the traditional approach provides a good estimate of PAF. However, this method does not capture onward transmission and is not able to incorporate heterogeneous mixing or other pathogen and population characteristics. The simulation approach is similar to estimating the future avoidable burden,¹⁸ and can incorporate almost any level of detail regarding the pathogen or population; however as a consequence, it is data hungry, computationally demanding and requires robust and often complex model fitting. The complexity of the simulation approach means that is it often not clear how the resulting PAF estimates relate to the input parameters. We demonstrated that the simulation approach leads to systematically larger PAF estimates than the traditional approach. The discrepancies are greatest when transmission is under control (below the epidemic threshold) in the general population.

The large differences between the two approaches arise from the fact that the traditional approach does not depend on baseline risk, whereas the simulation approach does. In the simulation approach, entire chains of transmission initiated by an individual in the risk group (including cases in the general population) are attributed to the presence of the risk factor, whereas in the traditional approach only cases in the risk group are attributed to the risk factor. Transmission from the risk group is sufficient to generate a chain of transmission in the general population, but not necessary. Attributing those cases to the risk group implies that the only way that they could occur is from the risk group, whereas in reality, infections sustained in the non-risk population are not uniquely attributable to the risk-group. Correlations in contact structure mean that infection trees are likely to overlap, and cases in the non-risk group would occur whether they were initiated by a risk-group individual or not. Therefore, the simulation approach is not an attributable fraction.

We have also shown that a major drawback of attributing second, third, fourth and subsequent generations to the risk group is that it decreases discriminatory power of the simulation-based statistic. Policy makers using these estimates would be unable to choose between whether to prioritize interventions between a risk group with relative risk of 5 or a different risk group with relative risk of 10.

We propose an approach based on the basic reproduction number with and without the presence of a risk group. Using the basic reproduction number captures onward transmission from the risk group to the general population, but does not attribute chains of transmission that do not involve the risk group to the presence of the risk factor. Calculating the basic reproduction number requires the same data input as the simulation approach, but significantly less computational time. Once a next generational matrix is defined, using the basic reproduction number is straightforward and can be used by non-specialists like the traditional approach, and pathogen and population characteristics are incorporated as with the simulation approach. A limitation of this approach is that reduced transmission due to herd immunity is not captured.

The PAF is one of a number of impact measures such as the number needed to treat (NNT)¹⁹ used to guide clinical and public health decision making. There is an argument that PAF and NNT provide individual-level information, whereas public health decision makers require population-level equivalent measures such as the number to be treated in your population (NTP) or number of events prevented in your population (NEPP).²⁰ Epidemiologists and modellers need to work with policy makers to define measures that are most useful for decision making and prioritization.

Funding

This work was supported by the National Institute for Health Research Health Protection Research Unit (NIHR HPRU) in Evaluation of Interventions, PEPFAR [P30AI094189] and the Canadian Institute of Health [232250]. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health.