Statistical Inference in the Wright–Fisher Model Using Allele Frequency Data

Abstract

The Wright–Fisher model provides an elegant mathematical framework for understanding allele frequency data. In particular, the model can be used to infer the demographic history of species and identify loci under selection. A crucial quantity for inference under the Wright–Fisher model is the distribution of allele frequencies (DAF). Despite the apparent simplicity of the model, the calculation of the DAF is challenging. We review and discuss strategies for approximating the DAF, and how these are used in methods that perform inference from allele frequency data. Various evolutionary forces can be incorporated in the Wright–Fisher model, and we consider these in turn. We begin our review with the basic bi-allelic Wright–Fisher model where random genetic drift is the only evolutionary force. We then consider mutation, migration, and selection. In particular, we compare diffusion-based and moment-based methods in terms of accuracy, computational efficiency, and analytical tractability. We conclude with a brief overview of the multi-allelic process with a general mutation model. [Allele frequency, diffusion, inference, moments, selection, Wright–Fisher.]

A central goal of population genetics is to infer the past history of populations and describe the evolutionary forces that have shaped their genetic variation. The Wright–Fisher model (Fisher 1930; Wright 1931) explicitly accounts for the effects of various evolutionary forces—random genetic drift, mutation, selection—on allele frequencies over time. This model can also accommodate the effect of demographic forces such as variation in population size through time and/or migration connecting populations. Information about these evolutionary and demographic forces can, in principle, be retrieved from allele frequency data. The questions that researchers can answer and the types of inference they can make depend on the type of genetic data available, which can be broadly divided into two categories.

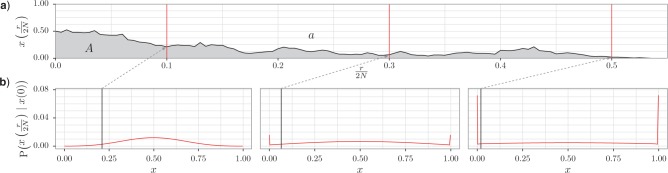
One type of data is a time series of allele frequencies from a single population (Fig. 1a). Here, the task is often to quantify the amount of drift that has influenced the changes in allele frequencies over time. This is done by estimating the size of the ideal Wright–Fisher population that best accounts for the patterns of genetic drift observed in the data, or, in other words, to estimate the effective population size. Furthermore, an important goal could be to identify those loci that have been under positive selection over the time interval considered.

Figure 1.

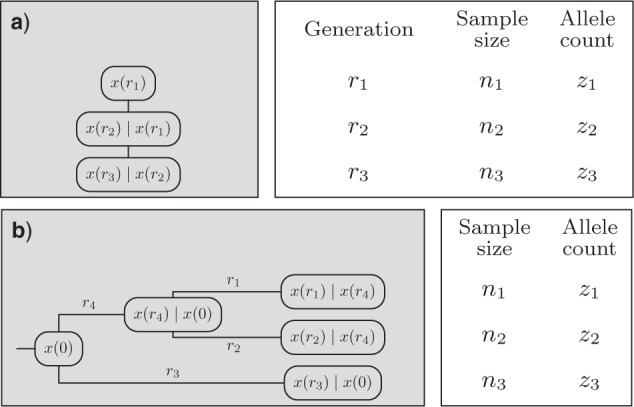
Data types. The gray boxes represent the unobserved history of the populations, together with the corresponding population allele frequency , whereas the white boxes indicate the observed data: the generation when the data are sampled, the size of the sample, and the allele count 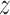, that is, how many alleles of a given type have been observed among the genotyped individuals. Given the population frequency 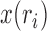, 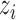follows a binomial distribution with size 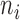and probability 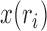. In order to calculate the likelihood of the data, the DAF of 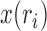is needed. a) Time series data where, typically, one population is sampled at different (known) generations. b) Single time-point data, where multiple populations are sampled just once, typically in the present. The history of the populations is given as a tree. The leaves and internal nodes represent the sampled and ancestral populations, respectively. The branch lengths reflect the amount of time populations have diverged since the split from the ancestral population.

The second type of data consists of allele frequencies from multiple populations, typically collected in the present (Fig. 1b). In this situation, the task is often to infer divergence times, population sizes, mutation rates, and, if applicable, migration rates between populations. Additionally, there is also considerable interest in evaluating the role of selection in shaping the observed data. Typical questions are: Do allele frequencies in regions of interest harbor footprints of selection? What is the overall importance of purifying selection on a specific set of sites (e.g., non-coding regions of functional interest or non-synonymous positions in gene coding regions)? We emphasize that this second type of data is very similar to the type of data analyzed in phylogenetics. In both instances, information is gained as new mutations arise at the nucleotide level and the fate of these mutations is influenced by the different evolutionary and demographic forces of interest. The difference between phylogenetics and population genetics essentially resides in the time scales that are modeled. Phylogenetics is often concerned with long time scales, and the data contain one sample per species. Differences among the sequences are most often substitutions. Population genetics typically considers data where several samples are available within a species, and many differences are detected due to mutations that are still segregating (polymorphic). Interestingly, these two time scales tend to merge when considering data sets containing sequences of individuals that comprise recently diverged species, as both types of differences—mutations that are still polymorphic and mutations that have been fixed as substitutions—have to be modeled jointly.

To infer the evolutionary history of a population, model-based approaches in population genetics have to rely on an explicit model for the evolution of populations. The Wright–Fisher model (Fisher 1930; Wright 1931) occupies a central position in this endeavour. It provides an elegant mathematical framework for modeling allele frequency data. The dynamics of the model are well understood (Kimura 1955a, 1955b, 1964; Crow and Kimura 1956; Crow and Kimura 1970; Ewens 1972; Crow 1987; Ewens 2004) but inference under the Wright–Fisher model is complicated due to the lack of a simple closed-form analytical expression for the distribution of allele frequencies (DAF). Common to all inference methods is the need to determine the DAF, either at equilibrium or over specified time intervals.

Here, we focus on how the DAF is influenced by demographic and evolutionary forces and concentrate on both classical and more recent attempts to calculate the DAF that enable accurate yet tractable population genetics inference. We begin our review with the basic bi-allelic Wright–Fisher model by considering, in turn, the forces of pure genetic drift, mutation, migration, and selection. For each of these forces, we provide expressions for the mean and variance of the DAF, and discuss and compare the approaches used to obtain the DAF. We also review implementations of the inference methods (Table 1).

Table 1.

Overview of recent inference methods for the bi-allelic Wright–Fisher model

Reference	Data	Mut	Mig	Sel	Approach	Availability
Markov chain theory
Mathieson and McVean (2013)a	T				Normal	-
Gompert (2015)a	T				Beta	spatpg
Diffusion approximation
Bollback et al. (2008)	T				Finite-difference	-
Gutenkunst et al. (2009)	S				Finite-difference	ai
Lukić and Hey (2012)	S				Spectral decomposition	MultiPop
Malaspinas et al. (2012)	T				Numerical approximation	upon request
Gautier and Vitalis (2013)	S				Spectral decomposition	KimTree
Steinrücken et al. (2014)	T				Spectral decomposition	spectralHMM
Vitalis et al. (2014)	S				Stationary DAF	SelEstim
Živković et al. (2015)	S				Spectral decomposition	upon request
Ferrer-Admetlla et al. (2016)	T				Numerical approximation	ApproxWF
Moment-based approximations
Sirén et al. (2011)	S				Beta	-
Pickrell and Pritchard (2012)	S				Normal	TreeMix
Lacerda and Seoighe (2014)	T				Normal	upon request
Hui and Burt (2015)	T				Beta	NB
Tataru et al. (2015)	S				Beta with spikes	SpikeyTree
Terhorst et al. (2015)	T				Normal	EandR-timeseries

The table indicates what type of data the method uses (Data): time series data from one population (T) or single time-point data from multiple populations (S); if the method models new mutations (Mut), migration (Mig) or selection (Sel); which type of approach is used for calculating the DAF (Approach); and whether the method is publicly available (Availability). All methods model genetic drift.

^a analyze jointly time series data from multiple populations. The table covers only the more recent inference methods.

Although the bi-allelic Wright–Fisher model captures a major part of data types, in particular single-nucleotide polymorphisms (SNPs), some loci are intrinsically multi-allelic. We therefore also briefly discuss recent progress to calculate the DAF under the general multi-allelic Wright–Fisher model. We investigate if one of the widely used approximations for the multi-allelic DAF can capture adequately the first two moments of the DAF, and point to limitations of the approximation.

A variety of methods that are grounded in the Wright–Fisher model use a range of tests and/or summary statistics to detect population differentiation (Balding and Nichols 1995; 1997; Nicholson et al. 2002; Gaggiotti and Foll 2010), or carry out genome-wide scans for selection (Foll and Gaggiotti 2008; Coop et al. 2010; Gautier et al. 2010; Gautier 2015). Several of these methods use some of the approaches for calculating the DAF discussed here. However, they do not directly use or estimate the effect of the different evolutionary forces on the DAF. Therefore, we do not review such methods and refer the reader instead to Haasl and Payseur (2015) for details.

Next to the Wright–Fisher model, the coalescent (Kingman 2000, 1982a, 1982b, 1982c) and Moran (Moran 1958) models occupy an important role in the field. The coalescent process is dual to the Wright–Fisher model: although the Wright–Fisher model describes the evolution of a population forward in time in discrete non-overlapping generations, the coalescent process is built backwards in time, and arises as an approximation to the Wright–Fisher model when the population size is large. Unlike the coalescent, the Moran model is a forward-in-time process, and it is often regarded as an equivalent to the Wright–Fisher model (but see Bhaskar and Song 2009). Both the coalescent and Moran models have been analyzed extensively and their dynamics are in several cases more amenable to mathematical analysis (Donnelly 1984; Ewens 2004; Hobolth et al. 2007; Muirhead and Wakeley 2009; Li and Durbin 2011; Paul et al. 2011; Vogl and Clemente 2012). However, the Moran model is hardly ever used for inference (but see, e.g., De Maio et al. 2013; 2015), whereas the coalescent is typically restricted to a handful of individuals (Hobolth et al. 2007; Li and Durbin 2011; Paul et al. 2011; Mailund et al. 2012; Sheehan et al. 2013; Schiffels and Durbin 2014; Rasmussen et al. 2014) and does not use allele frequency data (but see, e.g., Liu and Fu 2015). Therefore, we do not include the coalescent and Moran models in this review, and refer the reader instead to Fu and Li (1999); Durrett (2008); Kuhner (2009); Liu et al. (2009); Wakeley (2009); Nielsen and Slatkin (2013); Edwards et al. (2016).

BI-ALLELIC WRIGHT–FISHER MODEL

The Wright–Fisher model assumes a randomly mating population of finite size reproducing in discrete non-overlapping generations, by allowing the individuals in generation 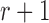to choose parents at random from the previous generation 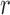. The model describes the stochastic behavior through time of the frequency of an allele at a locus. This frequency is influenced by a series of evolutionary forces that, as discussed below, change the probability of choosing a parent. Here, we consider a diploid population of size 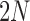which contains only two alleles, denote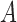d and 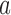. Below we review methods used to obtain the DAF of allele 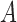after a certain amount of generations.

Pure Drift

The Wright–Fisher model, in its simplest form, only considers random genetic drift (Fig. 2), where the stochastic fluctuations in the allele frequency are purely determined by the random mating of the population. This assumption is appropriate for the analysis of loci that have small mutation rates and the analysis of recently diverged populations, leaving little time for mutation to create new alleles, and where we expect an overall negligible effect of selection.

Figure 2.

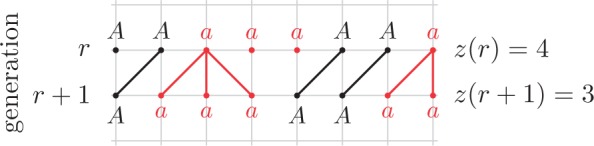
Dynamics in the pure drift bi-allelic Wright–Fisher model. The child inherits the parental allele.

Dynamics and moments.—

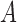Let be the number of alleles in generation 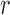and 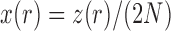be the corresponding allele frequency. The random mating of the population leads to a count of 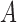alleles in generation 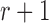that is binomially distributed (Fisher 1930; Wright 1931; Crow and Kimura 1970; Ewens 2004)

$$z(r+1)\mid z(r)\sim \mathrm{B}\mathrm{i}\mathrm{n}(2N,x(r)).$$ (1)

Here, 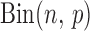is the binomial distribution with sample size 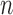and probability 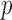. The genetic variation present in the population is due to ancestral polymorphism, and because no new variation is added, the 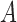allele is eventually fixed or lost (Fig. 3a).

Figure 3.

a) Simulation under the pure drift model (equation (1)) with 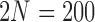and . The vertical bars indicate three sampled time-points. The 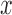-axis denotes the time measured in scaled number of generations. b) DAF at the three sampled time-points. The vertical bars indicate the simulated allele frequencies.

The goal is to determine the DAF: the distribution 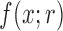of 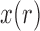, after evolving for 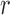generations from an initial frequency 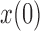(Fig. 3b). We first calculate the first two moments of the DAF. From the binomial sampling, the mean and variance over one generation are given by

$$\begin{array}{cc}\hfill \text{E}\left[x(r+1)\mid x(r)\right]& \hspace{0.17em}=x(r),\hfill \\ \text{Var}\left(x(r+1)\mid x(r)\right)\hfill & \hspace{0.17em}=\frac{1}{2N}x(r)(1-x(r)).\hfill \end{array}$$

The mean and variance after 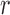generations can be obtained by iterating the two expressions above or from alternative derivations (Wright 1942; Crow 1954; Crow and Kimura 1970). The result is

$$\begin{array}{cc}\text{E}\left[x(r)\mid x(0)\right]\hfill & \hspace{0.17em}=x(0),\hfill \end{array}$$ (2)

$$\begin{array}{cc}\text{Var}\left(x(r)\mid x(0)\right)\hfill & \hspace{0.17em}=x(0)(1-x(0))(1-{(1-\frac{1}{2N})}^r).\hfill \end{array}$$ (3)

For large 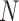, we can approximate the variance by

$$\text{Var}\left(x(t)\mid x(0)\right)\approx x(0)(1-x(0))(1-e^{-t}),$$ (4)

where 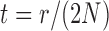. Note that this implies that 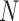can be estimated by equation (2) only if 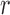is known, otherwise only the ratio 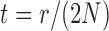can be estimated.

Markov chain theory.—

Because the allele frequency at generation 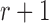only depends on generation 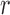, the Wright–Fisher model is a discrete-time finite-space Markov chain. Using this property, the DAF can be obtained from classical Markov chain theory (Karlin and Taylor 1975), where the transition probabilities are given by equation (1) (Williamson and Slatkin 1999). However, this procedure quickly becomes computationally infeasible, as the transition probability matrix has a size of 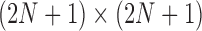. By recognizing that most of the probability mass from equation (1) is centered around 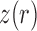, the computational demand can be reduced by evaluating, storing and using only the transition probabilities that are large enough to contribute significantly to the DAF (Wang 2001; Freeman et al. 2003).

Under the assumption of large 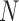, diffusion theory (see below) shows that the population size acts as a scaling factor (Feller et al. 1951; Wakeley 2005) and therefore one could calculate the DAF using a smaller 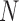. This approach was used by De Maio et al. (2013; 2015), though they relied on the Moran model rather than the Wright–Fisher. Alternatively, if 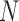is large enough such that the allele frequencies can be treated as continuous, the Markov chain can be built over discretized allele frequencies, and thus the computational burden is controlled by the number of bins. The original discrete binomial sampling probability from equation (1) is then replaced by the continuous normal or beta distributions (Mathieson and McVean 2013; Gompert 2015).

Diffusion approximation.—

One way to calculate the DAF is to take advantage of the diffusion approximation to the Wright–Fisher model, which is appropriate when the population size 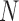is large, such that both allele frequencies and time can be treated as continuous. Diffusion theory uses two fundamental equations, the Kolmogorov forward and backward equations (Kolmogorov 1931). The forward equation was first used by Wright (1945) to calculate the rate of decay and stationary DAF, whereas Kimura (1957) used the backward equation first to study the problem of fixation. Let us define a new time scale by 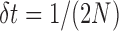such that one time unit corresponds to 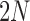generations. Then, we have

$$2Nx(t+\delta t)\mid x(t)\sim \mathrm{B}\mathrm{i}\mathrm{n}(2N,x(t)),$$

from which we can approximate

$$x(t+\delta t)\mid x(t)\approx \mathrm{N}(x(t),x(t)(1-x(t))\delta t).$$ (5)

Here, 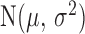is the normal distribution with mean 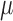and variance 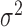. Equation (5) corresponds to the time-homogeneous stochastic differential equation

$$dx(t)=a(x)dt+\sqrt{b(x)}dw(t),$$ (6)

where 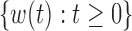is a standard Brownian motion, and 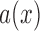and 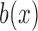are the infinitesimal mean and variance, respectively. For the Wright–Fisher model, 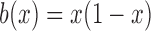, whereas has different forms depending on the evolutionary forces. Under pure drift, 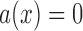, as is evident from equation (5).

The DAF 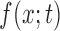at time 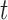is now determined by the forward Kolmogorov (or Fokker–Planck or diffusion) equation (Kolmogorov 1931; Crow and Kimura 1970; Ewens 2004)

$$\begin{array}{c}\begin{array}{cc}\frac{\mathrm{\partial }f(x;t)}{\mathrm{\partial }t}\hfill & \hspace{0.17em}=-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\{a(x)f(x;t)\}\hfill \\ & \hspace{0.17em}+\frac{1}{2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\{x(1-x)f(x;t)\},\hfill \end{array}\hfill \end{array}$$ (7)

with boundary condition 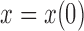for . This equation can be solved using different approaches (Table 1). Kimura first described how the DAF can be calculated under pure drift (Kimura 1955a) using the spectral decomposition of equation (7), which results in an infinite sum of scaled Gegenbauer polynomials. In practice, the infinite sum needs to be truncated and the optimal truncation level depends on the convergence properties. This controls the accuracy, but also the computational performance. The diffusion equation can also be solved using purely numerical methods. Chang and Cooper (1970) developed a finite-difference scheme to numerically solve any diffusion equation, whereas Zhao et al. (2013) proposed a finite-volume scheme to solve the Wright–Fisher diffusion equation.

Gautier and Vitalis (2013) relied on the solution proposed by Kimura (1955a) to estimate divergence times between populations that have been evolving under pure drift, from single time-point data.

Moment-based approximations.—

The use of the diffusion approximation is limited in practice due to the high computational burden. Cavalli-Sforza and Edwards (1967) approximated pure drift as a Brownian motion process, and current moment-based approximations are reminiscent of that approach, in that they are based on mathematically convenient instrumental distributions. By relying on the equations for the mean (2) and variance (3, 4), we can fit to the true DAF distributions that can be parameterized solely through the first two moments, such as the normal and beta distributions. These two distributions arise as special cases of the DAF approximated from the diffusion theory: the normal distribution is a transient distribution (equation (5)) which is appropriate for very short evolutionary times, whereas the stationary DAF under linear evolutionary pressure is given by a beta distribution (see Box 1, equation (B.9)).

Box 1.

Evolutionary models for the bi-allelic Wright–Fisher

Consider the general bi-allelic Wright–Fisher process, where 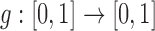captures the evolutionary pressures acting on the allele,

$$z(r+1)\mid z(r)\sim \mathrm{B}\mathrm{i}\mathrm{n}(2N,g(x(r))).$$ (B.1)

The function can take different forms.

General linear evolutionary pressure:

$$\begin{array}{c}g(x)=(1-a)x+b,\text{for\hspace{0.5em}}0\le b\le a<1,\hfill \end{array}$$ (B.2)

where 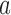and 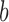are given by

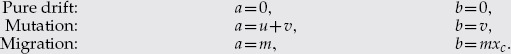(B.3)

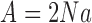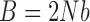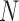Let , and . For large , the mean and variance for the DAF are given by (Tataru et al. 2015)

$$\begin{array}{cc}& \text{E}\left[x(t)\mid x(0)\right]=\frac{B}{A}+e^{-At}(x_0-\frac{B}{A}),\hfill \end{array}$$ (B.4)

$$\begin{array}{cc}& \text{Var}\left(x(t)\mid x(0)\right)\hfill \\ & \hspace{0.17em}=\frac{B}{A}(1-\frac{B}{A})\frac{1-e^{-(2A+1)t}}{2A+1}\hfill \\ & \hspace{0.17em}-{(x_0-\frac{B}{A})}^2{e}^{-2At}(1-e^{-t})\hfill \\ & \hspace{0.17em}+(1-\frac{2B}{A})(x_0-\frac{B}{A})e^{-At}\frac{1-e^{-(A+1)t}}{A+1}.\hfill \end{array}$$ (B.5)

For pure drift, 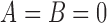and we set 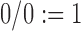. Note that equations (2), (4), (11), and (12) can be obtained as special cases of the above.

Selection (non-linear evolutionary pressure):

$$\begin{array}{cc}g(x)\hfill & \hspace{0.17em}=\frac{(1+s)x^2+(1+sh)x(1-x)}{(1+s)x^2+2(1+sh)x(1-x)+(1-x{)}^2}\hfill \end{array}$$ (B.6)

$$\begin{array}{cc}& \hspace{0.17em}\approx x+sx(1-x)(h+(1-2h)x),\hfill \end{array}$$ (B.7)

where the approximation relies on the selection coefficients 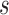and 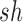being small (Crow and Kimura 1970).

Selection with linear evolutionary pressure: Alleles can undergo linear evolutionary pressure and selection jointly. Then,

$$\begin{array}{cc}g(x)\hfill & \hspace{0.17em}=(1-a)\{x+sx(1-x)(h+(1-2h)x)\}+b.\hfill \end{array}$$ (B.8)

Stationary distribution: When 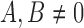, variation is constantly introduced in the population and the DAF has a stationary distribution given by (up to a normalization constant),

$$\begin{array}{c}f(x)\propto x^{2B-1}(1-x{)}^{2(A-B)-1}{e}^{Sx(2h+(1-2h)x)},\hfill \end{array}$$ (B.9)

where 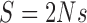is the scaled selection coefficient. When 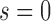, we obtain a beta distribution with shape parameters 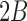and 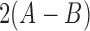, which is in agreement with the expressions for mean and variance in the limit .

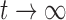Several authors used the normal distribution (Nicholson et al. 2002; Coop et al. 2010; Gautier et al. 2010; Pickrell and Pritchard 2012; Lacerda and Seoighe 2014; Terhorst et al. 2015), which takes the form

$$\begin{array}{c}x(r)\mid x(0)\sim \mathrm{N}(\mathrm{E}[x(r)\mid x(0)],\mathrm{V}\mathrm{a}\mathrm{r}(x(r)\mid x(0))).\hfill \end{array}$$ (8)

Equations (5) and (8) are equivalent under pure drift when the number of generations 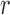is small relative to the population size 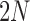. Then, by using the approximation

$$\begin{array}{c}1-{(1-\frac{1}{2N})}^r\approx 1-e^{-\frac{r}{2N}}\approx \frac{r}{2N},\hfill \end{array}$$

in the variance equation (3), we recover equation (5) from equation (8) with .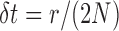

Balding and Nichols (1995; 1997) first proposed the use of the Dirichlet distribution, the multivariate generalization of the beta distribution, for the multi-allelic Wright–Fisher (see the multi-allelic section below). For the bi-allelic Wright–Fisher model, the DAF can be approximated with a beta distribution as follows,

$$\begin{array}{c}x(r)\mid x(0)\sim \mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}\left(\mathrm{E}[x(r)\mid x(0)],\mathrm{V}\mathrm{a}\mathrm{r}(x(r)\mid x(0))\right),\hfill \end{array}$$

where 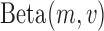is the beta distribution parameterized by mean 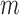and variance 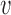. We note here that a beta distribution always verifies the condition 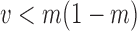. For the alternative parameterization with shapes 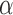and 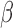, we have the relation

$$\begin{array}{c}\begin{array}{cc}\alpha \hfill & \hspace{0.17em}=(\frac{m(1-m)}{v}-1)m,\hfill \\ \beta \hfill & \hspace{0.17em}=(\frac{m(1-m)}{v}-1)(1-m).\hfill \end{array}\hfill \end{array}$$ (9)

Although both the normal and beta distributions have been used for inference, they differ in accuracy. One major difference comes from the support of the distributions. The allele frequency 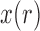always lies between 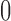and 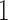, and, under the Wright–Fisher model, there can be a positive probability for 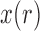being eithe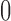r or 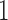(the allele is lost or fixed, respectively). The normal distribution is defined over the whole real line, and a positive probability can exist outside 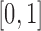. If 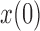is intermediate and 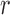is small, the probability that 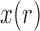falls outside of 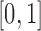is small and therefore can be ignored (Pickrell and Pritchard 2012; Lacerda and Seoighe 2014; Terhorst et al. 2015). If 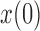is close to the boundaries, the normal distribution from equation (8) can be truncated to 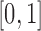. The probabilities in the intervals 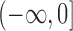and 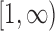are added as two atoms at 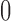and 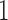and serve as the loss and fixation probabilities, respectively (Nicholson et al. 2002; Coop et al. 2010; Gautier et al. 2010). Gautier and Vitalis (2013) noted that the truncated normal distribution no longer has the true variance of the DAF.

Unlike the normal distribution, the beta distribution has support in 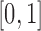. However, due to its continuous nature, the beta distribution cannot account for the discrete events that 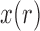can be 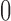or 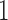. Tataru et al. (2015) addressed this issue and introduced a new approximation, the beta with spikes, a beta distribution for the polymorphic frequencies (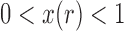), supplemented by two spikes at 0 and 1 accounting for the loss and fixation probabilities. Then the distribution of 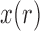is

$$\begin{array}{cc}x(r)\mid x(0)\sim {\mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}}^{\star }(\hfill & \text{E}\left[x(r)\mid x(0)\right],\text{Var}\left(x(r)\mid x(0)\right),\hfill \\ & p_0(r),p_1(r)),\hfill \end{array}$$

where 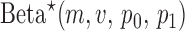is the beta with spikes distribution parameterized by mean 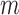, variance 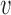, and probabilities 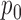and 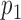found at 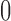and 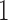, respectively. This is given by

$$\begin{array}{cc}{\mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}}^{\star }(x;m,v,p_0,p_1)\hfill & \hspace{0.17em}=p_0\delta (x)+p_1\delta (1-x)\hfill \\ & \hspace{0.17em}+\frac{1-p_0-p_1}{\text{B}({\alpha }^{\star },{\beta }^{\star })}\mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}(x;m^{\star },v^{\star }).\hfill \end{array}$$

Here, 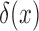is the Dirac delta function, introduced to account for the non-zero probabilities at the boundaries, and 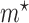and 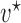are the mean and variance of the beta distribution for the polymorphic frequencies, given by (Tataru et al. 2015)

$$\begin{array}{cccc}{m}^{\star }\hfill & \hspace{0.17em}=\frac{m-p_1}{1-p_0-p_1},\hfill & v^{\star }\hfill & \hspace{0.17em}=\frac{v+m^2-p_1}{1-p_0-p_1}-{\left(m^{\star }\right)}^2.\hfill \end{array}$$

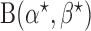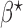The beta function acts as a normalization factor, where and are the shape parameters of 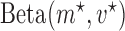(equation (9)).

Using the equations (2) and (3) for the mean and variance, the normal and beta approximations of the DAF can be written in closed form. However, the loss and fixation probabilities are not known in closed form, and therefore, the beta with spikes relies on a recursive approach to calculate these probabilities (see Tataru et al. (2015) for details).

The moment-based approximations have been used in a series of inference methods (Table 1). Hui and Burt (2015) used the beta distribution to infer the effective size of one population undergoing pure drift from time series data. Sirén et al. (2011) and Tataru et al. (2015) used single time-point data to infer divergence times between populations evolving under pure drift. Sirén et al. (2011) used the beta distribution, and therefore could not accurately model the alleles that are close to being lost or fixed. Tataru et al. (2015) used the beta with spikes approximation and demonstrated that the addition of spikes leads to a more accurate inference compared with merely using the beta distribution.

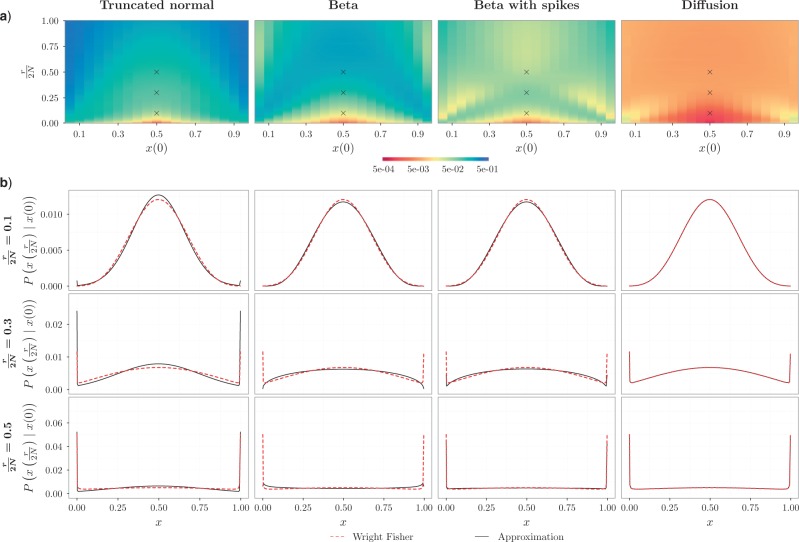
Quality of approximations.—

We evaluated the accuracy of the approximations to the true DAF obtained from the Markov chain property, using the Hellinger distance (Le Cam and Yang 2000), which lies between 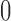and 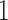, with 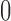indicating a perfect match of the two distributions. The diffusion approximation is the most accurate, whereas the truncated normal and beta distributions are the least accurate (Fig. 4). They approximate the true DAF well when the probability mass is away from the boundaries: 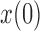is close to 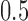and the generation 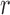is not too large. As 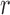increases, the frequency drifts away from 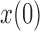and more and more probability accumulates at the boundaries. The beta distribution fails to capture this, whereas the atoms and spikes in the truncated normal and beta with spikes distributions, respectively, approximate these probabilities with various degrees of accuracy. Overall, the beta with spikes distribution is more accurate than both the truncated normal and beta distributions.

Figure 4.

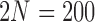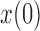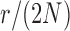Fit of various approximations to the pure drift true DAF, calculated using the Markov chain property for and a range of and . Each column shows a different type of approximation, indicated at the top of the figure. a) Hellinger distance on log scale between the approximated and true DAF. The three “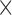”s in each of the heatmaps indicate the combinations of 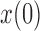and 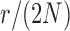used in b). b) True (dashed lines) and approximated (solid lines) DAF for 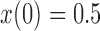and different values of 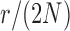. The truncated normal, beta and beta with spikes are discretized as in Tataru et al. (2015). The diffusion DAF is calculated as in Zhao et al. (2013), with 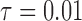and 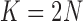. We used 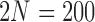for computational reasons, but we see similar patterns for larger .

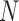Neutral Mutations

The most common way to introduce variation in a population is by allowing the alleles to mutate (Fig. 5).

Figure 5.

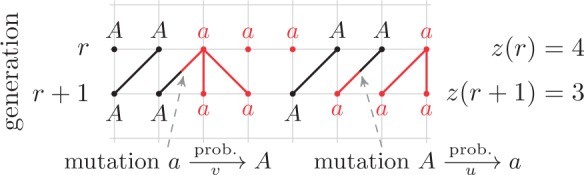
Dynamics in the bi-allelic Wright–Fisher model with mutations. If the parental allele is , the child has the same allele with probability , and a mutation occurs with probability 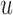. If the parental allele is 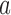, the child allele is 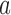with probability 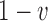, and becomes 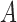with probability .

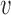Dynamics and moments.—

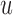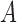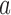If is the probability of a mutation from to , and 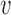is the probability for the reverse event, the sampling probability from equation (1) is changed by allowing each individual to undergo a mutation after choosing its parent. Therefore, the individual is carrying an 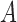allele if the parent had an 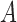allele (probability 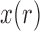) and there was no mutation (probability 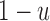), or the parent had an 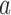allele (probability 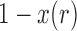) and it mutated (probability 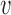), leading to a sampling probability

$$x(r)(1-u)+(1-x(r))v=(1-u-v)x(r)+v.$$

Then, the binomial distribution of 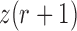becomes

$$z(r+1)\mid z(r)\sim \mathrm{B}\mathrm{i}\mathrm{n}(2N,(1-u-v)x(r)+v).$$ (10)

For large 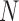, Crow and Kimura (1956) derived general formulas for all moments of 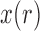. The mean and variance after 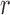generations of evolution can also be obtained by repeated use of the laws of total expectation and variance (Sirén 2012). Tataru et al. (2015) provided the formulas:

$$\begin{array}{cc}& \text{E}\left[x(t)\mid x(0)\right]=\frac{\nu }{\mu +\nu }+(x(0)-\frac{\nu }{\mu +\nu })e^{-(\mu +\nu )t},\hfill \end{array}$$ (11)

$$\begin{array}{cc}& \text{Var}\left(x(t)\mid x(0)\right)\hfill \\ & \hspace{0.17em}=\frac{\mu \nu }{(\mu +\nu {)}^2(2(\mu +\nu )+1)}(1-e^{-(2(\mu +\nu )+1)t})\hfill \\ & \hspace{0.17em}-{(x(0)-\frac{\nu }{\mu +\nu })}^2{e}^{-2(\mu +\nu )t}(1-e^{-t})\hfill \\ & \hspace{0.17em}+\frac{\mu -\nu }{(\mu +\nu )(\mu +\nu +1)}(x(0)-\frac{\nu }{\mu +\nu })\hfill \\ & \hspace{0.17em}\cdot e^{-(\mu +\nu )t}(1-e^{-(\mu +\nu +1)t}),\hfill \end{array}$$ (12)

where 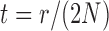, , 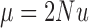and .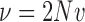

Diffusion approximation.—

The diffusion approximation of the Wright–Fisher with neutral mutations is obtained in a similar way as for pure drift. Let 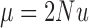and 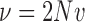be the scaled mutation rates, and we again scale the time in units of generations. Recall that the infinitesimal variance is independent of the evolutionary forces. For neutral mutations, the infinitesimal mean is given by

$$\begin{array}{cc}a(x)\hfill & \hspace{0.17em}=-\mu x+\nu (1-x).\hfill \end{array}$$ (13)

When new variation is constantly introduced in the population, after enough time, the allele frequency will reach a stationary distribution. This was first obtained by Wright (1931) by noting that at stationarity, the mean and variance are unchanged between successive generations. Later on, the stationary DAF was re-derived using alternative methods, including diffusion (Wright 1945; 1938). The stationary DAF for neutral mutations is given by a beta distribution with shape parameters 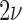and 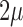(Crow and Kimura 1970; Ewens 2004). Note that this result is in agreement with the mean (equation (11)) and variance (equation (12)) in the limit .

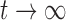The spectral decomposition method developed by Kimura (1955a) to calculate the DAF under pure drift was extended to calculate the DAF with recurrent mutation (Crow and Kimura 1956; 1970; Song and Steinrücken 2012), and to incorporate mutation rates and population sizes that vary in time in a piecewise constant manner (Steinrücken et al. 2016).

Moment-based approximations.—

Using the moments of the DAF for the bi-allelic Wright–Fisher with neutral mutations (equations (11) and (12)), the moment-based approximations are obtained just as for pure drift.

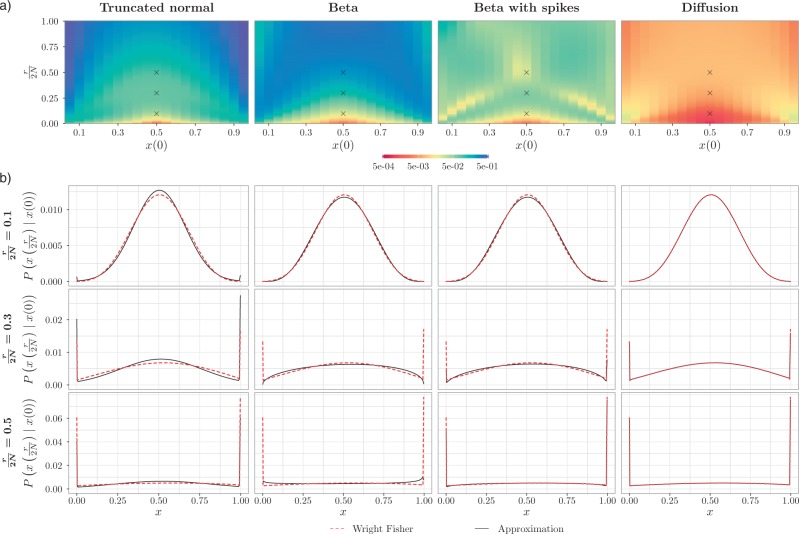
Quality of approximations.—

The non-zero mutation probabilities introduce variation in the population, and reduce the loss and fixation probabilities relative to pure drift (Figs. 4 and 6). For example, under pure drift, the probability that the mutation is lost (fixed) at 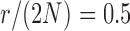is 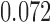, while when alleles mutate with 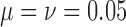, the probability is reduced to 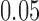. As more of the probability mass is now found away from the 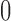and 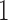boundaries, all approximations have an overall improved fit to the true DAF (Fig. 6).

Figure 6.

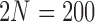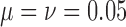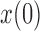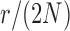Fit of various approximations to the true DAF with neutral mutations, calculated using the Markov chain property for , and a range of and . Each column shows a different type of approximation, indicated at the top of the figure. a) Hellinger distance on log scale between the approximated and true DAF. The three "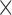"s in each of the heatmaps indicate the combinations of 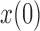and 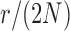used in b). b) True (dashed lines) and approximated (solid lines) DAF for 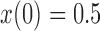and different values of 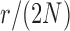. Calculations are performed as for Figure 4. For comparison purposes, the a) heatmap and b) 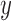-axis scales are the same as in Figure 4.

Migration

In its simplest form, the migration model describes the evolution of the allele frequency in one population that sends migrants, with probability , to an infinitely large population with constant allele frequency 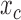, and receives immigrants such that the population size stays constant over time. Then the allele count at generation 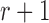is given by (Crow and Kimura 1970)

$$z(r+1)\mid z(r)\sim \text{Bin}(2N,(1-m)x(r)+m{x}_c).$$ (14)

Under pure drift, the sampling among the alleles in generation 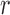is done uniformly (equation (1)). However, as different evolutionary pressures act on the allele, the sampling probability is changed, as observed for neutral mutations and migration in (14). We can capture all the evolutionary pressures acting on the allele in a function 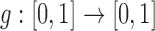which alters the sampling probability of the binomial distribution from equation (1). We then obtain the more general process

$$\begin{array}{c}z(r+1)\mid z(r)\sim \text{Bin}(2N,g(x(r))).\hfill \end{array}$$ (15)

The evolutionary pressures for pure drift, mutation, and migration are linear in 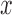(see Box 1) and are therefore collectively called linear pressure (Crow and Kimura 1970). It is this linearity that allows the calculation of the first two moments of the DAF in closed form. One can formulate a general linear evolutionary pressure model, where pure drift, mutation and migration are special cases (see Box 1).

The migration model from equation (14) is a good approximation if the immigrants represent a random sample of the entire species (Crow and Kimura 1970). This is often not the case, and migrants are typically exchanged by at least two populations that have non-constant allele frequencies. This leads to an evolutionary pressure 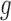that is dependent on the generation, and the DAFs of both populations need to be modeled jointly.

Markov chain theory.—

Mathieson and McVean (2013) inferred effective population sizes and migration rates from time series data (Table 1) while modeling multiple populations distributed on a lattice, where neighboring populations exchange migrants every generation.

Diffusion approximation.—

Gutenkunst et al. (2009) built a diffusion equation to model jointly the allele frequencies in multiple populations. They solved this equation using the finite-difference scheme to infer divergence time between populations, mutation, and migration rates. From the joint DAF, Gutenkunst et al. (2009) calculated the expected multi-population allele frequency spectrum (AFS), which summarizes allele frequency data. Because the dimension of the AFS depends on the number of populations, the time needed to compute the AFS grows exponentially with the number of populations. This limited their analysis to only three populations. Lukić and Hey (2012) also calculated the expected AFS, but they extended the spectral decomposition method to calculate the joint DAF of multiple populations that exchange migrants, while accounting for de novo mutations. The implementation of Lukić and Hey (2012) was optimized to use little memory, and can therefore tackle more than three populations. However, compared with Gutenkunst et al. (2009), it has a lower computational speed on two and three populations.

Moment-based approximations.—

Pickrell and Pritchard (2012) used the normal distribution to infer divergence times between populations that have been evolving under pure drift and have exchanged migrants. Due to their use of the normal distribution, the method is not accurate for alleles with frequencies close to 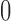or .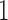

Quality of approximations.—

As both the neutral mutation ((10)) and migration (equation (14)) models are special cases of the general linear evolutionary pressure model (Box 1), the quality of the approximations is similar. The approximation quality shown in Figure 6, where 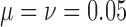, also applies for 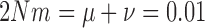and .

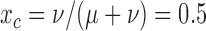Selection

When selection is present, the different genotypes are transmitted to the next generation with different probabilities, determined by their fitness. If the 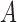allele has frequency 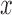and selection is parameterized by coefficient 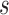and dominance parameter 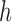, the three possible genotypes have the following frequencies (assuming Hardy–Weinberg equilibrium) and fitness (Crow and Kimura 1970)

Genotype
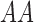
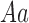
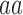
Frequency
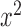
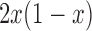
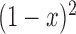
Fitness

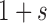
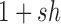
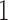
The allele count still follows the process given in equation (14), with the evolutionary pressure function from equation (B.7).

Dynamics and moments.—

The first two moments of the DAF for the general linear evolutionary pressure (equations (B.4) and (B.5)) can be obtained using the law of total expectation and variance, respectively. These take the form

$$\begin{array}{cc}& \text{E}\left[x(r+1)\mid x(0)\right]=\text{E}\left[g(x(r))\mid x(0)\right],\hfill \end{array}$$ (16)

$$\begin{array}{cc}& \text{Var}\left(x(r+1)\mid x(0)\right)\hfill \\ & \hspace{0.17em}=\frac{1}{2N}\text{E}\left[x(r+1)\mid x(0)\right]-\text{E}{\left[x(r+1)\mid x(0)\right]}^2\hfill \\ & \hspace{0.17em}+(1-\frac{1}{2N})\text{E}\left[g(x(r){)}^2\mid x(0)\right].\hfill \end{array}$$ (17)

The evaluation of 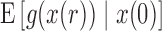and typically requires all moments of 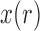. However, these can be written as functions of only the first two moments when 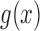is a linear function in 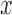, allowing the above recursions to be solved in closed form (Tataru et al. 2015). When the allele is under selection and 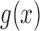is no longer linear, we can approximate 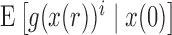by only using the first two moments by relying on a Taylor series. This will yield a recursion for calculating the mean and variance of the DAF. The Taylor series can be evaluated around the deterministic trajectory of 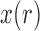(Barton and Otto 2005; Terhorst et al. 2015), or around the pre-calculated mean of 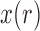(Lacerda and Seoighe 2014).

To obtain the Taylor series about the deterministic trajectory, we decompose 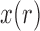as 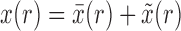, where 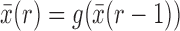represents the deterministic trajectory followed by the allele frequency in the infinite-population limit, and 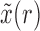is the random disturbance away from 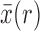. Then,

$$\begin{array}{cc}\text{E}\left[x(r)\mid x(0)\right]\hfill & \hspace{0.17em}=\overline{x}(r)+\text{E}\left[\tilde{x}(r)\mid x(0)\right],\hfill \end{array}$$ (18)

$$\begin{array}{cc}\text{Var}\left(x(r)\mid x(0)\right)\hfill & \hspace{0.17em}=\text{Var}\left(\tilde{x}(r)\mid x(0)\right).\hfill \end{array}$$ (19)

From equations (16) and (18) we obtain, using the Taylor series for 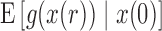about ,

$$\begin{array}{cc}\text{E}\left[\tilde{x}(r+1)\mid x(0)\right]\hfill & \hspace{0.17em}\approx \text{E}\left[\tilde{x}(r)\mid x(0)\right]\cdot \frac{\mathrm{d}g}{\mathrm{d}x}{\mid }_{\overline{x}(r)}\hfill \\ & \hspace{0.17em}+\frac{1}{2}\text{E}\left[\tilde{x}(r{)}^2\mid x(0)\right]\cdot \frac{{\mathrm{d}}^{2}g}{{\mathrm{d}}^{2}x}{\mid }_{\overline{x}(r)}.\hfill \end{array}$$

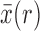Similarly, from the Taylor series of 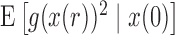about 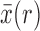, and using equations (17), (18), and (19) we obtain the recursion for ,

$$\begin{array}{cc}& \text{E}\left[\tilde{x}(r+1{)}^2\mid x(0)\right]\hfill \\ & \hspace{0.17em}\approx \frac{1}{2N}\overline{x}(r+1)(1-\overline{x}(r+1))\hfill \\ & \hspace{0.17em}+\frac{1}{2N}(1-2\overline{x}(r+1))\text{E}\left[\tilde{x}(r+1)\mid x(0)\right]\hfill \\ & \hspace{0.17em}+(1-\frac{1}{2N})\text{E}\left[\tilde{x}(r{)}^2\mid x(0)\right]{\left(\frac{\mathrm{d}g}{\mathrm{d}x}{\mid }_{\overline{x}(r)}\right)}^2.\hfill \end{array}$$

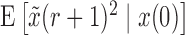By iterating the recursions above and calculating numerically the first two moments of 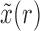, we can recover the mean and variance of the DAF after 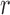generations.

Markov chain theory.—

Mathieson and McVean (2013) and Gompert (2015) inferred selection from time series data by discretizing continuous allele frequencies and building a Markov chain with normal and beta transition probabilities, respectively (Table 1). Gompert (2015) additionally allowed for variability in time of selection coefficients and population sizes.

Diffusion approximation.—

For a Wright–Fisher model with drift, mutation and selection, specified by equations (B.1), (B.2), (B.3), and (B.8), and letting 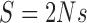, we obtain the following infinitesimal mean

$$\begin{array}{cc}a(x)\hfill & \hspace{0.17em}=-\nu x+\mu (1-x)+Sx(1-x)(h+(1-2h)x).\hfill \end{array}$$

The diffusion equation when selection is present is the most difficult to solve. However, the stationary distribution is known in closed form (Wright 1937; Crow and Kimura 1970; Ewens 2004) and is, up to a normalization constant, given by a tilted beta distribution

$$f(x)\propto x^{2\nu -1}(1-x{)}^{2\mu -1}{e}^{Sx(2h+(1-2h)x)}.$$ (20)

We note here that the diffusion limit to the Wright–Fisher model requires that the parameters involved in the evolutionary pressure, 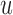, , 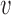, , 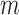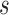and 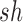, are all in the order of 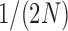, such that the resulting scaled parameters, 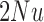, , 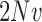, , 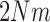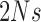and 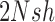, are in the order of 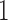. This is the source of the approximation of equation (B.6) with equation (B.7), and of the common practice of simplifying expressions by removing “small” terms (Feller et al. 1951; Wakeley 2005). It also indicates that in the diffusion limit, the population size 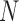acts as a scaling factor, and a rescaling of the parameters and time by a constant factor will not affect the DAF. This result is responsible for the notion that it is impossible to estimate, for example, the mutation rate and effective population size separately. However, although it may be true that there is low power in doing so, this is simply a consequence of the assumptions of the diffusion approximation. These might be expected to break down in cases in which the diffusion is not appropriate (Wakeley 2005). In this respect, the moment-based approximations are free of the small parameters assumption, especially because the mean and variance of the general linear evolutionary pressure can be calculated without making the approximation of large (Tataru et al. 2015). Therefore, moment-based approximations might be more appropriate when the evolutionary pressure is strong (Lacerda and Seoighe 2014).

Using the spectral decomposition of the diffusion equation, Kimura (1955b; 1957) found the DAF when selection is present. This approach was extended by Song and Steinrücken (2012) to improve the convergence properties for stronger selection, whereas Steinrücken et al. (2016) developed it further to model selection coefficients that vary over time in a piecewise constant manner. The DAF was also calculated using a finite-difference scheme (Bollback et al. 2008), finite-volume scheme (Zhao et al. 2013), a path integral formalism (Schraiber 2014) and other numerical approaches (Malaspinas et al. 2012; Ferrer-Admetlla et al. 2016).

Bollback et al. (2008); Steinrücken et al. (2014); Malaspinas et al. (2012) estimated jointly selection coefficients and effective population sizes from time series data from one population. Ferrer-Admetlla et al. (2016) could additionally infer mutation rates. Živković et al. (2015) used the spectral decomposition of Steinrücken (2012) to infer mutation, selection and variable population size from present data from one population. Vitalis et al. (2014) used the stationary distribution of the DAF when multiple populations exchange migrants and experience selection. As they used the stationary DAF, they could not recover any information about the divergence of the populations. We would like to note here that although the method of Gutenkunst et al. (2009) can in principle incorporate selection, the inference software does not estimate selection coefficients.

Moment-based approximations.—

Using the numerically approximated moments of the DAF, the truncated normal and beta distributions are obtained as previously. The beta with spikes approximation has not been extended to include selection. However, the approximation developed by Tataru et al. (2015) for the loss and fixation probabilities should still be reasonable if the selection pressure is small and the loss and fixation probabilities are mainly dominated by genetic drift.

Moment-based approximations have had limited use for inference of selection due to the difficulties in calculating the first two moments of the DAF. Both Lacerda and Seoighe (2014) and Terhorst et al. (2015) estimated effective population sizes and selection coefficients from time series data, using the normal distribution and the Taylor expansion approach. One critical difference between the two is that Lacerda and Seoighe (2014) assumed additive selection (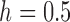) and used a Taylor series about the mean of 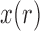, whereas Terhorst et al. (2015) made no assumptions about dominance and used a Taylor series about the deterministic trajectory. Additionally, Terhorst et al. (2015) were the first to incorporate linkage, but in practice their model is limited to jointly analyze only a small number of loci (typically 3).

Quality of approximations.—

Relative to pure drift, positive selection acts by increasing the expected frequency and probability of fixation of the allele, and decreasing the probability of loss (Figs. 4 and 7). For example, under pure drift and with a beginning frequency of 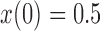, the probability that the mutation is lost (fixed) at 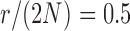is 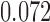(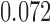), while when selection is present with 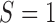, the probability is reduced (increased) to 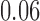(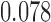). Overall, for 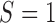, all approximations have a fit to the true DAF (Fig. 7) that is very similar to that for pure drift (Fig. 4). We note here that 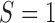is a very small selection coefficient. For larger values of 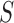, the Taylor series approach leads to estimated values for the mean 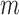and variance 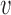for which 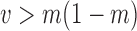, and these cannot be fitted by a beta distribution.

Figure 7.

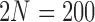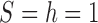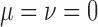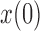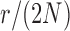Fit of various approximations to the true DAF with selection, calculated using the Markov chain property for , , and a range of and . Each column shows a different type of approximation, indicated at the top of the figure. a) Hellinger distance on log scale between the approximated and true DAF. The three “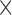”s in each of the heatmaps indicate the combinations of 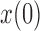and 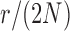used in b). b) True (dashed lines) and approximated (solid lines) DAF for and different values of 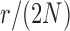. Calculations are performed as for Figure 4. For comparison purposes, the a) heatmap and b) -axis scales are the same as in Figure 4.

MULTI-ALLELIC WRIGHT–FISHER MODEL

The bi-allelic Wright–Fisher model is typically a very good approximation for SNP data (because the per-nucleotide mutation rate is typically small), but due to highly mutable sites, ancestral polymorphism, very large sample size or large evolutionary distance, a number of SNPs may contain 3 or 4 alleles. Furthermore, highly variable loci (e.g., short tandem repeats) are still widely used, especially in forensics (Balding and Nichols 1997; Balding and Steele 2015), and are typically multi-allelic. In these cases, the data can be analyzed using the multi-allelic Wright–Fisher model, an extension of the bi-allelic model. Instead of following the frequency of one allele, which is sampled from a binomial distribution from one generation to the next, the multi-allelic model describes the joint distribution of the 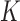alleles present in the population, which are now sampled from one generation to the next from a multinomial distribution.

Pure Drift

Similar to the bi-allelic model, the simplest form is the pure random genetic drift model, where the stochastic fluctuations in the allele frequencies are purely determined by the random mating of the finite population (Fig. 8).

Figure 8.

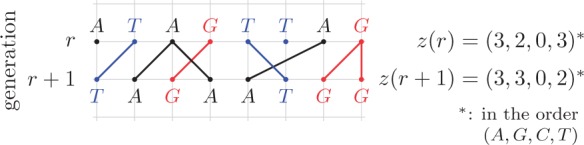
Dynamics in the pure drift multi-allelic Wright–Fisher model for . The child inherits the parental allele.

Dynamics and moments.—

Let 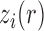be the number of 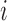alleles in generation 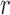, 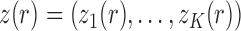and 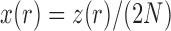be the corresponding allele frequency. The distribution of 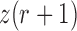is

$$\begin{array}{c}z(r+1)|z(r)\sim \mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}(2N,x(r)).\hfill \end{array}$$ (21)

Here, 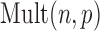is the multinomial distribution with sample size 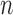and probability vector .

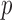To determine the mean and covariance of the DAF, we move from discrete generations to continuous time where one time unit corresponds to 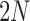generations, and set 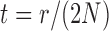. Then,

$$\begin{array}{cc}& \text{E}\left[x(t)\mid x(0)\right]=x(0),\hfill \end{array}$$ (22)

$$\begin{array}{c}\begin{array}{cc}& \text{Var}\left(x(t)\mid x(0)\right)\hfill \\ & \hspace{0.17em}=(1-e^{-t})(\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\{x(0)\}-x(0{)}^{\mathrm{\prime }}x(0)),\hfill \end{array}\hfill \end{array}$$ (23)

where 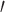denotes vector transpose. These formulas are natural extensions of equations (2) and (4).

Diffusion approximation.—

Diffusion theory can be extended from the bi-allelic to the multi-allelic case. We will not cover this here, but refer to Ewens (2004; section 4.8, p. 151) for a general discussion of multi-dimensional diffusion processes, and Ewens (2004; section 5.10, p. 192) for the 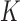-allele pure drift Wright–Fisher model. In particular, Ewens (2004) mentions that a generalization of equation (7) can be formulated and that a generalization of Kimura’s solution in terms of orthogonal polynomials exists.

Moment-based approximations.—

The beta distribution is a natural choice for approximating the DAF for the bi-allelic Wright–Fisher model, and it provides a good approximation when the allele is not close to being lost or fixed (Figs. 4, 6, and 7). It is therefore natural to approximate the DAF for the multi-allelic Wright–Fisher using the generalization of the beta distribution, the Dirichlet distribution (Balding and Nichols 1995; 1997). Just like for the bi-allelic case, where the beta distribution arises as the stationary DAF under linear evolutionary pressure, the Dirichlet distribution is the stationary DAF for a specific mutation model (Ewens 2004) (see below).

Under the Dirichlet model, also called the Balding–Nichols model (Balding and Steele 2015), the allele frequency vector 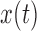follows a Dirichlet distribution

$$\begin{array}{cc}x(t)\mid x(0)\hfill & \hspace{0.17em}\sim \mathrm{D}\mathrm{i}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{h}\mathrm{l}\mathrm{e}\mathrm{t}(\alpha ),\hfill \end{array}$$

where 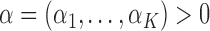. This implies that allele 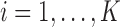has marginal distribution

$$\begin{array}{cccc}{x}_i(t)\hfill & \hspace{0.17em}\sim \mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}({\alpha }_i,{\alpha }_0-{\alpha }_i),\hfill & \text{with\hspace{0.5em}}{\alpha }_0\hfill & \hspace{0.17em}=\sum _{i=1}^K{\alpha }_i.\hfill \end{array}$$

Under the Dirichlet distribution, the mean and covariance of the DAF are

$$\begin{array}{cc}& \text{E}\left[x(t)\mid x(0)\right]=\frac{\alpha }{{\alpha }_0},\hfill \end{array}$$ (24)

$$\begin{array}{c}\begin{array}{cc}& \text{Var}\left(x(t)\mid x(0)\right)\hfill \\ & \hspace{0.17em}=\frac{1}{{\alpha }_0+1}(\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{\frac{\alpha }{{\alpha }_0}\right\}-{\left(\frac{\alpha }{{\alpha }_0}\right)}^{\mathrm{\prime }}\frac{\alpha }{{\alpha }_0}).\hfill \end{array}\hfill \end{array}$$ (25)

The mean and covariance of the DAF (equations (22) and (23)) are equivalent to those under the Dirichlet distribution (equations (24) and (25)) when

$$\begin{array}{cccccc}x(0)\hfill & \hspace{0.17em}=\frac{\alpha }{{\alpha }_0},\hfill & \text{and}\hfill & & 1-e^{-t}\hfill & \hspace{0.17em}=\frac{1}{{\alpha }_0+1}.\hfill \end{array}$$

Therefore, the Dirichlet distribution can accurately capture the true mean and covariance of the multi-allelic pure drift Wright–Fisher model.

Neutral Mutations

Just as is the case for the bi-allelic model (Fig. 3), when the alleles evolve under pure drift, eventually the process will reach a monomorphic state, where only one of the alleles will be present in the population. The variation can be maintained in the population by allowing mutations (Fig. 9).

Figure 9.

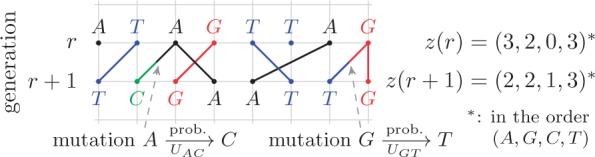
Dynamics in the multi-allelic Wright–Fisher model with mutations for . If the parental allele is , the child receives the same allele with probability 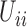and another allele 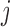with probability 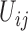, for .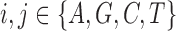

Dynamics and moments.—

If 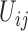is the probability of an 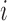allele to mutate to a 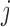allele, the multinomial distribution of 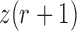becomes

$$z(r+1)\mid z(r)\sim \mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}(2N,x(r)U),$$

where the mutation probabilities are stored in a 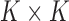matrix 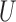. By specifying the structure of 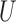, different evolutionary mutation models can be formulated, such as the Jukes–Cantor (JC) model, parent independent mutation model, infinite alleles model, Kimura model, and single-step mutation model (Felsenstein 2004).

The mean and covariance of the DAF in continuous time (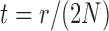) are obtained using the rate matrix 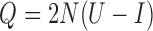, where 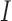is the identity matrix, from the diffusion approximation (Hobolth and Sirén 2016),

$$\begin{array}{cc}& \text{E}\left[x(t)\mid x(0)\right]=x(0)e^{Qt},\hfill \end{array}$$ (26)

$$\begin{array}{c}\begin{array}{cc}& \text{Var}\left(x(t)\mid x(0)\right)\hfill \\ & \hspace{0.17em}={\int }_0^t{e}^{-s}{\left(e^{Qs}\right)}^{\mathrm{\prime }}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\{x(0)e^{Q(t-s)}\}\left(e^{Qs}\right)ds\hfill \\ & \hspace{0.17em}-{\left(e^{Qt}\right)}^{\mathrm{\prime }}x(0{)}^{\mathrm{\prime }}x(0)e^{Qt}(1-e^{-t}).\hfill \end{array}\hfill \end{array}$$ (27)

These general formulas make it possible to numerically calculate the mean and covariance for any mutation model. In practice, the mean can be calculated using one of the many available numerical procedures for matrix exponentials (Moler and Van Loan 2003). Calculating the covariance, which involves integrals of matrix exponentials, is more tedious, but this can be done numerically using the eigenvalue decomposition of the rate matrix (Hobolth and Sirén 2016).

The JC is the most simple mutation model, where all mutation probabilities are equal, 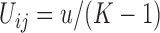, for all 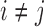. The entries in the rate matrix for the JC model are given by

$$\begin{array}{cc}{Q}_{ij}\hfill & \hspace{0.17em}=2N(U_{ij}-I_{ij})=\{\begin{array}{cc}{\displaystyle \frac{q}{K-1}}\hfill & \text{if\hspace{0.5em}}i\ne j\hfill \\ -q\hfill & \text{if\hspace{0.5em}}i=j\hfill \end{array}\hspace{0.17em}\hfill \end{array}$$

where 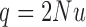. The rate matrix can be written in matrix form as

$$Q=\frac{q}{K-1}(E-IK),$$

where 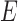is the 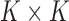matrix with 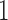in every entry. We can now obtain a closed-form solution for the matrix exponential 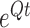, namely

$$\begin{array}{cc}{e}^{Qt}\hfill & \hspace{0.17em}=e^{-ϵ\frac{t}{2}}(I-\frac{E}{K})+\frac{E}{K},\hfill \end{array}$$

where 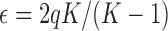. The mean and covariance in the JC model are found from equations (26) and (27) and given by

$$\begin{array}{cc}& \text{E}\left[x(t)\mid x(0)\right]=e^{-ϵ\frac{t}{2}}(x(0)-\frac{\mathbf{e}}{K})+\frac{\mathbf{e}}{K},\hfill \end{array}$$ (28)

$$\begin{array}{c}\begin{array}{cc}& \text{Var}\left(x(t)\mid x(0)\right)\hfill \\ & \hspace{0.17em}=\frac{1}{K}(I-\frac{E}{K})\frac{1}{1+ϵ}(1-e^{-(1+ϵ)t})\hfill \\ & \hspace{0.17em}-{(x(0)-\frac{\mathbf{e}}{K})}^{\mathrm{\prime }}(x(0)-\frac{\mathbf{e}}{K})e^{-ϵt}(1-e^{-t})\hfill \\ & \hspace{0.17em}+(\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\{x(0)-\frac{\mathbf{e}}{K}\}-{(x(0)-\frac{\mathbf{e}}{K})}^{\mathrm{\prime }}\frac{\mathbf{e}}{K}\hfill \\ & \hspace{0.17em}-\frac{{\mathbf{e}}^{\mathrm{\prime }}}{K}(x(0)-\frac{\mathbf{e}}{K}))\hfill \\ & \hspace{0.17em}\times e^{-ϵ\frac{t}{2}}\frac{1}{1+\frac{ϵ}{2}}(1-e^{-(1+\frac{ϵ}{2})t}),\hfill \end{array}\hfill \end{array}$$ (29)

where 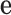is the 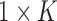vector with 1 in every entry.

For 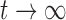, these reduce to

$$\begin{array}{cc}\hfill \text{E}\left[x(t)\mid x(0)\right]& \hspace{0.17em}=\frac{\mathbf{e}}{K},\hfill \\ \text{Var}\left(x(t)\mid x(0)\right)\hfill & \hspace{0.17em}=\frac{1}{K}(I-\frac{E}{K})\frac{1}{1+ϵ}.\hfill \end{array}$$

We note that these moments are the same as for a Dirichlet distribution with 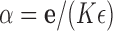, and indeed the Dirichlet distribution is the stationary DAF of the multi-allelic JC Wright–Fisher model (Ewens 2004).

Moment-based approximations.—

The mean and covariance of the Dirichlet distribution (equations (24) and (25)) are equivalent to those under the JC model if the covariance approximately fulfills the proportionality condition

$$\begin{array}{c}\begin{array}{cc}& \text{Var}\left(x(t)\mid x(0)\right)\hfill \\ & \hspace{0.17em}\propto \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\{\mathrm{E}[x(t)]\}-\mathrm{E}[x(t){]}^{\mathrm{\prime }}\mathrm{E}[x(t)]\hfill \\ & \hspace{0.17em}=\frac{1}{K}(I-\frac{E}{K})-{(x(0)-\frac{\mathbf{e}}{K})}^{\mathrm{\prime }}(x(0)-\frac{\mathbf{e}}{K})e^{-ϵt}\hfill \\ & \hspace{0.17em}+(\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\{x(0)-\frac{\mathbf{e}}{K}\}-{(x(0)-\frac{\mathbf{e}}{K})}^{\mathrm{\prime }}\frac{\mathbf{e}}{K}\hfill \\ & \hspace{0.17em}-\frac{{\mathbf{e}}^{\mathrm{\prime }}}{K}(x(0)-\frac{\mathbf{e}}{K}))e^{-ϵ\frac{t}{2}},\hfill \end{array}\hfill \end{array}$$ (30)

where we used the expression for the mean in equation (28). By comparing equations (29) and (30), we observe that the expressions are approximately proportional with proportionality constant 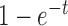when 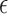is small, which corresponds to the pure drift case. Regardless of the parameter , the expressions are also approximately proportional, with proportionality constant 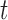, when the evolutionary distance 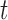is small. Finally, for large 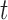, the proportionality constant is 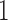, because the Dirichlet distribution is the stationary distribution for the JC model. These analytical considerations are confirmed by Figure 10. The Dirichlet distribution cannot accurately capture the mean and covariance of the JC model for intermediate values of 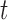, and the deviation is very clear for large values of 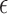(Fig. 10b). Therefore, care should be taken when using the Dirichlet distribution in practice. Because the JC is the most simple mutation model, with just one parameter, one could expect that the fit of the Dirichlet distribution could be even more problematic for more complex mutation models. An important step in developing more appropriate distributions for the DAF under the multi-allelic Wright–Fisher model is made by Sirén et al. (2013) and Hobolth and Sirén (2016), but in general more research is needed in this direction.

Figure 10.

Fit of the Dirichlet distribution (dotted lines) to the true mean and covariance of the multi-allelic JC Wright–Fisher model (solid lines) with a) 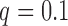( 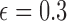small), and b) 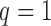( 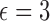large). All six plots are calculated for 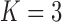, , 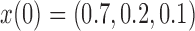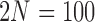and different values of .

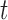CONCLUSION AND PERSPECTIVES

We have provided a broad overview of methods to calculate the DAF under the Wright–Fisher model. These methods have a number of working assumptions in common. Here, we discuss in turn each of these and how current methods tackle these issues or potentially could be improved to do so.

Virtually all methods presented here rely on unlinked loci, with an exception worth mentioning using a moment-based approach (Terhorst et al. 2015). Several inference methods built on the coalescent process analyze pairs of linked neutral loci (Li and Durbin 2011; Paul et al. 2011; Sheehan et al. 2013; Schiffels and Durbin 2014; Rasmussen et al. 2014). Some theoretical results do exist for linked bi-allelic selected loci in the limit of a large population size (Lessard and Kermany 2012), but these have limited use for inference methods. To our knowledge, equivalent results for the joint DAF of two loci are not available, but see Jenkins et al. (2014) for an approximation for loosely linked loci. These results could be used as the basis for including recombination in inference methods, but so far these types of approximations have not really permeated the field of inference under the Wright–Fisher model.

The methods we have presented here also implicitly assume very simplified demographic scenarios. In some instances, especially if the data contain individuals sampled from populations with complex demography, it might be easier, although more computationally intensive, to rely on simulations under the Wright–Fisher model to perform inference (Excoffier et al. 2013). In particular, much progress has been made in using Approximate Bayesian Computation (ABC) that relies on a series of summary statistics from simulations and either rejection sampling or more sophisticated methods to obtain approximated posterior distributions for the parameters of interest (Beaumont et al. 2002; Blum 2010; Marin et al. 2012). This is becoming very much a field of its own with active method development in the choice of relevant summary statistics, quasi-sufficiency (Joyce and Marjoram 2008), and various algorithms to obtain computationally efficient approximations of the likelihood (Excoffier et al. 2013). Simulation-based methods can be a source of inspiration for developing methods seeking to specify the DAF under a wider range of scenarios and less restrictive assumptions. Such an example is the inference of selection from time series data from experimental evolution, where the population size undergoes periodic bottlenecks, followed by population expansion. This is typical of most experimental setups, where the population size is experimentally controlled (Foll et al. 2014).

Ultimately, the directions of future method development are likely to be conditioned by the type of data modeled and the evolutionary or demographic questions of interest that motivate the need for inference. As genome-wide re-sequencing becomes increasingly common and replaces most SNP genotyping and exome sequencing, we can expect that the data will increasingly consist of polymorphism counts among tightly linked sites.

One direction worth exploring is using the Wright–Fisher model to learn about how selection varies along the genome, and thereby shapes genome-wide diversity. Some progress has been made in inferring mutation rates and selection coefficients by expressing expected local levels of nucleotide diversity as a function of the amount of selection affecting neutral sites due to linkage (Elyashiv et al. 2014).

Finally, at present, most software programs that implement inference methods have been developed for bi-allelic data, whereas inference for multi-allelic data is clearly lagging behind. We have discussed recent attempts to understand and formulate approximations for the DAF under the multi-allelic Wright–Fisher model with mutation. These developments are expected to improve modeling of short tandem repeat data that are still widely used in forensics (Balding and Steele 2015). They might also allow the analysis of a broader range of biological situations where the bi-allelic assumption is not always appropriate, for example, when there is extensive heterogeneity in the mutation rate or the product of effective population size and mutation rate is high, as is the case for microbial and viral genomes.

FUNDING

This work has been supported, in part, by the European Research Council under the European Unions Seventh Framework Program (FP7/20072013, ERC grant number 311341) and the Danish Research Council (grant number DFF4002-00382).