Spillover effects in epidemiology: parameters, study designs and methodological considerations

Abstract

Many public health interventions provide benefits that extend beyond their direct recipients and impact people in close physical or social proximity who did not directly receive the intervention themselves. A classic example of this phenomenon is the herd protection provided by many vaccines. If these ‘spillover effects’ (i.e. ‘herd effects’) are present in the same direction as the effects on the intended recipients, studies that only estimate direct effects on recipients will likely underestimate the full public health benefits of the intervention. Causal inference assumptions for spillover parameters have been articulated in the vaccine literature, but many studies measuring spillovers of other types of public health interventions have not drawn upon that literature. In conjunction with a systematic review we conducted of spillovers of public health interventions delivered in low- and middle-income countries, we classified the most widely used spillover parameters reported in the empirical literature into a standard notation. General classes of spillover parameters include: cluster-level spillovers; spillovers conditional on treatment or outcome density, distance or the number of treated social network links; and vaccine efficacy parameters related to spillovers. We draw on high quality empirical examples to illustrate each of these parameters. We describe study designs to estimate spillovers and assumptions required to make causal inferences about spillovers. We aim to advance and encourage methods for spillover estimation and reporting by standardizing spillover parameter nomenclature and articulating the causal inference assumptions required to estimate spillovers.

Introduction

Public health interventions may benefit those in close physical or social proximity to intervention recipients who do not receive the intervention themselves. When such ‘spillovers’ are present in the same direction as direct effects on recipients, direct effects alone do not capture the full health impact and cost-effectiveness of an intervention. Most epidemiological studies measuring spillover effects have evaluated herd effects of vaccines,^1,2 but spillovers are theoretically possible for numerous other interventions that could alter disease transmission or change health behaviours. Spillovers have increasingly been measured for other interventions, particularly in economics, since evidence of spillovers can support the case for scaling up or subsidizing an intervention.^3,4 However, to date, discussion of methods for estimating spillover effects and identifying them within a causal inference framework has largely remained confined to the vaccine literature,^5–14 with few articles extending methods to studies of other interventions.^15–18

Here we define spillover parameters using standardized notation and discuss causal inference assumptions for spillovers using non-technical language to provide an accessible introduction for epidemiologists. In conjunction with a systematic review we conducted on health spillovers of interventions in low- and middle-income countries,¹⁹ we classified types of spillovers to make their similarities and differences more transparent. By standardizing spillover parameter definitions and articulating causal inference assumptions for spillovers, we aim to advance methods for spillover study design, estimation and reporting.

Types of spillover parameters

We describe six classes of spillover parameters that were most common in our systematic review.¹⁹ We present individual-level counterfactual definitions of spillover effects in Box 1; the Supplement (available as Supplementary data at IJE online) contains average spillover effects as well as identification assumptions for each parameter. For simplicity we discuss spillovers among untreated individuals; however, spillover effects may also occur among the treated (Box 1). For example, HIV vaccine candidates provide imperfect protection to vaccinated individuals, but protection has been shown to increase as immunization coverage increases, due to reductions in transmission resulting from herd effects.²⁰ We define spillover parameters in the context of ‘intention-to-treat’ analyses, which estimate the true causal effect of interventions with high adherence. Inferences about spillovers are more complicated when there is imperfect adherence (e.g. in ‘per-protocol’ analyses),¹⁶ and a formal discussion of that setting is beyond the scope of this paper.

Box 1. Spillover parameter definitions

Here, we provide definitions of individual-level average spillover effects using counterfactual notation. The Supplement (available at IJE online) includes additional details and identification assumptions. Figures cited below provide visual representations of each parameter.

We present the first three types of parameters in a two-stage randomized trial in which the treatment regimen is defined such that at least one individual in a treated cluster receives treatment (α₁), and in control clusters, all individuals are allocated to control (α₀). Let Y_ij(a) be the potential outcome for individual j in cluster i, where a_i denotes a vector of treatment assignments for individuals in cluster i. The individual potential outcome averaging over different configurations of a_i is ${\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}$(α, a) and is a function of the treatment regimen (α) and the individual’s treatment assignment (a).

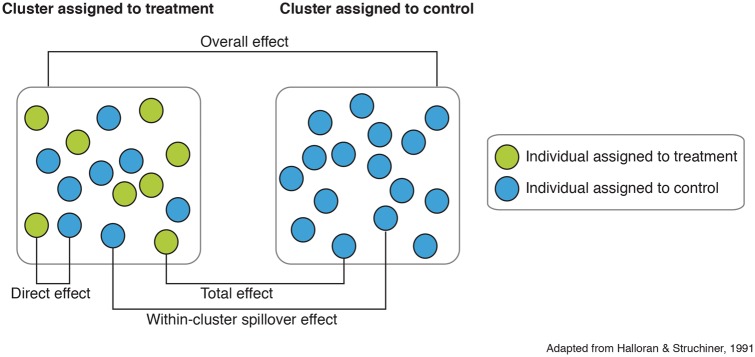
Cluster-level spillover effects (Figure 1)

Cluster-level spillover effect: ${\text{SE}}_{\mathit{\text{ij}}}\left({\text{α}}_1,{\text{α}}_0\right)\equiv {\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}\left({\text{α}}_1,0\right)-{\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}({\text{α}}_0,0)$

This parameter compares the mean potential outcome of an individual assigned to control in a treatment cluster with treatment regimen α₁ with their mean potential outcome if they were assigned to control in a cluster assigned to control (α₀).

Direct effect: ${\text{DE}}_{\mathit{\text{ij}}}\left({\text{α}}_1\right)\equiv {\overline{\text{Y}}}_{\mathit{\text{ij}}}\left({\text{α}}_1,1\right)-{\overline{\text{Y}}}_{\mathit{\text{ij}}}({\text{α}}_1,0)$

This parameter compares the mean potential outcome of an individual assigned to treatment in a treatment cluster with treatment regimen α₁ with their mean potential outcome if they were assigned to control in a cluster with treatment α₁.

Total effect: ${\text{TE}}_{\mathit{\text{ij}}}\left({\text{α}}_1,{\text{α}}_0\right)\equiv {\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}\left({\text{α}}_1,1\right)-{\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}({\text{α}}_0,0)$

This parameter compares the mean potential outcome of an individual assigned to treatment in a treatment cluster with treatment regimen α₁ their mean potential outcome if they were assigned to control in a cluster assigned to control (α₀).

Overall effect: ${\text{OE}}_{\mathit{\text{ij}}}\left({\text{α}}_1,{\text{α}}_0\right)\equiv {\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}\left({\text{α}}_1\right)-{\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}({\text{α}}_0)$

This parameter compares the mean potential outcome across individuals in a cluster with treatment regimen α₁ with their mean potential outcome had the cluster been assigned to control (α₀).

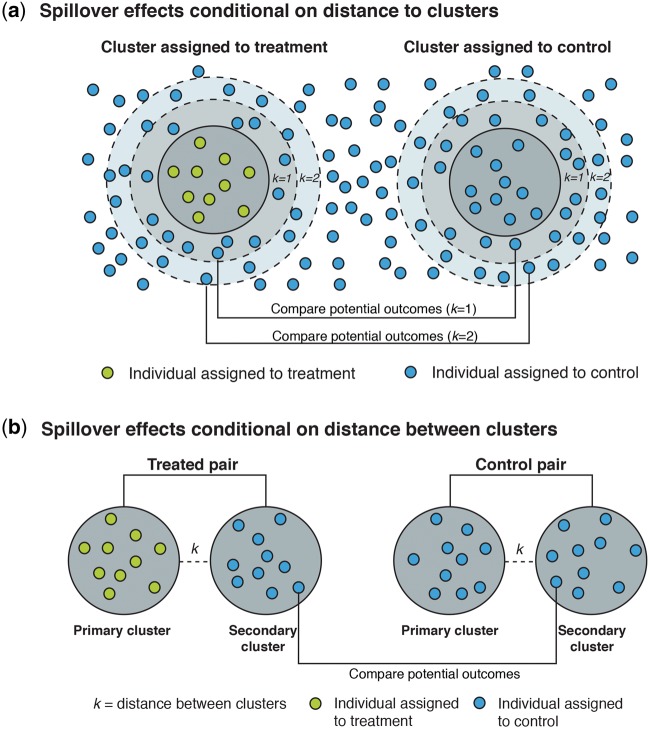
Distance-based spillover effects (Figure 2)

Spillover effect conditional on distance to clusters (Figure 2a): ${\text{SE}}_{\mathit{\text{ij}}}\left({\text{α}}_1,{\text{α}}_0,\mathit{\text{k}}\right)\equiv {\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}\left({\text{α}}_1|{\mathit{\text{K}}}_{\mathit{\text{i}}}=\mathit{\text{ k}}\right)-{\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}({\text{α}}_0|{\mathit{\text{K}}}_{\mathit{\text{i}}}=\mathit{\text{ k}})$

This parameter compares the mean potential outcome for individuals at distance k from a cluster with treatment regimen α₁ with the mean potential outcome at distance k from a cluster with treatment regimen α₀ (all individuals assigned to control).

Spillover effect conditional on distance between clusters (Figure 2b): ${\text{SE}}_{\mathit{\text{ij}}}\left({\text{α}}_1,{\text{α}}_0,{\text{β}}_0,\mathit{\text{k}}\right)\equiv {\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}\left({\text{α}}_1,{\text{β}}_0|{\mathit{\text{K}}}_{\mathit{\text{i}}}=\mathit{\text{ k}}\right)-{\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}({\text{α}}_0,{\text{β}}_0|{\mathit{\text{K}}}_{\mathit{\text{i}}}=\mathit{\text{ k}})$

This parameter compares the mean potential outcome of individuals in control clusters with treatment regimen β₀ within distance k of treatment clusters with treatment regimen α₁ with those in clusters assigned to control with treatment regimen β₀ within distance k of control clusters with treatment regimen α₀.

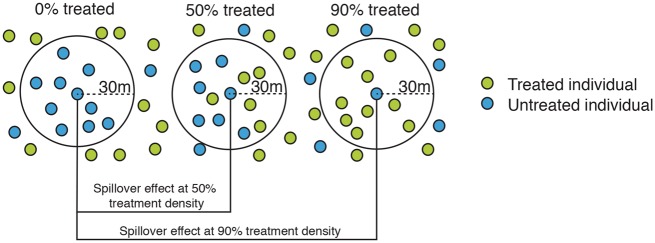
Spillover effect conditional on treatment density (Figure 3)

Define p_i as the proportion of individuals allocated to treatment in treatment clusters. In a two-stage randomized trial, in the first stage, clusters are randomly assigned to receive a certain proportion of treatment (E[a_i] = p_i), including clusters with p_i = 0. In the second stage, individuals are randomized to treatment (p_i > 0) or control (p_i = 0) in clusters.

$$\text{SE}({\mathit{\text{p}}}_{\mathit{\text{i}}},{\mathit{\text{p}}}_{\mathit{\text{i}}}^{\text{prime}})\equiv {\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}\left({\mathit{\text{p}}}_{\mathit{\text{i}}},0\right)-{\overline{\mathit{\text{Y}}}}_{\mathit{\text{ij}}}\left({\mathit{\text{p}}}_{\mathit{\text{i}}}^{\text{prime}},0\right)$$

This parameter compares the mean potential outcome of an individual assigned to control in clusters with different proportions of individuals assigned to treatment (p_i vs. p_i′, where p_i ≠ p_i′).

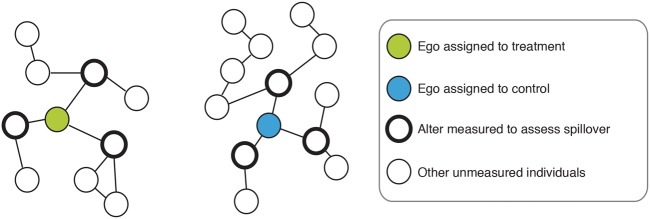
Social network spillover effect (Figure 4)

This parameter can be estimated as a trial that randomizes treatment to egos (the initially enrolled subjects) and compares the mean outcomes of alters (the persons socially connected to the egos) in the treatment vs control group. For this parameter, we define the potential outcome for alter j as Y_j(a₁, a₀), which is a function the treatment assignment of the ego (a₁) and the treatment assignment of the alter (a₀).

$$\text{SE}\equiv \text{E}\left[{\mathit{\text{Y}}}_{\mathit{\text{j}}}\left(1,0\right)-{\mathit{\text{Y}}}_{\mathit{\text{j}}}\left(0,0\right)\right]$$

This parameter compares the mean potential outcome among an untreated alter socially connected to a treated ego (Y_j (a₁ = 1, a₀ = 0)) with their mean potential outcome if they were connected to an untreated ego (Y_j (a₁ = 0, a₀ = 0)).

Vaccine efficacy for infectiousness (Figure 5)

This parameter is typically estimated in studies that enrol households with an infected individual (a ‘case’) and at least one uninfected individual (a ‘susceptible’). S is the outcome for the primary household case; Y is the outcome for the susceptible individual; and A is the treatment assignment for the case.

$${\text{VE}}_{\text{I}}=\text{ E}\left[\mathit{\text{Y|A }}=1,\mathit{\text{S }}=1\right]-\text{E}[\mathit{\text{Y}}|\mathit{\text{A }}=0,\mathit{\text{S }}=1]$$

The parameter compares the secondary attack rate among uninfected susceptible individuals in households with a vaccinated case with the rate among those in households with unvaccinated cases. Identification of this parameter requires assumptions that complicate the presentation of causal parameters, so we define a statistical parameter here and provide a causal parameter definition in the Supplement. The parameter is labelled ‘VE’ to be consistent with how it is presented in the vaccine literature.

To make causal inferences, investigators typically invoke the Stable Unit Treatment Value Assumption (SUTVA),²² which states that an individual’s potential outcome is not affected by the treatment assignment of other individuals in the population. This is also known as the assumption of no interference.²³ SUTVA does not hold when spillovers are present because an individual’s potential outcome depends on their own treatment assignment and the treatment assignment of other individuals connected to them. The most common and theoretically tractable method to make causal inferences about spillover effects is by making the ‘partial interference’ assumption,²⁴ which states that there are no spillovers between clusters of individuals but allows for spillovers among individuals within the same cluster.²⁴ This assumption underpins the validity of many cluster-randomized trials. Studies can minimize spillovers between clusters by including buffer zones between clusters, as is common in cluster-randomized trials.^25–27

Studies that assume no spillovers (i.e. that SUTVA holds) typically index counterfactuals only by an individual’s own treatment assignment (e.g. Y_a could indicate the potential outcome for a person with treatment assignment A = a). Under the partial interference assumption, the treatment assignment of each individual (j) in each cluster (i) can be summarized in a vector of treatments for n individuals: A_i ≡ (A_i1,…, $A_{i{n}_i}$). Similarly, A_i,-j ≡ A_i1,…, A_ij-1, A_ij+1,…, $A_{i{n}_i}$denotes the vector of treatments for individuals in cluster i for all individuals except for individual j.A_i can be considered a random treatment allocation regimen, and $\mathcal{A}\left(n_i\right)$ is the set of all possible treatment allocation regimens for n_i individuals (the set of values that A_i can assume). Specific regimens within $\mathcal{A}\left(n_i\right)$ can be denoted by α, the parameterization of the distribution of A_i for i = 1,…, N. For example, α₁ may include a scenario in which half of all individuals in a cluster are allocated to treatment and half are allocated to control, and α₀ may include a scenario in which all individuals in a cluster are allocated to control. In the following sections, we define individual-level average causal effects; see the Supplement for individual-level and group-level causal effects (available as Supplementary data at IJE online).

Cluster-level spillovers

Causal cluster-level spillover effects can be measured in a two-stage randomized trial⁹ in which treatment is randomized to independent clusters in the first stage, and in the second stage, individuals within treatment clusters are assigned to treatment or control (Figure 1). This is sometimes referred to as a double-randomized trial.¹¹ The cluster-level spillover effect may be defined as the difference in mean outcomes among untreated individuals in treated clusters and the outcomes among individuals in control clusters.^5,6,8,9 We provide the definition of this parameter from Hudgens and Halloran⁸ and Tchetgen Tchetgen.¹⁰ We present this and the parameters in subsequent sections on the additive scale. To be consistent with the causal inference literature,¹⁰ we reverse the order of treatment and control contrasts from those in Hudgens and Halloran,⁸ which subtract potential outcomes for those assigned to treatment from those assigned to control.

Figure 1.

Cluster-level spillover effects. This spillover parameter can be estimated in a two-stage randomized trial in which clusters are randomly allocated to treatment or control and then individuals within treatment clusters are randomly allocated to treatment or control. The direct effect compares potential outcomes of individuals allocated to treatment in treatment clusters to the potential outcomes of individuals allocated to control in treatment clusters. The cluster-level spillover effect compares potential outcomes of individuals allocated to control in treatment clusters to those of individuals in control clusters. The total effect compares the potential outcomes of individuals allocated to treatment in treatment clusters to those of individuals allocated to control in control clusters. The overall effect compares the potential outcomes of all individuals in clusters allocated to treatment to those of all individuals in clusters allocated to control.

Let Y_ij(a_i) be the potential outcome for individual j in cluster i, where a_i denotes a vector of treatment assignments for individuals in cluster i. Let a_i,-j be the vector of treatment for all individuals in cluster i except individual j. The potential outcome in this parameter, Y_ij(a_i,-j, a_ij), is a function of the individual’s own treatment assignment (a_ij) and the treatment assignment of other individuals (a_i,-j) in the cluster. In treatment clusters, the treatment regimen (α₁) is defined such that at least one individual receives treatment, and in control clusters, all individuals are allocated to control (α₀). The treatment vector a_i can vary for a given treatment regimen α. Thus, the individual potential outcome averaging over different configurations of a_i for a given α (i.e. averaging over all possible treatment regimens) is defined as:

$$\begin{array}{c}{\overline{Y}}_{ij}\left(\alpha ,a\right)={\displaystyle \sum }_{\mathit{s}\in \mathcal{A}(n-1)}{Y}_{ij}\left({\mathit{a}}_{i,-j}=\mathit{s},a_{ij}=a\right)\times \\ Pr{\hspace{0.5em}}_{\alpha }({\mathit{A}}_{i,-j}=\mathit{\text{s}}|A_{ij}=\mathit{\text{a}}) \end{array}$$ (1)

We assume that the proportion of individuals assigned to treatment (α₁) is the same among all treated clusters. A cluster-level spillover effect measures spillovers that occur among untreated individuals in a cluster that received treatment. This effect can be defined as:

$$S{E}_{ij}\left({\alpha }_1,{\alpha }_0\right)\equiv {\overline{Y}}_{ij}\left({\alpha }_1,0\right)-{\overline{Y}}_{ij}({\alpha }_0,0)$$ (2)

This parameter compares the mean potential outcome of an individual assigned to control in a treatment cluster with treatment regimen α₁ with their mean potential outcome if they were assigned to control in a cluster assigned to control (α₀). For example, Chong et al. estimated cluster-level spillovers by randomly assigning schools to receive a sexual health education programme and then randomly assigning the programme to classrooms within intervention schools; they compared sexual health knowledge among children in control classrooms in intervention schools with that of children in control schools (Table 1, Example 1).²⁸

Table 1.

Examples of empirical studies estimating different spillover parameters

Example	Study design	Spillover parameter	Intervention	Outcome	Spillover group	Comparison group
1. Chong et al., 2013	Double-randomized trial	Cluster-level spillover (Figure 1)	School-based sexual health education programme	Knowledge and attitudes about sexually transmitted infections and safe sex practices	Children in schools that received the programme but in classrooms that did not receive the programme	Children in schools that did not receive the programme
2. Banerjee et al., 2010	Cluster-randomized trial	Distance-based spillover (Figure 2)	Immunization campaign with and without incentives	Vaccination	Individuals in randomly selected, untreated villages within 6 km of villages randomized to treatment	Individuals in villages randomized to control
3. Hawley et al., 2003	Cluster-randomized trial	Distance-based spillover (Figure 2)	Insecticide-treated nets	Malaria, anaemia, child mortality	Untreated compounds 0–299 m, 300–599m and 600–899 m from treated compounds	Untreated compounds ≥ 900 m from treated compounds
4. Miguel and Kremer, 2004	Cluster-randomized trial	Spillovers conditional on treatment density (Figure 3)	School-based deworming	Soil-transmitted helminth infection	Untreated students at schools for which some pupils were treated at schools within 0–3 km and 4–6 km	Untreated students at schools for which no pupils were treated at schools within 0–3 km and 4–6 km
5. German et al., 2012	Randomized trial	Social network spillover (Figure 4)	Peer network intervention	Depression	Peers of individuals randomized to treatment	Peers of individuals randomized to control
6. Préziosi and Halloran, 2003	Secondary attack rate study	Vaccine efficacy for infectiousness (Figure 5)	Pertussis vaccine	Pertussis	Susceptibles living in households with treated cases	Susceptibles living in households with untreated cases

There are several related parameters that can also be estimated in a two-stage randomized trial (Figure 1). Direct effects compare the mean potential outcome of a treated individual in a treated cluster with treatment regimen α₁ with their mean potential outcome if they were assigned to control in the same cluster (${\overline{Y}}_{ij}\left({\alpha }_1,1\right)-{\overline{Y}}_{ij}({\alpha }_1,0)$); total effects compare the mean potential outcome of a treated individual in a treated cluster with treatment regimen α₁ with their mean potential outcome if they were assigned to control in control clusters (${\overline{Y}}_{ij}\left({\alpha }_1,1\right)-{\overline{Y}}_{ij}({\alpha }_0,0)$); and overall effects compare the mean outcome of all individuals in treated clusters with treatment regimen α₁ with the mean outcome had the cluster been assigned to control (${\overline{Y}}_{ij}\left({\alpha }_1\right)-{\overline{Y}}_{ij}({\alpha }_0)$) (see complete definitions in the Supplement, available as Supplementary data at IJE online). The direct effect defined in the spillover literature differs from other definitions in the causal mediation literature (effect of an exposure through no intermediate variables).²⁹ Similarly, in the spillover literature, the term ‘indirect effect’ is frequently used to describe spillover effects–in the mediation literature, an ‘indirect effect’ is the part of an intervention’s effect that is mediated through intermediate variables.

Cluster-level spillovers can be measured in studies that enrol clusters of any size. They are relatively convenient to estimate in studies with small- to medium-size clusters when the treatment status of most individuals in the cluster is known. Cluster-level spillover parameters often condition on other variables, such as eligibility to receive an intervention. For example, a comparison of outcomes among ineligible individuals in the treatment group with ineligible individuals in the control group estimates a cluster-level spillover effect (Figure 1).^30–37

Distance-based spillovers

Spillovers can be measured as a function of distance from treated individuals or clusters. We introduce two parameters: one conditional on individuals’ distance to clusters, and one conditional on distance between clusters. The first parameter measures spillover effects among individuals located a certain distance from the boundary of treatment and control clusters (Figure 2a). We define Y_ij(a_i | K_i = k) as the potential outcome for individual j residing within distance k from cluster i, with treatment vector a_i. The individual average potential outcome ${\overline{Y}}_{ij}$(α | K_i = k) is a function of the treatment regimen (α) and the individual’s distance to the nearest study cluster (k). Let α₁ be a treatment regimen in which at least one individual per cluster is allocated to treatment. Again, we assume that the treatment regimen is uniform (i.e. α₁ does not vary) among treated clusters. The spillover effect conditional on distance to treated clusters can be defined as:

$$SE\left({\alpha }_1,{\alpha }_0,k\right)\equiv {\overline{Y}}_{ij}\left({\alpha }_1|K_i=k\right)-{\overline{Y}}_{ij}\text{(}{\alpha }_0\text{|}{K}_i=k)$$ (3)

Figure 2.

Distance-based spillover effects. (a) Spillover effects conditional on distance to clusters can also be estimated in a two-stage randomized trial. This parameter compares the potential outcomes of untreated individuals within distance k of treated clusters to those of untreated individuals within distance k of control clusters. (b) Spillover effects conditional on distance between clusters can be estimated in a two-stage randomized trial. In the first stage, a study pair-matches clusters separated by distance k and then randomly allocates each pair to treatment or control. In the second stage, the study randomly selects one member from each pair to be the “primary” cluster; in the treated pairs, the primary cluster is assigned to treatment and the other cluster is assigned to control. Individuals in clusters assigned to treatment are randomly assigned to treatment or control. This parameter compares potential outcomes of individuals allocated to control in secondary clusters within distance k of treated clusters to those of individuals allocated to control in secondary clusters within distance k of control clusters.

This parameter compares the mean potential outcome of an individual distance k from a cluster with treatment regimen α₁ (at least one individual allocated to treatment per cluster) with their mean potential outcome at distance k from a cluster with treatment regimen α₀ (all individuals assigned to control). Studies estimating this parameter must ensure control clusters are at a distance from treatment clusters beyond which the intervention has an effect. Hawley et al. estimated a similar parameter in a re-analysis of a cluster-randomized trial to measure spillovers of insecticide-treated nets on malaria and other outcomes over different distances.³⁸ They compared individuals assigned to control clusters who were 0–299 m, 300–599 m and 600–899 m with those who were ≥ 900 m from the nearest individual in a treated cluster (Table 1, Example 3).

Spillover effects can also be measured as a function of distance between clusters using a pair-matched, two-stage design (Figure 2b). This parameter differs from the previous one because the individuals used to measure spillover effects reside in separate clusters rather than in the areas around the boundaries of the treatment clusters. To measure this type of spillover effect, first a study pair-matches clusters separated by distance k and then randomly allocates each pair to treatment or control. Second, the study randomly selects one member from each pair to be the ‘primary’ cluster; in the treated pairs, the primary cluster is assigned to treatment and the other cluster is assigned to control. In practice, the pairs of control clusters may be reduced to a single control cluster unless the second is needed to achieve sufficient statistical efficiency. Individuals in clusters assigned to treatment are randomly assigned to treatment or control. Let a_i be the treatment vector for primary clusters and b_i be the treatment vector for secondary clusters. Let Y_ij(a_i, b_i | K_i = k) be the potential outcome for individual j in secondary cluster i with treatment vector b_i within distance K_i = k from a primary cluster with treatment vector a_i. We define α as the treatment regimen for primary clusters and β as the treatment regimen for secondary clusters. The individual potential outcome averaging over different configurations of a_i and b_i for a given α and β is ${\overline{Y}}_{ij}$(α, β | K_i = k). The spillover effect conditional on distance between clusters may be defined as:

$$\begin{array}{c}S{E}_{ij}\left({\alpha }_1,{\alpha }_0,{\beta }_0,k\right)\equiv {\overline{Y}}_{ij}\left({\alpha }_1,{\beta }_0 | K_i=k\right)\\ -{\overline{Y}}_{ij}\text{(}{\alpha }_0,{\beta }_0 \text{|} K_i=k)\end{array}$$ (4)

This parameter compares the mean potential outcome of a control individual in a secondary control cluster (β₀) within distance K_i = k of a treatment cluster with treatment regimen α₁ with their mean potential outcome if they were assigned to a secondary control cluster (β₀) within distance K_i = k of a primary control cluster (α₀). Banerjee et al. conducted a study with a design similar to this to measure spillovers of a vaccine promotion campaign with and without subsidies (Table 1, Example 2).³⁹ They assigned clusters to treatment or control and then enrolled clusters within 6 km of treated clusters to measure spillovers. Their design assumes that clusters within 6 km of treatment clusters (the study’s spillover clusters) had similar baseline characteristics to control clusters; since spillover clusters were not included in the randomization, it is possible that there were systematic differences between spillover and control clusters, which could have confounded results.

Spillovers conditional on treatment density

We have defined spillover parameters with counterfactuals indexed by a vector of treatment assignments (a_i). In some cases, spillovers are a function not of the precise allocation of treatment to specific individuals, but instead of summaries of a_i, such as the proportion of those that get treatment (p_i). Thus, we can represent the model of the counterfactual distribution as Y_ij(p_i, a) = f(p_i,a), where f is a function of individual-level treatment assignment and low-dimensional summaries of treatment assignment among individuals in cluster i. Designs such as a two-stage randomized study can be tailored to estimate such effects. For instance, in the first stage, clusters are randomly assigned to receive a certain proportion of treatment (E[a_i] = p_i), and some clusters are assigned to p_i = 0. In the second stage, individuals are randomized to treatment or control in clusters with p_i > 0 (Figure 3).^8,10,13 We can define counterfactuals for individual j in cluster i as$Y_{ij}\left(p_i,a_{ij}\right)$, which is indexed by two scalars: the individual treatment assignment (a_ij) and the average proportion treated (p_i). The spillover effect among untreated individuals (a_ij = 0) conditional on treatment density is then:

$$SE(p_i,p_i^{\prime })\equiv {\overline{Y}}_{ij}\left(p_i,0\right)-{\overline{Y}}_{ij}\left(p_i^{\prime },0\right)$$ (5)

Figure 3.

Spillover effects conditional on treatment density. Spillover effects conditional on treatment density can be estimated in a two-stage randomized design that randomly allocates clusters to treatment or control and then randomly allocates individuals in treatment clusters to treatment or control. This parameter compares potential outcomes of untreated individuals in clusters allocated to treatment proportion p to those of untreated individuals in clusters allocated to a different treatment proportion p’. For example, in this figure, the treatment proportion within 30m of untreated individuals varies. This parameter compares potential outcomes of untreated individuals in clusters with treatment proportion 50% and 90% to those of untreated individuals in clusters with 0% of individuals allocated to treatment (i.e. control clusters).

In a two-stage randomized trial, this parameter compares the mean potential outcomes of an individual assigned to control in clusters with different proportions of individuals assigned to treatment (p_i vs. p_i′). This is equivalent to the cluster-level spillover effect on untreated individuals within the cluster (Equation 2), except for the simplifying assumption that the counterfactual is only a function of a summary of a_i,, namely p_i. This effect can also be estimated among treated individuals (see the Supplement for details, available as Supplementary data at IJE online). Miguel and Kremer estimated this parameter in a cluster-randomized trial of a school-based deworming programme in Kenya.³ They compared outcomes among children in untreated schools in areas with varying levels of density of treated children (Table 1, Example 4).³ This class of parameters can also be estimated by conditioning on the proportion of treated social network nodes within a given social distance metric of each untreated individual. For example, a study of a school-based deworming programme in Kenya estimated whether child deworming was associated with the number of social links to parents whose children received deworming at school.⁴⁰ Causal interpretation of this type of parameter requires that treatment be randomized to individuals within the social network rather than to individuals within a specific geographical area.

Social network spillovers

Social networks can be used to measure spillovers as a function of social proximity. A variety of designs can be employed to estimate different social network effects. For example, causal spillovers through social networks can be measured in a design that randomizes treatment to egos (the initially enrolled subjects) and compares the mean outcomes of alters (the persons socially connected to the egos) in the treatment vs control group (Figure 4). Counterfactuals in this design are a function of a joint treatment (a₁, a₀), where the treatment assignment for the ego is a₁, and the treatment assignment for the alter is a₀. The potential outcome for the alter j connected to the ego with treatment a₁ is Y_j (a₁, a₀). The social network spillover effect may be defined as:

$$SE\equiv E\left[Y_j\left(1,0\right)-Y_j\left(0,0\right)\right]$$ (6)

Figure 4.

Social network spillover effects. Social network spillover effects can be estimated in a study that randomizes treatment to egos (the initially enrolled subject) and compares the mean outcomes of alters (the person socially connected to the ego) in the treatment vs. control group.

This parameter compares mean outcomes among untreated alters socially connected to treated egos with their mean potential outcome had the egos been untreated. It is distinct from a parameter conditioning on treatment density among social network links (above) because it focuses on alters socially connected to specific egos, isolating the spillover effect through individual peer-to-peer connections. German et al. estimated this parameter in a randomized study that evaluated spillover effects of a peer network intervention. They compared depression scores among peers of treated vs control participants (Table 1, Example 5).⁴¹

Alternative parameters can be defined to estimate spillover effects through social networks. For example, spillover effects can be estimated for certain types of social ties (e.g. direct friends, social ties in the community, village members)⁴² or based on which type of social ties were targeted for intervention (e.g. villagers with the most social ties, nominated friends).⁴³ We presented social network spillovers among the untreated, but they can also be estimated among the treated by comparing counterfactual outcomes among treated alters connected to treated vs untreated egos. Many other types of social network spillover parameters have been described, and an overview of social network effects has been provided by Vanderweele and An.⁴⁴ We have described estimation of social network spillover effects in an individually randomized trial, but other study designs can be used to estimate spillover effects through social networks. For instance, Christakis et al. measured the spread of obesity⁴⁵ and smoking⁴⁶ through social networks in a large cohort study. Stochastic, actor-oriented models can also be used to estimate spillover effects in networks;^47,48 these models allow individuals to change their behaviour status and/or social ties at each time point and require strong assumptions.⁴⁴

When estimating social network spillover effects, both observational and randomized designs face unique threats to validity. First, socially connected individuals may have correlated outcomes and may inhabit the same environment, leading to environmental confounding.^49–53 Second, an individual may sever a social tie based on their present outcome status as a result of homophily, which may bias estimates of spillover effects.⁵¹ A randomized design can minimize homophily by randomizing individuals to peers in their social network, such as a room-mate, to ensure that potential confounders are balanced within ego and alter pairs.⁵⁴

Spillovers conditional on exposure to infection

Epidemiologists studying vaccines have developed parameters that condition on exposure to infected individuals to measure whether vaccines reduce transmission to uninfected individuals.^{6,9,12,55–58} These parameters are typically estimated in studies that enrol households with an infected individual (a ‘case’) and at least one uninfected individual (a ‘susceptible’). The vaccine efficacy for the infectiousness parameter (also referred to as the ‘infectiousness effect’⁵⁹) is a type of spillover parameter that compares the secondary attack rate among uninfected susceptible individuals in households with a vaccinated case, with the rate among those in households with unvaccinated cases (Figure 5; Table 1, Example 6).

Figure 5.

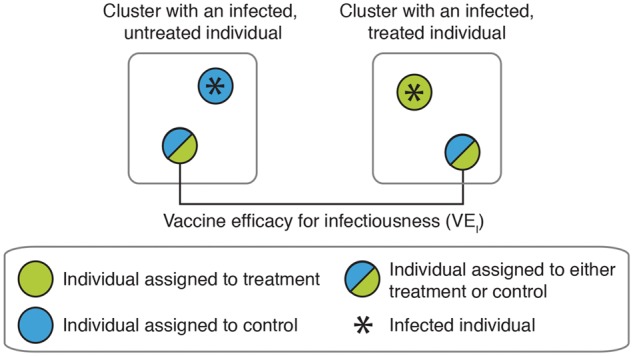
Vaccine efficacy for infectiousness. This parameter is typically estimated in studies that enroll households with an infected individual (a “case”) and at least one uninfected individual (a “susceptible“). The parameter compares the secondary attack rate among uninfected susceptible individuals in households with a vaccinated case to the rate among those in households with unvaccinated cases. Susceptibles may be either vaccinated or unvaccinated.

Conditioning on post-treatment outcome status can introduce selection bias because individuals who become infected may be systematically different from those who do not.⁶ Under standard causal inference assumptions this parameter is not identifiable;⁵⁸ to identify this parameter, relatively strong additional assumptions are required.^58–60 For example, one must assume that susceptibles are only exposed to infection in their household, i.e. that household members interact with each other but not with other households.⁶ Because these additional assumptions complicate the presentation of causal parameters, we define a parameter below that does not use counterfactuals (i.e. a statistical parameter); see the Supplement for a causal definition (available as Supplementary data at IJE online).

Let S be the outcome for the primary household case, Y be the outcome for the susceptible individual, and A be the treatment assignment for the case. The vaccine efficacy for infectiousness (VE) on the additive scale is:

$$V{E}_I=E\left[Y\text{|}A=1,S=1\right]-E[Y|A=0,S=1]$$ (7)

We present this parameter on the additive scale for consistency with other parameters, but it is most often estimated as a reduction in the relative risk [(1-RR) x 100%]. These parameters are similar to the cluster-level spillover effect (Equation 2) but condition on outcome status instead of treatment status. Préziosi and Halloran measured this parameter in a household secondary attack rate study of pertussis vaccination by comparing outcomes among susceptibles in households with vaccinated cases with those in households with unvaccinated cases.⁶¹

Designing studies to measure spillovers

In this section we discuss spillover study designs. Box 2 summarizes recommendations throughout this section.

Box 2. Recommendations for designing studies to estimate spillover effects

Importance of theory	Choose a spillover parameter and study design based on theory about how the intervention’s effects diffuse through a population. Especially when theory to support spillovers of an intervention is weak, use rigorous designs, such as the double-randomized design, in order to make causal inferences.
Causal inferences about spillovers	3.To estimate cluster-level spillovers, distance-based spillovers or spillovers conditional on treatment density, use a double-randomized design to maximize internal validity. 4.If it is only possible to use a cluster-randomized design, consider using multivariate matching techniques to match untreated individuals in the control clusters to untreated individuals in the treatment clusters. Matching may improve balance for measured confounders; however, unmeasured confounding may remain, and external validity may decrease depending on the subset of the population that is matched. 5.If a clustered study design is used, build in buffer zones between treated and control units in order to prevent contamination and ensure that there is a valid control group to serve as a counterfactual. 6.Use individual-level outcomes to measure spillovers when possible. Group-level measurements can be useful for hypothesis generation when individual-level measurements are unavailable.
Pre-specifying analyses	7.Pre-specify the specific spillover parameter(s) to be estimated. 8.Pre-specify the scale at which spillovers are expected and the hypothesized mechanism(s) of spillover. 9.If the spillover parameter incorporates measurement within specific distances or areas, pre-specify distance or area definitions and provide a rationale for them based on the hypothesized strength and scale of spillovers to avoid selectively choosing cutoffs that provide favourable results. For example, describe the specific distances in which measurement will take place or describe whether measurement will occur within quantiles of the observed distance distribution. 10.If the study protocol is registered, use the terms ‘spillovers’ or ‘indirect effects’ to refer to spillovers in the protocol because these are the most commonly used terms in the literature, and they provide a direct link to the theoretical literature on this topic.

Causal inferences about spillovers

Confounding of spillover effect estimates

Estimates of spillover effects will be confounded if there are factors associated with untreated individuals’ exposure to treatment and outcomes that are not controlled for. A two-stage randomized trial is ideal for estimating cluster-level spillovers, distance-based spillovers and spillovers conditional on treatment density, because it minimizes systematic differences other than treatment assignment between treated and untreated individuals in the treatment and control arms. Individually randomized trials can generate internally valid spillover estimates for certain parameters, such as social network spillover effects, if they ensure that there is sufficient physical or social distance between untreated individuals so that some individuals can serve as a valid counterfactual. For observational studies, strategies such as propensity scores,⁶² inverse probability weighting,^13,63–65 matching in the design stage,^66–68 regression discontinuity^69,70 and instrumental variables^28,29 can increase comparability between untreated individuals in proximity to treated individuals and untreated individuals not in proximity to treated individuals that serve as a control group. For example, cluster-randomized trials can measure cluster-level spillovers by matching individuals who were ineligible for treatment in treated clusters to similar individuals in control clusters and comparing outcomes.⁷³ However, this approach only ensures comparability on measured covariates, so unmeasured confounding may remain, and matching could potentially reduce the study’s external validity.⁷⁴ We note that some of these methods, such as regression discontinuity, have yet to be applied to estimation of spillover effects; to do so would require an extension of current theory, which is appropriate for total and overall effects.

Spillover effects conditional on distance can be confounded by factors that affect whether untreated individuals live near treated individuals and as well as their outcomes. Two-stage randomized designs (Figure 2) minimize this form of confounding by balancing the distribution of treatment across space. In observational studies, investigators can select comparison areas with similar geographical features to treatment areas to minimize confounding. Sensitivity analyses can estimate the extent of possible bias in studies with unmeasured confounding or studies that randomize treatment but condition on a post-treatment variable, such as the presence of an infected case in a household, which can also lead to bias.⁵²

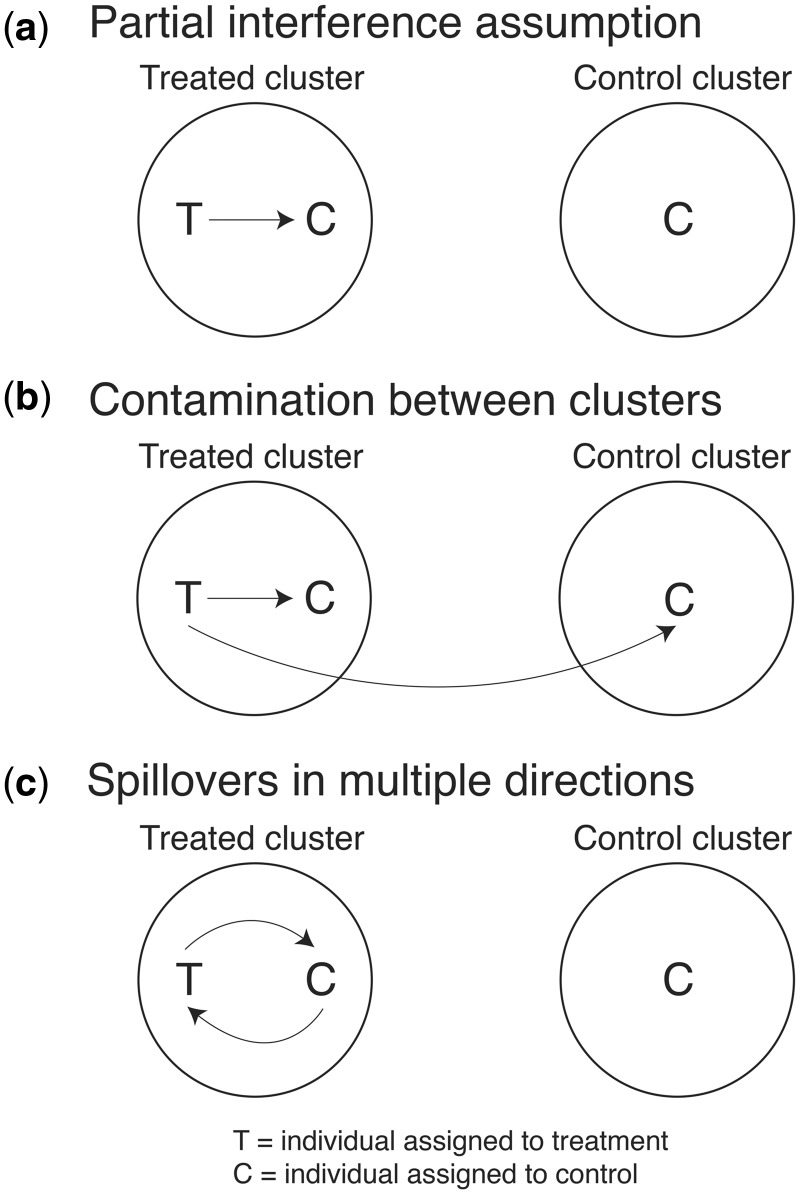
Violations of SUTVA and the partial interference assumption

SUTVA is one of the core assumptions required to make causal inferences; but when spillovers occur, the assumption can be relaxed to allow for spillovers within but not between clusters (partial interference)²⁴ (Figure 6a). Two-stage randomized designs can reasonably assume partial interference, but the assumption is difficult to assert in individually randomized studies unless enrolled individuals are separated by a large physical or social distance. In cluster-randomized trials, when interventions affect outcomes in the control clusters (‘contamination’), the partial interference assumption is violated (Figure 6b). In this case, spillover effects can generally be considered lower bounds of the true spillover effect under the assumption that the effect of treatment in the control group is less than or equal to its effect in the treatment group. However, if contamination causes re-composition of treatment and control units that alters transmission dynamics, treatment effects may be biased away from the null. Estimates will also be biased when spillovers occur in multiple directions—untreated individuals affect treated individuals’ outcomes and treated individuals affect untreated individuals’ outcomes (Figure 6c). For example, in a trial that randomizes improved latrines to a subset of households in a village, environmental contamination resulting from use of unimproved latrines by non-recipients may spread enteric infections to latrine recipients, diluting benefits from improved latrines.

Figure 6.

Schematic of spillovers within and between clusters. (a) The partial interference assumption states that there are no spillovers between clusters of individuals but allows for spillovers among individuals within the same cluster. (b) When an intervention affects individuals in a cluster assigned to control, this is often referred to as “contamination” in the cluster-randomized trial literature. This is an example of a violation of the partial interference assumption depicted in (a). (c) Spillovers may occur in multiple directions: individuals assigned to treatment may influence potential outcomes of individuals assigned to control and vice versa. When such multi-dimensional effects occur, causal inference becomes complicated.

To assess possible violations of SUTVA and the partial interference assumption, investigators can conduct Fisher’s permutation test of no effect, which assumes every study unit has the same outcome under all treatment assignments; in a cluster-randomized study, if the null hypothesis is true, there is no effect of intervention and there are no spillovers between clusters.^75–77 In some cases nothing can be done to prevent spillovers between individuals or clusters–a violation of the partial interference assumption. Recent efforts have explored causal inference in this setting, which is referred to as ‘general interference’. These studies have described statistical approaches and developed software packages⁷⁸ for analyzing network data in which individuals are not considered independent.^{17,64,79–90}

Causal epidemiological effects vs biological effects

Another consideration in estimating spillover effects is that the causal estimates from an epidemiological study may not be equivalent to the biological effects of intervention, even in a randomized trial.⁹¹ Comparing the quantities estimated in challenge studies vs epidemiological studies of vaccines illustrates this difference. The biological effect of a vaccine is the reduction in risk associated with exposure to a specific volume of inoculum. Challenge studies estimate this effect by comparing risk among individuals randomly assigned to receive a known quantity of inoculum or a placebo.⁹¹ On the other hand, epidemiological studies cannot control the level of exposure to pathogens targeted by vaccines;⁶ as a result, they produce estimates that are a function of the level of population mixing and frequency of exposure to illness, both of which are typically unknown. Because most trials do not condition on the level of exposure to infection, their causal estimates will differ from the biological effect for interventions that produce spillovers. In addition, spillover and total effects estimated in trials with differing levels of baseline transmission are not directly comparable.⁹¹ These principles may apply to studies of interventions other than vaccines, even if analogous biological effects cannot be estimated through challenge studies. For example, in a study led by German et al. of a peer network intervention to reduce depression,⁴¹ peers of study participants were recruited to measure spillovers, but the level of social contact between peers was not controlled by the investigator; estimates of spillover effects were a function of the extent and type of social contact between peers, which may vary across populations.

Importance of theory

Spillover estimates will be most meaningful when the theory about how the intervention diffuses through a population informs the parameter choice and study design. For example, to measure spillovers of an intervention that aims to reduce HIV transmission, social network spillovers are likely to provide information that is more useful for public health intervention than distance-based spillovers since transmission occurs through sexual contact. For spillovers of behaviour change interventions, network⁹² and diffusion theory^93,94 may inform how intervention effects diffuse over geographical areas or through social networks and whether spillovers occur evenly across a population or more strongly within subgroups. Interventions that diffuse through communication between individuals over great distances may cause spillovers over large geographical areas, even if no contact is made in person. If so, measuring spillovers through social networks is more appropriate than measuring spillovers through physical proximity since the latter may fail to capture the full spillover effect.

The strength of theory to support spillovers may inform design and analysis choices when estimating spillovers. When the causal mechanism for spillovers is not strongly grounded in theory, we encourage investigators to use a design that can effectively minimize confounding (e.g. two-stage randomization in Figure 1). However, for certain interventions such as vaccines, the biological mechanism for reducing pathogen transmission is often sufficiently clear for observational studies to provide strong inference about vaccine spillovers.⁹ In some cases, even if theory to support spillovers is strong, statistical models are required to make inferences about spillovers; this may occur if there is limited variation in treatment status within levels of confounders. Statistical models can yield biased estimates if they are mis-specified or if they extrapolate beyond the observed data, so model-based estimates should always be considered carefully in light of their potential assumptions and limitations.

Individual- vs group-level measurements

Spillovers can be estimated in studies that measure outcomes either in individuals or in groups. Two-stage randomized studies and other cluster-randomized studies produce individual-outcome level data. Studies have commonly attempted to measure spillover effects by assessing how rates of illness among untreated individuals change with the proportion of individuals treated in different areas, using group-level data from trials or observational studies.^95–102 Studies with individual-level outcome measurements typically have the strongest inference because they are better able to control for both individual-level and group-level confounders, whereas group-level studies can only control for the latter. Despite these drawbacks, group-level measurements can be useful for hypothesis generation when individual-level measurements are not available.

Measuring spillovers within geographic areas

Certain types of spillovers, such as spillovers conditional on treatment density and distance-based spillovers, measure intervention coverage and outcomes within specific geographical areas (e.g. neighbourhoods). Spillover estimates are likely to be very sensitive to the way areas are defined.¹⁰³ The size or shape of the area may determine whether spillovers are detected. Pre-specification of area definition before looking at outcomes prevents investigators from selectively using a definition that provides the most favourable result. Ideally, area definition is based on the hypothesized strength and scale of spillovers. For example, when spillover effects are expected to be weak, measurement is best within small areas where spillovers are most likely to be detected. Expected transmission dynamics may also inform area definition: a study of the cholera vaccine measured spillovers associated with immunization coverage near a shared water source, where cholera transmission was hypothesized to be the strongest.⁹⁷

Power calculations for spillovers

Typically, spillover effects are smaller than total or overall effects of interventions, so larger sample sizes are needed in order to detect them. We recommend that investigators conduct power calculations in the study design phase, to assess whether statistical power will be sufficient to detect spillovers. Several studies have provided sample size formulas to estimate spillovers using randomized designs and variants of them.^9,16 For non-standard study designs, simulations can be used to estimate statistical power.⁷⁸

Pre-specifying spillovers

We encourage investigators who plan to measure spillovers to pre-specify the specific spillover parameter(s), the scale at which spillovers are expected, and the hypothesized mechanism(s) of spillover be estimated in a study protocol. Pre-specification reduces the chance that the spillover parameters selected are those that detect positive spillovers, whether intentionally or not.¹⁰⁵ It also reduces the chance of publication bias.^106,107 We also encourage investigators to use the terms ‘spillovers’ or ‘indirect effects’ to refer to spillovers in protocols and manuscripts, because these are the most commonly used terms in the literature, and they provide a direct link to the theoretical literature on this topic.

Summary

We have defined different types of spillover effects relevant to a wide range of interventions using standardized notation to encourage estimation and reporting of spillovers by a broad range of investigators. We have also provided a general introduction to assumptions required to make causal inferences about spillover effects. Rigorous definition and study of spillover effects will improve the accuracy of estimates of the population-level impact and cost-effectiveness of interventions that have benefits beyond direct recipients.

Supplementary Data

Supplementary data are available at IJE online.

Conflict of interest: None declared.