Theory and Application of the Relationship between Steady-State Isotope Effects on Enzyme Intermediate Concentrations and Net Rate Constants

Abstract

Steady-state kinetic isotope effects on enzyme catalyzed reactions are often interpreted in terms of the microscopic rate constants associated with the elementary reactions of interest. Unfortunately, this approach can lead to confusion, especially when more than one elementary reaction is isotopically sensitive, because it forces one to consider the full catalytic cycle one step at a time rather than as a complete whole. Herein we argue that shifting focus from intrinsic effects to net rate constants and enzyme intermediate concentrations provides a more natural and holistic interpretation by which the effects of partial rate-limitation are more easily understood. In doing so, we demonstrate how the experimental determination of isotope effects on enzyme intermediate concentrations allows a direct determination of isotope effects on net rate constants. The chapter is divided into three main sections. The first outlines the basic theory and its interpretation. The second discusses an application of the theory in the study of the radical SAM enzyme DesII. The final section then provides the complete mathematical treatment.

1. Introduction

When studying enzymatic reaction mechanisms, a common experimental approach is to introduce a perturbation that affects the values of the microscopic (or intrinsic) rate constants in a predictable manner without altering the set of elementary reactions hypothesized to make up the catalytic cycle. This is a defining feature in the measurement of steady-state kinetic isotope effects (our focus here); however, it may also be applied to the study of viscosity effects, substrate specificity, and so on. In these studies, the perturbation effect is observed as the ratio of the parameter of interest measured in the absence of the perturbation, say y, to that measured in its presence, say y^*, or in the reigning notation (Cook and Cleland, 2007)

$${}^{\ast }y=y/y^{\ast }.$$ (1)

The difficulty with a such an experimental design, however, is that its interpretation requires compression of an entire kinetic model for the reaction into a single number. This can lead to ambiguity as well as qualitative, vague notions of rate-limiting reaction steps (Northrop, 1981b). Furthermore, the situation is made only more confusing when an emphasis is placed on intrinsic effects rather than parameters more representative of the steady-state condition.

In this chapter, we discuss a method of conceptualizing steady-state perturbation effects using kinetic isotope effects as the example. The approach focuses not on the elementary reactions but rather the related concepts of enzyme intermediate concentrations and net rate constants. It is general for models of steady-state enzymatic reactions that may be regarded as serial (i.e., unbranched with a clear forward direction of reaction flux) and suggests an experimental design by which useful information may be extracted from the measurement of steady-state isotope effects despite partially rate-limiting steps. This chapter is divided into three sections. The first is an informal discussion of the theory and its interpretation. The second describes an example of how the approach has been applied in a real experimental context. The final section then provides the mathematics behind the theory that is necessary for its rigorous justification.

2. Modeling steady-state isotope effects

2.1. Serial steady-state models

In modeling an enzymatic reaction, we make a distinction between enzyme species, denoted E₁,E₂,…, which are composed of the enzyme, and peripheral species, denoted X₁,X₂,…, which are not. Peripheral species may thus be substrates, products, cofactors, and so on, between which we make no distinction. The fixed, steady-state concentrations¹ of the peripheral species will be denoted by corresponding lowercase letters (e.g., x_i would represent the concentration of X_i). Finally, the pseudo-first-order rate constant for the elementary reaction converting E_i to E_j will be denoted k_ij. Each pseudo-first-order rate constant is a function of the fixed peripheral species concentrations and proportional to the microscopic rate constant for the associated elementary reaction (see Def. 4.1 in Sec. 4.3). If there is no elementary reaction connecting E_i to E_j in the model, then the corresponding microscopic rate constant is 0, and thus so too is the pseudo-first-order rate constant for all peripheral species concentrations.

For example, an enzymatic reaction modeled by

$$E_1\underset{-X_1}{\overset{+X_1}{\rightleftharpoons }}{E}_2\underset{-X_2}{\overset{+X_2}{\rightleftharpoons }}{E}_3\rightleftharpoons E_4\to E_5\stackrel{-X_3}{\to }{E}_1,$$ (2)

has five enzyme species (E₁ to E₅), three peripheral species (X₁, X₂ & X₃) and eight elementary reactions. The “irreversibility” of the E₅ → E₁ elementary reaction suggests that X₃ plays no part in the kinetics being modeled. Therefore, we really only need to be concerned with X₁ and X₂, thereby reducing the number of peripheral species in the model to just two. This model also has four key properties:

1. There are no interactions between the enzyme species.

2. The peripheral species interconvert only via the catalytic cycle.

3. There is one and only one connected cycle of all the enzyme species.²

4. The only other connected cycles contain just two enzyme species.

We call any steady-state kinetic model having these properties serial, which we can also define formally using graph theory (see Def. 4.4 in Sec. 4.4).

Serial models are in general unbranched and have at least one “irreversible” reaction by which a unique forward direction of reaction flux can be unambiguously identified (see Sec. 4.4).³ If all the peripheral species included in a serial model have steady-state concentrations greater than 0 (however small), then we can show (see Prp. 4.2) that all of the modeled steady-state enzyme species concentrations must also be greater than 0. It follows that given any set of nonzero peripheral species concentrations, we can always assign a nonzero, steady-state velocity to the serial model according to the flux through one of the irreversible elementary reactions (see Def. 4.6). Moreover, it can be demonstrated (see Prp. 4.3) that the steady-state velocity will be uniquely defined in this way regardless of how many irreversible reactions there may be in the serial model.⁴ This means that the velocity as well as the steady-state concentrations of each enzyme species are well-defined functions of the set of peripheral species concentrations.

In order to simplify the discussion of different sets of peripheral species concentrations, we will collect them together as the coordinates of a vector x. For example, in the case of (2) we would have

$$\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right].$$ (3)

The condition that all of the steady-state peripheral species concentrations are greater than 0 will then be expressed as x > 0. Therefore, if the velocity function is v and the concentration function for E_i is e_i, then the discussion in the preceding paragraph implies that a net rate function $k_i^{\prime }$ for each enzyme species E_i can be defined according to the ratio (see also Def. 4.7)

$$k_i^{\prime }(\mathbf{x})=\frac{v(\mathbf{x})}{e_i(\mathbf{x})},\mathbf{x}>\mathbf{0}.$$ (4)

The evaluation of $k_i^{\prime }$ at a given peripheral species concentration vector x is thus equivalent to the net rate constant for E_i that has been previously studied by Cleland (1975) and Noyes (1964). Furthermore, we can use the theory developed by King and Altman (1956) to derive (see Prp. 4.5) the familiar recursive expression,⁵

$$k_i^{\prime }(\mathbf{x})=\frac{k_{i,i+1}(\mathbf{x})k_{i+1}^{\prime }(\mathbf{x})}{k_{i+1,i}(\mathbf{x})+k_{i+1}^{\prime }(\mathbf{x})},$$ (5)

that was discovered by Cleland (1975) in his original work on net rate constants.

It is worth pointing out that up to this point we have not done anything particularly new. In fact, the uniqueness of the steady-state velocity as a function of the peripheral species concentrations will be familiar to anyone who has analyzed specific instances of serial models. What we have done, however, is outline a general framework for approaching serial kinetic models regardless of the number of elementary reactions and peripheral species it entails. We have also identified conditions where nonzero values of v(x), e_i(x) and $k_i^{\prime }(\mathbf{x})$ for all E_i associated with the steady-state serial model are guaranteed to exist in general sense, namely whenever x > 0. These results, which are justified rigorously in Sec. 4, are central to the validity of the following analysis of isotope effects.

2.2. Isotope effects on the steady-state velocity

Suppose we have two serial models that are equivalent in all respects except for the values of the nonzero microscopic rate constants. Recognizing one of the models as an unperturbed reference, we can then designate the steady-state velocity, enzyme species concentrations and net rate functions for the second, perturbed model with a post-superscript “*” (e.g., v^*, $e_i^{\ast },k_i^{\prime \ast }$ etc.). When the perturbation is understood to be induced by altering the isotopic composition of the reacting species, it corresponds to an isotope effect.

In Sec. 4.7 we refer to such models as being isomorphic, because there exists an invertible mapping between them that preserves structure and thus defines a pairing between the enzyme species of the first model (i.e., E₁,E₂,…) and those of the second (i.e., $E_1^{\ast },E_2^{\ast }$, …). Consequently, given our definition (4) of a net rate function, we can express the isotope effect on the steady-state velocity at x according to the function ^*v, where⁶

$${}^{\ast }v(\mathbf{x})=\frac{v(\mathbf{x})}{v^{\ast }(\mathbf{x})}=\frac{e_i(\mathbf{x})}{e_i^{\ast }(\mathbf{x})}·\frac{k_i^{\prime }(\mathbf{x})}{k_i^{\prime \ast }(\mathbf{x})}={{}^{\ast }e}_i(\mathbf{x}){{}^{\ast }k}_i^{\prime }(\mathbf{x}),$$ (6)

whenever x > 0. Note that this relationship is true for all pairs of corresponding enzyme species (i.e., $E_i\&E_i^{\ast }$) described by the models. Since the total enzyme concentration is a constant and the same for both the reference and perturbed reaction systems, we can also write

$${}^{\ast }v(\mathbf{x})={{}^{\ast }f}_i(\mathbf{x}){{}^{\ast }k}_i^{\prime }(\mathbf{x}),$$ (7)

where f_i(x) is the fractional steady-state concentration of enzyme species E_i at x, and ^*f_i(x) is the corresponding isotope effect.

Unfortunately, Eqn. (7) alone does not offer much intuition regarding the underlying kinetics. Nevertheless, a more insightful equation can be obtained by rearranging Eqn. (7) to obtain (see Sec. 4.8 for derivation)

$${}^{\ast }v(\mathbf{x})=\sum _{i=1}^n{f}_i(\mathbf{x}){{}^{\ast }k}_i^{\prime }(\mathbf{x}),$$ (8)

where n is the total number of enzyme species in the model. In other words, the isotope effect on the modeled steady-state velocity at x can be expressed as a weighted average of the isotope effects on each net rate constant, and the weighting terms are just the fractional concentrations of the enzyme species in the reference model.

Equations (7) & (8) are our first two key results. As one might expect, the latter demonstrates that if for some x the majority of the enzyme is piled-up in one enzyme species, then the isotope effect on the corresponding net rate constant will dominate the isotope effect on the observable steady-state velocity. The isotope effects on all other net rate constants will be obfuscated. Equation (7), however, provides a potential solution to this problem, because it can also be rearranged to provide

$${{}^{\ast }k}_i^{\prime }(\mathbf{x})={}^{\ast }v(\mathbf{x})/{{}^{\ast }f}_i(\mathbf{x}).$$ (9)

In other words, the isotope effect on a net rate constant is obtained immediately from a measure of the isotope effects on both the steady-state velocity and the enzyme intermediate concentration of interest. Section 3 will illustrate an example where this useful property of steady-state kinetic isotope effects was used in practice to study the mechanism of a radical SAM enzyme.

2.3. Isotope effects on V/K and V

We are typically not interested in isotope effects on the steady-state velocity but rather the steady-state kinetic parameters V/K and V. However, the corresponding isotope effects ^*(V/K) and ^*V are just limiting values of ^*v(x) as the coordinates of x each approach 0⁺ (i.e., 0 along the positive reals), increase without bound or approach some well-defined positive value (Northrop, 1981a). For example, the V isotope effect often refers to the limit of ^*v(x) as all peripheral species concentrations increase without bound. Likewise, a V/K isotope effect often refers to the limit of ^*v(x) as one peripheral species concentration approaches 0⁺ while all the remaining concentrations increase without bound. For models with multiple peripheral species, however, these isotope effects may also be defined according to limits where only one concentration approaches 0⁺ or ∞ and the remaining approach some set of finite, positive values.

It should be emphasized that these limits and hence isotope effects are not always guaranteed to exist for any serial model.⁷ Therefore, some care must be taken in the construction of a serial model if it is to be useful in the study of a real enzymatic reaction. However, if a limit for ^*v does exist for all positive intrinsic isotope effects in the model, then we can show (see Prps. 4.11 & 4.12) that the corresponding limit of each fractional enzyme concentration (i.e., f_i) and isotope effect on each net rate function (i.e., ${{}^{\ast }k}_i^{\prime }$) either exists or their product function (i.e., $f_i·{{}^{\ast }k}_i^{\prime }$) approaches 0. As previously suggested by Northrop (1981a) this is an important result, because it means that we may interpret isotope effects on the steady-state parameters in exactly the same way that we interpret isotope effects on the steady-state velocity despite the two being different mathematical constructs.

For example, suppose we continue with the model in (2) treating X₁ and X₂ as substrates for the reaction. The isotope effect on V would then correspond to the limit of ^*v(x) as both x₁ and x₂ increase without bound. In this case, both f₁(x) and f₂(x) approach 0, and we have

$${}^{\ast }V=f_{3V}{{}^{\ast }k}_{3V}^{\prime }+f_{4V}{{}^{\ast }k}_{4V}^{\prime }+f_{5V}{{}^{\ast }k}_{5V}^{\prime },$$ (10)

where f_iV and ${{}^{\ast }k}_{iV}^{\prime }$ denote the limiting values of f_i(x) and ${{}^{\ast }k}_i^{\prime }(\mathbf{x})$), respectively, as (x₁, x₂) → (∞, ∞). Likewise, if we define ^*(V/K)₁ as the limit of ^*v(x) as (x₁, x₂) → (0⁺, ∞), then we expect that all the enzyme will pile-up in the E₁ species such that f₁(x) → 1, and indeed we find that

$${{}^{\ast }(V/K)}_1=\underset{\begin{array}{c}{x}_1\to 0^{+}\\ x_2\to \infty \end{array}}{lim}{{}^{\ast }k}_1^{\prime }(\mathbf{x}),$$ (11)

where evaluation of this limit is discussed in the next section. Finally, if we define ^*(V/K)₂ as the limit of ^*v(x) as (x₁, x₂) → (∞, 0⁺), then we get

$${{}^{\ast }(V/K)}_2=\underset{\begin{array}{c}{x}_1\to \infty \\ x_2\to 0^{+}\end{array}}{lim}{{}^{\ast }k}_2^{\prime }(\mathbf{x}).$$ (12)

These latter two results should look familiar, since specificity constants (i.e., V/K), are generally understood (Cook and Cleland, 2007) to be equal to the normalized net rate function for the enzyme species that binds with the vanishing substrate. More complicated serial models and limiting conditions can be analyzed in exactly the same way so long as the limits that define the isotope effects on the kinetic parameters exist.

2.4. Isotope effects on net rate functions

The decomposition (8) of a steady-state isotope effect into a weighted average of isotope effects on the net rate functions naturally leads to the question as to how the latter should be interpretted. It is widely recognized that a net rate function for some enzyme species E_i only depends on the elementary reactions following E_i up to and including the first downstream reaction modeled as irreversible (Cleland, 1975; Cook and Cleland, 2007), and this can be proven from the definition in (4) (see Cor. 4.7.1). Thus, each net rate function is associated with a subsequence of the serial model that can be depicted graphically using an appropriately scaled (Ray, 1983) energy diagram.⁸ For example, the subsequence for E₁ that determines $k_1^{\prime }$ for the reaction in (2) corresponds to

$$E_1\underset{-X_1}{\overset{+X_1}{\rightleftharpoons }}{E}_2\underset{-X_2}{\overset{+X_2}{\rightleftharpoons }}{E}_3\rightleftharpoons E_4\to E_5,$$

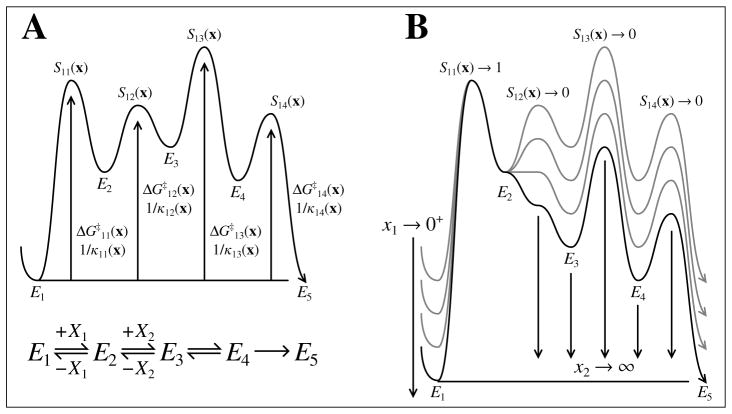
and a hypothetical energy diagram for this subsequence is shown in Fig. 1A.

Figure 1.

Graphical interpretation of rate-limiting steps with respect to the net rate function $k_1^{\prime }$ for the example in (2). In each plot the abscissa corresponds the subseqeunce of enzyme species and elementary reactions that contribute to $k_1^{\prime }$ (i.e., the reaction-coordinate). The ordinate represents the scaled energy of each enzyme species and the activated complexes that connect them. (A) Hypothetical plot for the E₁ subsequence given some well-defined x. In this case, the E₃ → E₄ elementary reaction has the largest activation energy with respect to E₁. Hence, the sensitivity index for the E₃ → E₄ reaction (i.e., S₁₃(x)) is closest to 1 making it the most rate-limiting with respect to $k_1^{\prime }(\mathbf{x})$. (B) Graphical heuristic of how the E₁ → E₂ elementary reaction alone becomes rate-limiting with respect to $k_1^{\prime }$ as the concentration of X₁ decreases and X₂ becomes saturating.

Along the energy diagram for each subsequence, we can identify an activation energy $\mathrm{\Delta }{G}_{ij}^{‡}(\mathbf{x})$ between the first enzyme species E_i in the subsequence and the j-th downstream activated complex (see Fig. 1A). This activation energy depends on the peripheral species concentration vector x and is therefore a heuristic rather than a fixed thermokinetic parameter. We can then associate what Noyes (1964) has labeled an equilibrated first-order rate constant κ_ij(x) with the activation energy $\mathrm{\Delta }{G}_{ij}^{‡}(\mathbf{x})$ such that (Stein, 1981; Murdoch, 1981; Ray, 1983; Tian, 1992)

$${\kappa }_{ij}(\mathbf{x})=K_{ij}(\mathbf{x})k_{j,j+1}(\mathbf{x}),$$ (13)

where k_j,j+1(x) is the pseudo-first-order rate constant given x for the E_j → E_j+1 elementary reaction, and K_ij(x) is the equilibrium constant between E_i and E_j constructed from the pseudo-first-order rate constants of the model and equal to unity if E_i = E_j. From the definition of a pseudo-first-order rate constant (see Def. 4.1), the isotope effect on κ_ij is a constant function for all x > 0, and therefore we may simply refer to it as the constant ^*κ_ij independent of x. These isotope effects reflect progression from E_i to each activated complex downstream and in general do not represent the intrinsic isotope effects associated with each individual elementary reaction (Stein, 1981; Ruszczycky and Anderson, 2006; Tian, 1992; Lewis and Schramm, 2006; Cleland, 1982).

As already pointed out by Schowen and Stein in their discussions of virtual transition states (Schowen, 1978; Stein, 1981; Alvarez et al., 1991), the isotope effect on the net rate function $k_i^{\prime }$ is itself a weighted average of the ^*κ_ij isotope effects along the subsequence for E_i. More specifically, it can be shown (see Secs. 4.7 & 4.8) that this isotope effect takes the form

$${{}^{\ast }k}_i^{\prime }(\mathbf{x})=\sum _{j\ge i}{S}_{ij}(\mathbf{x}){{}^{\ast }\kappa }_{ij},\mathbf{x}>\mathbf{0},$$ (14)

where the sum extends over all elementary reactions in the subsequence for E_i. Each weighting term S_ij, which is also a function of x, is equal to the sensitivity index of the i-th net rate function versus the j-th elementary reaction in the reference system (see Sec. 4.6 for the derivation). Sensitivity indices were defined by Ray (1983) to reflect the degree to which a steady-state parameter is affected by a change in the energy of an activated complex, all else being equal. For this reason, they may be regarded as a quantitative measure of rate-limitation for each elementary reaction with respect to V and V/K parameters (Murdoch, 1981; Ray, 1983). In agreement with this definition of rate-limitation, we extend this interpretation to sensitivity indices for the net rate functions.

Sensitivity indices for net rate functions can be expressed (Ray, 1983; Ruszczycky and Anderson, 2006) in terms of the familiar concepts (Northrop, 1981b,a; Cleland, 1982) of catalytic commitments; however, it can also be shown (Alvarez et al., 1991; Stein, 1981; Murdoch, 1981; Ray, 1983) that they are related to the reciprocals of the κ_ij according to

$$S_{ij}(\mathbf{x})=\frac{{\kappa }_{ij}^{-1}(\mathbf{x})}{{\sum }_{p\ge i}{\kappa }_{ip}^{-1}(\mathbf{x})},\mathbf{x}>\mathbf{0},$$ (15)

where the sum in the denominator again extends over all elementary reactions in the subsequence for E_i. This result follows immediately from Prps. 4.8 & 4.7 discussed in Secs. 4.5 & 4.6. Furthermore, the activation energy $\mathrm{\Delta }{G}_{ij}^{‡}(\mathbf{x})$ is affinely dependent on the logarithm of ${\kappa }_{ij}^{-1}(\mathbf{x})$ (Noyes, 1964; Stein, 1981; Ray, 1983). Therefore, the relative contribution of each isotope effect ^*κ_ij to ${{}^{\ast }k}_i^{\prime }(\mathbf{x})$ can readily be inferred from the difference in energy between each activated complex and the first enzyme species along the subsequence as shown in Fig. 1A (Ruszczycky and Anderson, 2006). Moreover, limits of the sensitivity indices follow the same rules as do the limits of perturbation effects on net rate functions (see Prp. 4.13) so that their interpretation remains the same with respect to the steady-state parameters V and V/K.

For example, returning to the model in (2), we have the following expression for ${{}^{\ast }k}_1^{\prime }(\mathbf{x})$:

$${{}^{\ast }k}_1^{\prime }(\mathbf{x})=\frac{{\kappa }_{11}^{-1}(\mathbf{x})}{{\sum }_{j=1}^4{\kappa }_{1j}^{-1}(\mathbf{x})}{{}^{\ast }\kappa }_{11}+\frac{{\kappa }_{12}^{-1}(\mathbf{x})}{{\sum }_{j=1}^4{\kappa }_{1j}^{-1}(\mathbf{x})}{{}^{\ast }\kappa }_{12}+\frac{{\kappa }_{13}^{-1}(\mathbf{x})}{{\sum }_{j=1}^4{\kappa }_{1j}^{-1}(\mathbf{x})}{{}^{\ast }\kappa }_{13}+\frac{{\kappa }_{14}^{-1}(\mathbf{x})}{{\sum }_{j=1}^4{\kappa }_{1j}^{-1}(\mathbf{x})}{{}^{\ast }\kappa }_{14},$$

which is shown diagramatically in Fig. 1. Furthermore, since

$${\kappa }_{1j}(\mathbf{x})\propto \{\begin{array}{ll}{x}_1,\hfill & j=1,\hfill \\ x_1{x}_2,\hfill & j=2,3,4,\hfill \end{array}$$

we find that

$$\underset{\begin{array}{c}{x}_1\to 0^{+}\\ x_2\to \infty \end{array}}{lim}{S}_{1j}(\mathbf{x})=\{\begin{array}{ll}1,\hfill & j=1,\hfill \\ 0,\hfill & j=2,3,4,\hfill \end{array}$$

and thus

$${{}^{\ast }(V/K)}_1={{}^{\ast }\kappa }_{11},$$

which is just the kinetic isotope effect on the E₁ → E₂ elementary reaction. This is what we expect, because binding of the limiting substrate (i.e., X₁) should dominate the ^*(V/K)₁ isotope effect as the second substrate (i.e., X₂) becomes saturating and thus introduces a large forward commitment on all subsequent steps as shown in Fig. 1B.

In contrast, when we consider $k_2^{\prime }(\mathbf{x})$ for the example in (2), we have the subsequence

$$E_2\underset{-X_2}{\overset{+X_2}{\rightleftharpoons }}{E}_3\rightleftharpoons E_4\to E_5,$$

and it follows that

$${\kappa }_{2j}(\mathbf{x})\propto x_2,$$

for all values of j between 2 and 4, inclusive. Therefore, the sensitivity indices are all constant values independent of x, because the x₂ just cancel out of the ratios in Eqn. (15). Consequently, ${{}^{\ast }k}_2^{\prime }(\mathbf{x})$ and by extension ^*(V/K)₂ are fixed averages of the four different ^*κ_2j isotope effects, and we can write

$${{}^{\ast }(V/K)}_2=S_{22}{{}^{\ast }\kappa }_{22}+S_{23}{{}^{\ast }\kappa }_{23}+S_{24}{{}^{\ast }\kappa }_{24},$$

treating the S_2j as constants.

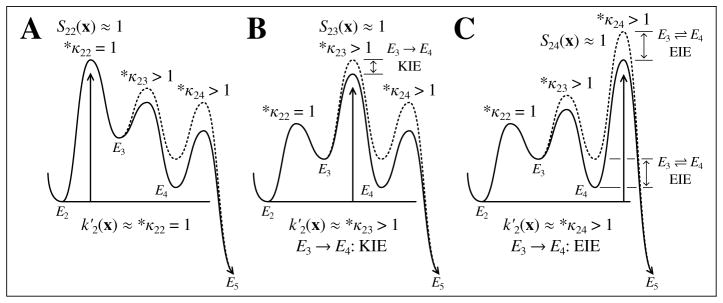
Now, suppose that the E₃ → E₄ reaction alone happens to be isotopically sensitive in the model. Equation (13) then implies that ^*κ₂₂ will be unity, ^*κ₂₃ will be equal to the intrinsic kinetic isotope effect on the E₃ → E₄ elementary reaction, and ^*κ₂₄ will be equal to the equilibrium isotope effect on this reaction as shown in Fig. 2. Therefore, if S₂₂ is close to unity so that S₂₃ and S₂₄ are close to 0, then ^*(V/K)₂ ≈ ^*κ₂₂ = 1, which corresponds to a large forward commitment on the the E₃ → E₄ reaction (see Fig. 2A). In contrast, if S₂₃ is close to unity, then E₃ → E₄ is “rate-limiting” for the net rate constant and ^*(V/K)₂ ≈ ^*κ₂₃ (see Fig. 2B). Finally, if S₂₄ is close to unity, then ^*(V/K)₂ is dominated by the equilibrium isotope effect ^*κ₂₄, which corresponds to a large reverse commitment on the E₃ → E₄ reaction as shown in Fig. 2C. Additional examples using this graphical approach to interpreting isotope effects on net rate constants as shown in Fig. 2 have been previously discussed (Ruszczycky and Anderson, 2006; Tian, 1992).

Figure 2.

Graphical interpretation of isotope effects on $k_2^{\prime }$ for the example in (2). Plots are drawn as in Fig. 1. The solid line corresponds to the reference model and the broken line to a model where there is a normal isotope effect on the E₃ → E₄ elementary reaction alone. (A) The E₂ → E₃ activated complex is highest in energy versus E₂ making this reaction most rate-limiting with respect to $k_2^{\prime }$. This introduces large forward commitments on both the E₃ → E₄ and E₄ → E₅ reactions. (B) The E₃ → E₄ reaction is rate-limiting for $k_2^{\prime }$, and the E₃ → E₄ kinetic isotope effect is strongly reflected in ${{}^{\ast }k}_2^{\prime }$, because there is a unit equilibrium isotope effect on E₂ ⇌ E₃. This places a large reverse commitment on E₂ → E₃ and a large forward commitment on E₄ → E₅. (C) The E₄ → E₅ reaction is most rate limiting, and the isotope effect reflects the bonding changes established in the E₃ → E₄ reaction, which is the E₃ ⇌ E₄ equilibrium isotope effect. This corresponds to large reverse commitments on the E₂ → E₃ and E₃ → E₄ reactions.

The previous sections have attempted to show that an intuitive and general framework for the interpretation of steady-state isotope effects is available by shifting the focus from intrinsic effects to parameters more representative of the steady-state, namely, net rate functions and their limits. Furthermore, the fundamental equations (8) and (14) along with their limits are completely general to all serial models and do not require that only one step be regarded as isotopically sensitive. Therefore, they permit one to reason holistically about steady-state isotope effects in terms of activation energy diagrams and the distribution of enzyme species at steady-state without the need to write out the full kinetic equations or focus on individual elementary reactions.

3. An example: DesII

3.1. Background

The theory outlined in the previous sections not only provides a framework for thinking about steady-state isotope effects (and perturbation effects in general) but also suggests an approach to their measurement, which is exemplified by studies on the radical SAM enzyme DesII. Radical SAM enzymes are characterized by an active site [4Fe-4S]¹⁺ cluster that serves to reductively homolyze S-adenosyl-L-methionine (SAM) to produce L-methionine and a 5′-deoxyadenosyl radical (Frey and Magnusson, 2003; Wang and Frey, 2007; Duschene et al., 2009; Frey, 2014). The 5′-deoxyadenosyl radical can then act as a radical initiator for a broad range chemical reactions catalyzed by this enzyme superfamily (Broderick et al., 2014; Frey, 2014; Mehta et al., 2015; Landgraf et al., 2016).

In the case of DesII, reductive homolysis of SAM results in abstraction of the hydrogen atom from the C3 carbon of its substrate TDP-4-amino-4,6-dideoxy-D-glucose thereby initiating a radical-mediated deamination reaction (1 → 2, see Fig. 3) (Szu et al., 2009; Ruszczycky et al., 2012; Ruszczycky and Liu, 2015). DesII can also accept TDP-D-quinovose (3), which has a hydroxyl rather than an amino group at C4, as a substrate with relatively little change in its kinetic profile (Szu et al., 2009; Ruszczycky et al., 2010; Ruszczycky and Liu, 2015). However, this small structural change converts DesII from a lyase into a radical-mediated dehydrogenase whereby the substrate radical reduces the [4Fe-4S]²⁺ cluster back to the [4Fe-4S]¹⁺ state with each turnover yielding the product 4 (see Fig. 3) (Ruszczycky et al., 2010). DesII has thus attracted attention as a model system for understanding how the fate of a radical intermediate is controlled in an enzyme active site (Ko et al., 2015).

Figure 3.

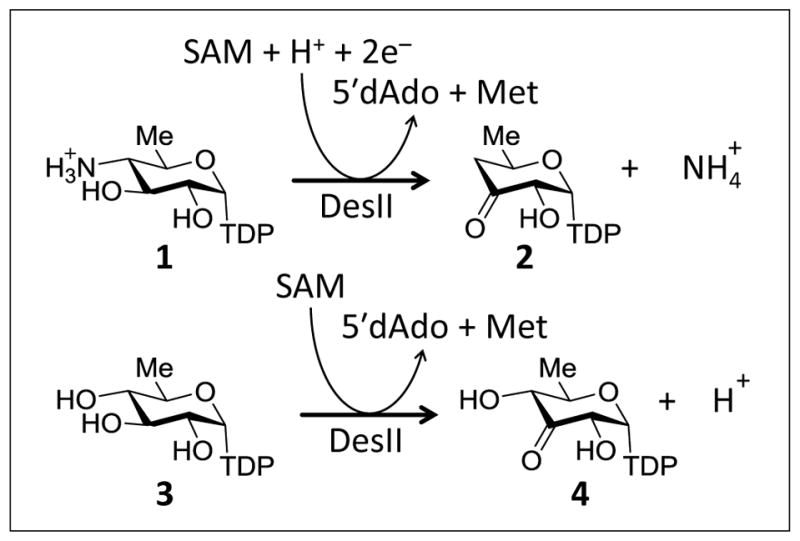
Reactions catalyzed by DesII.

3.2. Question and modeling

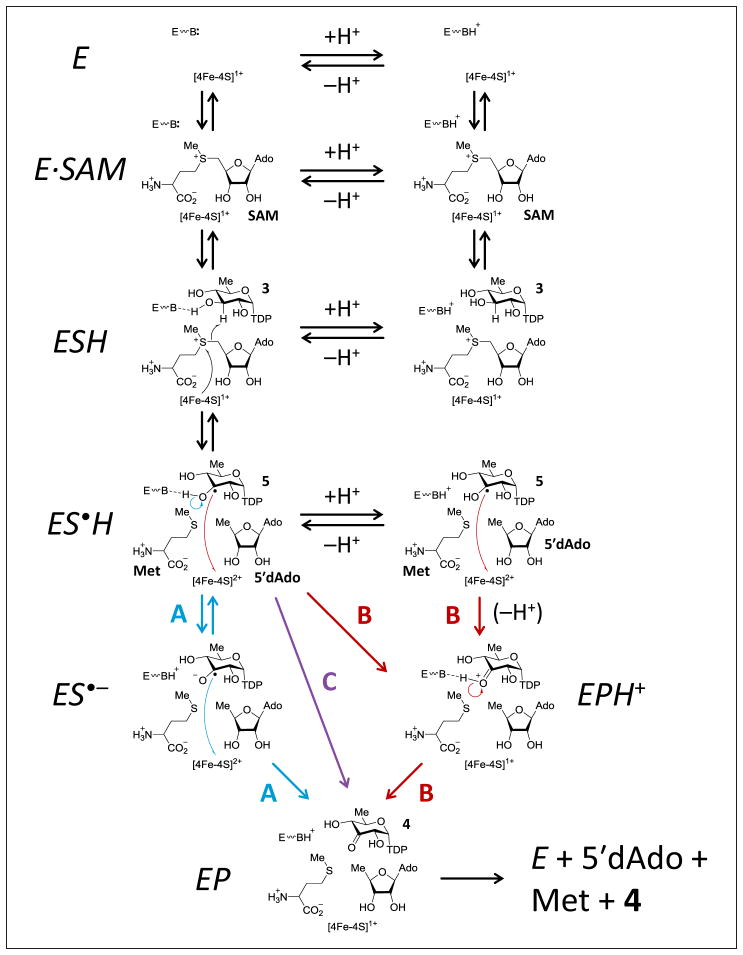
An initial electron paramagnetic resonance (EPR) investigation of the de-hydrogenation steady-state intermediates indicated that the substrate radical is an α-hydroxyalkyl radical (5, see Fig. 4) (Ruszczycky et al., 2011). This raised the question as to whether deprotonation of the α-hydroxyalkyl radical precedes (model A), follows (model B) or occurs concerted (model C) with electron transfer to the [4Fe-4S]²⁺ cluster. These three models, which are shown in Fig. 4, also take into account the observed pH-dependence of the DesII catalyzed dehydrogenation reaction that implicated titratable forms of the enzyme with decreasing activity as the pH is lowered (Ruszczycky et al., 2013).

Figure 4.

Models of catalysis for the DesII catalyzed dehydrogenation of TDP-D-quinovose (4). L-Methionine and 5′-deoxyadenosine are abbreviated Met and 5′dAdo, respectively.

While these models are clearly not serial due to the acid-base equilibria, they can be converted to serial form by treating the acid-base equilibra as rapid and applying Cha’s method (Cha, 1968). Furthermore, since the steady-state velocity exists and is nonzero in the limit as the concentrations of both SAM and 3 increase without bound, so too does the limit corresponding to the V isotope effect. Therefore, the discussion in Sec. 2.3 implies that we can consider these models under saturating conditions more simply as

$$\mathit{ESH}\underset{k_{RQ}^{\mathit{app}}}{\overset{k_{RG}^{\mathit{app}}}{\rightleftharpoons }}E{S}^{•}H\underset{k_{HR}}{\overset{k_{HT}^{\mathit{app}}}{\rightleftharpoons }}E{S}^{•-}\stackrel{k_{ET}}{\to }EP\stackrel{k_D}{\to }\mathit{ESH},$$ (A)

$$\mathit{ESH}\underset{k_{RQ}^{\mathit{app}}}{\overset{k_{RG}^{\mathit{app}}}{\rightleftharpoons }}E{S}^{•}H\stackrel{k_{ET}}{\to }{\mathit{EPH}}^{+}\stackrel{k_{HT}}{\to }EP\stackrel{k_D}{\to }\mathit{ESH},$$ (B)

$$\mathit{ESH}\underset{k_{RQ}^{\mathit{app}}}{\overset{k_{RG}^{\mathit{app}}}{\rightleftharpoons }}E{S}^{•}H\stackrel{k_{HE}^{\mathit{app}}}{\to }EP\stackrel{k_D}{\to }\mathit{ESH},$$ (C)

Here, the rate constants for radical generation ( $k_{RG}^{\mathit{app}}$), quenching ( $k_{RQ}^{\mathit{appa}}$) and hydron transfer ( $k_{HT}^{\mathit{app}}\&k_{HE}^{\mathit{app}}$) elementary reactions are apparent due to the acid-base equilbiria such that,

$$k^{\mathit{app}}(\mathbf{x})=\frac{K}{K+h}k(\mathbf{x}),$$ (16)

where K is the acid dissociation constant, and h is the fixed concentration of H₃O⁺. The radical generation step (i.e., ESH ⇌ ES^•H) is considered pH-dependent to account for the possibility that the active site needs to be in the correct ionization state to properly orient SAM and 3 for reductive homolysis and H-atom abstraction.

3.3. Experimental design

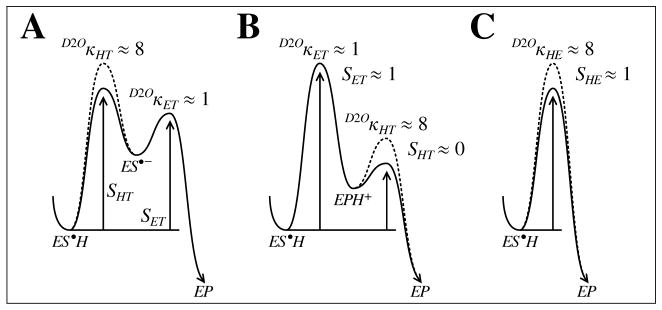
The three models can be distinguished experimentally if the solvent deuterium isotope effect on the net rate constant for ES^•H (i.e., the limit of ${{}^{D2O}k}_{ES•H}^{\prime }$ as 3 and SAM become saturating) can be measured as shown in Fig. 5. If proton abstraction precedes electron transfer (i.e., model A), then this isotope effect is given by the limiting weighted average (see Eqn. (14))

Figure 5.

Energy diagrams of the ES^•H subseqence for each model of the DesII reaction. The solid curve denotes the reaction in H₂O and the broken curve in D₂O. The energy levels of the ES^•H intermediate in H₂O and D₂O are aligned to make it easier to see the origin of the ^D2Oκ isotope effects. The deprotonation reaction is modeled with a near unit equilibrium isotope effect and a kinetic isotope of ca. 8 based on the experimental observations discussed in the text. Both the electron transfer and proton transfer steps are shown for model B for the sake of clarity; however, the electron transfer is treated as essentially irreversible. This is reflected in the values of the sensitivity indices.

$${{}^{D2O}k}_{ES•H}^{\prime }={s_{HT}}^{D2O}{\kappa }_{HT}+{S_{ET}}^{D2O}{\kappa }_{ET},$$ (17)

where S_HT and S_ET are the sensitivity indices for the hydron transfer and electron transfer steps, respectively, for $k_{ES•H}^{\prime }$ as the enzyme becomes saturated. After correction of the apparent rate constants for differences due to the acidbase equilibria (see below), the isotope effect ^D2Oκ_HT reflects bonding changes between ES^•H and the activated complex for hydron transfer and thus represents a primary deuterium kinetic isotope effect. In contrast, the isotope effect ^D2Oκ_ET reflects bonding changes between the subsequent activated complex for electron transfer and ES^•H and thus largely represents the equilibrium isotope effect on the ES^•H ⇌ ES^•− reaction (see Eqn. (13)). In other words, ${{}^{D2O}k}_{ES•H}^{\prime }$ should be large and normal if S_HT ≈ 1.

In model B, where electron transfer occurs before proton transfer, the isotope effect on the net rate constant for ES^•H is given by

$${{}^{D2O}k}_{ES•H}^{\prime }={{}^{D2O}\kappa }_{ET},$$ (18)

where the sensitivity index is 1, because electron transfer is the only step contributing to $k_{ES•H}^{\prime }$ in this model. In this case, ^D2Oκ_ET should be essentially unity, because there is neither a solvent hydron in flight in the corresponding activated complex nor is there a preceding reaction to introduce an equilibrium isotope effect with respect to ES^•H. Hence, model B always predicts ${{}^{D2O}k}_{ES•H}^{\prime }\approx 1$. In contrast, a concerted process (i.e., model C) predicts

$${{}^{D2O}k}_{ES•H}^{\prime }={{}^{D2O}\kappa }_{HE}.$$ (19)

Here, ^D2Oκ_HT, after correcting for acid-base equilibria (see below), reflects bonding changes between ES^•H and the activated complex for concerted electronhydron transfer. Thus, the concerted model always predicts a normal primary deuterium kinetic isotope effect on $k_{ES•H}^{\prime }$.

The solvent deuterium isotope effect ^D2OV on the DesII-catalyed dehydrogenation of 3 was measured by direct comparison and found to be 2.7 ± 0.4 at the suboptimal pH 8.0 Hepes buffer ratio,⁹ where the α-hydroxylalkyl substrate radical could be observed by EPR (Ruszczycky et al., 2013). This isotope effect seemed to suggest that there was indeed a hydron transfer reaction taking place during the catalytic cycle. However, the full expression for ^D2OV is given by

$${}^{D2O}V=f_{\mathit{ESH}}{{}^{D2O}k}_{\mathit{ESH}}^{\prime }+f_{ES•H}{{}^{D2O}k}_{ES•H}^{\prime }+f_{{\mathit{EPH}}^{+}}{{}^{D2O}k}_{{\mathit{EPH}}^{+}}^{\prime }+f_{EP}{{}^{D2O}k}_{EP}^{\prime },$$ (20)

for model B with similar expressions for models A and C as per the limit of Eqn. (8). While proton transfer from the protonated ketone in EPH⁺ should be fast and thus f_EPH⁺ low, there is no gaurantee that other steps (e.g., EP → ESH) would not involve transfer of solvent exchangeable hydrons. In other words, the modest, normal ^D2OV isotope effect alone did not convincingly rule out model B.

What one really wants to do is to increase the value of f_ES^•H closer to unity so that ^D2OV is more representative of ${{}^{D2O}k}_{ES•H}^{\prime }$. In the case of DesII, it was possible to reduce the value of f_ES^•H by running the reaction at the more optimal pH of 10 where the substrate radical could no longer be observed by EPR (Ruszczycky et al., 2013). Consequently, the value of ^D2OV decreased to 1.8±0.2 at this pH, thereby further supporting models A and C. This approach is identical to that first proposed by Cook and Cleland (1981a,b), whereby the degree to which an elementary reaction is rate-limiting can be modulated by examining the isotope effect at suboptimal pH. However, if the isotope effect on the steady-state concentration of ES^•H under saturating conditions can be determined (i.e., ^D2Of_ES^•H), then Eqn. (9) implies that ${{}^{D2O}k}_{ES•H}^{\prime }$ can be computed from the ratio

$${{}^{D2O}k}_{ES•H}^{\prime }=\frac{{}^{D2O}V}{{{}^{D2O}f}_{ES•H}}.$$ (21)

Note that this expression is independent of the exact form of the serial model. This was the approach taken with DesII, where ^D2Of_ES^•H was measured by integrating the EPR signal intensities for the ES^•H enzyme species in both H₂O and D₂O buffers and then taking their ratio.

In order to do this experiment with reasonable precision and minimal bias, a number of controls need to be in place in addition to proper replication. First, the enzyme must have the same specific activity in each sample preparation so that the concentration ratio reflects the isotope effect and not differences in total active enzyme. In the case of DesII, comparable H₂O and D₂O EPR samples were prepared from the same batch of enzyme at the same time. Furthermore, the same buffer exchange protocol was applied to the preparation of both the D₂O and H₂O reaction samples, and small aliquots of each enzyme preparation were extracted to determine the specific activity following buffer exchange. It is also important to make sure that the enzyme intermediate is trapped under the same conditions for both reaction systems. For example, if the reaction in H₂O buffer is significantly faster than in D₂O buffer, then the intermediate concentration differences could represent different levels of enzyme saturation and not the isotope effect. This was controlled for by both measuring the ratio at different freeze-quench times and also examining control quenches by HPLC to determine the extent of reaction in each system. The DesII enzyme also had a number of additional peculiarities requiring attention such as substrate inhibition and ensuring proper integration of the EPR signals, and these aspects are carefully addressed in the original work (Ruszczycky et al., 2013).

3.4. Results

The final value of ^D2Of_ES^•H was thus 0.22 ± 0.03 measured at the pH 8.0 Hepes buffer ratio indicating approximately 4–5 times more enzyme in the ES^•H state in D₂O versus H₂O (Ruszczycky et al., 2013). Consequently, ${{}^{D2O}k}_{ES•H}^{\prime \mathit{app}}$ was found to be 12 ± 3 prior to correction for acid-base equilibria. In the case of model B, k_ET and thus the net rate constant do not depend on the protonation state of the enzyme, such that¹⁰

$${{}^{D2O}k}_{ES•H}^{\prime }={{}^{D2O}k}_{ES•H}^{\prime \mathit{app}}=12\pm 3.$$ (22)

This is inconsistent with the model B prediction that this isotope effect be near unity. In contrast, the net rate constant for models A and C does depend on the protonation state of ES^•H via the apparent rate constants $k_{HT}^{\mathit{app}}$ and $k_{HE}^{\mathit{app}}$, respectively. In both cases, the dependence manifests as

$${{}^{D2O}k}_{ES•H}^{\prime \mathit{app}}={{}^{D2O}k}_{ES•H}^{\prime }\left(\frac{{}^{D2O}K/(h/d)+K/h}{1+K/h}\right),$$ (23)

where d is the concentration of D₃O⁺ at the pH 8.0 Hepes buffer ratio. In the original work, the correction factor on the right-hand-side was estimated to be approximately 1.6 ± 0.5, such that the corrected isotope effect on ${{}^{D2O}k}_{ES•H}^{\prime }$ was 8 ± 3, which is consistent with either of these models.

Collectively, these results ruled out model B indicating that proton transfer occurs either prior to or concerted with electron transfer during the DesII catalyzed dehydrogenation of TDP-D-quinovose. From a mechanistic perspective, the result implied that deprotonation of the α-hydroxyalkyl radical may be necessary to increase its oxidation potential to at least match the reduction potential of the active site [4Fe-4S]²⁺ cluster (Rao and Hayon, 1974; Hayon and Simic, 1974; Daley and Holm, 2003; Rao and Holm, 2004; Hinckley and Frey, 2006; Duschene et al., 2009). This would then facilitate what is presumably an outer-sphere electron transfer to yield the dehydrogenated product (4) and regenerate the active [4Fe-4S]¹⁺ form of the enzyme.

When investigating the steady-state of an enyzmatic reaction, the arguably most useful and experimentally accessible kinetic parameters are not the hypothesized microscopic rate constants but rather the net rate functions and enzyme intermediate concentrations. Hence, the study and manipulation of net rate functions and enzyme intermediate concentrations in their own right represent an important feature for developing and testing steady-state kinetic models of real enzymatic reactions. This thesis has been previously recognized in the works of Tittmann, Hübner and coworkers (Schütz et al., 2005; Tittmann et al., 2005b,a, 2003), who have studied intermediate concentrations directly, as well as those of Bollinger, Krebs and coworkers (Price et al., 2003; Hoffart et al., 2006; Xing et al., 2006; Tamanaha et al., 2016; Peck et al., 2017), who have also used isotope effects to manipulate the relative populations of intermediates observable by EPR. This conceptualization extends naturally to the general study of perturbation effects themselves providing well-defined, quantatitve concepts of partial rate-limitation that can be easily represented with activation energy diagrams.

4. Theory

4.1. Overview

This section provides a rigorous justification of the theory discussed informally in Sec. 2. As such, we take a completely mathematical approach and use the language of graph theory and vector calculus with no reliance on chemical intuition, despite some suggestive naming conventions. The section begins by establishing careful definitions of the mathematical constructs and then deriving their properties. A model that meets these definitions for any perturbation effect (whether it be an isotope effect, viscosity effect, etc.) will then have the derived properties. We first provide proofs that can be applied to steady-state serial models with more than two enzyme species and then show how this can be extended to models with only two enzyme species.

4.2. Basic terminology and notation

We use standard notation, with bold symbols representing real vectors and matrices or their functions. One exception is the use of the prime to denote a net rate function rather than single-variable differentiation. The sets ℝ, ℝⁿ and ℝ^n×n correspond to the sets of all real numbers, all vectors of n real numbers and all n × n matrices of real numbers, respectively. Standard notation is used to define functions and build sets. We use the basic definition of a digraph (i.e., a directed graph) that does not include multigraphs so that directed edges can only be represented once and there are no self-loops. Finally, if x is an element of ℝⁿ, then we will continue with the notation x > 0 from Sec. 2 to indicate that all n coordinates of the vector x are greater than 0.

4.3. Preliminary definitions and results

Definition 4.1 (Rate Function)

A rate function k parameterized in terms of a set of m nonnegative integer constants $B={\{b_i\}}_{i=1}^m$ and a nonnegative real number β is a function

$$\begin{gathered} k:{ℝ}^m\to ℝ, \\ k(\mathbf{x};\beta ,B)=\beta \prod _{i=1}^m{x}_i^{b_i}, \end{gathered}$$ (24)

where x_i is the i-th coordinate of the real column vector x in ℝ^m.

In the context of an elementary enzymatic reaction, a rate function is nothing more than a generalized pseudo-first-order rate constant that accounts for all possible peripheral species concentrations. The parameter β may then be regarded as the associated microscopic rate constant and the integer constant b_i as the molecularity of the elementary reaction with respect to peripheral species X_i. Note that if k is independent of x_i, then b_i = 0, and $x_i^0$ is defined to be 1 for all x_i ∈ ℝ such that k is a continuous function.

Definition 4.2 (Steady-State Model)

A steady-state model is an ordered triple (D_n, $A_n^m$, e₀) where n > 1 and

• D_n is a digraph with n vertices labeled E₁, E₂, …, E_n,

• $A_n^m$ is a set of n(n − 1) rate functions {k_ij}_i≠j defined on ℝ^m,

• e₀ is a positive real number,

  such that for each rate function k_ij(·; β_ij, B_ij) in $A_n^m$, β_ij > 0 if the ordered pair of vertices (E_i, E_j) exists in D_n, and β_ij = 0 if (E_i, E_j) does not exist in D_n.

Note that the ordered pairs (E_i, E_j) in a steady-state model represent the directed edges in the graphical representation of D_n. Therefore, the steady-state kinetics of an enzymatic reaction can be represented using a steady-state model by assigning each enzyme species to a vertex and defining x as a vector of m peripheral species concentrations. Note that this definition of a steady-state model establishes the first two conditions discussed in Sec. 2.1. The next definition follows the analysis of King and Altman (1956), which is built upon that by Matsen and Franklin (1950).

Definition 4.3 (King-Altman Function)

The King-Altman function A is defined for a steady-state model (D_n, $A_n^m$, e₀) as

$$\begin{gathered} \mathbf{A}:{ℝ}^m\to {ℝ}^{n\times n}, \\ {[\mathbf{A}(\mathbf{x})]}_{ij}=\{\begin{array}{ll}{k}_{ji}(\mathbf{x}),\hfill & i\ne j,\hfill \\ -{\sum }_{p\ne j}^n{k}_{pj}(\mathbf{x}),\hfill & i=j,\hfill \end{array} \end{gathered}$$ (25)

where [A(x)]_ij is the element in the j-column of the i-th row of A(x), and the k_ij are the elements of $A_n^m$.

Given a steady state model (D_n, $A_n^m$, e₀), if the rank of A(x) is n − 1, then there is an n-dimensional column vector e(x) that solves the linear system of equations given by

$$\mathbf{A}(\mathbf{x})\mathbf{e}(\mathbf{x})=\mathbf{0},$$ (26a)

$${\mathbf{1}}^{\top }\mathbf{e}(\mathbf{x})=e_0,$$ (26b)

where 1 is a column vector of n-ones, 0 is a column vector of n-zeros and ^⊤ denotes vector/matrix transposition. We can therefore treat e as an n-dimensional vector-valued function of x. Furthermore, if we denote the i-th coordinate of e(x) as e_i(x), then e_i is a real-valued function of x.

King and Altman (1956) have provided a detailed theoretical analysis of the solutions to Eqn. (26). In particular they have shown that if a solution e(x) exists, then it is given according to Cramer’s Rule as

$$e_i(\mathbf{x})=\frac{e_{0}det{\stackrel{\sim }{\mathbf{A}}}_i(\mathbf{x})}{{\sum }_{j=1}^{n}det{\stackrel{\sim }{\mathbf{A}}}_j(\mathbf{x})},1\le i\le n,$$ (27)

where Ã_i(x) is A(x) with the i-th row replaced by ones, the i-th column replaced by zeros, and [Ã_i(x)]_ii = 1. The notation det Ã_i(x) refers to the determinant of Ã_i(x). A defining achievement of King and Altman’s analysis is the theorem they proved for determining det Ã_i(x) from direct inspection of the digraph D_n. We will refer to this as the King-Altman theorem and state it here without proof. Note that this theorem along with Eqn. (27) also establishes a one-to-one correspondence (E_i ↔ e_i) between the vertices of D_n and the elements of e.

Theorem 4.1 (King-Altman)

If (D_n, $A_m^n$, e₀) is a steady-state model, then the determinant of Ã_i(x) is given by

$$det{\stackrel{\sim }{\mathbf{A}}}_i(\mathbf{x})={(-1)}^{n-1}\sum _P\alpha (\mathbf{x},P),$$ (28)

where the sum is over all products of n − 1 rate functions evaluated at x

$$\alpha (\mathbf{x},P)=k_{ab}(\mathbf{x})k_{bc}(\mathbf{x})\cdots k_{uv}(\mathbf{x})k_{vi}(\mathbf{x}),$$ (29)

such that

$$P=E_a{E}_b{E}_c\dots E_u{E}_v{E}_i,$$ (30)

is a connected (n − 1)-path with no cycles in D_n. Furthermore, if no such path exists, then the determinant is 0.

4.4. Serial models

Definition 4.4 (Serial Model)

A steady-state model (D_n, $A_n^m$, e₀) is called serial if D_n has one and only one n-cycle C_n and no p-cycle where 2 < p < n.

We can label the vertices of a serial model such that the unique n-cycle is represented by any circular shift of the path

$$C_n=E_1{E}_2{E}_3\dots E_{n-1}{E}_n{E}_1,$$ (31)

or written in terms of a sequence of edges,

$$C_n=(E_1,E_2)(E_2,E_3)\dots (E_{n-1},E_n)(E_n,E_1).$$ (32)

Since how we choose to index the vertices of a graph is arbitrary, we will always use an indexing such that C_n can be written according to Eqns. (31) and (32). This will allow us to use modular arithmetic when writing indices given a serial kinetic model, namely index i in k_i represents the least positive residual of i modulo n. For example, if n = 5, then E₂ = E₂, E₀ = E₅, E₋₂ = E₃ and E₇ = E₂. Two other properties of a serial model are worth emphasizing. First, there are no “branches” as this would otherwise introduce a cycle with more than 2 vertices. Second, if n > 2, then C_n defines an orientation for the model, which corresponds to the forward direction when applied to an enzymatic reaction.

Definition 4.5 (Irreversible Edge)

Given a directed graph D, if the ordered pair (E_i, E_j) exists in D and (E_j, E_i) does not exist in D, then (E_i, E_j) is called an irreversible edge of D.

Proposition 4.1

If a steady-state model (D_n, $A_n^m$, e₀) is serial and n > 2, then there is at least one irreversible edge in D_n.

Proof

Since the model is serial, there exists a sequence of edges forming the n-cycle C_n as in Eqn. (32). If there are no irreversible edges in D_n, then for every edge (E_i, E_j) in D_n the reverse edge (E_j, E_i) is also in D_n. The existence of C_n (see Eqn. (32)) then implies that all n edges in the set

$$\{(E_2,E_1),(E_3,E_2),\dots ,(E_n,E_{n-1}),(E_1,E_n)\},$$ (33)

exist in D_n, and thus D_n also contains the n-cycle given by the sequence

$$C_n^{\prime }=(E_1,E_n)(E_n,E_{n-1})\dots (E_3,E_2)(E_2,E_1).$$ (34)

However, if n > 2, then there is no permutation such that the sequences in Eqn. (32) and (34) become equal, hence $C_n^{\prime }\ne C_n$ and there must be two different n-cycles in D_n. This contradicts the hypothesis that the model is serial. Hence, there must be at least one irreversible edge in D_n.

Proposition 4.2

Given a serial model (D_n, $A_n^m$, e₀), if x > 0, then e_i(x) and k_i,i+1(x) are both positive for all vertices E_i in D_n.

Proof

The definition of a rate function implies that k_ij(x) > 0 whenever x > 0 and (E_i, E_j) exists in D_n. Thus, k_i,i+1(x) > 0. From the King-Altman theorem, the determinants det Ã_i(x) are all composed of sums of products of rate functions, and for every vertex there is a connected n−1 path corresponding to a subsequence of C_n. Therefore, for all E_i, det Ã_i(x) cannot be 0 when x > 0. Furthermore, the King-Altman theorem asserts that all of these determinants have the same sign; hence, Eqn. (26) implies e_i(x) > 0.

Proposition 4.3

Given a serial model (D_n, $A_n^m$, e₀), if (E_i, E_i+1) and (E_j, E_j+1) are both irreversible edges in D_n and x > 0, then

$$e_i(\mathbf{x})k_{i,i+1}(\mathbf{x})=e_j(\mathbf{x})k_{j,j+1}(\mathbf{x}).$$ (35)

Proof

Recognizing our use of modular indexing, the King-Altman theorem implies

$$det{\stackrel{\sim }{\mathbf{A}}}_i(\mathbf{x})={(-1)}^{n-1}{k}_{i+1,i+2}(\mathbf{x})\cdots k_{i-2,i-1}(\mathbf{x})k_{i-1,i}(\mathbf{x}),$$ (36a)

$$det{\stackrel{\sim }{\mathbf{A}}}_j(\mathbf{x})={(-1)}^{n-1}{k}_{j+1,j+2}(\mathbf{x})\cdots k_{j-2,j-1}(\mathbf{x})k_{j-1,j}(\mathbf{x}).$$ (36b)

Since every factor of the form k_p,p+1(x) is found in each product except k_i,i+1(x) in the first and k_j,j+1(x) in the second, we have

$$det{\stackrel{\sim }{\mathbf{A}}}_i(\mathbf{x})k_{i,i+1}(\mathbf{x})=det{\stackrel{\sim }{\mathbf{A}}}_j(\mathbf{x})k_{j,j+1}(\mathbf{x}),$$ (37)

and it follows immediately from Eqn. (26) that

$$e_i(\mathbf{x})k_{i,i+1}(\mathbf{x})=e_j(\mathbf{x})k_{j,j+1}(\mathbf{x}).$$ (38)

4.5. Steady-state velocity and net rate functions

Propositions 4.1, 4.2 and 4.3 are of particular importance for two reasons. First, they provide conditions under which e_i(x) ≠ 0 so that 1/e_i(x) exists. Second, they provide a mechanism for unambiguously defining a property of a serial model that we may equate with the steady-state velocity of an enzymatic reaction.

Definition 4.6 (Velocity)

If (D_n, $A_n^m$, e₀) is a serial model with n > 2, and (E_i, E_i+1) is any irreversible edge in D_n, then the velocity v of the model is the function

$$\begin{gathered} v:\{\mathbf{x}\in {ℝ}^m:\mathbf{x}>\mathbf{0}\}\to ℝ, \\ v(\mathbf{x})=e_i(\mathbf{x})k_{i,i+1}(\mathbf{x}). \end{gathered}$$ (39)

Definition 4.7 (Net Rate Function)

If (D_n, $A_n^m$, e₀) is a serial model with n > 2 vertices, then the net rate function for the i-th vertex is defined as the function

$$\begin{gathered} k_i^{\prime }:\{\mathbf{x}\in {ℝ}^m:\mathbf{x}>\mathbf{0}\}\to ℝ, \\ {k}_i^{\prime }(\mathbf{x})=v(\mathbf{x})/e_i(\mathbf{x}). \end{gathered}$$ (40)

Proposition 4.4

If (D_n, $A_n^m$, e₀) is a serial model with n > 2 and (E_i, E_i+1) is an irreversible edge in D_n, then $k_i^{\prime }(\mathbf{x})=k_{i,i+1}(\mathbf{x})$ whenever x > 0.

Proof

Since x > 0 we have e_i(x) > 0 by Prp. 4.2. Therefore, $k_i^{\prime }(\mathbf{x})$ exists and according to Prp. 4.3 is given by

$$k_i^{\prime }(\mathbf{x})=\frac{v(\mathbf{x})}{e_i(\mathbf{x})}=\frac{e_i(\mathbf{x})k_{i,i+1}(\mathbf{x})}{e_i(\mathbf{x})}=k_{i,i+1}(\mathbf{x}).$$ (41)

We are now in a position to prove the recursive expression for net rate constants first identified by Cleland (1975).

Proposition 4.5 (Cleland)

Given a serial model with n > 2 vertices, if x > 0, then the net rate function at x for the i-th vertex E_i is given by

$$k_i^{\prime }(\mathbf{x})=\frac{k_{i,i+1}(\mathbf{x})k_{i+1}^{\prime }(\mathbf{x})}{k_{i+1,i}(\mathbf{x})+k_{i+1}^{\prime }(\mathbf{x})}.$$ (42)

Proof

Let n be any integer greater than 2. Prp. 4.1 asserts that there is at least one irreversible edge in the digraph D_n of the serial model. We permute the indices of the vertices such that (E_n, E₁) is an irreversible edge. Therefore, D_n must contain the edges (E₁, E₂), (E_n, E₁) and possibly (E₂, E₁) but not (E₁, E_n). No other edges in D_n include E₁. Thus,

$${[\mathbf{A}(\mathbf{x})]}_{1i}=\{\begin{array}{ll}-k_{12}(\mathbf{x}),\hfill & i=1,\hfill \\ k_{i1}(\mathbf{x}),\hfill & i=2,n,\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$$ (43)

and and it follows from Eqn. (26) that

$$k_{21}(\mathbf{x})e_2(\mathbf{x})+k_{n1}(\mathbf{x})e_n(\mathbf{x})-k_{12}(\mathbf{x})e_1(\mathbf{x})=0.$$ (44)

Since x > 0, Prp. 4.2 implies that the net rate functions for E₁, E₂ and E_n are all positive at x, and we may write

$$k_{21}(\mathbf{x})\frac{v(\mathbf{x})}{k_2^{\prime }(\mathbf{x})}+k_{n1}(\mathbf{x})\frac{v(\mathbf{x})}{k_n^{\prime }(\mathbf{x})}-k_{12}(\mathbf{x})\frac{v(\mathbf{x})}{k_1^{\prime }(\mathbf{x})}=0.$$ (45)

Prp. 4.4 implies that $k_n^{\prime }(\mathbf{x})=k_{n1}(\mathbf{x})$, so Eqn. (45) rearranges to

$$k_1^{\prime }(\mathbf{x})=\frac{k_{12}(\mathbf{x})k_2^{\prime }(\mathbf{x})}{k_{21}(\mathbf{x})+k_2^{\prime }(\mathbf{x})},$$ (46)

since v(x) > 0. This proves the result for i = 1.

If 1 < i < n, then D_n must contain the edges (E_i−1,E_i), (E_i,E_i+1) and possibly the reverse of either. No other edges in D_n include E_i so that

$${[\mathbf{A}(\mathbf{x})]}_{ij}=\{\begin{array}{ll}-(k_{i,i-1}(\mathbf{x})+k_{i,i+1}(\mathbf{x})),\hfill & j=i,\hfill \\ k_{ji}(\mathbf{x}),\hfill & j=i\pm 1,\hfill \\ 0,\hfill & \text{otherwise.}\hfill \end{array}$$ (47)

We now make the inductive hypothesis that Eqn. (42) holds for some vertex E_i where 1 ≤ i < n−1 and consider the vertex E_i+1. Since 1 < i+1 < n, we may use (47) to write Eqn. (26) for e_i+1(x) as

$$k_{i,i+1}(\mathbf{x})e_i(\mathbf{x})-(k_{i+1,i}(\mathbf{x})+k_{i+1,i+2})(\mathbf{x})e_{i+1}(\mathbf{x})+k_{i+2,i+1}(\mathbf{x})e_{i+2}(\mathbf{x})=0.$$ (48)

Since x > 0, Prp. 4.2 implies that the net rate functions for E_i, E_i+1 and E_i+2 evaluated at x are all positive, and we may write

$$k_{i,i+1}(\mathbf{x})\frac{v(\mathbf{x})}{k_i^{\prime }(\mathbf{x})}-(k_{i+1,i}(\mathbf{x})+k_{i+1,i+2}(\mathbf{x}))\frac{v(\mathbf{x})}{k_{i+1}^{\prime }(\mathbf{x})}+k_{i+2,i+1}(\mathbf{x})\frac{v(\mathbf{x})}{k_{i+2}^{\prime }(\mathbf{x})}=0.$$ (49)

However, the inductive hypothesis implies that

$$k_{i,i+1}(\mathbf{x})\frac{v(\mathbf{x})}{k_i^{\prime }(\mathbf{x})}=\frac{k_{i+1,i}(\mathbf{x})+k_{i+1}^{\prime }(\mathbf{x})}{k_{i+1}^{\prime }(\mathbf{x})}v(\mathbf{x}).$$ (50)

Combining Eqns. (49) and (50) and rearranging we get

$$k_{i+1}^{\prime }(\mathbf{x})=\frac{k_{i+1,i+2}(\mathbf{x})k_{i+2}^{\prime }(\mathbf{x})}{k_{i+2,i+1}(\mathbf{x})+k_{i+2}^{\prime }(\mathbf{x})}.$$ (51)

Therefore, it follows inductively that Eqn. (42) holds for all i < n. All that is left is to show that it holds for i = n. Now, since (E_n, E₁) is an irreversible edge, the definition of a model implies that k_1n(x) = 0 for all x. Therefore, by Prp. 4.4 we have

$$k_n^{\prime }(\mathbf{x})=k_{n1}(\mathbf{x})=\frac{k_{n1}(\mathbf{x})k_1^{\prime }(\mathbf{x})}{0+k_1^{\prime }(\mathbf{x})}=\frac{k_{n1}(\mathbf{x})k_1^{\prime }(\mathbf{x})}{k_{1n}(\mathbf{x})+k_1^{\prime }(\mathbf{x})}.$$ (52)

Thus Eqn. (42) holds for all i ≤ n. Furthermore, since our choice of n > 2 was arbitrary, the result holds for all serial models with n > 2.

Definition 4.8 (Equilibrium Function)

Given a serial model with n vertices, the subgraph defined by the sequence of edges along C_n given by

$$(E_i,E_{i+1})(E_{i+1},E_{i+2})\dots (E_{j-2},E_{j-1})(E_{j-1},E_j),$$ (53)

where 1 ≤ i < j ≤ n has an associated equilibrium function given by

$$\begin{gathered} K_{ji}:\{\mathbf{x}\in {ℝ}^m:k_{p,p+1}(\mathbf{x})\ne 0\mathit{for}\mathit{all}i\le p<j\}, \\ {K}_{ji}(\mathbf{x})=\prod _{p=i}^{j-1}\frac{k_{p+1,p}(\mathbf{x})}{k_{p,p+1}(\mathbf{x})}, \end{gathered}$$ (54)

and K_ii(x) := 1 for all x.

Proposition 4.6

Given a serial model (D_n, $P_m^n$, e₀) with n > 2, if x > 0, then K_ji(x) ≥ 0 for any two vertices E_i and E_j where 1 ≤ i ≤ j ≤ n. Furthermore, if i < j and the sequence

$$(E_i,E_{i+1})(E_{i+1},E_{i+2})\dots (E_{j-1},E_j),$$ (55)

does not contain any irreversible edges in D_n, then K_ji(x) > 0.

Proof

Index the vertices such that (E_n,E₁) is irreversible. By definition,

$$0<v(\mathbf{x}):=e_n(\mathbf{x})k_{n1}(\mathbf{x})=\frac{e_{0}det{\stackrel{\sim }{\mathbf{A}}}_n(\mathbf{x})k_{n1}(\mathbf{x})}{{\sum }_{i=1}^{n}det{\stackrel{\sim }{\mathbf{A}}}_i(\mathbf{x})},$$ (56)

and therefore since x > 0, we have by the King-Altman theorem

$$\begin{array}{ll}0<det{\stackrel{\sim }{\mathbf{A}}}_n(\mathbf{x})k_{n1}(\mathbf{x}),\hfill & \hfill n\text{is}\text{odd},\\ 0>det{\stackrel{\sim }{\mathbf{A}}}_n(\mathbf{x})k_{n1}(\mathbf{x}),\hfill & \hfill n\text{is}\text{even},\end{array}$$

which implies

$$0<k_{12}(\mathbf{x})k_{23}(\mathbf{x})\cdots k_{n-1,n}(\mathbf{x})k_{n1}(\mathbf{x}),$$

so k_p,p+1(x) > 0 for all 1 ≤ p ≤ n, and thus K_ji(x) exists. The hypothesis that x > 0 also implies k_p+1,p(x) ≥ 0 for all p so that K_ji(x) ≥ 0. If the sequence in (55) does not contain any irreversible edges, then k_p+1,p(x) > 0 for all i ≤ p < j and K_ij(x) > 0.

The next proposition provides a nonrecursive expression for net rate functions. It was this form that Noyes (1964) discussed in his analysis of reaction kinetics under a uniform flux (i.e., steady-state) approximation. Our proof follows from the recursive expression provided by Prp. 4.5.

Proposition 4.7

Let (D_n, $A_n^m$, e₀) be a serial model with n > 2 and indexed such that (E_n,E₁) is an irreversible edge. If x > 0, then

$$\frac{1}{k_i^{\prime }(\mathbf{x})}=\sum _{j=i}^n\frac{K_{ji}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})},$$ (57)

Proof

By hypothesis, Prp. 4.2 implies that $k_i^{\prime }(\mathbf{x})>0$ for all i, so the reciprocals $1/k_i^{\prime }(\mathbf{x})$ exist for all i. Suppose first that i = n, then Prp. 4.4 asserts that

$$\frac{1}{k_n^{\prime }(\mathbf{x})}=\frac{1}{k_{n1}(\mathbf{x})}=\frac{K_{nn}(\mathbf{x})}{k_{n,n+1}(\mathbf{x})}=\sum _{j=n}^n\frac{K_{nj}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})},$$ (58)

such that Eqn. (57) holds for i = n. Now, assume the inductive hypothesis that expression (57) holds for some enzyme species E_i where 1 < i ≤ n and consider the species E_i−1. Since $k_{i-1}^{\prime }(\mathbf{x})>0$ we may write (see Prp. 4.5)

$$\frac{1}{k_{i-1}^{\prime }(\mathbf{x})}=\frac{k_{i,i-1}(\mathbf{x})}{k_{i-1,i}(\mathbf{x})}·\frac{1}{k_i^{\prime }(\mathbf{x})}+\frac{1}{k_{i-1,i}(\mathbf{x})}.$$ (59)

Applying the inductive hypothesis, we get

$$\frac{1}{k_{i-1}^{\prime }(\mathbf{x})}=\frac{k_{i,i-1}(\mathbf{x})}{k_{i-1,i}(\mathbf{x})}\sum _{j=i}^n\frac{K_{ji}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}+\frac{1}{k_{i-1,i}(\mathbf{x})}.$$ (60)

However, according to the definition of the equilibrium function,

$$\frac{k_{i,i-1}(\mathbf{x})}{k_{i-1,i}(\mathbf{x})}{K}_{ji}(\mathbf{x})=\frac{k_{i,i-1}(\mathbf{x})}{k_{i-1,i}(\mathbf{x})}\prod _{p=i}^{j-1}\frac{k_{p+1,p}(\mathbf{x})}{k_{p,p+1}(\mathbf{x})}=\prod _{p=i-1}^{j-1}\frac{k_{p+1,p}(\mathbf{x})}{k_{p,p+1}(\mathbf{x})}=K_{j,i-1}(\mathbf{x}).$$ (61)

Substitution of this expression into Eqn. (60), we get

$$\frac{1}{k_{i-1}^{\prime }(\mathbf{x})}=\sum _{j=i}^n\frac{K_{j,i-1}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}+\frac{1}{k_{i-1,i}(\mathbf{x})}=\sum _{j=i-1}^n\frac{K_{j,i-1}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}.$$ (62)

Thereby proving the inductive case. Since our choice of n > 2 was arbitrary, the result is true for all serial models where n > 2.

Corollary 4.7.1

If i ≤ q < n and (E_q,E_q+1) is an irreversible edge, then

$$\frac{1}{k_i^{\prime }(\mathbf{x})}=\sum _{j=i}^q\frac{K_{ji}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}.$$ (63)

Proof

By definition, k_q+1,q(x) = 0 for all x, because (E_q+1,E_q) does not exist in D_n. Therefore, K_ji(x) = 0 for all j > q.

4.6. Sensitivity indices

In the previous development, we have treated net rate functions as functions of x. However, they depend on x via the rate functions alone. Therefore, we can treat the rate functions as independent, parametric variables in their own right when analyzing the net rate functions. Following the example of Ray (1983), we can then consider the sensitivity index S_ij of the net rate function $k_i^{\prime }$ with respect to the rate function k_j,j+1 where i ≤ j as

$$S_{ij}(\mathbf{x}):=\frac{1/k_{j,j+1}(\mathbf{x})}{1/k_i^{\prime }(\mathbf{x})}·\left(\frac{\partial (1/k_i^{\prime })}{\partial (1/k_{j,j+1}(\mathbf{x}))}\right)(\mathbf{x}),$$ (64)

where the partial derivative holds K_j+1,j(x) as well as all evaluations of the rate functions other than k_j,j+1(x) and k_j+1,j(x) as constant values.

Proposition 4.8

Let (D_n, $A_n^m$, e₀) be a serial model with n > 2. If x > 0, then the sensitivity index of the i-th net rate function with respect to rate function k_j,j+1 where i ≤ j is given by

$$S_{ij}(\mathbf{x})=\frac{k_i^{\prime }(\mathbf{x})K_{ji}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}.$$ (65)

Proof

In order to evaluate the derivative in Eqn. (64), we replace the parametrically defined variable k_j+1,j(x) in Eqn. (57) with

$$k_{j+1,j}(\mathbf{x})=k_{j,j+1}(\mathbf{x})K_{j+1,j}(\mathbf{x}),$$ (66)

noting that K_j+1,j(x) exists by Prp. 4.6 and is to be treated as a constant when taking the partial derivative, to get

$$\frac{1}{k_i^{\prime }(\mathbf{x})}=\sum _{p=i}^{j-1}\frac{K_{pi}(\mathbf{x})}{k_{p,p+1}(\mathbf{x})}+\frac{K_{ji}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}+\sum _{p=j+1}^n\frac{K_{pi}(\mathbf{x})}{k_{p,p+1}(\mathbf{x})},$$ (67)

where the K_ji(x) depend only on k_j+1,j(x) and k_j,j+1(x) only via the constant ratio K_j+1,j(x). Therefore, the first and third terms on the right-hand-side of (67) are 0 when evaluating the derivative, and it follows that

$$\left(\frac{\partial (1/k_i^{\prime })}{\partial (1/k_{j,j+1}(\mathbf{x}))}\right)(\mathbf{x})=K_{ji}(\mathbf{x}).$$ (68)

Substituting this result into the definition Eqn. (64), we get for all x > 0,

$$S_{ij}(\mathbf{x})=\frac{k_i^{\prime }(\mathbf{x})K_{ji}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}.$$ (69)

Corollary 4.8.1

If x > 0, then 0 ≤ S_ij(x) ≤ 1 for all j ≥ i, and

$$\sum _{j=i}^n{S}_{ij}(\mathbf{x})=1.$$ (70)

Proof

The result that S_ij(x) ≥ 0 follows immediately from the result that $k_i^{\prime }(\mathbf{x})$, K_ji(x) and k_j,j+1(x) are all non-negative. If we consider the sum of S_ij(x) over all j ≥ i, then

$$\sum _{j=i}^n{S}_{ij}(\mathbf{x})=\left(\sum _{j=i}^n\frac{K_{ji}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}\right)k_i^{\prime }(\mathbf{x}).$$ (71)

However, using the result from Prp. 4.7, we find that

$$\sum _{j=i}^n{S}_{ij}(\mathbf{x})=\left(\sum _{j=i}^n\frac{K_{ji}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}\right)/\left(\sum _{j=i}^n\frac{K_{ji}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}\right)=1.$$ (72)

Corollary 4.8.2

If i ≤ q < n and (E_q,E_q+1) is an irreversible edge in D_n, then S_ij = 0 for all j > q, hence ${\sum }_{j=i}^q{S}_{ij}=1$.

Proof

The proof follows from Cor. 4.8.1 and is essentially identical to that for Cor. 4.7.1.

4.7. Isomorphic models

Definition 4.9 (Isomorphic Models)

Suppose $M=(D_n,A_n^m,e_0)$ and $M^{\ast }=(D_n^{\ast },A_n^{\ast m},e_0^{\ast })$ are steady-state models where $e_0=e_0^{\ast }$. We say that M and M^* are isomorphic if there exists a set of n(n − 1) positive real numbers ${\{{{}^{\ast }k}_{ij}\}}_{i\ne j}^{n,n}$ and an isomorphism g between D_n and $D_n^{\ast }$ such that whenever (E_i,E_j) is an edge in D_n and $g(E_i)=E_p^{\ast }$ and $g(E_j)=E_q^{\ast }$, we have $k_{ij}(\mathbf{x})={{}^{\ast }k}_{ij}{k}_{pq}^{\ast }(\mathbf{x})$ for all x ∈ ℝ^m.

Note that if two steady-state models are isomorphic, there may be more than one isomorphism between the two digraphs where the condition on $A_n^m$ and $A_n^{\ast m}$ is fulfilled. When working with isomorphic steady-state models, we will always assume an indexing that follows one of these isomorphisms g so that $g(E_i)=E_i^{\ast }$ for all indices i. Furthermore, it is straightforward to show that if models 1 and 2 are isomorphic, and models 2 and 3 are isomorphic, then models 1 and 3 are isomorphic. In other words, the relation is transitive.

Proposition 4.9

Suppose (D_n, $A_n^m$, e₀) and ( $D_n^{\ast },A_n^{\ast m}$, e₀) are isomorphic serial models. If (E_i,E_i+1) is an irreversible edge in D_n, then

$$\frac{k_i^{\prime }}{k_i^{\prime \ast }}={{}^{\ast }k}_{i,i+1},$$ (73)

and if there are no irreversible edges in the sequence

$$(E_i,E_{i+1})(E_{i+1},E_{i+2})\dots (E_{q-1},E_q),$$ (74)

with (E_q,E_q+1) being an irreversible edge in D_n, then

$$\frac{k_i^{\prime }}{k_i^{\prime \ast }}=S_{ii}{{}^{\ast }k}_{i,i+1}+\sum _{j=i+1}^q\left(S_{ij}{{}^{\ast }k}_{j,j+1}\prod _{p=i}^{j-1}\frac{{{}^{\ast }k}_{p,p+1}}{{{}^{\ast }k}_{p+1,p}}\right),$$ (75)

where the ratio function $k_i^{\prime }/k_i^{\prime \ast }$ is defined for all x > 0.

Proof

Let x be any vector in ℝ^m such that x > 0. Proposition 4.8 implies

$$S_{ii}(\mathbf{x})=\frac{k_i^{\prime }(\mathbf{x})}{k_{i,i+1}(\mathbf{x})}=\frac{k_i^{\prime }(\mathbf{x})}{{{}^{\ast }k}_{i,i+1}{k}_{i,i+1}^{\ast }(\mathbf{x})}=\frac{k_i^{\prime }(\mathbf{x})}{k_i^{\prime \ast }(\mathbf{x})}·\frac{S_{ii}^{\ast }(\mathbf{x})}{{{}^{\ast }k}_{i,i+1}}.$$ (76)

However, if (E_i,E_i+1) is irreversible, Cor. 4.8.2 implies

$$S_{ii}(\mathbf{x})=S_{ii}^{\ast }(\mathbf{x})=1,$$

for all x > 0 and therefore

$$\frac{k_i^{\prime }(\mathbf{x})}{k_i^{\prime \ast }(\mathbf{x})}·\frac{1}{{{}^{\ast }k}_{j,j+1}}=1,$$ (77)

which rearranges immediately to Eqn. (73). If, however, (E_i,E_i+1) is not irreversible, then for any i < j ≤ q in sequence (74), Prp. 4.8 asserts

$$S_{ij}(\mathbf{x})=\frac{k_i^{\prime }(\mathbf{x})K_{ji}(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}=\frac{k_i^{\prime }(\mathbf{x})}{k_{j,j+1}(\mathbf{x})}\prod _{p=i}^{j-1}\frac{k_{p+1,p}(\mathbf{x})}{k_{p,p+1}(\mathbf{x})}.$$ (78)

Therefore, it follows that

$$S_{ij}(\mathbf{x})=k_i^{\prime }(\mathbf{x})\left(\frac{1}{k_{j,j+1}^{\ast }(\mathbf{x})}\prod _{r=i}^{j-1}\frac{k_{r+1,r}^{\ast }(\mathbf{x})}{k_{r,r+1}^{\ast }(\mathbf{x})}\right)\left(\frac{1}{{{}^{\ast }k}_{j,j+1}}\prod _{p=i}^{j-1}\frac{{{}^{\ast }k}_{p+1,p}}{{{}^{\ast }k}_{p,p+1}}\right).$$ (79)

Applying the results of Prp. 4.8 for ( $D_n^{\ast },A_n^{\ast m}$, e₀), we find that

$$S_{ij}(\mathbf{x})=\frac{k_i^{\prime }(\mathbf{x})}{k_i^{\prime \ast }(\mathbf{x})}{S}_{ij}^{\ast }(\mathbf{x})\left(\frac{1}{{{}^{\ast }k}_{j,j+1}}\prod _{p=i}^{j-1}\frac{{{}^{\ast }k}_{p+1,p}}{{{}^{\ast }k}_{p,p+1}}\right),$$ (80)

which we can rearrange to get

$$\frac{k_i^{\prime }(\mathbf{x})}{k_i^{\prime \ast }(\mathbf{x})}{S}_{ij}^{\ast }(\mathbf{x})=S_{ij}(\mathbf{x})\left({{}^{\ast }k}_{j,j+1}\prod _{p=i}^{j-1}\frac{{{}^{\ast }k}_{p,p+1}}{{{}^{\ast }k}_{p+1,p}}\right),i<j\le q.$$ (81)

Summing (81) over all j for i < j ≤ q and adding Eqn. (76), we have

$$\frac{k_i^{\prime }(\mathbf{x})}{k_i^{\prime \ast }(\mathbf{x})}\sum _{j=i}^q{S}_{ij}^{\ast }(\mathbf{x})=S_{ii}(\mathbf{x}){{}^{\ast }k}_{i,i+1}+\sum _{j=i+1}^q\left(S_{ij}(\mathbf{x}){{}^{\ast }k}_{j,j+1}\prod _{p=i}^{j-1}\frac{{{}^{\ast }k}_{p,p+1}}{{{}^{\ast }k}_{p+1,p}}\right),$$ (82)

and use of Cor. 4.8.2 yields Eqn. (75).

4.8. Perturbation effects

Prp. 4.9 is our key result, and while the notation is useful for ensuring that all of the ratios exist (i.e., there is no division by zero), it is rather ungainly. Having established this result, however, we can simplify the notation considerably to match that in Sec. 2.4 by defining the constants ^*κ_ij (where j ≥ i) such that

$$\begin{gathered} {{}^{\ast }\kappa }_{ij}:={{}^{\ast }k}_{i,i+1},j=i, \\ {{}^{\ast }\kappa }_{ij}:={{}^{\ast }k}_{j,j+1}\prod _{p=i}^{j-1}\frac{{{}^{\ast }k}_{p,p+1}}{{{}^{\ast }k}_{p+1,p}},j>i. \end{gathered}$$ (83)

This will allow us to write both Eqns. (73) and (75) together using the more compact expression

$$\frac{k_i^{\prime }}{k_i^{\prime \ast }}=\sum _{j\ge i}{S}_{ij}{{}^{\ast }\kappa }_{ij},$$ (84)

where the sum is understood to extend from i to q for the first irreversible edge (E_q,E_q+1). It is also worth pointing out for the sake of clarity that we have defined the ^*κ_ij in Eqn. (83) differently than we did in Sec. 2.4, though the results are equivalent. In Sec. 2.4, they represented constant-valued functions defined informally based on chemical intuition. Here they are constants defined rigorously with respect to two isomorphic serial models.

The definition of a net rate function also implies that whenever x > 0, we can write for any pair of isomorphic serial models

$$\frac{v(\mathbf{x})}{v^{\ast }(\mathbf{x})}=\frac{k_i^{\prime }(\mathbf{x})}{k_i^{\prime \ast }(\mathbf{x})}·\frac{e_i(\mathbf{x})}{e_i^{\ast }(\mathbf{x})},$$ (85)

for any vertex E_i, since Prp. 4.2 asserts that v(x) and v^*(x) are both positive. We can rearrange this expression to also get

$$\frac{v(\mathbf{x})}{v^{\ast }(\mathbf{x})}{e}_i^{\ast }(\mathbf{x})=\frac{k_i^{\prime }(\mathbf{x})}{k_i^{\prime \ast }(\mathbf{x})}{e}_i(\mathbf{x}),$$ (86)

and summing over all the vertices, we have

$$\sum _{i=1}^n\frac{k_i^{\prime }(\mathbf{x})}{k_i^{\prime \ast }(\mathbf{x})}{e}_i(\mathbf{x})=\sum _{i=1}^n\frac{v(\mathbf{x})}{v^{\ast }(\mathbf{x})}{e}_i^{\ast }(\mathbf{x})=\frac{v(\mathbf{x})}{v^{\ast }(\mathbf{x})}\sum _{i=1}^n{e}_i^{\ast }(\mathbf{x})=\frac{v(\mathbf{x})}{v^{\ast }(\mathbf{x})}{e}_0,$$ (87)

which rearranges immediately to provide

$$\frac{v(\mathbf{x})}{v^{\ast }(\mathbf{x})}=\sum _{i=1}^n\frac{e_i(\mathbf{x})}{e_0}·\frac{k_i^{\prime }(\mathbf{x})}{k_i^{\prime \ast }(\mathbf{x})}.$$ (88)

This defines a function on all x > 0 that we can write

$$\begin{gathered} {}^{\ast }v:\{\mathbf{x}\in {ℝ}^m:\mathbf{x}>\mathbf{0}\}\to ℝ, \\ {}^{\ast }v(\mathbf{x})=v(\mathbf{x})/v^{\ast }(\mathbf{x}). \end{gathered}$$ (89)

This function is thus defined for any pair of isomorphic serial models.

The expression for ^*v(x) can be simplified if we introduce the notation

$$f_i(\mathbf{x}):=e_i(\mathbf{x})/e_0,$$ (90)

so that for all x > 0, we have

$${}^{\ast }v(\mathbf{x})=\sum _{i=1}^n{f}_i(\mathbf{x})k_i^{\prime }(\mathbf{x})/k_i^{\prime \ast }(\mathbf{x})=\sum _{i=1}^n\sum _{j\ge i}{f}_i(\mathbf{x})S_{ij}(\mathbf{x}){{}^{\ast }\kappa }_{ij}.$$ (91)

Proposition 4.2 implies 0 < f_i(x) < 1 for all x > 0, and from Eqn. (26b),

$$\sum _{i=1}^n{f}_i(\mathbf{x})=1.$$ (92)

Combining this result with Cor. 4.8.2, it follows that

$$\sum _{i=1}^n\sum _{j\ge i}{f}_i(\mathbf{x})S_{ij}(\mathbf{x})=1.$$ (93)

Hence, ^*v(x) is a weighted average of the constant values ^*κ_ij.

4.9. Limits

We now want to consider limits of the function ^*v as discussed in Sec. 2.3. Since the entire vector x is to be considered in the limit, we will express limits using the compact notation

$$\mathbf{x}\to \mathbf{y}={[y_1,y_2,\cdots ,y_m]}^{\top },$$ (94)

where each y_i represents 0⁺, a positive real number or ∞. As discussed in Sec. 2.3, it is not always guaranteed that such a limit exists for ^*v given any pair of isomorphic serial models. Nevertheless, results useful for the interpretation of the limits of ^*v are given by the following propositions.

Proposition 4.10

Let v₁ be the velocity function for a serial model ${(D_n,A_n^m,e_0)}_1$ and let v₂ be the velocity function for an isomorphic model ${(D_n{A}_n^m,e_0)}_2$. If

$$\underset{\mathbf{x}\to \mathbf{y}}{lim}{v}_1(\mathbf{x})/v^{\ast }(\mathbf{x})$$ (95)

exists for all models ( $D_n^{\ast },A_n^{\ast m}$, e₀) isomorphic to ${(D_n,A_n^m,e_0)}_1$, then

$$\underset{\mathbf{x}\to \mathbf{y}}{lim}{v}_2(\mathbf{x})/v^{\ast }(\mathbf{x})$$ (96)

exists for all models ( $D_n^{\ast },A_n^{\ast m}$, e₀) isomorphic to ${(D_n,A_n^m,e_0)}_2$.

Proof

Since ${(D_n,A_n^m,e_0)}_2$ is isomorphic to ${(D_n,A_n^m,e_0)}_1$, the limit

$$\underset{\mathbf{x}\to \mathbf{y}}{lim}{v}_1(\mathbf{x})/v_2(\mathbf{x}),$$ (97)

exists by hypothesis. Furthermore, Prp. 4.9 and Eqns. (91) and (93) imply that the ratio v₁(x)/v₂(x) is bounded below on x > 0 by a positive value such that the limit must also be positive. Therefore, the limit

$$\underset{\mathbf{x}\to \mathbf{y}}{lim}{v}_2(\mathbf{x})/v_1(\mathbf{x})$$ (98)

also exists. If ( $D_n^{\ast },A_n^{\ast m}$, e₀) is any model isomorphic to ${(D_n,A_n^m,e_0)}_2$, then it is also isomorphic to ${(D_n,A_n^m,e_0)}_1$, and the existence of the limit in Eqn. (96) follows from

$$\underset{\mathbf{x}\to \mathbf{y}}{lim}\frac{v_2(\mathbf{x})}{v^{\ast }(\mathbf{x})}=\underset{\mathbf{x}\to \mathbf{y}}{lim}\frac{v_2(\mathbf{x})v_1(\mathbf{x})}{v_1(\mathbf{x})v^{\ast }(\mathbf{x})}=\left(\underset{\mathbf{x}\to \mathbf{y}}{lim}\frac{v_2(\mathbf{x})}{v_1(\mathbf{x})}\right)\left(\underset{\mathbf{x}\to \mathbf{y}}{lim}\frac{v_1(\mathbf{x})}{v^{\ast }(\mathbf{x})}\right).$$ (99)

Proposition 4.11

Let (D_n, $A_n^m$, e₀) be a serial model with n > 2. If the limit lim_x→y ^*v(x) exists for some condition y and all isomorphic models, then the limit lim_x→y f_i(x) exists for all i.

Proof

Let ( $D_n^{\ast },A_n^{\ast m}$, e₀) be a serial model isomorphic to (D_n, $A_n^m$, e₀) such that all elements of {^*k_up} are unity except ^*k_i,i+1 = ^*k_i,i−1 = 2, and thus

$${{}^{\ast }\kappa }_{up}=\{\begin{array}{ll}1,\hfill & u\ne i,\hfill \\ 2,\hfill & u=i.\hfill \end{array}$$ (100)

Equations (91) and (93) then imply that for all x > 0,

$$\begin{gathered} {}^{\ast }v(\mathbf{x})=2f_i(\mathbf{x})+\sum _{u\ne i}\sum _{p\ge u}{f}_u(\mathbf{x})S_{up}(\mathbf{x}), \\ =2f_i(\mathbf{x})+(1-f_i(\mathbf{x})), \\ =f_i(\mathbf{x})+1. \end{gathered}$$ (101)

Hence, the existence of lim_x→y f_i(x) follows from

$$\underset{\mathbf{x}\to \mathbf{y}}{lim}{f}_i(\mathbf{x})=\underset{\mathbf{x}\to \mathbf{y}}{lim}({}^{\ast }v(\mathbf{x})-1).$$ (102)

Proposition 4.12

Let (D_n, $A_n^m$, e₀) be a serial model with n > 2. If the limit lim_x→y ^*v(x) exists for some condition y and all isomorphic models, then for any isomorphic serial model and any i, ${lim}_{\mathbf{x}\to \mathbf{y}}{k}_i^{\prime }(\mathbf{x})/k_i^{\prime \ast }(\mathbf{x})$ exists or

$$\underset{\mathbf{x}\to \mathbf{y}}{lim}{f}_i(\mathbf{x})k_i^{\prime }(\mathbf{x})/k_i^{\prime \ast }(\mathbf{x})=0.$$ (103)

Proof

From Eqn. (84) and Cor. 4.8.2, we have

$$f_i(\mathbf{x})min\{{{}^{\ast }\kappa }_{ij}\}\le f_i(\mathbf{x})k_i^{\prime }(\mathbf{x})/k_i^{\prime \ast }(\mathbf{x})\le f_i(\mathbf{x})max\{{{}^{\ast }\kappa }_{ij}\}.$$ (104)

If lim_x→y f_i(x) = 0, then Eqn. (103) follows from the Squeeze Theorem. Furthermore, Eqn. (86) and Prps. 4.10 & 4.11 imply the existence of

$$\underset{\mathbf{x}\to \mathbf{y}}{lim}{f}_i(\mathbf{x})k_i^{\prime }(\mathbf{x})/k_i^{\prime \ast }(\mathbf{x})=\underset{\mathbf{x}\to \mathbf{y}}{lim}{f}_i^{\ast }{(\mathbf{x})}^{\ast }v(\mathbf{x}).$$ (105)

Therefore, if lim_x→y f_i(x) ≠ 0, then ${lim}_{\mathbf{x}\to \mathbf{y}}{k}_i^{\prime }(\mathbf{x})/k_i^{\prime \ast }(\mathbf{x})$exists according to

$$\underset{\mathbf{x}\to \mathbf{y}}{lim}\frac{k_i^{\prime }(\mathbf{x})}{k_i^{\prime \ast }(\mathbf{x})}=\underset{\mathbf{x}\to \mathbf{y}}{lim}\frac{f_i(\mathbf{x})k_i^{\prime }(\mathbf{x})}{f_i(\mathbf{x})k_i^{\prime \ast }(\mathbf{x})}=\frac{{lim}_{\mathbf{x}\to \mathbf{y}}{f}_i(\mathbf{x})k_i^{\prime }(\mathbf{x})/k_i^{\prime \ast }(\mathbf{x})}{{lim}_{\mathbf{x}\to \mathbf{y}}{f}_i(\mathbf{x})}.$$ (106)

Proposition 4.13

Let (D_n, $A_n^m$, e₀) be a serial model with n > 2 and suppose the limit lim_x→y ^*v(x) exists for some condition y and all isomorphic models. If lim_x→y f_i(x) ≠ 0, then lim_x→y S_ij(x) exists for all j ≥ i.

Proof

Choose an isomorphic model such that all elements of {^*k_up} are unity except for ^*k_j,j+1 = ^*k_j+1,j = 2. It then follows from Eqn. (84) that

$$k_i^{\prime }(\mathbf{x})/k_i^{\prime \ast }(\mathbf{x})=2S_{ij}(\mathbf{x})+(1-S_{ij}(\mathbf{x}))=S_{ij}(\mathbf{x})+1.$$ (107)

Therefore, the existence of lim_x→y S_ij(x) is implied by Prp. 4.12, because

$$\underset{\mathbf{x}\to \mathbf{y}}{lim}{S}_{ij}(\mathbf{x})=\underset{\mathbf{x}\to \mathbf{y}}{lim}(k_i^{\prime }(\mathbf{x})/k_i^{\prime \ast }(\mathbf{x})-1).$$ (108)

4.10. Two-vertex models

The development in Secs. 4.5–4.9 only considered serial mechanisms where n > 2, because directed graphs with only two vertices are unoriented. Nevertheless, it is easy to show that the preceding results are also applicable to two-vertex serial models of the form

$$E_1\underset{k_{21}(\mathbf{x})}{\overset{k_{12}(\mathbf{x})}{\rightleftharpoons }}{E}_2.$$ (109)

To do so, a forward direction to the model must be imposed by splitting the E₂ → E₁ reaction into reverse and forward components governed by rate functions k_r and k_v, respectively, where k_v ≠ 0 such that

$$k_{21}(\mathbf{x})=k_r(\mathbf{x})+k_v(\mathbf{x}).$$ (110)

Next, we construct a three-vertex model of the form

$${\stackrel{\sim }{E}}_1\underset{2k_r(\mathbf{x})}{\overset{k_{12}(\mathbf{x})}{\rightleftharpoons }}{\stackrel{\sim }{E}}_2\stackrel{2k_v(\mathbf{x})}{\to }{\stackrel{\sim }{E}}_3\stackrel{2k_v(\mathbf{x})}{\to }{\stackrel{\sim }{E}}_1.$$ (111)

It is straightforward to show that the solutions to Eqn. (26) for the models in (109) and (111) are related according to

$$e_1(\mathbf{x})={\stackrel{\sim }{e}}_1(\mathbf{x}),$$ (112a)

$$e_2(\mathbf{x})={\stackrel{\sim }{e}}_2(\mathbf{x})+{\stackrel{\sim }{e}}_3(\mathbf{x}),$$ (112b)

and that ṽ(x) = v(x) = k_v(x)e₂(x). It follows then that the net rate function for E₁ is equal to that for Ẽ₁, and we have

$$\begin{gathered} {}^{\ast }v(\mathbf{x})={\stackrel{\sim }{f}}_1(\mathbf{x})\frac{k_1^{\prime }(\mathbf{x})}{k_1^{\prime \ast }(\mathbf{x})}+{\stackrel{\sim }{f}}_2(\mathbf{x})\frac{k_v^{\prime }(\mathbf{x})}{k_v^{\prime \ast }(\mathbf{x})}+{\stackrel{\sim }{f}}_3(\mathbf{x})\frac{k_v^{\prime }(\mathbf{x})}{k_v^{\prime \ast }(\mathbf{x})}, \\ =f_1(\mathbf{x})\frac{k_1^{\prime }(\mathbf{x})}{k_1^{\prime \ast }(\mathbf{x})}+f_2(\mathbf{x})\frac{k_v^{\prime }(\mathbf{x})}{k_v^{\prime \ast }(\mathbf{x})}, \end{gathered}$$ (113)

since the factor of two cancels in the ratio functions ^*k_v.