Thermal Expansion in Layered Na_xMO₂

Abstract

Layered oxide Na_xMO₂ (M: transition metal) is a promising cathode material for sodium-ion secondary battery. Crystal structure of O3- and P2-type Na_xMO₂ with various M against temperature (T) was systematically investigated by synchrotron x-ray diffraction mainly focusing on the T-dependences of a- and c-axis lattice constants (a and c) and z coordinate (z) of oxygen. Using a hard-sphere model with minimum Madelung energy, we confirmed that c/a and z values in O3-type Na_xMO₂ were reproduced. We further evaluated the thermal expansion coefficients (α_a and α_c) along a- and c-axis at 300 K. The anisotropy of the thermal expansion was quantitatively reproduced without adjustable parameters for O3-type Na_xMO₂. Deviations of z from the model for P2-type Na_xMO₂ are ascribed to Na vacancies characteristic to the structure.

Introduction

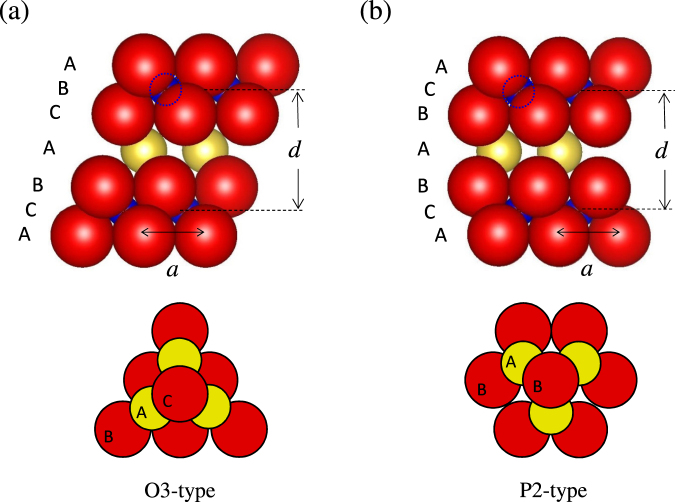
Sodium-ion-secondary battery (SIB) stores electrochemical energy through Na⁺ intercalation/deintercalation process. Due to large Clark number (=2.63) of Na compared with that (=0.006) of Li, SIBs can be a promising next-generation battery for storage of natural energy at a power plant and for a large-scale device such as electrical vehicle. Layered oxide Na_xMO₂ (M: transition metal) is a typical cathode material for SIBs^1–3. Crystal structure of this material is categorized into two typical structures: O3 and P2 types⁴. Figure 1 shows schematic structures of (a) O3-type and (b) P2-type NaMO₂. Red, yellow, and blue spheres represent O, Na, and M, respectively. M is surrounded by six oxygens, and a MO₆ octahedron is formed. The edge-sharing MO₆ octahedra form a MO₂ layer. Both O3- and P2-type NaMO₂ exhibit alternately stacked MO₂ layers and Na sheets. The sodium sheet, upper and lower oxygen sheets stack as BAC resulting in the octahedral Na site. In the P2-type NaMO₂, the sodium and oxygen sheets stack as BAB resulting in the prismatic Na site. O3-type NaMO₂ (M = Ti, Cr, Mn, Co, Ni) and P2-type Na_xMO₂ (M = Mn and Co) were found to exhibit Na⁺ intercalation/deintercalation in early 1980s^5–9. Concerning the discovery of hard carbon (≥200 mAh/g) as anode material of SIB¹⁰, electrochemical properties of Na_xMO₂ are extensively reported^11–20. Very recently, substitution effects on the battery properties in O3-type structure^21–27 and P2-type structure^28–45 were extensively studied to reduce expensive element and improve the cyclability and capacity.

Figure 1.

Schematic figure of (a) O3- and (b) P2-NaMO₂ structure. Red, yellow, and blue spheres represent O, Na, and M (transition metal element), respectively. M is sandwiched by upper and lower oxygen layers. In the P2-type structure, only the Na1 site [the atomic coordinates of Na1 are $\left(\frac{1}{3},\frac{2}{3},\frac{3}{4}\right)$] is shown. The bottom panels show top views of O-Na-O stackings in the O3- and P2-type structures, respectively. The BAC stacking in O3 forms NaO₆ octahedron, and the BAB stacking in P2 forms NaO₆ triangular prism.

Not only electrochemical properties but also superconductivity⁴⁶, crystal structure^47–57, magnetism^58–61, thermoelectric effect^62,63, and first-principle calculation^64–67 of the end family are also studied. Fujita et al. found that Na_xCoO_2−δ single crystal shows a large dimensionless figure-of-merit of ZT = 1 at 800 K⁶³, which has motivated practical use for waste heat recovery at high temperatures (T). An isostructural O3-type LiMO₂ is widely used as a cathode material in lithium-ion-secondary battery (LIB)^68,69. This family is also studied as a thermoelectric material⁷⁰ and a cathode material of solid oxide fuel cell (SOFC)⁷¹. In particular, Lan and Tao found that Li_xAl_0.5Co_0.5O₂ shows good proton conductivity of 0.1 Scm⁻¹ at 773 K⁷¹, which is the highest among those of known polycrystalline proton-conducting materials. During operation of energy devices such as LIB(SIB), thermoelectric device, and SOFC, these materials are exposed to a variation and/or a gradient of temperature. A mismatch in thermal expansion coefficients in between the components can result in high stresses around the interface leading to deterioration of the device. Thus, evaluation and systematical comprehension of thermal expansion behaviors in this class of materials are important.

In this paper, we report systematic structural analysis of four O3- and five P2-type Na_xMO₂ samples against T (300 K ≤ T ≤ 800 K) performed by synchrotron x-ray diffraction focusing on thermal expansion. To understand the thermal expansion behavior, we constructed a hard-sphere model with constraint that M, upper and lower oxygens are connected each other. We confirmed that the calculated d/a [d: interlayer distance, a: a-axis lattice constant] and z well reproduced the experimental values for O3-type Na_xMO₂. By introducing T-linear expansion of the hard sphere, the anisotropy of the thermal expansion was quantitatively reproduced without adjustable parameter for O3-type Na_xMO₂.

Results

Temperature dependence of a(c)-axis lattice constants and z coordinate of oxygen

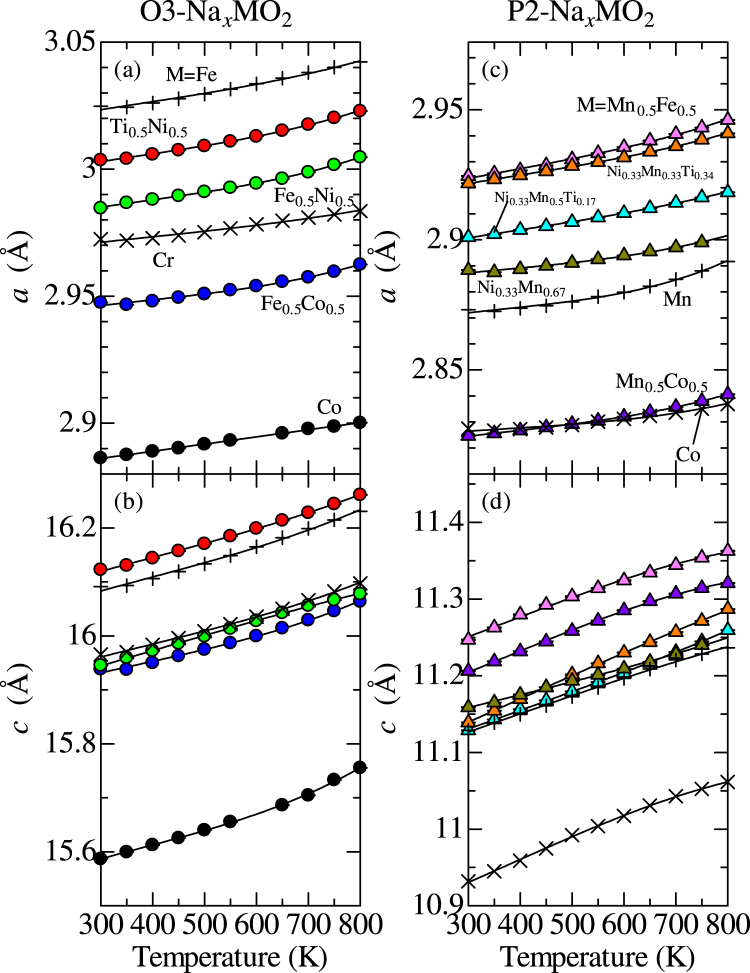
Figure 2(a) and (b) show a-axis lattice constant (a), and (b) c-axis lattice constant (c) of O3-type Na_0.99CrO₂, Na_0.99FeO₂, Na_1.00CoO₂, Na_0.98Fe_0.5Co_0.5O₂, Na_0.99Fe_0.5Ni_0.5O₂, and Na_0.94Ti_0.5Ni_0.5O₂ against T. With T, a and c monotonically increase. Raw x-ray diffraction data and results of Rietveld refinements at 300 K are shown in Figs S1–S3. The solid line represents a least-square fitting with use of a degree 3 polynomial function. By using ${\alpha }_{a(c)}=\frac{d\ln a(c)}{dT}$, a linear thermal expansion coefficient along a- and c-axis was evaluated. Figure 2(c) and (d) show a and c of P2-type Na_0.52MnO₂, Na_0.59CoO₂, Na_0.50Mn_0.5Co_0.5O₂, Na_0.70Ni_0.33Mn_0.67O₂, Na_0.69Ni_0.33Mn_0.5Ti_0.17O₂, Na_0.70Ni_0.33Mn_0.33Ti_0.34O₂, and Na_0.48Mn_0.5Fe_0.5O₂. The P2-type compounds also show monotonical T-dependences of a and c. In Table 1, the values of a, c at 300 K, α_a, and α_c of O3- and P2-type Na_xMO₂ at 300 K were listed.

Figure 2.

Temperature (T) dependence of (a) a-axis, (b) c-axis lattice constants (a and c) of O3-type Na_xMO₂. T dependence of (c) a, and (d) c of P2-type Na_xMO₂. The solid line represents a least-square fitting with use of a degree 3 polynomial function for a and c. a and c values of O3-Na_0.99CrO₂, O3-Na_0.99FeO₂, P2-Na_0.52MnO₂, and P2-Na_0.59CoO₂ were referred from our previous reports^56,57.

Table 1.

a-axis, c-axis lattice constants (a and c), z coordinate of oxygen (z) at 300 K, the linear thermal expansion coefficient [α_a (α_c)] along a(c)-axis, and α_c/α_a of O3- and P2-type Na_xMO₂ at 300 K.

Compound	a (Å)	c (Å)	z	αa (10−5 K−1)	αc (10−5 K−1)	αc/αa
56O3-Na0.99CrO2	† 2.97247(3)	†15.96540(18)	0.23213(13)	*0.73	*1.52	*2.07
56O3-Na 0.99 FeO 2	†3.02477(2)	†16.09135(10)	0.23389(12)	*1.07	*1.63	*1.52
O3-Na1.00CoO2	2.88627(2)	15.58680(12)	0.23046(9)	0.98	1.71	1.74
O3-Na0.98Fe0.5Co0.5O2	2.94748(3)	15.93844(23)	0.23238(12)	0.79	1.37	1.73
O3-Na0.99Fe0.5Ni0.5O2	2.98463(9)	15.94545(63)	0.23334(17)	1.01	1.76	1.74
O3-Na0.94Ti0.5Ni0.5O2	3.00358(4)	16.12273(24)	0.23382(13)	1.06	1.61	1.51
57P2-Na0.52MnO2	†2.87311(9)	†11.1287(5)	0.0858(3)	*0.81	*2.11	*2.59
57P2-Na0.59CoO2	†2.82748(4)	†10.9319(2)	0.0881(3)	*0.48	*2.70	*5.61
P2-Na0.50Mn0.5Co0.5O2	2.82459(5)	11.20617(33)	0.08704(24)	0.84	2.42	2.87
P2-Na0.70Ni0.33Mn0.67O2	2.88835(5)	11.15881(29)	0.09120(28)	0.67	1.51	2.26
P2-Na0.69Ni0.33Mn0.5Ti0.17O2	2.90101(3)	11.12868(16)	0.09263(17)	1.07	2.20	2.05
P2-Na0.70Ni0.33Mn0.33Ti0.34O2	2.92173(4)	11.13896(22)	0.09381(21)	1.12	2.72	2.42
P2-Na0.48Mn0.5Fe0.5O2	2.92452(8)	11.24690(48)	0.08592(32)	1.30	2.26	1.74

^†The original data were referred from previous reports^56,57. ^*α_a and α_c were reevaluated in a T-range of 300–800 K.

Figure 3(a) shows z coordinate of oxygen for O3- and P2-type structure (z_O3 and z_P2) against a at 300 and 700 K. Blue and red circles represent z_O3 at 300 and 700 K, respectively. Light green and pink triangles represent z_P2 at 300 and 700 K, respectively. The values were almost independent of T. Figure 3(b) shows a ratio of interlayer distance (d) to a against a at 300 K, where d is c/3 for O3-type and c/2 for P2-type structure. Light blue and purple circles represent d/a of O3-type compounds at 300 and 700 K, respectively. Green and yellow triangles represent d/a of P2-type compounds at 300 and 700 K, respectively. d/a slightly decreases with an increase in a.

Figure 3.

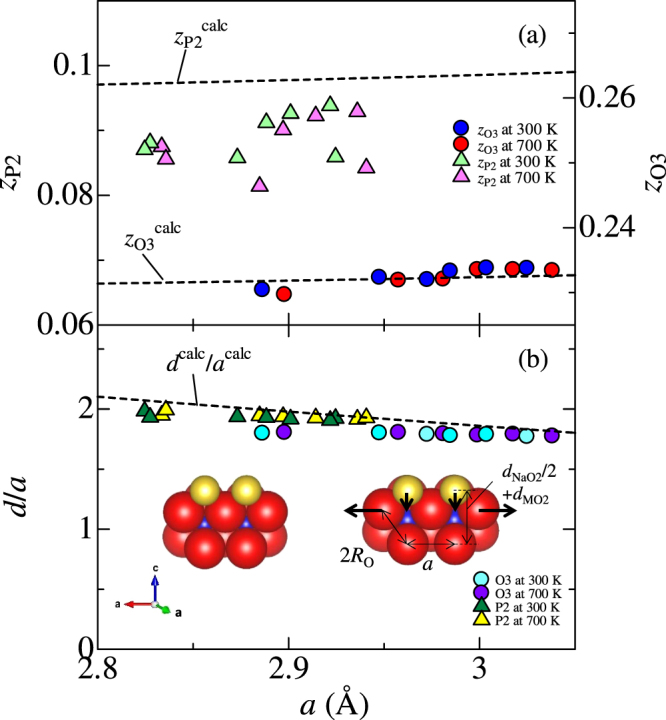
(a) z coordinate of oxygen for O3- (z_O3) and P2-type (z_P2) structure against a-axis lattice constant (a). Blue and red circles represent z_O3 at 300 and 700 K, respectively. Light green and pink triangles represent z_P2 at 300 and 700 K, respectively. The broken lines represent z calculated by the hard sphere model with minimum Madelung energy for O3 and P2-type compounds ($z_{\mathrm{O}3}^{\mathrm{calc}}$ and $z_{\mathrm{P}2}^{\mathrm{calc}}$) against a, respectively. (b) The ratio of interlayer distance (d) to a against a. Light blue and purple circles represent d/a of O3-type compounds at 300 and 700 K, respectively. Green and yellow triangles represent d/a of P2-type compounds at 300 and 700 K, respectively. The broken line represents d/a calculated by the hard sphere model with minimum Madelung energy (d^calc/a^calc) against a. The inset of Fig. 3(b) shows a schematic view of the local atomic configuration around M.

Thermal expansion coefficients

Figure 4 shows (a) α_a, (b) α_c, and (c) α_c/α_a against a. α_a and α_c of O3-type Na_1.00CoO₂ were 0.98 × 10⁻⁵ K⁻¹ and 1.71 × 10⁻⁵ K⁻¹, respectively. These values are comparable to those of inorganic compounds; α_a = 1.44 × 10⁻⁵ K⁻¹ for LiMn₂O₄⁷², and α_a(α_c) = 0.85(2.5) × 10⁻⁵ K⁻¹ for layered BaFe_1.84Co_0.16As₂⁷³. α_a(α_c) in Fig. 4 is rather scattered against a around the averaged value of 0.92(1.96) × 10⁻⁵ K⁻¹. The ratio α_c/α_a is also scattered around the averaged value (=2.30). However, the data point for P2-Na_0.59CoO₂ are seriously deviated from the average value. This is probably due to the Na ordering⁶⁷.

Figure 4.

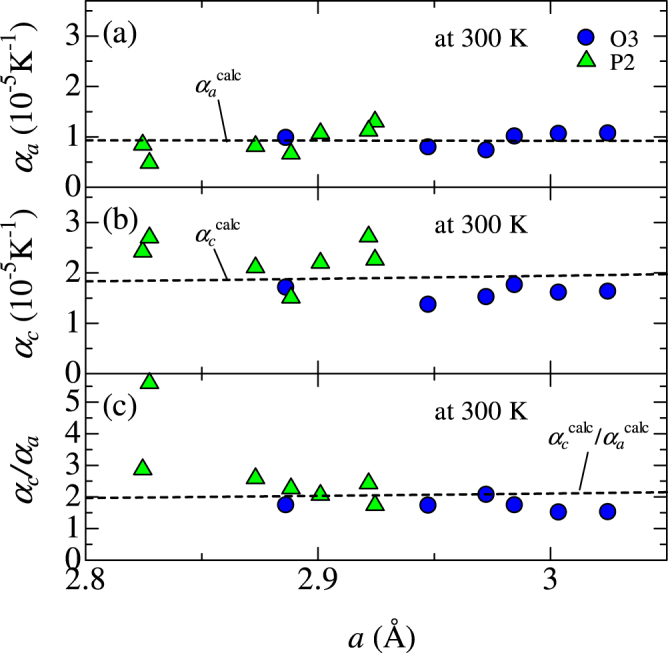
Linear thermal expansion coefficient (a) along a-axis (α_a), (b) along c-axis (α_c), and (c) α_c/α_a against a-axis lattice constant (a). The broken lines in Fig. 4(a,b and c) represent α_a, α_c, and α_c/α_a against a calculated by the hard-sphere model with minimum Madelung energy (${\alpha }_a^{\mathrm{calc}}$, ${\alpha }_c^{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}}$, and ${\alpha }_c^{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}}$/${\alpha }_a^{\mathrm{calc}}$).

Discussion

A hard-sphere model with minimum Madelung energy

We have constructed a hard-sphere structural model for O3- and P2-type NaMO₂ to reproduce the experimental results (d/a, z, α_c/α_a). Firstly, imagine a sheet consists of hard spheres that were arrayed on triangular lattice, and then the sheet is alternately stacked as shown in Fig. 1. In the model, hard spheres of Na, M, and O were assumed to have Shannon’s ionic radius⁷⁴; R_Na = 1.02 Å, R_O = 1.40 Å, and R_M is a variable parameter that takes 0.58–0.7 Å, respectively. Since the ionic radius of the hard sphere is different from one another, the structure can not be the hexagonal close-packed structure, and several structures with different a are possible for the unique value of R_M. Here, we adopted a constraint that M, upper, and lower oxygens coroneted each other, because the constraint minimizes the Madelung energy against a (vide infra). For a calculation of thermal expansion coefficient, the hard sphere is assumed to expand in proportion to the temperature difference (ΔT). ΔT dependence of R_Na is expressed as $R_{\mathrm{Na}}(\mathrm{\Delta }T)=R_{\mathrm{Na}}+A{m}_{\mathrm{Na}}^{-1}{R}_{\mathrm{Na}}\mathrm{\Delta }T$, where m_Na(=22.99) is atomic weight of Na atom. Similarly, ΔT dependences of R_O and R_M are expressed as $R_{\mathrm{O}}(\mathrm{\Delta }T)=R_{\mathrm{O}}+A{m}_{\mathrm{O}}^{-1}{R}_{\mathrm{O}}\mathrm{\Delta }T$, and $R_{\mathrm{M}}(\mathrm{\Delta }T)=R_{\mathrm{M}}+A{m}_{\mathrm{M}}^{-1}{R}_{\mathrm{M}}\mathrm{\Delta }T$, where m_O(=16.00) and m_M(=55.85) (We used 55.85 of the atomic weight of Fe as m_M although M is not only Fe but also mixture of Ti, Mn, Fe, and Co. When we used 47.88 of the atomic weight of Ti as m_M, the calculated α_c/α_a worse reproduces the experiments.) are atomic weights of O and M, respectively.

Now, let us derive the expression (a^calc) of a-axis lattice constant as a function of ΔT. Note that the in-plane nearest-neighbor oxygen distance is a for both the P2- and O3-structure. Considering the above-mentioned constraint, a^calc(ΔT) for both O3- and P2-structures is expressed as

$$a^{\mathrm{calc}}(\mathrm{\Delta }T)=2\sqrt{{[R_{\mathrm{O}}(\mathrm{\Delta }T)+R_{\mathrm{M}}(\mathrm{\Delta }T)]}^2-R_{\mathrm{O}}{(\mathrm{\Delta }T)}^2}\mathrm{.}$$ 1

This equation is easily derived using Pythagorean theorem. As shown in Eq. 1, a^calc strongly depends on R_M value. Due to the finite ionic radius of oxygen (R_O = 1.40 Å), minimum value of a^calc is 2.80 Å. At a^calc = 2.80 Å, R_M is evaluated to be ≈0.5799 Å using Eq. 1. With an increase in R_M, the oxygen triangular lattice expands in order to keep the connection between M, upper and lower oxygens.

Na sheet is sandwiched by the MO₂ layers as BAC (BAB) in the O3-type (P2-type) structure. We noted that the expression (d^calc) of interlayer distance is independent of the stacking manner, and the ΔT-dependence of d^calc for O3- and P2-type structure is expressed as,

$$d^{\mathrm{calc}}(\mathrm{\Delta }T)=\sqrt{{\mathrm{[2}{R}_{\mathrm{O}}(\mathrm{\Delta }T)]}^2-\frac{a^{\mathrm{calc}}{(\mathrm{\Delta }T)}^2}{3}}+2\sqrt{{[R_{\mathrm{O}}(\mathrm{\Delta }T)+R_{\mathrm{Na}}(\mathrm{\Delta }T)]}^2-\frac{a^{\mathrm{calc}}{(\Delta T)}^2}{3}}\mathrm{.}$$ 2

The first and the second terms correspond to $d_{{\mathrm{MO}}_2}^{\mathrm{calc}}$ and $d_{{\mathrm{NaO}}_2}^{\mathrm{calc}}$, where $d_{{\mathrm{MO}}_2}^{\mathrm{calc}}$ and $d_{{\mathrm{NaO}}_2}^{\mathrm{calc}}$ are the thicknesses of MO₂ and NaO₂ layers, respectively. A relationship between d^calc and the expression of c (c^calc) is expressed as $3d^{\mathrm{calc}}(\mathrm{\Delta }T)=c_{\mathrm{O}3}^{\mathrm{calc}}(\mathrm{\Delta }T)$ and $2d^{\mathrm{calc}}(\mathrm{\Delta }T)=c_{\mathrm{P}2}^{\mathrm{calc}}(\mathrm{\Delta }T)$ for O3- and P2-type structures. By using Pythagorean theorem, Eq. 2 is easily derived. Expressions of z (z^calc) for O3- and P2-type structures are derived as

$$z_{\mathrm{O}3}^{\mathrm{calc}}(\mathrm{\Delta }T)=\frac{1}{6}+\frac{1}{6d^{\mathrm{c}alc}(\mathrm{\Delta }T)}\sqrt{{\mathrm{[2}{R}_{\mathrm{O}}(\mathrm{\Delta }T)]}^2-\frac{a^{\mathrm{calc}}{(\mathrm{\Delta }T)}^2}{3}},$$ 3

and

$$z_{\mathrm{P}2}^{\mathrm{calc}}(\mathrm{\Delta }T)=\frac{1}{4d^{\mathrm{calc}}(\mathrm{\Delta }T)}\sqrt{{\mathrm{[2}{R}_{\mathrm{O}}(\mathrm{\Delta }T)]}^2-\frac{a^{\mathrm{calc}}{(\mathrm{\Delta }T)}^2}{3}},$$ 4

respectively.

Now, let us consider the stability of the hard-sphere model with the constraint that M, upper and lower oxygens coroneted to each other. For this purpose, we calculated the Madelung energy at a specific R_M (=0.65 Å) against a. We show that this model exhibits minimum Madelung energy (E_ME). Figure 5 shows E_ME of O3- and P2-type NaMO₂ against a. Our constraint gives a^calc ≈ 2.995 Å [Eq. 1] at R_M = 0.65 Å. With the O3 structure, the a^calc value corresponds to the minimum position of E_ME (−8.67 eV). With an increase in a from 2.995 Å, M becomes isolated from the surrounding oxygens (the right-side inset of Fig. 5), and E_ME increases (Note that the oxygen positions were controlled by Eqs 3 and 4). With an decrease in a from 2.995 Å, the upper and lower oxygens are separated (the left-side inset of Fig. 5), and E_ME increases as well (We used $d^{\mathrm{calc}}\mathrm{=2}\sqrt{{(R_{\mathrm{M}}+R_{\mathrm{O}})}^2-\frac{a^2}{3}}+2\sqrt{{[R_{\mathrm{O}}+R_{\mathrm{Na}}]}^2-\frac{a^2}{3}}$, $z_{\mathrm{O}3}^{\mathrm{calc}}=\frac{1}{6}+\frac{1}{6d^{\mathrm{calc}}}\sqrt{{(R_{\mathrm{M}}+R_{\mathrm{O}})}^2-\frac{a^2}{3}}$, and $z_{\mathrm{P}2}^{\mathrm{calc}}=\frac{1}{4d^{\mathrm{calc}}}\sqrt{{(R_{\mathrm{M}}+R_{\mathrm{O}})}^2-\frac{a^2}{3}}$ for the calculation below a = 2.995 Å). Similar results are obtained for the P2 structure. Thus, our model is energetically stable against the variation of a. Our constraint that M, upper and lower oxygens connected to each other causes the compact layered structure and minimized the long-range Coulomb energy between the layers. We call our model “hard-sphere model with minimum Madelung energy”.

Figure 5.

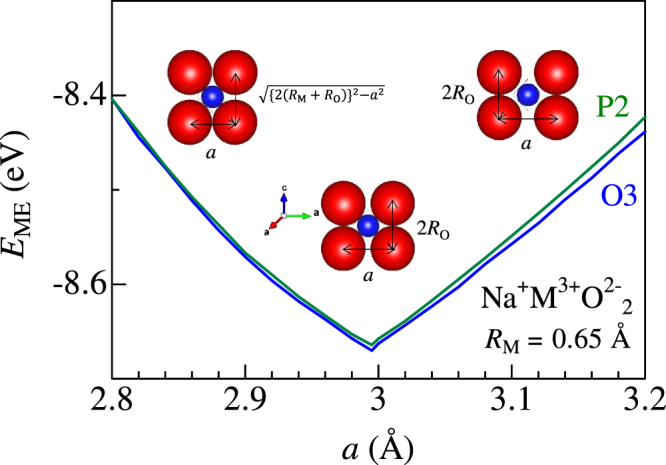
Madelung energy (E_ME) of O3- and P2-type NaMO₂ against a for the hard-sphere model. R_M was fixed at 0.65 Å.

Companion of the structural parameters and the thermal expansion coefficients with the model

The broken line in Fig. 3(b) is the calculated d/a based on the hard-sphere model with minimum Madelung energy (see Eqs 1 and 2). d^calc/a^calc decreases with an increase in a^calc, which reproduces experimental results. The decrease in d^calc/a^calc is schematically depicted in the inset of Fig. 3(b). When O-O distance along in-plane direction elongates due to increase in R_M, Na atoms relatively sink down along out-of-plane direction. (Decrease in $d_{{\mathrm{NaO}}_2}\mathrm{/(2}a)$ against a is displayed in Fig. S5). We further calculated z and plotted them in Fig. 3(a). In the O3-type compounds, z^calc well reproduces the experimental data. In the P2-type compounds, however, z^calc is slightly smaller than $z_{\mathrm{P}2}^{\mathrm{calc}}$. We ascribed the smaller z_P2 to the Na vacancies characteristic to the P2 structure. With the vacancies, the nominal valence of M became higher, and hence R_M becomes smaller. Our model tells us that $z_{\mathrm{P}2}^{\mathrm{calc}}$ becomes smaller if R_M becomes smaller.

The broken lines in Fig. 4 represent the calculated α_a, α_c, and α_c/α_a (${\alpha }_a^{\mathrm{calc}}$, ${\alpha }_{\mathit{c}}^{\mathrm{calc}}$, and ${\alpha }_c^{\mathrm{calc}}$/${\alpha }_a^{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}}$), respectively. ${\alpha }_a^{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}}$(${\alpha }_c^{\mathrm{calc}}$) was evaluated by using the equation, $\frac{d\ln a^{\mathrm{calc}}(\mathrm{\Delta }T)}{d\mathrm{\Delta }T}$ $\left[\frac{d\ln c^{\mathrm{calc}}(\mathrm{\Delta }T)}{d\Delta T}\right]$. The only fitting parameter A (=2.56 × 10⁻⁴ K⁻¹) was chosen to fit the average value of α_a (=0.92 × 10⁻⁵ K⁻¹). Using the same value of A, ${\alpha }_c^{\mathrm{calc}}$ was found to reproduce the magnitude of experimental value for the O3 materials. On the other hand, larger α_c for the P2 materials is possibly due to Na vacancies except for the data point of Na_0.59CoO₂. We note that $\frac{{\alpha }_c^{\mathrm{calc}}}{{\alpha }_a^{\mathrm{calc}}}$ is expressed without the adjustable parameter A,

$$\begin{array}{lll}\hfill {\frac{{\alpha }_c^{\mathrm{calc}}}{{\alpha }_a^{\mathrm{calc}}}|}_{\mathrm{\Delta }T=0}& \hfill =\hfill & \frac{\frac{2m_{\mathrm{O}}^{-1}{R}_{\mathrm{O}}^2}{m_{\mathrm{M}}^{-1}{R}_{\mathrm{M}}{R}_{\mathrm{O}}+(m_{\mathrm{O}}^{-1}{R}_{\mathrm{O}}+m_{\mathrm{M}}^{-1}{R}_{\mathrm{M}})R_{\mathrm{M}}}-\frac{2}{3}}{4\sqrt{\left\{{\left(\frac{2R_{\mathrm{O}}}{a_0}\right)}^2-\frac{1}{3}\right\}\left\{{\left(\frac{R_{\mathrm{O}}+R_{\mathrm{Na}}}{a_0}\right)}^2-\frac{1}{3}\right\}}+2\left\{{\left(\frac{2R_{\mathrm{O}}}{a_0}\right)}^2-\frac{1}{3}\right\}}\hfill \\ \hfill & \hfill & +\frac{\frac{(m_{\mathrm{O}}^{-1}{R}_{\mathrm{O}}+m_{\mathrm{Na}}^{-1}{R}_{\mathrm{Na}})(R_{\mathrm{O}}+R_{\mathrm{Na}})}{2m_{\mathrm{M}}^{-1}{R}_{\mathrm{M}}{R}_{\mathrm{O}}+\mathrm{2(}{m}_{\mathrm{O}}^{-1}{R}_{\mathrm{O}}+m_{\mathrm{M}}^{-1}{R}_{\mathrm{M}})R_{\mathrm{M}}}-\frac{2}{3}}{\sqrt{\left\{{\left(\frac{2R_{\mathrm{O}}}{a_0}\right)}^2-\frac{1}{3}\right\}\left\{{\left(\frac{R_{\mathrm{O}}+R_{\mathrm{Na}}}{a_0}\right)}^2-\frac{1}{3}\right\}}+2\left\{{\left(\frac{R_{\mathrm{O}}+R_{\mathrm{Na}}}{a_0}\right)}^2-\frac{1}{3}\right\}},\hfill \end{array}$$ 5

where $a_0=2\sqrt{2R_{\mathrm{O}}{R}_{\mathrm{M}}+R_{\mathrm{O}}^2}$. The hard-sphere model examined in this paper gives intuitive and easy comprehension of the thermal expansion behavior of the layered oxides. The density-functional-thery (DFT) calculation successfully reproduces the linear thermal expansion coefficients of several materials such as Al⁷⁵, S⁷⁶, 4d transition metals^77,78, Os⁷⁸, MgO⁷⁹, CaO⁷⁹, and ZnO⁸⁰, which is beyond the scope of this paper.

Conclusion

We systematically determined the temperature dependent lattice constant and z-coordinates of P2- and O3-type NaMO₂. We proposed a simple hard-sphere model with constraint that M, upper and lower oxygens are coroneted to each others. The model quantitatively reproduced a, c, z, α_a and α_c for O3-type Na_xMO₂. On the other hand, z coordinate of P2-type Na_xMO₂ deviates from the hard-sphere model possibly due to Na vacancies. This simple model can be easily applied for the other layered compounds to intuitively understand and design the thermal expansion behaviors.

Methods

Sample preparation

Powders of O3- and P2-Na_xMO₂ (M: transition metal) were synthesized by using conventional solid state reaction. For O3-Na_1.00CoO₂, Na₂O₂ and Co₃O₄ were mixed under the molar ratio of Na:Co = 1.1:1, and calcined at 550°C in O₂ for 16 h. Then, the product was finely ground, and again calcined in the same condition (this process was repeated once again.). For O3-Na_0.98Fe_0.5Co_0.5O₂, Na₂CO₃, Fe₃O₄ and Co₃O₄ were mixed under the molar ratio of Na:Fe:Co = 1.05:0.5:0.5, and calcined at 900 °C in air for 15 h. For O3-Na_0.99Fe_0.5Ni_0.5O₂, Na₂O₂, Fe₂O₃ and NiO were mixed under the molar ratio of Na:Fe:Ni = 1.2:0.5:0.5, and calcined at 650°C in O₂ for 15 h. Then the product was finely ground and again calcined in the same condition. For O3-Na_0.94Ti_0.5Ni_0.5O₂, Na₂CO₃, TiO₂ and NiO were mixed under the molar ratio of Na:Ti:Ni = 1.05:0.5:0.5, and calcined at 900°C in air for 15 h. Then the product was finely ground and again calcined in the same condition.

For P2-Na_0.50Mn_0.5Co_0.5O₂, Na₂CO₃, MnCO₃ and Co₃O₄ were mixed under the molar ratio of Na:Mn:Co = 0.7:0.5:0.5, and calcined at 900°C in air for 12 h, Then, the product was finely ground and again calcined in the same condition. For P2-Na_0.70Ni_0.33Mn_0.67O₂, Na₂CO₃, NiO and Mn₂O₃ were mixed in ethanol under the molar ratio of Na:Ni:Mn = 0.7:0.33:0.67, and calcined at 900°C in air for 24 h. Then, the product was finely ground and again calcined in the same condition. For P2-Na_0.69Ni_0.33Mn_0.5Ti_0.17O₂, Na₂CO₃, NiO, Mn₂O₃ and TiO₂ were mixed under the molar ratio of Na:Ni:Mn:Ti = 0.7:0.33:0.5: 0.17, and calcined at 900°C in air for 18 h. For P2-Na_0.70Ni_0.33Mn_0.33Ti_0.34O₂, Na₂CO₃, NiO, Mn₂O₃ and TiO₂ were mixed under the molar ratio of Na:Ni:Mn:Ti = 0.7:0.33:0.33:0.34, and calcined at 900°C in air for 12 h. For P2-Na_0.48Mn_0.5Fe_0.5O₂, Na₂O₂, Mn₂O₃ and Fe₂O₃ were mixed under the molar ratio of Na:Mn:Fe = 0.7:0.5:0.5, and calcined at 900°C in air for 12 h. Then, the product was finely ground and again calcined in the same condition. All the samples were taken out from the hot furnace (>200°C), and then immediately transferred into a vacuum desiccator to avoid moisture in air.

X-ray diffraction

The synchrotron radiation x-ray diffraction (XRD) patterns were measured at BL02B2 beamline⁸¹ at SPring-8. The capillary was placed on the Debye-Scherrer camera at the beamline. The sample temperature was controlled by blowing a hot N₂ in the temperature range of 300 K ≤ T ≤ 800 K. The XRD patterns were detected with an imaging plate (IP). The exposure time was 5 min. The wavelength of the x-ray was 0.499420 Å for P2-Na_0.48Mn_0.5Fe_0.5O₂ and P2-Na_0.50Mn_0.5Co_0.5O₂, and 0.499892 Å for O3-Na_0.98Fe_0.5Co_0.5O₂ and Na_0.94Ti_0.5Ni_0.5O₂, and 0.499838 Å for the others. The wavelengths are calibrated by the cell parameter of standard CeO₂ powders. Crystal structure was analyzed by RIETAN-FP program⁸². Schematic figure of the crystal structure were drawn by VESTA program⁸³. All the reflections can be indexed with the O3-type ($R\overline{3}m$) or P2-type (P6₃/mmc) structures except for a tiny amount of impurity of O3-type Fe-rich phase for Na_0.99Fe_0.5Ni_0.5O₂ and NiO for Na_0.94Ti_0.5Ni_0.5O₂. All the structural parameters against T (300 K ≤ T ≤ 800 K) were listed in Tables S1–S9. During heating process, any extra impurity peaks were not appeared. We observed no tendency of Na deintercalation due to heating (Fig. S4).

The actual Na concentrations in the compound were determined by the Rietveld refinement based on the synchrotron XRD patterns at 300 K. We note that ref.⁴⁵ reported a consistency of Na contents determined by ICP-AES (Inductively Coupled Plasma Atomic Emission Spectroscopy) and Rietveld refinement using synchrotron x-ray diffraction for P2-Na_xMn_1/2Fe_1/2O₂ phase.

Madelung energy calculation

Madelung energy (E_ME) was computed by the MADEL program in the VESTA software using the Fourier method⁸³. The site potential ϕ_i is calculated by the formula ${\phi }_i={\sum }_j\frac{g_j{Z}_j}{4\pi {\epsilon }_0{l}_{ij}}$, where g_j is the occupancy of the j th ion, Z_i is the valence of the j th ion, ε₀ is the vacuum permittivity, and l_ij is the distance between ions i and j. E_ME is calculated by using the formula $E_{\mathrm{ME}}=\frac{1}{2}{\sum }_i{\phi }_i{Z}_i{W}_i$, where W_i is a factor depending on g_i and the number of equivalent atomic positions at the site i in the unit cell. For O3-type structure (space group: $R\overline{3}m$), we put +1, +3, and −2 charges on 3a Na (0,0,0), 3b M (0,0, $\frac{1}{2}$), and 6c O (0,0, z) sites in stoichiometric NaMO₂. In the calculation of the P2-type structure (P6₃/mmc), we assume a stoichiometric NaMO₂ with fully occupied 2d Na site. We put +e, +3e, and −2e charges on 2d Na $\left(\frac{1}{3},\frac{2}{3},\frac{3}{4}\right)$, 2a M (0,0,0), and 4f O $\left(\frac{1}{3},\frac{2}{3},z\right)$. A radius (s) of the hard sphere was set to 0.3 Å, and Fourier coefficients are summed up to 10 Å⁻¹ in the reciprocal space.

Author Contributions

W.K. measured synchrotron XRD patterns, analyzed the XRD data, calculated linear thermal expansion coefficient based on a hard-sphere model, and wrote the manuscript. A.Y. synthesized O3-type layered oxides, and measured synchrotron XRD patterns. T.A., T.S., and D.T. synthesized P2-type layered oxides, and measured synchrotron XRD patterns. Y.M. contributed discussion and critically examined the manuscript.

Competing Interests

The authors declare no competing interests.