Influence of a Confined Methanol Solvent on the Reactivity of Active Sites in UiO‐66

Abstract

UiO‐66, composed of Zr‐oxide bricks and terephthalate linkers, is currently one of the most studied metal–organic frameworks due to its exceptional stability. Defects can be introduced in the structure, creating undercoordinated Zr atoms which are Lewis acid sites. Here, additional Brønsted sites can be generated by coordinated protic species from the solvent. In this Article, a multilevel modeling approach was applied to unravel the effect of a confined methanol solvent on the active sites in UiO‐66. First, active sites were explored with static periodic density functional theory calculations to investigate adsorption of water and methanol. Solvent was then introduced in the pores with grand canonical Monte Carlo simulations, followed by a series of molecular dynamics simulations at operating conditions. A hydrogen‐bonded network of methanol molecules is formed, allowing the protons to shuttle between solvent methanol, adsorbed water, and the inorganic brick. Upon deprotonation of an active site, the methanol solvent aids the transfer of protons and stabilizes charged configurations via hydrogen bonding, which could be crucial in stabilizing reactive intermediates. The multilevel modeling approach adopted here sheds light on the important role of a confined solvent on the active sites in the UiO‐66 material, introducing dynamic acidity in the system at finite temperatures by which protons may be easily shuttled from various positions at the active sites.

1.  Introduction

UiO‐66 is a metal–organic framework (MOF) which has received significant attention from both experimental and theoretical researchers since its discovery in 2008.1 Its attractiveness can be mainly traced back to its exceptional thermal, chemical and mechanical stability2 and to the relative facility by which (linker) defects can be induced in the structure.3 These linker defects create under‐coordinated metal sites which act as Lewis acid sites that can be used for catalysis.4 The chemical formula for a defect‐free UiO‐66 unit cell is [Zr₆O₄(OH)₄][C₆H₄(COO)₂]₆, as displayed in Figure 1. Each Zr‐brick represents a six‐centered zirconium oxyhydroxide cluster (octahedron of Zr atoms whose faces are capped by μ₃‐oxo and μ₃‐hydroxyl groups in an alternating fashion), linked via terephthalate or benzenedicarboxylate (bdc) linkers to form a face‐centered‐cubic net (fcu‐a topology). As has been reported by Lillerud and co‐workers,1 each Zr metal is fully coordinated by 12 organic linkers to form a highly connected framework if no linker defects are present. This high connectivity lies on the basis of its exceptional structural stability and rigidity.

Figure 1.

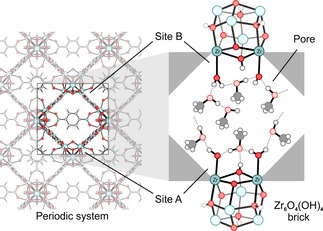
Schematic representation of a pore in UiO‐66. Left: periodic lattice; right: the pore where the missing linker defect is located, with included guest molecules. The active sites site A and B are indicated on the left.

Another feature that makes UiO‐66 very attractive for catalysis is the presence of both acid and basic centers within molecular distances, yielding active sites with bifunctional behavior.5 In addition, the presence of water has a distinct influence on the acidity and basicity of the active sites. Recently, Ling and Slater6 used molecular dynamics simulations to show the existence of some dynamic acidity, created by a double proton transfer involving two physisorbed water molecules and a hydroxide anion in the defect structure. The findings of Ling and Slater have been confirmed independently by some of the present authors.7 Its remarkable properties lie on the basis of the numerous coordination bonds of the linkers with the metal centers. When focusing on the catalytic behavior of the UiO‐66 material, knowledge of the molecular structure of the active sites created by linker defects is an essential ingredient to understand the reactivity of the node with coordinating species such as water and methanol, and eventually to tune its catalytic properties. These species introduce additional Brønsted sites which can play a role in reactions catalyzed by the material. A combined experimental‐theoretical work8 demonstrated that the topology of the OH/OH₂ defect coordinating species on the Zr₆ node‐face can be tuned with intermediate steps in which methanol replaces water on the Zr sites. Insight in the nature of active sites and the methanol substitution process was obtained, indicating that the thermodynamically most favorable structure was obtained with a node‐face containing a methoxide and an open Zr metal site.8 Further understanding of the broad variety of defect structures in the UiO‐66 material was obtained by several recent theoretical works,6, 7, 8, 9 investigating possible structures where up to three defect coordinating molecules are involved. These metal‐oxide‐like nodes of UiO‐66 unveil acid‐base properties which are beneficial for a series of catalytic reactions such as the jasminaldehyde condensation, the Oppenauer oxidation5, 10 and the Fischer esterification of carboxylic acids with alcohols.9 More precisely, special attention was given to the role of coordinated species to generate additional Brønsted acid and base sites in the UiO‐66 material. Water was shown to have a beneficial effect on the reactivity by providing additional Brønsted sites and extra stabilization for various intermediates through hydrogen bonding. The bifunctional character of the catalyst has been highlighted. This conclusion was based on a concerted acid‐base reaction mechanism that was found for the esterification reaction of propionic acid with methanol, in which water formed a combined Lewis/Brønsted network in defective UiO‐66 material. However, it may be anticipated that such behavior is not restricted to water only but may also be extended to other protic molecules, such as methanol. This is especially important as many reactions take place in protic solvents like alcohols.

Herein we investigate the remarkable dynamic complexity of defect termination of UiO‐66 in a methanol solution. This is of high importance as many heterogeneous catalytic reactions are performed in solution, where the solvent can play a notable role in facilitating or hindering the reaction due to its interactions with the catalyst and the solute. We particularly study the role of the solvent present in the confined cavities of the material and its interaction with the active sites, as displayed schematically in Figure 1. A major unresolved challenge lies in the characterization of the active sites at operating conditions when more molecules are confined in the pores of the material. It remains unclear in how far the presence of extra methanol molecules in the pores of the material affects the accessibility and nature of the active sites. For instance, solvent molecules can play a role by connecting the two active sites that are generated by local defects by means of linker vacancies and can shuttle protons of reactive species from one site to the other. The simplest theoretical model includes only species that are directly bonded to the Zr atoms. A more complex system could be generated by introducing additional molecules to reproduce the first solvation spheres. However, a more realistic behavior of the system at operating conditions can only be obtained by following the system in time under realistic temperatures and pressures and taking the full solvent environment in the pores of the material into account.

In this work, we study the nature of the active sites in the UiO‐66 material at operating conditions in the presence of a realistic loading of methanol molecules confined in the pores of the material. To this end, a multistep modeling approach is used. First, a series of static periodic density functional theory (DFT) calculations were performed to estimate structures of the active sites with coordinated water or methanol molecules. Second, a full loading of the unit cell with methanol was considered. The number of methanol molecules was estimated by means of a series of grand canonical Monte Carlo (GCMC) calculations. In these simulations, we estimated the maximum uptake of solvent molecules in the pores of the defective hydrated UiO‐66 unit cell with two water molecules capping the Zr metal sites at each defect site. Then, a series of molecular dynamics simulations was performed in the NVT ensemble, after an equilibration run in the NPT ensemble at 330 K, which is below the boiling point of methanol. The followed modeling approach yields insight into the role of a confined methanol solvent in the pores of the UiO‐66 framework and its influence on the nature of the active sites. We will show that the active sites show a remarkable dynamic behavior where protons can be easily shuttled among various position on the defective sites.

Computational Methods

To estimate the influence of a methanol solvent loading on the active sites in the UiO‐66 material, a multistep modeling approach was used. First, the active sites were explored with static periodic calculations, investigating the role of defect capping species with different topologies. These calculations are necessary in order to get realistic starting structures and to obtain insight on the species directly coordinated to the Zr atoms. In a second step, a full loading of methanol solvent was considered. The initial loading in the pores was estimated by means of grand canonical Monte Carlo simulations, using an empirical force‐field model. Subsequently, DFT‐based molecular dynamics simulations were performed on a defective UiO‐66 where Zr atoms are capped with water molecules. For our study, it is crucial to model hydrogen bonding and proton transfer mechanisms. These phenomena involve bonds being broken and formed and need an electronic level treatment in order to be correctly reproduced. Force‐field based molecular dynamics would never capture these features even after long simulation times. Therefore, an ab initio treatment is required. The computational details for each of these calculations are outlined below.

Static DFT Calculations

The various structures at the active site were investigated with a static DFT approach using a periodic model to correctly describe the environment surrounding the active sites. In this work, the same methodology and level of theory of previous work of the authors are adopted.9, 10 The calculations were performed with the Vienna Ab Initio Software Package (VASP),11 applying the projector augmented wave approximation (PAW),12 and limiting the sampling of the Brillouin zone to the Γ point. The structures were optimized with PBE exchange‐correlation functional13 complemented by the Grimme D314 dispersion corrections. The energy cutoff for the plane waves was set to 700 eV, and the convergence threshold for the electronic self‐consistent field (SCF) calculations was fixed to 10⁻⁵ eV. To improve convergence, a Gaussian smearing of 0.025 eV was also included. The used periodic unit cell is built following the crystallographic structure provided by Cavka et al..1 Following a methodology already established in earlier works of present authors,5, 7, 9, 10, 15 frequency calculations were performed on each periodic structure with a partial Hessian approach.16 Firstly, they indicate if all structures were correctly optimized. Only positive values for the frequencies of the reported states ensure that they correspond to minima in the potential energy surface. Secondly, frequencies are used to account for the finite temperature effects in the calculation of free energy differences. For this purpose, thermal corrections were computed using the in‐house developed processing toolkit TAMkin.17

Active Sites in the Defective UiO‐66 Unit Cell

In this work, we will restrict ourselves to active sites which are created by the removal of two terephthalate linkers in the conventional unit cell of four inorganic Zr‐bricks. Many possibilities exist to remove two linkers. A rationalization of these two‐linker defects has been done in Ref. 18. The defect structure denoted as type 6 in the work of Rogge18b was chosen here, as this structure ensures the highest accessibility for guest species, as shown in our earlier work.5, 9, 10 We gave preference to the situation where active sites were created showing the best perspective for guest intrusion and accessibility of the metal center. In addition, the symmetry of this linker deficiency allows to reduce the dimension of the unit cell to two bricks. The structure of these active sites has been extensively outlined in previous works of the authors.5, 7, 9, 15

The defective brick <Zr₆O₆(OH)₂>¹⁰⁺ is tenfold coordinated, and shows two distinct active sites which lie on opposite sides of the brick, as displayed in Figure 1. We will refer to these sites as site A and B. When atmospheric water is present, the Zr‐brick becomes hydrated: water molecules physisorb on the coordinatively unsaturated metal centers. One of the water molecules then dissociates into a hydroxyl group adsorbed on the Zr‐atom and a proton is adsorbed on the adjacent μ₃‐oxygen, to give a more stable structure, as discussed in literature.6, 7, 8, 9 The unit cell of this hydrated UiO‐66 material with two missing terephthalate linkers is displayed in Figure 1. The two hydrated node surface sites A and B exhibit the same structure. Further static periodic DFT calculations are performed with different types of coordination with water and methanol on site A while keeping the hydrated site B as passive.

Grand Canonical Monte Carlo

To estimate the number of methanol molecules which can be inserted in the UiO‐66 framework, we used Grand Canonical Monte Carlo (GCMC) simulations as implemented in the RASPA software package.19 The employed force field describes the short‐range repulsion and long‐range van der Waals attraction by a Lennard‐Jones potential, and electrostatics via point‐charge Coulombic interactions. The methodology is the same as used by Ghosh et al.20 to describe water and CO₂ adsorption in UiO‐66. The Lennard‐Jones parameters of the framework atoms are obtained from Dreiding21 (except for Zr for which the UFF22 parameters are used) and framework charges are computed using the Extended Charge Equilibration method.23 The TraPPE24 model is used for the methanol guest atoms. In the GCMC simulations, van der Waals interactions are truncated beyond a distance of 12.8 Å, which is compensated by analytical tail corrections. For the electrostatic interaction, the Ewald summation to account for the long‐range nature of this interaction is used. Each run consists of 10 000 equilibration cycles and 20 million production cycles, where a cycle consists of at least 20 Monte Carlo move attempts. The concept of a 2‐brick unit cell is systematically employed in all calculations performed in the frame of this work. It implies that structures are easily interchangeable between the different approaches. Snapshots belonging to GCMC runs can be directly used as starting configurations for the ab initio molecular dynamics simulations. A temperature of 330 K and a pressure of 50 atm is applied and it is verified that methanol in UiO‐66 shows liquid behavior under these conditions.25

Molecular Dynamics

DFT‐based molecular dynamics simulations were performed with the CP2K software package,26 that employs a hybrid Gaussian Plane Wave basis sets approach.27 The DFT functional is taken to be the PBE,13 which was supplemented by Grimme D3 dispersion corrections.14b A DZVP‐GTH basis set was used for C, O and H atoms together with pseudopotentials.28 For Zr the DZVP‐MOLOPT‐SR basis set was taken into account. The time step for integration of the equation of motion was set to 0.5 fs, and the temperature was controlled by a Nosé‐Hoover chain thermostat consisting of five beads and a time constant of 0.3 ps.29 The unit cell used was taken from the static calculations and the methanol configurations were extracted from the GCMC simulation. A first simulation of 25 ps was performed in the NPT ensemble at 330 K and 1 bar, using a MTK barostat with a time constant of 0.1 ps.30 The final structure is then used as starting configuration in an NVT simulation of 50 ps keeping the unit cell parameters fixed.

2.  Results and Discussion

2.1.  Free‐Energy Balance—Water and Methanol Coordination on Defective Metal Sites

A first step towards a thorough understanding of the influence of methanol on the active sites in the UiO‐66 material may be done by studying the stability of the various coordinated systems, involving physisorbed and chemisorbed water and methanol molecules on the active Zr sites. This first step can best be accomplished by means of static periodic calculations, as already done for the case of water in a recent paper of some of the authors.9 As a result, insight is obtained into the structural topology of the Zr₆ node and the associated chemistry. To allow for a comparative discussion on coordination energies, the structure of site B (facing site A at the opposite brick (Figure 1)) is kept fixed in all structure calculations and is assumed to show a hydrated node surface. The results of these static periodic calculations are shown in Figure 2.

Figure 2.

Coordination free energies at temperature of 330 K of water and methanol at coordinatively unsaturated Zr‐oxide bricks in defective UiO‐66, with respect to a water coordination free node face R. We assume a hydrated site B which is kept fixed in the static calculations for the different structures of site A. Free energies (in black) are given in kJ mol⁻¹ and their decompositions into enthalpic (blue) and entropic contributions (grey). Energies resulting from periodic calculations at PBE‐D3 level of theory.

In an environment with atmospheric water, the bare Zr₂O₂ face will be hydrated immediately. The stabilization caused by one water molecule physisorbed to one of the undercoordinated Zr‐atoms amounts to 17.7 kJ mol⁻¹ at 330 K (structure 1 of Figure 2). The molecule can be deprotonated to the μ₃‐oxygen atom (structure 2), lowering the free energy with an additional 22.7 kJ mol⁻¹. The remaining open metal site acts as a Lewis acid center while a Brønsted acid and basic site arise on the μ₃‐hydroxyl and the hydroxyl bonded to the metal. The most stable configurations at 330 K are complexes with two or three water molecules. In configuration 3, both Zr sites are capped with a physisorbed and a chemisorbed water molecule, respectively, stabilizing the complex with an extra 64.7 kJ mol⁻¹. Adding a third molecule yields a complex (structure 6 in Figure 2) which is slightly more stabilized (≈9.4 kJ mol⁻¹) than the complex with two coordinated water molecules. The additional water molecule is coordinated to the μ₃‐hydroxyl group and the Zr‐OH group in accordance with what has been reported by Ling and Slater,6 and Vandichel et al..7 However, the small additional coordination energy will lead to a spontaneous decoordination of this water molecule from the active site. With the presence of a solvent molecule like methanol in the vicinity of the active site, one could expect that water can be displaced to allow for coordination by methanol. This may be important for reactions where methanol takes an active role in the chemical conversion which is for example, the case for esterification. Configuration 4 in Figure 2 is characterized by methanol which is settled along the hydrated face (structure 3) by means of hydrogen bonds with the Zr adsorbed water and hydroxide anion and with the μ₃‐hydroxyl group. This complex has an extra stabilization energy of 18.4 kJ mol⁻¹ compared to the well‐known configuration 3. Another possible arrangement is structure 5, with two water molecules physisorbed to the two adjacent under‐coordinated Zr‐centers and a methanol coordinated to the μ₃‐oxygen atom. Summarizing, the static calculations give a good picture of how the active sites created by linker deficiencies are capped with water in atmospheric conditions, and how methanol can easily replace water when coordinated to the hydrated site. Structure 4, in which methanol is hydrogen‐bonded with the μ₃‐hydroxyl group and Zr‐OH, is even the most stable. Therefore, based on the static calculations one could predict that configuration 4 will be the most visited configuration in a MD simulation at operating conditions and with the pores filled with liquid methanol. Further in this paper, as part of our multilevel modeling approach, we will elaborate in how far these initial results correspond to a dynamic loading of the pores at operating conditions.

2.2.  GCMC Calculations to Estimate the Loading of Methanol in the Pores of Defective UiO‐66

As a next step of our multilevel approach, we estimate the number of methanol molecules in the pores of the UiO‐66 material at a temperature of 330 K and a pressure of 50 atmospheres, where methanol is in liquid phase. To this end, a series of GCMC calculations have been performed at various pressures. This yields a methanol adsorption isotherm for defective UiO‐66 displayed in Figure 3 a at a temperature of 330 K. Convergence is almost reached at 1 atm. Probability distributions for the uptake of methanol molecules at a high pressure of 50 atm (convergence is now absolutely assured) are plotted in Figure 3 b and a maximum probability is reached at an uptake of 29 molecules in the pores of the unit cell (restricted to two bricks) with a spreading of ±3 molecules. For the sake of completeness GCMC calculations have also been performed in a 2×2 x 2 supercell. The maximum loading becomes now 38 molecules (Figure 3 a). This higher number is expected since in the small simulation cell a lot of space is lost in the boundaries, which could host additional methanol molecules. To compensate for the usage of a reduced unit cell, a maximum loading of 32 methanol molecules is considered in the following NPT and NVT molecular dynamics simulations. The impact of this number on the structure of the active site and immediate vicinity is scarcely visible, since the number of methanol molecules surrounding the active sites is constant and stabilized by hydrogen bonds, while other molecules occupy the adjacent pores.

Figure 3.

a) Methanol adsorption isotherm in defective UiO‐66 at 330 K indicating also the 1σ width of the probability distribution; b) Probability distribution at different loading of methanol molecules as predicted by GCMC at 330 K and a pressure of 50 atm.

2.3.  Molecular Dynamics: Active Sites at Operating Conditions

In previous work of some of the present authors, reactions were modeled at the active site of defective UiO‐66 taking into account only the molecular species which are directly included in the reaction and possibly some directly coordinating protic molecules. However, at real catalytic operating conditions, a solvent is present in the pores of the material. Even when the solvent molecules do not play an active role in the reaction mechanism, they frequently affect the reaction rate in a substantial and beneficial manner. We have shown in the GCMC calculations that the methanol solvent in the pores can be represented by an uptake of about 29–32 methanol molecules per unit cell (restricted to two bricks). To describe the active (hydrated) site and its immediate surroundings at operating conditions we perform a series of MD simulations starting from some random structures encountered at the end of the GCMC calculations near convergence. In particular, first an NPT simulation has been run with full loading of methanol during 25 ps to equilibrate the system, with two water molecules at each active site A and B (structure 3 of Figure 2). The empty framework has been kept fixed during the loading of the solvent molecules in the GCMC procedure, and the NPT simulation allows the system to relax which is clearly visible when examining the change of the unit cell volume, as visualized in Figure S2.

The final configuration of the NPT simulation is used as initial structure of the NVT simulation. During this simulation, attention is drawn to the mobility of the methanol molecules and its concentration and network formation in the pores of the unit cell. In the starting hydrated configuration, two water molecules are coordinated to each of the two active sites A and B (structure 3 in Figure 2). During the timescale of our simulations, the methanol solvent does not succeed in replacing a water molecule coordinated to the metal. At the beginning of the simulation, the two active sites A and B are equivalent, but at a certain moment a methanol is nestled between the water coordinated to the metal and the hydroxyl group bonded to the other Zr‐center, bridging the two Zr‐atoms and forming three hydrogen bonds with the node face. In this configuration, the aqua ligands give rise to a highly stabilized complex, as shown in Figure 4. This behavior takes place at the beginning of the simulation and breaks the symmetry of the two sites. In a completely arbitrary way we associate the appearance of this trigonal network with the water‐hydroxo pair to site A. The system remains in this structure during the whole simulation (displayed in Figure 4). In the static calculations, it is also found that this configuration is the most stable (structure 4 in Figure 2). This trigonal network obviously interacts with other methanol molecules of the pore, but they do not succeed in breaking this bridge. One may expect that the replacement of the water by a methanol molecule is to some extent activated. An important and interesting aspect is the continuous proton shuttle observed between one Zr‐bound water and the other via the connecting methanol molecule. We are here confronted with a dynamic Brønsted acidity: the role of the acid proton of the water and the OH‐anion is similar as there is a systematic switch between the two configurations, as clearly visualized in Figure 4. The observed dynamic acidity resembles that of Ling and Slater6 but in the latter no methanol is present between the two groups.

Figure 4.

Dynamic Brønsted acidity in one of the structures established on the active site in defective UiO‐66 and liquid methanol in the pores.

At site B (opposite to site A) we observe a more complex variation of structures, going from single closed loops of hydrogen bonded methanol and water molecules to connected loops and open methanol chains with a length of 5–6 molecules. The total time of appearance of these three types of networks and the probability of occurrence during the 50 ps of simulation are displayed in Figure 5. These loops and chains are formed and disappear in a completely random way. The size of the loops and chains varies dynamically and may easily amount to a network of 6 oxygens tied together with hydrogen bonds. Three of the possible and distinct patterns that are observed are shown in the top pane of Figure 5. In all these patterns, the node‐ligated‐aqua and hydroxyl species remain intact. None of these species have been replaced by methanol. One of the patterns at site B which appears the most frequently, is the six‐membered ring formed by four methanol molecules and the two capping water molecules. We clearly see a boat or chair conformation for the six‐membered ring analogous to the cyclohexane molecule. One methanol lies between the two water molecules, forming a hydrogen bond with the μ₃‐oxygen atom, while other three methanol molecules are located on the same site of the μ₃‐OH group. This configuration is stable for a part of the simulation time, with the position of the oxygens kept fixed in a network of hydrogen bonds, while some of the hydrogens are shuttled by the methanol molecules. The system then, after about 22 ps (Figure 5), evolves to an open 5‐membered ring structure as a methanol molecule decoordinates from the Zr‐OH group. The open ring structure further arranges to form a 4 or 5‐membered ring as shown in the Figure. This structure allows a methanol molecule to come closer to the μ₃‐OH group, presumably enhancing the stability by forming tighter hydrogen bonds.

Figure 5.

Top: Ring configurations observed at site A and site B originating from the interaction between the Zr‐bonded hydroxo and water and the solvent molecules. Bottom: Appearance of the various structures during the simulation. The frequency of occurrence of the different structures is also reported. A threshold of 2.2 Å for the donor‐acceptor distance was chosen to determine a hydrogen bond and observations were smoothed over 0.5 ps.

It is instructive to verify possible similarities with the microscopic structure of liquid methanol in bulk. It is unambiguously shown in a combined experimental‐theoretical paper31 that liquid methanol in bulk is a mixture of ring and chain structures dominated by six and eight methanol units. However, in bulk the methanol molecules are not hindered by any boundary effects. In general, the influence of the internal surfaces of the pores of a nanoporous material disturbs the presence of regular patterns in the structure of the methanol liquid. Here, boundary and surface effects will have a substantial influence on the length of the chain and ring structure. Nevertheless, the tendency to form chains of 4 methanol molecules which are eventually hydrogen‐bonded to the coordinated water is clearly present. It is interesting to observe that the structure of bulk methanol has similarities with the structure in a confined environment. It must however be emphasized that such behavior will be critically dependent on the particular cavity and channel structure of this nanoporous material. The pores on UiO‐66, where the included sphere diameter ranges from 6 to 9 Å,18b are large enough to enable structuring of the methanol molecules, certainly when defects are present.

Besides single closed loops also open chains of hydrogen‐bonded methanol molecules are occurring during the simulation (for at least 30 % of the simulation time), as displayed in the bottom line of Figure 5. In some events these chains connect the two opposite sites, but no proton transfer has been observed through this chain of methanol molecules. It is striking that all the different patterns that have been observed involve methanol molecules that are located in the space between the two active sites. Assuming a total loading of 32 methanol molecules in the pore of the unit cell, many other molecules are not part of the observed patterns around the active sites. They also form chains of hydrogen bonds, which are generally of short length and which show similarities with those that have been observed in bulk methanol solution.32

In all these scenarios which take place during the NVT simulation, we observe a rather peculiar role of the acid proton on the μ₃‐OH group. It does not only play a fundamental role in the formation of the ring structures, as already noticed, but it also provides an additional stabilization. This is certainly also the case in the structure on site A where a single methanol molecule is coordinated to the μ₃‐OH, Zr‐OH and Zr‐OH₂ group, acting as an intermediary in the proton transfer between the Zr‐OH and Zr‐OH₂ groups. The proton of the μ₃‐OH group prefers to stay in its protonated state and only participates in the network by forming a hydrogen bond with a methanol molecule. Summarizing, the presence of liquid methanol in the pores of defective UiO‐66 gives rise to a dynamic network of hydrogen bonds which surround the active sites and directly involve Brønsted sites, which could take part in reactive processes.

No proton transfer has been observed between the two opposite sites (site A and site B) during the simulation time. The distance between the two sites can easily be bridged by two methanol molecules forming a hydrogen bond with the waters coordinated at the Zr‐centers in both opposite sites. During the simulation, such a bridge is formed several times, but there was no driving force to induce a proton transfer. During the simulation, we never saw a replacement of a water molecule coordinated to the metal by a methanol and also reversely, no replacement of a methanol by a water molecule has been observed. In configuration 5 of Figure 2 we see that deprotonation of the μ₃OH group at site A is energetically not favored, as it is 30 kJ mol⁻¹ less stable than configuration 4. This transition 4 → 5 needs breaking of two chemical bonds and is probably highly activated. We have not estimated this barrier but we never encountered the occurrence of configuration 5 during the NVT simulations. Another striking feature is the breaking of the symmetry in the structures formed at the two active sites. At one of the two sites, a methanol molecule acts as bridge to allow a proton shuttle between the terminating water and hydroxide, creating a dynamic Brønsted acidity center. These simulations shed light on a series of dynamic processes that cannot be observed with static calculations. Herein, we see that methanol molecules actively take part in the active sites via dynamic hydrogen bonds, and change the behavior of the Brønsted sites at the defect level, by exchanging protons with the water molecules. In general, the multilevel modeling approach allows to go one step beyond the static representation of the active sites by adding a realistic loading of solvent, making it possible to model the system at operating conditions.

2.4.  Proton Mobility in Liquid Methanol Confined in the Pores of UiO‐66

So far, we have seen how protons are dynamically shuttled by methanol from one Zr‐bound water to the other. It is however also interesting to investigate the transport mechanism of charged defects in a protic environment. Transport dynamics of charged defects in hydrogen‐bonded liquids have their importance in numerous biological and technological systems [Ref32b and refs therein]. A substantial amount of theoretical and computational studies has addressed this topic. They all support the structural diffusion or Grotthuss mechanism in which a charge defect migrates through a hydrogen bond network via a series of proton transfer steps. All this work was restricted to liquids in bulk. The present simulations allow to extract information about the way a proton or charge can move through a confined liquid, by removing a proton artificially from the active site and inserting it elsewhere in the pore, as displayed in Figure 6. This way, one creates a positively and a negatively charged site in the pore of the unit cell and can investigate how the system responds to this charged defect in the pore of the material.

Figure 6.

Three snapshots of the molecular dynamics simulation which starts from a deprotonated site A and a protonated methanol molecule, with corresponding schematic representation of the process (above). 1) starting structure with protonated solvent; 2) a snake‐like chain of hydrogen bonds is formed which leads a proton to site B; 3) site B is protonated, while site A is missing a proton.

In a methanol solvent, a particular charge transfer mechanism was detected, which involve a series of subsequent hydrogen bonds, as displayed in Figure 6. In this context, it is interesting to see whether methanol in the pores of a nanoporous material shows similarities with the earlier observations. A proton shuttle generates a transfer of charge. The proton transfer occurs through a hydrogen bonded network and implies a shuffle of a hydrogen between two neighboring oxygens. In a methanol chain or ring each non‐terminating oxygen atom can play a role as hydrogen acceptor and donor, via hydrogen bonds. The positive charge is transferred from the acceptor to the donor since CH₃OH₂ ⁺ owns a coordination pattern which is similar to that of CH₃OH. If we assume a proton transfer from A to B over a chain of methanol molecules tight together with hydrogen bonds, a charge displacement is generated yielding a change in the electrical potential between A and B. The main pore in the reduced UiO‐66 unit cell shows two opposite sites A and B filled with methanol liquid in between. Starting from a neutral system with no charged species we may assume that the two active sites A and B have the same electrical potential, and thus no proton transfer is indeed observed between these sites even when some network of methanol molecules appears in the simulation connecting the two sites. This was indeed observed in the previous section.

To study the effect of charge mobility in the UiO‐66 material, three NVT simulations were performed, where in each of the simulations, a hydrogen atom was removed from site A and donated to one of the methanol molecules outside the first solvation sphere, as schematically shown in Figure 6. This creates a charge separation in the system. If the proton is allowed to move without restraints, the system will eventually seek to stabilize the charge. In two of the simulations, the protonated methanol is stabilized by the surrounding solvent molecules. In the third simulation, a chain of hydrogen bonds acts as a backbone for a cascade of exchange of protons, which leads to the donation of a proton from the solvent to the active site B. Snapshots of this path are displayed in Figure 6. Site A, therefore, remains deprotonated, while there is an extra proton on site B. This configuration is retained for the whole time of the simulation, and is apparently stabilized by the presence of solvent molecules. Static periodic calculations in the absence of any solvent molecules show a difference in free energy of 89.6 kJ mol⁻¹ in favor of the structure with neutral sites (structure 3 of Figure 2) with respect to the structure where one proton is moved from site A to site B (Supporting Information, Figure S5). The observation that these protonated/deprotonated sites are maintained in the molecular dynamics simulations is an indication that solvent molecules have a decisive role in the stabilization of these charged configurations. Moreover, the active sites undergo also changes in the geometry. On site B, in particular, the orientation of the two Zr bonded water molecules are slightly altered by the presence of an extra proton. The distance between the oxygens and the Zr atoms increases, and they become more loosely bonded. Moreover, the distance between the two oxygens themselves is larger, and has large fluctuations (up to 2 Å). This could be related to a higher tendency of water to leave the active site, and such a process could be the initiator of the substitution process of a water molecule with a methanol molecule, or with a generic reactant present in solution. The methanol substitution process in UiO‐66 has been investigated by Yang et al.8 showing that at room temperature the interexchange of one water molecule by one methanol molecule is not thermodynamically favorable. Proton mobility has also been studied in liquid methanol by inducing an excess proton as a defect structure.32b It is found that the defect structure associated with the excess proton is a hydrogen‐bonded cationic chain whose length may exceed the average chain length in pure liquid methanol. This agrees perfectly with what we observed in the path discussed in Figure 6 where the excess proton as defect structure migrates/diffuses through the hydrogen‐bonded network. The proton transfer satisfies a “snake‐like” mechanism, as suggested by Morrone et al.32b

2.5.  Conclusions

In this work, we investigated static and dynamic properties of the active sites on the hydrated UiO‐66 in the presence of a realistic loading of methanol solvent. The behavior of a liquid in a confined space is substantially different from the one in bulk. The methanol molecules of the solvent mediate and aid proton transfers and are kept in stable configurations near the active sites by a network of hydrogen bonds. Moreover, the solvent has the capability of transferring protons to the active sites. The presence of a solvent like methanol assists in the proton mobility, which is observed in the case of a deprotonation of the active site. When an excess proton is introduced in the solution, it can be transferred to the active site via the methanol molecules. In this case, we show that the solvent can stabilize a charge on the active site, with dynamic interactions that are impossible to consider in static calculations. This could also play a role in reactions where charged intermediates are present and can be stabilized by the solvent. The interaction with the solvent sheds light on the relative stability of both Brønsted acid and base sites of the material. The μ₃‐hydroxo group is involved in the solvent network, but does not exchange protons during the simulation time, which indicates that protons from water and hydroxyl group are preferential donors and show higher acidity. This remarkable behavior of the protons on these sites may have a substantial impact on many heterogeneous catalytic reactions which take place in protic solvents, such as Fischer esterification or hydrogenation reactions and could also affect the rearrangement of the framework itself, such as in the linker exchange process. A solvent can activate or deactivate the reaction, can serve as a substrate, influence the formation of different isomers, affect reaction mechanism and even influence the rate and selectivity due to its interactions with the starting materials or products. Hydrogen bonds between solvents and substrates can strongly influence the reaction, revealing the important role of solvent‐stabilized catalytic intermediates, thus going far beyond the solvation alone. In general, this multilevel modeling approach brings insights on the interactions of the solvent in the confined pores of the material and how the active sites are modulated via these dynamic interactions.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

C. Caratelli, J. Hajek, S. M. J. Rogge, S. Vandenbrande, E. J. Meijer, M. Waroquier, V. Van Speybroeck, ChemPhysChem 2018, 19, 420.