Two-stage patterning dynamics in conifer cotyledon whorl morphogenesis

Abstract

Background and Aims

Conifer embryos, unlike those of monocots or dicots, have variable numbers of cotyledons, even within the same species. Cotyledons form in a single whorl on a dome-shaped embryo. The closely spaced cotyledons are not found outside this ring, indicating a radial control on where they can form. Polar transport of the hormone auxin affects outgrowth of distinct cotyledons, but not the radial aspect of the whorl or the within-whorl spacing between cotyledons. A quantitative model of plant growth regulator patterning is needed to understand the dynamics of this complex morphogenetic process.

Methods

A two-stage reaction–diffusion model is developed for the spatial patterning of growth regulators on the embryo surface, with a radial pattern (P1) constraining the shorter-wavelength cotyledon pattern (P2) to a whorl. These patterns drive three-dimensional (3-D) morphogenesis by catalysing local surface growth.

Key Results

Growth driven by P2 generates single whorls across the experimentally observed range of two to 11 cotyledons, as well as the circularly symmetric response to auxin transport interference. These computations are the first corroboration of earlier theoretical proposals for hierarchical control of whorl formation. The model generates the linear relationship between cotyledon number and embryo diameter observed experimentally. This accounts for normal integer cotyledon number selection, as well as the less common cotyledon fusings and splittings observed experimentally. Flattening of the embryo during development may affect the upward outgrowth angle of the cotyledons.

Conclusions

Cotyledon morphogenesis is more complex geometrically in conifers than in angiosperms, involving 2-D patterning which deforms a surface in three dimensions. This work develops a quantitative framework for understanding the growth and patterning dynamics involved in conifer cotyledon development, and applies more generally to the morphogenesis of whorls with many primordia.

INTRODUCTION

Angiosperm monocots and dicots are tightly constrained to form one or two cotyledons, respectively. By contrast, Pinaceae conifers can have highly variable numbers of cotyledons (n_c), both between and within species (von Aderkas, 2002). Average n_c for species are reported as low as 3 (in Tsuga) and as high as 9 (in Cedrus) (Butts and Buchholz, 1940). Within species, n_c typically ranges ±1 from these averages for zygotic embryos (Butts and Buchholz, 1940). For somatic cultures (of clonal lines), embryos with n_c from 3 to 10 are common in Larix, Pseudotsuga and Picea, which have species averages of 5 to 6 (Harrison and von Aderkas, 2004; Holloway et al., 2016).

The positioning of three or more cotyledons on an embryo is geometrically more complex than is the case for monocots or dicots, in which the most complex arrangement defines a one-dimensional (1-D) line between two cotyledons. By contrast, three or more cotyledons can be arranged two-dimensionally (on the embryo surface), and patterned either regularly or irregularly. With this additional complexity, and without the rigid constraint on cotyledon number seen in angiosperms, conifer cotyledon formation can provide unique insights into the developmental mechanisms for the spatial positioning of organs.

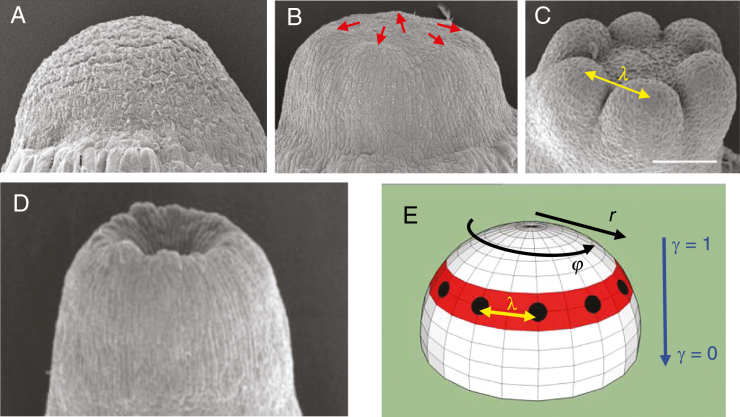
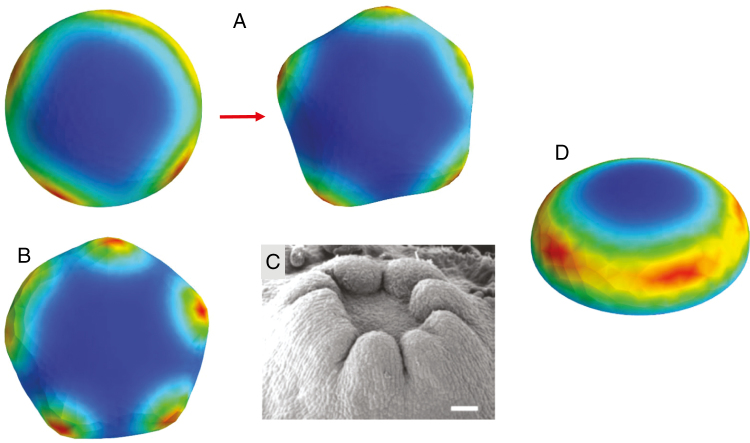
Among the possibilities for 2-D patterning, conifer cotyledons notably do not form all over the surface, but arise simultaneously in a single whorl (Fig. 1C). For the circular geometries involved – embryos go from a domed (Fig. 1A) to a flattened shape (Fig. 1B) during cotyledon development – formation of the whorl indicates pattern control along the radial dimension (Fig. 1E, ‘r’: distance on the surface from the embryo tip or centre, or ‘latitude’ on a hemisphere). Within this whorl, regular cotyledon-to-cotyledon spacing (Fig. 1C, ‘λ’) indicates pattern control in the circumferential dimension (Fig. 1E, ‘φ’: ‘longitude’ on the hemisphere). The linear variation of n_c with diameter expected for regular spacing in a ring (Fig. 1E, black spots) has been found experimentally in Larix (Harrison and von Aderkas, 2004), Pseudotsuga and Picea (Holloway et al., 2016), indicating that n_c variability reflects embryo-to-embryo diameter variability. Without radial constraint, the short wavelength cotyledon spacing (λ) would position cotyledons over the entire embryo, which is not observed: arrangement of primordia in a single whorl involves the combination of a longer spatial scale radial control with a shorter scale circumferential control.

Fig. 1.

Cotyledon patterning in conifer development. (A) An early dome-shaped embryo. (B) At a later stage, embryos have flattened and cotyledons are just beginning to appear (red arrows). (C) Cotyledons subsequently grow out, in a whorled (ring) pattern, with a distinct inter-cotyledon spacing, λ. Scale bar = 200 µm. (D) Cup-shaped embryos, with no distinct cotyledons, can occur spontaneously or be induced by NPA treatment (blocking polar auxin transport). This indicates two linked patterning events (E): the first (pattern P1, red) controlling the radius (r coordinate) of the cotyledon ring (or its ‘latitude’ on the dome); the second (pattern P2, black spots) controlling the spacing, λ, between cotyledons in the ring (along φ, the circumferential coordinate, or ‘longitude’ on the dome). P2 patterning is disrupted in cup-shaped embryos. γ denotes the flatness of the embryo (as defined in Nagata et al., 2013: γ = 1, hemisphere; γ = 0, flat disc). A–C and E are adapted from Holloway et al. (2016), D from Harrison and von Aderkas (2004), with permission. (A–D) Larch (Larix) embryos are shown.

In conifers, the radial and circumferential aspects of cotyledon outgrowth are experimentally separable: disrupting transport of the hormone auxin with NPA (1-N-naphthylphthalamic acid) results in loss of circumferential patterning (Larsson et al., 2008; Hakman et al., 2009), producing circularly symmetric cup-shaped embryos which lack distinct, separated cotyledons (Fig. 1D).

In this paper, we develop a quantitative model for conifer cotyledon positioning, in order to create a framework for understanding the dynamics involved in normal development as well as in response to NPA treatment. The model is two-stage, with mechanisms for radial positioning (pattern 1, P1; red, Fig. 1E) and for the circumferential between-cotyledon positioning (pattern 2, P2; λ, Fig. 1E). The mechanisms are linked hierarchically: P1 control of where the short-wavelength P2 pattern occurs provides the radial constraint necessary for cotyledon whorl formation. NPA affects P2-patterned cotyledon outgrowth, not the circularly symmetric P1 component.

To couple the spatial patterning to embryo shape change, the surface is grown in proportion to the local P1/P2 concentrations; i.e., the P1/P2 mechanism models the dynamic distribution of plant growth regulators corresponding to whorl morphogenesis. As size and geometry changes of the surface in turn affect spatial patterning, the model is ‘morphodynamic’ (Salazar-Ciudad et al., 2003), encompassing the full feedback cycle between growth regulator patterning and surface deformations. The P1 and P2 patterns are stable to this induced growth, as well as being stable over experimental ranges of embryo diameters and to the geometric flattening occurring during cotyledon formation.

Turing (1952) proposed the first mathematical model for chemical pattern formation, which he and subsequent researchers applied to spatial patterning in plant development. His reaction–diffusion (RD) theory shows how reactions between two or more chemicals (morphogens) having unequal diffusivities can self-organize stable concentration waves with a characteristic spacing or wavelength. RD patterns have been confirmed in the development of both animals (e.g. Sick et al., 2006; Sheth et al., 2012; Raspopovic et al., 2014) and plants (e.g. Digiuni et al., 2008). RD has been applied to many cases of plant development, both for ‘morphostatic’ (Salazar-Ciudad et al., 2003) patterning on growing domains (e.g. Harrison et al., 1981; Meinhardt, 1982; Jönsson et al., 2005; Digiuni et al., 2008; Fujita et al., 2011) and for ‘morphodynamic’ patterning of growth regulators driving morphogenesis (Harrison and Kolář, 1988; Holloway and Harrison, 1999, 2008). In RD, chemical transport is via simple diffusion down a concentration gradient.

More recently, it has been discovered that the growth regulator auxin has unique intercellular transport properties (reviewed by Friml, 2003). In addition to simple diffusion, auxin has its own cellular efflux transporters, PIN proteins. Localization of PINs to subregions of the cell membrane produces a polar auxin transport (PAT). PAT, in conjunction with simple diffusion, can self-organize auxin concentration patterns (shown analytically, for example, by Jönsson et al., 2006; Draelants et al., 2013; Farcot and Yuan, 2013). PAT can include a with-the-flux localization of PIN1 (a down-the-gradient facilitated diffusion), which has been applied to canalization and venation (e.g. Mitchison, 1981; Rolland-Lagan and Prusinkiewicz, 2005; Feugier et al., 2005), or an up-the-gradient localization of PIN1, which has been applied to the sequential placement of organs in phyllotaxis (e.g. Jönsson, et al., 2006; de Reuille et al., 2006; Smith et al., 2006). Models of complex auxin patterning, such as for phyllotaxis plus venation, can include terms for intracellular reactions, simple diffusion, up-the-gradient PAT and down-the-gradient PAT (e.g. Bayer et al., 2009). Such mechanisms can have very complex dynamics, because even subsets of the terms – such as reaction and diffusion (Turing, 1952), or diffusion and up-the-gradient PAT (e.g. Jönsson, et al., 2006) – are capable of self-organization.

Previous models of whorled phyllotaxis have focused on the successive formation of whorls, and have defined organ initiation at a fixed radius R₀ from the centre of an apical or floral meristem (Douady and Couder, 1996; Kitazawa and Fujimoto, 2015). In these models, the occurrence of whorls (as compared to spirals) depends on R₀ and on the timing and size of sequential primordia initiation. Initiation sites are affected by the positions of older primordia. In conifer embryos, however, a single whorl of cotyledons forms simultaneously, and the single whorl is robust to large changes in radius: experimental measurements show whorl radii increase by about 150 µm over the range of observed n_c (Holloway et al., 2016; whorl radius is approx. 125 µm less than embryo radius). This indicates an adaptive self-organizing P1 mechanism (in the r coordinate) to position the single cotyledon whorl 150 µm closer to the centre in small embryos with low n_c than in large embryos with high n_c, and argues against a fixed radius R₀ (for instance set by diffusion of a morphogen from the embryo centre), which would not adapt to embryo size variation as observed.

The induction of cup-shaped embryos by NPA treatment indicates a PAT dependence for the circumferential P2 cotyledon pattern (along the φ coordinate), but not for the circularly symmetric P1 ring pattern. Turing dynamics in intracellular reactions and simple diffusion can self-organize pattern in the absence of PAT dynamics. RD is therefore used as a framework for quantitatively characterizing the PAT-independent P1 pattern. This is similar to the recent application of RD dynamics to the radial control of shoot apical meristem size (Fujita et al., 2011). Quantifying radial patterning in this way allows us to characterize the dynamics involved in forming a single whorl robust to the wide range of embryo sizes found in conifers.

For the circumferential P2 pattern, the NPA effect appears to be primarily on the outgrowth of cotyledons: while most embryos do not grow cotyledons at moderate NPA concentrations, those that do tend to show normal circumferential spacing (Holloway et al., 2016). This indicates that the outgrowth of distinct cotyledons from the ring is PAT-dependent (perhaps via supply of a critical factor), but that the spacing λ between cotyledons is PAT-independent. In wave terminology, PAT appears to affect P2 amplitude, not its wavelength. We therefore use a PAT-independent RD mechanism to model self-organization of the P2 cotyledon–cotyledon wavelength λ. The NPA effect on P2 amplitude is modelled as a PAT-dependent factor that affects whether the RD mechanism can actively form a pattern.

While RD can be used to study de novo pattern formation from an unpatterned state, the more common occurrence in development is for patterns to form on prior patterns, as with the P1/P2 stages studied here. Harrison et al. (1981) first proposed such hierarchical patterning for whorl formation in the alga Acetabularia, with subsequent experiments indicating that RD was involved in circumferential spacing in the whorl (Harrison et al., 1988, 1997). Turing identified RD parameter conditions for spatial patterns to grow (amplify) from initially uniform concentration states (PAT models can be analysed similarly). We refer to this self-organizing generation of new pattern as active patterning. RD can also generate active pattern from a pre-patterned state (termed ‘Turing models of the 2^nd kind’, Hunding, 1987); in these cases the pre-pattern limits where the RD pattern forms (by controlling where the Turing conditions are met for active patterning, although linear Turing analysis is an approximation with pre-patterns). For the conifer model, P1 controls where P2 can actively generate the circumferential cotyledon pattern. However, when conditions do not support P2 active patterning (e.g. if a critical factor is affected by NPA reduction of PAT), P2 relaxes to a passive pattern: this is not a uniform concentration, but rather reflects the radial P1 ring pattern.

The P1/P2 model for patterning and morphogenesis allows us to quantify the dynamic constraints involved in forming conifer cotyledon whorls. For patterning, these include constraints on reaction and transport kinetics, the response to NPA interference with PAT, and how the P1 and P2 stages are coupled. For morphogenesis, these include constraints on P1/P2 catalysed surface growth, the effect of that growth on patterning and the effect of 3-D embryo geometry on morphogenesis. The model provides a framework for interpreting current data and guiding new experiments to understand conifer cotyledon development and the establishment of whorled structures in general.

MODEL AND METHODS

As discussed above, the P1 and P2 spatial patterns are each generated by an RD mechanism. The annular P1 pattern specifies the radial position at which cotyledons form. P1 affects a rate constant in the P2 mechanism, constraining the P2 circumferential patterning to this ring. P2 is morphogenetic, altering 3-D shape by locally catalysing surface growth.

The Brusselator RD mechanism (Prigogine and Lefever, 1968) is used for the P1 pattern:

$$\frac{\partial X_1}{\partial t}=a_1{A}_1-b_1{B}_1{X}_1+c_1{X}_1{}^2{Y}_1-d_1{X}_1+D_{X_1}{\nabla }^2{X}_1$$ (1a)

$$\frac{\partial Y_1}{\partial t}=b_1{B}_1{X}_1-c_1{X}_1{}^2{Y}_1+D_{Y_1}{\nabla }^2{Y}_1$$ (1b)

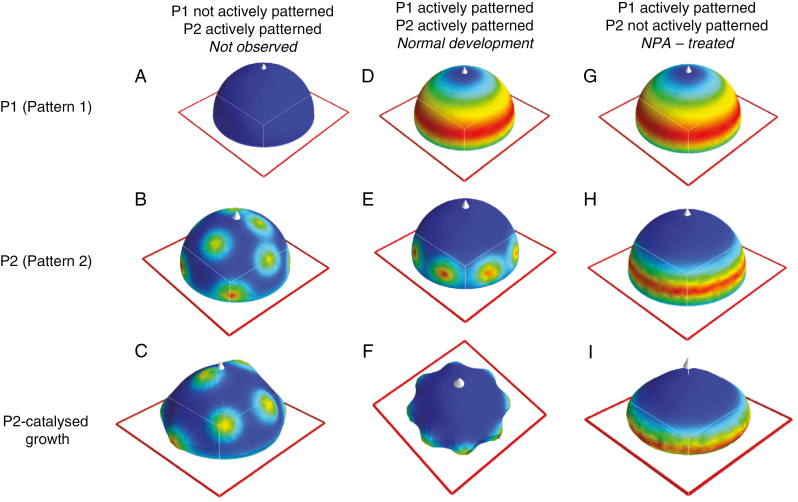
where X₁ and Y₁ are the concentrations of the spatially patterned Turing morphogens (subscript 1 for P1). A and B are precursor concentrations; a, b, c and d are reaction rate constants; and the final terms are for diffusion of X₁ and Y₁ with diffusivities D_X1 and D_Y1, respectively. X₁ self-amplifies (cX²Y term), but this increase is limited by using up Y₁. This depletion-type kinetics tends to form regular patterns in X₁ and Y₁ very close to predictions from linear analysis (e.g. Lacalli, 1981; Harrison, 1993; Holloway and Harrison, 1995) and has been used extensively for regular branching processes in morphogenesis (Harrison and Kolář, 1988; Holloway and Harrison, 1999, 2008; Nagata et al., 2003, 2013; Jönsson et al., 2005; Rozada et al., 2013). Due to this regularity, the Brusselator was used to model formation of the P1 annulus (Fig. 2D, G).

Fig. 2.

Two-stage model for conifer cotyledon morphogenesis. Top row, spatial pattern 1 (P1), colour-mapped for morphogen X₁; middle row, spatial pattern 2 (P2), colour-mapped for morphogen X₂; bottom row, 3-D shape generated by X₂-catalysed growth (colour-mapped for X₂). The top two rows are hemispherical surfaces, while the shapes on the bottom row grow from initial hemispheres. Red outlines are in the x–y plane; white arrow, z-axis. P1 and P2 patterns are generated by reaction–diffusion (RD) mechanisms (eqns 1 and 2, respectively); X₁ and X₂ concentrations are shown colour-mapped from blue (lowest concentration) to red (highest concentration). The X₁ concentration (top row) affects a production rate constant in P2 (eqn 3), constraining where P2 forms (middle row). (A–C) When P1 is not actively patterned, X₁ (A) and Y₁ revert to uniform steady-state concentrations. This allows the short-wavelength P2 pattern to form all over the domain (B), catalysing a ‘spots-all-over’ bumpy morphogenesis (C), which is not seen in conifer embryogenesis. (D–F) When P1 is actively patterned, X₁ forms a ring defining the radial position of the cotyledon whorl (D). This (by eqn 3) constrains P2 to form only within the ring (E). Outgrowth of regularly spaced primordia corresponds to normal cotyledon morphogenesis (F). (G–I) If P2 is not actively patterning, it has a steady-state pattern (H) which follows that of P1 (G), and outgrowth is circularly symmetric (I), like NPA-treated cup-shaped morphogenesis.

The depletion kinetics of the Brusselator, however, make it unsuitable for a P2 pattern, which is controlled by P1. Without loss of generality, a, b, c and d can be set to unity, and the A and B concentrations become the only reaction parameters in the model (Nicolis and Prigogine, 1977). A feedforward from P1 to a P2 Brusselator could be made by identifying one of the P1 morphogens (X₁ or Y₁) with the A₂ or B₂ precursors for P2. This P1-patterned feedforward must be into A₂ to produce a passive P2 ring pattern when simulating NPA treatment, as the passive steady state of X₂ is proportional to A₂ and does not depend on B₂. However, active patterning happens at lowA in the Brusselator (Herschkowitz-Kaufman, 1975), which contradicts forming P2 concentration peaks in the high A₂ annulus specified by P1. That is, such a mechanism cannot form active normal cotyledon pattern in the same radial position as the passive NPA-treated ring, as is observed experimentally.

We therefore used an activator–inhibitor kinetic mechanism in which both active and passive P2 pattern are in-phase with the P1 annulus (Fig. 2E, H). This Gierer–Meinhardt (GM) mechanism (Gierer and Meinhardt, 1972) is given by:

$$\frac{\partial X_2}{\partial t}=a_2{A}_2+\frac{c_2{A}_2{X}_2{}^2}{Y_2}-d_2{X}_2+D_{X_2}{\nabla }^2{X}_2$$ (2a)

$$\frac{\partial Y_2}{\partial t}=b_2{B}_2{X}_2{}^2-e_2{Y}_2+D_{Y_2}{\nabla }^2{Y}_2$$ (2b)

for the morphogens X₂ and Y₂, with subscript 2 for P2.

P1 to P2 feedforward is implemented by setting

$$c_2=n{X}_1$$ (3)

as gradients in c₂ strongly affect GM pattern localization (Holloway and Harrison, 1995). Equations (1)–(3) establish the necessary chemical prepatterns for morphogenesis of a single simultaneously initiated whorl of primordia (Fig. 2D–F).

Equations (1)–(3) were solved by an implementation of the finite element method (FEM) in Python (version 2.7.3), using the Fenics 1.5 (https://fenicsproject.org/;Logg and Wells, 2010; Logg et al., 2012; Alnaes et al., 2015), numpy (http://www.numpy.org/) and scipy (https://www.scipy.org/) libraries. Mayavi2 graphics were used for visualization (http://mayavi.sourceforge.net/). The initial triangulated mesh specifying the surface was generated by gmsh 2.5.1 (http://gmsh.info/). Initial shapes were hemispherical caps, specified by flatness parameter γ between 1 (hemisphere) and 0 (flat disc) (see Fig. 1E). Initial surfaces were defined on between 793 and 801 vertices (exact value depended on the radius specified). All surfaces had 65 boundary (equatorial) vertices, but surfaces with γ < 1 had fewer total vertices than γ = 1 at any given radius, in proportion to the decrease in pole height. Boundary conditions were fixed-value (Dirichlet), with X and Y concentrations (eqns 1 and 2) specified as their passive steady-state values (X₀, Y₀) on the boundary (equatorial positions). (No-flux boundary conditions would create maxima at the pole or equator, which would not correspond to the observed whorls.)

To couple this prepattern to morphogenesis, local growth of the surface was implemented as in Harrison et al. (2001) and Holloway and Harrison (2008): in each iteration, finite elements intersecting at a mesh vertex were increased in area proportional to the local X₂ concentration; mesh vertices were then moved along the local normal vector (averaged from the normals of the neighbouring finite elements) to accommodate this area change (e.g. Fig. 2C, F, I). Vertex positions were updated simultaneously for the whole surface. Boundary (equatorial) vertices had fixed positions.

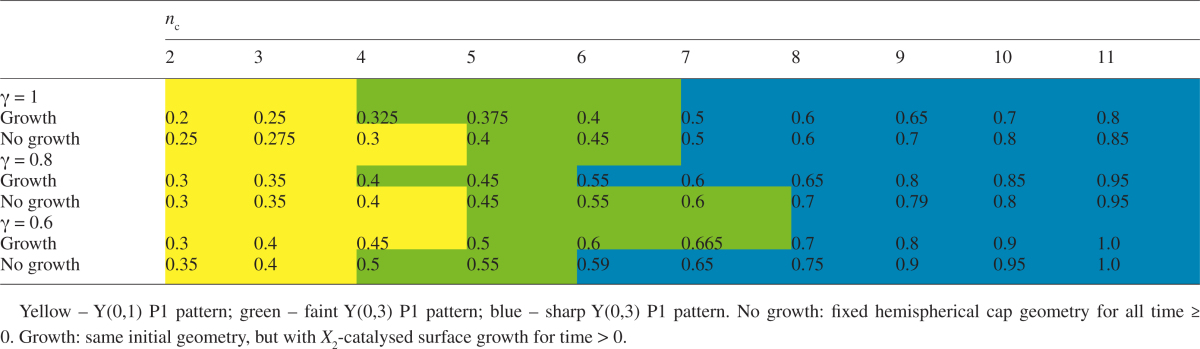
The spatial solutions of eqn (1) (or any pattern-forming mechanism) on a hemispherical geometry are composed of the surface spherical harmonics, Y(m,l), which are polynomials with m repeated structures in the φ dimension (longitude) and l latitudes at which the solution passes through the passive steady-state value. Occurrence of the P1 ring depends on the fit between the domain (embryo) size and the spacing of the chemical patterning mechanism (wavelength). The parameters in Table 1 (reaction rate constants from Holloway and Harrison, 2008) generate a P1 Y(0,3) ring pattern (e.g. Fig. 2D, G) which is stable over more than a doubling of domain radius, or, equivalently, to a more than halving of pattern spacing. This represents robustness to at least a factor of two change in reaction or diffusion constants (since these have a less than linear effect on RD spacing; Harrison, 2011, chapter 5).

Table 1.

Model parameters

Equation (1)	Equation (2)	Other
a 1 = 0.01	a 2 = 0.0006	n = 0.00125
b 1 = 1.5	b 2 = 0.025	c g = 0.001
c 1 = 1.8	c 2 = 0.005 (initial)	Δt = 0.01
d 1 = 0.07	d 2 (normal) = 0.21; d2 (NPA) = 0.14	Number of vertices (γ = 1) ~ 800
	e 2 = 0.27
A 1 = 10.0	A 2 = 0.4
B 1 = 1.0	B 2 = 0.4
D X1 = 0.01	D X2 = 0.0004
D Y1 = 0.1	D Y2 = 0.008

GM (eqn 2) reaction rate parameters are as in Holloway and Harrison (1995), except for initial c₂ = 0.005 (for t > 0, c₂ follows eqn 3), with diffusivities selected to give a wavelength λ = 0.52 (calculated from linear analysis), corresponding to 12 P2 primordia at radius 1 (and γ = 1). The feedforward constant n (eqn 3) scales X₁ to keep P2 in the active patterning region of the linear parameter space. NPA treatment is simulated by reduction of d₂, which shuts off active P2 patterning without strongly affecting wavelength (Holloway and Harrison, 1995). Linear analysis predicts this qualitative active-to-passive change for decreasing d₂; numerical simulations were used to find this boundary value for the non-linear system of eqns (1) and (2). Local growth is proportional to X₂ (parameter c_g), and is calculated once for every 50 iterations (of size Δt) of the RD solver. Simulations were run for 30 000 iterations.

RESULTS

Whorl formation: P1 constraint of P2

Lack of constraint.

An essential feature of single whorl formation is that a relatively short wavelength spacing (the inter-cotyledon λ shown in Fig. 1) is constrained to a ring. In the absence of a radial (or latitudinal) constraint, a mechanism with such a short wavelength would generate pattern all over the domain. This is illustrated in Fig. 2A–C, in which active patterning is turned off in the P1 Brusselator (by setting diffusivities D_X1 and D_Y1 to zero), resulting in unpatterned, uniform X₁ and Y₁ concentrations (Fig. 2A). Active patterning in P2 is then spatially unconstrained, and concentration peaks form all over the surface (Fig. 2B). If this P2 pattern catalyses surface expansion, outgrowths occur over the whole domain (Fig. 2C): this is not observed in conifer cotyledon morphogenesis (or single whorl morphogenesis in general).

Normal patterning and morphogenesis.

With P1 actively patterning and generating a relatively long-wavelength annular pattern (Fig. 2D), feedforward (eqn 3) constrains the short-wavelength P2 to form in a whorl and not over the centre of the domain (Fig. 2E). Growth catalysed by P2 generates the regularly spaced whorl of primordia associated with normal cotyledon morphogenesis (Fig. 2F). Equations (1)–(3) provide a framework for the dynamics needed for the morphogenesis of a single simultaneous whorl of primordia.

NPA effect on P2 patterning

Cup-shaped morphogenesis (spontaneous or due to NPA treatment) is associated with loss of P2 patterning (lack of distinct cotyledon outgrowth). With normal active P1 patterning (Fig. 2G), loss of active P2 patterning reverts to a passive steady state reflecting the P1 annular pattern (Fig. 2H). The PAT-dependent shut-off of P2 self-organization is modelled via reduction of the decay parameter d₂, from 0.21 (normal) to 0.14 (NPA-treated). Growth catalysed by the resulting annular passive P2 pattern generates the circularly symmetric morphogenesis of cup-shaped embryos (Fig. 2I). Partial reduction of d₂, to 0.18, produces active P2 pattern, but at lower amplitude than normal. This corresponds to the decreased amplitude outgrowth but relatively unaffected P2 spacing observed experimentally under moderate NPA treatments (Holloway et al., 2016).

Effect of geometry on morphogenesis

Cotyledons in vivo tend to point upwards (Fig. 1C), and this upwards tendency is retained even in cup-shaped embryos lacking cotyledons (Fig. 1D). The radial location of the P1 ring on the dome could potentially affect this outgrowth angle, with higher latitude rings giving smaller angles between the outgrowth and the z-axis. The single-ring solution of the P1 eqn (1) on a hemispherical cap is the annular Y(0,3) surface spherical harmonic (Fig. 2D, G), which has a characteristic inset from the equator. Higher latitude rings could arise for higher-order harmonics (e.g. Y(0,7)), but this would also produce multiple rings, which are not seen in normal conifer development.

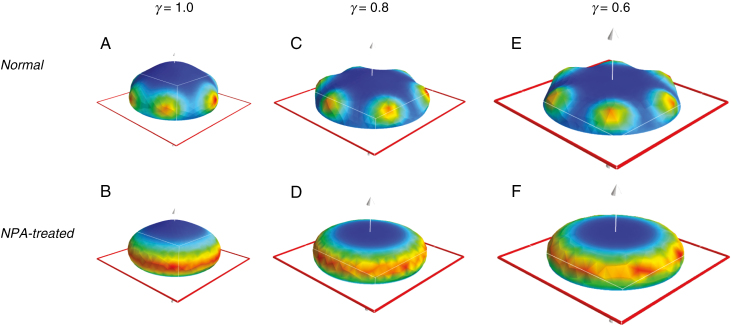
Geometry could also contribute to upward growth. Flattening of a hemispherical geometry, as seen during conifer embryogenesis (Fig. 1A to Fig. 1B), decreases the angles between the z-axis and normal vectors on the surface. Therefore, P1 patterning on a flattened dome should direct more upwards growth than on a hemisphere. To test this geometric effect, we ran series of computations at different values of γ, the parameter specifying dome flatness (varying between 1 for a hemisphere and 0 for a flat disc; see Fig. 1E and Nagata et al., 2013). Figure 3 compares morphogenesis from hemispherical initial shapes (Fig. 3A, B) to increasingly flat initial shapes (Fig. 3C, D to Fig. 3E, F). Decreasing γ decreases the outgrowth angle from the z-axis, producing closer fits to observations, both for cotyledon outgrowth and for NPA-induced cups. This indicates that establishment of the P1 pattern on geometries intermediate between a hemisphere (γ = 1) and a flattened disc (γ = 0), i.e. patterning after the dome stage (Fig. 1A), could contribute to the observed upwards growth.

Fig. 3.

The effect of geometry on patterning and morphogenesis. Top row, normal morphogenesis (both P1 and P2 actively patterning); bottom row, NPA-treated cup morphogenesis (P1 actively patterning, P2 not actively patterning). Colour-map, red outline and white arrow as in Fig. 2. (A, B) Growth starting from hemispherical initial shapes, γ = 1.0 (see Fig. 1E legend). (C–E) Progressively flattened domains: (C, D) γ = 0.8; (E, F) γ = 0.6, shown to scale. The radius increase as γ decreases keeps the number of primordia (6, here) constant. As the domain flattens, the angle between the z-axis (pole) and the P1 ring decreases, directing the primordia upwards, more closely matching the observed morphogenesis (Fig. 1C). This corresponds to cotyledons being positioned during tip flattening, after the dome stage (Fig. 1A) of embryogenesis.

Linear relation between primordia number and diameter

A characteristic wavelength, λ, for P2 spacing within the P1 ring implies a linear relationship between domain diameter, d, and the number of primordia, n_c:

$$d=(\lambda /\pi )n_c+b$$ (4)

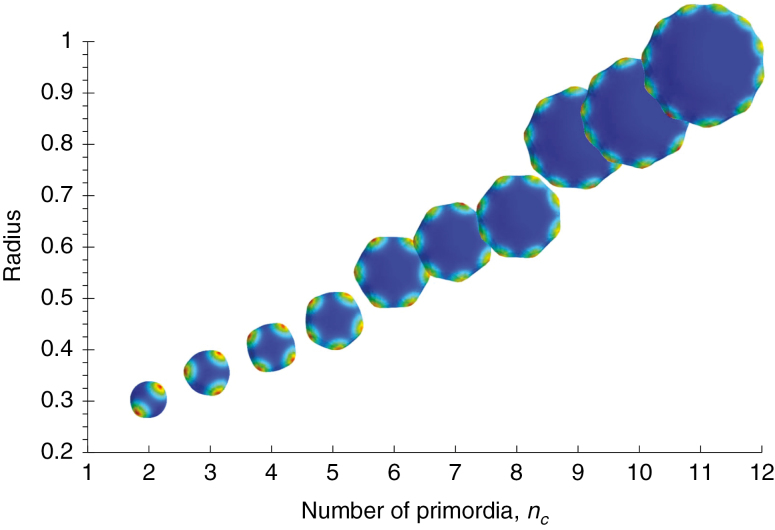
where b/2 is the inset of the ring from the equator. This relationship is seen experimentally (Harrison and von Aderkas, 2004; Holloway et al., 2016). For the P1/P2 RD simulations, Fig. 4 shows this linear increase in radius with primordia number. The linear trend is observed at different γ values, and with or without P2-catalysed growth (Table 2; P < 0.05 for all regressions).

Fig. 4.

Linear relationship between number of primordia (n_c) and radius, as predicted from eqn (4) and corresponding to the trend seen experimentally (Harrison and von Aderkas, 2004; Holloway et al., 2016). Top-view shapes, colour-mapped for X₂ concentration, shown to scale. The P1 ring stabilizes formation of a single whorl of primordia over the observed range of two to 11 cotyledons (Holloway et al, 2016). γ = 0.8 with X₂-catalysed growth is shown; see Table 2 for the linear relationship at other geometries.

Table 2.

Initial radii at particular number of primordia n_c, for different tip flatness γ

The single ring of primordia is stable across the two to 11 cotyledons observed experimentally. This stability of whorl formation depends on P1 pattern stability with respect to radius increase. Spatial solutions of dynamic mechanisms such as eqn (1) depend on domain size, with a progression from lower to higher complexity patterns as size increases. At small radius, the domain size is too small for the annular Y(0,3) spherical harmonic: P1 forms a lower-order, pole-high Y(0,1) pattern in these cases. P2 can form n_c = 2 to 4 on these small-radius P1 patterns (Table 2, yellow). This is consistent with previous results, in which we observed whorl patterns up to n_c = 6 for a single Brusselator pattern-former on a Y(0,1) fixed pre-pattern (Holloway and Harrison, 2008). For larger radii, however, the Y(0,3) annular pattern generated by the dynamic P1 mechanism (as in Fig. 2D, G) is critical for stabilizing P2 whorl formation (as compared to ‘spots all over’, e.g. Fig. 2B). The P1 annulus stabilizes whorls to the upper end of the experimentally observed range: up to n_c = 11 is shown in Table 2 (green and blue); n_c = 12 and 13, of which single cases were observed in Holloway et al. (2016), can also be generated. At higher radii than these, P1 begins to transition to a multiple ring Y(0,7) pattern, which would correspond to radially nested P2 whorls, which are not seen in normal development. Simulation of NPA treatment, decreasing d₂ to shut off active P2 patterning, gave circularly symmetric morphologies for all radii in Fig. 4.

Variations in patterning

Transitions between distinct patterns can be gradual for P1 and P2. In Table 2, for instance, the P1 transition between the Y(0,1) pole-high and Y(0,3) annular patterns occurs over a range of radii (green cells), with the Y(0,3) polar minima becoming more distinct as radius increases. For P2, radii between those shown in Table 2 can give mixed patterns, resulting in either splittings (e.g. an initial n_c = 4 going to n_c = 5, Fig. 5A) or fusions (long circumferentially extended maxima which fail to resolve into distinct primordia, Fig. 5B). Splittings are seen experimentally, for example with an embryo showing four cotyledons on an initial measurement showing five cotyledons a week later. Fusions are also observed, where, for example, space for two cotyledons is occupied by a single broad structure (Fig. 5C). The simulations indicate that such indeterminate n_c could be a natural consequence of the radial dependence of the P2 pattern, i.e. that these embryos are at a transitional size between radii with distinct integer n_c.

Fig. 5.

Variation in patterns. The model can generate some of the anomalous morphologies seen experimentally. (A) Concentration peak splitting, in this case from an earlier pattern of four peaks (left) to a later pattern of five peaks (right), corresponds to readjustments seen experimentally, where additional cotyledons are sometimes seen a week after the earliest count. (B) Peak fusions, where a ring with space for, in this case, between five and six peaks, has several peaks ‘smeared’ together, corresponding to fused or extra-width cotyledons sometimes observed experimentally (C; from Harrison and von Aderkas, 2004, with permission; scale bar = 250 µm). Such cases of indistinct peak number tend to occur at transitional radii between distinct integer peak numbers (i.e. between the shapes shown in Fig. 4). (D) Transient pattern in early stages of an ‘NPA-treatment’ simulation (at later stages, this passive P2 pattern is distributed in a smooth ring). Such transient pattern could correspond to the ‘bumpy cup’ morphology sometimes observed in NPA-treated embryos, where the cup rim is not smooth (Holloway et al., 2016).

NPA treatment tends to abolish outgrowth of distinct cotyledons, but in rare cases vestigial ‘bumps’ can be observed along the rims of the cup-shaped embryos (Holloway et al., 2016). Since NPA treatment appears to reduce P2 amplitude without altering the P2 spacing λ, these bumps may be due to a remaining very low-amplitude P2 pattern during their development. Figure 5D shows that in cases where P2 is not actively patterning, and has a steady state which will follow the P1 annular pattern, transient circumferential pattern can still be observed at early stages, which could contribute to vestigial bumps prior to the pattern fully relaxing to the annular steady state.

DISCUSSION

Cotyledon morphogenesis in conifers is complex, with positioning and outgrowth controlled in radial and circumferential directions on a flattening dome geometry. Fundamental questions in this process include: how are cotyledons constrained radially to form in a whorl; how are cotyledons evenly spaced circumferentially within that whorl; what is the role of auxin in cotyledon formation; and how do spatial patterning dynamics affect the morphology of the cotyledon crown in early embryos? We developed a dynamic model of pattern formation and growth in three dimensions to investigate these questions.

Induction of cup-shaped morphogenesis by NPA treatment suggests that an underlying PAT-independent patterning mechanism, P1, sets the radial position of the cotyledon whorl. This ring pattern is robust – even in NPA-treated embryos showing partial cotyledon growth or embryos with missing cotyledons (gaps), outgrowth occurs at a clear radius from the tip (Larsson et al., 2008; Holloway et al., 2016). The consistent formation of whorls in conifer cotyledon development depends on the stability of this single-ring pattern solution to changes in domain size, embryo geometry and mechanism parameters (e.g. reaction rates, transport rates, potentially mechanical properties). The size stability of the whorl pattern is notable in the broader developmental context, given that within-species conifer embryo sizes are far more variable (s.d./mean ≈ 30 % for diameters; Holloway et al., 2016) than those in Drosophila (s.d./mean ≈ 8 % for lengths; Holloway et al., 2006), a model organism intensively studied for such pattern scaling to variable size (e.g. Houchmandzadeh et al., 2002; He et al., 2015). On flattening dome geometries, the single-ring whorl pattern corresponds to the Y(0,3) spherical harmonic. We have shown that an RD P1 mechanism (the Brusselator) can stabilize single whorls across the range of two to 11 cotyledons observed experimentally. In particular, Y(0,3) P1 solutions are critical in maintaining single whorls at larger diameters. Our simulations indicate that P1 ring stabilization is important for diameters associated with n_c > 4; this is highly applicable to many common conifers, in which species averages are n_c = 5 and above (Butts and Buchholz, 1940).

To constrain cotyledon formation to the ring, P1 needs a feedforward control on the short-wavelength P2 pattern. The formation of P1 and P2 patterns in-phase in the whorl is consistent with GM activator–inhibitor kinetics for P2, and not with Brusselator depletion kinetics. P1 is coupled to P2 via the X₁ morphogen affecting the X₂ self-reinforcement rate parameter c₂. Active pattern formation by the GM P2 mechanism produces even spacing between primordia within the P1 ring. This is the first computed confirmation that a hierarchical double-RD mechanism can generate single whorl morphogenesis on a dome, as first suggested by Harrison et al. (1981).

The loss of distinct cotyledon outgrowth with NPA treatment indicates a PAT effect on P2 pattern amplitude. This is modelled as an effect on active vs. passive patterning, with NPA treatment (decrease of PAT) decreasing parameter d₂. At low d₂, active circumferential patterning dies out and the resulting passive steady-state of P2 reflects the underlying P1 ring pattern (Fig. 2H). Turing analysis shows how d₂ decrease causes this loss of self-organization; the decreased decay could also be associated with a pooling of unpatterned P2 morphogen in the P1 ring.

NPA-induced reversion of a distinct cotyledon pattern to a ring pattern supports the two-stage P1/P2 model over a one-stage RD model. For a single Brusselator, Nagata et al. (2013) found the stability conditions for different pattern harmonics on spherical caps. Transitions from cotyledon-like patterns, Y(n_c, 1), to the annular Y(0,3) would require different specific variations in parameters for each n_c. In comparison, loss of active patterning in P2 can be effected over a range of values for any of the parameters in eqn (2), more consistent with a systemic NPA treatment reliably converting all potential n_c (or all diameters, given eqn 4) to Y(0,3).

P1 control constrains a potentially 2-D P2 pattern (all over the surface) into a quasi-1-D pattern in a ring. This produces the linear dependence between inter-cotyledon spacing λ and embryo diameter (eqn 4) observed experimentally (Harrison and von Aderkas, 2004; Holloway et al., 2016). In such a ring arrangement, each increment of the whorl circumference by the inter-cotyledon spacing allows another cotyledon to fit in. Table 2 shows radii for each integer n_c in the experimentally observed range. Since radius can vary continuously, radii intermediate to those shown in Table 2 can produce mixed n_c: the cotyledon fusions or splittings observed experimentally could be due to the diameter–n_c dependence contained in eqn (4).

Morphogenetically, P2-driven growth generates the evenly spaced primordia of normal cotyledon morphogenesis, as well as the circularly symmetric outgrowth of NPA-induced cup-shaped morphogenesis. The pattern formation is stable to this induced growth. Computations on different embryo geometries (dome flatness γ) suggest that P1/P2 cotyledon positioning occurs during flattening, after the early dome stage: decreasing γ from 1 (hemispherical) decreases the angle between outgrowth and the z-axis, generating increasingly upward-pointing primordia which more closely match experimental observations.

Visualization of growth regulator patterning in conifer embryos is rudimentary compared to Arabidopsis; the model provides a quantitative framework for interpreting the data currently available and guiding new experiments. For instance, new experiments in auxin labelling could clarify whether auxin localizes to the P1 ring, indicating a localized PAT delivery of the P2 ‘amplitude factor’ and perhaps some dependence of PAT on P1; or whether auxin is more ubiquitous at these stages, and loss of PAT would produce a more generic loss of the P2 ‘amplitude factor’ across the embryo. While the molecular identity of the X₂ growth catalyst is unknown at this point, the model indicates that it is patterned by activator–inhibitor kinetics, as found earlier in plants for trichome patterning (Digiuni et al., 2008) and in shoot apical meristems (Fujita et al., 2011).

The dynamic mechanism developed here for conifer cotyledons may apply more generally to single whorl formation in development, or to successive simultaneously forming whorls (independent of earlier primordia position) such as vegetative growth in Acetabularia (Dumais and Harrison, 2000) or Equisetum. These phenomena are in contrast to phyllotactic whorls formed by successively initiated primordia (e.g. Douady and Couder, 1996; Kitazawa and Fujimoto, 2015), and also to the PAT self-organization model of floral whorls, in which earlier organs (sepals) affect the positioning of later organs (van Mourik et al., 2012). The stability of the P1/P2 system over a large size range is especially applicable to simultaneous whorls with large numbers of primordia. In these cases, the short spacing between primordia relative to domain size requires a radial constraint to form in a whorl, and not have patterning all over the available space. While current data supports RD patterning for both P1 and P2 in conifer cotyledon whorls, the current model establishes more general constraints for whorl formation which could be realized with other pattern-forming mechanisms, such as PAT. In particular, the current model establishes constraints on the linkage between the radial and circumferential patterning systems, the coupling to growth, and the stability of the patterns to embryo size variability and geometric changes during morphogenesis: these apply to any mechanism for regular spacing, RD or otherwise.

In this broader context, the current characterization of the two-stage process in conifer cotyledon development shows parallels with previous findings of multi-component mechanisms with separable effects (and dependences on PAT) in different dimensions. These include results in tomato and Arabidopsis, in which exogenous application of auxin could alter circumferential patterning on the shoot, but not within a critical radial distance of the meristem (Reinhardt et al., 2000); the PIN1 dependence of floral initiation compared to the partial PIN1 independence of leaf initiation (Guenot et al., 2012); the separable surface and inward PAT flows found in the shoot apex (Furutani et al., 2014); and the PAT-dependent lateral and PAT-independent medial components of gynoecial development (Larsson et al., 2014).

Conifer polycotyledony offers a unique system for studying developmental mechanisms for the positioning of organs. Development of a 3-D finite element model of conifer cotyledon whorl formation has allowed us to study the dynamics involved in this complex morphogenetic process. This clarifies the role of the radial patterning (P1) and its stability over the size ranges found experimentally; the constraint of cotyledons to this ring; the spacing of cotyledons within the ring (P2 pattern); and the loss of P2 patterning with NPA treatment. This quantitative model for the dynamics of growth regulator patterning and consequent morphogenesis provides a synthesis of current data and can serve as a framework to guide future experiments into the molecules and mechanisms involved in conifer cotyledon development, with implications for whorl formation in general.