A BAYESIAN SPATIAL AND TEMPORAL MODELING APPROACH TO MAPPING GEOGRAPHIC VARIATION IN MORTALITY RATES FOR SUBNATIONAL AREAS WITH R-INLA

Abstract

Hierarchical Bayes models have been used in disease mapping to examine small scale geographic variation. State level geographic variation for less common causes of mortality outcomes have been reported however county level variation is rarely examined. Due to concerns about statistical reliability and confidentiality, county-level mortality rates based on fewer than 20 deaths are suppressed based on Division of Vital Statistics, National Center for Health Statistics (NCHS) statistical reliability criteria, precluding an examination of spatio-temporal variation in less common causes of mortality outcomes such as suicide rates (SRs) at the county level using direct estimates. Existing Bayesian spatio-temporal modeling strategies can be applied via Integrated Nested Laplace Approximation (INLA) in R to a large number of rare causes of mortality outcomes to enable examination of spatio-temporal variations on smaller geographic scales such as counties. This method allows examination of spatiotemporal variation across the entire U.S., even where the data are sparse. We used mortality data from 2005–2015 to explore spatiotemporal variation in SRs, as one particular application of the Bayesian spatio-temporal modeling strategy in R-INLA to predict year and county-specific SRs. Specifically, hierarchical Bayesian spatio-temporal models were implemented with spatially structured and unstructured random effects, correlated time effects, time varying confounders and space-time interaction terms in the software R-INLA, borrowing strength across both counties and years to produce smoothed county level SRs. Model-based estimates of SRs were mapped to explore geographic variation.

1. Introduction and motivation

The use of Bayesian methods in the areas of disease mapping, epidemiology, and small area health applications is well established. The Bayesian inference combines the prior distribution on model parameters and the data likelihood to derive the posterior distribution which summarizes the behavior of the parameters in light of the observed data. (Lawson, A. (2013)) Bayesian hierarchical models that incorporate time and area effects provide additional insights in terms of the interpretability and similarity based on the neighborhood structure of areas and adjacent times. However, incorporating time and area effects results in increasingly complex model structures which can substantially increase the computational time required to estimate these models.

Traditionally, Markov Chain Monte Carlo (MCMC methods) have been used to approximate the posterior marginals in Bayesian Hierarchical models and are computationally intensive and time consuming. Two basic methods, namely, Gibbs sampling and Metropolis-Hastings are designed in Winbugs software (Ntzoufras, I. (2009)) to approximate the posterior distributions via MCMC. The computation time in reaching convergence for the different parameters in the model can often be measured in days or weeks of time for big datasets or large models. (Barker, L. E. et al. (2013), Bivand, R.S. et. al. (2015), Khan, D. et. al. (2018), Martins, T.G. et al. (2013), Rue, H. et al. (2009), Rue, H. and Martino, S. (2009)) Further, the highly multivariate structure of the models limits the ability to approximate the full posterior distributions. Several other packages exist for example, STAN (Stan Development Team (2016)) but require a certain level of programming expertise. Spatial models are not built-in in JAGS (Plummer, M. (2003)) and hence need to be programmed.

The INLA method has been introduced as an alternative to MCMC to approximate the posterior marginals of latent Gaussian models and significantly reduces the computation time. (Rue, H. et.al. (2009) The INLA method does not use iterative computation techniques like MCMC. The posterior approximation is achieved by applying numerical integrations for fixed effects and Laplace integral approximation to the random effects (Chen, C. et al. (2014), Martins, T.G. et al. (2013), Rue, H. et al. (2009), Rue, H. and Martino, S. (2009)). Models are built-in and can be fitted in R-INLA, using R commands (Bivand, R. S. (2015))

In this study, we examine existing Bayesian spatio-temporal models in the software R-INLA for the purposes of mapping less common causes of mortality outcomes on small geographic scales and consider suicide rates (SRs) at the county level as one particular application. Mapping county level estimates provides greater understanding of the trends and variability in spatio-temporal patterns of less common causes of mortality outcomes not possible by examination of direct national and state estimates (Schaible, W.L. (1996)) or by examination of direct county level estimates. Additionally, mapping county-level estimates can help highlight areas where estimates are higher or lower than the national average, and provide additional insights on how county-level estimates have changed over time across the U.S. Due to the potential instability of the direct estimates of less common causes of mortality outcomes at smaller geographic scales such as counties, compounded by small population sizes, the annual county level direct estimates are typically not reported. For example, the majority of counties across the U.S. report fewer than 20 suicide deaths in any given year, the criterion for suppression of death rates due to concerns about statistical reliability by the Division of Vital Statistics at the National Center for Health Statistics. (Kochanek, K.D. et al. (2016), page 118) To account for the problems encountered in examining spatio-temporal variations with county level direct estimates for less common causes of mortality outcomes such as SRs over time, as outlined above, we propose to examine existing hierarchical Bayesian spatio-temporal models that account for extra uncertainty, inherent spatial autocorrelation, and the time dependent structure of the data to produce smoothed model based yearly county level SRs in the software R-INLA to examine broad scale trend and variability in spatiotemporal patterns in SRs across 3,140 U.S. counties from 2005 through 2015. (Knorr-Held, L. and Besag, J. (1998), Lawson, A. (2013), Lawson, A. (2015), Lagazio, C. et al. (2001), Wall, M. M. (2004), Xia, H., et al. (1997))

Specifically, in a Bayesian spatio-temporal model, the spatially structured and unstructured random effects are used to model the inherent spatial autocorrelation in the data, the correlated and uncorrelated time effects model the time dependent structure of the data, time varying covariates model the extra uncertainty in the data due to measured confounders, and the space-time interaction effects model the residual spatio-temporal variation that are unaccounted for by the county and time random effects to produce reliable model based yearly county level estimates.

The posterior distributions for the parameters in Bayesian Hierarchical spatio-temporal models in this study are simulated in the software R-INLA, to reduce the computation time often incurred when analyzing large spatial datasets. A variety of prior distributions for model parameters and random effects can be specified in R-INLA. The Bayesian spatio-temporal modeling approach borrows strength across both counties and years to produce smoothed yearly county level estimates and allows examination of spatial and temporal variability in less common causes of mortality outcomes over time. This method can be applied to a large number of rare causes of mortality outcomes to examine small-scale geographic variation and temporal variability with model based smoothed and robust small area estimates. The accuracy of the INLA estimates compared to MCMC estimates have been examined in large number of study areas. (Fong, Y. et al. (2010), Martins, T.G. et al. (2013), Paul, M. et al. (2010), Riebler, A. et al. (2012), Rue, H. et al. (2009), Rue, H. and Martino, S. (2009), Schrodle, B. (2011))

The spatiotemporal models in R-INLA smooth the time trends by borrowing strength from adjacent times. Since 2015 is the most recent year of data that is available from the National Vital Statistics System (NVSS) files, this study incorporates the years 2005–2015 to examine the county level spatio-temporal variation in SRs using 11 years of NVSS data. The smoothed model based county level SRs are mapped and compared for the years 2005 and 2015 to examine the geographic variations and the broad scale trend in spatio-temporal patterns. The absolute difference in the increase in SRs over time is also mapped to examine the overall increase in SRs from the start of the analyses year (2005) to the end of the analyses year (2015).

Section 2 describes the general space-time model for analyzing rare causes of mortality outcomes on small geographic scales, such as counties. Section 3 describes one particular application of the proposed existing methodology to examine county level spatio-temporal variation in SRs. Specifically, Section 3.1 contains information on SRs data and the respective sources of covariates used in this study. Section 3.2 describes model and prior distribution assumptions for modeling county level SRs, and Section 3.3 discusses model selection criteria for selecting the best model for county level SRs. In Section 3.4 we discuss model accuracy. Section 3.5 discusses results with respect to model covariates, and Section 3.6 outlines the broad scale trend and variability in geographic patterns and the usefulness of the Bayesian spatio-temporal technique in mapping small area outcomes such as SRs by using the proposed existing Bayesian spatio-temporal technique in R-INLA. Sections 4 summarizes the discussion.

2. Methods

2.1 Hierarchical Bayesian Model Specification

The hierarchical Bayes statistical models employ multiple levels of modeling specified in a hierarchical order to estimate the posterior distributions of the model parameters using the Bayes method. The observed data is combined with the multiple sub-level model specifications (prior distributions) and possible covariates to estimate the posterior distribution via Bayes theorem. The hierarchical Bayes models can be used to model to model grouped data: temporally (repeated in time) or spatially structured (exhibiting spatial autocorrelation).

The small-scale geography (e.g. county level) data for a less common cause of mortality outcome, in general, often exhibits strong spatial autocorrelation. (Besag et.al. (1991)) Time varying covariates can account for some of the spatial and temporal autocorrelation. (Lawson, A. (2013)) The residual spatial autocorrelation is accounted for by the introduction of spatially structured random effects into the model. The modeling of spatially structured random effects via the adjacency matrix of the counties by conditional autoregressive priors was first proposed by Besag et.al. (1991). (Besag, J. and Kooperberg, C (1995), Wall, M. M. (2004)) To account for potential linear and non-linear trends and extra variation in county level estimates over time, fixed, correlated and uncorrelated time effects and space time interaction effects are incorporated. (Böhning, D. et al. (2000), Knorr-Held, L. and Besag, J. (1998), Knorr-Held, L. and Rasser G (2000), Lagazio, C. et al. (2001), Lawson, A. (2013), Xia, H. et al. (1997)) Several models can be implemented using the R-INLA package accounting for the time and county, fixed and random effects. (Bivand, R (2015), Martins, T.G. et al. (2013), Rue, H. and Martino, S. (2009), Rue, H. et al. (2009)) Specifically, if y_it = counts of deaths for a rare outcome of interest in county i and year t, and n_it = counts of population of county i in year t. Then, y_it ~ Binomial (n_it, p_it); i = 1,…, m counties and t =1,…, T years, where p_it = probability of a rare outcome of interest in county i at time t. The general hierarchical Bayes space-time model structure for modeling p_it can be specified as (Lawson et.al. (2013)):

logit (p_it) = α₀ + A_i + B_t + C_it + X_it′β, where, the regression models include:

1. Grand intercept α₀.

2. Spatial component accounting for existent spatial autocorrelation A_i.

3. Time component accounting for fixed and random time effects B_t.

4. Space-time interaction term accounting for residual spatial variation not accounted for by the main time and space effects C_it.

5. Covariates which can be time varying or time-invariant X_it′β accounting for uncertainty due to measured confounders, where, X_it is the covariates matrix for county i and time t and β is a vector of regression parameters.

The posterior distributions of the parameters in the hierarchical Bayesian model can be estimated via Integrated Nested Laplace Approximation (INLA) in R, borrowing strength across both counties and years to produce smoothed yearly county level estimates even where the data are sparse. Depending on the nature of the data, a variety of latent models such as random walk-1, random walk-2, besag, convolution etc. can be implemented via R-INLA software package to model the small area outcome and produce reliable smoothed estimates. (Bivand et.al. (2015)) Full list of the latent models, likelihoods and prior assumptions can be found in the R-INLA website at http://www.r-inla.org/

3 Application to US county level suicide rates

3.1 Data

Data were obtained from the 2005–2015 National Vital Statistics System (NVSS) Multiple Cause of Death Files (restricted-use geography files). (Centers for Disease Control and Prevention (2016)) The number of suicides by county of residence and year were identified based on the International Classification of Diseases, 10th Revision (ICD-10) underlying cause codes U03, X60-X84, and Y87.0. Population denominators for SRs were obtained from the U.S. Census intercensal (2005–2009), decennial (2010) and postcensal (2011–2015) population estimates. (Statistics NCHS (2011), Statistics NCHS (2016a), Statistics NCHS (2016b)) Because suicide is not an allowable cause of death for persons under 5 years of age, population estimates were limited to those age 5 and older.

Data on time-varying county-level characteristics were obtained from several sources, including Area Health Resource Files, (AHRF (2015)), Uniform Crime Reporting Program Data: County-Level Detailed Arrest and Offense Data, (Uniform Crime Reporting Program Data (2014)), National Survey of Drug Use and Health (NSDUH) Substate Estimates, (NSDUH (2016)), Housing and Urban Development Small Area Foreclosure Rates (HUD 2017). County-level covariates considered for inclusion in the model were selected based on previous studies that demonstrated an association between these factors and SRs such as prevalence of suicidal thoughts and behaviors, (Crosby, A.E. et al. (2011)) and economic factors (e.g., unemployment levels, foreclosure rates, poverty rates ) etc. (Brenner, B. et al. (2011), Crosby, A.E. et al. (2011), Haws, C. A. (2009), Hempstead, K. (2006), Kerr, W.C. et al. (2016), Kim, N. (2011), Lester, D. (1995), Middleton N. (2008), Miller, M. et al. (2006), Opoliner, A. et al. (2014), Siegel, M. and Rothman, E. F. (2016)) A table of included covariates and their respective sources is provided in Table s1 in the supplemental online information. While most values for covariates were at the county-level, estimates from NSDUH data (e.g., drug use, prevalence of major depressive episodes and serious mental illness) were measured at the sub-state level (aggregates of counties). (NSDUH (2016)) All covariates were standardized to have a mean of zero and standard deviation of one before inclusion in the model.

Geographic boundaries for some counties changed during the study period. To provide constancy in the total number of counties during the study period (2005–2015), several counties in Alaska were aggregated and Bedford City, VA was merged with Bedford County, VA, resulting in a combined national file that included 3,140 counties (National Center for Health Statistics (2016c)).

3.2 Modeling assumptions for county level SRs

The total numbers of crude counts and percentages of the numbers of suicides equal to zero, less than 10, and less than 20 that were extracted from the NVSS files are shown in Table 1 for the years 2005, 2009 and 2015. Several models were implemented for modeling the county level SRs based on the general space-time modeling framework specified in Section 2. The general hierarchical Bayesian model incorporating time varying covariates and several time and county random effects for i = 1,…, m counties and t =1,…, T years, is:

Table 1.

Counts and percentages for numbers of suicides extracted from the NVSS data files reported to be equal to 0, less than 10, and less than 20 for years 2005, 2009, and 2015 respectively.

	Equal to 0		Less than 10		Less than 20
Year	Count	Percent	Count	Percent	Count	Percent
2005	475	15.12	2405	76.59	2775	88.37
2009	427	13.6	2349	74.8	2716	86.5
2015	360	11.5	2186	69.6	2646	84.3

logit (p_it) = α₀ + u_i + v_i + φ_1t + φ_2t + ψ_it + X_it′β, where, the regression models include:

1. logit link function log (p_it/(1 − p_it)); where, p_it is the probability of suicides in county i at time t.

2. an overall intercept term α₀. The intercept, α₀ was assigned a flat prior: P(α₀) ∝ constant, (where, P indicates probability).

3. X_it′β where, X_it : is the i th row and t th column of the covariates matrix X and β is a vector of regression parameters. The β for fixed effects (X_it′β) were assigned Normal priors. β ~ N (0,100)

4. the spatial effects, u_i, by county to account for strong spatial autocorrelation, and were modeled via normal conditionally autoregressive priors (CAR) ( Besag, J. et al. (1991)) where weights were assigned to each county according to adjacency; neighboring counties receive a weight of one while non-neighboring counties receive a weight of zero. Specifically, for i = 1,…, m, counties and j = 1,…, T, years;

   $$u_i\mid u_j,{\tau }_u~N\left(\frac{1}{{\mathrm{\sum }}_{j=1}^m{\omega }_{ij}}\sum _{j\in {\delta }_i}{\omega }_{ij}{u}_j,\frac{1}{n_{{\delta }_i}{\tau }_u}\right)i\ne j,$$
   where, τ_u is the conditional precision of spatial random effects and δ_i is the neighborhood of the i th region, n_δi is the number of neighbours, ${\mathrm{\sum }}_{j=1}^m{\omega }_{ij}$, and the spatial weight, ω_ij equals 1 for counties i and j that are deemed neighbors and otherwise 0. Delaunay triangulation was used to establish spatial weights. This method generates Voronoi triangles from county centroids. Nodes connected by a triangle edge are considered neighbors. (Bivand, R (2017)) Each county has at least one neighbor, and the number of neighbors is determined empirically based on the spatial distribution of the counties. Sphere of influence spatial weighting scheme was also investigated as an alternative and sensitivity results are discussed in the results section (Sterrantino, A.F. et al. (2017)). The conditional precision of the spatial random effect was assigned τ_u ~ Gamma (1, 0.001) prior. The Gamma (α, β) density is defined as:

   $$\begin{gathered} \pi (\tau )=\frac{{\beta }^{\alpha }}{(\alpha -1)!}{\tau }^{\alpha -1}exp(-\beta \tau ),\text{for} \\ \tau >0,\text{where} \\ \alpha >0,\mathit{the}\mathit{shape}\mathit{parameter},\mathit{and} \\ \beta >0,\mathit{the}\mathit{inverse}\mathit{scale}\mathit{parameter}. \end{gathered}$$

5. non-spatial random effects v_i by county, to model residual spatial variation not dealt with by our spatial random effects and were assigned a Normal prior, $v_i~N(0,\frac{1}{{\tau }_v})$, with precision, τ_v. The conditional precision of the unstructured random effect was assigned τ_v ~ Gamma (1, 0.001) prior.

6. correlated random time effects, φ_1t, to account for time dependence, were modeled via first order random walk. (Böhning, D (2000), Knorr-Held L and Rasser G (2000), Lawson, A. (2013)) This component assumes that the values for a given county in a given year depend upon the values observed for that county in the prior year plus a residual. The correlated temporal random effect, φ_1t, which has a random walk prior distribution, with precision, τ_φ1; where ${\phi }_{1t}~N({\phi }_{1,t-1},\frac{1}{{\tau }_{\phi 1}})$. The conditional precision of the unstructured random effect was assigned τ_φ1 ~ Gamma (1, 0.001) prior.

7. an uncorrelated time dependent random effect φ_2t, to account for independent time effects, which were modeled as normal distributed with precision, τ_φ2; ${\phi }_{2t}~N(0,\frac{1}{{\tau }_{\phi 2}})$. The conditional precision of the unstructured random effect was assigned τ_φ2 ~ Gamma (1, 0.001) prior.

8. the space time interaction term, ψ_it, to account for any residual spatiotemporal variation that was not captured by the spatial or temporal main effects, and were assumed to be independently and identically distributed. (Knorr-Held, L. and Rasser G (2000), Lawson (2015)); ${\psi }_{it}~N(0,\frac{1}{{\tau }_{\psi }})$. The conditional precision of the unstructured random effect was assigned τ_ψ ~ Gamma (1, 0.001) prior.

(The precisions for the intercept, fixed effects and the random effects are assigned priors that are default in R-INLA. INLA assigns log (precisions) ~log-gamma (1, 0.001) priors) (Bivand, R. S. (2015), Martins, T.G. et al. (2013), Rue, H. and Martino, S. (2009), Rue, H. et al. (2009)))

A set of models following the above general space time modeling approach were explored to determine the contribution of different components, namely, the correlated and uncorrelated random time effects, spatially structured and unstructured random effects, space time interaction term and the different covariates to examine spatio-temporal variation in county level SRs. Alternative models such as proper CAR, Besag proper, and (ZIP) were also explored but did not provide any improvement in model fit, as assessed using the Deviance Information Criterion (DIC). (Spiegelhalter, D.J. et al. (2002)) Sensitivity analysis was also conducted to examine the effect of different priors. The six best competing models that incorporated a variety of time and county effects describing the features of the SRs data are presented here.

3.3 Model selection criteria

Model fit was evaluated using the Deviance Information Criterion (DIC) with lower values indicating better fit. For context, a DIC difference of 3–5 is considered significant. (Lawson (2015), Spiegelhalter, D.J. et al. (2002)) The best fitting model should have the lowest DIC and small effective number of parameters to estimate (n.eff). Several models were examined to determine the best fitting model via DIC, as seen in Table 2. The first model incorporated a normal random effect for each county and a grand intercept. Moran’s I test (Lee, D. (2013)) on the yearly county level direct SRs in this study indicated strong spatial autocorrelation as expected. Thus, the addition of a spatially structured random effect for each county to the first model reduced the DIC by 405 points, accounting for the existence of strong spatial autocorrelation but n.eff remained the same. The fixed year effects accounting for linear trends in time, did not provide any improvement in the DIC value and were not included in the model. To account for potential non-linearities in the county level SRs over time, correlated random time effects with a Type II random walk prior distribution were incorporated which resulted in a reduction in DIC by 1958 points and n.eff reduced to 1884, indicating the strong non-linear temporal dependence in the SRs at the county level not evident at the state level. The model with uncorrelated time effects resulted in a slight increase in DIC as compared to the model with correlated time effects and n.eff remained approximately the same. Hence, correlated time effect was retained in the model. The DIC for models incorporating both uncorrelated and correlated time effects suggested no improvement in model fit. To account for residual spatiotemporal variation unaccounted for by the main effects, an independent identically distributed space time interaction term was included which further reduced the DIC by 186 points but n.eff increased to 2766. Models including a space-time interaction term with a random walk prior distribution did not result in an appreciably lower DIC value and increased the computation time substantially, and thus was not included. The final model included county and time random effects, a space time interaction term, and the full set of time-varying covariates to account for measured confounders. The model with time varying covariates and without time varying covariates had a DIC difference of 640 points. Thus, the model with the full set of time varying covariates provided the best fit, providing the least value of DIC amongst all the models that were explored and a lower value of n.eff (1896) as compared to the null model and hence was selected as the best fitting model. The best hierarchical Bayesian model incorporating time varying covariates and several time and county random effects for SRs is:

$$\text{logit}(p_{it})={\alpha }_0+u_i+v_i+{\phi }_{1t}+{\psi }_{it}+{{\mathit{X}}_{\mathit{i}}}^{\prime }\mathit{\beta }.$$

Table 2.

Alternative Model Specification and Fit Statistics

Terms: α0 represents the intercept or grand mean; ui is a spatial random effect; vi is a non-spatial random effect;
Model	Components	DIC	n.eff
1. Simple random effects, vi	α0 + vi	150371.4	2316
2. Spatial ui and non-Spatial vi, random effects	α0 + ui + vi	149966.2	2316
Random time effects
3. Correlated time effects, φ1t	α0 + ui + vi + φ1t	148008.6	1884
4. Uncorrelated time effects, φ2t	α0 + ui + vi + φ2t	148010.3	1886
Full Model
5. Space time interaction term, ψit	α0 + ui + vi + φ2t + ψit	147821.9	2766
Full Model with Covariates
6. All components and covariates	α0 + ui + vi + φ1t + ψit + Xit′β	147181.1	1896

φ_1t and φ_2t are the temporal random effects, ψ_it is the space-time interaction term, which is independently and identically distributed, accounting for any residual spatiotemporal variation; and X_it′β represent the matrix of time-varying covariates and the corresponding coefficients.

The county level SR estimates from the best model and more parsimonious models (no covariates or only a subset of statistically significant covariates) were highly correlated (R2 from 0.88–0.99, see Supplemental Figure S1 in online supplemental information). However, the DIC value indicated a better fit for the model incorporating time varying covariates accounting for the extra uncertainty due to measured confounders. Since a better fitting model provides lower posterior mean deviance and the number of effective parameters to estimate, the best model incorporated all the time varying covariates and was selected as the best fit.

The estimated marginals of the coefficients of the fixed effects and the estimated marginals of the precisions of the prior variances for all the random components from the best model were also checked for convergence. Table 3 shows the posterior means, posterior standard deviations, 95 % Bayesian credible intervals and the posterior mode for all the estimated marginals of the precisions of the prior variances for the random effects in the best model. The mode of the posterior density of the precision of the prior variance for the spatial effect, u_i is small accounting for a large amount of spatial autocorrelation as compared to the precision of the prior variance for the non-spatially structured random effect v_i, indicating the borrowing effect amongst counties. The mode of the posterior density of the precision of the prior variance for the space time interaction term, ψ_it is also small capturing the temporal dependence of SRs and indicates borrowing of strength across years. The residual spatio-temporal variation is accounted for by fixed effects and the correlated time effects, φ_1t for which the mode of the posterior density of the precision on the prior variance is comparatively small validating our belief in statistical modeling assumptions for the SRs and supporting our choice of spatio-temporal model accounting for year and county effects. Figure S3, in the supplemental online information shows the distribution plots of the estimated marginals of the precisions of the prior variances for the random components from the best model. This model accounts for non-linear effects in time at the county level, which are not evident at the state level, via the correlated random time effects, φ_1t, a distinct feature of the space-time modeling methods in R-INLA which can be considered in future small area mapping studies for the small scale-geography data. This model is an improvement on the past Bayesian spatio-temporal models accounting for linear trends via MCMC in the software Winbugs and captures the non-linearity in time at the county level via the correlated random effects. (Khan, D. et. al. (2018), Lawson, A. (2015))

Table 3.

Model hyperparameters: posterior mean, posterior standard deviation, 95% Bayesian credible intervals and posterior mode for the estimated marginals of the precisions of the prior variances of non-spatial effects, τ_v, spatial effects, τ_u, correlated time effect, τ_φ1 and iid space time interaction effect, τ_ψ.

Precisions	Posterior mean	Posterior standard deviation	0.025 quantile	0.975 quantile	Posterior mode
τv	22380.75	2009.316	2523.08	75191.57	7201.39
τu	21.27	1.439	18.85	24.46	20.68
τφ1	5935.05	3180.924	2062.85	14120.89	4046.36
τψ	461.13	78.305	335.38	641.15	428.46

3.4 Model check and accuracy

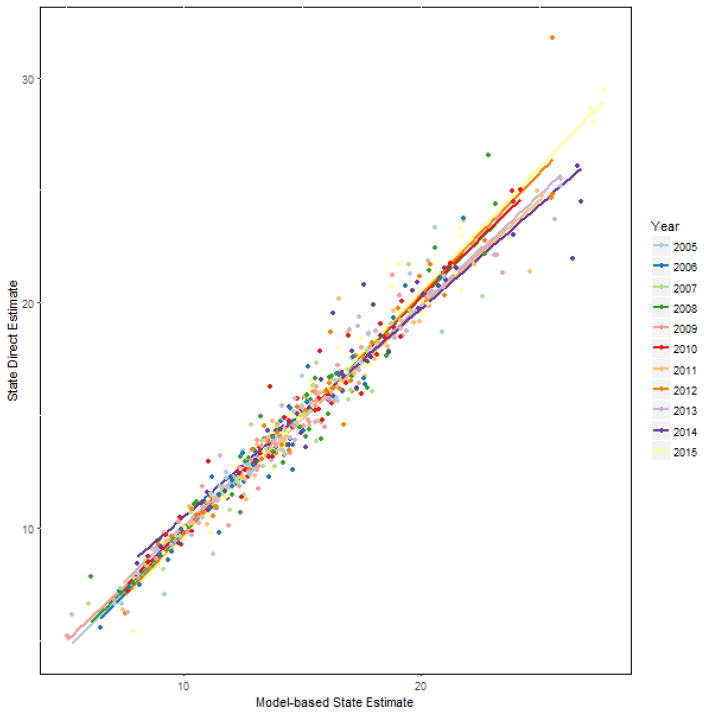
Residual analysis was conducted to compare the state level direct estimates with the aggregated state level model-based estimates to check the model accuracy and performance. The county-level model-based posterior predictions for each year were summed by state, weighted by county population size as a proportion of state population size, to calculate the state-level model-based estimates. The comparison of the state-level directly estimated SRs and the aggregated model-based state-level SRs for the best model for different years is shown in Figure 1. The majority of the estimates fall on the line of equality, indicating the lack of any major model failures that would result in large deviations from the state-level direct estimates. The national direct SRs and the aggregated national model-based SRs were also plotted in Figure S2 in the supplemental online information, illustrating that for the US, the model-based estimates corresponded very closely to the national direct estimates of suicide rates from 2005–2015.

Figure 1.

Comparison of state-level direct estimates (y-axis) and model-based estimates (x-axis), by year.

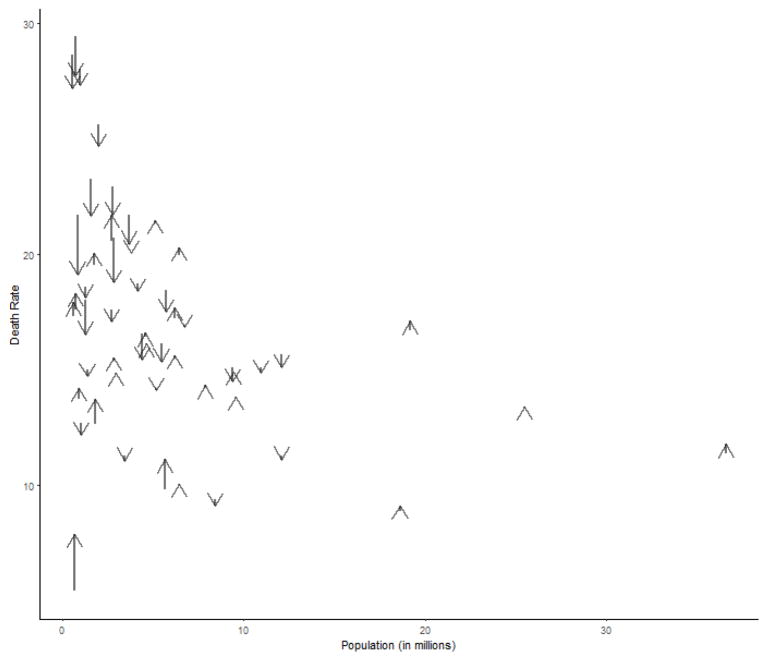
As an additional model check, the shrinkage between the direct state-level SRs and the aggregated model-based state-level SRs is plotted and can be seen in Figure 2. States with small populations show larger shrinkage in model-based SRs, a tendency of the aggregated model-based state-level SRs to scale towards local area (county/state) model-based mean SRs, indicating borrowing of strength from neighboring areas (counties/states).

Figure 2.

Shrinkage of suicide rates for each state, by population size for 2015. Crude death rates are plotted at the start of the arrows, and model-based death rates are located at the end of the arrows. Shrinkage is greater in states with smaller populations (left side of the chart) and more extreme suicide rates.

Sensitivity analysis was conducted to compare the Delaunay triangulation and sphere of influence spatial weighting schemes. The estimated county level SRs and the associated posterior standard deviations from the two spatial weighting schemes were highly correlated (R2 =0.99) as seen in Figure S4 in the Appendix.

3.5 Covariates

The inclusion of covariates can enhance the predictive power of small area estimation models. (Rao, J.N.K. (2003)) Several covariates were significant predictors of county-level SRs (i.e., 95% Bayesian Credible Intervals excluded zero). Coefficients and 95% Bayesian credible intervals for covariates and a list of significant as well as non-significant variables included in the full model are shown in the supplemental online information in Table s2. Covariates were included in this study to enhance the small area predictions. Thus, the coefficients should be interpreted with caution, as they represent ecological relationships and are not suggestive of causal pathways or individual-level risk factors. Broadly, covariates significantly associated with SRs included: demographic characteristics (e.g., household size, racial and ethnic distribution, urbanization level, divorce rates), socioeconomic factors (e.g., median home value, median gross rent, household crowding, median per capita income, % persons with college education, unemployment rate, high-cost loan rate), and health-related characteristics (e.g., % abusing or dependent on illicit drugs or alcohol in the previous year, treatment gap for alcohol and drug use, prevalence of major depressive episode, and county-level model-based estimates of age-adjusted death rates due to drug poisoning). This is consistent with prior analyses reporting county-level (i.e., ecological) associations between socioeconomic, demographic and/or health-related factors and suicide rates. (Brenner, B. et al. (2011), Crosby, A.E. et al. (2011), Haws, C. A. (2009), Hempstead, K. (2006), Kerr, W.C. et al. (2016), Kim, N. (2011), Lester, D. (1995), Miller, M. et al. (2006), Opoliner, A. et al. (2014), Siegel, M. and Rothman, E. F. (2016))

3.6 Spatio-temporal variation

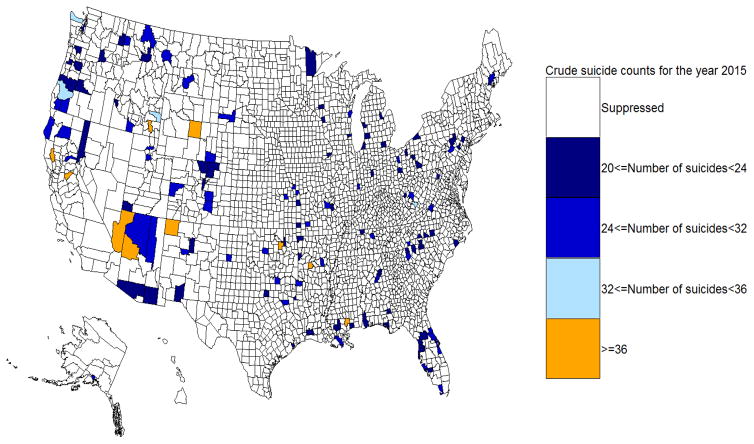
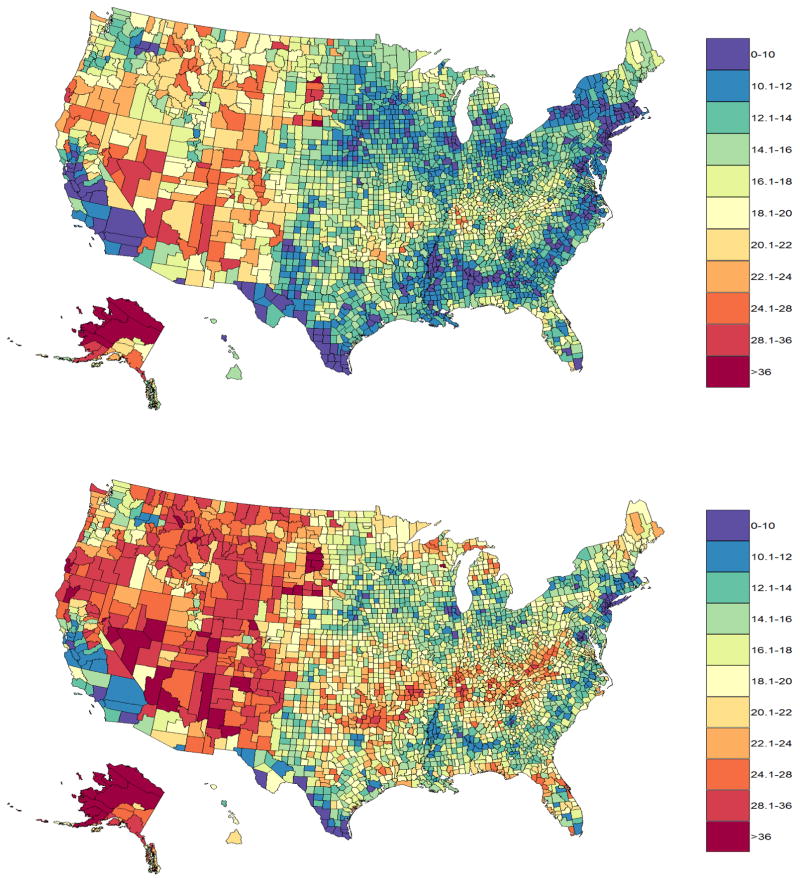
The actual number of deaths due to suicide at the county level for the year 2015 (number of deaths less than 20 are suppressed) are shown in Figure 3. This map precludes examination of geographic variations in county level SRs because most of the actual county level data extracted from the NVSS files are suppressed. The majority of counties across the U.S. report fewer than 20 suicide deaths in any given year, the criterion for suppression of death rates due to concerns about statistical reliability by the Division of Vital Statistics at the National Center for Health Statistics. (Kochanek, K.D. et al. (2016), page 118). The maps obtained by mapping stable posterior predictions from the best fitting Bayesian spatio-temporal for the county-level SRs for the years 2005 (Figure 4 (top)) and 2015 (Figure 4 (bottom)) enable examination of the geographic patterns and broad scale trend in spatio-temporal variability for the years 2005 and 2015 for all of the counties. The uncertainty associated with the estimated county level SRs for the years 2005 and 2015 is very small as shown in Figure S5 (2005 (top) and 2015 (bottom)) in the Appendix. A comparison of the aggregated state level SRs obtained by aggregating county level SRs via MCMC simulations in the software Winbugs with the same modeling assumptions as in Section 3.2 and vague prior distributions specifications, showed that the predictions are almost the same (Figure S6 in the Appendix), further solidifying our belief in the INLA based predictions. However, the MCMC programs took 8 weeks to converge in the software Winbugs.

Figure 3.

Crude county level deaths due to suicides for the year 2015. Number of deaths less than 20 are suppressed.

Figure 4.

Predicted county-level suicide death rates in 2005 (top) and 2015 (bottom).

In 2005 and 2015, counties with the highest model-based SRs were predominantly located across the western US while the lowest rates were observed across southern California, western Texas, along the Mississippi river, and in areas along the East Coast. These patterns were largely consistent over time. Multiple studies have described state-level variation in suicide rates (SRs), with higher rates noted in Western states lending credibility to the model based county level SRs. (Karch, L.D. et al. (2009), Kposowa, A.J. (2013)) This further validates our belief in statistical modelling assumptions. Additionally, the maps for the years 2005 (Figure 4 (top)) and 2015 (Figure 4 (bottom)) with robust and reliable county level estimates highlight all counties with high and low suicides mortality which can be used to target prevention programs and for more effective allocation of resources. Hence, the existing Bayesian spatio-temporal techniques in R-INLA outlined in this study can be useful in analyzing the trend and changing spatial patterns of a small area outcome such as SRs at the county level not afforded by examination of direct state estimates, national estimates and direct county level estimates.

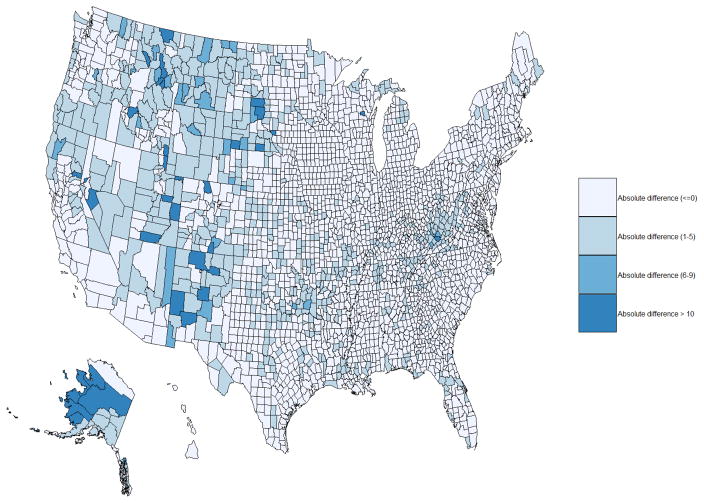
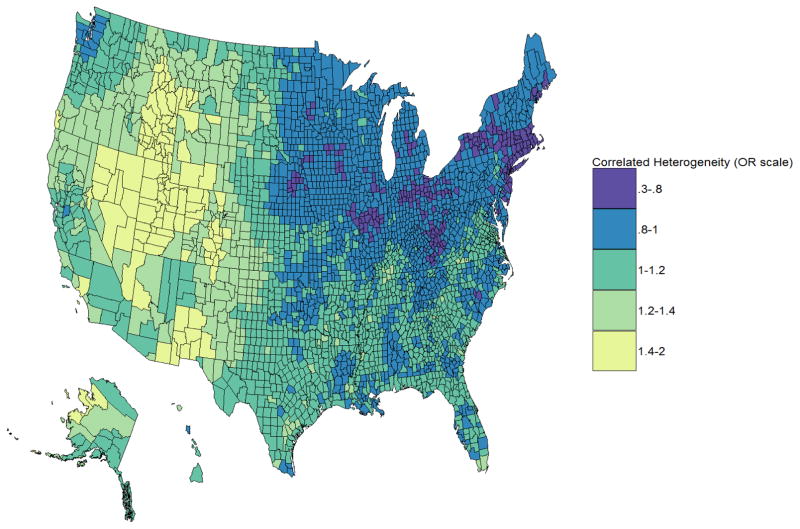
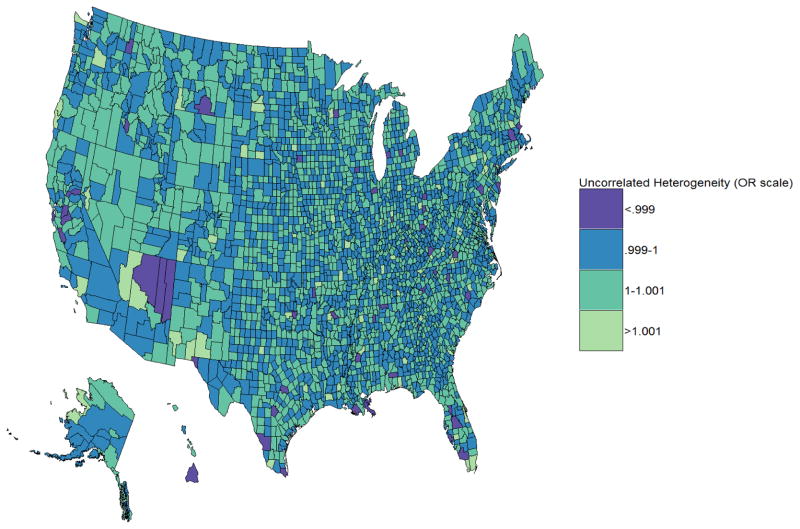
The absolute differences in the model based county level SRs in the U.S. from 2005–2015 are shown in Figure 5. The absolute differences map of the posterior predictions of the county level SRs depicts the magnitude of change in spatio-temporal variability in county level SRs for the years 2005 and 2015. Approximately 77% (2418) counties reported an absolute difference between 1 and 5 in the model based county level SRs for the years 2005 and 2015. The spatial patterning of the random effects can be seen in Figure 6 accounting for the large correlated heterogeneity in areas where the SRs are high. This supports our choice of using a spatially structured random effects model. The extra uncorrelated variability is seen in Figure 7. Thus, the existing hierarchical Bayesian spatio-temporal models in R-INLA can account for the differences in time and the challenges associated with examining unreliable direct estimates for less common causes of mortality outcomes for small scale geographic data and produce robust and reliable estimates enabling examination of spatiotemporal variations

Figure 5.

Absolute differences in model based county level suicide rates in the U.S. from 2005–2015. (The legend corresponds to the increase in suicide number of deaths per 100,000)

Figure 6.

Spatially structured random effect representing correlated heterogeneity in suicide rates across U.S. counties.

Figure 7.

Spatially unstructured random effect representing uncorrelated heterogeneity in suicide rates across U.S. counties.

4 Discussion

County-level direct estimates of less common mortality outcomes are often highly unstable. Many prior studies on county-level variations in less common causes of mortality outcomes have relied on estimates aggregated over time or larger geographic areas. However, this type of aggregation precludes the examination of detailed temporal and spatial trends. To overcome these limitations, this study uses hierarchical Bayesian methods to generate robust model-based estimates of yearly county-level SRs to examine the spatio-temporal variations across a span of 11 years.

This study contributed to the existing literature by applying an existing methodology, namely hierarchical Bayesian spatio-temporal models in R-INLA to estimate county-level SRs in order to examine spatiotemporal variation in SRs. Although there are a variety of alternative models with different assumptions that we did not explicitly explore, this study is the first to incorporate spatiotemporal random effects along with time varying confounders to estimate annual county level estimates for SRs for the years 2005–2015. There was substantial geographic variation in SRs. The majority of the counties across the U.S. demonstrated an increase in suicide death rates over this time period and no counties exhibited a decline. The existing Bayesian spatio-temporal modeling techniques in R-INLA can potentially be applied to a large number of rare causes of mortality-related outcomes from vital statistics data to examine geographic and temporal variation.

The use of R-INLA method resulted in substantially reduced computation time for this study, an average of twenty four for the best model with a full set of covariates and six to twenty four hours for models with no or few covariates, as opposed to weeks of time required for simulations based Markov Chain Monte Carlo (MCMC) via WINBUGS with large spatial datasets. (Khan, D. et al. (2018), Martins, T.G. et al. (2013), Rockett, I.R. et al. (2012), Rue, H. and Martino, S. (2009)) A variety of models incorporating space and time random effects could be tested in R-INLA without an overwhelming burden of computation time. INLA provides substantial flexibility with several built-in model components and specifications to examine a variety of models such as proper CAR (Conditionally autoregressive), ZIP (Zero Inflated Poisson) and Besag Proper without the need of further programming expertise. Moreover, the functional form of the covariates in R-INLA can be specified in different forms and can be other than linear as well.

The model fit was examined via DIC comparisons. Amongst the models fitted, the contribution of different space and time components was examined by the subsequent reduction in DIC values and the effective number of parameters to estimate. The best-fitting model captured the spatial autocorrelation and the time dependence structure of the data and was further improved by using time varying covariates accounting for the extra variability that was not captured by the main time and county effects. The best fitting model was found to have the lowest DIC with small number of effective parameters to estimate as compared to the model without time varying covariates. However, the temporal random effect was found to be an autoregressive process of order 1 which dampens out after a certain period of time. This suggests that future analyses might not require too long of a stretch of data in time in order to compute stable county level SRs. The comparison of state-level directly estimated SRs and the aggregated model-based state-level SRs for the different years showed that the majority of estimates fell on the line of equality indicating a close correspondence between the model-based state SRs and the direct state SRs at larger geographic scales.

The limitations of this study are as follows. Although a large number of models were implemented, alternative models incorporating different covariates from other data sources and space and time components might have improved the predictions. Secondly, R-INLA software can implement a variety of traditional models that are built-in, however there are a class of models such as latent mixture models that still need to be implemented. Moreover, the prior specifications that are not built-in in R-INLA need to be programmed. Thirdly, this study incorporated a large number of covariates to account for measured covariates, however suicides rates vary by gender and age groups and future studies can look at suicide rates by these mechanisms. Lastly, there is underreporting in suicides numbers and the actual number of suicides are always larger than the reported. Underreporting and measurement errors in suicides cannot be understated and have been studied in the literature (Claassen, C.A. et al. (2010)). Future studies can consider more explicit handling of the prior distributions other than the default priors specified in R-INLA (Simpson, D. et al. (2017)).

Future research exploring spatial clustering of less common causes of mortality outcomes over time, including at sub-county levels, would provide further understanding of how the small-scale geographic variation may be spatially patterned across the U.S. Lastly, the R-INLA package has provided a new, flexible and substantially faster alternative to MCMC methods.