Abstract
Previous studies examining future changes in heat/cold waves using climate model ensembles have been limited to grid cell-average quantities. Here, we make use of an urban parameterization in the Community Earth System Model (CESM) that represents the urban heat island effect, which can exacerbate extreme heat but may ameliorate extreme cold in urban relative to rural areas. Heat/cold wave characteristics are derived for U.S. regions from a bias-corrected CESM 30-member ensemble for climate outcomes driven by the RCP8.5 forcing scenario and a 15-member ensemble driven by RCP4.5. Significant differences are found between urban and grid cell-average heat/cold wave characteristics. Most notably, urban heat waves for 1981–2005 are more intense than grid cell-average by 2.1°C (southeast) to 4.6°C (southwest), while cold waves are less intense. We assess the avoided climate impacts of urban heat/cold waves in 2061–2080 when following the lower forcing scenario. Urban heat wave days per year increase from 6 in 1981–2005 to up to 92 (southeast) in RCP8.5. Following RCP4.5 reduces heat wave days by about 50%. Large avoided impacts are demonstrated for individual communities; e.g., the longest heat wave for Houston in RCP4.5 is 38 days while in RCP8.5 there is one heat wave per year that is longer than a month with some lasting the entire summer. Heat waves also start later in the season in RCP4.5 (earliest are in early May) than RCP8.5 (mid-April), compared to 1981–2005 (late May). In some communities, cold wave events decrease from 2 per year for 1981–2005 to one-in-five year events in RCP4.5 and one-in-ten year events in RCP8.5.
1 Introduction
Extreme heat and cold are a leading cause of weather-related human mortality and morbidity in the U.S. (Dixon et al. 2005; Medina-Ramón and Schwartz 2007; Anderson and Bell 2011; Guirguis et al. 2014). For example, Dixon et al. (2005) reported that during 1979–1999, 8015 deaths in the U.S. were heat related, using the Centers for Disease Control and Prevention National Center for Health Statistics’ compressed mortality database. Despite the recent “hiatus” in the increase of global mean temperature (Kosaka and Xie 2013), observational data show a continued increase of hot extremes over land (Seneviratne et al. 2014). As temperatures continue to increase due to climate change, heat waves are expected to increase in intensity (e.g., hotter days and nights), frequency (more frequent heat waves) and duration (longer heat waves), while cold waves are expected to decrease (Meehl and Tebaldi 2004; Collins et al. 2013). However, determining patterns and trends in extreme heat events and attributing changes to anthropogenic influence is not straightforward due to internal climate variability (Perkins and Fischer 2013) and uncertainty in the underlying forced response. While the uncertainty due to internal variability is large and essentially irreducible at local scales, multi-model and/or multi-member ensembles can inform more robust statements about extreme events (Fischer et al. 2013).
Future changes in extreme heat events due to climate change have been investigated using both multi-model and multi-member approaches. Coumou and Robinson (2013) showed that the multi-model mean of CMIP5 models predicts a several-fold increase in the frequency of heat extremes over global land by 2040 in the Representative Concentration Pathway 2.6 (RCP2.6) and RCP8.5 scenarios, but a strong reduction in heat extremes by the second half of the 21st century in RCP2.6 compared to RCP8.5. Fischer et al. (2013) used both the CMIP5 models and a multi-member Community Earth System Model (CESM) ensemble to show that while internal variability produces large irreducible uncertainties at the local scale, models agree that within only three decades about half of the global land surface will see significantly more intense hot extremes. Gao et al. (2012) used a high resolution regional model and single realizations of present-day and RCP8.5 climate to show that heat waves will become more severe by mid-century in most regions of the eastern U.S. Diffenbaugh and Ashfaq (2010) also used a regional model to conduct a multi-member ensemble of simulations using the A1B emissions scenario and found that substantial intensification of hot extremes could occur within the next three decades in the U.S. Monier and Gao (2014) analyzed changes in extreme events over the U.S. using a 60-member ensemble simulation with an integrated assessment model for various values of climate sensitivity, emission scenarios, and initial conditions. They found an intensification and increase in frequency of extreme hot temperatures and a decrease in intensity and frequency of extreme cold temperatures. The choice of emission scenario was found to be the largest source of uncertainty.
All of the above studies use grid cell-average quantities of surface temperature to assess extreme events. However, it is known that extreme heat can be exacerbated in urban areas because of the urban heat island (UHI) effect, which may also ameliorate extreme cold in urban relative to rural areas (Stone 2012; Mishra et al. 2015). Furthermore, analysis of extreme heat events has indicated a role of UHI effects in enhancing premature mortality and morbidity (e.g., Conti et al. 2005). The land surface model within CESM is unique among global climate models in that it includes an urban canyon model that is capable of representing the most important factors responsible for the UHI (Oleson 2012). The combination of the capability of the urban canyon model to simulate urban air temperature and the availability of CESM ensemble simulations provides a unique opportunity to investigate heat/cold waves in urban areas.
This paper is part of a larger project on the Benefits of Reducing Anthropogenic Climate changE (BRACE; O’Neill and Gettelman, in prep.). The BRACE project focuses on characterizing the difference in impacts driven by climate outcomes resulting from the forcing associated with RCP 8.5 and 4.5 (van Vuuren et al. 2011). Here, we apply a multi-member ensemble approach using the CESM version 1 (CESM1) with the Community Atmosphere Model version 5 [CESM1(CAM5); Hurrell et al. 2013] to calculate heat and cold waves for present day (defined here as 1981–2005) and a future time period defined as 2061–2080 externally forced by RCP8.5 and RCP4.5. The objectives of this paper are to 1) Contrast and characterize urban heat/cold waves with those calculated from grid cell-average and rural land, 2) Assess the changes in future heat/cold waves in the U.S. if the RCP4.5 scenario is followed instead of RCP8.5. Three other papers in the BRACE study carry out related analyses. The projections developed here are used in Anderson et al. (in prep.) to project future changes in the frequency of high-mortality heat waves in U.S. communities, in Jones et al. (in prep.) to project future exposure of populations to heat extremes globally, and in Tebaldi et al. (submitted) to assess avoided impacts from average and extreme temperature increases on crops.
2 Materials and Methods
2.1 CESM Ensemble Simulations
The CESM community recently designed the CESM Large Ensemble (CESM-LE) with the goal of enabling assessment of climate change in the presence of climate variability (Kay et al. 2014). The simulations used here replay the 20–21st century (1920–2100) 30 times under historical and RCP8.5 external forcing with small atmospheric initial condition differences. The global mean land surface temperature, averaged across ensemble members, increases by 4.2 K from 1981–2005 to 2061–2080, with internal variability producing a range of 0.2 K warming across ensemble members. The CESM-LE experimental design is described fully in Kay et al. (2014).
The same experimental design was applied to a Medium Ensemble (15 members) using RCP4.5 external forcing (CESM-ME; Sanderson et al., submitted). In response to RCP4.5 forcing, global mean land surface temperature, averaged across ensemble members, increases by 2.5 K with variability of 0.2 K across ensemble members. Here, we use daily maximum and minimum 2-m reference height temperature (“Tmax” and “Tmin”) for grid cell-average and sub-grid urban and rural landunits from these simulations.
The Community Land Model version 4 (CLM4; Lawrence et al. 2011) is the land surface model used in CESM1(CAM5). The land surface in CLM4 is described by sub-grid fractions of landunits such as vegetation/soil (referred to here as the rural surface) which consists of mixtures of plant functional types derived from satellite data as well as other landunits such as glaciers, wetlands, lakes, and urban. The rural surface is intended to represent areas where people might live other than in urban areas (thus excluding glaciers, lakes, and wetlands). The urban landunit consists of five components: roof, sunlit wall, shaded wall and a canyon floor subdivided into pervious (e.g., representing green space within the city) and impervious (e.g., representing roads, parking lots, sidewalks) fractions (CLMU; Oleson 2012). The five urban components are arranged in an urban canyon configuration in which the canyon geometry is described by building height (H) and street width (W). The spatial resolution of the climate model is 0.9375° latitude by 1.25° longitude. The urban canyon model then is a parameterization for the sub-grid urban fraction that exists within each model grid cell as a landunit. Thus, urban climate variables such as temperature are on the same spatial grid as the climate model. The urban model has been satisfactorily evaluated against measured fluxes and temperatures for several flux tower sites, performed well against other models in the International Urban Energy Balance Models Comparison Project, and produces known features of urban climatology, as discussed by Oleson (2012).
Urban fraction is aggregated from the 1 km data of Jackson et al. (2010) to the model grid. Urban properties are also provided by Jackson et al. (2010). These include thermal (e.g., thermal conductivity and heat capacity), radiative (e.g., albedo and emissivity), and morphological (e.g., H/W, roof fraction, average H, and pervious fraction of canyon floor) properties for each urban surface. These properties are defined uniquely for thirty-three geographic regions across the world [see Figure 3 in Jackson et al. (2010)] which broadly represents variations in urban morphology and building construction (the U.S. is divided into six unique regions).
A significant limitation of this study is that the model as currently structured is not capable of representing changes in urban extent and properties in transient climate simulations. This likely implies that the increases in heat waves (and decreases in cold waves) that we expect here may be underestimated (overestimated) since a common assumption is that urban areas may continue to warm faster than rural areas due to increases in urbanization driven by population growth (Stone 2007). The extent of this disparity between urban and rural warming will be a function of the degree and type of urbanization (sprawl versus increased density) and the ability of communities to implement mitigation measures such as albedo and greening strategies. The current study thus provides estimates of changes in urban heat/cold wave characteristics under greenhouse gas forcing only. Changes due to possible future urban land cover change is the subject of future model development and research.
2.2 Bias correction
In this paper we focus on future changes in heat/cold waves relative to present day. However, several other statistics of these events derived here and used elsewhere in this special issue (Anderson et al., in prep.; Jones et al., in prep; Tebaldi et al., submitted) are absolute measures and thus some corrections are required to account for systematic model biases. The process of bias correction adjusts present day model climate to better match observed climate conditions. The bias correction derived from this process is then applied to the future climate projections under the assumption that the model biases are stationary (they do not change over time).
Here, we apply a new robust technique called Kernel Density Distribution Mapping (KDDM; McGinnis et al. 2015) that has been shown to have the best overall performance among several other common approaches for bias correcting daily climate model data that is non-parametric. In this method, kernel density estimates of the distribution are first calculated for model and observed present day datasets. Cumulative distributions are constructed by integrating the density estimates. The cumulative distributions are generalized into regular and inverse cumulative distribution functions (CDF) for the model and observed datasets, respectively, via interpolation. Lastly, the future model data is bias corrected by mapping it from value to probability using the present day CDF, and from probability back to value using the observed inverse CDF. This procedure is applied to mean-zero data to correct the shape of the distribution; the means are corrected separately.
The bias correction procedure requires an observation-based dataset of the desired climate variables on the same grid as the model and at the same temporal resolution and time span as the model data [here our heat/cold wave definition (section 2.3) requires daily Tmax and Tmin at a nominal horizontal resolution of 1° in latitude and longitude for 1981–2005]. We derived an observation-based daily Tmax and Tmin dataset from an hourly 0.5° reanalysis product [Modern-Era Retrospective Analysis for Research and Applications (MERRA; Rienecker et al. 2011)] that itself has been bias corrected using Climate Research Unit (CRU) TS3.10 monthly mean Tmax and Tmin data by Wang and Zeng (2013). This data (hereinafter MERRA-BC) was re-gridded to the model grid.
The bias correction procedure can modify the diurnal temperature range (DTR) and in some cases can result in unrealistic behavior in Tmax and Tmin (Tmin > Tmax) primarily because of model biases at high latitudes possibly associated with snow albedo feedback during snowmelt (Thrasher et al. 2012). Therefore, as recommended by Thrasher et al. (2012), we bias correct model Tmax and DTR and then derive Tmin from the bias corrected Tmax and DTR. We follow the approach of Girvetz et al. (2012) in removing the trends in MERRA-BC and model Tmax and DTR before bias correction and reapplying the trends after correction to preserve interannual variability and the underlying trend.
The complete bias correction procedure was applied to all CESM-LE and CESM-ME members for 1980–2080. The resulting Tmax and Tmin bias corrections are then applied directly to the sub-grid urban and rural Tmax and Tmin. This approach effectively assumes that the urban heat island simulated by the model is reasonable. An improved bias correction procedure for the urban Tmax and Tmin would require an observation-based global urban air temperature dataset which currently does not exist. Urban and rural data are not available for the first ensemble member, resulting in 29 CESM-LE and 14 CESM-ME members for the urban/rural analysis. Details on the bias correction procedure and justification for the choice of the MERRA-BC dataset can be found in Online Resource 1 (OR1; Fig. S1–S4). The effects of the bias correction on heat/cold wave characteristics are discussed in OR1 as well.
2.3 Heat/cold wave definition
We calculate heat/cold waves for present day (defined as 1981–2005) and contrast them with those calculated for 2061–2080 under the RCP8.5 and RCP4.5 scenarios. There are many definitions of heat/cold waves, perhaps due to the diversity of research communities involved in extreme events research (Smith et al. 2013). Here we use a definition that has been shown to be related to human mortality risk (Anderson and Bell 2011) and used by Anderson et al. (in prep.) to project future changes in the frequency of high-mortality heat waves in U.S. communities.
Heat waves are defined as two or more consecutive days with daily mean temperature (Tmean) greater than the 98th percentile of Tmean for 1981–2005. Tmean is calculated from the average of daily Tmax and Tmin. Heat wave intensity is defined as the average Tmean during the heat wave. Cold waves are defined similarly except that we use the 2nd percentile of Tmean.
In previous studies that utilized the same urban/rural model applied here, urban-related quantities such as, for example, high heat stress days/nights, were calculated using the distributions taken from the rural temperature data to emphasize the contrast between urban and rural land cover (Oleson et al. 2013). Here, we assume that urban dwellers are adapted to their climate environment and the urban heat/cold waves are based on the urban temperature distribution. We also assume that there is no further adaption to warming temperatures. However, Anderson et al. (in prep.) consider two adaptation cases; a mid-time period (with distributions from 2023–2042; lagged adaptation) and 2061–2080 (on-pace adaptation) and the effect on future very dangerous heat waves. Although all heat/cold wave calculations are performed on the global land data (see Jones et al., in prep., for an application of those results), our analysis here is focused on the U.S. only. We use seven regions as defined in Peterson et al. (2013) (Northwest, Great Plains North, Midwest, Northeast, Southwest, Great Plains South, Southeast) (Fig. 2). Results for heat/cold waves for 82 individual communities selected by Anderson et al. (in prep.) are also presented here and in OR1. We also use Houston, Texas and Denver, Colorado to illustrate some important aspects of changes in heat/cold waves.
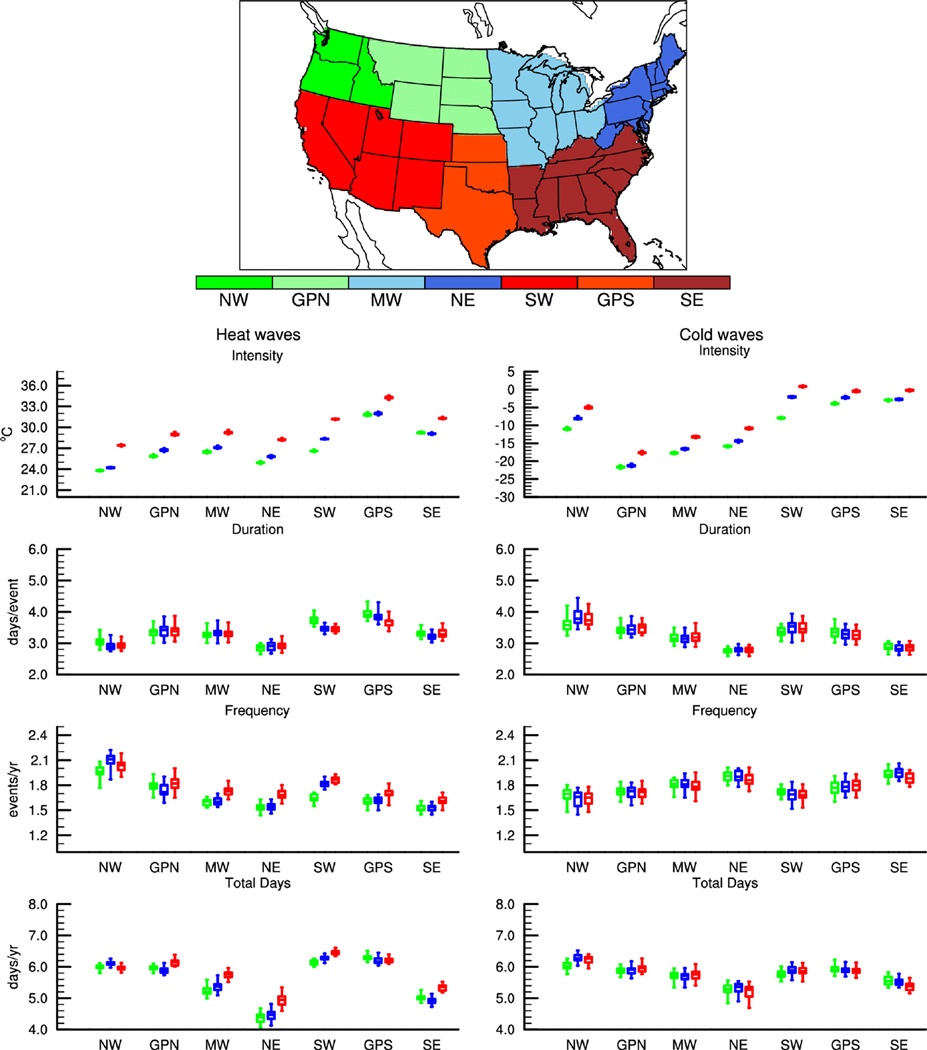
Fig. 2.
Boxplots of grid cell-average (green), rural (blue), and urban (red) heat and cold wave intensity (°C), duration (days per event), frequency (events per year), and total days (days per year) for 1981–2005 by U.S. region. Boxplots show CESM-LE ensemble median (middle horizontal bar), 75th and 25th percentiles (top and bottom horizontal bars) and at top and bottom, the maximum and minimum values. Grid cell-average is calculated from 30 ensemble members and rural and urban from 29 ensemble members. Regions (top map) are from Peterson et al. (2013). NW (Northwest), GPN (Great Plains North), MW (Midwest), NE (Northeast), SW (Southwest), GPS (Great Plains South), SE (Southeast).
We note that the heat/cold wave definition used here is less stringent than some of the definitions used in the studies referenced in section 1 (e.g., Fischer et al. (2013) used the annual maximum value of Tmax to define extreme heat) and thus we expect to identify a larger number of them in this study. As a consequence, we should be able to statistically distinguish relatively small differences in heat/cold wave characteristics in these regions with these ensembles. Statistical significance (at the 95% level) is assessed using the Wilcoxon signed-rank test for urban/rural comparisons (where the sample sizes are equal, e.g., for CESM-LE) and the Wilcoxon rank-sum test for avoided impacts comparisons (where the sample sizes are unequal, e.g., for CESM-LE and CESM-ME).
3. Results
3.1 Present day climatology
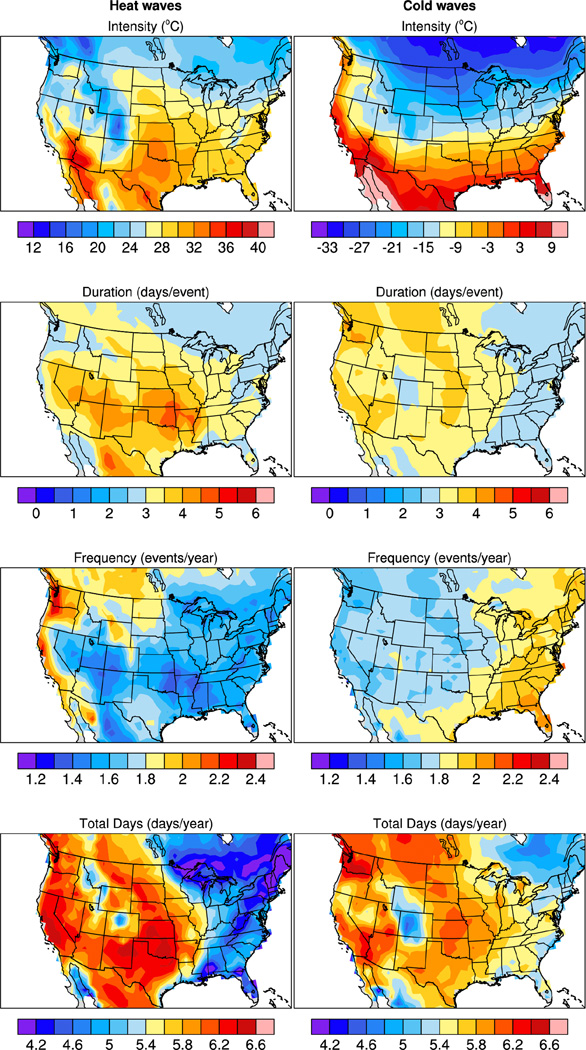
We start with an analysis of the present day heat/cold waves calculated from grid cell-average data. Fig. 1 shows ensemble mean heat/cold wave intensity, duration, frequency, and total days for 1981–2005. The spatial patterns of heat/cold wave intensity across the U.S. show a predictable dependence on latitude and topography. The most intense heat waves occur in the southern Great Plains and the most intense cold waves in the northern Great Plains (see green boxplots in Fig. 2 for regional averages). In general, heat waves are longer in regions of highest intensity, while cold waves are longest in the western U.S. Heat waves are more frequent in the western U.S. while cold waves are more frequent in the eastern U.S. Mean total heat wave days (duration multiplied by frequency in days per year) range from 4.4 (northeast) to 6.3 (southern Great Plains), with a similar range for cold wave days. Note that unlike intensity, the results for heat/cold wave duration, frequency, and total days are tightly constrained by the definition of heat/cold waves used here. We can expect a maximum of about 7 total heat/cold wave days per year (2% multiplied by 365 days). Regional variation is controlled by whether these days meet the consecutive day requirement.
Fig. 1.
CESM-LE mean (30 ensemble members) of grid cell-average heat and cold wave intensity (°C), duration (days per event), frequency (events per year), and total days (days per year) for 1981–2005.
As noted in Smith et al. (2013), comparison of heat/cold wave results between studies is difficult because of differences in definitions, time period of analysis, data sources, and spatial resolution, as well as future emission pathways. For example, heat wave days calculated for 1979–2011 by Smith et al. (2013) using data from the North American Land Data Assimilation System were consistently lower than ours likely partly due to the fact that only warm season data were used by Smith et al. (2013).
Next, we discuss the differences between grid cell-average and urban heat/cold waves for 1981–2005 to illustrate the value of the urban model (Fig. 2). We also show rural results but note that they are generally similar to the grid cell-average, except that rural area excludes wetland and lakes. In general, the largest differences between grid cell-average and rural are are seen in the intensity metric where the grid cell-average is less intense than rural for heat waves and is more intense than rural for cold waves because of the influence of wetlands and lakes.
The urban heat island effect is readily apparent in the heat/cold wave intensities. Urban heat waves are more intense than grid cell-average while cold waves are less intense (Fig. 2). Mean urban heat wave intensities are warmer than grid cell-average by 2.1°C (southeast) to 4.6°C (southwest). Urban cold wave intensities are less than grid cell-average by 2.8°C (southeast) to 8.8°C (southwest). All differences between urban and grid cell-average and urban and rural heat/cold wave intensities shown in Fig. 2 are statistically significant.
On the other hand, urban and grid-cell average heat/cold wave duration, frequency, and total heat/cold wave days are more similar to each other (Fig. 2). As mentioned above, this is due in part to the heat/cold wave definition applied to each temperature distribution. It is also due to the fact that the landunits in each grid cell are forced by the same atmospheric variables (e.g., temperature, solar/longwave radiation). The largest difference in duration is in the northwest where urban cold waves are on average 0.3 days less in duration than the grid cell-average. The largest difference in frequency is in the southwest where there are 0.2 more urban heat waves per year than the grid cell-average. Total days differ by at most 0.6 days per year (heat waves in the northeast). Although the differences between the urban and grid cell-average total heat/cold wave days are small, the differences in the medians are statistically significant except for heat waves in the northwest and cold waves in the Midwest and southern Great Plains.
3.2 Projected heat/cold waves
We also compared heat/cold wave characteristics for RCP8.5 (2061–2080) as calculated from the urban model compared to those calculated with grid cell-average data. Again, the impact of the urban model is most important for heat/cold wave intensity (Fig. S5). Mean urban heat wave intensities are warmer than the grid cell-average by 2.1°C (southeast) to 4.5°C (southwest). Urban cold waves are less intense than the grid cell-average by 2.7°C (southeast) to 8.6°C (southwest). These differences are similar to those found for present day.
Differences between urban and grid cell-average for other heat wave characteristics in RCP8.5 are generally larger in an absolute sense than those for present day (Fig. S5). For example, differences in duration and frequency result in differences in total heat wave days. Urban total heat wave days are less than grid cell-average by 10 (northwest) and 7 days (southwest) per year due to shorter durations and more than grid cell-average by 3 days per year (northeast) due to longer durations (all statistically significant). Differences in cold waves are small and not significant mainly because of the relative lack of cold waves in RCP8.5.
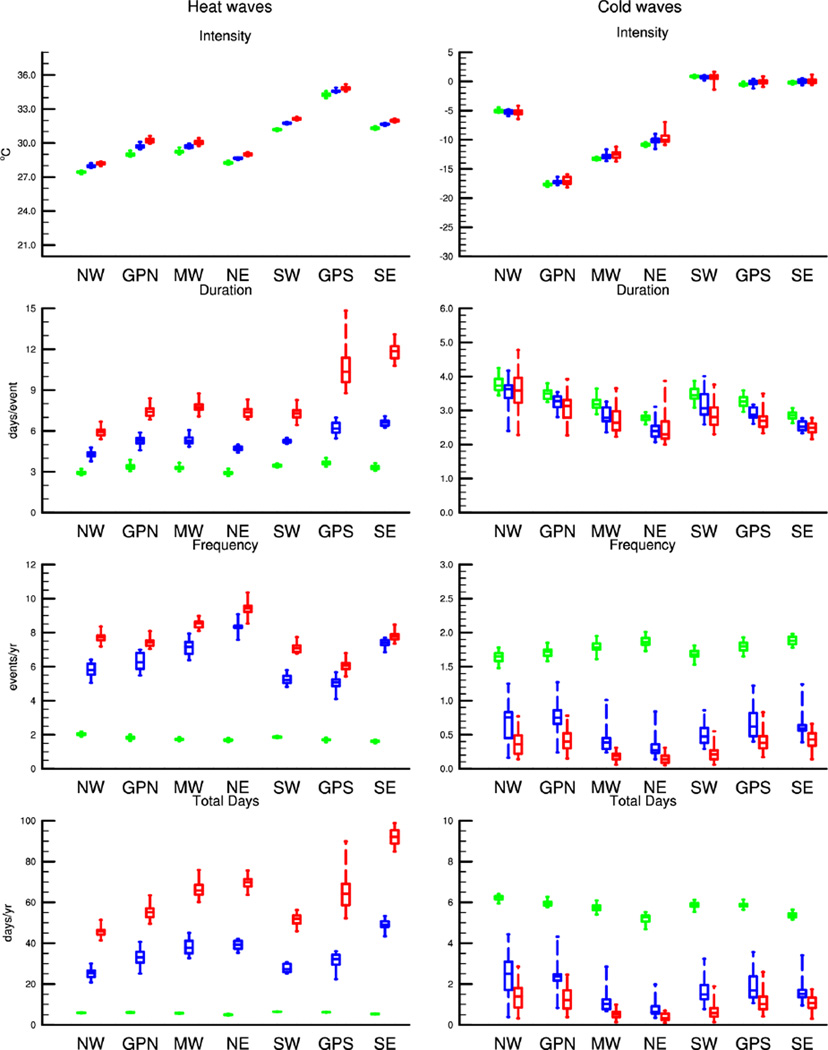
We now turn to the subject of avoided climate impacts of choice of RCP4.5 versus RCP8.5, focusing on urban areas. Fig. 3 compares urban heat/cold wave characteristics for RCP8.5 and RCP4.5 (2061–2080) and present day (1981–2005). Both RCP8.5 and RCP4.5 result in more intense, longer, and more frequent urban heat waves compared to present day. This is consistent with grid cell-average results from previous studies (e.g., Gao et al. 2012). If the RCP4.5 scenario is followed, there is a substantial reduction in heat wave days per year relative to RCP8.5, mean heat wave days per year are reduced by 21 (northwest) to 43 (southeast) due to a reduction in both duration and frequency. Heat wave intensities are also lower in RCP4.5 compared to RCP8.5 but the differences are small (0.2–0.5°C; the differences from present day are small as well). All differences in the mean heat wave characteristics between RCP8.5 and RCP4.5 are statistically significant.
Fig. 3.
Boxplots of urban heat and cold wave intensity (°C), duration (days per event), frequency (events per year), and total days (days per year) for 1981–2005 (green; 29 ensemble members), 2061–2080 RCP4.5 (blue; 14 ensemble members) and 2061–2080 RCP8.5 (red; 29 ensemble members).
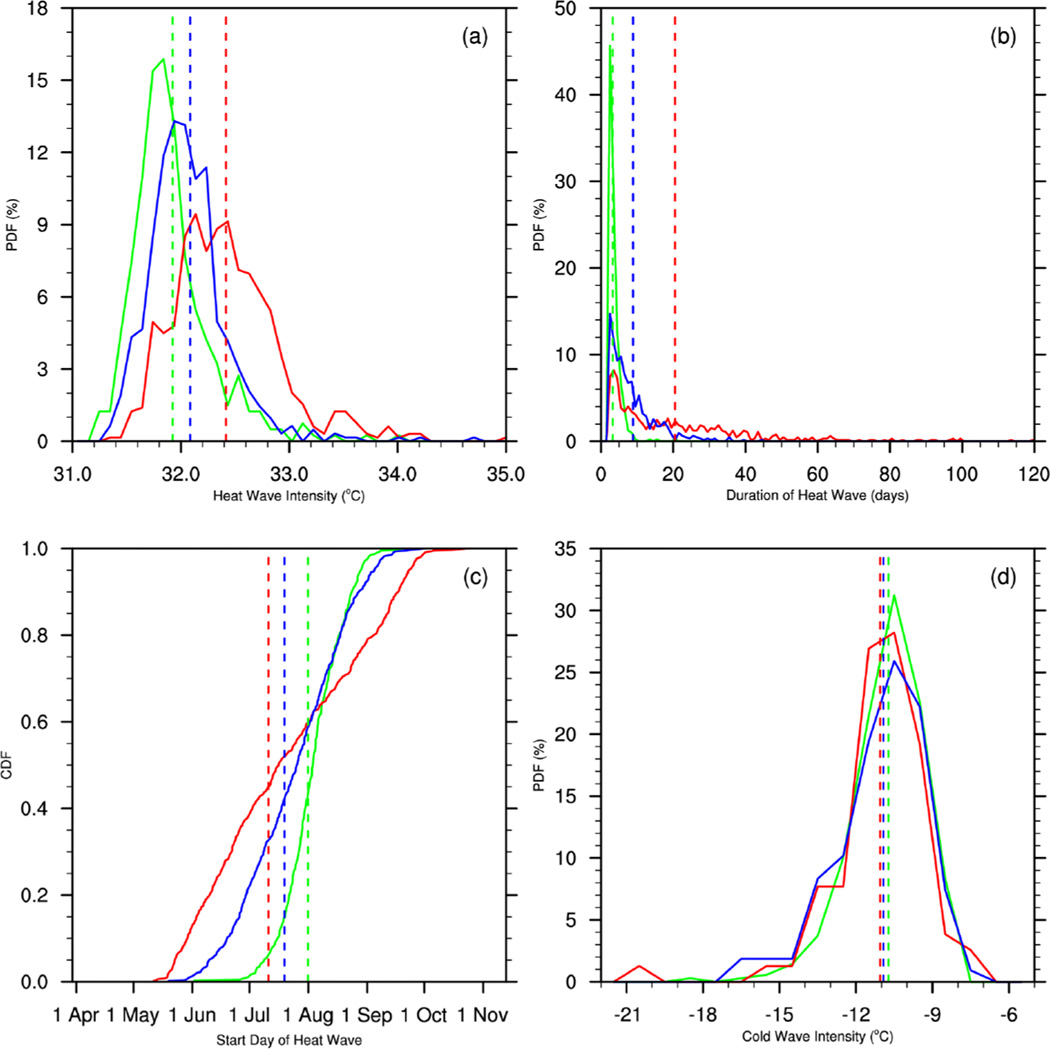
The relatively small increase in heat wave intensity for both RCP8.5 and RCP4.5 compared to present day, and thus the differences between the two scenarios, is somewhat counterintuitive because it does not follow the overall warming in these scenarios. The reason for this can be seen in Fig. 4a, which compares the frequency distribution of ensemble mean heat wave intensity for RCP8.5, RCP4.5, and present day for urban Houston, Texas. The 98th percentile of present day Tmean for Houston ranges from 31.1 to 31.4°C, depending on ensemble member. The frequency distributions of heat wave intensity in RCP4.5 and RCP8.5 shift to higher intensities compared to present day, however, the distributions are also broader such that the mean change in intensity is relatively small (the mean increase in intensity is about 0.2°C in RCP4.5 and 0.5°C in RCP8.5).
Fig. 4.
Frequency distributions of ensemble mean urban heat/cold wave characteristics for 1981–2005 (green lines), 2061–2080 RCP4.5 (blue lines), 2061–2080 RCP8.5 (red lines). Vertical dashed lines indicate the mean of each distribution. a) intensity of heat waves for urban Houston, Texas, b) as in (a) but for duration of heat waves, c) as in (a) but for cumulative distribution function of starting day of heat waves, d) intensity of cold waves for urban Denver, Colorado.
Ensemble mean heat wave results for 82 communities are shown in Fig. 5 and summarized in Table S1. Here we focus on duration, frequency, and total days since avoided impacts for intensity are small. In general, the differences between the RCPs and present day as well as the avoided impacts follow the geographic patterns shown in Fig 3. However, communities within the same region do sometimes have differing responses. For instance, the largest increases in duration in the RCPs are in the southern Great Plains and southeast (Fig. 3). In the southern Great Plains much of this is due to communities in southern Texas (e.g., Corpus Christi and Houston) where heat waves are about 6 and 17 days longer in RCP4.5 and RCP8.5 compared to 1981–2005, respectively. Thus the avoided impact is 10–12 days (Fig. 5; Table S1). The avoided impacts in communities to the north (e.g., Oklahoma City and Dallas-Ft. Worth) are much less (heat waves are only 2–3 days shorter in RCP4.5 than RCP8.5). Overall, avoided total heat wave days are larger in the south (e.g., 45 days in Houston) than the north (21 days in Oklahoma City). Similar behavior can be seen in the southeast where the regional mean avoided impact in total heat wave days is 43. For example, avoided impacts for southern coastal cities such as Miami and St. Petersburg are 53 and 44 days, respectively, while northern cities such as Knoxville and Charlotte are 37 and 35 days.
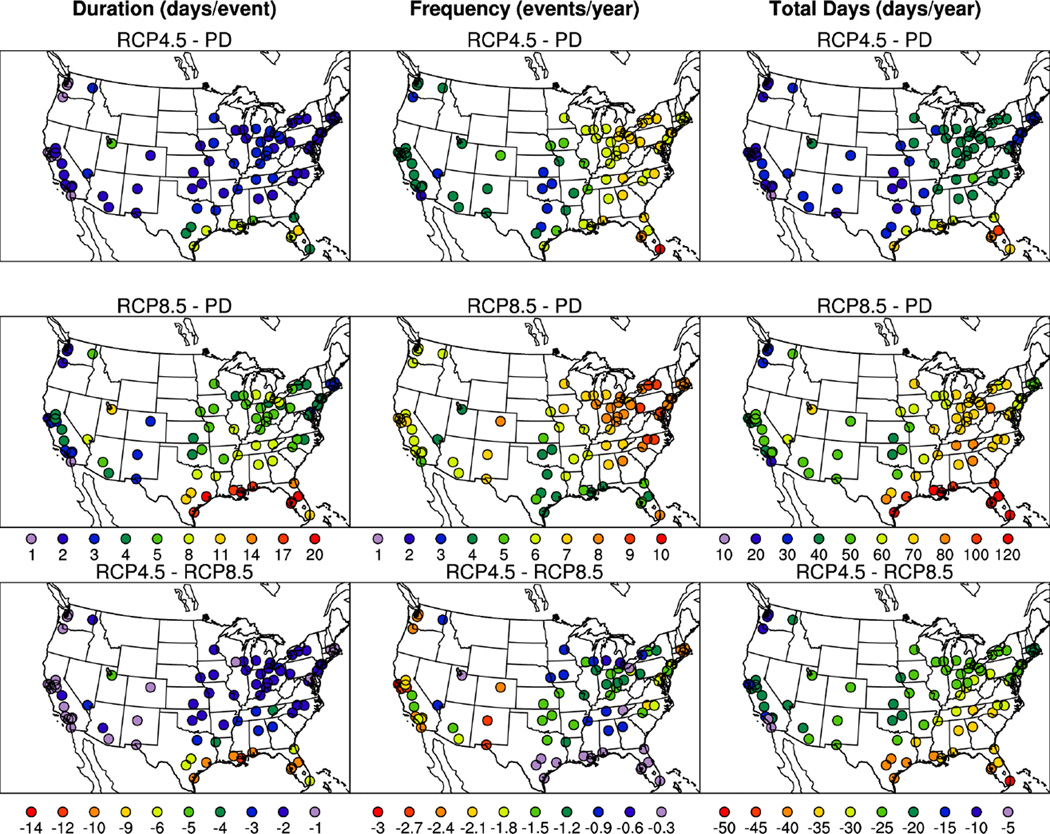
Fig. 5.
Ensemble mean heat wave duration (days per event), frequency (events per year) and total heat wave days (days per year) for 82 U.S. communities selected by Anderson et al. (in prep.). Top three panels show values for RCP4.5 (2061–2080) minus PD (present day; 1981–2005). Middle three panels show RCP8.5 (2061–2080) minus PD. Bottom three panels show RCP4.5 minus RCP8.5. A summary of community names, locations, and heat wave characteristics can be found in Table S1.
There is some notable spatial variability in avoided impacts within the southwestern U.S. as well (Fig. 5). Most cities in California have similar avoided impacts in total heat wave days, ranging from 18 days (Los Angeles) to 23 days (Bakersfield). However, San Diego and Santa Ana are exceptions to this with about half as many days (10). Avoided impacts appear to be less spatially variable within the midwest and northeast in terms of total days. In the Midwest (mean of 28), avoided impacts are between 25 days (Madison and Milwaukee) and 32 days (Columbus), while they vary a bit more in the northeast (mean of 31) and are between 22 days (Boston, Providence, Worcester; note that these three communities are located within the same grid cell) and 34 days (Pittsburg).
In some communities, the heat wave season consists of shorter but more frequent heat waves in RCP4.5 than RCP8.5. This occurs exclusively in the southern Great Plains (Corpus Christi and Houston) and the southeast (Baton Rouge, Jacksonville, Miami, Mobile, New Orleans, Orlando, St. Petersburg, Tampa) (Table S1). For example, in New Orleans heat waves are about 13 days shorter but there are almost 3 more heat waves per year in RCP4.5 compared to RCP8.5.
The large avoided impacts in average heat wave duration for urban Houston (12 days) are demonstrated in Fig. 4b for individual ensemble members. RCP8.5 has numerous significantly longer heat waves than RCP4.5. For example, CESM-LE#15 has heat waves with durations of 39, 40, 41, 48 (2), 49, 52, 56, 62, 68, 76 (2), 88 (2), 93, 95, 102, and 107 days, while the longest heat wave in CESM-ME#15 is 38 days (Fig. S6). This implies that in RCP8.5 there is nearly one heat wave per year that is more than a month in duration, with a few of these lasting the entire summer.
Heat waves start earlier and also later in the season in RCP8.5 than RCP4.5 (Fig. 4c). For the ensemble mean in RCP8.5, there are 78 and 164 heat waves that start in May and June, respectively, and 7 and 117 heat waves in RCP4.5. Heat waves in individual ensemble members start as early as mid-April in RCP8.5 and as late as early November (Fig. S8). In RCP4.5, the earliest heat waves begin in early May and the very latest begin in early October (Fig. S8). There are far fewer heat waves in RCP8.5 that start during July and August compared to RCP4.5 because there is a large probability that a long duration heat wave is already in progress by July (note the smaller slope of the CDF for RCP8.5 compared to RCP4.5 in Fig. 4c).
Houston is the most extreme example with respect to heat wave duration and start dates for the most populous community in each of the seven regions (Fig. S6–S9). However, these other communities (Omaha, Chicago, New York, Seattle, Jacksonville, and Los Angeles) all share the common characteristics of significantly longer heat wave durations and earlier start dates in RCP8.5 compared to RCP4.5. These characteristics may have adverse consequences for human health (Anderson and Bell 2011; Peng et al. 2011).
In terms of avoided impacts for cold waves, again there are only small differences in intensity (Fig. 3) (only the differences between RCP4.5 and RCP8.5 for the Midwest are significant). Fig. 4d shows an example of cold wave intensity for urban Denver, Colorado. The 2nd percentile of present day Tmean for Denver ranges from −7.9 to −6.7°C, depending on ensemble member. The frequency distributions have similar width and the mean intensities for the three cases are similar. Extreme cold waves are also possible in either RCP. For example, cold waves in Denver in CESM-LE#4 and CESM-LE#6 (RCP8.5) have intensities of about −21 and −19°C, respectively, while CESM-ME#12 and CESM-ME#8 (RCP4.5) have cold waves with intensities of about −20 and −19°C, respectively (not shown).
There are only small avoided impacts in cold wave duration as well (Fig. 3). Only the differences for southern Great Plains (RCP4.5 durations are longer than RCP8.5 by 0.2 days per event) and southwest (RCP4.5 durations are longer by 0.3 days per event) are significant. Differences in cold wave frequencies are significant but small in all regions ranging from 0.1 to 0.3 more events per year in RCP4.5 compared to RCP8.5. Thus, cold wave days per year increase by 0.4 to 1.2 in RCP4.5 compared to RCP8.5 (all significant). In some communities in the midwest and northeast, cold wave events decrease from almost 2 per year to as low as a one-in-five year event in RCP4.5 and a one-in-ten year event in RCP8.5 (e.g., Cleveland, Detroit, Grand Rapids, Toledo, Buffalo, Rochester, Syracuse; Fig S10, Table S2).
4. Discussion and Conclusions
The results indicate statistically significant differences between heat/cold wave characteristics obtained from temperature distributions predicted by the urban model compared to the grid cell-average temperatures used in previous studies. In particular, urban heat wave intensities are higher than grid cell-average intensities as a result of the urban heat island. Differences in heat/cold wave duration, frequency, and total days are smaller but still significant. Given that more than 50% of the world’s population lives in urban communities and this percentage is expected to increase in the future, these results indicate the value of embedding an urban model within a climate model. The results also show that the avoided climate impacts of heat waves by following a lower emissions scenario are significant and substantial.
These results should be interpreted in the context of the limitations of the modeling framework used here. A major limitation of this study is that the urban areas are static in time, in other words, urban thermal, radiative, and morphological properties do not change in the future nor does urban extent. We are currently developing future urban datasets that will allow us to examine the relative roles of urban development and climate change in determining future heat/cold wave characteristics.
Monier et al. (2014) argue that a modeling framework to address uncertainty in regional climate change should include the roles of internal variability, model structural uncertainty, model parameters (e.g., climate sensitivity), and emissions scenario. The modeling framework we use here consists of ensembles of opportunity conducted by the CESM community to enable assessment of climate change in the presence of internal climate variability (Kay et al. 2014; Sanderson et al., submitted.). The availability of urban output makes these ensembles a unique resource as there is only one other global climate model with an urban representation that submitted simulations to CMIP5 that we are aware of. However, this modeling framework means that we can only address the roles of internal variability and emissions scenarios and our results are thus subject to uncertainty from choices in model design (and their effect on climate sensitivity). These additional uncertainties could be addressed through multi-model urban simulations when urban models in climate models become more widely available.
For the heat/cold wave events examined here, the range of results obtained are generally much more dependent on emission scenario than on internal variability. This result agrees with Hawkins and Sutton (2009) who demonstrate that for time horizons of many decades or longer, the dominant sources of uncertainty at regional or larger spatial scales are scenario uncertainty and model uncertainty, the latter of which is not addressed here. On the other hand, for some heat wave metrics such as frequency there are cases where the ensemble members are useful for distinguishing whether the differences between RCP4.5 and RCP8.5 are significant (Fig. 3). The ensemble members are also useful for describing the sensitivity of the tails of the distribution for a given emissions scenario. A notable example of this is RCP8.5 heat waves in the southern Great Plains, where duration ranges from 9 to 15 days and total days per year range from 52 to 90, depending on ensemble member (Fig. 3). Internal variability still clearly plays a significant role at 2061–2080 and by looking at extremes, one sees a larger role than one would observe by looking at changes in the mean as in Monier et al. (2014) and Hawkins and Sutton (2009).
Supplementary Material
Acknowledgements
This material is based upon work supported by the National Science Foundation (NSF) under Grant Number AGS-1243095. K.W. Oleson was supported in part by NASA grant NNX10AK79G (the SIMMER project) and the NCAR Weather and Climate Impacts Assessment Science Program (WCIASP). G.B. Anderson was supported by NIEHS grants K99ES022631 and R21ES020152. We thank C. Tebaldi and B. O’Neill for comments on an earlier draft of this paper, and J.-F. Lamarque for useful discussions about heat/cold waves. We thank the reviewers for their insightful and constructive comments that substantially improved the manuscript. NCAR is sponsored by the NSF.
Contributor Information
K.W. Oleson, National Center for Atmospheric Research, P.O. Box 3000, Boulder, CO 80307, 303-497-1332, FAX: 303-497-1348, oleson@ucar.edu
G.B. Anderson, Colorado State University, Department of Environmental & Radiological Health Sciences, Fort Collins, CO 80523
B. Jones, CUNY Institute for Demographic Research, New York, NY 10010-5585
S.A. McGinnis, National Center for Atmospheric Research, P.O. Box 3000, Boulder, CO 80307
B. Sanderson, National Center for Atmospheric Research, P.O. Box 3000, Boulder, CO 80307
REFERENCES
- Anderson GB, Bell ML. Heat waves in the United States: mortality risk during heat waves and effect modification by heat wave characteristics in 43 U.S. communities. Environmental Health Perspectives. 2011;119:210–218. doi: 10.1289/ehp.1002313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins M, Knutti R, Arblaster J, et al. Long-term climate change: projections, commitments and irreversibility. In: Stocker TF, Qin D, Plattner G-K, et al., editors. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press; 2013. [Google Scholar]
- Conti S, Meli P, Minelli G, et al. Epidemiologic study of mortality during the Summer 2003 heat wave in Italy. Environ Res. 2005;98:390–399. doi: 10.1016/j.envres.2004.10.009. [DOI] [PubMed] [Google Scholar]
- Coumou D, Robinson A. Historic and future increase in the global land area affected by monthly heat extremes. Environ Res Lett. 2013;8:034018. [Google Scholar]
- Diffenbaugh NS, Ashfaq M. Intensification of hot extremes in the United States. Geophys Res Lett. 2010;37:L15701. [Google Scholar]
- Dixon PG, Brommer DM, Hedquist BC, et al. Heat mortality versus cold mortality: a study of conflicting databases in the United States. B Am Meteorol Soc. 2005;86:937–943. [Google Scholar]
- Fischer EM, Beyerle U, Knutti R. Robust spatially aggregated projections of climate extremes. Nature Clim Change. 2013;3:1033–1038. [Google Scholar]
- Gao Y, Fu JS, Drake JB, et al. Projected changes of extreme weather events in the eastern United States based on a high resolution climate modeling system. Environ Res Lett. 2012;7:044025. [Google Scholar]
- Girvetz EH, Maurer E, Duffy P, et al. Making climate data relevant to decision making: the important details of spatial and temporal downscaling. [Accessed 01 October 2014];The World Bank Group. 2012 http://sdwebx.worldbank.org/climateportal. [Google Scholar]
- Guirguis K, Gershunov A, Tardy A, Basu R. The impact of recent heat waves on human health in California. J Appl Meteorol Clim. 2014;53:3–19. [Google Scholar]
- Hawkins E, Sutton R. The potential to narrow uncertainty in regional climate predictions. B Am Meteorol Soc. 2009;90:1095–1107. [Google Scholar]
- Hurrell JW, Holland MM, Gent PR, et al. The Community Earth System Model: a framework for collaborative research. B Am Meteorol Soc. 2013;94:1339–1360. [Google Scholar]
- Jackson TL, Feddema JJ, Oleson KW, et al. Parameterization of urban characteristics for global climate modeling. A Assoc Am Geog. 2010;100:848–865. [Google Scholar]
- Kay JE, Deser C, Phillips A, et al. The Community Earth System Model (CESM) large ensemble project: a community resource for studying climate change in the presence of internal climate variability. B Am Meteorol Soc. 2014 [Google Scholar]
- Kosaka Y, Xie S-P. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature. 2013;501:403–407. doi: 10.1038/nature12534. [DOI] [PubMed] [Google Scholar]
- Lawrence DM, Oleson KW, Flanner MG, et al. Parameterization improvements and functional and structural advances in version 4 of the Community Land Model. J Adv Model Earth Syst. 2011;3:M03001. [Google Scholar]
- McGinnis S, Nychka D, Mearns LO. A new distribution mapping technique for climate model bias correction. In: Lakshmanan V, Gilleland E, McGovern A, Tingley M, editors. Machine Learning and Data Mining Approaches to Climate Science: Proceedings of the Fourth International Workshop on Climate Informatics. Springer; 2015. [Google Scholar]
- Medina-Ramón M, Schwartz J. Temperature, temperature extremes, and mortality: a study of acclimatisation and effect modification in 50 US cities. Occupational and Environmental Medicine. 2007;64:827–833. doi: 10.1136/oem.2007.033175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meehl GA, Tebaldi C. More intense, more frequent, and longer lasting heat waves in the 21st century. Science. 2004;305:994–997. doi: 10.1126/science.1098704. [DOI] [PubMed] [Google Scholar]
- Mishra V, Ganguly AR, Nijssen B, Lettenmaier DP. Changes in observed climate extremes in global urban areas. Environ Res Lett. 2015;10:024005. [Google Scholar]
- Monier E, Gao X. Climate change impacts on extreme events in the United States: an uncertainty analysis. Climatic Change. 2014 [Google Scholar]
- Monier E, Gao X, Scott JR, et al. A framework for modeling uncertainty in regional climate change. Climatic Change. 2014 [Google Scholar]
- Oleson KW. Contrasts between urban and rural climate in CCSM4 CMIP5 climate change scenarios. J Climate. 2012;25:1390–1412. [Google Scholar]
- Oleson KW, Monaghan A, Wilhelmi O, et al. Interactions between urbanization, heat stress, and climate change. Climatic Change. 2013 [Google Scholar]
- Peng RD, Bobb JF, Tebaldi C, et al. Toward a quantitative estimate of future heat wave mortality under global climate change. Environmental Health Perspectives. 2011;119:701–706. doi: 10.1289/ehp.1002430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perkins SE, Fischer EM. The usefulness of different realizations for the model evaluation of regional trends in heat waves. Geophys Res Lett. 2013;40 2013GL057833. [Google Scholar]
- Peterson TC, Heim RR, Jr, Hirsch R, et al. Monitoring and understanding changes in heat waves, cold waves, floods, and droughts in the United States: state of knowledge. B Am Meteorol Soc. 2013;94:821–834. [Google Scholar]
- Rienecker MM, Suarez MJ, Gelaro R, et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J Climate. 2011;24:3624–3648. doi: 10.1175/JCLI-D-16-0758.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seneviratne SI, Donat MG, Mueller B, Alexander LV. No pause in the increase of hot temperature extremes. Nature Clim Change. 2014;4:161–163. [Google Scholar]
- Smith TT, Zaitchik BF, Gohlke JM. Heat waves in the United States: definitions, patterns and trends. Clim Change. 2013;118:811–825. doi: 10.1007/s10584-012-0659-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone B., Jr Urban and rural temperature trends in proximity to large US cities: 1951–2000. Int J Clim. 2007;27:1801–1807. [Google Scholar]
- Stone B. The city and the coming climate: Climate change in the places we live. New York: Cambridge University Press; 2012. [Google Scholar]
- Thrasher B, Maurer EP, McKellar C, Duffy PB. Technical Note: Bias correcting climate model simulated daily temperature extremes with quantile mapping. Hydrol Earth Syst Sci. 2012;16:3309–3314. [Google Scholar]
- van Vuuren DP, Edmonds J, Kainuma M, et al. The representative concentration pathways: an overview. Clim Change. 2011;109:5–31. [Google Scholar]
- Wang A, Zeng X. Development of global hourly 0.5° land surface air temperature datasets. J Climate. 2013;26:7676–7691. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.