Abstract
Understanding the mechanical factors that drive the biological responses of chondrocytes is central to our interpretation of the cascade of events that lead to osteoarthritic changes in articular cartilage. Chondrocyte mechanics is complicated by changes in tissue properties that can occur as osteoarthritis (OA) progresses and by the interaction between macro-scale, tissue level, properties and micro-scale pericellular matrix (PCM) and local extracellular matrix (ECM) properties, both of which cannot be easily studied using in vitro systems. Our objective was to study the influence of macro- and micro-scale OA-associated structural changes on chondrocyte strains. We developed a multi-scale finite element model of articular cartilage subjected to unconfined loading, for the following three conditions: (i) normal articular cartilage, (ii) OA cartilage (where macro and micro-scale changes in collagen content, matrix modulus and permeability were modeled), and (iii) early-stage OA cartilage (where only micro-scale changes in matrix modulus were modeled). In the macro-scale model, we found that a depth-dependent strain field was induced in both healthy and OA cartilage and that the middle and superficial zones of OA cartilage had increased tensile and compressive strains. At the micro-scale, chondrocyte shear strains were sensitive to PCM and local ECM properties. In the early-OA model, micro-scale spatial softening of PCM and ECM resulted in a substantial increase (30%) of chondrocyte shear strain, even with no structural changes in macro-scale tissue properties. Our study provides evidence that micromechanical changes at the cellular level may affect chondrocyte activities before macro-scale degradations at the tissue level become apparent.
Keywords: Cartilage, Osteoarthritis, Cell, Multi Scale, Finite Element Modeling
1. Introduction
Articular cartilage is a swollen, hydrated tissue with an extracellular matrix (ECM) composed of negatively charged proteoglycans (PGs) and a uniquely organized type II collagen network. When articular cartilage is mechanically loaded, tissue-level deformations are transferred through the hierarchical structure of the ECM, through a proteoglycan and type VI collagen rich region surrounding each chondrocyte1–3 – the pericellular matrix (PCM) – to the embedded chondrocytes. Chondrocytes respond to deformation by regulating metabolic and matrix synthesis activities.4 For example, excessive chondrocyte strains can result in enhanced secretion of catabolic effectors, e.g. matrix metalloproteinases (MMPs) and PG degrading aggrecanases, thereby leading to the progression of cartilage and joint degeneration over time.4–6 In pathological conditions, such as osteoarthritis (OA), decreased modulus and increased permeability at the tissue-explant level (i.e. macro-scale) occur,7–9 while decreases in the spatial elastic modulus of the ECM and PCM (i.e. micro-scale level) surrounding the chondrocyte have also been reported.10 Oftentimes, the more subtle micro-scale changes can occur before macro-scale tissue-level changes are evident.11 Our understanding of the mechano-biological responses of chondrocytes is therefore complicated by the interaction of the macro- and micro-scale properties. For example, while it has been suggested that the mechanical properties of both the PCM and the ECM regulate the transmission of the deformation to the chondrocyte12–17,18,19 the mechanics of this interaction have not yet been defined.
Computational models have been used to simulate chondrocyte deformation and chondrocyte-matrix interactions in articular cartilage,7,20,21 and have demonstrated that the PCM plays an important role in regulating the equilibrium and transient micro-mechanical environment of chondrocytes. Furthermore, it has been shown that changes in tissue level properties which occur in OA affect chondrocyte volumetric behavior under mechanical loading.21 However, the role of micro-scale spatial inhomogeneities in ECM and PCM modulus10 on chondrocyte deformation, has not been investigated.
Our objective was to study the influence of macro- and micro-scale OA-associated structural changes on chondrocyte strain. To achieve this objective, we developed a multi-scale finite element model of articular cartilage. We hypothesized that micro-scale changes in local ECM and PCM modulus would affect chondrocyte deformations, even with no apparent changes in macro-scale tissue properties.
Methods
General approach
An axisymmetric macro-scale finite element model of an articular cartilage explant subjected to unconfined loading was created in Abaqus v6.16 (Dassault Systems, Providence, RI). The model was designed to mimic the anisotropic, inhomogeneous, fibril-reinforced, poroelastic, and swelling behavior of articular cartilage. A micro-scale axisymmetric finite element model was also created which included a chondrocyte (‘cell’) surrounded by PCM and ECM (Fig. 1). Using a multi-scale modeling approach, the deformations from the middle zone of the macro-scale model were used as input boundary conditions for the micro-scale model.22
Figure 1.
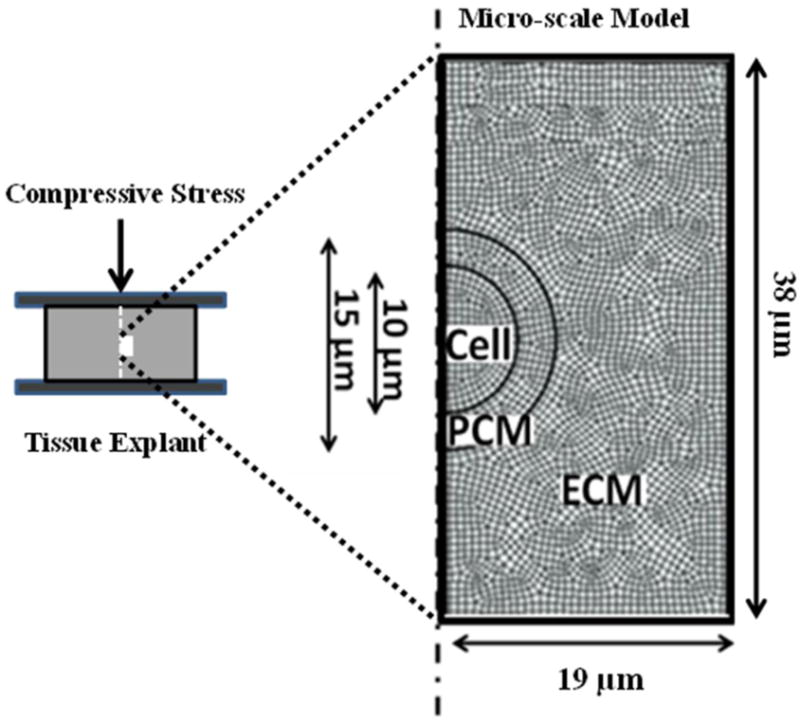
Axisymmetric micro-scale (right) finite element mesh of a cylindrical cartilage explant (left) under unconfined compression. Boundary conditions of the micro-scale model were obtained from the solution of a macro-scale axisymmetric finite element model of the explant. The local ECM in the micro-scale model had the same properties as the ECM of the macro-scale model except that the spatial variation of the shear modulus in the local ECM was adjusted as depicted in Figure 2.
Material Model
We adopted a composition-based fibril-reinforced poroelastic swelling model prescribed in an Abaqus user subroutine (UMAT). The same material model was used for ECM of the macro-scale model and ECM and PCM of the micro-scale models. The material was considered to consist of a fluid phase and a porous solid phase with swelling properties. The porous solid phase of the biphasic tissue consisted of a swelling solid ground substance representing proteoglycan (PGs) non-fibrillar matrix, and a fibrillar component representing the oriented collagen network.23–25
The governing stress equation is given by:24,26
| (1) |
where μf is the fluid pressure, I the unit tensor, Δπ the osmotic pressure gradient, ns,0 the initial solid volume (in the unloaded and non-swollen state), J the volumetric deformation, σpgm the stress in the solid ground substance, σicol the collagen fibril stress in the ith fibril direction, i detonated the number of the fibril compartment and totcol the total number of the fibrils. Depth-dependent composition description of the collagen fibers and the solid ground substance can be found in Wilson et al. (2004-2007).24,25 Since collagen and PG constituents compose the total solid phase, the fractions of collagen and PG constituents in our model are defined with respect to the total solid phase.
Fluid flux has been modeled with Darcy’s law:
| (2) |
where w is the flux of the fluid relative to the solid, nf is the current fluid fraction, is the relative velocity of the fluid with respect to the solid matrix, k is cartilage permeability and is the pressure gradient.27
The permeability k is a function of the current extra-fibrillar fluid fraction:24,25
| (3) |
where M and are positive material parameters and is the current extra-fibrillar fluid fraction. It is noted that when obtaining this formulation, the fact that only the extra-fibrillar fluid can flow out of the tissue has been accounted for. For further details of the calculation of permeability the reader is referred to Wilson et al. (2006-2007).24,25
For the solid ground substance, a compressible Neo-Hookean model was used of which the compressibility is dependent on the solid fraction:24
| (4) |
where Gm was the shear modulus of the solid ground substance and was the deformation gradient tensor.
The total Cauchy stress for collagen expressed as a function of the deformation is given by:24
| (5) |
where λ is the elongation of the fibril, is the current fibril direction, Pcol is the 1st Piola Kirchhoff fibril stress, and σiso is represented the isotropic stiffness of the fibers. The isotropic stress σiso was described with the same Neo-Hookean model used to describe the stress in the solid ground substance (σpgm, Eq. 2), yet with Gm replaced by Gmcol, representing the shear modulus of the collagen fiber network.26
Elongation of the fibril λ is calculated by:
| (6) |
where is the initial fibril orientation.
The 1st Piola Kirchhoff fibril stress is given by:
| (7) |
with P1 and P2 defined as:
| (8) |
| (9) |
and E1, k1, E2 and k2 positive material constants. Collagen was modeled as a double-spring-dashpot where is the total fibril logarithmic strain in a first spring, the logarithmic strain of the second spring which is parallel to the first spring, and is the logarithmic strain of the dashpot which is in series configuration with the second spring. The strains in the upper part of the double-spring dashpot (i.e. the first spring) and lower part of the double-spring dashpot (i.e. the second spring and dashpot) of the spring system are the same. As such, the strain in the first spring is equal to the summation of the strains in the second spring and the dashpot. For more details on the collagen fiber material model the reader is referred to Wilson et al. (2004-2007).24,25
The osmotic pressure gradient Δπ, as a result of the fixed-charge density (FCD) of the negative glycosaminoglycan (GAG) concentration embedded in the ground substance matrix, is given by:28
| (10) |
where is effective fixed charge density, cext the external salt concentration ϕα osmotic coefficient, γα activity coefficients, T the temperature, and R the gas constant. For further details of the material model the reader is referred to Wilson et al.25
Study Design
Three cases were simulated:
Case 1, Healthy cartilage model - The ECM of the macro-scale model and local ECM and PCM of the micro-scale model were assigned material properties to mimic that of normal articular cartilage.
Case 2, OA cartilage model - The ECM of the macro-scale model and the ECM and PCM of the micro-scale model were assigned material properties to mimic OA cartilage.
Case 3, Early-stage OA cartilage model - The ECM of the macro-scale model as assigned material properties to mimic normal cartilage, while the local ECM and PCM of the micro-scale model was assigned properties to mimic OA cartilage.
Macro-scale Model
The circular tissue explant was 5.6 mm diameter and 1 mm thickness. The base of the explant was restricted from displacements in all directions in order to represent cartilage attachment to the subchondral bone. The displacements at the nodes along the axis of symmetry were confined in the radial direction. The nodes on the lateral edge were prescribed zero pore pressure to simulate free fluid flow. Compressive stress of 7.75 MPa was applied to the top surface of the explant. This stress magnitude corresponded to the reaction force divided by the explant’s surface area when an impermeable platen applied a 10% compression to the healthy explant. At the macro-scale, the healthy and OA cartilage models were simulated by adjusting the content and properties of the ECM components, as presented in Table 1. Based on data from literature,7–9 the ECM of the OA cartilage model was considered to have 40% less collagen content, 40% lower matrix stiffness, and twice (2X) the permeability as that of healthy cartilage. Output: Tensile and compressive strain fields in the ECM of the healthy and early OA cartilage models which had identical macroscale ECM properties (Case 1 and Case 3) and of the OA cartilage model (Case 2) were calculated. Tensile and compressive strains at the middle zone of the explant were computed and used as inputs to their respective micro-scale model.
Table 1.
Material parameters of normal and OA ECM.
| Parameter | Description | Normal value | OA value | |
|---|---|---|---|---|
| nf,0 | Initial fluid volume fraction | 0.9-0.2(z#) | Same as normal | |
| ns,0 | Initial solid volume fraction | 1−[0.9-0.2(z#)] | Same as normal | |
| CF0 | Initial fixed charge density | 0.1(−z#)2−0.24(z#)+0.035 | Same as normal | |
| ncol | Depth dependent collagen fraction | 1.4(z#)2−1.1(z#)+0.59 | 0.4 × Normal value | |
| Npgm | Depth dependent PG fraction | 1-ncol | Same as normal | |
| Gm | Shear modulus of PG matrix | 0.7722 (MPa) | 0.4 × Normal value | |
| Gcol | Shear modulus collagen isotropic matrix | 0.01144 (MPa) | Same as normal | |
|
|
Permeability constant | 1.767 ×10−17 m4/N s | 2.0× Normal value | |
| M | Permeability constant | 1.339 | Same as normal | |
| E1 | Collagen type II material constant | 4.362 (MPa) | Same as normal | |
| K1 | Collagen type II material constant | 14.39 | Same as normal | |
| E2 | Collagen type II material constant | 20.25 (MPa) | Same as normal | |
| K2 | Collagen type II material constant | 43.96 | Same as normal | |
| η | Collagen type II viscoelasticity dashpot constant | 1.532 × 105 (MPa s) | Same as normal |
z# was the normalized depth of the explant (0 at the articular surface and 1 at the explants-bone interface)
Micro-scale Model
The sub-modeling option in Abaqus was used to prescribe the displacement and fluid pore pressure fields derived from the solution of the macro-scale model to the boundary of the micro-scale model. The inner and outer diameters of the chondrocyte and PCM were 10 μm, 10 μm and 15 μm, respectively (Fig 1). The chondrocyte was modeled as an homogeneous biphasic material.7,29,30 The PCM was modeled using the same material model as ECM, with fluid fraction of 0.85, fixed charge density of 0.2 (mEq/ml), Poisson’s ratio of 0.15 and permeability of 1.9 ×10−15 m4/N s.21 The collagen fibril stiffness of the PCM was 10% (type VI collagen) of that of the ECM (type II collagen)21 (Table 2). The spatial softening of PCM and ECM for Cases 2 and 3 was modeled by adjusting the shear modulus of the ground substance Gm.10 Accordingly Gm of the PCM and ECM were increased from the inner edge of the PCM towards the ECM (Fig. 2). The ratio of the increase in Gm was the same as the ratio of increase in the elastic modulus of PCM towards ECM measured in experiments which used atomic force microscopy.10 In Fig. 2, the Gm of the ECM and PCM are normalized to that of the normal ECM (Gm= 0.7722 MPa). Output: Tensile, compressive and shear strains at the micro-scale were calculated for the studied cases using the micro-scale model. Tensile strain refers to logarithmic lateral strain (LE11), compressive strain refers to logarithmic axial strain (LE22) and shear strain is logarithmic in-plan shear strain (LE12).
Table 2.
Material parameters of the PCM and chondrocyte in the micro-scale model.
| Parameter | Description | Value |
|---|---|---|
| PCM | ||
| nf,0 | Initial Fluid Volume Fraction | 0.85 |
| CF0 | Initial Fixed Charge Density | 0.2 (mEq/ml) |
| KPCM | Permeability (constant) | 1.9 ×10−15 m4/N s |
| E1 | collagen type VI material constant | 0.4362 (MPa) |
| K1 | collagen type VI material constant | 14.39 |
| E2 | collagen type VI material constant | 2.025 (MPa) |
| K2 | collagen type VI material constant | 43.96 |
| η | Collagen type VI viscoelasticity dashpot constant | 1.532 ×105 (MPa s) |
| Chondrocyte | ||
| nf,0 | Initial Fluid Volume Fraction | 0.83 |
| EChondrocyte | Young’s modulus | 0.0007 (MPa) |
| VChondrocyte | Poison’s ratio | 0.4 |
| KChondrocyte | Permeability (constant) | 0.5×10−14 m4/N s |
Figure 2.
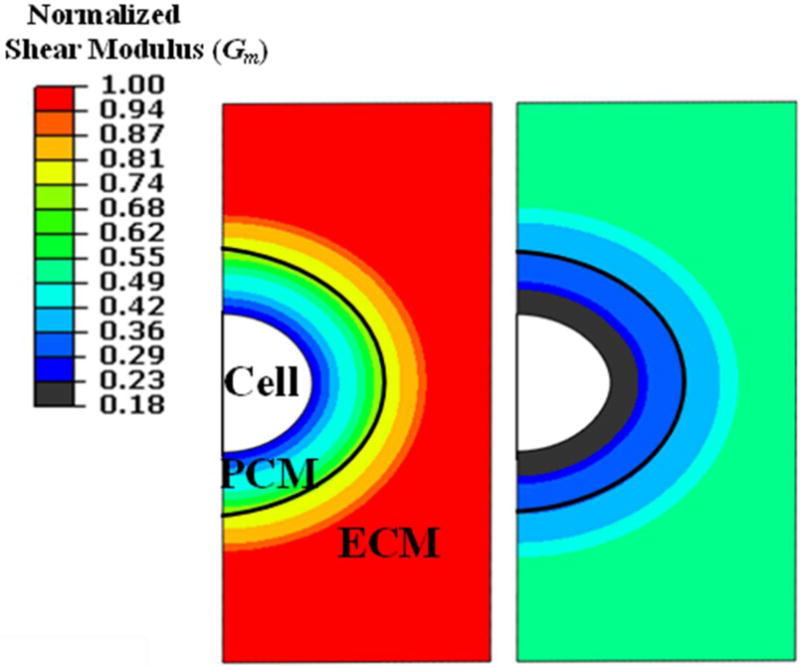
Spatial variation of the shear modulus from PCM inner edge towards ECM in the micro-OA condition (right) is different from that in the healthy condition (left). The shear modulus is normalized to that of normal ECM.
Solution approach
Galerkin method, direct equation solver and Full Newton solution technique were employed. 8-node axisymmetric quadrilateral, biquadratic displacement, bilinear pore pressure elements were used. A mesh refinement study was performed by reducing by increasing the number of elements to a level that the results were independent of the mesh resolution. Based on the mesh refinement study, the number of element of the macroscale and microsclae models were 3069 and 13064, respectively.
Results
At the macro-scale
At the macro-scale, a highly non- homogeneous strain field was induced in the healthy and OA models (Fig. 3). The magnitude of the tensile (Fig. 3a) and compressive (Fig. 3b) strains throughout the depth of the tissue were variable between each case, with largest tensile and compressive strains occurring in the superficial zone. In the middle zone of the healthy cartilage model (Case 1), tensile strain of 6% and compressive strain of 12% were induced. In OA cartilage (Case 2) these strains were 9% and 17%, respectively, an increase of 50% and 41% strains in the OA explant compared to those in the healthy explant.
Figure 3.
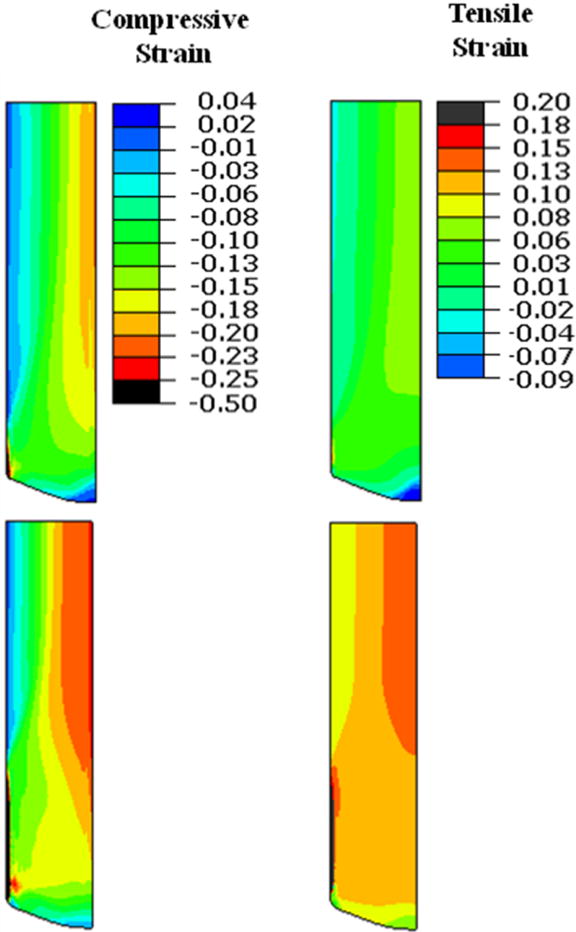
Depth-dependent variations in tensile (a) and compressive (b) strains at the macro-scale in the normal (left) and OA (right) explants.
At the micro-scale
At the micro-scale, the distribution of the shear strains through the cell-ECM-PCM structure was different between all cases (Fig 4). In particular, peak shear strains for the normal cartilage model (Case 1) were concentrated within the PCM region (Fig 4a). However, in Case 2 and 3 there were elevated shear strains in part of the chondrocyte periphery (Fig. 4b and 4c). In contrast, the distributions of the compressive and tensile strains were consistent between all three Cases (Fig. 5 and 6). In particular, (i) the compressive and tensile strains were amplified within the chondrocyte, (ii) the intersecting boundary region between the chondrocyte and PCM had the highest strains, and (iii) the central region of the chondrocyte had lower compressive and tensile strains compared to its periphery.
Figure 4.
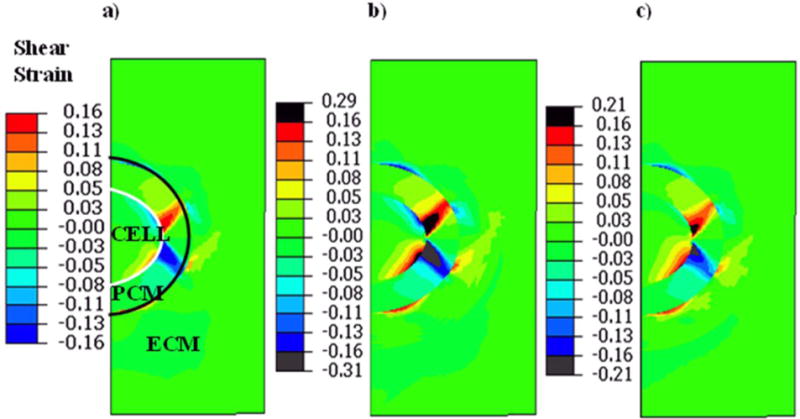
Shear strains induced within the chondrocyte and PCM in Case 1 (a) Case 2 (b), and Case 3 (c). The shear strains are increased in OA (Case 2) and early OA (Case 3) conditions as compared to the healthy condition (Case 1). Note that black regions in Case 2 and Case 3 show strains values which exceed those in the healthy cartilage (Case 1). Also note that the peak strains induced in each case is different as indicated by the corresponding legends.
Figure 5.
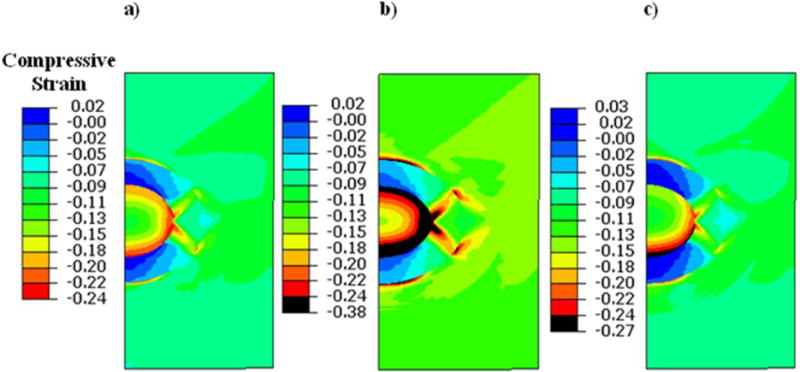
Compressive strains induced within the chondrocyte and PCM in Case 1 (a) Case 2 (b), and Case 3 (c). The compressive strains are elevated in OA (Case 2) and early OA (Case 3) conditions as compared to the healthy condition (Case 1).
Figure 6.
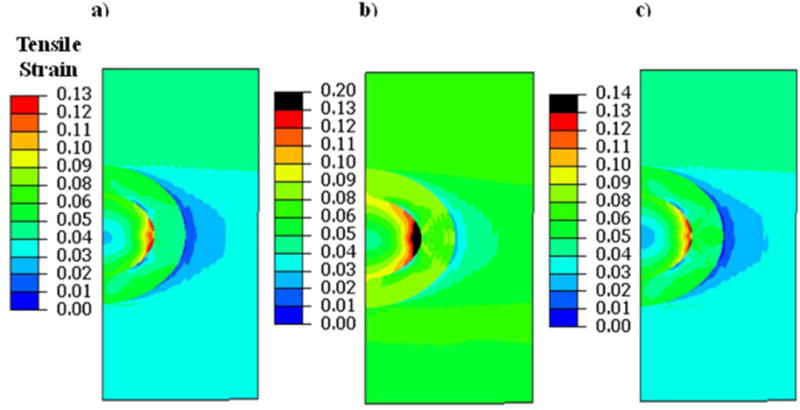
Tensile strains induced within the chondrocyte and PCM in Case 1 (a) Case 2 (b), and Case 3 (c). The tensile strains are increased in OA (Case 2) as compared to the healthy condition (Case 1).
In the healthy cartilage model (Case 1), the chondrocyte had a peak shear strain of 13%, which was localized to the internal periphery of the chondrocyte (Fig. 4a). The compressive and tensile strains had peak magnitudes of 24% (Fig. 5a) and 13% (Fig. 6a), respectively, which were concentrated at the intersecting boundary region between the chondrocyte and PCM. The central region of the chondrocyte had less strains compared to its periphery.
In the OA cartilage model (Case 2), substantially higher strain magnitudes were induced in the chondrocyte when compared to Case 1. Peak shear strains increased to 31% at the PCM region and the peripheral area of the chondrocyte at its periphery also had high shear strains of up to 22% (Fig. 4b). Peak compressive strain increased to 38% in PCM region and 32% in the chondrocyte (Fig. 5b), and peak tensile strain increased to 20% in the chondrocyte (Fig. 6b).
In the early-stage OA model (Case 3), peak shear strain was 21% at the PCM region while a region close to the periphery of the chondrocyte had a shear strain of 17% (Fig. 4a). Peak compressive strain was 27% (Fig. 4b) and peak tensile strain was 14% (Fig. 4c).
Discussion
We studied the influence of macro- and micro-scale OA-associated structural changes on chondrocyte deformations using a multi-scale, biphasic, swelling, fiber-reinforced, nonlinear computational model of adult articular cartilage, subjected to unconfined compressive load. At the macro-scale, we found that a depth-dependent strain field was induced in healthy and OA cartilage, and that the superficial and middle zones of OA cartilage experience increased tensile and compressive strains compared to healthy cartilage. At the micro-scale, we found that chondrocyte shear strains were sensitive to PCM and local ECM properties. In particular, micro-scale spatial softening of PCM and ECM resulted in a substantial increase (by up to 30%) in chondrocyte shear strain, even with no structural change in macro-scale tissue properties, leading us to accept our hypothesis. When macro-scale and micro-scale structural changes were present in the OA model, there were 70%, 53% and 33% higher shear, tensile and compressive strains in the chondrocyte, respectively.
The factors that affect the mechanobiological response of chondrocytes are still being understood.4–6 In vitro studies have found that eexcessive compressive strains can result in mechanical injury to chondrocyte, leading to reduced remodelling, maintenance and repair,31–33 although the magnitude of strain that is deemed excessive, is highly variable across studies.34–35 The mechanical mechanisms driving chondrocyte responses to deformations are difficult to study using in vitro modeling systems. To avoid the limitations associated with in vitro tests, computational models of the micromechanical environment of chondrocytes have been used.7,20,21,36–39 These studies have suggested that collagen orientation and depth-dependent negative fixed charge densities of articular cartilage can modulate the mechanical environment in the vicinity of chondrocytes.38 It has also been found that tissue level changes in the ECM (e.g. fibrillation of the superficial zone of cartilage) cause cell volume increase in OA cartilage under compressive loads.21 Furthermore, it is suggested that at the cellular level, the PCM plays an important role in regulating chondrocyte strains and exhibits a significant stress shielding effect.7 However, the micro-scale spatial inhomogeneities in ECM and PCM modulus which were recently revealed in atomic force microscopy studies,10 have not been included in these micro-scale computational models.
The cartilage material model adopted in the present study has previously been validated and used for studies at macroscopic24,25,40,41 and microscopic scales.20,21,36–39 The predictions of cell deformations using our multi-scale method have also been compared to experimentally quantified axial deformations of chondrocytes embedded in agarose gel.42,43 In the current study, we used our macro-scale finite element model to determine the strain field throughout healthy cartilage. By changing the properties of the ECM (i.e. collagen content, shear modulus of the ECM ground substance and permeability) we simulated an osteoarthritic-like cartilage explant. Using a multi-scale approach, the strains obtained from the macro-scale model were used as inputs to the micro-scale model, which included a representation of the cell, the PCM and the local ECM. In doing so, we could mimic changes at the PCM and local ECM level,10 both of which are reported to occur prior to macro-tissue level changes,11 and thereby mimic the early stages of OA.
Consistent with previous studies7 we found that in healthy cartilage the PCM amplifies compressive strains in chondrocytes located at the middle zone of cartilage. In OA cartilage, however, our results indicate that the level of strain amplification is increasing and results in the induction of high compressive strains on chondrocytes. Excessive magnitudes of compression have been shown to result in mechanical injury to cells.32 Injurious magnitudes of deformation activate proinflammatory mediators and ultimately catabolic pathways that lead to cartilage degeneration.4 Further to these insights, our study also indicated that in healthy cartilage shear strains are attenuated by the PCM and as a result can shield the chondrocytes from distortional deformations. Yet in the OA cartilage models, where loss of structural properties in ECM and PCM occurred, chondrocytes were not as effectively protected against excessive shear strains. Of interest, increases in shear stresses have been shown to lead to increased release of nitric oxide, a reactive oxygen metabolite implicated in joint pathogenesis.44,45 It has also been found that the exposure of human osteoarthritic chondrocytes to a continuously applied shear stress upregulated nitric oxide synthase gene expression and increased nitric oxide release. In yet another study it was reported that increased shear strains applied to isolated human chondrocytes resulted in increased glycosaminoglycan synthesis, longer chondroitin sulfate glycosaminoglycan chains, and elevated expression of interleukin-6 (markers typical of osteoarthritic cartilage).46 Given the increase in chondrocyte shear strains in OA cartilage observed in our study, we suggest that when the effects of cell deformations on their biological response are computationally or experimentally investigated, shear strains as well as compressive and tensile strains should be determined, reported, and analyzed. In the literature, the physiological significance of shear vs. compressive or tensile strains has not been explored in a consistent setting yet. Future studies may shed more lights on relative influence of these strains on cellular activities.
In our study, OA cartilage was modeled by altering three parameters of collagen content, matrix stiffness, and permeability at the tissue level which are believed to be the most influential and prominent parameters affected in OA cartilage as compared to normal cartilage.4,12 Alteration in some other parameters may be captured by the changed parameters. For example, the reduction in collagen stiffness may have similar effects on stress and strains as the reduction in the collagen content. Similarly, the reduction in water content may have a similar effect on stresses and strains as an increase in permeability or decrease in stiffness. A comprehensive parametric study is required to isolate the influence of variations in all possible material parameters on the mechanical behavior of OA cartilage, but was beyond the scope of the current study.
A limitation to this study and other modeling studies20,30 is that the chondrocyte was idealized as a homogeneous continuum.47 Models incorporating sub-cellular components, such as the nucleus and cytoskeletal fibers, may provide further insights into intracellular mechanotransduction mechanisms.48 For such models, the assumption of continuous attachment between chondrocytes and their environment could also be updated to discrete focal cell-matrix attachment sites.49 Direct validation of chondrocyte strains in the cartilage ECM have yet to be performed and may become more feasible in the near future with new developments in the field.50 Finally, we focused on analyzing the micromechanical environment of chondrocytes located in the middle zone of the cartilage under unconfined compression. Given the depth-varying non-homogeneous strain field that was induced in both healthy and OA conditions, the effects of depth-wise variations in the chondrocyte shapes and PCM thickness and properties on chondrocyte deformations should be accounted for in future studies.
Conclusion
In conclusion, our multiscale computational model incorporated detailed cartilage ultrastructure as well as spatially varying microstructural mechanical properties of the PCM and ECM to reflect those found in healthy and OA cartilage. We found that in early stages of OA, independent of the macro-scale structural degradation, microstructural changes at the cellular level may substantially change the transfer of tissue-level loads to the chondrocytes. This finding suggests that micromechanical changes at the cellular level may affect chondrocyte activities before macro-scale degradations at the tissue level become apparent.
Acknowledgments
Research reported in this publication was supported in part by the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the National Institutes of Health under Award Numbers AR057343 and AR066635. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. We thank the Russell Warren Chair in Tissue Engineering for their support of this research.
Footnotes
Author Contribution Statement: All authors were involved in the study design, interpretation of data, and drafting/revising the paper. Mehdi Khoshgoftar created and ran the Finite Element Models. He helped to interpret the data and wrote the manuscript. Peter Torzilli helped with study design, data interpretation, and manuscript writing and editing. Suzanne Maher helped with study design, data interpretation, and manuscript writing and editing.
References
- 1.Poole CA, Matsuoka A, Schofield JR. Chondrons from Articular Cartilage .3. Morphologic Changes in the Cellular Microenvironment of Chondrons Isolated from Osteoarthritic Cartilage. Arthritis Rheum. 1991;34(1):22–35. doi: 10.1002/art.1780340105. [DOI] [PubMed] [Google Scholar]
- 2.Wilusz RE, Sanchez-Adams J, Guilak F. The structure and function of the pericellular matrix of articular cartilage. Matrix Biol. 2014;39(2014):25–32. doi: 10.1016/j.matbio.2014.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zelenski NA, Leddy HA, Sanchez-Adams J, et al. Type VI collagen regulates pericellular matrix properties, chondrocyte swelling, and mechanotransduction in mouse articular cartilage. Arthritis Rheumatol. 2015;67(5):1286–1294. doi: 10.1002/art.39034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sanchez-Adams J, Leddy HA, McNulty AL, et al. The mechanobiology of articular cartilage: bearing the burden of osteoarthritis. Curr Rheumatol Rep. 2014;16(10):451. doi: 10.1007/s11926-014-0451-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Quinn TM, Grodzinsky AJ, Hunziker EB, Sandy JD. Effects of injurious compression on matrix turnover around individual cells in calf articular cartilage explants. J Orthop Res. 1998;16(4):490–499. doi: 10.1002/jor.1100160415. [DOI] [PubMed] [Google Scholar]
- 6.McCulloch RS, Ashwell MS, Maltecca C, et al. Progression of Gene Expression Changes following a Mechanical Injury to Articular Cartilage as a Model of Early Stage Osteoarthritis. Arthritis. 2014;2014:1–9. doi: 10.1155/2014/371426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Alexopoulos LG, Setton La, Guilak F. The biomechanical role of the chondrocyte pericellular matrix in articular cartilage. Acta Biomater. 2005;1:317–325. doi: 10.1016/j.actbio.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 8.Setton LA, Mow VC, Müller FJ, et al. Mechanical Properties of Canine Articular Cartilage Are Significantly Altered Following Transection of the Anterior Cruciate Ligament. J Orthop Res. 1994;12(4):451–463. doi: 10.1002/jor.1100120402. [DOI] [PubMed] [Google Scholar]
- 9.Alexopoulos LG, Williams GM, Upton ML, et al. Osteoarthritic changes in the biphasic mechanical properties of the chondrocyte pericellular matrix in articular cartilage. J Biomech. 2005;38(3):509–517. doi: 10.1016/j.jbiomech.2004.04.012. [DOI] [PubMed] [Google Scholar]
- 10.Wilusz RE, Zauscher S, Guilak F. Micromechanical mapping of early osteoarthritic changes in the pericellular matrix of human articular cartilage. Osteoarthr Cartil. 2013;21(12):1895–1903. doi: 10.1016/j.joca.2013.08.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Workman J, Thambyah A, Broom N. The influence of early degenerative changes on the vulnerability of articular cartilage to impact-induced injury. Clin Biomech. 2017;43:40–49. doi: 10.1016/j.clinbiomech.2017.01.003. [DOI] [PubMed] [Google Scholar]
- 12.Alexopoulos LG, Setton LA, Guilak F. The biomechanical role of the chondrocyte pericellular matrix in articular cartilage. Acta Biomater. 2005;1:317–325. doi: 10.1016/j.actbio.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 13.Lee DA, Bader DL. Compressive strains at physiological frequencies influence the metabolism of chondrocytes seeded in agarose. J Orthop Res. 1997;15:181–188. doi: 10.1002/jor.1100150205. [DOI] [PubMed] [Google Scholar]
- 14.Guilak F, Alexopoulos LG, Upton ML, et al. The pericellular matrix as a transducer of biomechanical and biochemical signals in articular cartilage. Ann N Y Acad Sci. 2006;1068:498–512. doi: 10.1196/annals.1346.011. [DOI] [PubMed] [Google Scholar]
- 15.Knudson W, Loeser RF. CD44 and integrin matrix receptors participate in cartilage homeostasis. Cell Mol life Sci C. 2002;59:36–44. doi: 10.1007/s00018-002-8403-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lee V, Cao L, Zhang Y, et al. The roles of matrix molecules in mediating chondrocyte aggregation, attachment, and spreading. J Cell Biochem. 2000;79:322–333. doi: 10.1002/1097-4644(20001101)79:2<322::aid-jcb150>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- 17.Julkunen P, Wilson W, Jurvelin JS, Korhonen RK. Composition of the pericellular matrix modulates the deformation behaviour of chondrocytes in articular cartilage under static loading. Med Biol Eng Comput. 2009;47(12):1281. doi: 10.1007/s11517-009-0547-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Haider MA, Schugart RC, Setton LA, Guilak F. A mechano-chemical model for the passive swelling response of an isolated chondron under osmotic loading. Biomech Model Mechanobiol. 2006;5(2–3):160–171. doi: 10.1007/s10237-006-0026-1. [DOI] [PubMed] [Google Scholar]
- 19.Vincent TL, Hermansson MA, Hansen UN, et al. Basic Fibroblast Growth Factor Mediates Transduction of Mechanical Signals When Articular Cartilage Is Loaded. Arthritis Rheum. 2004;50(2):526–533. doi: 10.1002/art.20047. [DOI] [PubMed] [Google Scholar]
- 20.Julkunen P, Wilson W, Isaksson H, et al. A review of the combination of experimental measurements and fibril-reinforced modeling for investigation of articular cartilage and chondrocyte response to loading. Comput Math Methods Med. 2013;2013:326150. doi: 10.1155/2013/326150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tanska P, Turunen SM, Han SK, et al. Superficial collagen fibril modulus and pericellular fixed charge density modulate chondrocyte volumetric behaviour in early osteoarthritis. Comput Math Methods Med. 2013;2013:164146. doi: 10.1155/2013/164146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kim E, Guilak F, Haider MA. The dynamic mechanical environment of the chondrocyte: a biphasic finite element model of cell-matrix interactions under cyclic compressive loading. J Biomech Eng. 2008;130:61009. doi: 10.1115/1.2978991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wilson W. Stresses in the local collagen network of articular cartilage: a poroviscoelastic fibril-reinforced finite element study. J Biomech. 2004;37:357–366. doi: 10.1016/s0021-9290(03)00267-7. [DOI] [PubMed] [Google Scholar]
- 24.Wilson W, Huyghe JM, Van Donkelaar CC. Depth-dependent compressive equilibrium properties of articular cartilage explained by its composition. Biomech Model Mechanobiol. 2007;6:43–53. doi: 10.1007/s10237-006-0044-z. [DOI] [PubMed] [Google Scholar]
- 25.Wilson W, Huyghe JM, Van Donkelaar CC. A composition-based cartilage model for the assessment of compositional changes during cartilage damage and adaptation. Osteoarthr Cartil. 2006;14:554–560. doi: 10.1016/j.joca.2005.12.006. [DOI] [PubMed] [Google Scholar]
- 26.Quiroga JMP, Wilson W, Ito K, van Donkelaar CC. Relative contribution of articular cartilage’s constitutive components to load support depending on strain rate. Biomech Model Mechanobiol. 2017;16(1):151–158. doi: 10.1007/s10237-016-0807-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ehlers W, Karajan N, Markert B. An extended biphasic model for charged hydrated tissues with application to the intervertebral disc. Biomech Model Mechanobiol. 2009;8(3):233–251. doi: 10.1007/s10237-008-0129-y. [DOI] [PubMed] [Google Scholar]
- 28.Huyghe JM, Houben GB, Drost MR, Van Donkelaar CC. An ionised/non-ionised dual porosity model of intervertebral disc tissue. Biomech Model Mechanobiol. 2003;2:3–19. doi: 10.1007/s10237-002-0023-y. [DOI] [PubMed] [Google Scholar]
- 29.Jones WR, Ting-Beall HP, Lee GM, et al. Alterations in the Young’s modulus and volumetric properties of chondrocytes isolated from normal and osteoarthritic human cartilage. J Biomech. 1999;32:119–127. doi: 10.1016/s0021-9290(98)00166-3. [DOI] [PubMed] [Google Scholar]
- 30.Guilak F, Mow VC. The mechanical environment of the chondrocyte: a biphasic finite element model of cell–matrix interactions in articular cartilage. J Biomech. 2000;33:1663–1673. [PubMed] [Google Scholar]
- 31.Wong BL, Bae WC, Chun J, et al. Biomechanics of cartilage articulation: Effects of lubrication and degeneration on shear deformation. Arthritis Rheum. 2008;58(7):2065–2074. doi: 10.1002/art.23548. [DOI] [PubMed] [Google Scholar]
- 32.Loening AM, James IE, Levenston ME, et al. Injurious Mechanical Compression of Bovine Articular Cartilage Induces Chondrocyte Apoptosis. Arch Biochem Biophys. 2000;381(2):205–212. doi: 10.1006/abbi.2000.1988. [DOI] [PubMed] [Google Scholar]
- 33.Chen CT, Bhargava M, Lin PM, Torzilli PA. Time, stress, and location dependent chondrocyte death and collagen damage in cyclically loaded articular cartilage. J Orthop Res. 2003;21(5):888–898. doi: 10.1016/S0736-0266(03)00050-0. [DOI] [PubMed] [Google Scholar]
- 34.Wong M, Siegrist M, Cao X. Cyclic compression of articular cartilage explants is associated with progressive consolidation and altered expression pattern of extracellular matrix proteins. Matrix Biol. 1999;18(4):391–399. doi: 10.1016/s0945-053x(99)00029-3. [DOI] [PubMed] [Google Scholar]
- 35.Widmyer MR, Utturkar GM, Leddy HA, et al. High body mass index is associated with increased diurnal strains in the articular cartilage of the knee. Arthritis Rheum. 2013;65(10):2615–2622. doi: 10.1002/art.38062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Korhonen RK, Han S-K, Herzog W. Osmotic loading of articular cartilage modulates cell deformations along primary collagen fibril directions. J Biomech. 2010;43:783–787. doi: 10.1016/j.jbiomech.2009.10.022. [DOI] [PubMed] [Google Scholar]
- 37.Turunen SM, Han SK, Herzog W, Korhonen RK. Cell deformation behavior in mechanically loaded rabbit articular cartilage 4 weeks after anterior cruciate ligament transection. Osteoarthr Cartil. 2013;21:505–513. doi: 10.1016/j.joca.2012.12.001. [DOI] [PubMed] [Google Scholar]
- 38.Korhonen RK, Julkunen P, Wilson W, Herzog W. Importance of collagen orientation and depth-dependent fixed charge densities of cartilage on mechanical behavior of chondrocytes. J Biomech Eng. 2008;130:21003. doi: 10.1115/1.2898725. [DOI] [PubMed] [Google Scholar]
- 39.Korhonen RK, Herzog W. Depth-dependent analysis of the role of collagen fibrils, fixed charges and fluid in the pericellular matrix of articular cartilage on chondrocyte mechanics. J Biomech. 2008;41:480–485. doi: 10.1016/j.jbiomech.2007.09.002. [DOI] [PubMed] [Google Scholar]
- 40.Julkunen P, Wilson W, Jurvelin JS, et al. Stress-relaxation of human patellar articular cartilage in unconfined compression: prediction of mechanical response by tissue composition and structure. J Biomech. 2008;41:1978–1986. doi: 10.1016/j.jbiomech.2008.03.026. [DOI] [PubMed] [Google Scholar]
- 41.Julkunen P, Kiviranta P, Wilson W, et al. Characterization of articular cartilage by combining microscopic analysis with a fibril-reinforced finite-element model. J Biomech. 2007;40:1862–1870. doi: 10.1016/j.jbiomech.2006.07.026. [DOI] [PubMed] [Google Scholar]
- 42.Khoshgoftar M, Ito K, van Donkelaar CC. The Influence of Cell-Matrix Attachment and Matrix Development on the Micromechanical Environment of the Chondrocyte in Tissue-Engineered Cartilage. Tissue Eng Part A. 2014;20(23–24):3112–3121. doi: 10.1089/ten.TEA.2013.0676. [DOI] [PubMed] [Google Scholar]
- 43.Lee DA, Bader L. The development and characterization of anin vitro system to study strain-induced cell deformation in isolated chondrocytes. In Vitro Cellular & Developmental Biology-Animal. 1995;31(11):828–835. doi: 10.1007/BF02634565. [DOI] [PubMed] [Google Scholar]
- 44.Lee MS, Trindade MCD, Ikenoue T, et al. Effects of shear stress on nitric oxide and matrix protein gene expression in human osteoarthritic chondrocytes in vitro. J Orthop Res. 2002;20(3):556–61. doi: 10.1016/S0736-0266(01)00149-8. [DOI] [PubMed] [Google Scholar]
- 45.Smith RL, Carter DR, Schurman DJ. Pressure and shear differentially alter human articular chondrocyte metabolism: a review. Clin Orthop Relat Res. 2004;427(Suppl):S89–S95. [PubMed] [Google Scholar]
- 46.Lane Smith R, Trindade MC, Ikenoue T, et al. Effects of shear stress on articular chondrocyte metabolism. Biorheology. 2000;37(1–2):95–107. [PubMed] [Google Scholar]
- 47.Durrant LA, Archer CW, Benjamin M, Ralphs JR. Organisation of the chondrocyte cytoskeleton and its response to changing mechanical conditions in organ culture. J Anat. 1999;194(3):343–353. doi: 10.1046/j.1469-7580.1999.19430343.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Slomka N, Gefen A. Finite Element Modeling of Cellular Mechanics Experiments. Stud Mechanobiol Tissue Eng Biomater. 2011;4:331–344. [Google Scholar]
- 49.Gilmore AP, Burridge K. Molecular mechanisms for focal adhesion assembly through regulation of protein-protein interactions. Struct London Engl. 1996;4:647–51. doi: 10.1016/s0969-2126(96)00069-x. [DOI] [PubMed] [Google Scholar]
- 50.Bartell LR, Fortier LA, Bonassar LJ, Cohen I. Measuring microscale strain fields in articular cartilage during rapid impact reveals thresholds for chondrocyte death and a protective role for the superficial layer. J Biomech. 2015;48(12):3440–3446. doi: 10.1016/j.jbiomech.2015.05.035. [DOI] [PMC free article] [PubMed] [Google Scholar]


