Material Properties of the Brain in Injury-Relevant Conditions – Experiments and Computational Modeling

Abstract

Material properties of the brain have been extensively studied but remain poorly characterized. The vast variations in constitutive models and material constants are well documented. However, no study exists to translate the variations into disparities in impact-induced brain strains most relevant to brain injury. Here, we reviewed a subset of injury-relevant brain material properties either characterized in experiments or adopted in recent head injury models. To highlight how variations in measured brain material properties manifested in simulated brain strains, we selected six experiments that have provided a complete set of brain material model and constants to implement a common head injury model. Responses resulting from two extreme head impacts representing a high-rate concussive event and a low-rate in vivo head rotation, respectively, varied substantially. We hypothesized, and further confirmed, that the time-varying shear moduli at the appropriate time scales (e.g., ~5 ms and ~40 ms corresponding to the impulse durations of the major acceleration peaks for the two impacts, respectively), rather than the initial or long-term shear moduli, were the most indicative of impact-induced brain strains. These results underscored the need to implement measured brain material properties into an actual head injury model for evaluation. They may also provide guidelines to better characterize brain material properties in future experiments and head injury models. Finally, our finding provided a practical solution to satisfy head injury model validation requirements at both ends of the impact severity spectrum. This would improve the confidence in model simulation performance across a range of time scales relevant to concussion and sub-concussion in the real-world.

Graphical abstract

1. Introduction

The brain is arguably the most important and most complex organ in our body that determines who we are. Understanding its mechanical properties across length scales from individual neurons to the whole brain (Goriely et al., 2015a) is crucial to the investigation of neuromechanics in a multitude of disciplines including neurodevelopment, disease, and injury (Goriely et al., 2015b). The brain mechanical properties are well known to be heterogeneous and anisotropic in the white matter (WM), and are characterized both by time-independent hyperelasticity and time-dependent viscoelasticity (de Rooij and Kuhl, 2016). Mechanical modeling of the brain, for example, via appropriate constitutive models, is central to bridging brain mechanical responses across length and time scales to synthetize information important to regulate brain structure and function (Goriely et al., 2015b; Lytton et al., 2017). One key area necessitating such applications is to develop a biofidelic computational head injury model to investigate the mechanisms of traumatic brain injury (TBI).

TBI is well recognized as a worldwide health and socioeconomic problem (Meaney et al., 2014; Peden et al., 2004). In the United States alone, 1.6–3.8 million new cases of TBI are estimated to occur each year, amounting to an economic burden of over $60 billion in associated direct and indirect costs (Daneshvar et al., 2011; Langlois et al., 2006). Much of the work in TBI biomechanics has so far focused on developing a scalar kinematic variable to characterize head impact severity and to predict the occurrence of injury (Yang et al., 2006). The use of linear and/or rotational acceleration peak magnitude is ubiquitous. Numerous more advanced variants have also been developed. However, a critical and inherent limitation of these empirical scalar injury metrics is their inability to inform regional brain deformation such as strain and strain rate thought to cause injury (King et al., 2003). Consequently, while they are effective in mitigating moderate-to-severe brain injury risks and incident rates such as in automobile crashes, they are likely insufficient to study mild TBI (mTBI), including concussion, that presents wide-spread neuroimaging alterations (Bigler, 2016) and a diverse spectrum of clinical signs and symptoms (Duhaime et al., 2012). Presumably, these clinical observations are a result of mechanical insult to specific anatomical regions and/or structural and functional networks of the brain. Not surprisingly, a recent study has questioned the clinical utility of simple kinematic impact indicators such as linear acceleration peak magnitude in sports concussion (Mihalik et al., 2017). These concerns are likely to grow even further, given the cumulative effects from repetitive sub-concussive head impacts now starting to be realized (Bahrami et al., 2017; Talavage et al., 2014).

There is consensus that a computational head injury model is a critical tool to bridge the gap between head external impacts and tissue/cellular tolerance criterion to assess brain injury risk (Goriely et al., 2015b; Meaney et al., 2014). A computational head injury model is composed of three basic constituents: model geometry, boundary conditions, and tissue material properties. With properly measured impact loading conditions as input for simulation, whole-brain mechanical responses can then be estimated. The accuracy of model geometry can be quantified by comparing its mesh with high-resolution neuroimaging (Ji et al., 2015). Some inconsistencies exist in handling the brain-skull boundary conditions, but most models allow a certain degree of relative tangential motion at the interface, either through a frictional boundary condition (Kleiven, 2007), or by incorporating a soft cerebrospinal fluid layer with either a low shear modulus (Ji et al., 2015; Mao et al., 2013; Takhounts et al., 2008) or an equation of state (Garimella and Kraft, 2016). However, much larger variations exist in material properties of the brain. In fact, there is no consensus on even what type of material constitutive model to adopt (de Rooij and Kuhl, 2016; Yang et al., 2006), or, for a given material model, what material property constants to use.

The vast variations in brain material properties are documented in abundant literature reviews. They focus on comparison of raw data from various test methods and conditions (Cheng et al., 2008), in vitro test conditions (Hrapko et al., 2008), comparison between in vitro and in vivo tests (Chatelin et al., 2010), imaging techniques such as magnetic resonance elastography (MRE; (Bayly et al., 2012; Di Ieva et al., 2010)), and on constitutive models (de Rooij and Kuhl, 2016; van Dommelen et al., 2009). Another review also compared the diverse spectrum of brain material properties adopted in human and animal head injury models (Yang et al., 2006). However, no study exists to translate these vast variations into disparities in estimated brain strains that are most relevant to injury prediction.

A recent study parametrically identified significant differences in estimated regional brain mechanical responses from three “validated” finite element head models (Ji et al., 2014). However, the selected models differed not only in brain material properties, but also in head size and geometry, brain-skull boundary conditions, mesh resolution, and even in simulation software package. It was infeasible to isolate the effect of brain material properties, even though this was critical for providing insight into how this crucial injury model component affects impact-induced brain strains and subsequent injury prediction. This is important, considering that an ultimate use of brain material properties is to develop a biofidelic head injury model in the first place (in the context of TBI investigation).

There are numerous ongoing efforts to measure and characterize brain material properties, both analytically and experimentally (de Rooij and Kuhl, 2016; Goriely et al., 2015b). Surprisingly, however, little efforts exist to translate these findings into practical applications via an actual head injury model. For example, while the brain’s hyperelasticity is well-known (de Rooij and Kuhl, 2016), quite some injury models continue to adopt linear elasticity instead (coupled with viscoelasticity; (Mao et al., 2013; Miller et al., 2016; Shigeta et al., 2009; Takhounts et al., 2008)). A viscoelasticity model limited to small strains measured over 40 years ago (Shuck and Advani, 1972) remains in active use for large strain impact simulations (Chatelin et al., 2013; Garimella and Kraft, 2016). Further, nearly all head injury models scale the brain shear modulus of a selected material model in order to satisfy model validation, rather than applying the measured properties directly. To some degree, this would defeat the purpose of experimental work on brain material properties in the first place. Apparently, there is a significant disconnect between material property measurement/characterization and the intended real-world applications in head impact simulation.

Unless this disconnect is resolved, the value of numerous work on brain material properties would be significantly undermined. As a first step to bridge the gap, we conducted the following study to link measured brain material properties with other brain biomechanics data at both high- and low-rates used for head injury model validation. This allowed understanding how brain material properties influence brain strains via an actual head injury model across time scales relevant to concussion and sub-concussion in the real-world. This study has three components. First, we review a subset of experiments that characterize brain material properties relevant to brain injury, as well as brain material properties adopted in recent head injury models. Based on the review, representative material models are selected and implemented into a common head injury model for response comparison. Finally, we parametrically identify that the time-varying shear modulus at the appropriate time scales for a given impact is the most indicative of the induced brain strains. The latter effort is important, as it potentially offers a practical solution to enable future head injury models for applications across a spectrum of head impact severities, rather than being limited to only high-rates in most current injury models. Such a further model advancement is critical to investigate the cumulative effects of sub-concussive head impacts that are emerging as an important contributor to neural health (Bahrami et al., 2017; Talavage et al., 2014).

We expect that our findings will shed important insights into how experimentally measured brain material properties perform in an actual head injury model for impact simulation. They may also provide guidelines for future experiments as well as development of head injury models how best to yield reliable brain responses across a range of time scales and impact conditions. This is an important and timely contribution to bridge the gaps among isolated efforts in material property characterization, brain biomechanics for head injury model validation, real-world head impacts, and the ultimate use of head injury models for a concerted effort to study TBI in the future.

2. Materials and Methods

2.1 Experimentally Characterized Brain Material Properties Relevant to Brain Injury

There are numerous experimental studies characterizing in vitro and in vivo brain tissue samples with an array of test conditions and tissue preparation protocols (Chatelin et al., 2010; Cheng et al., 2008). Here, we limit our review only to studies that provide either the time-independent hyperelastic or time-dependent viscoelastic properties relevant to blunt head impact modeling. Table 1 briefly summarizes their main findings relevant to our study, their limitations/caveats or other notes, and their applications in head injury models.

Table 1.

Summary of the previous experimental studies (listed chronologically) related to simulations of blunt head impacts. The more recent experimental work has not yet been incorporated into a head injury model.

Experimental study	Main findings related to modeling	Limitations, caveats, or other notes	Applications in head injury models
(Shuck and Advani, 1972)	Dynamic shear tests on human brain tissue; Viscoelastic model with two-term Prony series	Limited to small strains (1.3%)	(Chatelin et al., 2013; Garimella and Kraft, 2016)
(Mendis et al., 1995)	Used Abaqus to fit previous test data; Mooney-Rivlin hyperelastic and viscoelastic models	Shear modulus overly stiff	Used in early head injury models (Yang et al., 2006); had to be scaled to 10% (Kleiven and Hardy, 2002)
(Prange and Margulies, 2002) (Gefen and Margulies, 2004)	Shear tests on porcine and fresh human cortex; First-order Ogden model with two-term Prony series; Extended to indentation relaxation to derive linear viscoelastic models	Low strain rates (up to 8.33/s and 3 mm/s, respectively); WM more compliant than GM but opposed to some other findings	Scaled to use in an infant (Coats et al., 2007) and a pig head (Sullivan et al., 2014) model
(Nicolle et al., 2004) and (Nicolle et al., 2005)	Stress-strain isochrones on porcine WM; Third-order Ogden hyperelastic model; Oscillatory shear for viscoelasticity over an extensive frequency range, fitted to a 5 or 8-term Prony series	Limited to low strain levels; No significant difference between viscoelastic behaviors of porcine and human brain tissue; WM and GM similar at small strains	Data refitted into a 6-term Prony series (Kleiven, 2007); Adopted in (Ji et al., 2015; Kleiven, 2007)
(Ning et al., 2006)	Shear tests on porcine brainstem at a strain rate of 25/s; Transversely isotropic hyper-viscoelastic model	No standard implementation available in Abaqus, relied on a user subroutine	Incorporated in WM anisotropy (Chatelin et al., 2013; Giordano and Kleiven, 2014a)
(Velardi et al., 2006)	Tensile tests on porcine WM at a displacement rate of 0.5 mm/s or strain rate of ~0.01/s; Transversely isotropic hyperviscoelastic model	Limited to slow strain rate; No standard implementation available in Abaqus	Incorporated in WM anisotropy (Chatelin et al., 2013; Ganpule et al., 2017; Wright et al., 2013; Wright and Ramesh, 2012)
(Franceschini et al., 2006)	Uniaxial cyclic tension and compression on human brain tissue; Second-order Ogden hyperelastic model	Quasi-static tests; observed non-linear mechanical behavior and hysteresis	Adopted in (Ji et al., 2015; Kleiven, 2007)
(Tamura et al., 2008, 2007)	Uniaxial compression and extension on fresh porcine brain; 3-term Prony series for viscoelasticity	Conducted at a number of rates and magnitudes; Long-term shear modulus not included when focusing on short time duration	N/A
(Rashid et al., 2014, 2013, 2012)	Compression, simple shear, and dynamic tension on porcine brain; First-order Ogden, Gent, Fung, and Mooney-Rivlin hyperelastic models with two-term Prony series for viscoelasticity	Conducted at a number of strain rates; A separate hyperelastic and viscoelastic model was generated for each loading condition	N/A
(Jin et al., 2013)	Tension, compression, and shear tests using post mortem human brain; Data can be used to fit a hyperelastic model	Three strain rates; No relaxation tests were conducted to derive viscoelasticity	N/A
(Feng et al., 2016)	Asymmetric indentation on porcine corpus callosum; Transversely isotropic, hyperelastic material model with two anisotropic invariants	Indentation strain rate low (~0.2/s); implementation not available in Abaqus and required user subroutine	N/A
(Finan et al., 2017)	Microindentation on healthy human brain tissue waste from epilepsy surgery; Linear viscoelastic model with two- or three-term Prony series	Property provided for each brain region and for both gender	N/A

2.2 Material Properties Implemented in Recent Head Injury Models

Material properties of the brain are a key component of a head injury model. However, there is no consensus on what material model or material constants to use for the brain. In this section, we highlight the diverse material models adopted in recent adult head injury models, as earlier or animal head injury models have been summarized previously (Yang et al., 2006). Table 2 briefly summarizes isotropic and anisotropic brain material property models used in recent head injury models. The Total HUman Model for Safety (THUMS; (Shigeta et al., 2009)), the most recent model developed by the Wayne State University, GHBMC (Mao et al., 2013), ABM (an atlas-based brain model; (Miller et al., 2016)), and SIMon (Simulated Injury Monitor; (Takhounts et al., 2008)) continue to adopt a linear viscoelastic model for the entire brain. Other models (KTH (Kleiven, 2007), University of Strasbourg model (Chatelin et al., 2013), The Worcester Head Injury Model, WHIM (Ji et al., 2015)) and work (Ganpule et al., 2017; Wright et al., 2013; Wright and Ramesh, 2012) generally employ an isotropic or an anisotropic hyperelastic model. Alternatively, (Garimella and Kraft, 2016) adopted a different strategy by explicitly modeling the axonal fiber network using an embedded method, and their brain material properties were identical to those in (Chatelin et al., 2013).

Table 2.

Summary of the brain material properties adopted in recent head injury models or modeling work

Isotropic		Anisotropic
Linear viscoelastic	Hyperviscoelastic	Puso-Weiss	Quadratic Reinforcing (Meaney, 2003)	HGO (Gasser et al., 2006)
THUMS (Shigeta et al., 2009); GHBMC (Mao et al., 2013): both assumed WM 25% stiffer than gray matter (GM), but the initial (long-term) moduli in THUMS is 67% (307%) higher than that in GHBMC ABM (Miller et al., 2016): properties were optimized by maximizing cadaveric validation performance SIMon (Takhounts et al., 2008)	KTH (Kleiven, 2007) and WHIM (Ji et al., 2015): 2nd order Ogden model based on data from (Franceschini et al., 2006); 6-term Prony viscoelasticity based on data from (Nicolle et al., 2005)	University of Strasbourg model (Chatelin et al., 2013): Mooney-Rivlin hyperelastic model based on in vivo MRE tests; WM reinforcement ratio based on both high-rate shear (Ning et al., 2006) and quasi-static tensile (Velardi et al., 2006) tests; Viscoelasticity from (Shuck and Advani, 1972)	(Wright and Ramesh, 2012): Transversely isotropic hyperelastic model based on uniaxial tensile data on porcine WM (Velardi et al., 2006)	(Giordano and Kleiven, 2014a): WM reinforcement based on highrate shear test (Ning et al., 2006); viscoelasticity same as (Kleiven, 2007); (Wright et al., 2013) (Ganpule et al., 2017): WM reinforcement based on quasi-static tensile test on porcine WM (Velardi et al., 2006)

2.3 Material Property Comparisons in Model-Estimated Brain Strain Responses

Previous review studies have summarized the diverse variations in brain material properties (Chatelin et al., 2010; Cheng et al., 2008; de Rooij and Kuhl, 2016). Here, we further extended the studies to understand how the reported variations manifested in terms of disparities in brain strain responses most relevant to brain injury prediction (King et al., 2003). The WHIM (Fig. 1 (Ji et al., 2015)) was used as a common platform to implement selected material property models. WHIM was extensively employed recently to integrate modeling with neuroimaging (Zhao et al., 2017a, 2016) and to develop a real-time simulation strategy (Ji and Zhao, 2015; Zhao et al., 2017b; Zhao and Ji, 2016). The WHIM mesh was developed based on high-resolution MRI of an individual. It had approximately 56.6 k nodes and 55.1 k hexahedral elements for the brain, with an average element size of 3.3±0.79 mm. The average distance from the WHIM brain mesh outer boundary nodes to the corresponding MRI segmented surface was 1.5±0.8 mm. Relative brain-skull tangential movement was allowed at the interface through a cerebrospinal fluid layer modeled as a soft viscoelastic medium. Except for the brain, the material property assignment for all other components remained identical to those used in previous studies.

Fig. 1.

The WHIM showing color-coded head exterior (a) and intracranial components (b). It was employed to implement a number of brain material property models to translate the diverse variation into disparities in impact-induced brain strains via a common head injury model. Except for the brain material properties, all other components of the WHIM remained identical to the baseline model reported previously (Ji et al., 2015; Zhao et al., 2016). The X, Y and Z directions correspond to posterior-anterior, right-left, and inferior-superior, respectively.

Whole-brain strains were obtained by simulating two head impacts: a cadaveric impact (Kleiven and Hardy, 2002) and an in vivo, volunteer head rotation (Sabet et al., 2008). The two sets of data have been used for model validation at the high- and low-rate conditions (Ganpule et al., 2017; Ji et al., 2015; Kleiven, 2007; Mao et al., 2013; Miller et al., 2016; Takhounts et al., 2008; Wright et al., 2013). For each selected brain material model, relative brain-skull displacements (for the cadaveric impact) and strain responses (for both) were obtained from the corresponding simulation. CORA scores were calculated by comparing with the experiments. The two selected head impacts represented extreme cases of high- and ultra-low-rate impacts corresponding to concussive and in vivo brain biomechanics far from the injury level, respectively. They provided insight into the variations in brain strain responses across a range of time scales and impact loading conditions.

2.3.1 Selection of brain material property models

The earlier review section revealed that it was typical for a given head injury model to combine fitted hyperelasticity from one study by a research group with fitted viscoelasticity from another study by another group. Yet, the material constants also had to be retroactively adjusted in order to yield a successful model validation (Kleiven, 2007; Miller et al., 2016; Sullivan et al., 2014). To avoid similarly combining different “ingredients” of brain material properties, here we selected a number of experiments that have provided a complete set of material property models and constants required for head injury model implementation. This allowed translating the originally measured brain material properties directly into a common platform for more objective comparison. Material models that required non-standard, customized user subroutines were excluded from evaluation (Feng et al., 2016; Ning et al., 2006). Table 3 compares model parameters for the selected material property models (2 linear viscoelastic and 4 hyper-viscoelastic models). For completeness, we also included a recent model derived under quasi-static conditions to investigate how, properties intended for physiological applications, perform in impact simulations (S. Budday et al., 2017b). This study fitted material properties for four brain regions under unconditioned or conditioned state either separately or simultaneously for shear, compression, and tension.

Table 3.

Brain material property models and constants from the six selected experiments. μ₀ and μ_∞: initial and long-term shear modulus, respectively; α_i: hyperelasticity parameter; g_i and τ_i: viscoelasticity parameters; GM: gray matter; WM: white matter; CR: corona radiata; C: cortex

Parameters	(Prange and Margulies, 2002)	(Tamura et al., 2008)	(Rashid et al., 2014)	(Finan et al., 2017)		(S. Budday et al., 2017b)
	Shear	Tension	Tension	Microindentation		Combined compression, tension, and shear
	1st-order Ogden hyperelastic	Linear viscoelastic	1st-order Ogden hyperelastic	Linear viscoelastic		1st-order Ogden hyperelastic
	Whole brain	Whole brain	Whole brain	GM	WM	C	CR
μ0 (Pa)	295.7	12566.9*	2780	1062.1	1811.7	2960	1940
μ∞ (Pa)	60.3	12.6	303.3	99.1	193.6	360	350
α	0.0323	N/A	6.0	N/A	N/A	−16.07	−20.80
g1	0.335	0.416	0.5663	0.603	0.637	0.601	0.608
g2	0.461	0.327	0.3246	0.169	0.256	0.277	0.211
g3	N/A	0.256	N/A	0.136	N/A	N/A	N/A
τ1 (s)	2.4	0.0096	0.0350	0.014	0.025	5.719	2.127
τ2 (s)	0.146	0.0138	0.0351	0.425	1.420	851.070	99.317
τ3 (s)	N/A	1.5080	N/A	5.290	N/A	N/A	N/A
Nicolle et al., 2004		3rd-order Ogden hyperelastic
Oscillatory shear		μ1 (Pa)	μ2 (Pa)	μ3 (Pa)	α1	α2	α3
Whole brain		1353	−1092	10.19	0.0451	−3.9	16.3
g1	g2	g3	g4	g5	g6	g7	g8
0.79	0.0958	0.0452	0.0212	0.0120	0.0036	0.0072	0.0206
τ1 (s)	τ20	τ3 (s)	τ4 (s)	τ5 (s)	τ6 (s)	τ7 (s)	τ8 (s)
1.0E-5	1.2E-04	1.2E-3	1.49E-2	0.11	1.1	11.11	333.33

^*μ₀ was calculated from the initial Young’s modulus given in (Tamura et al., 2008).

An Ogden form hyperelastic model with N-terms has the following strain energy function, U:

$$U={\sum }_{i=1}^N\frac{2{\mu }_i}{{\alpha }_i^2}({\lambda }_1^{{\alpha }_i}+{\lambda }_2^{{\alpha }_2}+{\lambda }_3^{{\alpha }_3}-3),$$ (1)

where λ_i are deviatoric principal stretches, μ_i and α_i are material constants. The viscoelasticity is expressed in an N-term Prony series:

$$\mu (t)={\mu }_0\times \left(1-{\sum }_{i=1}^N{g}_i\left(1-e^{\raisebox{1ex}{$\_t$}\!\left/ \!\raisebox{-1ex}{${\tau }_i$}\right.}\right)\right),$$ (2)

where μ₀ is the initial shear modulus, and g_i and τ_i are material constants.

Some research groups provided different material models for a range of test conditions. Only one was chosen here. For example, (Tamura et al., 2008, 2007) provided different sets of material constants for brain compression and extension at different loading rates and strain magnitudes. The one corresponding to the highest rate (25/s) and largest strain (30%) from extension was selected. Different material models/constants were also given for tension, compression, and shear in (Rashid et al., 2014, 2013, 2012). Only the one corresponding to tension at a strain rate of 30/s was chosen. For the (Finan et al., 2017) study, the properties for the average male subjects were used. For the (S. Budday et al., 2017b) study, we chose the unconditioned state for the cortex and corona radiata under the combined mode for implementation (assigned to the gray matter (GM) and WM, respectively).

Most of the studies (except for (S. Budday et al., 2017b; Finan et al., 2017) do not separately report material properties for the GM and WM. The same material properties were used for the entire brain. Three studies (S. Budday et al., 2017b; Finan et al., 2017; Prange and Margulies, 2002) reported material properties for the human brain while others were based on porcine brain tissues. We chose to use the reported properties directly without considering the possible inter-species differences because of inconsistency in finding (Nicolle et al., 2005; Prange and Margulies, 2002). Fig. 2a compares the shear relaxation moduli for the six selected brain material models.

Fig. 2.

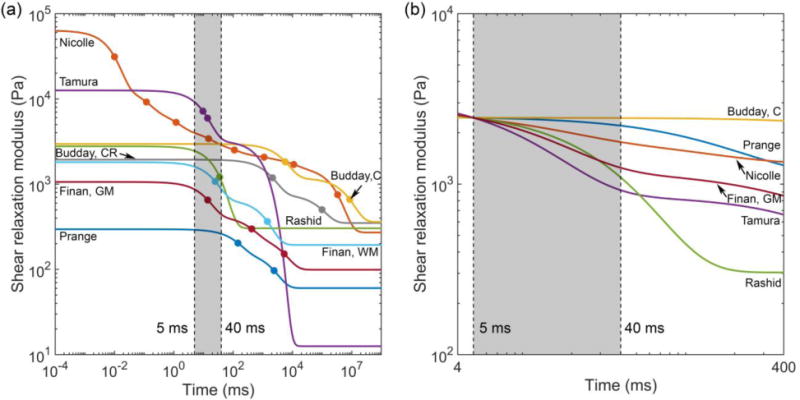
(a) Shear relaxation moduli for the 6 selected brain material models. Markers on each curve indicate the τ values used in the corresponding Prony series. For (Rashid et al., 2014), the two τ values were 0.0350 s and 0.0351 s, and the two markers virtually coincided. (b) Scaled shear relaxation moduli, where their μ₅ values (i.e., shear moduli at 5 ms) were scaled to match that of (Rashid et al., 2014) (see Section 2.4). GM: gray matter; WM: white matter; CR: corona radiata; C: cortex

2.3.2 Selection of head impacts for brain strain estimation

(Hardy et al., 2007, 2001) conducted a series of cadaveric tests to measure relative brain-skull displacements under high-rate impacts using imbedded radiopaque, neutral density targets (NDT). At the other extreme, (Sabet et al., 2008) used tagged MRI to measure 2D brain strains under low-rate head rotations in live humans. A representative parietal cadaveric impact (C291-T1; peak resultant linear/rotational acceleration magnitude of ~42.5 g/7.8 krad/s²; acceleration profile relatively “clean” with one major acceleration peak; (Kleiven, 2006; Kleiven and Hardy, 2002; Miller et al., 2017) and an in vivo head rotation (~299 rad/s²) were selected as input for model simulations. The time durations for the major acceleration peak in the two experiments were approximately 5 ms and 40 ms, respectively. Example kinematics from the two sets of experiments have been used previously to validate head injury models (Ganpule et al., 2017; Ji et al., 2016; Kleiven, 2007; Mao et al., 2013; Miller et al., 2016; Takhounts et al., 2008; Wright et al., 2013).

For all simulations, the skull and facial components were simplified as rigid bodies as they did not influence intracranial responses when the kinematics were prescribed to the rigid skull through the head center of gravity. For each selected brain material model, the resulting predicted brain-skull displacements (for the cadaveric impact) and in-plane radial-circumferential shear strains (for the in vivo head rotation) were compared with measurements. In addition, cumulative maximum principal strains for the whole brain, regardless of the time of occurrence during the course of impact, were obtained for the cadaveric impact for comparison among the six brain material models. This strain measure is often used for injury prediction (Yang et al., 2006), and is the basis for cumulative strain damage measure, CSDM (Takhounts et al., 2008) and many kinematics-based injury metrics.

2.4 Parametric scaling of brain material property based on time-varying μ_t

The initial and long-term shear moduli of the brain material properties, μ₀ and μ_∞, describe the brain’s instantaneous response and quasi-static behavior, respectively. For a given head impact with an impulse duration of t ms for the major acceleration peak, we hypothesized that the impact-induced brain strains were mostly relevant to the brain’s corresponding time-varying shear modulus at this time scale, μ_t, rather than μ₀ or μ_∞. To test the hypothesis, we scaled all material models so that their μ₅ values (i.e., shear moduli at 5 ms, corresponding to the impulse duration of ~5 ms for C291-T1) were identical to the median of the six material models (corresponding to that of (Rashid et al., 2014)). This allowed us to test whether their corresponding brain responses in the high-rate cadaveric impact were similar. Their viscoelastic Prony series parameters, g_i and τ_i, were maintained to preserve the shear relaxation moduli shapes (Fig. 2b). For both the (Finan et al., 2017) and (S. Budday et al., 2017b) material models, their GM/cortex material properties were used for the entire brain, for simplicity. With the scaled material properties, the two impacts were rerun to compare their strain responses.

2.5 Data analysis

All simulations were conducted using Abaqus/Explicit (Version 2016; Dassault Systèmes, France) on a high-end computer (15 CPUs with GPU acceleration; Intel Xeon E5-2698 with 256 GB memory, and 4 NVidia Tesla K80 GPUs with 12 GB memory). For each material model, CORA scores were reported based on the predicted relative brain-skull displacements in comparison with the measurement for the cadaveric impact. Element-wise cumulative maximum principal strains were also obtained. Pearson correlations between the peak maximum principal strain in the whole brain (evaluated at the 95^th percentile level) and μ₅, μ₀, and μ_∞ were calculated.

For the in vivo impulse, radial-circumferential shear strains were obtained from the selected material models and compared with the measurement. Area fractions of above-threshold shear strains were reported and compared in terms of CORA. The same Pearson correlations were also conducted between the peak shear strains and μ₄₀ (i.e., shear moduli at 40 ms, corresponding to the impulse duration for the in vivo head rotation), μ₀, and μ_∞.

Finally, all material models were scaled so that their μ₅ values were identical. Impact simulations were repeated to compare their resulting strain responses. All data analyses were performed in MATLAB (R2017b; Mathworks, Natick, MA). Statistical significance was defined at the level of 0.05.

3. Results

Fig. 3 compares relative brain-skull displacement time histories for a total of 12 NDT locations resulting from simulating the cadaveric impact. Apparently, different brain material models led to a wide range of relative brain-skull displacement magnitudes (e.g., peak magnitude from 1.91 mm to 5.21 mm for NDT_a3 along Y, and from 0.95 mm to 3.63 mm for the same location along Z). With different brain material models, there was a general trend that when the relative displacement magnitude increased, its occurrence also happened at a later time. For example, for the same NDT location, the peak was reached at 14 ms using (Tamura et al., 2008), but it was much later at 26 ms using (Prange and Margulies, 2002). Table 4 summarizes the CORA ratings when using each brain material model for simulation. The same two material models that led to the smallest (Tamura et al., 2008) and largest displacement magnitude (Prange and Margulies, 2002) also yielded the best and the worst CORA score, respectively, for this impact.

Fig. 3.

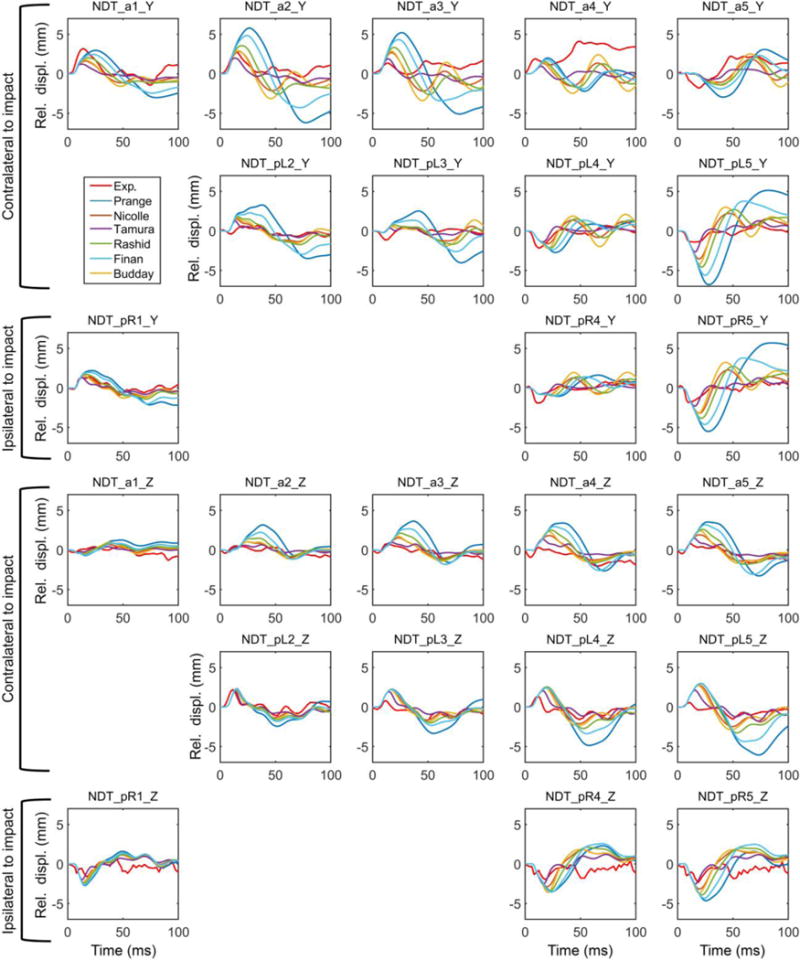
Relative brain-skull displacements for the 12 NDT locations (5 anterior, a1 to a5; 4 posterior left, pL2 to pL5; and 3 posterior right, pR1, pR4 and pR5) along the Y and Z directions using each of the 6 selected brain material models to implement a common head injury model, in comparison with those measured (C291-T1). Displacements along the X direction were not reported in a biplane system.

Table 4.

CORA scores for the two simulations using six selected brain material models based on either relative brain-skull displacement (Fig. 3) or above-threshold shear strain (Fig. 6) time histories.

Material Properties	Overall CORA scores
	C291-T1	Volunteer test
Prange 2002	0.240	0.419*
Nicolle 2004	0.357	0.132**
Tamura 2008	0.437	0.099**
Rashid 2014	0.326	0.348
Finan 2017	0.259	0.406
Budday 2017	0.338	0.116

^*When the magnitude was outside of the corridor, the CORA “corridor method” reported a rating of zero. However, in the “correlation method” category, the “cross correlation function” reported a high rating. This led to an overall high score.

^**Nonzero CORA was reported for virtually zero response curves because the phase category reported a perfect rating of 1.0.

Similar to the large variations in displacement (Fig. 3), significant disparities were also found in their cumulative maximum principal strains (Fig. 4). (Prange and Margulies, 2002) showed the highest strain overall, while (Tamura et al., 2008) had the lowest. The peak maximum principal strain in the whole brain ranged 0.11–0.44 among the six material models, and it ranged 0.08–0.9 in the corpus callosum (peak values were assessed at the 95^th percentile level, thus, yielding a peak value in the whole-brain lower than that in the corpus callosum). Their magnitudes decreased with the increase in μ₅ (Fig. 5). However, their Pearson correlation did not reach a statistical significance (r of −0.75; p = 0.085; compared to correlations with μ₀ and μ_∞: r of −0.41 and −0.38, and p of 0.41 and 0.45, respectively), likely because a non-linear relationship existed instead for this large-deformation impact.

Fig. 4.

Comparison of element-wise cumulative maximum principal strains from the selected six material models resulting from simulating cadaveric impact C291-T1. The responses shown are resampled on a representative coronal plane. The (S. Budday et al., 2017b) apparently produced a different strain pattern. This was because of the large absolute value of the negative α in its hyperelasticity model (Table 3).

Fig. 5.

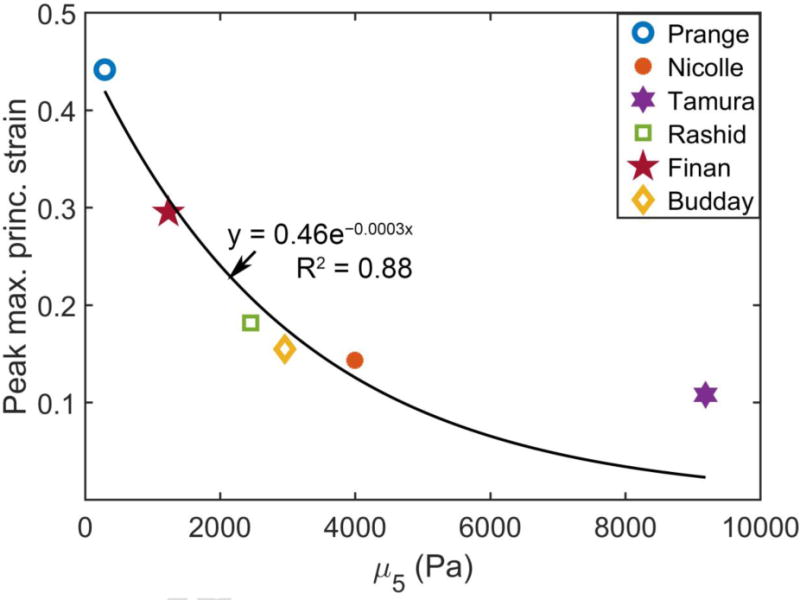
The peak maximum principal strains in the whole brain are compared with their corresponding μ₅ values for the cadaveric impact. For the Finan et al. (Budday et al.) material model, its μ₅ was averaged from values of the GM (cortex) and WM (corona radiata). A non-linear relationship was apparent for this cadaveric impact case involving large deformation (fitted for illustration only).

Regardless, except for the (S. Budday et al., 2017b) property, all of the brain material property models produced high strain regions to be near the cortex and deep in the brain (corpus callosum and midbrain). This was consistent with a recent study that analogously simulated a group of pure coronal head rotations (scaled to the same peak rotational velocity) using the baseline WHIM (Zhao and Ji, 2017). An animated movie was provided to show the simulated head motion and brain strains using the Rashid property, along with the linear/rotational acceleration profiles (see Supplementary).

Fig. 6 compares the area fractions of above-threshold radial-circumferential shear strains over time using the in vivo head rotation from each selected brain material model. Their corresponding CORA scores are reported in Table 4. The shear strains are further compared in Fig. 7 at a selected time frame, along with the measurement. While (Prange and Margulies, 2002) was too compliant and substantially over-estimated strain, (Nicolle et al., 2004) and (Tamura et al., 2008) were too stiff to predict any above-threshold area fraction at all. Interestingly, (Rashid et al., 2014) produced reasonable responses for both the high-rate cadaveric impact and the in vivo head rotation.

Fig. 6.

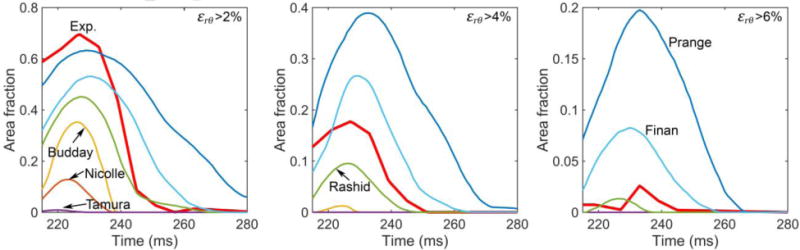
Area fractions of above-threshold radial-circumferential shear strains (ε_rθ) at three threshold levels ((a) >2% (b) >4% (c) >6%) on an axial plane by simulating an in vivo head rotation using the selected six brain material models.

Fig. 7.

Radial-circumferential shear strains on a selected axial plane (corresponding to the +2 cm plane at 228 ms (Sabet et al., 2008)) for the six selected brain material models in comparison with the experiment.

Similar to the cadaveric impact, the peak shear strains were significantly, and negatively correlated with μ₄₀ (r of −0.88, p = 0.02; Fig. 8a), but not with μ₀ or μ_∞ (r of −0.46 and −0.48; p = 0.36 and 0.34, respectively). This indicated that higher μ₄₀ values led to lower peak shear strains, as expected. An animated movie was provided to show the estimated shear strains on four axial planes for this impact using the Rashid property (see Supplementary).

Fig. 8.

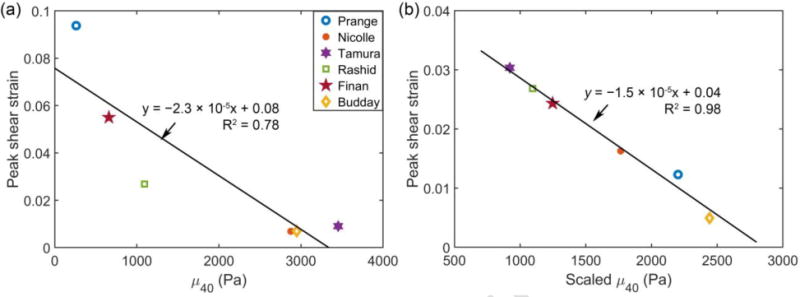
Peak radial-circumferential shear strain vs. (a) unscaled and (b) scaled μ₄₀ for the six selected material models. For the Finan et al. (Budday et al.) material model in (a), μ₄₀ was averaged from that of the GM (cortex) and WM (corona radiata) for comparison.

Using the scaled material models with an identical μ₅, their cumulative maximum principal strain responses for the cadaveric impact now became largely similar (Fig. 9, top; perhaps, except for (S. Budday et al., 2017b)). The variation in peak maximum principal strain in the corpus callosum region was 0.18–0.28, substantially less than that of 0.08–0.9 with the original μ₅ values (Fig. 4). Much less variations were also observed for the in vivo case (Fig. 9, bottom). Similar to the results from the un-scaled μ₄₀ values, a significant and negative correlation was found between peak shear strain and the scaled μ₄₀ (r of −0.99, p < 0.001) to yield a strong linear relationship (Fig. 8b). However, they were not correlated with the scaled μ₀, or μ_∞ (r of −0.14 and −0.61; p = 0.80 and 0.20, respectively).

Fig. 9.

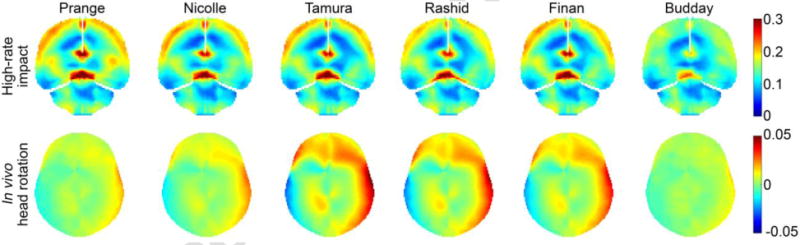
(a) Cumulative maximum principal strains using each scaled material model of the brain in the high-rate cadaveric impact; (b) radial-circumferential shear strains resulting from the in vivo head rotation. To improve visualization, the color scale in (b) was reduced from 0.1 in Fig. 7 to 0.05. The Rashid shear strains were identical in the two figures.

4. Discussion

A proper mechanical model of the brain is crucial to a head injury model for studying brain biomechanics across a range of time scales and impact conditions. While material properties of the brain have been extensively studied, they are far from being well characterized for application in a head injury model. Here, we significantly extended previous review studies to translate the vast variations into disparities in model estimated brain strains for comparison. In addition, we hypothesized, and further confirmed, that the time-varying shear modulus, rather than the initial or long-term shear moduli, were the most important to the brain mechanical behavior for a given impact. These findings may provide guidelines for future experimental studies and computational modeling to better characterize brain material properties for real-world applications.

4.1 Cadaveric impact

The relative CORA scores from the predicted displacements (Fig. 3) were consistent with the strain response magnitude – the brain material model that yielded the largest CORA was also the stiffest with the smallest overall strain magnitude ((Tamura et al., 2008); Fig. 4). In contrast, the one with the lowest CORA was also the most compliant with the highest strain magnitude (Prange and Margulies, 2002). It was interesting to note that for the selected impact (C291-T1), the CORA scores obtained here (range of 0.240–0.437; Table 2) were largely similar to (and even higher than) other established head injury models including AMB, SIMon, GHBMC, THUMS, and KTH (ranging from 0.221 for GHBMC to 0.389 with KTH using Ogden properties; (Miller et al., 2017)). Yet, for the six material models evaluated here, their strain responses varied greatly. For example, the maximum strain in the corpus callosum ranged from 0.08 (Tamura et al., 2008) to 0.90 (Prange and Margulies, 2002). This large disparity in model-estimated brain strains, while all with an “acceptable” CORA rating (according to (Miller et al., 2017)), once again suggested the danger of directly comparing model-estimated responses between different injury models, even if they have been “validated” (Ji et al., 2014).

Concerns further arose whether it was sufficiently reliable to exclusively rely on CORA rating and sparsely measured brain-skull relative displacements to “validate” and rank head injury models (Miller et al., 2017), especially given the caveats about CORA, itself (Table 4). Admittedly, most head injury models were validated against multiple cadaveric impacts rather than a single case assessed here. Nevertheless, the notion that past cadaveric impacts tests were not “totally suited” for head injury model validation was not new, as “they were not designed for validation” (Yang et al., 2006). This was somewhat implied in a pig head injury study, where strain, rather than displacement, was used for material property optimization and validation (Sullivan et al., 2014). There, the authors had the luxury to transect piglet heads and calculate 2D strains using full-field displacements measured from a high-speed camera.

4.2 Strain responses in high-rate cadaveric impacts

While full-field, 3D brain strain measurements are not yet available in high-rate human head impacts, averaged brain strains were measured at one or two NDT cluster locations in a few cadaveric impacts (Hardy et al., 2007). They were used to validate the KTH model (Giordano and Kleiven, 2014b). However, the strain magnitudes, as calculated based on a triad using the measured brain-skull displacements as input via finite element modeling, appeared rather low when compared to findings from the in vivo head rotation.

The average peak magnitudes of maximum principal strain and shear strain were mostly around 1.5–3% in three cadaveric tests, C380-T5, C380-T4, and C288-T3 (offset parietal, temporal, and occipital impact, respectively (Hardy et al., 2007); with one exception of ~7% in peak principal strain in C288-T3 that had a peak rotational acceleration of 26.3 krad/s²; see Fig. 10). In comparison, the area fraction of in-plane shear strain (lower bound of 3D shear strain) above 2% reached ~70% on a selected axial plane in the in vivo head rotation for two subjects (Sabet et al., 2008). The similar strain magnitudes in the two sets of experiments, in fact, suggested substantial inconsistency, as their peak head rotational accelerations differed greatly (range of approximately 7.0–26.3 krad/s² for the three cadaveric impacts vs. ~300 rad/s², i.e., 22.3–86.7 times higher than the latter; albeit, their head rotational directions also differed). Both THUMS and GHBMC reported ~8-10% (and even higher, for GHBMC in C380-T4) peak principal/shear strains in these cadaveric impacts, while the KTH model mostly reported about 2–4% (Giordano and Kleiven, 2016). Unfortunate, strain responses under in vivo head rotations have not been reported for any of the three injury models. Caution must be exercised when assessing their fidelity at very low impact severities relevant to sub-concussion (more below).

Fig. 10.

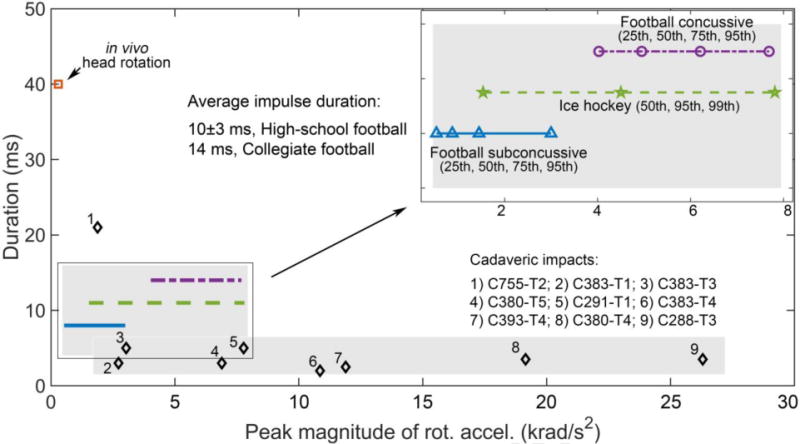
Distribution comparisons of peak rotational acceleration magnitudes and impulse durations of the major acceleration peaks for 1) cadaveric impacts often selected for head injury model validation, 2) on-field football/ice hockey measurements in the real-world, and 3) in vivo head rotation. Most on-field impacts were within the ranges between cadaveric and in vivo impacts in both acceleration peak magnitude and impulse duration. Validating a head injury model at both ends of the impact severity spectrum may improve the confidence for application especially in sub-concussive impacts in the real-world.

4.3 In vivo head rotation

While currently limited to 2D and low-rate far below injurious levels, in vivo head rotation provided full-field strains that could facilitate the validation of head injury models at the low end of impact severities (Ganpule et al., 2017; Ji et al., 2015; Wright et al., 2013). At this extreme, substantial disparities in strain were similarly observed, with above-threshold area fractions varied from virtually zero to much higher levels than the measurement (Fig. 6 and Fig. 7). Both (Prange and Margulies, 2002) and (Tamura et al., 2008) continued to produce the highest and lowest strains, respectively. Interestingly, (Rashid et al., 2014) performed reasonably well in both the high- and low-rate impacts (Fig. 4, Fig. 6 and Fig. 7). The difference between its shear moduli, μ₅ and μ₄₀, was 1356.5 Pa (2450.6–1094.1 Pa), representing a 55.4% decrease. This clearly confirmed the significant viscoelasticity across the 5–40 ms time window (Fig. 2).

4.4 Head injury model validation at both ends of the impact severity spectrum

The majority of head injury models were only validated using high-rate cadaveric impacts potentially causing injury in live humans (Miller et al., 2017). Fig. 10 compares the distribution of peak rotational acceleration magnitudes and impulse durations of the major acceleration peaks for nine cadaveric impact cases commonly used for validation (Ji et al., 2015; Kleiven, 2007; Miller et al., 2017). The details of the tests were reported in (Hardy et al., 2007, 2001). Except for one case, they all had an impulse duration of approximately 3–5 ms. Most of them also had a rotational acceleration peak magnitude above 7.9 krad/s² and could even reach up to 26.3 krad/s². In comparison, head impacts on the sports-field were often considerably lower than the cadaveric impacts in peak rotational acceleration. For example, the 95^th percentile concussive peak rotational acceleration was ~7.7 krad/s² in collegiate football (Rowson et al., 2012), similar to the 99^th percentile peak value in ice-hockey (~7.8 krad/s²; (Ji et al., 2014)). Sub-concussive head impacts were even much lower (~3 krad/s² for the 95^th percentile value; Fig. 10).

At the opposite extreme, a typical in vivo head rotational acceleration peak (range of 244–370 rad/s² for 3 subjects (Sabet et al., 2008)) was much lower than the injury level (e.g., 5260 rad/s² for a nominal injury risk of 10% in collegiate football (Rowson et al., 2012)). However, it was on the same order relative to the 25^th percentile sub-concussive rotational acceleration peak (531–682 rad/s²). In terms of impulse duration, on-field head impacts (~10±3 ms for high-school football (Broglio et al., 2010) and 14 ms on average for collegiate football (Rowson et al., 2009)) were within the range given by typical cadaveric impacts and the in vivo data (~3–5 ms vs. 40 ms, respectively; Fig. 10).

Conceptually, a head injury model is analogous to a continuous (no sudden jump in response), monotonic (response increases with the increase in severity, it never decreases), and non-linear (due to non-linearity in geometry and brain material properties) hyper-function to map head impact kinematics into estimates of mechanical responses. Model features, including brain material properties, analogously serve as important parameters to define the functional mapping. The continuity assumption is likely reasonable for a large spectrum of brain biomechanics ranging from in vivo conditions to sub-concussion and concussion, even though it could become invalid for higher impact severities involving tissue mechanical breakdown (e.g., tissue tear, hemorrhage and skull fracture).

Nevertheless, when a head injury model was only validated at the high-end extreme using cadaveric impacts, it was necessary to “extrapolate” the performance when applied to simulate the majority of head impacts on the sports field. This, unfortunately, could lead to substantial uncertainty in performance for lower-rate impacts, as clearly shown (and exaggerated) here using an in vivo head rotation as input (Fig. 6 and Fig. 7).

In contrast, if a head injury model can be successfully validated against experiments under impact conditions at both ends of the extreme (Ji et al., 2015), assessing its performance in simulating typical concussive and sub-concussive impacts then becomes analogous to a functional “interpolation”, as opposed to “extrapolation”. This could improve the confidence in model performance in real-world applications. This is important, given the growing concern on the cumulative effects from repetitive sub-concussive head impacts (Bahrami et al., 2017; Talavage et al., 2014) that are significantly below the severities in cadaveric impacts (Fig. 10).

With these considerations, therefore, it may be necessary to revisit the notion that the in vivo brain biomechanics data are not relevant for TBI studies because they are far from injurious levels (Giordano and Kleiven, 2016; Ji et al., 2014).

4.5 The importance of time-varying shear modulus, μ_t

For the brain’s viscoelasticity, the co-dependent μ₀ and μ_∞ are important to define the constitutive model. However, they are not directly relevant to the brain responses under impact conditions across the time-scales relevant to concussion/sub-concussion. For example, while (Nicolle et al., 2004) had a much greater than that in (Tamura et al., 2008) (Fig. 2), the latter was actually stiffer in the high-rate impact (Fig. 4). Similarly, while (Tamura et al., 2008) had the lowest μ_∞, its strain responses in both impacts were the stiffest (comparable to (S. Budday et al., 2017b; Nicolle et al., 2004) in the in vivo condition; Fig. 4 and Fig. 5).

Our property scaling parametric study directly supported the hypothesis that the time-varying μ_t at the appropriate time scale, rather than μ₀ or μ_∞, was the most indicative of brain strains for the corresponding impact. With an identical μ₅, all of the material models produced largely similar strains for the cadaveric impact (Fig. 9 top). Some differences remained, likely because of secondary acceleration peaks that could have played a role in response. In addition, the material models also differed in elasticity – either a linear or a hyperelastic model was used which could be important for this high-rate impact involving large deformation. The apparent difference in strain pattern when using (S. Budday et al., 2017b) property (Fig. 9 top) was also a direct consequence of their unique hyperelasticity model that included negative with α large absolute values (confirmed; Table 3).

Regardless, the significance of μ_t on brain strains was reinforced by the negative correlations between the peak strains and μ₅ (for the cadaveric impact) or μ₄₀ (either original unscaled or scaled values; for the in vivo head rotation). The strong linear relationship between the peak shear strain and the scaled μ₄₀ (Fig. 8b) was a direct evidence, which was also expected because of the small deformation in the in vivo case. The degraded linear relationship with respect to unscaled μ₄₀ (Fig. 8a) was likely because of significant differences in μ_t prior to reaching the end of head rotation. In contrast, for the cadaveric impact case involving much larger deformation, a more complex non-linear relationship was observed (Fig. 5). A monotonic relationship was apparent, regardless.

4.6 Material property scaling

It was no secret that a head injury model often scaled the shear modulus, μ₀, (or, equivalently, μ_∞) in order to yield a satisfactory validation performance. Unfortunately, to some degree, this would defeat the purpose of numerous and meticulous experimental efforts aimed at establishing an accurate brain material property model in the first place. Nearly all of the head injury models maintained the viscoelastic Prony series without altering the shape of the modulus relaxation function (Kleiven, 2007; Sullivan et al., 2014; Wright and Ramesh, 2012). While this could yield an “acceptable” validation in a given high-rate impact condition, the performance at lower rates (e.g., relevant to sub-concussion) was undefined, as clearly shown (and exaggerated) in Fig. 9 (bottom). Both (Prange and Margulies, 2002) and (S. Budday et al., 2017b) had their τ values significantly outside of the 5–40 ms range (minimum τ of 0.146 s and 2.127 s, respectively; Table 3). Therefore, when they were scaled to match μ₅, their μ₄₀ became too stiff to produce any meaningful response in the low-rate, in vivo condition.

The shape of μ_t was controlled by the Prony series parameters, g_i and τ_i (Table 1). Only ABM (Miller et al., 2016) considered the full set of parameters using a one-term Prony series linear viscoelastic model. Effectively, this could be used to optimize both the magnitude and shape of μ_t, so that to satisfy model validations at both ends of the impact severity. Unfortunately, this was not the intention of their study, as only high-rate cadaveric impacts were used for optimization. In addition, the parameters selected for optimization also included other irrelevant parameters such as well-defined density and bulk modulus of the brain.

Regardless, our finding potentially offers an effective strategy for future head injury model development. By optimizing μ_t, g_i and τ_i, rather than simply scaling μ₀ or μ_∞ alone, it is possible to satisfy validation requirements across a range of time scales and impact conditions (e.g., using (Rashid et al., 2014) as a starting point, as it achieved reasonable agreement with the two selected experiments). For the majority of real-world applications in simulating concussive and sub-concussive events (Fig. 10), the model performance can then be assessed in the sense of “interpolation”. This strategy does not appear to have been recognized before in head injury model development, and will be the subject of our future investigation.

Conversely, to successfully measure the brain’s viscoelasticity in experiment for use in impact simulations, it is important to have sufficient strain rate in order to characterize the brain mechanical behavior within the transitional time window most relevant to concussion and sub-concussion. The strain rates in (Prange and Margulies, 2002), (Feng et al., 2016) and (S. Budday et al., 2017b) up to 8.33/s, ~0.2/s, and 2 mm/min, respectively, were insufficient to describe the viscoelasticity required for simulating the range of real-world impacts (e.g., from in vivo to concussive impacts as conducted here). In contrast, the 8-term Prony series in (Nicolle et al., 2004) was excessive, as its transitional time window was several orders larger than necessary.

4.7 Brain material properties in head injury models: further thoughts

Most experiments measure brain material properties under a single loading mode, which cannot fully describe the brain mechanical behavior in a complex whole-head impact condition. Therefore, it is common to combine data from different experiments to implement a complete material model required in a head injury model. While this is a limitation in the current state-of-the-art, still, it is important to recognize the caveats that these “ingredients” may not be “compatible”. For example, the viscoelasticity based on oscillatory shear on porcine WM over a large frequency range (Nicolle et al., 2004) may not behave the same in uniaxial cyclic tension/compression on postmortem human brain in quasi-static conditions (Franceschini et al., 2006), and vice versa. Yet, they were directly combined in KTH (Kleiven, 2007) and WHIM (Ji et al., 2015). Similarly, hyperelasticity from in vivo MRE data may not be the same in dynamic shear tests on postmortem tissue to derive viscoelasticity (Shuck and Advani, 1972). However, they were simply combined in (Chatelin et al., 2013) and (Garimella and Kraft, 2016) studies as well.

Nevertheless, the need to characterize and model the brain mechanical behavior under arbitrary loading conditions with the same tissue sample has already been recognized (S. Budday et al., 2017b). The authors conducted a series of multiaxial compression/tension/shear tests to systematically investigate the time-dependent characteristics of the brain mechanical behaviors (S Budday et al., 2017; S. Budday et al., 2017a, 2017b). They identified that an isotropic modified one-term Ogden model suitable of representing the hyperelastic behavior under a combined loading condition. Interestingly, although their material model was intended for applications in physiological conditions, still, it generated strain responses within the bounds of those from other material properties (Fig. 5 and Fig. 8a). However, the minimum τ values for this property (~5 s and ~2 s for the cortex and corona radiata, respectively) were orders of magnitude larger than the 5–40 ms time window evaluated here. Therefore, similarly to other models (Feng et al., 2016; Prange and Margulies, 2002), it cannot be used to capture the brain viscoelasticity across the spectrum of head impacts relevant to concussion/sub-concussion (S. Budday et al., 2017b).

On the other hand, the (S. Budday et al., 2017b) hyperelastic model was unique, as the authors emphasized the need for a negative rather than a positive (Prange and Margulies, 2002; Rashid et al., 2014) α value to induce compression-tension asymmetry (i.e. higher stress in compression than in tension). However, it remains to be seen whether this notion was applicable in impact-rate loading conditions. In this case, using a head injury model could substantially facilitate future experimental studies along this line.

A computational head injury model is an important tool to bridge the gap between external head impacts and clinical indicators of injury (Meaney et al., 2014). Indeed, it is the weakest link of a system that defines its overall performance in real-world applications (de Rooij and Kuhl, 2016). However, it is likely debatable which one is the weakest, given the uncertainty and potential errors across diverse disciplines (e.g., from biomechanics to neuroimaging, and to cognition and concussion diagnosis). For the development and application of head injury model, itself, both the brain’s material properties as well as model validation data appear to be limiting sufficient confidence in model simulation. For example, all of the six selected material models yielded “acceptable” response for the cadaveric impact based on relative brain-skull displacements and CORA scores, as compared to other existing head injury models (Miller et al., 2017). Yet, they differed greatly in strain for both the high-rate impact and in vivo rotation (Fig. 4 and Fig. 7). Nevertheless, by “validating” a head injury model at both ends of the impact severity spectrum, essentially to maximize the use of all of the valuable but imperfect experimental data available, the confidence in model simulation may be improved for the majority of real-world head impacts.

5. Limitations

We have only used one injury model (WHIM), two extreme impacts, and six brain material models for evaluation. For each selected material model, although the experimental studies may have provided multiple material models suitable for different loading conditions, only one had to be selected. Conceivably, it may be possible to implement a more appropriate material model for each impact condition. However, this would introduce an unwanted challenge in determining the appropriate model for mid-rate impacts, and could induce discontinuity in response over impact rate. Using a single model to capture the brain responses across the time scales is desirable, even though this remains a challenge.

Further, we did not formally investigate the significance of hyperelasticity parameters on brain responses that was mostly relevant to high-rate impacts involving large deformation, as only one cadaveric impact was used. However, it remains to be seen whether the sparsely measured brain-skull relative displacements (Fig. 3) and the CORA metric are sufficient to discriminate suitable hyper- or linear elastic material models for use in concussion and sub-concussion simulations. Finally, the material property implementations were bounded to the existing Abaqus capabilities. Other non-standard implementations were not considered (Feng et al., 2016; Ning et al., 2006).

6. Conclusion

We have significantly extended previous review studies on brain material properties by translating their vast variations into brain response disparities under both high- and low-rate impact conditions. The time-varying shear moduli at the appropriate time scales were the most indicative of impact-induced brain strains. This would enable future head injury models to optimize the material properties in order to satisfy validation requirements at both ends of the impact severity spectrum. However, this will likely require better-quality validation datasets to discriminate the performance. Scaling properties derived from (semi-) quasi-static conditions may still be used to simulate head impact at a particular time scale, but not across a range of time scales as they are unable to capture the viscoelasticity within the corresponding time window. Finally, there is an apparent disconnect between material property analytical/experimental work and the intended applications in impact simulation. Understanding how brain material properties govern the responses through an actual head injury model would provide critical insights into how they can be better characterized in experiment, and further implemented in injury models, for practical, real-world applications.

Highlights.

• Vast variations in brain material properties manifested in impact-induced brain strains

• Time-varying shear moduli are most indicative of impact-induced brain strains

• Properties from quasi-static conditions cannot capture viscoelasticity in a range of impacts

• Model validated at both ends of impact severities would improve simulation confidence

• Should bridge gap between material property measurement and real-world applications