Quantitative chemical analysis at the Nanoscale using the PTIR technique

Abstract

Photothermal induced resonance (PTIR), also known as AFM-IR, is a scanning probe technique that provides sample composition information with a lateral resolution down to 20 nm. Interest in PTIR stems from its ability to identify unknown samples at the nanoscale thanks, in first approximation, to the direct comparability of PTIR spectra with far-field infrared databases. The development of rapidly tuning quantum cascade lasers has increased the PTIR throughput considerably, making nanoscale hyperspectral imaging within a reasonable timeframe possible. Consequently, a better understanding of PTIR signal generation and of the fine details of PTIR analysis become of paramount importance for extending complex IR analysis methods developed in the far-field, e.g. for classification and hyperspectral imaging, to nanoscale PTIR spectra. Here we calculate PTIR spectra via thin film optics, to identify subtle changes (band shifts, deviation from linear approximation, etc.) for common sample parameters in the case of PTIR with total internal reflection illumination. Results show signal intensity linearity and small band shifts as long as the sample is prepared correctly, with band shifts typically smaller than macroscale ATR spectroscopy. Finally, a generally applicable algorithm to retrieve the pure imaginary component of the refractive index (i.e. the chemically specific information) is provided to overcome the PTIR spectra non-linearity.

TOC image

Infrared (IR) absorption spectroscopy is a widespread analytical technique because it provides rich molecular conformation and chemical composition information, without any a priori knowledge of the sample.^1,2 The power of IR spectroscopy greatly relies on the Lambert and Beer’s approximation that establishes a proportionality between IR transmission spectral intensities and the sample absorption coefficient (α). Such proportionality enables material identification and the determination of the concentrations (c_i) of the sample constituents

$$\alpha \left(\lambda \right)={\displaystyle \sum _i{c}_i{\epsilon }_i\left(\lambda \right)}$$ (1)

where ε_i is the molar absorption coefficients of specimen i and λ is the wavelength of light. The absorption coefficient α is related to the commonly used decadic absorption coefficient $\left(a\right)\alpha \left(\lambda \right)=a\left(\lambda \right)\ln \left(10\right)$ and to the complex refractive index $(\widehat{n}=n+i\kappa )$ of the sample by

$$\alpha \left(\lambda \right)=\frac{4\pi \kappa \left(\lambda \right)}{\lambda }$$ (2)

Within the Lambert-Beer approximation, the absorbance (A) is given by:

$$A=\alpha \left(\lambda \right)l$$ (3)

where l is the optical path length in the sample.

With imaging optics, IR spectroscopy yields spatially resolved, chemical images;^2–5 however, its spatial resolution (ξ) is limited by diffraction (Rayleigh limit) and gets worse with increasing wavelength:

$$\xi =\frac{0.61\lambda }{\text{NA}}$$ (4)

where NA is the objective numerical aperture. The lateral resolution limit of IR microscopy is of the order of 1 to 10 μm,⁴ but such resolution is hardly achieved in practice.

It is important to realize that the Lambert and Beer’s approximation is accurate if i) the sample is homogenous, ii) the sample is weakly absorbing iii) scattering is negligible, iv) there are no reflections at interfaces.⁶ In the solid state however, n(λ) commonly shows dispersion in proximity of strong IR absorption peaks⁷ and the intensity, band shape and peak position of IR spectra can be affected by sample preparation and sampling methods, such as attenuated total reflection (ATR)⁸ or when analyzing microscopic portions of a sample.⁹ Data reduction routines based on multivariate analysis typically enable “compact” visualization and interpretation of the large and complex dataset in the form of chemical maps,^3,5 principal components, etc. However, because chemometric techniques often implicitly assume a linear relation between the IR signal and the concentrations of the sample components, deviations from the Lambert and Beer’s approximation must be understood to pretreat the data (baseline correction etc.) and to eliminate artefacts due to the sampling method and to scattering at interfaces.

Methods to improve the spatial resolution of IR spectroscopy are of great interest because measurement of the nanoscale chemical composition is critically important for engineering nanomaterials,^10–13 to understand the origin of diseases,¹⁴ and for their diagnosis,^1,15 based on chemical signatures. However, to translate the power of IR spectral analysis to the nanoscale, ideally, nanoscale IR spectra should resemble far-field IR spectra and not require complex calculations or prior-knowledge of the sample. Photothermal induced resonance (PTIR), scattering scanning near field microscopy (s-SNOM) and photo induced force microscopy (PIFM) are three scanning probe methods that provide IR spectra with nanoscale resolution.

s-SNOM^16,17 measures the amplitude and the phase of light scattered from a tip in proximity of the sample. These quantities are complex functions of the sample’s n(λ) and κ(λ) and depend on the tip-sample-substrate near-field interactions. For weak IR absorption peaks, s-SNOM phase spectra resemble somewhat far-field IR absorption spectra.^16–18 However, sophisticated modelling¹⁹ and knowledge of the sample is necessary to analytically invert the near-field scattering problem and determine both n(λ) and κ(λ).

PIFM²⁰ measures the photoinduced force resulting from the dipole-dipole interactions between a metallized AFM (atomic force microscope) tip and the sample when illuminated by a laser. Although the measured signal is subject of debate,²¹ the resulting photoinduced force depends on the balance between the real and imaginary polarizabilities of the sample and of the tip. Depending on the balance of those forces the PIFM spectra can be more closely related to κ(λ)²⁰ or n(λ).²¹

In PTIR,^17,22 an AFM tip transduces the sample thermal expansion induced by the absorption of light pulses in the sample into cantilever oscillations (Fig 1). The amplitude of the oscillations, captured by the AFM detector, is proportional to the energy absorbed by the sample. Nanoscale IR spectra are obtained by plotting the amplitude of the cantilever oscillations while tuning the laser wavelength. Although PTIR has been implemented initially in the mid-IR,²³ and it is also known as AFM-IR, its mechanical detection scheme works in principle for all wavelengths and its operating range has been recently extended to the visible.^24,25 Among nanoscale IR techniques, PTIR has attracted the most attention from analytical chemists because, in first approximation, PTIR spectra are proportional to κ(λ),^26–28 i.e. are similar to far-field transmission spectra, and enable material identification by comparison with far-field IR databases.²⁹ Furthermore, while s-SNOM and PIFM are primarily surface sensitive techniques, PTIR probes samples thicknesses even in excess of 1 μm.^17,27 PTIR is finding ever growing applications in polymer science,^28,30,31 plasmonics,^32–35 photovoltaics,^11,25,36 pharmaceutics,³⁷ biology^14,38,39 and medicine¹⁴ etc.

Figure 1.

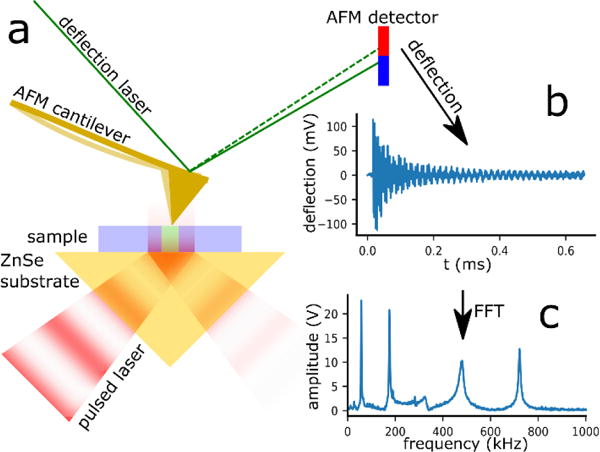
a) Sketch illustrating the PTIR setup and signal generation. The sample (blue) is placed on a ZnSe Prism (yellow) and illuminated from below with a pulsed, infrared laser beam (red). The sample locations that absorb IR light, heat up and expand during each laser pulse. The expansion induced motion of the AFM tip (gold), deflection signal, is detected by the AFM detector. b) time domain PTIR signal (ring-down). c) The fast Fourier transform (FFT) on the deflection signal, yields the amplitudes of the cantilever oscillation modes which are proportional to the local infrared absorption.

Recent innovations such as resonance enhanced PTIR,⁴⁰ the use of sensitive nano-sized picogram-scale probes,⁴¹ and the development of tapping-mode PTIR, have considerably increased the PTIR sensitivity and throughput, opening the door for nanoscale hyperspectral imaging. This novel PTIR capability has recently been commercialized, driven by the desire for translating the power of chemometric analysis² to the nanoscale. Although the spectral distortions in PTIR spectra are typically much less prominent than in s-SNOM¹⁶ or PIFM,²¹ it is important to gain an accurate understanding on the factors that influence PTIR peak shapes, positions and intensities, to ensure proper interpretation of the minute spectral differences highlighted by chemometric algorithms,² and avoid spectra misinterpretation⁴². Although such optical analysis is closely related to modelling in far-field IR microscopy, where samples are prepared with homogeneous thickness (i.e. ≈ 8 μm for dry cells), the sample topography in PTIR typically varies and must be considered as an additional parameter.

In this work, we consider PTIR with ATR illumination and calculate optical absorption as a function of the sample thickness, absorption coefficient, dispersion and light polarization, to understand the PTIR linearity range, band shifts, peak ratios and the effect of sample stratification. The ATR geometry is chosen to avoid complications due to Fabry-Pérot interference that may modulate the PTIR intensity for top-down illumination. The calculations presented here provide guidelines for optimal sample preparation and data analysis. Furthermore, we propose a general non-linear multivariate data fitting algorithm that allows deriving pure κ(λ) spectra from PTIR spectra, thus overcoming the non-linear dependence of the PTIR signal on α (λ).

Experimental

Transfer Matrix Method (TMM) calculations

All simulated PTIR spectra were calculated using the tmm Python package,⁴³ which provides a well-tested implementation of the TMM. The refractive index of the ZnSe substrate was 2.4, unless otherwise stated, in which case we refer to literature data.⁴⁴ The complex refractive index for Poly-methyl-methacrylate (PMMA) was obtained from literature⁴⁵ (see fig. S1). Calculations were performed using Python 3.5.1, numpy 1.11.1 and scipy 0.18.1 libraries.⁴⁶ Matplotlib 2.0.0⁴⁷ was used for preparing plots.

In all calculations, the illumination was from the bottom through a ZnSe optical element at 45° angle of incidence, unless otherwise noted. The PTIR signal was calculated as the fraction of the incident light intensity absorbed in the sample layer as detailed in the text.

Non-linear least squares (NLS) fits were performed using the Limited-Memory Broyden–Fletcher–Goldfarb–Shanno algorithm as implemented in scipy optimize package.

Sample Preparation

All chemicals were used as received without further purification. PMMA wedges with thickness ranging from 43 nm ± 5 nm to 1243 nm ± 10 nm, as measured by AFM, were prepared by spin coating and electron beam lithography as previously described.²⁷ Uncertainties through the manuscript represent a single standard deviation.

PTIR measurements

PTIR measurements were obtained with a modified commercially available PTIR setup interfaced with an external cavity quantum cascade laser (EC-QCL) array. Spectra were obtained in the range from 1700 cm⁻¹ to 1760 cm⁻¹. The laser was operated with 1 kHz repetition rate and 400 ns long pulses.

Five consecutive PTIR spectra were acquired for each sampling position (i.e. each PMMA thickness). AFM topography images were obtained before and after each set of 5 spectra to evaluate any possible sample position drift. PTIR spectra were obtained by stepping the laser at 2 cm⁻¹ intervals and referenced to the laser power measured with a power meter positioned in place of the sample on the AFM stage (background spectrum). To obtain high signal-to-noise (SNR) background spectra the laser was operated at 200 kHz repetition rate. Changing the repetition rate did not change the shape of the laser emission spectrum.

Results and Discussion

The signal transduction in PTIR is the following: 1) optical energy into absorbed energy, 2) absorbed energy in local heat, 3) local heat in to local thermal expansion, 4) local thermal expansion into AFM cantilever motion, 5) cantilever motion into AFM detector signal (see Fig. 1). Dazzi et al. established a framework to describe the PTIR signal, based on the electric dipole approximation, and identified the linear relationship between the PTIR signal (S_PTIR) and κ(λ)²⁶ by factoring the PTIR signal transduction chain into a series of multiplicative contributions.²⁶ For convenience, here we rewrite Dazzi’s original expression to include k(λ) in the optical contribution (H_opt) and factorize the intensity of the laser incident power (I_inc), typically accounted for by the background spectrum:

$$S_{\mathit{PTIR}}\propto H_{\mathit{AFM}}{H}_m{H}_{\mathit{th}}{H}_{\mathit{opt}}\left(\lambda \right)I_{\mathit{inc}}\left(\lambda \right)$$ (5)

where

• H_AFM is the cantilever contribution, that depends on the cantilever modal stiffnesses, frequencies, shapes and deflection sensitivity,

• H_m is the mechanical contribution to the signal that depends on the sample thermal expansion coefficient,

• H_th is the thermal contribution, which describe the sample thermalization dynamics which is determined by the laser pulse length and by the sample thermal properties,

• H_opt is the optical contribution, defined here as the fraction of incident light absorbed by the sample, i.e. its absorptance. For ATR illumination, H_opt is a functionof the refractive index of sample $\left({\widehat{n}}_1=n_1+i{\kappa }_1\right)$ and substrate $\left({\widehat{n}}_0=n_0\right)$, sample thickness, light polarization and incidence angle. In short, the new definition of H_opt is better suited to go beyond the approximation proposed in Dazzi’s²⁶ original work. This step is necessary to include cases with strongly absorbing groups, such as carbonyls that show a non-negligible anomalous dispersion in the mid-IR.

The main focus of this study, H_opt, is the only term in eq. (5) that directly depends on the wavelength and that includes the absorption coefficient, κ, the primary quantity of interest to IR spectroscopists. The PTIR signal produced by a sufficiently fast cantilever is directly proportional to the total absorbed optical energy H_opt, independently from the wavelength. Because I_inc is determined via a separate background measurement, knowledge of H_opt is sufficient to describe the PTIR spectral shape in such cases. However, we note that in addition to the total absorbed optical energy, λ also influences the initial distribution of the absorbed power and the temperature inside the sample. Because differences in the initial temperature distribution can change the sample thermal relaxation dynamics, λ can indirectly influence the cantilever response amplitude for slower cantilevers. Such indirect λ-dependence of the PTIR signal will not be considered here and will be the subject of future work.

H_opt is calculated here using plane waves incident on a sample consisting of a stack of parallel homogeneous layers that are illuminated in a total internal reflection (TIR) configuration. Unless otherwise noted, we consider a 3-layer sample composed of a ZnSe substrate (layer 0), a PMMA sample layer with different thickness (layer 1) and an air top layer (layer 2). TIR occurs at interfaces for light incident from the higher refractive index material (n₀ > n₁) at angles of incidence θ larger than ${\theta }_c=\arcsin \left(\frac{n_1}{n_0}\right)$,. In such conditions, light cannot propagate into layer 1, and only the evanescent tail of the incident electromagnetic field stretches into the sample layer with a decay length (1/e), or depth of penetration (d_p). For a non-absorbing sample $d_p=\frac{{\lambda }_0}{2\pi \sqrt{n_0^2{\sin }^2\theta -n_1^2}}$, where λ₀ is the free space wavelength of the incident light. If absorption occurs in the sample (κ₁ > 0), only a fraction of the incident light is reflected (i. e. R < 1) which is referred as attenuated total reflection (ATR)⁸. It can be shown, that the absorbance (A) can be approximated by a Beer’s law like expression⁴⁸:

$$A=-{\log }_{10}R\left(\lambda \right)=\alpha \left(\lambda \right)l_{\mathit{eff}}$$ (6)

That linearly relates it to the absorption coefficient α(λ) and to the effective path length (l_eff) of the sample, provided that the sample is not strongly absorbing (i.e. if the real part of the refractive index is essentially constant). It is well known that ATR spectra show peak shifts (particular for strongly absorbing peaks) and that the relative ATR peak intensities differ from transmission spectra because d_p is λ-dependent. An introduction to mid-IR ATR spectroscopy is available elsewhere.⁴⁹

However, in macroscale ATR experiments the sample thickness is typically either far greater than d_p or far smaller than d_p. In the first case, the semi-infinite medium approximation allows the use of Fresnel equations to accurately calculate the reflection coefficient at the interface.⁵⁰ In the second case, the refractive index of the thin sample does not influence the electric field at the interface significantly and the imaginary part of the refractive index is sufficient to calculate the reflected light attenuation.⁴⁸ In contrast, for PTIR the thickness of the sample is often of the order of d_p, typically between 100 nm and 1 μm.^27,40,51 Because, in PTIR the sample thickness lies somewhere in between the commonly used thin film and semi-infinite ATR case limits,⁴⁸ the thickness is an important additional variable influencing PTIR spectra, making calculations using at least three layers (substrate, sample, top layer) necessary. As long as there is no traveling wave in the top layer $\left(\text{air}\right)H_{\mathit{opt}}=1-{\left|r\right|}^2$. The reflection r of a three layer system has been described by Hansen:⁵²

$$r=\frac{r_{01}+r_{12}{e}^{2i{\delta }_1}}{1+r_{01}{r}_{12}{e}^{2i{\delta }_1}}$$ (7)

Here, r₀₁ and r₁₂ are the Fresnel reflection coefficients at the substrate-sample and sample-air interfaces, respectively. The $e^{2i{\delta }_1}$ term, describes the phase shift and attenuation the wave experiences while traveling in the sample layer,

$${\delta }_1=\frac{2\pi {\widehat{n}}_1}{\lambda }{l}_1\cos \left({\mathrm{\theta }}_1\right)$$ (8)

where l₁ and ${\widehat{n}}_1$ are the sample thickness and complex refractive index respectively. θ₁ is the complex angle of refraction determined from Snell’s law

$${\widehat{n}}_0\sin \left({\theta }_0\right)={\widehat{n}}_1\sin \left({\theta }_1\right)$$ (9)

Depending on the polarization of the incident wave, the reflection coefficients for s or p polarization must be used. Expressions similar to (7) for systems with more than three layers can be obtained, however, they are quite cumbersome. Instead, the transfer matrix method (TMM) formalism used here generalizes the result to electro-magnetic fields in thin films with an arbitrary number of parallel layers (see section S-2 of the supporting information).

Signal intensity

Given the well-known λ-dependent differences between band ratios in transmission and ATR spectra it is reasonable to expect similar effects in PTIR. To understand the effect of sample thickness on the PTIR signal intensity it is instructive to consider the case of an artificial material with constant complex refractive index across the whole mid-IR range. Figure 2 displays the TMM calculated PTIR intensities normalized to the intensity at 1300 cm⁻¹ in the case of n = 1.4 for a weakly (a = 0.02 μm), medium (a = 0.10 μm) and strongly (a = 0.50 μm) absorbing artificial sample with thickness up to 1000 nm. For l₁< 100 nm the relative PTIR intensities resemble those seen in transmission, with deviations smaller than 10 % across the whole spectral range. Thicker samples tend to display larger deviations from Beer’s law compliant transmission spectra, with deviations less pronounced for strongly absorbing samples because the rapid decay of the field in the sample due to absorption, lessens the effect of the wavelength on d_p.

Figure 2.

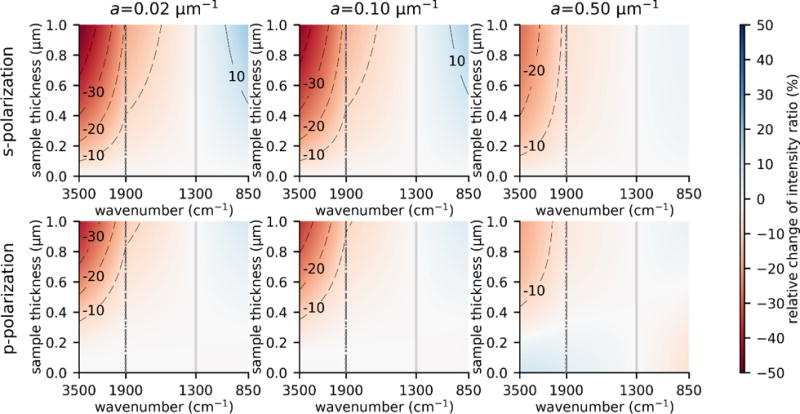
Effect of ATR illumination on the PTIR band intensity ratios with respect to 1300 cm⁻¹ (vertical grey lines). The graphs display deviations from 1 for the TMM calculated PTIR band intensity ratios with respect to 1300 cm⁻¹ for an artificial sample with n = 1.4 and constant decadic absorption coefficient in the case of a weakly (left column), medium (central column) and strongly (right column) absorbing sample. 0 % deviation from 1 would indicate that the relative band intensity ratios are the same as in a Lambert and Beer law compliant transmission spectrum. Calculations were obtained for s-polarization (top row) and p-polarization (bottom row). The horizontal scales above 1900 cm⁻¹ and below 1900 cm⁻¹ are different to highlight changes in the mid-IR fingerprint region.

Importantly, the effect of the sample height on the PTIR intensity ratio is generally limited (< 10 %) within the 850 cm⁻¹ to 1900 cm⁻¹ spectral range for samples up to 400 nm thick and within 1050 cm⁻¹ to 1600 cm⁻¹ for samples up to 1.0 μm thick.

Linearity of the PTIR signal

Quantitative use of infrared spectroscopy leverages the linear relationship between sample absorption and analyte concentration. As for the relative intensities, the sample thickness must be considered in addition to the wavelength when assessing the linearity of the PTIR signal.

To gain insight on the PTIR signal linearity, TMM was used to calculate H_opt as a function of the decadic absorption coefficients (from 10⁻⁷ μm⁻¹ to 0.5 μm⁻¹) for artificial samples with constant absorption and constant refractive index (n = 1.4). The calculations were carried out in the case of a thin (100 nm), medium (500 nm) and thick (1000 nm) sample layer. The results were compared to the H_opt obtained in case of a small decadic absorption coefficient (a₀= 0.02 μm⁻¹) and linearly extrapolated to a higher a (Fig. 3). Figure 3 highlights the deviations of the PTIR signal from perfect linearity with respect to a. The deviation from linearity is less accentuated for smaller sample thickness and for smaller absorption coefficients. For a given sample thickness, excitation with s-polarization leads on average to a 0.7 times smaller deviation from linearity than for p polarization.

Figure 3.

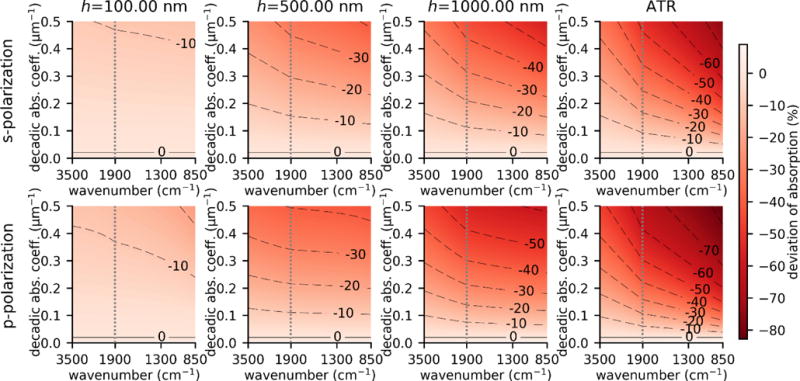
Estimate of the maximum deviation of the PTIR signal from perfect linearity with respect to the absorption coefficient. For the estimate, we considered an artificial weakly absorbing material with constant a₀= 0.02 μm⁻¹ and n = 1.4 and calculated $H_{\mathit{opt}}\left(a\right)-a\left(\frac{H_{\mathit{opt}}\left(a_0\right)}{a_0}\right)$, normalized to $a\left(\frac{H_{\mathit{opt}}\left(a_0\right)}{a_0}\right)$ Sample parameters were n₀=2.4, n₁ = 1.4 + iκ, n₂=1. Calculations were carried out for 100 nm thick (1^st column), 500 nm thick (2^nd column),1000 nm thick (3^rd column) sample and for a semi-infinite sample (4^th column, labelled ATR). The horizontal scales above 1900 cm⁻¹ and below 1900 cm⁻¹ are different to highlight changes in the mid-IR fingerprint region.

For moderately absorbing samples (a < 0.1 μm⁻¹) PTIR spectra display close adherence to linearity even for thick samples (<10 % error for samples up to 710 nm in s polarization and up to 520 nm in p polarization). However, for strongly absorbing samples (a ≥ 0.5 μm⁻¹) for best results quantitative analysis (< 10 % deviation) should be carried out on thin samples (< 75 nm in s polarization).

The non-linear effects described here are even more accentuated in the case of a semi-infinite-medium, as typical in macroscale ATR spectroscopy. However, in ATR spectroscopy these effects are typically mitigated plotting the logarithm of the reflection signal; a procedure that in principle could also be applied to PTIR spectra if either H_AFMH_mH_th or S_PTIR in the case of total absorption were known.

Influence of anomalous dispersion

Because band positions, widths and shapes of IR spectra are routinely interpreted to derive the secondary structure of proteins,⁵³ it is important to understand and evaluate, optical effects that may also distort these spectral features.

Although band shifts due to anomalous dispersion in correspondence of strong absorption peaks are common in ATR,⁸ because d_p increases with the wavelength across the peak width, such effect has been typically ignored in PTIR experiments.-Figure 4 shows that, for the strongest PMMA band, the narrow linewidth (< 1 cm⁻¹) of an external-cavity quantum cascade laser (EC-QCL) allows to clearly resolve small band shifts (< 5 cm⁻¹) in PTIR spectra as a function of the sample thickness. It should be noted, that the combination of a large change in sample thickness and a strong band is the least favorable scenario in regard to band shifts in PTIR spectra.

Figure 4.

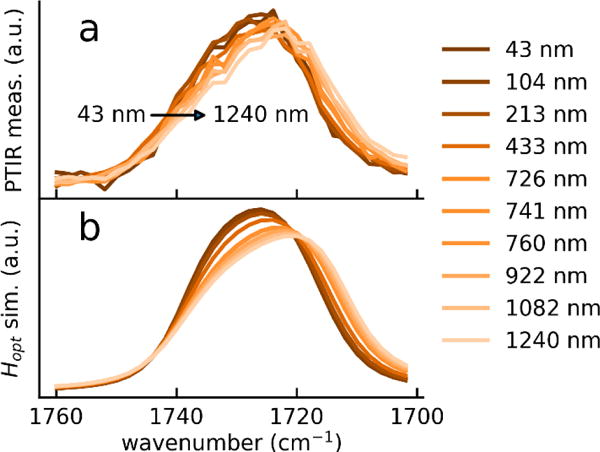
Band shifts of the PMMA carbonyl band in the case of p-polarization. a) measured PTIR spectra on a PMMA wedge and b) simulated H_opt signal (using literature values for ZnSe⁴⁴ and PMMA⁴⁵).The sample thickness used in the simulations correspond to those measured in panel a. The spectral intensities are displayed in arbitrary units for clarity. (For s-polarization see fig. S-2).

The experimentally measured peak shifts are comparable with calculations for PMMA films of equivalent thickness (Fig. 4 and Fig S2). Although in the mid-IR the peak shape of absorption peaks is better described by the Voigt peak shape (a convolution of a Lorentzian and Gaussian peak shapes), for simplicity, in our calculations we use a Lorentzian peak shape⁵⁴ because it captures peak shifts with sufficient accuracy. Calculations with Lorentzian bands (with the corresponding anomalous dispersion) across a range of halfwidths and band positions shows that the shift (typically downshift) is always larger for s polarization than for p polarization and the shift increases the broader the bands (see Figure S-3).

In the limit of sufficiently thick samples, PTIR peak shifts coincide with those measured in ATR spectroscopy. In general, the peak redshift becomes more pronounced as the sample thickness and the absorption coefficient increase (see Figure 5).

Figure 5.

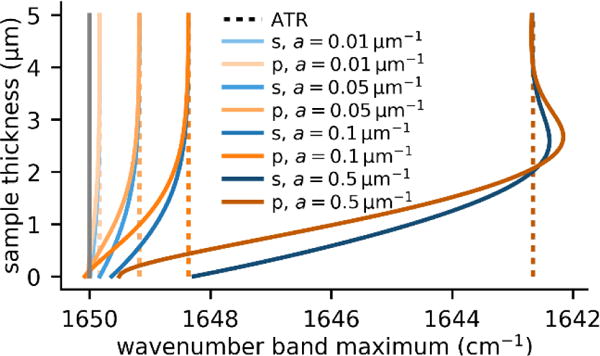
Band shifts in PTIR and ATR spectra: calculated band shifts for a Lorentzian band (10 cm⁻¹ half width) centered at 1650 cm⁻¹ (typical spectral position of the amide I band), for absorption coefficients ranging from a = 0.01 μm⁻¹ to 0.5 μm⁻¹ as a function of the sample thickness (up to 5 μm). The band position in the PTIR spectrum approaches the band position measured in ATR spectroscopy, as the sample height increases. Note that typical PTIR samples are significantly thinner than 5 μm.

Preliminary calculations with our model, obtained with illumination from the air side at 70° angle from the sample normal (a common illumination geometry) and neglecting the effect of the AFM tip, show (Figures S-4 and S-5) slightly smaller and generally upshifted peak positions. Furthermore, for top illumination although the sample thickness appears to have a weak effect on the shift, the substrate refractive index shows a non-negligible effect due to reflection at the sample-substrate interface (compare Fig S4 and S5).

Vertically heterogeneous samples

The influence of the sample stratification on the PTIR spectra is a commonly asked question, which however has not been yet addressed in the literature.

Here we consider a 1 nm thick, weakly absorbing (a= 10⁻³ μm) layer embedded in a non-absorbing matrix characterized by the same (n = 1.4) refractive index and calculate the PTIR absorption of such thin layer as a function of the layer vertical position in the matrix. Figure 6 shows that the calculated absorption in the layer follows the expected exponential decay for the cases of a thin (100 nm), medium (500 nm) and thick (1000 nm) matrix. It should be noted, that in case of a vertically heterogenous sample, H_th will also depend on the position of the absorber, but the analysis of this secondary effect is outside the scope of this work.

Figure 6.

Calculated PTIR signal intensity (a) and band position shift (b) for a 1 nm thick, weakly absorbing layer (a = 10⁻³μm, n = 1.4) within a non-absorbing matrix (n = 1.4) as a function of the layer distance from the prism-matrix interface. Calculations were carried out for matrix thicknesses ranging from 100 nm to 1000 nm and for s and p polarization. Band positions were calculated considering the band maximum of a Lorentzian band 10 cm⁻¹ wide centered around 1650 cm⁻¹.

Notably, light absorption in the thin layer at a given distance from the substrate increases for thicker matrices because the electric field amplitude in the sample increases (see fig. 6a) In contrast, considering a Lorentzian halfwidth of 15 cm⁻¹, the peak shift is negligible as the absorbing layer is positioned further away from the substrate (Fig 6b).

Derivation of α(λ) from PTIR spectra

Algorithms that derive κ(λ) from ATR spectra (hereafter inverse problem) are well established,⁵⁵ once κ(λ) is known, α(λ) can be calculated. Equation (7) can in principle be used to derive the unknown κ(λ) of the sample from an experimentally measured PTIR spectrum. Compared to ATR spectroscopy, in PTIR the sample is usually thin enough to be considered vertically homogeneous and, most importantly, the sample thickness can be measured concurrently with the spectrum. Consequently, if the PTIR signal transduction factors (H_AFM,H_m, H_th in eq. 5) were known, a single PTIR spectrum would be sufficient to determine κ(λ) (see fig. S-6). However, because the transduction factors are generally unknown and sample-dependent, they provide a challenge for the problem inversion. Essentially, the fraction of light absorbed in the sample is not known, because H_opt(λ) represents only a quantity proportional to it via the scaling factor H_AFMH_mH_th.

Here, for each PMMA thickness from 100 nm to 1 μm, we leverage pairs of calculated s and p polarized H_opt spectra to evaluate whether the inverse problem for PTIR spectra can be solved without knowledge of scaling factors. The relative band intensities in the calculated H_opt spectra show marked difference across the large range of sample thicknesses (see fig. 7a), as expected based on Fig 2. The spectra were scaled by the same, arbitrary number and then used as input to a NLS fit of equation (7) to derive the sample κ(λ) spectrum which was benchmarked against literature data for PMMA⁴⁵ (see Fig.7). For each PMMA thickness, in addition to the pair of PTIR spectra (s and p-polarization), the NLS algorithm also uses the sample n value at a single wavelength away from absorption bands and the layer thickness as input parameters. The real part of the refractive index spectrum was calculated from the imaginary part via a numeric Kramers-Kronig transformation.⁵⁶

Figure 7.

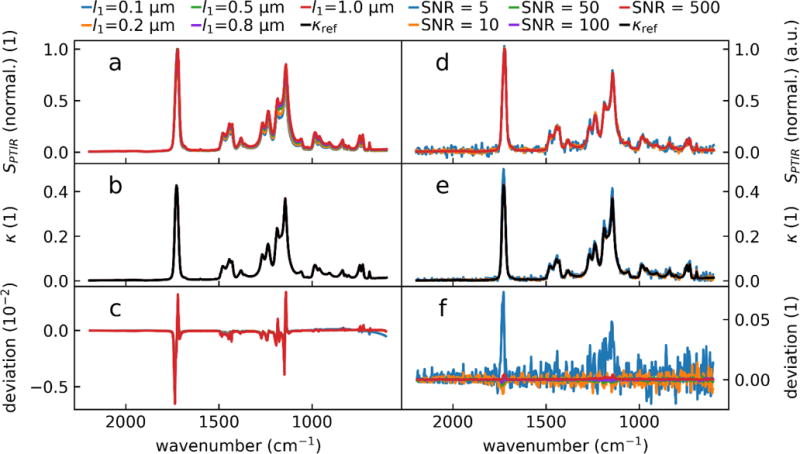
Calculated κ(λ) from pairs of H_opt spectra (s- and p-polarization) for PMMA using a NLS fit a) Calculated H_opt (s-polarization only) for a series of film thicknesses. The spectra intensities were normalized at ≈ 1725 cm⁻¹ to highlight the intensity ratio differences as a function of the sample thicknesses. For each thickness, the pair of spectra (s- and p-polarization) were scaled by an arbitrary number before the NLS fit to ensure that the scaling of the spectrum did not influence the fit. b) κ(λ) spectra as output by the NLS fit function. c) Difference between κ_ref reference literature values and fit results. Panels d-e showcase NLS fit noise resilience. d) Noise (Gaussian distribution with standard deviation σ) was added to the simulated PTIR spectra for a 0.5 μm thick slab of PMMA. The added noise resulted spectra with SNRs (calculated from 8× the standard deviation of the noise and the maximum of the carbonyl peak). e) Recovered κ spectra from noisy input data. f) The difference of the recovered spectra and the noiseless κ_ref Note the different scales on panels c and f.

The resulting κ(λ) spectra closely match reference data (see fig. 7b) demonstrating that the PTIR signal inversion can be achieved for two spectra affected by the same scaling (i.e. PTIR spectra at a given location with different light polarization). We note that the NLS fitting for κ introduced here, works especially well for thick samples and for strongly absorbing bands, where the contribution of non-linearity between α(λ) and the PTIR signal is more noticeable (see fig. 7c). Essentially the method works best for the cases that most need such correction.

To test the stability of the NLS fit procedure, Gaussian noise was added to the input data to the simulated PTIR spectra yielding SNRs ranging from 1000 (close to perfect measurement) to 10 (noisy measurement). The SNR was defined as the ratio of the maximum signal intensity in the spectrum and the noise peak to peak value (8× the standard deviation). Obviously, some noise (with peak to peak comparable the input noise) is noticeable in the recovered κ(λ) spectrum (see fig. 7d–f), but it doesn’t impede the fitting procedure.

Conclusions

Because band positions generally present smaller shift in PTIR spectra than in ATR spectra, PTIR chemical identification of unknown species is expected to work at least as well as ATR and is not affected by the stratification of the sample.

This work provides guidelines for selecting the sample parameters for best PTIR quantitative measurements. To obtain PTIR signals that closely follow a linear behavior, the sample should be thin (< 500 nm), flat and vertically homogenous, as in the case of many PTIR applications to date.^17,22 For quantitative analysis on thicker samples weakly absorbing (≤ 0.1 μm⁻¹) bands should be used. For proper quantitation of strongly absorbing samples, measurements should be obtained for small sample thickness (< 75 nm) and using s polarization.

Thus far band ratios have been leveraged to compare PTIR signal intensity from materials of different thermal and mechanical properties.⁵⁷ However, to properly compare PTIR spectra of samples that have also different heights, it recommended to ratio bands with similar center wavelengths and similar absorptions coefficients to ensure best linearity.

In general, if the sample cannot be prepared thin enough or if no weakly absorbing bands are available for analysis, inverting the PTIR signal to obtain the absorption spectrum, is a general approach, demonstrated here, to enable quantitative analysis of PTIR data and requiring measurement of only 2 spectra with different polarization for each location.

We believe that the guidelines for sample preparation and data analysis provided here will foster PTIR quantitative analysis at the nanoscale across the broad PTIR application space ranging from material science to biology and medicine.