Using observational data to emulate a randomized trial of dynamic treatment-switching strategies: an application to antiretroviral therapy

Abstract

Background: When a clinical treatment fails or shows suboptimal results, the question of when to switch to another treatment arises. Treatment switching strategies are often dynamic because the time of switching depends on the evolution of an individual’s time-varying covariates. Dynamic strategies can be directly compared in randomized trials. For example, HIV-infected individuals receiving antiretroviral therapy could be randomized to switching therapy within 90 days of HIV-1 RNA crossing above a threshold of either 400 copies/ml (tight-control strategy) or 1000 copies/ml (loose-control strategy).

Methods: We review an approach to emulate a randomized trial of dynamic switching strategies using observational data from the Antiretroviral Therapy Cohort Collaboration, the Centers for AIDS Research Network of Integrated Clinical Systems and the HIV-CAUSAL Collaboration. We estimated the comparative effect of tight-control vs. loose-control strategies on death and AIDS or death via inverse-probability weighting.

Results: Of 43 803 individuals who initiated an eligible antiretroviral therapy regimen in 2002 or later, 2001 met the baseline inclusion criteria for the mortality analysis and 1641 for the AIDS or death analysis. There were 21 deaths and 33 AIDS or death events in the tight-control group, and 28 deaths and 41 AIDS or death events in the loose-control group. Compared with tight control, the adjusted hazard ratios (95% confidence interval) for loose control were 1.10 (0.73, 1.66) for death, and 1.04 (0.86, 1.27) for AIDS or death.

Conclusions: Although our effective sample sizes were small and our estimates imprecise, the described methodological approach can serve as an example for future analyses.

Introduction

Many clinical decisions involve switching or discontinuing treatment. The most effective switching strategies are dynamic, that is, they involve switching different individuals at different times depending on the evolution of their time-varying covariates. However, very few randomized trials compare dynamic strategies for switching treatments. Despite this lack of clinical evidence, many clinical guidelines provide recommendations in the form of dynamic switching strategies.

For example, the guidelines for the management of HIV-infected patients issued by the United States Department of Health and Human Services (DHHS)¹ and the International AIDS Society-USA Panel² recommend switching a patient's antiretroviral regimen immediately after a confirmed virological failure (i.e. two consecutive HIV-1 RNA measurements ≥ 200 copies/ml). The European AIDS Clinical Society³ and British HIV Association⁴ guidelines recommend switching immediately if HIV-1 RNA > 500 copies/ml or > 400 copies/ml, respectively, but suggest repeating a viral load measurement if HIV-1 RNA is detected below the threshold for switching. The World Health Organization⁵ guidelines recommend waiting to switch until confirmation of HIV-1 RNA > 1000 copies/ml, the lowest level that can be used when measuring viral load from dried blood spots. Generally, the harder to implement tight-control strategies are recommended to avoid the use of failing antiretrovirals in the presence of ongoing viral replication which may lead to drug-resistant mutations, use of more expensive drugs and limitations on future treatment options.^6–9

Here we review a framework for the comparison of dynamic switching strategies using observational data.^10–14 We begin by describing the protocol of the hypothetical randomized trial we would like to conduct (the target trial). We then review an approach to emulate this target trial using observational data. To overcome the limitations of standard methods for adjustment for time-varying confounders,^15,16 we use inverse-probability weighting of a dynamic marginal structural model.¹⁷

The protocol of the target trial

The target trial is a hypothetical randomized trial that is specified in order to guide our analysis of observational data. Key components of its design are eligibility criteria, treatment strategies being compared, follow-up period, outcomes, causal contrasts of interest and analysis plan. Discussions between colleagues with clinical and statistical backgrounds are generally needed to specify a target trial whose results would be most useful to resolve uncertainties in clinical practice. We describe the components of the target trial below.

Eligibility criteria

The trial includes individuals who initiated antiretroviral therapy in 2002 or later, achieved suppression of viral replication (defined as at least one measurement of HIV-1 RNA ≤ 200 copies/ml) within 360 days of initiating treatment, and then experienced confirmed virological failure (defined as the second of two measurements of HIV-1 RNA > 200 copies/ml 7–180 days apart). At confirmed virological failure (baseline), individuals are required to be 18 years of age or older and to have had a CD4 cell count measurement in the previous 90 days. Eligible antiretroviral regimens before first virological failure are listed in Table 1.

Table 1.

Eligible initial regimens

Regimen classification	Eligible initial regimensa
PI + ≥ 2 NRTI	All regimens where the PI is either fosamprenavir (FAPV) or atazanavir (ATV) except those containing the NRTI tenofovir (TNV) or an excluded drugb
bPI + ≥ 2 NRTI	All regimens except those containing an excluded drugb
NNRTI + ≥ 2 NRTI	All regimens except those containing an excluded drugb
< 6 drugs including FI/INSTI (+ entry inhibitors)	All drug regimens with ≥ 3 drugs except those containing an excluded drugb

PI, protease inhibitor; NRTI, nucleoside reverse transcriptase inhibitor; bPI, boosted protease inhibitor; NNRTI, non-nucleoside reverse transcriptase inhibitor; FI, fusion inhibitor; INSTI, integrase strand transfer inhibitor.

^aEligible regimens were determined by a panel of clinicians on the basis of treatment guidelines.

^bThe following drugs are excluded from initial regimens: enfuvirtide (ENF), zalcitabine (DDC), tipranavir (TPV), alovudine (ALO), capravirine (CPV), DPC 083 (DPC083), delavirdine (DLV), emivirine (EMV), lodenosine (DDA or LDN), loviride (LOV), mozenavir (MOZ), vicriviroc (VIC) and any unspecified drugs (ART, PI, NNRTI, NRTI).

Treatment strategies

Eligible individuals are randomized to either tight- or loose-control strategies at confirmed virological failure. The tight-control strategy is ‘switch within 90 days of HIV-1 RNA crossing above 400 copies/ml’. The loose-control strategy is ‘switch within 90 days of HIV-1 RNA crossing above 1000 copies/ml’. In both arms, individuals should switch from regimens at baseline to new regimens (as indicated in Table 2) and switches are expected to occur uniformly¹¹ during the 90-day grace period. After the initial switch, individuals may subsequently switch to another regimen or discontinue treatment if clinically indicated or recommended by their treating physicians. All individuals should be seen and have their CD4 cell count/HIV-1 RNA measured on average every 12–16 weeks and at least once every 52 weeks. As in all randomized trials, we expect that some individuals will not adhere to the target trial protocol.

Table 2.

Changes from initial regimens to new regimens that are considered switches^a

Regimen classification	Switch from (PI + ≥ 2 NRTI)?	Switch from (bPI + ≥ 2 NRTI)?	Switch from (NNRTI + ≥ 2 NRTI)?	Switch from (< 6 drugs including FI/INSTI + (entry inhibitors))?
PI + ≥ 2 NRTI	Nob	No	Yes	Yes
bPI + ≥ 2 NRTI	Yes	Yes if PI changesb	Yes	Yes
NNRTI + ≥ 2 NRTI	Yes	Yes	Yes if NNRTI to etravirine (ETV)b	Yes
bPI + PI/NNRTI (+ other)	Yes	Yes	Yes if NNRTI to etravirine (ETV)b	Yes
< 6 drugs including FI/INSTI (+ entry inhibitors)	Yes	Yes	Yes	Yes if FI/II/entry inhibitor changes or addition of a FI/II/entry inhibitorb

If the cell reads ‘no’, this type of change is never considered a switch. Changes to regimen classifications other than those in the table are never switches. If the cell reads ‘yes’, this type of change is always considered a switch. If the cell reads ‘yes if …’, the condition(s) listed must be met for the change to be considered a switch. Other aspects of the regimen may also change or stay the same.

Individuals must change to regimens that do not include any of the following drugs: zalcitabine (DDC), alovudine (ALO), capravirine (CPV), DPC 083 (DPC083), delavirdine (DLV), emivirine (EMV), lodenosine (DDA or LDN), loviride (LOV), mozenavir (MOZ), vicriviroc (VIC) or any unspecified drugs (ART, PI, NNRTI, NRTI).

PI, protease inhibitor; NRTI, nucleoside reverse transcriptase inhibitor; bPI, boosted protease inhibitor; NNRTI, nonnucleoside reverse transcriptase inhibitor; FI, fusion inhibitor; INSTI, integrase strand transfer inhibitor.

^aEligible regimens were determined by a panel of clinicians on the basis of treatment guidelines.

^bOur primary definition of switching above does not include NRTI-only changes. An alternative definition includes some NRTI-only changes (i.e. any NRTI to tenofovir (TNV) and tenofovir (TNV) to zidovudine (AZT)). According to this alternative definition, a change where the regimen classification does not change is considered a switch if any part of the regimen changes (according to the conditions above).

Outcomes

The clinical outcomes of interest are all-cause mortality and a combined endpoint of AIDS-defining illness¹⁸ or death.

Follow-up period

Individuals are followed from baseline (randomization) until the outcome, loss to follow-up (52 weeks after the most recent laboratory measurement) or the administrative end of follow-up (3 years after baseline), whichever occurred first.

Causal contrasts of interest

To compare the two switching strategies, we estimate the intention-to-treat effect and the per-protocol effect (i.e. the effect that would have been observed if all participants had switched as indicated in this protocol, regardless of the treatment they received subsequently).

Analysis plan

Intention-to-treat analysis: We estimate 3-year Kaplan-Meier survival curves by randomization arm. Despite its limitations as an effect measure,¹⁹ we also estimate the mortality hazard ratio via the pooled logistic model $\text{logit Pr}\left(D_{t+1}=1\text{|}{D}_t=0, X\right)={\beta }_{0t}+{\beta }_{1}X$, where D_t is an indicator (1: yes, 0: no) for death in week t, ${\beta }_{0t}$ is a time-specific intercept (the baseline hazard, estimated via linear and quadratic terms for t), X is an indicator for randomization arm (1: loose-control, 0: tight-control) and ${\beta }_1$ is the log odds ratio of mortality for loose vs tight control. Because mortality is rare in each time interval, the parameter ${\beta }_1$ approximates the log of the intention-to-treat mortality hazard ratio that would have been estimated from a proportional hazards Cox model.²⁰ In case of a chance imbalance of pre-treatment prognostic factors V between arms, the model would include them as covariates.

Per-protocol analysis: Individuals are censored when they deviate from their assigned switching strategy. In particular, individuals are censored at the time they change treatment prematurely (i.e. between baseline and when HIV-1 RNA first crosses above 400 copies/ml for tight control and above 1000 for loose control), change to an ineligible regimen during the 90-day grace period and at the end of the grace period if the individual has not yet switched to an eligible regimen. Because this censoring may be informative, adjustment for both baseline (pre-randomization) and time-varying (post-randomization) covariates may be necessary.¹¹

To estimate a per-protocol mortality hazard ratio, we fit a weighted model logit $\mathrm{Pr}\left(D_{t+1}=1\text{|}{D}_t=0,C_t=0, X, V\right)={\theta }_{0t}+{\theta }_{1}x+{\theta }_2^{\prime }V$, where C_t is an indicator (1: yes, 0: no) for censoring due to deviating from the assigned switching strategy in week t and V is a vector of the baseline (time-fixed) covariates: sex, age (<35, 35–49, ≥50 years), race (White, Black, other or unknown), geographical origin (North America, Western Europe, sub-Saharan Africa, other or unknown), mode of acquisition (heterosexual, homosexual/bisexual, injection drug use, other or unknown), CD4 cell count (<200, 200–499, ≥500 cells/mm³), HIV RNA (≤400, 401–1000, > 1000 copies/ml), calendar year (2002–04, 2005–07, ≥ 2008), regimen class at initiation [non-nucleoside (NNRTI)-based or non-NNRTI based] and regimen class at baseline (NNRTI-based or non-NNRTI based).

To adjust for time-varying selection bias that is induced by the censoring required for the per-protocol analysis, we use inverse-probability weighting to eliminate the dependence between measured time-varying prognostic factors and censoring. Informally, an uncensored individual’s weight at time t is inversely proportional to his/her probability of remaining uncensored through time t conditional on having survived to time t (D_t), his/her covariate history (${\overline{L}}_t$), and his/her switching history (${\overline{A}}_{t-1}$), where A_t = 2 indicates that the individual has switched to an eligible regimen, A_t = 1 indicates that the individual has changed to an ineligible regimen, and A_t = 0 indicates that the individual has not changed treatment by week t. We weight each individual by the time-varying inverse-probability weight: $W_t=\prod _{k=0}^t\frac{1}{f(A_k|{\overline{A}}_{k-1},D_k=0,{\overline{L}}_k)},$ where $f\left(A_k\text{|}{\overline{A}}_{k-1},D_k=0,{\overline{L}}_k\right)$ is the conditional probability mass function $f_{A_k|{\overline{A}}_{k-1},D_k=0,{\overline{L}}_k}(a_k|{\overline{a}}_{k-1},d_k=0,{\overline{l}}_k)$ with $(a_k|{\overline{a}}_{k-1},d_k=0,{\overline{l}}_k)$ evaluated at the random argument $\left(A_k\text{|}{\overline{A}}_{k-1},D_k=0,{\overline{L}}_k\right)$and $A_{-1}=0$.

As previously described,²¹ these probabilities are estimated using pooled multinomial logistic models including a time-specific intercept (estimated via linear and quadratic terms for t), the baseline covariates previously listed and the time-varying covariates: CD4 cell count (restricted cubic spline with 5 knots at 10, 200, 350, 500 and 1000 cells/mm³), HIV-1 RNA (≤400, 401–1000, >1000 copies/ml), AIDS-defining illness (when the outcome was death alone) and time since last laboratory measurement (<4, 4–7, 8–11, ≥12 weeks). For an explanation of why the probability of treatment changes can be used to estimate the probability of remaining uncensored, please see Cain et al. 2010.¹¹

Under the assumptions that: (i) we measured and successfully adjusted for all baseline and time-varying confounders; (ii) there is positivity (i.e. no deterministic treatment assigned given the confounders); and (iii) the weight models are not misspecified, the above logistic model consistently estimates the parameter of a dynamic marginal logistic structural model:^17,22–24logit $\mathrm{Pr}\left(D_{t+1}^x=1\text{|}{D}_t^x=0,V\right)={\theta }_{0t}^{*}+{\theta }_1^{*}x+{\theta }_2^{*\prime }V$, where $D_t^x$ is the counterfactual indicator that an individual would have developed the outcome during week t under strategy X = x.

To estimate per-protocol survival curves, we fit a similar model that included a product (‘interaction’) term between X and f(t), where f(t) is a flexible function of time (estimated via linear and quadratic terms for t). The model's predicted values are then used to estimate the 3-year survival from baseline as previously described^11,19 (nonparametric estimation of survival curves would result in very unstable estimates). The estimated 3-year survival can be interpreted as the survival that would have been estimated had all individuals switched according to the study protocol (regardless of the treatment they subsequently received).

The same analytical approach is then applied to the combined endpoint of AIDS-defining illness or death. Inverse-probability weighting may be used to adjust for potential selection bias due to loss to follow-up²⁵ in both the intention-to-treat and the per-protocol analyses.

Emulating the target trial using observational data

In the absence of a randomized clinical trial for switching, we emulated one using observational data²² from the Antiretroviral Therapy Cohort Collaboration (ART-CC), the Centers for AIDS Research (CFAR) Network of Integrated Clinical Systems (CNICS) and the HIV-CAUSAL Collaboration. These collaborations have been described elsewhere.^26–29 The cohorts that make up these collaborations are listed in Appendix 1 (available as Supplementary data at IJE online). All overlaps between and within collaborations were removed. Each cohort collected data prospectively, including CD4 cell count, HIV-1 RNA (limit of detection ≤ 200 copies/ml), dates of treatment initiation and treatment changes, AIDS-defining illness and death.

We designed our analysis of the observational data to match the eligibility criteria, the treatment strategies, and the outcomes of the target trial as much as possible.

Eligibility criteria

We applied the same eligibility criteria as in the target trial. Our analysis was restricted to HIV-infected persons who initiated antiretroviral therapy after 1 January 2002 (2004 for CoRIS, 2005 for FHDH and Frankfurt when information on their treatment interruptions became available).

Treatment strategies

We compared the same tight- and loose-control switching strategies as in the target trial. To reduce the influence of data errors, new drug prescriptions of duration of 14 days or less were disregarded when determining the existence of switching. Instead, the time was assigned to the nearest regimen of duration longer than 14 days before the short regimen. In sensitivity analyses, point estimates did not vary (data not shown) for durations of 31 and 62 days, when we assigned the disregarded time to the nearest longer regimen after the short regimen, and when we used an alternative definition of switching (see Table 2).

Outcomes

We considered the same two outcomes as in the target trial: all-cause mortality and a combined endpoint of AIDS-defining illness¹⁸ or death. The date of death was identified using a combination of national and local mortality registries and clinical records as described elsewhere,²⁸ and AIDS-defining illnesses were ascertained by the treating physicians.

Follow-up period

Follow-up started at baseline and ended at the occurrence of the outcome, loss to follow-up (52 weeks after the most recent laboratory measurement) or the cohort-specific administrative end of follow-up (up to November 2012), whichever occurred first.

Causal contrast of interest

For the reasons explained below, only the per-protocol effect comparing the two switching strategies can be estimated.

Analysis

We used the same pooled logistic model described for the target trial, except that we fitted the model to an expanded dataset constructed as follows. Because all individuals had data consistent with both strategies at confirmed virological failure (baseline), we created an expanded dataset that included two replicates (clones) of each individual, and assigned each replicate to one of the strategies. We censored replicates if and when their data were no longer consistent with their assigned strategy.¹⁷ In particular, replicates were censored if and when the individual changed treatment too soon (i.e. between baseline and when HIV-1 RNA first crossed above 400 (1000) copies/ml), if and when the individual changed to an ineligible regimen during the 90-day grace period and at the end of the grace period if the individual had not yet switched to an eligible regimen.

A consequence of using grace periods with cloning and censoring is that an intention-to-treat effect cannot be estimated because each individual is assigned to all strategies at baseline. Therefore, a contrast based on baseline assignment (i.e. an intention-to-treat analysis) will compare groups with essentially identical outcomes. Analyses with a grace period at baseline are geared towards estimating a per-protocol effect of a target trial.

The inverse-probability weights were the same as for the target trial except that we added a numerator¹¹ to emulate uniform switching during the grace period. This numerator equals $\frac{1}{m+1-j}$ when j = m and when 0 ≤ j < m if the individual initiates, and $(1-\frac{1}{m+1-j})$ when 0 ≤ j < m if the individual does not initiate, where m is the length of the grace period in weeks and j is the position in the grace period such that j = 0 is the beginning of the grace period and j = m is the end of the grace period. The weights were truncated at the 99th percentile;³⁰ however, truncation had little effect on the estimates (data not shown).

The inclusion of inverse-probability weights to adjust for censoring at 52 weeks without a laboratory measurement in addition to the previously described weights had little effect on our estimates (data not shown).

All 95% confidence intervals (CIs) were estimated via a nonparametric bootstrap with 500 samples. All analyses were conducted with SAS 9.4 (SAS Institute, Cary, NC, USA).

Results

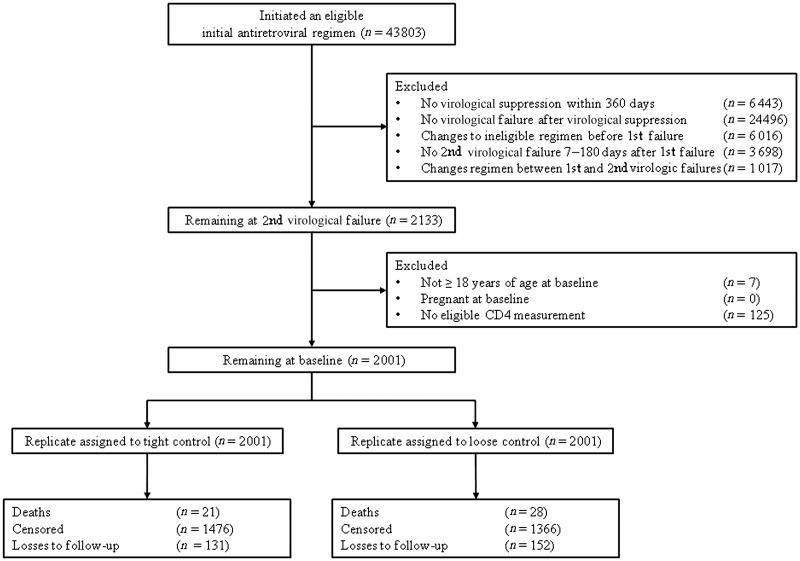
Of 43 803 potentially eligible individuals, 2001 met the baseline inclusion criteria for the mortality analysis and 1641 for the AIDS or death analysis. The most common reason for being excluded was never experiencing virological failure after achieving virological suppression. A flowchart of patients for the mortality analysis is provided in Figure 1.

Figure 1.

Modified CONSORT flow diagram for the mortality analysis in the ART-CC, the CNICS and the HIV-CAUSAL Collaboration, 2002–12.

Table 3 shows the baseline characteristics of the study population for the mortality analysis. Of the 4002 replicates in the expanded dataset, 74% of the tight-control group and 68% of the loose-control group were censored during follow-up. In the tight-control group, 11% were censored for changing treatment prematurely, 14% were censored for changing to an ineligible regimen during the grace period and 75% were censored for not having switched to an eligible regimen by the end of the grace period. In the loose-control group, the respective numbers were 23%, 14% and 63%. Among the uncensored, the median [interquartile range (IQR)] follow-up time was 89 (38, 168) weeks for the tight-control group (1673 person-years) and 82 (40, 166) weeks for the loose-control group (2009 person-years). The numbers were similar in the AIDS or death analysis.

Table 3.

Characteristics of 2001 HIV-infected individuals in the mortality analysis at baseline in the ART-CC, the CNICS and the HIV-CAUSAL Collaboration, 2002–12

Characteristic		No. of individuals (%)
		Western Europe		North America
		1503		498
Sex	Male	959	(63.8)	418	(83.9)
	Female	544	(36.2)	80	(16.1)
Age, years	< 35	540	(35.9)	92	(18.5)
	35–50	774	(51.5)	278	(55.8)
	> 50	189	(12.6)	128	(25.7)
Geographical Origin	North America	0	(0.0)	498	(100.0)
	Western Europe	587	(39.1)	0	(0.0)
	Sub-Saharan Africa	516	(34.3)	0	(0.0)
	Other/unknown	400	(26.6)	0	(0.0)
Race	White	509	(33.9)	176	(35.3)
	Black	398	(26.5)	215	(43.2)
	Other/unknown	596	(39.7)	107	(21.5)
Acquisition group	Heterosexual	836	(55.6)	102	(20.5)
	Homosexual	482	(32.1)	158	(31.7)
	Injection drug use	97	(6.5)	81	(16.3)
	Other/unknowna	88	(5.9)	157	(31.5)
CD4 cell count, per mm3	< 200	387	(25.7)	150	(30.1)
	200–499	801	(53.3)	250	(50.2)
	≥ 500	315	(21.0)	98	(19.7)
HIV-1 RNA, copies/ml	≤ 400	317	(21.1)	147	(29.5)
	401–1000	270	(18.0)	95	(19.1)
	>1000	916	(60.9)	256	(51.4)
Calendar year	2002–04	256	(17.0)	157	(31.5)
	2005–07	714	(47.5)	226	(45.4)
	≥ 2008	533	(35.5)	115	(23.1)
Regimen class at initiation	PI + ≥ 2 NRTI	8	(0.5)	9	(1.8)
	bPI + ≥ 2 NRTI	703	(46.8)	219	(44.0)
	NNRTI + ≥ 2 NRTI	785	(52.2)	268	(53.8)
	< 6 drugs including FI/INSTI (+ entry inhibitors)	7	(0.5)	2	(0.4)
Regimen class at baseline	PI + ≥ 2 NRTI	15	(1.0)	10	(2.0)
	bPI + ≥ 2 NRTI	732	(48.7)	229	(46.0)
	NNRTI + ≥ 2 NRTI	747	(49.7)	257	(51.6)
	< 6 drugs including FI/INSTI (+ entry inhibitors)	9	(0.6)	2	(0.4)

HIV, human immunodeficiency virus; PI, protease inhibitor; NRTI, nucleoside reverse transcriptase inhibitor; bPI, boosted protease inhibitor; NNRTI, nonnucleoside reverse transcriptase inhibitor; FI, fusion inhibitor; INSTI, integrase strand transfer inhibitor.

^aOther/unknown acquisition group included all VACS-VC participants.

There were 21 deaths and 33 AIDS or death events in the tight-control group, and 28 deaths and 41 AIDS or death events in the loose-control group (Table 4; see Appendix 2 for details, available as Supplementary data at IJE online). Among those who died, the median (IQR) time to death was 31 (11, 52) weeks for the tight-control group and 42 (14, 113) weeks for the loose-control group. Among those who developed AIDS or died, the median (IQR) time to AIDS or death was 11 (2, 29) weeks for the tight-control group and 15 (7, 60) weeks for the loose-control group. Compared with tight control, the fully-adjusted hazard ratios (95% CI) for loose control were 1.10 (0.73, 1.66) for death and 1.04 (0.86, 1.27) for AIDS or death. Adjustment for either baseline or time-varying variables did not materially change the hazard ratio estimates (Table 4). The estimated inverse-probability weights had mean 3.1 (interquartile range 1.2, 3.2, 99th percentile 15.5) for the mortality analysis, and 3.1 (interquartile range 1.1 − 3.4, 99th percentile 17.2) for the AIDS or death analysis. The main predictors of switching were HIV-1 RNA and time since last laboratory measurement (see Appendix Table 1, available as Supplementary data at IJE online).

Table 4.

Hazard ratios of clinical outcomes under tight- and loose-control switching strategies in the ART-CC, the CNICS and the HIV-CAUSAL Collaboration, 2002–12

Outcome	Strategy (HIV-1 RNA threshold in copies/ml)	No. of outcomes (overlap with tight)	Median (IQR) time to event in weeks	Hazard ratio, 95% confidence interval
				Unadjusted		Baseline-adjusted		Baseline and time- varying adjusteda,b
Death	Tight (400)	21	31 (11, 52)	1 (ref.)		1 (ref.)		1 (ref.)
	Loose (1000)	28 (20)	42 (14, 113)	1.11	0.88, 1.41	1.13	0.93, 1.38	1.10	0.73, 1.66
AIDS or death	Tight (400)	33	11 (2, 29)	1 (ref.)		1 (ref.)		1 (ref.)
	Loose (1000)	41 (31)	15 (7, 60)	1.08	0.90, 1.28	1.05	0.90, 1.23	1.04	0.86, 1.27

HIV, human immunodeficiency virus; IQR, interquartile range; ref., reference.

^aAdjusted for the baseline covariates (sex, age, race, geographical origin, mode of acquisition, CD4 cell count, HIV RNA, calendar year, regimen class at initiation, and regimen class at baseline and time-varying covariates (CD4 cell count, HIV RNA, AIDS-defining illness and time since last laboratory measurement).

^bTime-varying adjustment carried out by inverse-probability weighting with weights truncated at the 99th percentile.

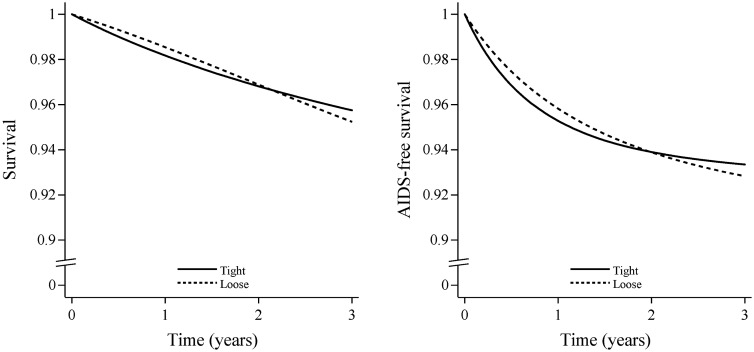
Figure 2 plots the estimated 3-year survival and 3-year AIDS-free survival. The survival at 3 years was 95.7% (93.4%, 98.1%) for tight control and 95.2% (92.8%, 97.6%) for loose control. The 3-year survival difference was −0.5% (−2.3%, 1.2%). The AIDS-free survival proportion was 93.3% (90.5%, 96.1%) for tight control and 92.8% (89.7%, 95.9%) for loose control. The 3-year AIDS-free survival difference was −0.5% (−1.9%, 0.8%).

Figure 2.

Survival (left) and AIDS-free survival (right) under tight- and loose-control switching strategies in the ART-CC, the CNICS and the HIV-CAUSAL Collaboration, 2002–12. The curves are standardized by the baseline covariates and inverse-probability weighted by the time-varying covariates listed under Table 4.

As a sensitivity analysis, we also considered an alternative trial in which we did not require confirmation of virological failure. In this case, baseline becomes the time of first virological failure (defined as one measurement of HIV-1 RNA > 200 copies/ml) following virological suppression. Estimated hazard ratios using this definition of baseline were similar (see Appendix 3 for details, available as Supplementary data at IJE online).

Discussion

We have described how to use observational data to emulate a target trial that compares different treatment switching strategies. As an illustration, we applied the method to the question of when to switch from a first-line antiretroviral regimen to a new regimen, following virological failure.

Our results suggest that there is little difference between switching within 90 days of HIV-1 RNA crossing above a threshold of either 400 copies/ml or 1000 copies/ml in terms of preventing short-term death and AIDS-defining illness. However, even after pooling data from three large consortia of HIV cohorts, our effective sample size was small and the effect estimates imprecisely estimated. This was due, in large part, to the strict eligibility criteria of our target trial, which were defined by a panel of clinicians on the basis of the treatment guidelines. Of the 43 803 potentially eligible individuals, 95% were excluded because they did not meet the baseline inclusion criteria. Most individuals excluded were doing well on their first-line antiretroviral regimen and did not experience virological failure. Had we been able to observe individuals for longer periods of time, more of them would likely have experienced virological failure and could have been included in our analyses.

Most individuals in our analyses contributed to both arms of the target trial. Because one cannot generally observe the exact moment at which HIV-1 RNA thresholds were crossed, 59% of individuals crossed both thresholds at baseline (those with baseline HIV-RNA ≤ 400 copies/ml had the potential to cross both thresholds simultaneously later in their follow-up). In the main analysis, 20 of 29 individuals who died and 31 of 43 individuals who developed AIDS or died contributed events to both groups (see Appendix 2 for details). Similar difficulties have been encountered when trying to emulate target trials that compare two dynamic strategies in cancer patients.³¹

The validity of our methodology relies on two key assumptions in addition to positivity. First, we assume there is no unmeasured confounding given the measured covariates, i.e. that all joint predictors of switching and the outcome were included in the estimation of the inverse-probability weights. The assumption might not hold, even approximately, if for example previous adherence to treatment and antiretroviral drug resistance remained important predictors of treatment switching and the outcome, even after adjustment for the measured covariates (some of which may be viewed as proxies for adherence and resistance). To further protect our estimates from unmeasured confounding, we defined the dynamic treatment strategies in terms of initial switching regardless of subsequent adherence to treatment. Defining the strategies this way makes it unnecessary to adjust for joint determinants of future switching and is perhaps more clinically meaningful, as at the time of deciding whether or not to switch, future adherence is unknown.

Second, we assumed a correct specification of the model for switching as a function of the measured confounders. To reduce bias due to model misspecification that results in apparent outliers, we truncated the estimated weights at the 99th percentile of the distribution of the estimated weights.³⁰

Our analyses only focused on the decision to switch regimens after treatment failure, but in practice switching may occur for other reasons, including regimen simplification, toxicity management and avoidance of teratogenic effects during pregnancy. The dates of pregnancies were not available for the majority of individuals in this analysis, and we restricted the analysis to those who became virologically suppressed and therefore were more likely to adhere and less likely to experience treatment-related toxicities (more common in the early stages of therapy).

We defined our treatment strategies for switching based on HIV-1 RNA viral load only. The majority of clinical guidelines^1–4 also recommend investigating the reasons for failure, addressing any adherence issues and performing resistance testing while the individual is on the failing regimen before switching. Data on adherence and the results of resistance testing were not available for the majority of individuals in this analysis, but we hope to be able to incorporate these data in the future. These considerations may suggest that even with reasonable eligibility criteria and minimal unmeasured confounding, our target trial was of limited clinical relevance in the populations and periods during which the observational data for our study were collected.

In summary, we described an approach to compare dynamic strategies of treatment switching via censoring and inverse-probability weighting. We expect that the methodological approach described here for the comparison of dynamic switching strategies using observational data will serve as an example for future analyses. Future applications may consider switching strategies for which more HIV-infected individuals are eligible and the use of alternative methods for comparing dynamic strategies of treatment switching, including the parametric g-formula, which may result in more precise estimates at the expense of additional modelling assumptions.^16,32–34

Supplementary Data

Supplementary data are available at IJE online.

Funding

The ART-CC is supported by the UK Medical Research Council [grant numbers G0700820, MR/J002380/1] and the Department for International Development (DFID). The CNICS is supported by the National Institutes of Health [grant number R24 AI067039], which was made possible by the National Institute of Allergy and Infectious Diseases (NIAID) and the National Heart, Lung and Blood Institute (NHLBI). The HIV-CAUSAL Collaboration is supported by the National Institutes of Health [grant number R01-AI073127]. J.S. is funded by National Institute for Health Research Senior Investigator award [NF-SI-0611-10168]. The UK CHIC Study is funded by the Medical Research Council (MRC) UK (grant numbers G0000199, G0600337, G0900274 and M004236). The views expressed in this manuscript are those of the researchers and not necessarily those of the MRC.

Conflict of interest: Andrea Antinori currently receives honoraria for consultancy agreement from Gilead Sciences, Bristol Myers Squibb, Merck, Janssen-Cilag, ViiV Healthcare, AbbVie. His institution receives research grants from Gilead Sciences, Bristol Myers Squibb, Janssen-Cilag. All these conflicts are outside the submitted work. Heiner Bucher has received honoraria from BMS and Gilead Sciences in the past 6 months. His institution has received grants from BMS and Gilead Sciences and funds for travel reimbursement from Gilead Sciences and ViiV Healthcare. Joseph J. Eron is a consultant to Merck, BMS, ViiV Healthcare, Janssen and Gilead Sciences. His university receives grant support in his name from Janssen and ViiV Healthcare. Richard Haubrich is an employee of Gilead Sciences. Michael Mugavero is a consultant with Janssen Therapeutics, Georgetown University / amfAR, NASTAD, Bristol-Myers Squibb and Gilead Sciences, and has received fees for his services as a consultant. Peter Reiss through his institution has received independent scientific grant support from Gilead Sciences, Janssen Pharmaceutical Inc., Merck & Co., Bristol-Myers Sqiubb and ViiV Healthcare; he has served on scientific advisory board for Gilead Sciences; he serves on a data safety monitoring committee for Janssen Pharmaceutical Inc and chaired a scientific symposium by ViiV Healthcare, for which his institution has received remuneration. Michael Saag has received research grant support paid to his institution from Merck, Gilead, BMS, ViiV and AbbVie. Caroline Sabin is a member of the speakers' bureau for Gilead Sciences. She provides educational training materials for Gilead Sciences, ViiV Healthcare and Janssen-Cilag. She is a member of Data Safety and Advisory Boards for Janssen-Cilag and ViiV Healthcare and has given talks for Bristol Myers Squibb. Ramon Teira has occasionally served as a speaker in symposia or other events organized by: Janssen Cilag, Abbvie, ViiV Healthcare and Gilead Sciences.