On Enrichment Strategies for Biomarker Stratified Clinical Trials

Summary

In the era of precision medicine, drugs are increasingly developed to target subgroups of patients with certain biomarkers. In large all-comer trials using a biomarker stratified design (BSD), the cost of treating and following patients for clinical outcomes may be prohibitive. With a fixed number of randomized patients, the efficiency of testing certain treatments parameters, including the treatment effect among biomarker positive patients and the interaction between treatment and biomarker, can be improved by increasing the proportion of biomarker positives on study, especially when the prevalence rate of biomarker positives is low in the underlying patient population. When the cost of assessing the true biomarker is prohibitive, one can further improve the study efficiency by oversampling biomarker positives with a cheaper auxiliary variable or a surrogate biomarker that correlates with the true biomarker. To improve efficiency and reduce cost, we can adopt an enrichment strategy for both scenarios by concentrating on testing and treating patient subgroups that contain more information about specific treatment parameters of primary interest to the investigators. In the first scenario, an enriched biomarker stratified design (EBSD) enriches the cohort of randomized patients by directly oversampling the relevant patients with the true biomarker, while in the second scenario, an auxiliary-variable-enriched biomarker stratified design (AEBSD) enriches the randomized cohort based on an inexpensive auxiliary variable, thereby avoiding testing the true biomarker on all screened patients and reducing treatment waiting time. For both designs, we discuss how to choose the optimal enrichment proportion when testing a single hypothesis or two hypotheses simultaneously. At a requisite power, we compare the two new designs with the BSD design in term of the number of randomized patients and the cost of trial under scenarios mimicking real biomarker stratified trials. The new designs are illustrated with hypothetical examples for designing biomarker-driven cancer trials.

1. Introduction

There is a large literature on study designs integrated with treatment-selection biomarkers. See Mandrekar and Sargent (2009), Freidlin et al. (2010) and Tajik et al. (2013) for recent reviews. Biomarker stratified clinical trials have been frequently used to evaluate the effect and safety of an experimental therapy relative to a control therapy as well as to evaluate the utility of using the biomarker in directing treatments. A trial with a biomarker stratified design (BSD) randomizes all patients to one of the treatment therapies with biomarker as a stratification factor. Such an all-comer trial allows hypothesis testing on treatment parameters related to treatment effects among biomarker positive patients, biomarker negative patients and the overall populations as well as the value of utilizing biomarker to direct treatments. A BSD trial is especially useful when the biomarker of interest has weak or moderate credentials in directing treatments based on pre-existing data (Korn and Freidlin, 2016).

In this paper, we investigate two improved designs based on biomarker stratified clinical trials. The standard BSD design is an all-comer design, in which all eligible patients are enrolled, tested for biomarker, and then randomized. The proportion of patients with given biomarker values is not optimized for efficiency in testing specific treatment parameters. Also, the number of enrolled patients in such trial is often limited by the prohibitive cost associated with treating patients and following them for clinical outcomes. For example, when the prevalence rate of biomarker positives is low, say less than 20%, with a given trial size, the efficiency for testing the treatment effect among biomarker positives and the interaction between treatment and biomarker can be very low, while the contribution of a relatively large number of biomarker negatives to the power of testing the two treatment parameters is small. In one of the improved designs, referred to as the enriched biomarker stratified design (EBSD), we increase (enrich) the relative proportion of biomarker positives among the randomized patients from 20% to 50% or higher by keeping all biomarker positives and retaining only a proportion of biomarker negatives. With the same number of randomized patients, the EBSD design is able to include more patients with more information on the relevant treatment parameters than the BSD design. In another situation where the cost associated with testing the true biomarker is high and there exists some inexpensive auxiliary variables that is positively correlated to the true biomarker, we can utilize the same enrichment strategy to enrich the randomized patients with more information about specific treatment parameters by oversampling based on the auxiliary biomarker. This improved design is referred to as an auxiliary-variable-enriched biomarker stratified design (AEBSD). Unlike the EBSD design, AEBSD avoids testing the true maker status for all screened patients and can be a useful design when testing for the true biomarker is expensive or time-consuming and there exists a cheaper auxiliary variable or surrogate biomarker that correlates with the true biomarker and thus achieves greater cost-efficiency.

Both EBSD and AEBSD designs use an enrichment strategy - oversampling patients who contain more information about specific treatment parameters and undersampling those who do not - to improve the study efficiency of biomarker stratified trials. Like the biomarker stratified design, these improved designs permit inference on the biomarker negative population, overall population and the interaction effect between treatment and biomarker. But unlike the biomarker stratified design, the enrichment designs usually use a smaller sample of biomarker negative patients, resulting in a more cost-efficient design. In this paper, we will study how to determine the optimal enrichment proportions for both new designs to maximize the testing efficiency for specific treatment parameters. We will compare the relative efficiency of the two designs over BSD in term of the number of randomized patients and the cost of the trial conduct. Yang et al. (2015) investigated a variant of an enriched biomarker design and demonstrated that this design can improve testing efficiency in treatment effect among biomarker positives with continuous outcome. Both EBSD and AEBSD represent new enrichment sampling strategies to improve trial efficiency and they should be distinguished from the commonly used term “enrichment design” for a targeted design or biomarker positive only design (e.g. Simon and Maitournam (2004)).

The rest of the paper is organized as follows. Section 2 introduces the background of a biomarker stratified design (BSD). In Section 3, we describe the enriched biomarker stratified design (EBSD) and discuss how to design a EBSD trial at the optimal enrichment proportion for testing specific treatment parameters. In Section 4, we describe the auxiliary-variable-enriched biomarker stratified design (AEBSD) and explain how to obtain the optimal probabilities for selecting patients based on auxiliary biomarkers. In Section 5, we compare the two enrichment designs with BSD in several settings mimicking real biomarker stratified trials. In Section 6, we illustrate EBSD with a hypothetical Herceptin trial in breast cancer and AEBSD with a EGFR-inhibitor trial in lung cancer. In Section 7, we conclude the paper with several remarks.

2. Biomarker Stratified Design (BSD)

A biomarker stratified design (BSD) is a commonly used all-comer design for evaluating treatment effects in various biomarker subgroups and the predictive value of the biomarker for optimal treatments. As illustrated in Figure 1a, in a BSD design all screened patients will be randomized to one of two treatments (Experimental E or Control C) with biomarker as a stratification factor. Denote κ₁ the selection probability for the biomarker positives and κ₀ the biomarker negatives. In a BSD design, both κ₁ and κ₀ are equal to one so that the expected proportion of biomarker positives in the randomized cohort is equal to π, the prevalence rate of biomarker positives in the underlying patient population.

Figure 1.

Diagram for (a) Biomarker stratified design (BSD), (b) Enriched biomarker stratified design (EBSD) and (c) Auxiliary-variable-enriched biomarker stratified design (AEBSD). For BSD and EBSD, π is the prevalence of biomarker positives in the population; κ₁ and κ₀ are the selection probability for biomarker positives and biomarker negatives into the randomized cohort, respectively. For AEBSD, π̃ is the prevalence of auxiliary positives in the population; κ̃₁ and κ̃₀ are the selection probability for auxiliary positives and auxiliary negatives into the randomized cohort, respectively.

2.1 Notation and Assumptions

For illustrative purpose, we focus on a biomarker stratified trial in which the effect of an experimental therapy E over a control therapy C on a binary outcome, such as tumor response (yes vs. no), on patients with positive biomarker and negative biomarker. Let M = {+, −} or M = {1,0} denote the biomarker status with P(M+) = π and P(M−) = 1 − π. Let D = {E,C} or D = {1,0} denote the treatment to which a patient is assigned by random allocation and Y represent the response outcome (Y = 1 for response; Y = 0 for no response). Denote the response rates for patients with D = {E,C} and M = {1,0} as η_E1 = P(Y = 1|D = 1, M = 1), η_E0 = P(Y = 1|D = 1, M = 0), η_C1 = P(Y = 1|D = 0, M = 1) and η_C0 = P(Y = 1|D = 0, M = 0). Several treatment effects can be defined based on the data arising from a BSD design. In this paper, we focus on the response rate, although other related measures, such as log odds, could also be used.

• Treatment effect in M+ patients: B₁ = η_E1 − η_C1

• Treatment effect in M− patients: B₀ = η_E0 − η_C0

• Overall treatment effect: B = πB₁ + (1 − π)B₀, which is average treatment effect weighted by the prevalence of biomarker positivity in the population.

• Interaction between treatment and biomarker: δ = B₁ − B₀ = (η_E1 − η_C1) − (η_E0 − η_C0)

• Clinical benefit between biomarker-guided approach and a standard biomarker-unguided approach:

  $${\theta }_{\gamma }=\text{response rate in biomarket}-\text{guided patients}-\text{response rate in biomarket}-\text{unguided patients}=[\pi {\eta }_{E1}+(1-\pi ){\eta }_{C0}]-[\gamma \pi {\eta }_{E1}+\gamma (1-\pi ){\eta }_{E0}+(1-\gamma )\pi {\eta }_{C1}+(1-\gamma )(1-\pi ){\eta }_{C0}]=(1-\gamma )\pi B_1-\gamma (1-\pi )B_0$$

  where γ is the proportion of patients treated by the experimental therapy E in the biomarker-unguided approach. θ_γ is a measure of treatment benefit difference of two strategies: a biomarker-guided strategy in which optimal treatment is determined by biomarker and a biomarker-unguided strategy where treatment is assigned to a proportion γ of patients without considering biomarker status. Notice that θ_γ can be directly estimated from biomarker-strategy trials (e.g. Sargent et al. (2005)). When γ = 0 we have θ₀ = πB₁, commonly used as a global measure for biomarker performance in treatment selection (Brinkley et al., 2010; Janes et al., 2011, 2014).

Let n denote the total number of randomized patients in a BSD trial. Let n_E1, n_C1, n_E0, n_C0 denote the sample sizes in the D = {E,C} and M = {1,0} groups, respectively. Let m_E1, m_C1,m_E0, m_C0 denote the number of responding patients in the corresponding patient groups. The unbiased estimators for these parameters and the corresponding variance estimators can be written as:

• B̂₁ = η̂_E1−η̂_C1 and $\widehat{\mathit{\text{var}}}({\hat{B}}_1)={\hat{\eta }}_{E1}(1-{\hat{\eta }}_{E1})/n_{E1}+{\hat{\eta }}_{C1}(1-{\hat{\eta }}_{C1})/n_{C1}$, where η̂_E1 = m_E1/n_E1 and η̂_C1 = m_C1/n_C1 are the estimates for the response rates for groups E1 and C1, respectively.

• B̂₀ = η̂_E0−η̂_C0 and $\widehat{\mathit{\text{var}}}({\hat{B}}_0)={\hat{\eta }}_{E0}(1-{\hat{\eta }}_{E0})/n_{E0}+{\hat{\eta }}_{C0}(1-{\hat{\eta }}_{C0})/n_{C0}$, where η̂_E0 = m_E0/n_E0 and η̂_C0 = m_C0/n_C0 are the estimates for the response rates for groups E₀ and C₀, respectively.

• B̂ = πB̂₁ + (1 − π)B̂₀ and

  $$\widehat{\mathit{\text{var}}}(\hat{B})={\pi }^2\widehat{\mathit{\text{var}}}({\hat{\eta }}_{E1})+{\pi }^2\widehat{\mathit{\text{var}}}({\hat{\eta }}_{C1})+{(1-\pi )}^2\widehat{\mathit{\text{var}}}({\hat{\eta }}_{E0})+{(1-\pi )}^2\widehat{\mathit{\text{var}}}({\hat{\eta }}_{C0})$$

• δ̂ = B̂₁ − B̂₀ and $\widehat{\mathit{\text{var}}}(\hat{\delta })=\widehat{\mathit{\text{var}}}({\hat{B}}_1)+\widehat{\mathit{\text{var}}}({\hat{B}}_0)$

• θ̂_γ = (1 − γ)πB̂₁ − γ(1 − π)B̂₀ and $\widehat{\mathit{\text{var}}}({\hat{\theta }}_{\gamma })={\pi }^2{(1-\gamma )}^2\widehat{\mathit{\text{var}}}({\hat{B}}_1)+{\gamma }^2{(1-\pi )}^2\widehat{\mathit{\text{var}}}({\hat{B}}_0)$.

For B̂ and θ̂_γ we have assumed that π is known. If π is unknown it can be estimated by n₁/n where n₁ is the total number of biomarker positives in the randomized cohort. In this case, the variance expressions are more complicated.

2.2 Hypothesis testing on treatment parameters

A typical BSD trial is designed to test one or more hypotheses involving the aforementioned treatment parameters and the results of these tests reveal different aspects of the effect of the experimental therapy over the control therapy conditional or unconditional on biomarker status. Several common scenarios are listed in Table 1. The primary task designing a BSD trial is to ensure that the design is adequately powered for testing the chosen hypothesis. Let ξ = (B₁, B₀, B, δ, θ_γ) and ξ̂ = (B̂₁, B̂₀, B̂, δ̂, θ̂_γ). Each element of ξ̂ is a linear combination of (η̂_E1, η̂_C1, η̂_E0, η̂_C0), which follows a multivariate normal distribution by the central limit theorem. As a result, each element of ξ̂ has an asymptotic normal distribution by Slutsky’s theorem. That is, when n is large, $Z_i=\frac{{\hat{\xi }}_i-{\xi }_i}{\sqrt{\widehat{\mathit{\text{var}}}({\hat{\xi }}_i)}}\dot{~}𝒩(0,1)$ for i = 1, ⋯, 5. Standard normal distribution results can be used to derive the coverage probability for the 95% confidence interval and calculate the power for testing each treatment parameter. As an illustration, a proof that B̂ has an asymptotic normal distribution is given in the supplementary materials.

Table 1.

Tests on different treatment parameters and their combinations

Case	Hypothesis	Interpretation
1	H0: B1 = 0 vs. Ha: B1 ≠ 0	Test on B1
2	H0: B0 = 0 vs. Ha: B0 ≠ 0	Test on B0
3	H0: B = 0 vs. Ha: B ≠ 0	Test on B
4	H0: δ = 0 vs. Ha: δ ≠ 0	Test on δ
5	H0: θγ = 0 vs. Ha: θγ ≠ 0	Test on θγ
12	H10: B1 = 0 vs. H1a: B1 ≠ 0	Test on B1 and B0
	H20: B0 = 0 vs. H2a: B0 ≠ 0
13	H10: B1 = 0 vs. H1a: B1 ≠ 0	Test on B1 and B
	H20: B = 0 vs. H2a: B ≠ 0
14	H10: B1 = 0 vs. H1a: B1 ≠ 0	Test on B1 and δ
	H20: δ = 0 vs. H2a: δ ≠ 0
15	H10: B1 = 0 vs. H1a: B1 ≠ 0	Test on B1 and θγ
	H20: θγ = 0 vs. H2a: θγ ≠ 0

3. Enriched Biomarker Stratified Designs (EBSD)

Figure 1b shows a diagram for the EBSD design, in which biomarker positive patients will be selected into the cohort of randomized patients with probability κ₁ and the biomarker negative patients will be selected into the randomized cohort with probability κ₀, and only those patients in the randomized cohort will be treated and followed up. In this paper, our discussion is focused on equal allocation of patients to the two treatment arms. The proposed approach can be easily extended to unequal allocation between treatment arms. Indeed, the allocation ratio between treatment arms can be another design parameter subject to optimization for the power of testing specific hypotheses. For all scenarios of hypothesis testing listed in Table 1, we will search for the optimal enrichment proportion π_e > 0. The expected proportion of positives in the trial is $\frac{{\kappa }_1\pi }{{\kappa }_1\pi +{\kappa }_0(1-\pi )}$. If we set the above = π_e then ${\kappa }_0={\kappa }_1\frac{\pi /(1-\pi )}{{\pi }_e/(1-{\pi }_e)}$. Any pair (κ₀, κ₁) satisfying the above will work. Thus, there is no unique solution pair (κ₀, κ₁) for any given π_e > 0. However, we want to minimize the number of patients omitted from the study (i.e., maximize the number selected for randomization among screened patients), so we choose κ₀ and κ₁ to be as large as possible. This additional consideration yields the following unique values for κ₀ and κ₁:

$${\kappa }_0={\kappa }_1=1\text{ if }{\pi }_e=\pi$$

$${\kappa }_0=\frac{\pi /(1-\pi )}{{\pi }_e/(1-{\pi }_e)},{\kappa }_1=1,\text{ if }{\pi }_e>\pi$$

$${\kappa }_0=1,{\kappa }_1=\frac{{\pi }_e/(1-{\pi }_e)}{\pi /(1-\pi )},\text{ if }{\pi }_e<\pi$$

Thus, for any given π_e, including the optimal ${\pi }_e^{\mathit{\text{opt}}}$, the values of κ₀ and κ₁ are uniquely determined as above.

3.1 Test on B

The variance for the estimate of the overall treatment effect B̂ = πB̂₁ + (1 − π)B̂₀ can be written as

$$\mathit{\text{var}}(\hat{B})={\pi }^2\frac{2{\eta }_{E1}(1-{\eta }_{E1})}{n{\pi }_e}+{\pi }^2\frac{2{\eta }_{C1}(1-{\eta }_{C1})}{n{\pi }_e}+{(1-\pi )}^2\frac{2{\eta }_{E0}(1-{\eta }_{E0})}{n(1-{\pi }_e)}+{(1-\pi )}^2\frac{2{\eta }_{C0}(1-{\eta }_{C0})}{n(1-{\pi }_e)}$$ (1)

For an EBSD trial with n randomized patients, the optimal enrichment proportion ${\pi }_e^{\mathit{\text{opt}}}$ for biomarker positive patients can be obtained by minimizing $\widehat{\mathit{\text{var}}}(\hat{B})$. It is straightforward to show the optimal enrichment proportion for biomarker positives

$${\pi }_e^{\mathit{\text{opt}}}=\frac{1}{1+\frac{1-\pi }{\pi }\sqrt{\varphi }}$$ (2)

where

$$\varphi =\frac{{\eta }_{E0}(1-{\eta }_{E0})+{\eta }_{C0}(1-{\eta }_{C0})}{{\eta }_{E1}(1-{\eta }_{E1})+{\eta }_{C1}(1-{\eta }_{C1})}$$ (3)

Note that ${\pi }_e^{\mathit{\text{opt}}}$ approaches π when ϕ approaches 1.

3.2 Test on δ

For an EBSD trial with n randomized patients, the optimal enrichment proportion ${\pi }_e^{\mathit{\text{opt}}}$ for biomarker positive patients in testing δ can be obtained by finding the minimizer for var(δ̂)

$$\mathit{\text{var}}(\hat{\delta })=\frac{2{\eta }_{E1}(1-{\eta }_{E1})}{n{\pi }_e}+\frac{2{\eta }_{C1}(1-{\eta }_{C1})}{n{\pi }_e}+\frac{2{\eta }_{E0}(1-{\eta }_{E0})}{n(1-{\pi }_e)}+\frac{2{\eta }_{C0}(1-{\eta }_{C0})}{n(1-{\pi }_e)}$$ (4)

The optimal enrichment proportion in this case is given by

$${\pi }_e^{\mathit{\text{opt}}}=\frac{1}{1+\sqrt{\varphi }}$$ (5)

where ϕ is defined in (3). Note that ${\pi }_e^{\mathit{\text{opt}}}$ approaches 0.5 when ϕ approaches 1.

3.3 Test on θ_γ

When testing θ_γ = (1 − γ)πB₁ − γ(1 − π)B₀ with an EBSD design with 0 ≤ γ ≤ 1, one can minimize

$$\mathit{\text{var}}({\hat{\theta }}_{\gamma })=\frac{2{(1-\gamma )}^2{\pi }^2}{n{\pi }_e}·({\eta }_{E1}(1-{\eta }_{E1})+{\eta }_{C1}(1-{\eta }_{C1}))+\frac{2{\gamma }^2{(1-\pi )}^2}{n(1-{\pi }_e)}·({\eta }_{E0}(1-{\eta }_{E0})+{\eta }_{C0}(1-{\eta }_{C0}))$$ (6)

It is straightforward to obtain the solution

$${\pi }_e^{\mathit{\text{opt}}}=\frac{1}{1+\frac{\gamma (1-\pi )}{(1-\gamma )\pi }\sqrt{\varphi }}$$ (7)

where ϕ is defined in (3). Note that when γ = 0 we have θ₀ = πB₁ and ${\pi }_e^{\mathit{\text{opt}}}=1$ and when γ = 1 we have θ₁ = −(1 − π)B₀ and ${\pi }_e^{\mathit{\text{opt}}}=0$.

3.4 Testing two hypotheses

Without loss of generality, we will use an α splitting approach in the discussion of simultaneously testing two hypotheses. Other testing procedures for control of the overall type I error involving multiple hypotheses can be adopted (e.g. (Matsui et al., 2014)) but these will not be discussed in this paper. When testing two hypotheses, as in cases 12, 13, 14, 15 in Table 1, we can find the optimal enrichment proportion π_e by minimizing the maximum of the required sample sizes for the first hypothesis and the second hypothesis at given type I errors (α₁, α₂) and type II errors (β₁, β₂). For example, for testing B₁ and δ, the sample size n(π_e; H_1a) for the first hypothesis is given as

$$n({\pi }_e;H_{1a})=\frac{{(z_{{\alpha }_1/2}+z_{{\beta }_1})}^2}{B_1^2/{\mathit{\text{var}}}^{\ast }({\hat{B}}_1)}$$ (8)

For the second hypothesis, the sample size n(π_e; H_2a) is

$$n({\pi }_e;H_{2a})=\frac{{(z_{{\alpha }_2/2}+z_{{\beta }_2})}^2}{{\delta }^2/{\mathit{\text{var}}}^{\ast }(\hat{\delta })}$$ (9)

where var*(B̂₁) = nvar(B̂₁) and var*(δ̂) = nvar(δ̂). The optimal π_e, i.e. ${\pi }_e^{\mathit{\text{opt}}}$, such that n_max = max(n(π_e; H_1a), n(π_e; H_2a)) is minimized can be obtained straightforwardly by numerical method.

4. Auxiliary-variable-enriched Biomarker Stratified Design (AEBSD)

The cost of the assessment of the true status of a biomarker M for all patients is often prohibitive. However, suppose that we have an auxiliary variable or a biomarker based on another assay M̃ that is predictive of M and can be easily and cheaply assessed. One can enrich the study with true biomarker positive patients by selecting patients to be randomized based on the values of M̃. Only the patients selected for randomization will have their true biomarkers M measured. Let π and π̃ denote the prevalence rates of patients with positive true biomarker (M = 1) and positive auxiliary biomarker (M̃ = 1) respectively in the population. The positive predictive value PPV is the probability that a patient with positive auxiliary biomarker (M̃ = 1) also has a positive true biomarker (M = 1). That is, PPV = Pr(M = 1|M̃ = 1). Let κ̂₁ ∈ [0, 1] and κ̂₀ ∈ [0, 1] represent the probability of patients with positive and negative auxiliary variable M̃ being selected into the randomized cohort, respectively. The enrichment proportion for an auxiliary positive patient is ${\stackrel{\sim }{\pi }}_e=\frac{\stackrel{\sim }{\pi }{\stackrel{\sim }{\kappa }}_1}{\stackrel{\sim }{\pi }{\stackrel{\sim }{\kappa }}_1+(1-\stackrel{\sim }{\pi }){\stackrel{\sim }{\kappa }}_0}$. The probability of a randomized patient with a positive true biomarker can be written as

$${\pi }_e=\mathit{\text{PPV}}{\stackrel{\sim }{\pi }}_e+\left(\frac{\pi -\stackrel{\sim }{\pi }\mathit{\text{PPV}}}{1-\stackrel{\sim }{\pi }}\right)(1-{\stackrel{\sim }{\pi }}_e)$$ (10)

For statistical testing and inference concerning B or θ_γ we need a consistent estimate for π when π is unknown. We may estimate π by noting π = e₁₁κ̃₁π̃ + e₀₁κ̃₀(1 − π̃), where e₁₁ = P(M = 1|M̃ = 1, R = 1) and e₀₁ = P(M = 1|M̃ = 0, R = 1) and R = 1 indicates that the patient is selected into the randomized cohort.

4.1 Testing one hypothesis

In designing an AEBSD trial, our goal is to find the optimal π̃_e that minimizes the number of randomized patients for testing a specific hypothesis (or hypotheses) as in Table 1. Here we illustrate the idea for testing H₀ : δ = 0 against H_a : δ = δ*, where δ is the interaction between treatment and biomarker. To minimize the number of randomize patients we minimize var(δ̂), which is

$$\mathit{\text{var}}(\hat{\delta })=\frac{2{\eta }_{E1}(1-{\eta }_{E1})}{n{\pi }_e}+\frac{2{\eta }_{C1}(1-{\eta }_{C1})}{n{\pi }_e}+\frac{2{\eta }_{E0}(1-{\eta }_{E0})}{n(1-{\pi }_e)}+\frac{2{\eta }_{C0}(1-{\eta }_{C0})}{n(1-{\pi }_e)}$$ (11)

where the denominator of each term is the expected number of patients in subgroups defined by D and M. Thus, for given n, π, π̃, PPV, η_E1, η_C1, η_E0, η_C0, we can find the optimal π̃_e in [0, 1] that minimizes var(δ̂). The result is given by

$${\stackrel{\sim }{\pi }}_e^{\mathit{\text{opt}}}=\frac{(1-\stackrel{\sim }{\pi }){\pi }_e^{\mathit{\text{localopt}}}-\pi +\stackrel{\sim }{\pi }\mathit{\text{PPV}}}{\mathit{\text{PPV}}-\pi }$$ (12)

where ${\pi }_e^{\mathit{\text{localopt}}}$ is the local optimal solution whose global optimal solution is the same as ${\pi }_e^{\mathit{\text{opt}}}$ in Section 3.2 but adjusted according to π and PPV. When ${\pi }_e^{\mathit{\text{opt}}}\in [\text{min}(\pi ,\mathit{\text{PPV}}),\text{max}(\pi ,\mathit{\text{PPV}})],{\pi }_e^{\mathit{\text{localopt}}}={\pi }_e^{\mathit{\text{opt}}}$. Otherwise ${\pi }_e^{\mathit{\text{localopt}}}=\pi$ or PPV, whichever is closer to ${\pi }_e^{\mathit{\text{opt}}}$.

4.2 Testing two hypotheses

When testing two hypotheses is of interest, as the cases 12, 13, 14, 15 in Table 1, we can find the optimal π̃_e by minimizing the maximum of the required sample sizes for the first hypothesis and the second hypothesis at given α₁, β₁, α₂, β₂. For example, for case 13, the sample size n(π̃_e; H_1a) for the first hypothesis is given as $n({\stackrel{\sim }{\pi }}_e;H_{1a})=\frac{{(z_{{\alpha }_1/2}+z_{{\beta }_1})}^2}{B_1^2/{\mathit{\text{var}}}^{\ast }({\hat{B}}_1)}$ where z_α1 and z_β1 is the standard normal distribution percentile for α₁/2 and β₁. For the second hypothesis, the sample size n(π̃_e; H_2a) is $n({\stackrel{\sim }{\pi }}_e;H_{2a})=\frac{{(z_{{\alpha }_2/2}+z_{{\beta }_2})}^2}{{\delta }^2/{\mathit{\text{var}}}^{\ast }(\hat{\delta })}$ where z_α2/2 and z_β2 is the standard normal distribution percentile for α₂/2 and β₂. The goal is to find the optimal π̃_e such that n_max = max(n(π̃_e; H_1a), n(π̃_e; H_2a)) is minimized. The local optimal ${\pi }_e^{\mathit{\text{localopt}}}$ can be determined by π, PPV, ${\pi }_e^{\mathit{\text{opt}}}$, the global optimal solution in Section 4.1 and the solution for n(π̃_e; H_1a) = n(π̃_e; H_2a). Details are given in supplementary materials. The optimal π̃_e in this case, ${\stackrel{\sim }{\pi }}_e^{\mathit{\text{opt}}}$, can also be calculated by equation (12) using ${\pi }_e^{\mathit{\text{localopt}}}$.

5. Numerical Studies

5.1 EBSD design

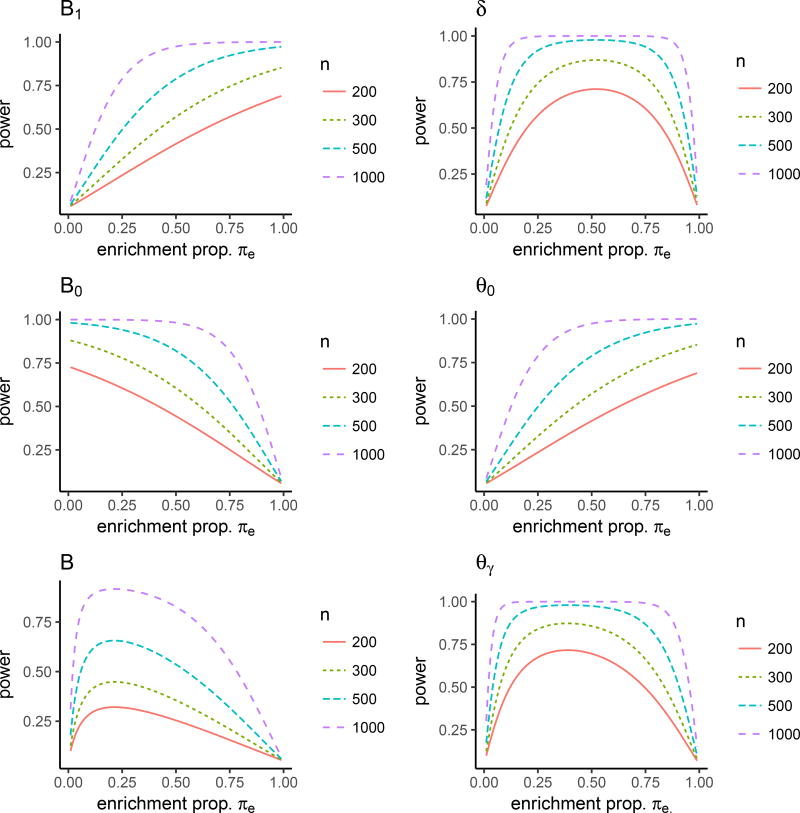
In this numerical study, we assume that the prevalence of biomarker positive patients in the population is 0.2 and that selected patients will be randomized with equal allocation to treatment D = {1,0}. For the sake of illustration, we assume the response of each patient follows a logistic regression model logit(Y = 1|D, M) = b₀+b₁D+b₂M+b₃TM. We consider two types of interaction between treatment and biomarker, quantitative and qualitative (Polley et al., 2013). In the case of quantitative interaction between treatment and biomarker, we set b₀ = −0.5, b₁ = 0.4, b₂ = −0.8, b₃ = 0.6, as seen in Figure 2a, and the logistic model yields the response rates 0.43, 0.21,0.48 and 0.38 for patient groups in E1, C1, E0 and C0, respectively. Figure 3 describes the relationship between statistical power for testing specific treatment parameters B, B₁, B₀, δ and θ_γ and the enrichment proportion π_e at the given number of randomized patients n = 200, 300, 500, 1000. These plots demonstrate that the optimal enrichment proportion π_e varies by the specific testing parameter and π_e reaches the highest power for B₁ at 1, B₀ at 0, B at 0.19, δ at 0.48 and θ_γ at 0.68. Note that the BSD design corresponds to π_e = 0.2 in these plots, demonstrating the EBSD design can achieve significant efficiency gain for a given sample size at optimal enrichment proportion ${\pi }_e^{\mathit{\text{opt}}}$.

Figure 2.

Illustration for (a) quantitative interaction with response rates η_E1 = 0.43, η_C1 = 0.21, η_E0 = 0.48 and η_C0 = 0.38 and (b) qualitative interaction with response rates η_E1 = 0.21, η_C1 = 0.10, η_E0 = 0.12 and η_C0 = 0.11

Figure 3.

The power for testing a specific treatment parameter at different enrichment proportions π_e for EBSD for quantitative interaction

As seen in Figure 2b, for the case of qualitative interaction between treatment and biomarker, we set b₀ = −0.5, b₁ = −0.8, b₂ = −0.1, b₃ = 1.5, which yields the response rates 0.21,0.10, 0.12 and 0.11 for patient groups E1, C1, E0 and C0, respectively. Figure 4 describes the relationship between the power for the specific treatment parameters B, B₁, B₀, δ and θ_γ and the enrichment proportion π_e at the number of randomized patients n = 200, 300, 500, 1000. Again, these plots show that the optimal enrichment proportion π_e varies by the specific testing parameter and π_e reaches the highest power for B₁ at 1, B₀ at 0, B at 0.21, δ at 0.52 and θ_γ at 0.71.

Figure 4.

The power for testing a specific treatment parameter at different enrichment proportions π_e for EBSD for qualitative interaction

To further verify the performance of the proposed treatment parameter estimators and their variance estimators under EBSD, simulation was conducted based on 1000 simulations. At a given sample size n = 500, Table 2 lists the estimates for B, B₁, B₀, δ, θ_γ for EBSD at ${\pi }_e^{\mathit{\text{opt}}}$ and BSD. Other quantities, including the standard errors based on the proposed variance estimators (std.p), the simulated standard error (std.e), and the 95%CI coverage probability based on the estimated standard error (coverage), are also provided. It can be seen that the proposed estimators yield consistent estimates with negligible bias and variance estimators yield standard errors close to the simulated one and a satisfying 95% nominal coverage probability. It can also be seen that the EBSD design at ${\pi }_e^{\mathit{\text{opt}}}$ yields much smaller standard error than the BSD design, indicating the EBSD design is significantly more efficient that the BSD, except for testing the overall treatment effect B, where BSD at π = 0.2 is very close to its optimal ${\pi }_e^{\mathit{\text{pt}}}=0.19$ for the quantitative interaction and 0.21 for the qualitative interaction and understandably the BSD at the setting yields similar performance as the EBSD.

Table 2.

Simulation results for EBSD and BSD for testing a single hypothesis (n = 500)

Test	B1		B0		B		δ		θγ
	BSD	EBSD	BSD	EBSD	BSD	EBSD	BSD	EBSD	BSD	EBSD
				quantitative interaction
$\pi ,{\pi }_e^{\mathit{\text{opt}}}$	0.2	1	0.2	0	0.2	0.188	0.2	0.480	0.2	0.675
true	0.211	0.211	0.097	0.097	0.120	0.120	0.114	0.114	0.030	0.030
estimate	0.211	0.212	0.097	0.098	0.120	0.118	0.110	0.113	0.030	0.030
std.p	0.090	0.041	0.049	0.044	0.043	0.043	0.103	0.084	0.017	0.011
std.e	0.091	0.040	0.049	0.044	0.044	0.043	0.103	0.085	0.017	0.011
coverage	0.943	0.952	0.949	0.945	0.951	0.949	0.942	0.946	0.944	0.947
				qualitative interaction
$\pi ,{\pi }_e^{\mathit{\text{opt}}}$	0.2	1	0.2	0	0.2	0.214	0.2	0.521	0.2	0.710
true	0.171	0.171	−0.163	−0.163	−0.097	−0.097	0.334	0.334	0.044	0.044
estimate	0.171	0.171	−0.162	−0.164	−0.097	−0.096	0.335	0.333	0.044	0.044
std.p	0.097	0.044	0.045	0.040	0.042	0.041	0.107	0.084	0.018	0.011
std.e	0.100	0.044	0.045	0.041	0.042	0.041	0.108	0.085	0.018	0.011
coverage	0.944	0.948	0.951	0.941	0.949	0.945	0.947	0.948	0.941	0.951

γ = 0.1 is assumed for θ_γ. We also set π = 20%, α = 0.05, n_sim = 1000

Table 3 summarizes the results of designing a EBSD trial to test two treatment parameters simultaneously at given powers, 90% for H₁ and 80% for H₂. The results for EBSD are obtained at ${\pi }_e^{\mathit{\text{opt}}}$ with the method described in Section 3.4. The coverage probability for all treatment effect estimates achieves their corresponding nominal levels; for B̂₁ the coverage probability is close to 99% and for the second treatment effect estimate the coverage probability is close to 96%. It can be seen that the EBSD needs significantly less randomized patients to achieve requisite powers for testing two hypotheses than BSD in all combinations of hypothesis testing. Also, the efficiency gain for testing two hypotheses is generally larger than that of testing a single hypothesis.

Table 3.

Simulation results for EBSD and BSD for testing two hypotheses at targeted powers

Test	B1 & B0		B1 & B		B1 & δ		B1 & θγ
	BSD	EBSD	BSD	EBSD	BSD	EBSD	BSD	EBSD
			quantitative interaction
$\pi ,{\pi }_e^{\mathit{\text{opt}}}$	0.2	0.244	0.2	0.416	0.2	0.480	0.2	0.675
n	1374	1130	1374	661	3449	2315	1374	538
	B1		B1		B1		B1
true	0.211	0.211	0.211	0.211	0.211	0.211	0.211	0.211
estimate	0.211	0.211	0.211	0.212	0.211	0.212	0.211	0.211
std.p	0.055	0.054	0.055	0.055	0.035	0.027	0.055	0.047
std.e	0.055	0.055	0.055	0.054	0.034	0.027	0.054	0.048
coverage	0.987	0.988	0.989	0.987	0.991	0.991	0.987	0.990
	B0		B		δ		θγ
true	0.097	0.097	0.120	0.120	0.114	0.114	0.030	0.030
estimate	0.097	0.097	0.120	0.120	0.113	0.114	0.030	0.030
std.p	0.030	0.034	0.026	0.041	0.039	0.039	0.010	0.010
std.e	0.030	0.033	0.027	0.041	0.039	0.039	0.010	0.011
coverage	0.963	0.961	0.958	0.962	0.961	0.960	0.955	0.951
			qualitative interaction
$\pi ,{\pi }_e^{\mathit{\text{opt}}}$	0.2	0.658	0.2	0.495	0.2	0.873	0.2	0.939
n	2444	742	2444	988	2444	560	2444	520
	B1		B1		B1		B1
true	0.171	0.171	0.171	0.171	0.171	0.171	0.171	0.171
estimate	0.170	0.170	0.171	0.172	0.171	0.171	0.171	0.171
std.p	0.044	0.044	0.044	0.044	0.044	0.044	0.044	0.044
std.e	0.045	0.044	0.046	0.044	0.044	0.045	0.045	0.045
coverage	0.988	0.990	0.987	0.990	0.989	0.990	0.990	0.989
	B0		B		δ		θγ
true	−0.163	−0.163	−0.097	−0.097	0.334	0.334	0.044	0.044
estimate	−0.163	−0.164	−0.096	−0.096	0.335	0.335	0.044	0.044
std.p	0.020	0.056	0.019	0.033	0.049	0.114	0.008	0.015
std.e	0.021	0.057	0.019	0.034	0.049	0.116	0.008	0.015
coverage	0.958	0.958	0.954	0.956	0.960	0.954	0.957	0.941

γ = 0.1 is assumed for θ_γ. We also set π = 20%, α₁ = 0.01, α₂ = 0.04, β₁ = 0.1; β₂ = 0.2, n_sim = 1000

5.2 AEBSD design

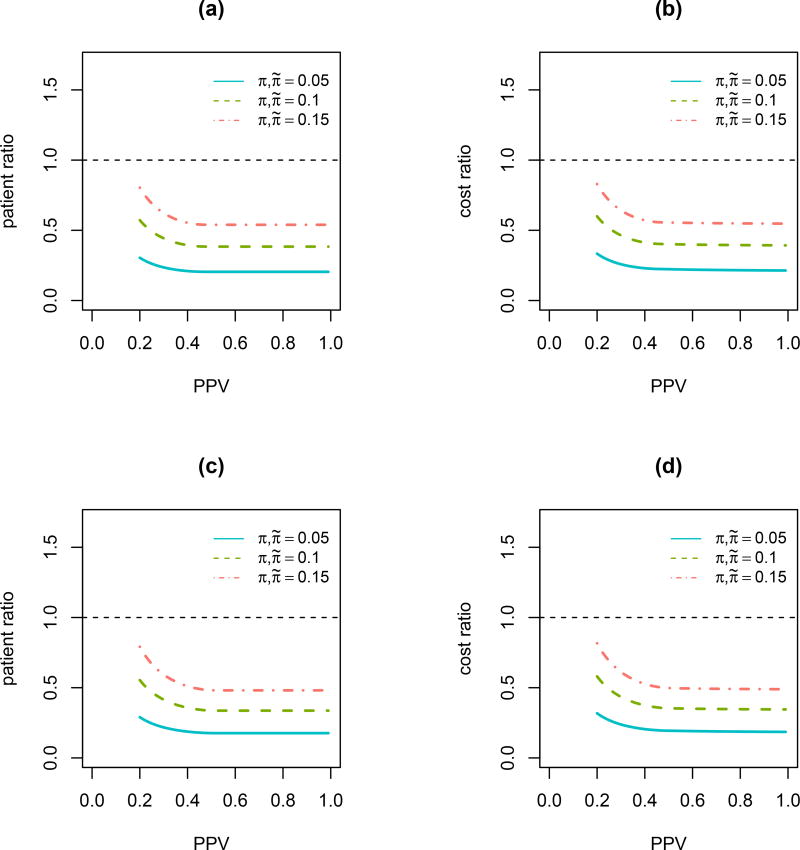
In this numerical study, we investigate the relationship of patient ratio and cost ratio with PPV for testing the interaction δ under AEBSD. Quantitative and qualitative interactions are both investigated. For a quantitative interaction, η_E1 = 0.43, η_C1 = 0.21, η_E0 = 0.48 and η_C0 = 0.38. For a qualitative interaction, η_E1 = 0.53, η_C1 = 0.35, η_E0 = 0.21 and η_C0 = 0.38. We assume α = 0.05, β = 0.1 in the calculation. The unit cost is 500 for biomarker assay and the average unit cost is 10, 000 for treating and following each patient. Figure 5 shows decreasing trends for both patient ratio and cost ratio with an increasing PPV for both quantitative and qualitative interactions. Table 4 gives further details on the screening ratio ns_ratio for AEBSD over BSD. Similar results are obtained for testing two treatment parameters simultaneously. Details can be found in the supplementary materials.

Figure 5.

Relationship of patient and cost ratio with PPV for testing the interaction between treatment and biomarker δ under AEBSD. (a) Patient ratio with quantitative interaction; (b) Cost ratio with quantitative interaction; (c) Patient ratio with qualitative interaction; (d) Cost ratio with qualitative interaction.

Table 4.

Numerical results for AEBSD design for testing δ

π	π̃	PPV	${\stackrel{\sim }{\pi }}_e^{\mathit{\text{opt}}}$	naebsd	nsaebsd	nbsd	nratio	cratio	nsratio
				quantitative interaction
0.05	0.05	0.2	1.000	4325	86500	14199	0.305	0.334	6.092
		0.5	0.958	2902	55592	14199	0.204	0.223	3.915
		0.8	0.595	2902	34516	14199	0.204	0.216	2.431
0.1	0.1	0.2	1.000	4325	43251	7559	0.572	0.599	5.722
		0.5	0.955	2902	27716	7559	0.384	0.401	3.667
		0.8	0.589	2902	17082	7559	0.384	0.395	2.260
0.15	0.15	0.2	1.000	4325	28834	5381	0.804	0.829	5.358
		0.5	0.951	2902	18408	5381	0.539	0.556	3.421
		0.8	0.582	2902	11252	5381	0.539	0.549	2.091
				qualitative interaction
0.05	0.05	0.2	1.000	546	10920	1882	0.290	0.318	5.802
		0.5	1.000	333	6660	1882	0.177	0.194	3.539
		0.8	0.647	332	4296	1882	0.176	0.187	2.283
0.1	0.1	0.2	1.000	546	5461	986	0.554	0.580	5.539
		0.5	1.000	333	3330	986	0.338	0.354	3.377
		0.8	0.642	332	2131	986	0.337	0.347	2.161
0.15	0.15	0.2	1.000	546	3640	690	0.791	0.816	5.275
		0.5	1.000	333	2220	690	0.483	0.498	3.217
		0.8	0.635	332	1407	690	0.481	0.491	2.039

${\stackrel{\sim }{\pi }}_e^{\mathit{\text{opt}}}$ is optimal enrichment proportion for auxiliary positive patient; n_aebsd is the number of randomized patients for AEBSD; n_bsd is the number of randomized patients for BSD; n_bsd is the number of randomized patients for BSD; n_ratio is the ratio of n_EBSD and n_BSD; ns_ratio is the ratio of the number of screened patients for AEBSD versus BSD; c_ratio is the cost ratio for conducting AEBSD and BSD. α = 0.05, β = 0.1. The unit cost is 500 for ascertaining true biomarker, the average unit cost is 10,000 for treatment and follow-up, and the unit cost is 50 for ascertaining auxiliary variable.

6. Case Studies

6.1 Herceptin trial with EBSD

The breast cancer chemotherapy Herceptin is a well-known success story of personalized medicine. Human epidermal growth factor receptor-2 protein (HER2) is over-expressed in approximately 20% of breast cancer patients (Korkaya and Wicha, 2013). Herceptin, a target agent on HER2, was shown to be effective in patients with HER2+ metastatic breast cancer (Baselga, 2001; Joensuu et al., 2006). Retrospective studies also suggested that HER2− patients could also benefit from Herceptin (Paik et al., 2008). For illustration, we assume that the overall response rate (ORR), a binary endpoint based on the percentage of patients whose cancer shrinks or disappears after treatment, is to be used in designing a first-line metastatic breast cancer therapy for Herceptin plus chemotherapy E versus chemotherapy C. We assume that these response rates for groups E1 and C1 are η_E1 = 45% and η_C1 = 29% respectively in HER2+ patients and that the response rates for groups E0 and C0 is 45% and 40%, respectively. Our goal is to illustrate how to design a EBSD trial at the optimal enrichment proportion π_e when the investigators are primarily interested in testing a single hypothesis involving a single treatment parameter from (B₁, B₀, B, δ, θ_γ) with γ = 0.2. The optimal enrichment proportion ${\pi }_e^{\mathit{\text{opt}}}$ is obtained by the method described in Section 3 to achieve the maximum efficiency for the specific test for given n. The top panel of Table 5 shows the required number of randomized patients for EBSD and BSD at two-sided α = 0.05 and β = 0.1. The ratio of randomized patents n_ratio and the cost ratio c_ratio for EBSD versus BSD are also provided, where the unit cost for ascertaining true biomarker is 300 and the unit cost for treating and following patient is averaged 10, 000 for one year (Schmidt, 2011). In this case, the cost of screening and IHC testing for HER2 is significantly lower than the cost of treatment and patient follow-up.

Table 5.

Herceptin trial: Testing one or two hypotheses with EBSD at optimal enrichment proportion ${\pi }_e^{\mathit{\text{opt}}}$ compared to BSD

Test	true	${\pi }_e^{\mathit{\text{opt}}}$	nebsd	Pebsd	nbsd	Pbsd	nratio	nsratio	cratio
		Testing a single hypothesis
B1	0.160	1.000	372	0.900	1861	0.900	0.200	1.000	0.216
B0	0.050	0.000	4098	0.900	5122	0.900	0.800	1.000	0.804
B	0.072	0.194	1948	0.900	1949	0.900	1.000	1.007	1.000
δ	0.110	0.491	3267	0.900	4996	0.900	0.654	1.605	0.673
θ0	0.032	1.000	372	0.900	1861	0.900	0.200	1.000	0.216
θγ	0.025	0.685	1071	0.900	2643	0.900	0.405	1.387	0.425
		Testing two hypotheses
B1 & B0	0.160, 0.050	0.139	3797	0.980	4087	0.997	0.929	1.000	0.930
B1 & B	0.160, 0.072	0.318	1663	0.961	2635	0.985	0.631	1.002	0.638
B1 & δ	0.160, 0.110	0.491	2607	1.000	3986	0.985	0.654	1.606	0.673
B1 & θ0	0.160, 0.032	0.999	528	0.965	2635	0.964	0.200	1.001	0.216
B1 & θγ	0.160, 0.025	0.685	855	0.940	2635	0.909	0.325	1.111	0.340

${\pi }_e^{\mathit{\text{opt}}}$ is optimal enrichment proportion for biomarker positives; n_ebsd is the number of randomized patients for EBSD; P_ebsd is the power of testing a single hypothesis and the probability of success of testing two hypotheses for EBSD; n_bsd is the number of randomized patients for BSD; P_bsd is the power of testing a single hypothesis and the probability of success of testing two hypotheses for BSD; n_ratio is the ratio of n_EBSD and n_BSD; ns_ratio is the ratio of the number of screened patients for EBSD versus BSD; c_ratio is the cost ratio for conducting EBSD and BSD. γ = 0.2 is assumed for θ_γ. We also assume π = 0.2, the unit cost is 300 for ascertaining true biomarker and the average unit cost is 10, 000 for treatment and follow-up. For testing on a single hypothesis, α = 0.05, β = 0.1. For testing two hypotheses, α₁ = 0.01, β₁ = 0.1, α₂ = 0.04, β₂ = 0.2.

Table 5 also illustrates the case of designing an EBSD trial when testing two hypotheses. We consider the first hypothesis of interest to be the test on treatment effect among HER2+ patients B₁, which is often the primary goal in a biomarker-driven clinical trial. The second hypothesis will be chosen from (B₀, B, δ, θ_γ), testing the treatment effect in biomarker negatives, the treatment effect in the overall population, the interaction between treatment and biomarker, and the clinical benefit of selecting treatment by biomarker. The response rates for the four groups of patients defined by treatment and biomarker are the same for the case of single hypothesis testing. To control the overall type error at the level of two-sided 0.05, we split the α between the first hypothesis and the second hypothesis. The number of randomized patients for testing each hypothesis for given α₁ = 0.01, β₁ = 0.10, α₂ = 0.04 and β₂ = 0.2 are calculated, and the maximum of the two sample sizes is chosen as the size of the trial. The optimal enrichment proportion ${\pi }_e^{\mathit{\text{opt}}}$ for the EBSD design is obtained by numerical methods to achieve the smallest of the maximum number of randomized patients required by testing both hypotheses with respective power greater than 1 − β₁ and 1 − β₂ for the two hypotheses. In the bottom panel of Table 5, the ratio of randomized patents of the two designs n_ratio and the ratio of cost c_ratio are listed. P_ebsd indicates the probability of success when testing two hypotheses for EBSD. In designing trials with two primary hypotheses, one can obtain the probability of success, i.e. the probability of rejecting either null hypothesis under the alterative (Matsui et al., 2014). The probability of success is calculated using the joint distribution of two testing statistics $Z_1=\frac{{\hat{B}}_1}{\sqrt{\widehat{\mathit{\text{var}}}({\hat{B}}_1)}}$ and $Z_2=\frac{\hat{\delta }}{\sqrt{\widehat{\mathit{\text{var}}}(\hat{\delta })}}$.

6.2 EGFR-inhibitor trial using AEBSD

In this case study, we consider designing a hypothetical AEBSD trial for comparing the 5-month progression-free-survival (5mPFS) rate of gefitinib (E) versus carboplatin and paclitaxel (C) in patients with non-small-cell lung cancer (NSCLC). The example is hypothetical, but the 5mPFS for each patient group is based on the results of an actual clinical trial (IPASS) (Mok et al., 2009). The mutation of epidermal growth factor receptor (EGFR) is thought predictive of the effect of gefitinib in treating non-small cell lung cancer. The prevalence of EGFR mutations in approximately 50% in Asia, significantly higher than the 10% prevalence in North America (Shi et al., 2015; Kerr, 2013). As a result of the high prevalence rate of EGFR mutants, IPASS was successfully conducted in Asia and found that gefitinib significantly extended PFS among patients with EGFR mutations, but resulted in significantly shorter PFS for patients with EGFR wild types (Mok et al., 2009; Maemondo et al., 2010).

We consider a biomarker stratified trial to be conducted in North America with the goal of testing two primary hypotheses: H₁: the treatment effect among patients with EGFR mutations B₁ and H₂: the interaction between treatment and EGFR mutation δ. We set two-sided α₁ = α₂ = 0.025 and β₁ = β₂ = 0.1. A BSD design with the objectives of testing B₁ and δ is very inefficient, as it would enroll, treat and follow a large number of patients who are EGFR wild-types and therefore would entail a waste of limited resource. For an AEBSD design, it is known that EGFR mutations are more commonly observed in patients with adenocarcinomas and no prior history of smoking, as well as in females and those of Asian descent (Kerr, 2013). A predictive score, the auxiliary variable in this case, can be built using these easily and cheaply assessed prognostic factors. We have assumed the prevalence rate of “high-score” patients is 15% and the true EGFR mutations is at least 60% among the “high-score” patients.

Mimicking the IPASS trial, we choose the median PFS for groups E1, C1, E0, C0 as 9.82, 4.71, 2.00 and 5.70 months, respectively, indicating a strong qualitative interaction between treatment and biomarker. Under the exponential hazards, we assume the 5mPFS for these groups are 0.65, 0.41,0.13 and 0.48, respectively. Under these design parameters, we find the optimal selection probability κ̃₁ = 1 for auxiliary positive patients and κ̃₀ = 0 for the auxiliary negative patients. The number of randomized patients for the two designs are n_AEBSD = 338 and n_BSD = 2023 with n_ratio = 0.167, and the cost ratio c_ratio = 0.172. In the calculation of the trial cost, we assume that the unit cost of testing EGFR mutation is 1,000, the average treatment cost and the average follow-up cost are 7, 500 and 2, 500 for each patient in the randomized cohort while the unit cost for determining the EGFR predictive score is 50. These cost estimates are based on the literature reflecting the experience of the United States (Horgan et al., 2011; Sauter and Butnor, 2016).

7. Discussion

In this paper, we propose two new enrichment designs for biomarker stratified clinical trials. The key idea of enrichment sampling is to oversample patients who contain more information about specific treatment parameters and undersample those who do not. We demonstrate that the new designs can significantly improve study efficiency in term of increased power and higher estimation precision with a fixed number of randomized patients and therefore reduce the cost of conducting trials. We give analytic solutions or numerical algorithms for finding the optimal probabilities for selecting patients with positive and negative biomarkers into the randomized cohort for the EBSD design and the optimal probabilities of selecting patients with positive and negative auxiliary biomarkers for the AEBSD design. We also demonstrate how to determine the sample size for EBSD and AEBSD designs when testing a single treatment parameter or two treatment parameters simultaneously. The numerical studies and the case studies demonstrate the superior performance of the new designs over the BSD.

Enrichment sampling strategies have been proposed and successfully used in observational studies to test association between disease and risk factors (Morara et al., 2007; Wang and Zhou, 2010; Strauss et al., 2010) and to estimate the accuracy of biomarkers in predicting disease condition (Wang et al., 2012, 2013). These papers demonstrate that biased sampling with enrichment of relevant patient subgroups, those that contain more information on estimands, leads to more efficient studies that requires significantly fewer patients and study cost. The enrichment strategies can be applied to other biomarker-driven clinical trial designs, such as the biomarker strategy design. See Freidlin et al. (2010) for a review. In a biomarker strategy design, patients are randomly assigned to a biomarker-guided arm that uses the biomarker to determine whether a patient receive the experimental therapy or the control therapy or to a biomarker-unguided arm that randomly assign the patients to the experimental therapy and control therapy regardless of biomarker status.

In this paper we consider a binary endpoint such as tumor response or survival rate at a landmark time. The extension of our discussion to an unequal randomization ratio is straightforward. Indeed, the allocation ratio between treatment arms can be optimized for additional efficiency gains to test specific treatments parameters. An enrichment strategy is equally applicable to trials involving more than two treatments.

Compared to the BSD design, one limitation of the EBSD and AEBSD designs is that they may significantly prolong the time of trial completion, as the latter designs require longer time to accrue sufficient number of biomarker positive patients. In this paper, the cost introduced by prolonged trial completion time has not been considered. In practice, this issue can be addressed by verifying that the EBSD and AEBSD designs under the optimal selection on κ̃₁ and κ̃₀ will lead to an estimated time of trial completion that the investigators can accept. If not, the standard BSD design may be used.