Complementarity in False Memory Illusions

Abstract

For some years, the DRM illusion has been the most widely studied form of false memory. The consensus theoretical interpretation is that the illusion is a reality reversal, in which certain new words (critical distractors) are remembered as though they are old list words rather than as what they are—new words that are similar to old ones. This reality-reversal interpretation is supported by compelling lines of evidence, but prior experiments are limited by the fact that their memory tests only asked whether test items were old. We removed that limitation by also asking whether test items were new-similar. This more comprehensive methodology revealed that list words and critical distractors are remembered quite differently. Memory for list words is compensatory: They are remembered as old at high rates and remembered as new-similar at very low rates. In contrast, memory for critical distractors is complementary: They are remembered as both old and new-similar at high rates, which means that the DRM procedure induces a complementarity illusion rather than a reality reversal. The conjoint recognition model explains complementarity as a function of three retrieval processes (semantic familiarity, target recollection, and context recollection), and it predicts that complementarity can be driven up or down by varying the mix of those processes. Our experiments generated data on that prediction and introduced a convenient statistic, the complementarity ratio, which measures (a) the level of complementarity in memory performance and (b) whether its direction is reality-consistent or reality-reversed.

False memory phenomena have figured centrally in a broad range of research domains. At one time or another, they have been prominent topics in abnormal psychology (e.g., McNally, Clancy, & Schacter, 2001), aging and dementia (e.g., Budson et al., 2006), autism spectrum disorders (e.g., Beversdorf et al., 2000), criminology (e.g., Wells et al., 1998), developmental psychology (e.g., Bouwmeester & Verkoeijen, 2010), differential psychology (e.g., Gallo, 2010), cognitive neuroscience (e.g., Dennis, Bowman, & Vandekar, 2012), pediatric psychology (e.g., Goodman, Quas, Batterman-Faunce, Riddlesberger, & Kuhn, 1994), psychotherapy (e.g., Poole, Lindsay, Memon, & Bull, 1995), special education (e.g., Weekes, Hamilton, Oakhill, & Holliday, 2007), and of course, mainstream memory research (for a review, see Brainerd & Reyna, 2005). Although a wide assortment of procedures has been implemented, there are two preeminent methodologies, the misinformation paradigm (Loftus, 1975) and the Deese/Roediger/McDermott (DRM; Deese, 1959; Roediger & McDermott, 1995) illusion. Loftus’ misinformation procedure was dominant in early research, owing to a focus on the effects of manipulative interviewing practices in police investigations and psychotherapy, but more recently, the DRM illusion has become the dominant methodology (for reviews, see Gallo, 2006, 2010; Brainerd, Reyna, & Zember, 2011).

From a practical point of view, the DRM illusion’s preeminence is easily understood. It combines high efficiency in the production of false memories with great simplicity and adaptability. The core methodology is summarized in Table 1, where it can be seen that the illusion consists of falsely remembering words that were not presented on lists of related words. With respect to efficiency, levels of false memory are quite high, relative to most other paradigms, especially for the new-similar words in Table 1 that are labeled “strong.” Concerning simplicity, only a brief induction phase, in which subjects encode a few short lists, is required to achieve high levels of false memory. Indeed, reliable levels of false memory have been detected a few seconds after the presentation of a single four-word DRM list (Atkins & Reuter-Lorenz, 2011). Concerning adaptability, the core methodology is so flexible that it can be adjusted to meet the requirements of most experimental designs. This includes the very restrictive requirements of fMRI studies (see Dennis, Bowman, & Vandekar, 2012; Kurkela & Dennis, 2016) and studies of cognitively impaired populations (see Brainerd, Forrest, Karibian, & Reyna, 2006; Budson et al., 2006).

Table 1.

Experimental materials and procedures for the Deese/Roediger/McDermott illusion

Old list words (O)	New-but-similar words (NS)	New-different words (ND)
table, couch, desk, sofa, …	chair (strong), seat (weak)	city, music
rest, awake, tired, dream, …	sleep (strong), yawn (weak)	cold, soft
mad, fear. hate, temper, …	anger (strong), mean (weak)	spider, thief

Note. Subjects study word lists composed of 12–15 related items, such as those in the left hand column, and they respond to a recognition test on which three types of test probes are presented: old (O) list words, new-but-similar (NS) words, and new-different (ND) words. For each test probe, the subjects’ task is to decide whether it is O.

The dominance of the DRM procedure means that much of our knowledge about false memory is now tied to that paradigm, and hence, it is essential to understand exactly what type of illusion it creates. It might be thought that this question has long since been answered, by what we shall call the reality-reversal hypothesis. According to that notion, DRM lists foment reversals in the perceived reality states of certain types of new-similar (NS) items—the strong NS items in Table 1, which are usually called critical distractors or critical lures. Specifically, after list presentation, list items and strong NS items are both perceived to be old on memory tests, rather than list items being perceived as old and strong NS items being perceived as new-similar. This reality-reversal hypothesis, which is exemplified by the label “DRM illusion,” has become the consensus interpretation by virtue of some compelling lines of evidence.

Consider four examples. First, not only are raw false alarm probabilities high (e.g., the bias-corrected mean is .39 for the DRM lists in the Roediger, Watson, McDermott, & Gallo, 2001, norms), they approach hit rates for list items. To illustrate, Gallo (2006, Table 4.1) reviewed 36 sets of data in which the mean false alarm rate was within ±.02 of the mean hit rate, and Stadler, Roediger, and McDermott (1999) identified 18 DRM lists for which the mean false alarm rate did not differ reliably from the mean hit rate. Second, when subjects introspect on the conscious experiences that items stimulate on memory tests, critical distractors and list items both provoke reports of realistic study-phase details at high levels, and confidence ratings for false alarms approach those for hits (for a review, see Arndt, 2012). Across the data sets that Gallo reviewed, for example, false alarms and hits provoked recollection of realistic details (e.g., voices in which lists were spoken, fonts in which they were printed) 57% and 65% of the time, respectively (see also, Prohaska, DelValle, Toglia, & Pittman, 2016). Third, the brain regions whose activity is correlated with DRM true and false memory have been investigated in fMRI studies (e.g., Atkins & Reuter-Lorenz, 2011), and the modal finding is substantial overlap among those regions. Here, Dennis et al. (2012) reviewed medial temporal, parietal, and frontal regions that exhibit such overlap. Fourth, several experiments have been conducted in which investigators enriched memory test instructions with explicit warnings about the types of NS items that subjects are apt to mistake for old (O) items and with examples of the qualities of retrieved memories that can be used to discriminate them (e.g., Gallo et al,, 1997). The modal finding is that such warnings produce only small reductions in false alarms to critical distractors (Brainerd & Reyna, 2005).

Such evidence seems to add up to convincing proof that following list presentation, the perceived reality states of critical distractors and list items are indistinguishable to subjects: Both are remembered as belonging to the old state. However, support for this reality-reversal hypothesis is limited by how memory performance has been measured—explicitly, by the ubiquitous practice of only measuring whether subjects perceive that test items are old—without regard to whether they may also perceive that such items belong to other, logically incompatible, reality states. This practice generates data that speak to whether critical distractors and list items are both remembered as old when the task is to judge whether they belong to that state (O? tests), but not to whether they are both remembered as old when the task is to judge whether they belong to the complementary new-similar state (NS? tests). The minimum rational condition for confirmation of the reality-reversal hypothesis is that performance is compensatory across these incompatible judgments (Brainerd & Reyna, 2005). More particularly, pools of list words will exhibit high hit rates (O? tests) coupled with very low false alarm rates (NS? tests), and pools of critical distractors will exhibit high false alarm rates (O? tests) coupled with very low hit rates (NS? tests).

However, a theoretical case can be made that this will not happen, and instead, performance will be compensatory for list items but complementarity (high false alarm and hit rates) for critical distractors. This possibility falls out of one of the main theoretical accounts of false memory, fuzzy-trace theory (FTT), which posits that memory can be noncompensatory over mutually incompatible judgments as a by-product of storing dissociated verbatim and gist traces that favor different reality states (Brainerd, Wang, Reyna, & Nakamura, 2015). There is another recent theory that makes related dual-trace assumptions, Nelson and Shiffrin’s (2013) storing-and-retrieving-knowledge-and-events (SARKAE) model. FTT and SARKAE differ in several particulars, and they evolved from different experimental traditions, but they share two fundamental principles. First, both of them posit that episodic memory generates two types of traces, verbatim and gist traces in the case of FTT or item and knowledge traces in the case of SARKAE. Second, both theories use dual traces to explain dissociations in performance on traditional memory tests, which focus on the distinction between old and new, and on memory tests that focus on other content, such as meaning or inference.

In this article, we investigate whether DRM lists actually induce a reality-reversal illusion or whether, instead, they induce a complementarity illusion. We begin by discussing the notion of memory compensation among incompatible reality states and consider the fact that although intuition favors compensation, some familiar theoretical distinctions about verbatim and gist memory predict that NS items could display complementarity. In subsequent sections, we present a series of experiments that evaluated compensation versus complementarity for NS items by determining whether the known tendency of critical distractors to be falsely remembered at high rates on O? tests means that they are not correctly remembered at high rates on NS? tests. As an advance organizer, the answer will prove to be no. The type of false memory illusion that DRM lists are found to induce, then, is something more novel than reality reversal—namely, complementarity, in which both false alarm rates and hit rates are high for critical distractors. In contrast, compensation dominates memory for list items (high hit rates and low false alarm rates). Thus, although memory for critical distractors may be largely indistinguishable from memory for list items on O? tests, the two prove to be quite distinctive when data from both O? and NS? tests are analyzed.

Compensation and Complementarity in False Memory

We now sketch some familiar memory mechanisms that could move memory for NS items away from compensation toward complementarity. It will turn out that complementarity emerges from two distinctions. First, some NS items will be perceived as belonging to both the O and NS states, despite their incompatibility, by virtue of a retrieval processed that is called semantic familiarity. Second, a pair of recollective phenomenologies operate in the DRM paradigm, one (target recollection) that involves vivid reinstatement of specific list items and another (context recollection) that involves reinstatement of realistic details that accompany the presentation of DRM lists (Brainerd, Gomes, & Moran, 2014). These two forms of recollection generate contrasting perceptions of NS items’ reality states. The perceived state is new-similar for target recollection but is old for context recollection, allowing items that induce context recollection to be remembered as old on both O? and NS? probes while allowing other items that induce target recollection to be remembered new-similar on both O? and NS? probes Thus, it is easy to see that the two recollections will produce similar false alarm and hit rates (complementarity) for critical distractors to the extent that their memory effects are comparable.

Dual Recollection Processes in False Memory

It is traditional in false memory experiments to test memory for items from three reality states: O (e.g., table, rest, mad in the left column of Table 1), NS (e.g., chair, sleep, anger in the middle column of Table 1), and new-different (ND) (e.g., music, soft, thief in the right column of Table 1). The task is merely to decide whether each type of item maps with the O state, which we refer to as O? probes. Affirmative judgments for NS items count as false memories, affirmative judgments for O items count as true memories, and affirmative judgments for ND items count as response bias and are used to adjust the first two types of responses for the influence of bias. Suppose that the task is expanded to include NS? probes, so that subjects also decide whether the same three types of items map with the logically incompatible NS state. Now, affirmative judgments for NS items count as true memories, affirmative judgments for O items count as false memories, and affirmative judgments for ND items still count as response bias. For pools of NS items, what should the relation be between affirmative judgments on O? and NS? probes?

The intuitive answer is compensation. Because O and NS are mutually incompatible reality states, our naïve intuition is that if the tendency to judge items such as chair and anger as old on O? probes is high, the tendency to judge them as new-similar on NS? probes will be low, and conversely. Although this intuition is powerful, we mentioned that FTT anticipates that it may be wrong empirically, owing to the fact that subjects store traces of list words that are consistent with both the O and NS states. Specifically, subjects are assumed to store verbatim traces of individual list words and gist traces of their semantic content, especially meanings that connect different words (Reyna & Brainerd, 1995). According to FTT, connecting meaning across different words is central to the illusion. Here, Brainerd, Yang, Howe, Reyna, and Mills (2008) and Cann, McRae, and Katz (2011) noted three semantic properties of the DRM paradigm. First, list words share salient meanings (e.g., two-thirds of the words on the chair list are household furniture; two-thirds of the words on the anger list are emotions). These authors noted that as a group, DRM lists exemplify six distinct types of semantic relations. Second, critical distractors are very familiar exemplars of those shared meanings. Third, false memory increases as the number of list words that share a salient meaning with the critical distractor increases (Cann et al., 2011). The third property also holds for other types of semantically-related lists, such as categorized lists (Brainerd & Reyna, 2007; Dewhurst, 2001).

Brainerd et al. (2015) pointed out that in false memory experiments, whether or not performance is compensatory across probes for incompatible reality states is a multi-dimensional proposition that depends on the mix of verbatim and gist retrieval, which generates three subjective reactions to test items: (a) semantic familiarity, (b) target recollection, and (c) context recollection. Taking semantic familiarity first, a key property of the meaning information in gist traces is that it supports complementary perceptions of incompatible reality states, for both O and NS items. Consider the chair and anger lists (Table 1, left column), which produce verbatim traces of table, couch, desk, …, verbatim traces of mad, fear, hate, …, and gist traces of these words’ semantic content. Because semantic information is congruent with any exemplar of a target meaning, regardless of whether the exemplar was presented, it supports contradictory responses to O? and NS? probes. For instance, the “household furniture” and “emotion” meanings are consistent with chair and anger being O (there are many exemplars of those concepts on the respective lists) and also with them being NS (many exemplars of those concepts were not on the respective lists). Thus, when the phenomenology is semantic familiarity, individual items can be perceived as a simultaneously occupying both the O and NS reality states. However, as we now show, complementarity can also result when individual items are perceived as occupying only one of these states because the state is different for target recollection than for context recollection.

Taking target recollection first, it is a by-product of retrieving verbatim traces of list items. It is compensatory across incompatible reality states, for individual O and NS items, because verbatim traces identify particular items as having been present on the study list, causing O items to be perceived as old and NS items to be perceived as new-similar. Hence, processing verbatim traces of, say, table and mad supports acceptance of NS? probes and rejection of O? probes for chair and anger, while simultaneously supporting acceptance of O? probes and rejection of NS? probes for table and mad, because the latter are perceived to old and the former are perceived to be new-similar. In the false memory literature, the rejection halves of these paired judgments have been widely studied, where they are usually called recollection rejection or recall-to-reject (e.g., Lampinen & Odegard, 2006).

Turing to context recollection, this form of recollection was emphasized by Jacoby (1991) in his process dissociation model, which measures subjects’ ability to distinguish items that were presented on different lists via conscious reinstatement of contextual details that differentiate the lists (e.g., visual vs. oral presentation). More recent work has shown that some gist traces are compensatory because they recruit realistic study-phase contextual details when they are retrieved (Brainerd et al., 2014). Here, several findings suggest that gist traces sometimes recruit vivid recollective support for test items, in the form of contextual details that accompanied list presentation, and this process has been tied to the high levels of phantom recollective phenomenology that subjects experience for critical distractors (for a review, see Arndt, 2012). These particular gist traces are compensatory because they identify both O and NS items, not just O items, as being O and not NS. Note that for NS items, this is a reality reversal, but for O items it is reality-consistent. Note, too, that for NS items, context recollection induces a perceived reality state that is logically incompatible with the reality state that target recollection induces.

A key point about target and context recollection is that although we have seen that they are compensatory, paradoxically they are jointly complementary. Obviously, they will produce complementarity for a pool of NS items (i.e., similar hit and false alarm rates) when the effects of the two recollections are roughly comparable; that is, when the percentage of NS items that provokes target recollection is roughly the same as the percentage that provokes context recollection. In contrast, O items are not subject to this paradox because, as we saw, the two recollections are both individually and jointly compensatory for such items. The denouement is that complementarity should occur at far higher rates for NS items than for O items. For the latter, only semantic similarity can produce it (because individual items will be perceived as being both O and NS). For NS items, however, complementarity can be produced by semantic familiarity and by the countervailing effects of target and context recollection.

Conjoint Recognition

A model is required in order to spell out exactly how these processes combine to generate responses to O? and NS? probes. The relevant model is conjoint recognition, and it is known to fit DRM data well (Bouwmeester & Verkoeijen, 2010; Brainerd & Wright, 2005; for a review, see Brainerd et al, 2014). The conjoint recognition model contains parameters that disentangle the effects of the three processes by defining them over O? and NS? probes and also over a third type of probe that is analogous to inclusion tests in the process dissociation paradigm (O-or-NS?) To see how that works for NS items, consider the bias-corrected expressions for accepting O? and NS? probes:

$$p_{NS}(\mathrm{O}?)=(1-R)P+(1-R)(1-P)S_{NS}\text{and}$$ (1)

$$p_{NS}(\text{NS}?)=R+(1-R)(1-P)S_{NS},$$ (2)

where S_NS, R, and P are the probabilities of semantic familiarity, recollection rejection, and phantom recollection, respectively. Recollection rejection and phantom recollection are forms of performance that are produced by different recollective processes: Recollection rejection is the act of both rejecting O? probes and accepting NS? probes by virtue of target recollection, and phantom recollection the act of doing the opposite by virtue of context recollection (Brainerd et al., 2014). Two conclusions about complementarity emerge from these expressions. First, a pool of NS items will exhibit at least partial complementarity [i.e., the mean values of p_NS(O?) and p_NS(NS?) will both be > 0] as long as S_NS > 0 and the other two parameters are < 1. Second, complete complementarity [i.e., the mean values of p_NS(O?) and p_NS(NS?) will both be > 0 and will be roughly equal], can also occur because certain combinations of the values of R and P will produce it—even though, paradoxically, the processes that these parameters measure are individually compensatory. Explicitly, note that whether NS items exhibit complete complementarity [i.e., p_NS(O?) = p_NS(NS?)] or strong complementarity [i.e., p_NS(O?) ≈ p_NS(NS?)] cannot depend on S_NS because the term (1− R)(1− P)S_NS vanishes when p_NS(NS?) is subtracted from p_NS(O?). That subtraction leaves p_NS(O?) − p_NS(NS?) = (1−R)R − P, which means that performance will be completely complementary whenever P = R/(1−R).

The exact quantitative tradeoff between levels of complementarity and values of these parameters is shown in Figure 1. This curve represents the paired values of P and R that, for a pool of NS items, will produce equivalent mean values of p_NS(O?) and p_NS(NS?), even though individual items are perceived to occupy O state and not the NS state by virtue of context recollection, or the NS state and not the O state by virtue of target recollection. To the right and left of the curve are, respectively, the regions in which performance for NS items is partially complementary and reality-consistent [because p_NS(O?) < p_NS(NS?)] versus partially complementary and reality-reversed [because p_NS(O?) > p_NS(NS?)]. It can be seen that reality reversal occurs for a smaller region of the R-P coordinate space than reality consistency and that it cannot occur whenever R > .5.

Figure 1.

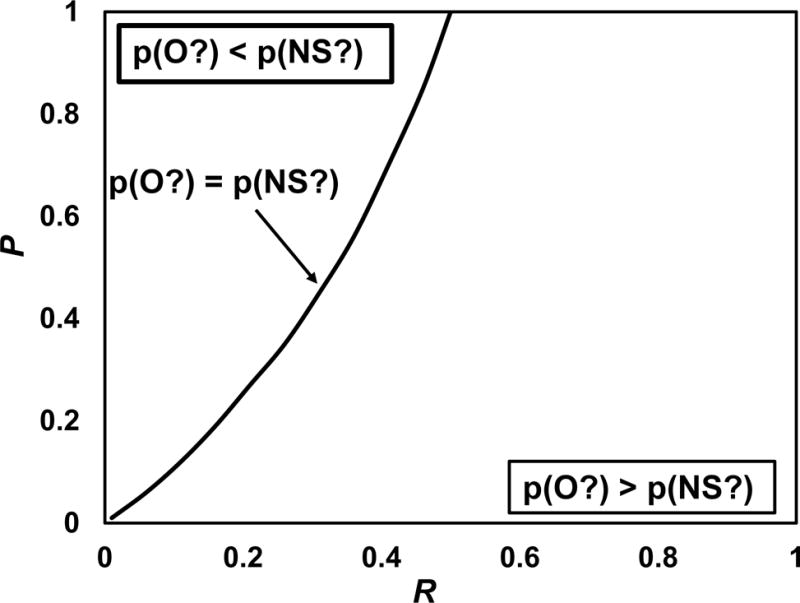
The mathematical relation between levels of complementarity for new-similar items and the processes of target recollection (parameter R of the conjoint recognition model) and context recollection (parameter P). p(O?) is the probability of accepting new-similar items on old probes, and p(NS?) is the probability of accepting them on new-similar probes. Complete complementarity [the p(O?) = p(NS?) curve] is observed when P = R/(1− R). Partial complementarity that is realty-consistent [p(O?) > p(NS?); right side of graph] is observed when P < R/(1− R)), and partial complementarity that is realty-reversed [p(O?) < p(NS?); left side of graph] is observed when P > R/(1− R).

Turning to O items, we mentioned that for such items, target and context recollection are both reality-consistent. The model’s expressions for accepting O? and NS? probes for these items are:

$$p_O(\mathrm{O}?)=R_O+(1-R_O)S_O,\text{and}$$ (3)

$$p_O(\text{NS}?)=(1-R_O)S_O,$$ (4)

where S_O is the probability of semantic familiarity and R_O is the combined probability of the two forms of recollection (i.e., it is the probability of accepting O? probes and rejecting NS probes due to target recollection or context recollection). It is easy to see that observing complete or strong complementarity for targets rests on R_O being 0 or close to it, which will be rare events. Also, note another feature of Equations 3 and 4 that reinforces our earlier comment that complementarity is far more likely for NS items than for O items. For O items, the relation between p_O(O?) and p_O(NS?) is constrained such that p_O(O?) ≥ p_O(NS?) because R_O + (1−R_O)S_O, ≥ (1− R_O)S_O. The relation between p_NS(O?) and p_NS(NS?) is not similarly constrained; it will turn on the relative magnitudes of R and P.

Complementarity in Judgment and Decision Making

Complementarity has not been a topic of focused research in the memory literature, and as we saw, it violates our naïve intuition that episodic memory ought to be compensatory across judgments about incompatible reality states. In that light, it is useful to remind ourselves, before moving on to data, that there are established instances of complementarity in other areas of cognitive psychology—most notably in the judgment and decision making literature.

Preference reversals (e.g., Slovic & Lichtenstein, 1983; Tversky, Slovic, & Kahneman, 1990) are classic examples. Similar to memory complementarity, subjects exhibit such reversals by affirming logically contradictory preference states for the same item, on slightly different probes. A textbook illustration involves one group of subjects affirming a preference for option A over option B, when choosing between them on one type of probe, but another group of subjects affirming a preference for B over A when choosing between them on another type of probe. For instance, suppose that subjects read descriptions of various features of apartment A and apartment B—location, age, size, distance from subway stations, and so on. Half the subjects express their preference by indicating which apartment they would be willing to live in, and the other half express their preference by indicating which apartment they would be willing to pay more rent for. The apartment with the higher average preference on the first task is the opposite of the apartment with the higher average preference on the second task (Corbin, Reyna, Weldon, & Brainerd, 2015). A further parallel with memory complementarity is that preference reversals have been tied to the mix of verbatim and gist retrieval on these probes (Stone, Yates, & Parker, 1994).

Overview of Experiments

In Experiment 1, we investigated whether DRM lists and other common false memory materials induce reality-reversal illusions or complementarity illusions with a large corpus of conjoint recognition data sets; that is, whether that average value of p_NS(O?) for critical distractors is far higher than the average value of p_O(NS?) or whether they are more comparable. We introduce a quantitative index, the complementarity ratio. This is a convenient statistic that simultaneously conveys information about the level of complementarity in performance and about whether its direction is reality-consistent or reality-reversed. For DRM data sets, the corpus allowed levels of complementarity for strong NS items, weak NS items, and O items to be averaged across many experiments and a range of experimental conditions. For other false memory tasks, the corpus allowed us to compare the levels of complementarity for other common procedures to DRM levels.

In Experiments 2 and 3, we determined whether the group-level results from Experiment 1 generalized to individual subjects. The subjects studied large numbers of DRM lists and responded to both O? and NS? probes about test items. The individual-level results were similar to the group results. The next experiment was a housekeeping study in which we considered whether the high levels of complementarity that were observed for recognition in the first three experiments are also observed for recall.

In Experiments 5 and 6, we attempted to gain experimental control of complementarity with theoretically-derived manipulations. According to Equations 1 and 2, complementarity can be forced in a reality-consistent direction by increasing target recollection (parameter R), relative to some baseline condition, and complementarity can be forced in a reality-reversed direction by decreasing target recollection. We investigated a manipulation of the former sort in Experiment 5 (repetition) and a manipulation of the latter sort in Experiment 6 (speeded retrieval).

Experiment 1

The aim of this experiment was to secure baseline findings on the type of illusion that DRM lists induce by determining the degree to which memory for critical distractors is compensatory or complementary over the O and NS reality states. In order to do that, we took advantage of a corpus of conjoint recognition data that Brainerd et al. (2014) assembled. It currently consists of 293 data sets divided into 2 sub-corpora: 169 sets of DRM data and 124 sets of data from other standard semantic false memory paradigms. The first sub-corpus is derived from experiments in which subjects were exposed to lists drawn from the DRM norms (Roediger et al., 2001; Stadler et al., 1999) under a variety of conditions that are common in DRM research (e.g., deep vs. shallow encoding, high vs. low backward associative strength, auditory vs. visual presentation, fast vs. slow presentation rate, younger vs. older subjects). This sub-corpus is further divided into 104 data sets in which the NS items were strong (critical distractors) and 65 data sets in which the NS items were weak. The second sub-corpus is derived from false memory experiments with tasks other than the DRM illusion. The study materials consisted of such things as sentences (Singer & Spear, 2015), picture lists (Bookbinder & Brainerd, 2017), lists of unrelated words (Odegard & Lampinen, 2005), and short narratives (Brainerd, Reyna, & Estrada, 2006). As in DRM experiments, subjects responded to O, NS, and ND items on memory tests, but false memory levels are generally lower than in the DRM experiments. Also, these other procedures do not as often produce the compelling phenomenological evidence of realty reversal that we mentioned in connection with the DRM illusion. Hence, the levels of complementarity that are observed with these other procedures are useful benchmarks for interpreting the levels that are observed with the DRM procedure.

The feature of conjoint recognition that makes it applicable to complementarity is that different groups of subjects respond to different types of memory probes—namely, O?, NS?, and O-or-NS? In other words, some subjects respond to “Is it old?” with test items, others respond to “Is it new-similar?” and still others respond to “Is it either old or new-similar?” Conjoint recognition is a member of a class of procedures that have figured in the memory literature for some years. The core feature of those procedures is that subjects are administered two types of tests: (a) traditional episodic memory tests (recognition or recall) and (b) inferential tests, which require that subjects use episodic memories to make judgments that go beyond those memories. Examples of the latter include conditions in which subjects make judgments about the theme of a series of events (Abadie, Waroquier, & Terrier, 2013), about category membership (Koutstaal, 2003), about spatial relations (Gekens & Smith, 2004), about logical implication (Kintsch, Welsch, Schmalhofer, & Zimny, 1990), about reversals of meaning (Odegard & Lampinen, 2005), and about pragmatic truth (Singer & Remillard, 2008). These procedures have been applied in neuroscience research, where the goal is to isolate differences in the brain regions that are active when subjects access episodic memories versus when they use them to make various judgments (e.g., Garoff, Slotnick, & Schacter, 2005.; Slotnick, 2010). Relative to other members of this class of procedures, the distinguishing property of conjoint recognition is that it includes a mathematical model that quantifies the retrieval processes that control performance on both episodic memory and judgment tests (cf. Equations 1–4). Although that property does not figure in Experiment 1, it is exploited later (see General Discussion).

Returning to whether and to what extent memory is compensatory versus complementary, this question can be examined with the data of two of the three conjoint recognition conditions, by analyzing the values of p(O?) and p(NS?) for both NS and O items. Naturally, the values of p(O?) and p(NS?) will vary over these data sets, and we know that such variability is predicted as a function of variability in target recollection, context recollection, and semantic familiarity (Equations 1–4). The question, as p(O?) and p(NS?) vary over data sets, is whether the overall relation between them is compensatory or complementary—for critical distractors, weak NS items and O items. That question can be answered by analyzing the grand means of p(O?) and p(NS?) for different types of test items, where three patterns are possible empirically.

First, performance for a given type of item might square with our intuition and be completely compensatory, so that either p(O?) > 0 or p(NS?) > 0, but not both. Logically, however, compensation could be either reality-consistent or reality-reversed: It is reality-consistent when the quantity that is > 0 refers to an item’s correct reality state [p(O?) for O items and p(NS?) for NS items], and it is reality-reversed when it refers to the item’s incorrect reality state [p(O?) for NS items and p(NS?) for O items]. Note that the latter arrangement corresponds to the hypothesis that DRM lists foment reality reversals for critical distractors [e.g., p(O?) > 0 and p(NS?) = 0]. The second possible pattern is that memory for a given type of item may exhibit partial complementarity, and if so, p(O?) and p(NS?) will both be reliability > 0. The exact level of complementarity is determined by the spread between the two (the smaller the spread, the greater the complementarity), which is conveniently measured by the ratio p(NS?)/[p(O?) + p(NS?)] for NS items and the ratio p(O?)/[p(O?) + p(NS?)] for O items. Complementarity becomes stronger as these ratios approach .5. We will say that memory is partially complementary if the (a) p(O?) and p(NS?) are both > 0, and (b) either p(O?) > p(NS?) or p(O?) < p(NS?). From the definition of the complementarity ratio, partial complementarity is reality-consistent when the ratio is > .5, and it is reality-reversed when the ratio is < .5. The third possible pattern is that memory for a given type of item may be completely complementary, and if so, p(O?) and p(NS?) will both be reliably > 0 and p(O?) = p(NS?), which means that the complementarity ratio will be .5. In the two subsections that follow, we investigated levels of complementarity displayed by O and NS items in both the DRM and non-DRM sub-corpora.

DRM Sub-corpus

Overall results are shown in Figure 2, where bias-corrected grand means of p(O?) and p(NS?) for O and NS items are displayed separately for the strong NS (critical distractor) data sets (Panel A) and the weak NS data sets (Panel B). The results in Figure 2 and in the remainder of this article are based on the widely used two-high-threshold (2HT) method of correcting recognition data for response bias (e.g., Snodgrass and Corwin, 1998). It has been suggested that 2HT may occasionally produce different results than some other familiar correction methods—in particular, signal detection theory statistics such as d′ and A′ (Healy & Kubovy, 1978). Hence, all of the analyses that are reported below and in subsequent experiments were repeated using d′ and A′. As none of the results were different, we confine attention to the 2HT results in what follows.

Figure 2.

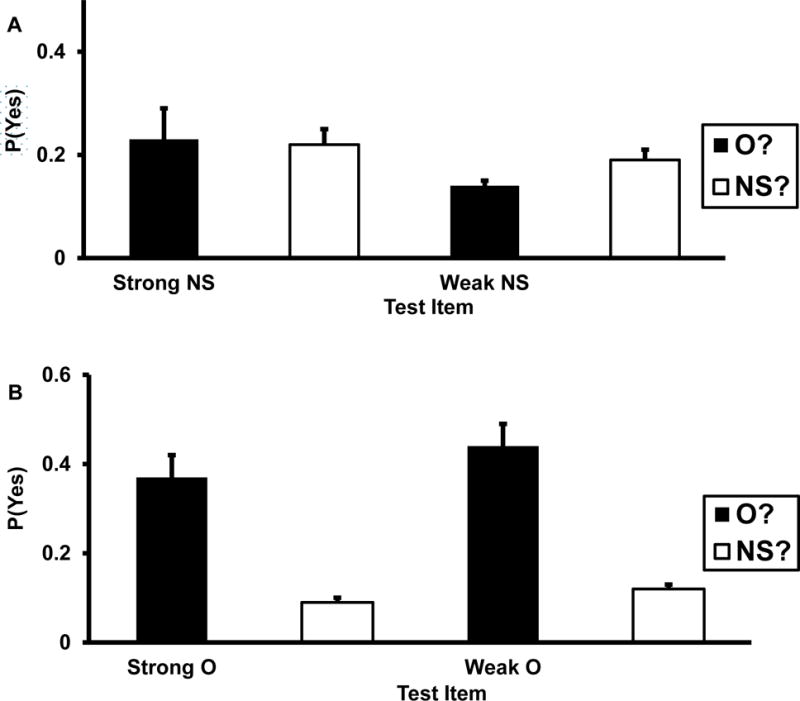
Means and variances of bias-corrected acceptance rates [P(Yes)] for NS (new-similar) and O (old) items in Panels A and B, respectively. O? refers to old probes, and NS? refers to new-similar probes. Strong O refers to O items from strong NS data sets, and weak O refers to O items from weak NS data sets in Experiment 1. Strong NS performance is completely complementary because p(O?) ≈ p(NS?). Weak NS performance is moderately complementary and reality-consistent because p(O?) < p(NS?). O performance is weakly complementary and reality-consistent because p(O?) > p(NS?).

Strong NS Data Sets

Taking the critical distractor results first, as expected the values of p(O?) and p(NS?) varied widely over data sets, with the ranges being 0–.77 for p(O?) and 0–.73 for p(NS?). When it came to the relation between them, however, complementarity was the clear pattern [i.e., p(O?) ≈ p(NS?) for the grand means]. The main analysis was a 2 (condition: O? vs. NS? probes) X 2 (item: O vs. NS) analysis of variance (ANOVA). We noted earlier that according to Equations 1–4, complementarity should be far more pronounced for NS items than for O items. That result would fall out as a Condition X Item interaction, such that the difference between the p(O?) and p(NS?) acceptance rates is smaller for NS items (and perhaps not reliable) than for O items. A large interaction of this sort was the major result, F(1, 102) = 76.10, MSE = .03, η_p² = .43. It can be seen in Figure 2A that the interaction was a cross-over such that (a) p(NS?) was larger for NS items than for O items, but (b) p(O?) was larger for O items than for NS items. With respect to the question of central interest, memory complementarity, post hoc analyses of this interaction revealed that memory for NS items was completely complementary, whereas memory for O items displayed weak complementary that was reality-consistent; that is, critical distractors such as chair and anger were remembered as being old and new-similar as comparable rates, whereas list items such as table and mad were remembered as being old at much higher rates than they were remembered as being new-similar. The detailed results for those patterns follow, but first, we describe the method of analysis because the same two-step analysis will be repeated in all of the experiments that are reported in this paper.

Earlier, in the preamble to this experiment, we mentioned that three relations between p(O?) and p(NS?) are possible—complete compensation, partial complementarity, or complete complementarity. Statistically, the specific relation can be determined in two steps, which consist of one-sample t tests followed by a paired-samples t test. First, the unique feature of complete compensation is that either p(O?) or p(NS?) must not be reliably > 0. That can be determined by evaluating the null hypotheses that p(O?) = 0 and p(NS?) = 0 with one-sample t tests. If one is rejected and the other is not, we stop there and conclude that memory was completely compensatory. Otherwise, second, the unique feature of complete complementarity is that p(O?) = p(NS?), which can be evaluated with a paired-samples t test. When the first step rejects both null hypotheses, the second decides whether complementarity is partial (null hypothesis is rejected) or complete. If complementarity is partial, whether it is reality-consistent or reality-reversed follows from the direction of the difference between p(O?) and p(NS?).

Analyzing the strong NS data first, we tested the null hypotheses that p(O?) = 0 and p(NS?) = 0 with one-sample t tests, and both were rejected at high levels of confidence, t(103) = 10.00 and t(103) = 12.26, respectively. (The .05 level of confidence is used for all significance tests in this article.) Thus, critical distractors were remembered as belonging to each of these incompatible states at reliable levels. Next, we evaluated the null hypothesis that p(O?) = p(NS?) with a paired-samples t test. That null hypothesis could not be rejected, t(103) = .37, indicating complete complementarity between memory for the two reality states. Consistent with that, the complementarity ratio p(NS?)/[p(O?) + p(NS?)] = .49. In this pool of data sets, then, rather than inducing a reality reversal in which strong NS items were erroneously perceived to be O and not NS, on average these items were erroneously perceived to be O on O? tests and correctly perceived to be NS on NS? tests at comparable levels.

Turning to O items, one-sample t tests rejected the null hypotheses that p(O?) = 0, t(103) = 17.16, and p(NS?) = 0, t(103) = 2.14. We then evaluated the null hypothesis that p(O?) = p(NS?) with a paired-samples t test. That null hypothesis was rejected at a high level of confidence, t(103) = 15.08, and the complementarity ratio p(O?)/[p(O?) + p(NS?)] = .76. Hence, DRM lists also induced a moderate degree of complementarity for list items, which was reality-consistent because the complementarity ratio was > .5.

In sum, subjects correctly remembered the traditional critical distractors of DRM lists as being new-similar at approximately the same rate as they erroneously remembered them as being old. Thus, over the conditions of this sub-corpus, DRM lists did not foment a reality reversal but, instead, did something more novel. They stimulated a complementarity illusion in which memory for these items was mapped with each of these incompatible states at similar levels. As predicted on theoretical grounds, this illusion was not observed for list words, which displayed a moderate level of reality-consistent complementarity.

Weak NS Data Sets

Turning to the weak NS portion of the sub-corpus, the pattern was somewhat different for weak than for strong NS items but was the same for O items (Figure 2B). As with the strong NS data sets, the values of p(O?) and p(NS?) varied widely over the weak NS data sets, with the ranges being 0–.43 for p(O?) and 0–.55 for p(NS?). When it came to the relation between them, however, partial complementarity that was reality consistent was the clear pattern [i.e., p(O?) > 0, p(NS?) > 0, and p(O?) < p(NS?)]. As before, the main analysis was a 2 (condition: O? vs. NS? probes) X 2 (item: O vs. NS) ANOVA. Also as before, the main result was a large Condition X Item cross-over interaction, F(1, 65) = 83.11, MSE = .03, η_p² = .56. Post hoc analysis of this interaction produced results that were similar to those reported above, except that the level of complementarity for weak NS items was slightly less marked than it was for strong NS items.

For weak NS items, we first tested the null hypotheses that p(O?) = 0 and p(NS?) = 0 with one-sample t tests, and both were rejected at high levels of confidence, t(65) = 10.34 and t(65) = 10.45, respectively. Thus, memory displayed complementarity for weak NS items, but unlike critical distractors, it was imperfect because when we tested the null hypothesis that p(O?) = p(NS?), it was rejected. However, consider the values of p(O?) and p(NS?) in Figure 2B (.14 and .19). With those values, the complementarity ratio was .58, which is obviously close to .5, even though it is reliably larger. Further, notice that the direction of the difference is reality-consistent, which means that there is no sense in which DRM lists induced reality reversals for either strong or weak NS items. The bottom line is that like critical distractors, weak NS items displayed marked complementarity because the complementarity ratios was close to .5, and the hit rate on NS? probes was slightly but reliably higher than the false alarm rate on O? probes.

With respect to O items, one-sample t tests rejected the null hypothesis that p(O?) = 0, t(65) = 15.67, and the null hypothesis that p(NS?) = 0, t(65) = 8.06. We then evaluated the null hypothesis that p(O?) = p(NS?) with a paired-sample t test. That null hypothesis was rejected at a high level of confidence, t(65) = 12.66. As in the strong NS data sets, then, DRM lists fomented only moderate complementarity for list items because the complementarity ratio was .79, which is close to its value for the strong NS data sets (.76).

Non-DRM Sub-corpus

Turning to the non-DRM sub-corpus, the hallmark of these tasks is that they generate lower average levels of false memory (judging NS items to be O) than DRM critical distractors. Referring to Equations 1 and 2, the two changes, relative to the DRM sub-corpus, that would have the largest suppressive effect on false memory would be increases in target recollection, which would decrease O? acceptances and increase NS? acceptances, and decreases in context recollection, which would have the same two consequences. Considering that memory for critical distractors was found to be completely complementary, the outcome of either change would be to reduce complementarity in a reality-consistent direction. This could only fail to happen if both R and P decreased in such a way that the paired values fall on the curve in Figure 1 [i.e., the values satisfy P = R/(1−R)]. For purely statistical reasons, it is improbable that the data would always arrange themselves in just that way over a wide assortment of conditions, and hence, the straightforward prediction is that NS items in the non-DRM sub-corpus should exhibit lower levels of complementarity, as well as lower levels of false memory.

Bias-corrected grand means for the non-DRM sub-corpus are displayed in Figure 3 for the O? and NS? conditions. First, we conducted the same 2 (condition: O? vs. NS? probes) X 2 (item: O vs. NS) ANOVA of the p(O?) and p(NS?) means for the various conditions in this sub-corpus. As in the ANOVAs of the DRM sub-corpus, there was a large Condition X Item crossover interaction, F(1, 123) = 386.16, MSE = .03, η_p² = .66. Post hoc analysis of this interaction produced more modest complementarity for both list items and NS items than the DRM sub-corpus did.

Figure 3.

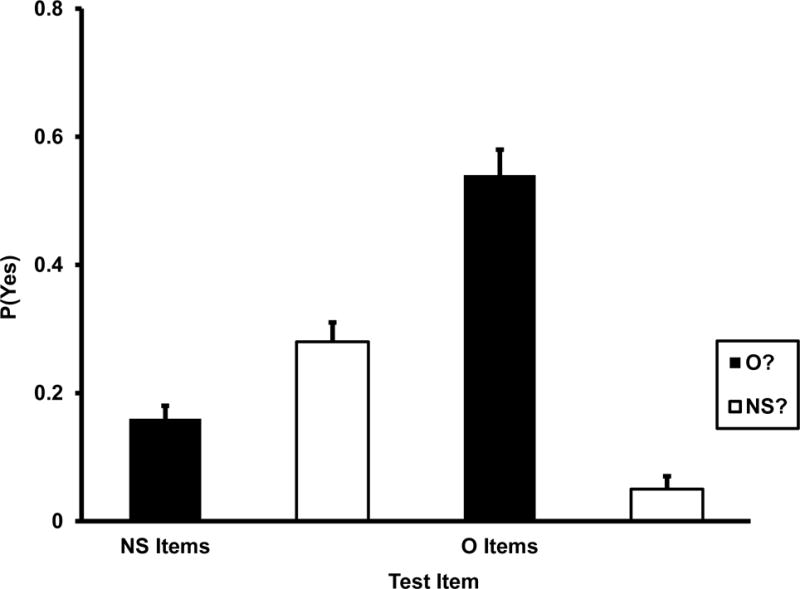
Means and variances of bias-corrected acceptance rates [P(Yes)] for NS (new-similar) and O (old) items. O? refers to old probes, and NS? refers to new-similar probes. These are the relations between p(O?) and p(NS?) for NS items and O items in the non-DRM sub-corpus of Experiment 1. Performance on NS items is partially complementary and reality-consistent because p(O?) < p(NS?). Performance on O items is very weakly complementary and reality-consistent because p(O?) > p(NS?).

Analyzing the NS data for complementarity first, the null hypotheses p(O?) = 0, p(NS?) = 0, and p(O?) = p(NS?), were all rejected high levels of confidence, ts(123) = 11.08, 20.40, and 6.84, respectively. Note in Figure 3 that the mean of p(O?) for NS items was not only well above 0 (.16), but there was a sizeable difference between that value and the mean of p(NS?) for these items (.28) in the reality-consistent direction. That difference (.12) is far larger than the differences for strong and weak NS items in the DRM illusion—producing a complementarity ratio of .67, which is noticeably closer to 1 than the ratios for strong and weak NS items in the DRM sub-corpus (.49 and .58, respectively). Another important point is that over the DRM and non-DRM sub-corpora, complementarity for NS items does seem to be simply a monotonic function of the level of false memory level: The level of false memory for NS items in the non-DRM sub-corpus [i.e., p(O?) for such items] was roughly the same as for weak NS items in the DRM sub-corpus (.16 vs. .14), but the level of complementarity was more moderate.

With respect to O items, complementarity was weaker than for NS items, as Equations 1–4 predict. First, a one-sample t test showed that the null hypothesis that p(O?) = 0 could be rejected, t(123) = 29.23, and although the value of p(NS?) in Figure 3 is very close to 0 (.05), a one-sample t test showed that the null hypothesis that p(NS?) = 0 could also be rejected, t(123) = 4.02. Naturally, the large difference between p(O?) and p(NS?) in Figure 3 (.49) meant that the p(O?) = p(NS?) null hypothesis was rejected by a paired-samples t test, t(123) = 22.98. With the values of p(O?) and p(NS?) in Figure 3, the complementarity ratio (.91) approaches perfect compensation, although it is reliably < 1.

The most instructive finding is that the non-DRM result buttress the stature of the DRM paradigm as a unique procedure that induces especially high levels of complementarity for NS items. Regardless of whether one compares the results for strong or weak NS items in the DRM sub-corpus to the result for NS items in the non-DRM sub-corpus, complementarity is much more robust for the DRM paradigm and is complete for critical distractors.

Experiments 2 and 3

Experiment 1 was a study of convenience inasmuch as it relied on an existing corpus that happened to include the complementary O? and NS? conditions, in order to gain leverage on the type of illusion that DRM lists induce. The next two experiments were designed to generate new data on this question, using procedures that are familiar in the literature—except for the fact that the O and NS reality states were both tested within-rather than between-subjects, for all items. In each experiment, subjects were exposed to a large number of DRM lists that produce the highest levels of false recognition of critical distractors in extant norms, followed by O? and NS? tests for O, strong NS, weak NS, and ND items.

The difference between the two experiments was the presence of delayed tests in the second one. The design of Experiment 2 simply exposed subjects to DRM lists, followed by O? and NS? probes for the four types of items. However, an often-discussed feature of the DRM illusion is its stability over time, with reliable levels of distortion being detectable a day, a week, or a month after list presentation (Payne, Elie, Blackwell, & Neuschatz, 1996; Toglia, Neuschatz, & Goodwin, 1999). Clearly, it is important to know whether complementarity is similarly stable and whether the complementarity ordering of strong NS > weak NS > O is also stable. Those questions were investigated in Experiment 3 by adding delayed tests to the design of Experiment 2. Several DRM lists were again presented, followed by O? and NS? probes for half of these lists. One to two weeks later, O? and NS? probes were administered for all of the lists. By comparing delayed performance for lists that were tested versus were not tested a week earlier, we were able to determine how prior testing affects the stability of complementarity.

Another notable feature of Experiments 2 and 3 is that O? and NS? probes were varied within-subject. In conjoint recognition experiments, the normal procedure is for different groups of subjects to participate in the different testing conditions, and that procedure figured in nearly all of the data sets there were analyzed in Experiment 1. Therefore, at this point, the evidence that DRM lists induce complementarity illusions is restricted to between-subject comparisons of O? and NS? performance. That is a significant limitation because the false memory literature contains examples of variables that produce robust effects with between-subject comparisons but no effect or small effects with within-subject comparisons. In order to address this uncertainty, all subjects in Experiments 2 and 3 responded to recognition probes for all four types of items that were half O? and half NS?

Method

Subjects

The subjects in Experiment 2 were 114 undergraduates, who participated to fulfill a course requirement. The subjects in Experiment 2 were 168 undergraduates, who participated to fulfill a course requirement. The research protocol for these two experiments and for Experiments 4, 5, and 6 was approved by the local Institutional Review Board and was in compliance with the ethical standards of the American Psychological Association.

Materials

The materials came from a pool of DRM lists that had been drawn from the Stadler et al. (1999) norms, which report levels of true and false recognition for 36 lists. Each list consists of the first 15 forward associates of a missing word, the critical distractor (cf. Table 1). For each subject, we randomly selected 16 of these lists for presentation. Those lists supplied the items that were presented during the study phase of each experiment, and they supplied the O, strong NS, and weak NS items that were subjected to immediate and delayed memory tests. The remaining 20 lists in the norms supplied the ND items for immediate and delayed tests.

Procedure

The procedure for Experiment 2 consisted of two steps, list presentation followed by immediate memory tests. The procedure for Experiment 3 consisted of three steps, list presentation, followed by immediate memory tests, followed by delayed memory tests. At the start of Experiment 2, subjects received general memory instructions that described the overall structure of the experiment. Next, the 16 DRM lists were presented in random order via prerecorded audio files, as the subject sat at a computer to which headphones were attached. The individual words on each list were presented in descending order of forward associative strength, as is traditional in DRM research. In order to make the subjects’ memory task manageable, the first eight words of each DRM list were presented in Experiment 2. At the start of list presentation, the subject was told that he or she would be listening to 16 short word lists and that a memory test would be administered after all the lists had been presented. Next, list presentation began with the announcement “first list,” followed by the words of the first DRM list being read at a 3 sec rate. There was a 10 sec pause after the last word of the first list, at the end of which the subject heard “next list,” followed by the words of the next list, presented at a 3sec rate. This procedure of presenting a list, followed by a 10 sec pause, followed by the next list was continued until all 16 lists had been presented.

Following list presentation, the subject read instructions that described the upcoming memory test and provided concrete examples. The instructions explained that the test would consist of words that they had just heard on the lists (O), new words that were semantically similar to list words (NS), and new words that were unrelated to list words (ND). Examples of each type of word were provided. The instructions also informed subjects that they would make one of two types of judgments about individual test words. They were told that for half the words, they would be asked whether the words were old list words, whereas for the other half, they would be asked if the words were new-similar. Further examples were provided of correct and incorrect judgments of both types, and they were accompanied by a series of O? and NS? practice probes. Correct answers were provided for the practice probes, and the subject was encouraged to ask any questions about the nature of the upcoming test.

The subject then responded to a 144-item self-paced memory test for the 16 DRM lists, with the test items administered in random order. The test items were of four types: (a) 48 O words (3 from each presented list); (b) 16 strong NS words (the critical distractors for the presented lists); (c) 32 weak NS words (two unpresented words from each presented list, drawn at random from positions 9–15); and (d) 48 ND words. Concerning the ND words, they were further subdivided into 16 words that were the critical distractors for 16 of the unpresented DRM lists in the Stadler et al. (1999) norms, and 32 words that were targets from those same unpresented lists (2 per list, selected at random). On this test, subjects responded to O? probes for half the words in each of the four groups of words, and they responded to NS? probes for the other half of the words in each group.

The design of Experiment 3 was the same as that of Experiment 2, except for (a) the content of the memory test that followed the presentation of the 16 lists and (b) the addition of a delayed memory test. Concerning a, the initial memory test that followed presentation of this lists was a self-paced recognition test that consisted of 72 items, rather than 144, because only 8 of the 16 DRM lists were tested. Thus, the test consisted of the following types of items: 24 O words (3 from each of 8 presented lists, selected at random); 8 strong NS words (the critical distractors for the 8 tested lists); 16 weak NS items (2 unpresented words from each of the 8 tested lists, drawn at random from positions 9–15); 24 ND items (the 8 critical distractors from 8 unpresented DRM lists, plus 2 list words from each of those lists). Following this initial test, subjects were scheduled to return to the laboratory for a delayed test at intervals of 7–14 days. Overall, the mean length of time between the immediate and delayed tests for these subjects was 10 days. The content of the delayed test was identical to the immediate test in Experiment 2; that is, all 16 presented lists were tested, the 8 that had been tested on the immediate test and the 8 that had not been.

Results and Discussion

Experiment 2

In Figure 4A, we display the bias-corrected acceptance probabilities in the O? and NS? conditions for strong NS, weak NS, and O items. Visually, it is apparent that the same complementarity pattern that was detected in the conjoint recognition corpus was also present in this experiment. For strong NS items, it can be seen that the probability of judging them to be old list items was virtually the same as the probability of judging them to be new-similar. Complementarity was less marked for weak NS items and was reality-consistent. Subjects were less likely to incorrectly judge weak NS items to be old than to correctly judge them to be new-similar. Complementarity was even more moderate and reality-consistent for O items subjects were far more likely to correctly judge them to be old than to incorrectly judge them to be new-similar. The corresponding complementarity ratios are .43, .66, and .80 for strong NS, weak NS, and O items, respectively, and hence, complementarity was robust for strong NS items, moderate for weak NS items, and modest for O items.

Figure 4.

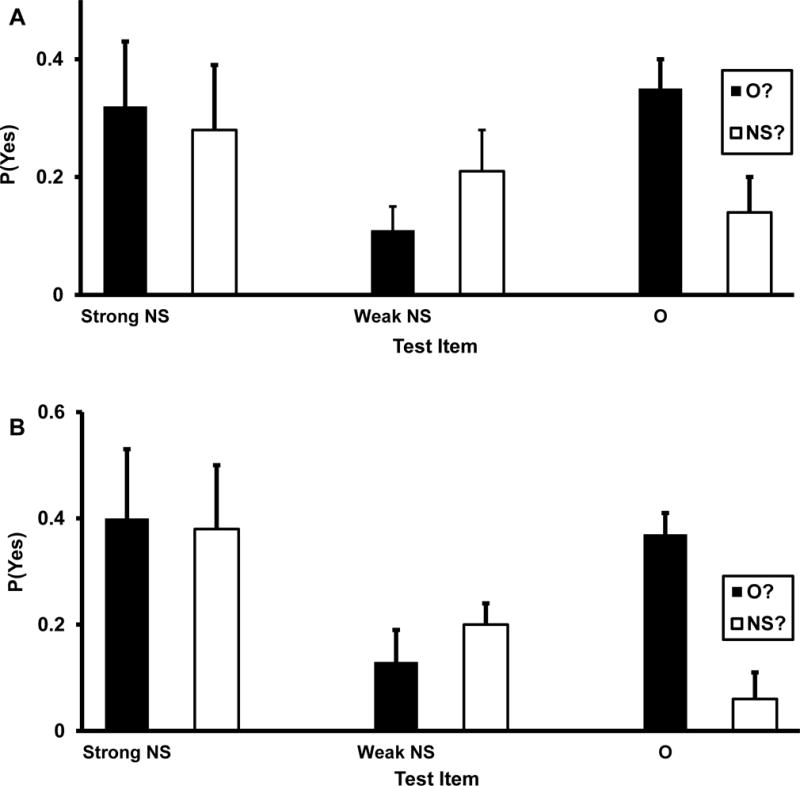
Means and variances of bias-corrected acceptance rates [P(Yes)] for NS (new-similar) and O (old) items. O? refers to old probes, and NS? refers to new-similar probes. These are the relations between p(O?) and p(NS?) for strong NS items, weak NS items, and O items in Experiment 2 (Panel A) and in the immediate testing condition of Experiment 3 (Panel B). In both panels, strong NS performance is completely complementary because p(O?) ≈ p(NS?), weak NS performance is partially complementary and reality-consistent because p(O?) < p(NS?), and O performance is weakly complementary and reality-consistent because p(O?) > p(NS?).

The main statistical analysis was a 2 (condition: O? vs. NS? probes) X 3 (item: strong NS vs. weak NS vs. O) ANOVA of the bias-corrected means of p(O?) and p(NS?) for the three types of items. The key result, as in the conjoint recognition corpus, was a large Condition X Item interaction, F(1, 224) = 25.88, MSE = .09, η_p² = .19. The reason for the interaction is the variation in complementarity is apparent in the above ratios.

The detailed complementarity analyses produced the following patterns for the three types of items. First, for strong NS items, we tested the null hypotheses p(O?) = 0 and p(NS?) = 0 with one-sample t tests and the null hypothesis p(O?) = p(NS?) with a paired-samples t test. The first two hypotheses were rejected at high levels of confidence, t(112) = 10.50 and t(112) = 9.07, respectively, but the third null hypothesis could not be rejected, t(112) = 1.01. Statistically, then, memory for strong NS items was completely complementary, although numerically, the complementary ratio was < .5. Second, for weak NS items, we also tested the null hypotheses p(O?) = 0 and p(NS?) = 0 with one-sample t tests and the null hypothesis p(O?) = p(NS?) with a paired-samples t test. Similar to strong NS items, the first two hypotheses were rejected at high levels of confidence, t(112) = 5.73 and t(112) = 8.22, respectively, but unlike strong NS items, the third null hypothesis was also rejected, t(112) = 2.96. Thus, memory for weak NS items was complementary [because p(O?) and p(NS?) were both reliably > 0] and moderately so [because p(NS?) was reliably > than p(O?)]. Third, for O items, we again tested the null hypotheses that p(O?) = 0 and p(NS?) = 0 with one-sample t tests and the null hypothesis that p(O?) = p(NS?) with a paired-samples t test. Similar to both types of NS items, the first two hypotheses were rejected at high levels of confidence, t(112) = 11.49 and t(112) = 2.77, respectively, and similar to weak NS items, the third null hypothesis was also rejected, t(112) = 8.94. Hence, the pattern for both O items was only weak complementarity, considering that the complementarity ratio was closer to 1 than to .5.

Summing up, in this experiment we measured complementary within-subjects by administering both O? and NS? probes to them. However, the overriding conclusions that emerged were the same as when complementarity was measured between-subjects (Experiment 1). First, there was no evidence that DRM lists induce reality reversals, in which critical distractors are remembered as being what they are not (old) and not as what they are (new-similar). Second, there was consistent evidence that DRM lists induce complementarity illusions for NS items and that the overall complementarity ordering is strong NS > weak NS > O.

Finally, notice an interesting asymmetry between O? and NS? probes that is relevant to a previously mentioned finding about the DRM illusion—namely, that levels of true and false recognition often do not differ. The asymmetry is that this finding depends on which reality state subjects were responding to. With O? probes, the standard result was obtained; acceptance probabilities for O and strong NS items were virtually the same (Figure 3A). In contrast, with NS? probes, the level of true memory (acceptance of NS items) was two times the level of false memory (acceptance of O items).

Experiment 3

Complementarity was measured on two occasions in this experiment, immediately after list presentation and 10 days later. We report the results for the immediate test first, followed by the results for the delayed test.

Immediate test

The bias-corrected acceptance probabilities in the O? and NS? conditions are displayed in Figure 3B for the three types of test items. Obviously, the complementarity picture is broadly the same as in Experiments 1 and 2. For strong NS items, the probability of judging them to be old list items was virtually the same as the probability of judging them to be new-similar. Complementarity was also evident for weak NS items but was less marked and was only weakly present for O items. For weak NS items, subjects were somewhat less likely to incorrectly judge them to be old than to correctly judge them to be new-similar, and for O words, subjects were far more likely to correctly judge them to be old than to incorrectly judge them to be new-similar. The corresponding complementarity ratios were .49, .59, and .86 for strong NS, weak NS, and O items, respectively. Thus, complementarity was complete for strong NS items, quite robust for weak NS items, and very weak for O items. Note that the ratios for weak NS and O items are both reality-consistent.

As in Experiment 2, the main statistical analysis was a 2 (condition: O? vs. NS? probes) X 3 (item: O vs. strong NS vs. weak NS) ANOVA of the bias-corrected means of p(O?) and p(NS?) for the three types of items. Also as in Experiment 2, the key result was a large Condition X Item interaction, F(1, 334) = 49.69, MSE = .08, η_p² = .23. The reason for the interaction is that as the just-mentioned complementarity pattern indicates, the spread between p(O?) and p(NS?) varied considerably as a function of which type of item was being tested.

We repeated the same detailed analyses of complementarity effects for the three types of items. For strong NS items, we tested the null hypotheses p(O?) = 0 and p(NS?) = 0 with one-sample t tests and the null hypothesis p(O?) = p(NS?) with a paired-samples t test. The first two hypotheses were rejected at high levels of confidence, t(168) = 14.50 and t(168) = 14.42, respectively, but the third could not be rejected, t(167) = .42. Once again, then, memory for critical distractors was completely complementary. Next, for weak NS items, we also tested the null hypotheses p(O?) = 0 and p(NS?) = 0 with one-sample t tests and the null hypothesis p(O?) = p(NS?) with a paired-samples t test. Similar to strong NS items, the first two hypotheses were rejected, t(168) = 7.13 and t(168) = 11.94, respectively, but unlike strong NS items, the third null hypothesis was also rejected, t(167) = 2.79. Thus, memory for weak NS items was partially complementary but was strongly so because the complementarity ratio (.59) approached .5. Last, for O items, we again tested the null hypotheses p(O?) = 0 and p(NS?) = 0 with one-sample t tests and the null hypothesis p(O?) = p(NS?) with a paired-samples t test. Similar to weak NS items, the first two hypotheses were rejected, t(168) = 22.76 and t(168) = 3.49, respectively, and the third null hypothesis was also rejected, t(167) = 13.18. Therefore, memory for O was also partially complementary, and only very weakly so because the complementarity ratio (.86) was far from .5. Finally, the complementarity ordering was again strong NS > weak NS > O.

Note in Figure 3B that the data of the immediate test exhibited the same asymmetry between O? and NS? probes that was present in Experiment 2. On the one hand, the standard finding that true and false recognition levels are virtually the same for O and strong NS items, respectively, was again obtained with O? probes. With NS? probes, on the other hand, the true recognition level was much higher than the false recognition level.

Delayed test

Recall that these subjects received a delayed test whose content was identical to the immediate test in Experiment 2; that is, all 16 DRM lists were tested, whereas only 8 had been tested on the immediate test. This means that there was an additional design factor for the delayed test: Half of the items in each of the four categories (O, strong NS, weak NS, ND) had been previously tested, and the other half were tested for the first time. A well-known finding about how prior testing affects performance on delayed tests is that it helps preserve both verbatim and gist traces of study materials, elevating both true and false memory on subsequent tests (for a review, see Brainerd & Poole, 1995). Because, as we saw, complementarity depends on the mix of gist and verbatim processing, we measured it separately for previously tested versus previous untested items.

The bias-corrected acceptance probabilities in the O? and NS? conditions are displayed in Figure 4A for previously tested items and in Figure 4B for previously untested items. Taking previously tested items first, the complementarity picture is qualitatively the same as on the immediate test for strong NS items (complete complementarity) and O items (partial complementarity) but is different for weak NS items. Although it is still the case that memory for weak NS items was partially complementary, the complementarity ratio was in the reality-reversed direction, whereas it was reality-consistent in Experiment 1 and on the immediate tests of Experiments 2 and 3. The relevant complementarity ratios are .53, .29, and .63 for strong NS, weak NS, and O items, respectively. Turning to the previously untested items, the qualitative picture was the same for strong and weak NS items but different for O items. Complementarity was complete for strong NS items and partial but reality-reversed for weak NS items, whereas memory was completely compensatory and reality-consistent for O items. The relevant complementarity ratios are .46, .30, and .91 for strong NS, weak NS, and O items, respectively, and the O ratio was not reliably < 1 (see below).

The main statistical analysis was a 2 (prior testing: tested vs. untested) X 2 (condition: O? vs. NS? probes) X 3 (item: O vs. strong NS vs. weak NS) ANOVA of the bias-corrected means of p(O?) and p(NS?) for the three types of items. As in all prior ANOVAs, there as a large Condition X Item interaction, F(2, 304) = 14.32, MSE = .06, η_p² = .09. Also as in prior ANOVAs, the reason for this interaction is that the spread between p(O?) and p(NS?) varied as a function of the type of item that was being tested. This ANOVA contained a new factor, prior testing, that was not present in previous ANOVAs, which produced an important but anticipated finding: There was a large main effect for this factor, F(1, 304) = 48.69, MSE = .11, η_p² = .24, which was due to the fact that the grand means of p(O?) and p(NS?) were larger for previously tested items than for previously untested items. We report the detailed analyses of complementarity effects separately for previously tested and previously untested items.

Taking previously tested items first, for strong NS items, we tested the null hypotheses p(O?) = 0 and p(NS?) = 0 with one-sample t tests and the null hypothesis p(O?) = p(NS?) with a paired-samples t test. The first two hypotheses were rejected, t(1152) = 7.06 and t(152) = 8.32, respectively, but the third null hypothesis could not be rejected, t(167) = .73. As in all prior analyses, then, memory for previously tested strong NS items was completely complementary. For weak NS items, we also tested the null hypotheses p(O?) = 0 and p(NS?) = 0 with one-sample t tests and the null hypothesis p(O?) = p(NS?) with a paired-samples t test. Similar to strong NS items, the first two hypotheses were rejected, t(152) = 8.89 and t(152) = 3.40, respectively, but the third null hypothesis was also rejected, t(152) = 3.78. Hence, memory for weak NS items was partially complementary, and it was also reality-reversed because p(O?) > p(NS?). Finally, for O items, we tested the null hypotheses that p(O?) = 0 and p(NS?) = 0 with one-sample t tests and the null hypothesis that p(O?) = p(NS?) with a paired-samples t test. Similar to weak NS items, the first and second hypotheses were rejected, t(152) = 12.01 and t(152) = 5.98, respectively, and the third was also rejected, t(152) = 3.36. Therefore, memory for O items was also partially complementary, but it was reality-consistent because p(O?) > p(NS?).

Continuing with previously untested items, the complementarity results for NS items were similar to those for their previously untested counterparts, but they were different for O items. For strong NS items, we tested the null hypotheses p(O?) = 0 and p(NS?) = 0 with one-sample t tests and the null hypothesis p(O?) = p(NS?) with a paired-samples t test. The first two hypotheses were rejected, t(1152) = 5.41 and t(152) = 3.97, respectively, but the third could not be rejected, t(167) = .78. As in all prior analyses, then, memory for strong NS items was completely complementary. For weak NS items, we also tested the null hypotheses p(O?) = 0 and p(NS?) = 0 with one-sample t tests and the null hypothesis p(O?) = p(NS?) with a paired-samples t test. Similar to strong NS items, the first two hypotheses were rejected, t(152) = 8.77 and t(152) = 3.83, respectively, but the third null hypothesis was also rejected, t(152) = 9.54. Hence, memory for weak NS items was partially complementary, and the direction of the difference between p(O?) and p(NS?) was reality-reversed. Finally, for O items, we tested the null hypotheses that p(O?) = 0 and p(NS?) = 0 with one-sample t tests. The first hypothesis was rejected, t(152) = 7.31, but the second hypothesis was not, t(152) = .88. Thus, memory was completely compensatory and reality-consistent for O items. This is the only instance in any of our DRM experiments in which memory was not at least weakly complementary.

Summary

These experiments generated a large amount of additional data on the question of whether DRM lists induce a reality reversal or a complementarity illusion. Consistent with Experiment 1, performance was completely complementary for critical distractors. This pattern held for delayed as well as immediate tests. Also as in Experiment 1, the complementarity effect generalized to weak NS items, with complementarity being partial rather than complete in both instances. Pooling over all of the conditions in the Experiments 2 and 3, the complementarity ordering was strong NS > weak NS > O, as it was in Experiment 1. Recall that the fact that complementarity is always more marked for new-similar items than for list items is a prediction of the conjoint recognition model.

Relative to Experiment 1 and the immediate tests of Experiments 2 and 3, there was one difference in the detailed results for the delayed tests in Experiment 3. For both previously tested and previously untested weak NS items, the partial complementarity pattern was reality-reversed, whereas it was reality-consistent in all earlier comparisons. Statistically speaking, on delayed tests weak NS items were remembered as being both NS and O, but they were remembered as being O at higher rates (the mean value of the complementarity ratio was .30). Ironically, then, although there was no evidence of reality reversals for critical distractors in any of our data, there was some slight evidence of it, under special testing conditions, for a type of new-similar item that is not tested in most DRM experiments.

Experiment 4

The data up to this point show that under standard conditions, DRM lists induce complementarity illusions rather than reality reversals. Considering that strong NS items, weak NS items, and O items exhibited complementarity in a graded fashion that is congruent with theoretical expectations, it is time to move on to the question of whether the levels of complementarity that critical distractors display can be altered with manipulations that are motivated by the same theoretical distinctions. In particular, is it possible to shift memory for critical distractors away from complete complementarity toward partial complementarity that is both reality-reversed and reality-consistent?

Before taking up that question, however, we briefly report a housekeeping experiment that dealt with a pair of residual questions. The bulk of contemporary DRM experiments focus on recognition rather than recall, but several recall experiments have been reported, too (e.g., Howe, Candel, Otgaar, Malone, & Wimmer, 2010; Toglia et al., 1999). Although most manipulations have similar effects when the DRM illusion is measured with recognition or recall, a few have different effects (e.g., Howe et al., 2010). Also, false memory levels are lower with recall than with recognition (cf. Roediger et al., 2001; Stadler et al., 1999), suggesting that the mix of verbatim and gist retrieval is different (Brainerd & Reyna, 2005). Thus, it is natural to wonder whether the pattern of strong complementarity for critical distractors will be observed with recall as well as recognition.

To answer that question, we conducted a standard type of experiment (e.g.., Payne et al., 1996) in which subjects studied a series of DRM lists that were presented in small blocks and recalled the lists in each block after presentation. The subjects were 60 undergraduates who participated to fulfill a course requirement, with each subject being randomly assigned to one of two recall conditions: O? or NS? Each subject studied 12 15-word DRM lists that were randomly selected from the 36 lists in the Stadler et al. (1999) norms. The procedure was the same for each subject. First, the subject received general memory instructions, which stated that he/she would listen to several short lists of words presented in three groups and would be given a memory test after each group of lists. Next, the subject listened to audio files of four lists, with each being read in the traditional “forward” order (strongest-to-weakest forward associates of the critical distractor), at a rate of 2.5 sec per word and with a 10 sec pause between consecutive lists. Before list presentation began, the subject was told to focus on each word as it was presented and to avoid thinking of other words. Following the first block of lists, subjects solved arithmetic problems for 1 min, read instructions for the recall test, and then performed 3 min of written free recall. The instructions for the O? condition told subjects to recall only words from the lists that had just been presented and to avoid recalling unpresented words with similar meanings, whereas the instructions for the NS? condition told subjects to recall only unpresented words that were similar in meaning to list words and to avoid recalling words that actually been presented. The instructions provided examples of the types of words that should and should not be recalled. The procedure was the same for the second and third blocks. No lists were repeated over blocks.

The results were simple—namely, complete complementarity for critical distractors and weak complementarity that was reality-consistent for list words. On the one hand, critical distractors were recalled at virtually that same rate in the two conditions: p(O?) = .29 and p(NS?) = .28, for a complementarity ratio of .49. On the other hand, list words were recalled at much higher levels in the O? condition than in the NS? condition: p(O?) = .40 and p(NS?) = .07, for a complementarity ratio of .85. In short recall, was completely complementary over the O and NS reality states for critical distractors and was only weakly so for list words.

We conducted a follow-up analysis to determine whether complementarity varied as a function of the strength of the DRM illusion. Normed levels of false recall vary widely for the Stadler et al. (1999) lists, ranging from a high of p(O?) = .65 (window) to a low of p(O?) = .10 (king), with a grand mean of .46. Although complete complementarity for critical distractors was observed for the list pool as a whole, it is natural to wonder whether it varies as a function of level of false memory. An intuitive hypothesis is that complementarity might be weaker and reality-reversed for lists that produce higher levels of false recall. To evaluate that, we spilt the list pool into the 18 lists with the highest levels of false recall (M_p(O?) = .51) and the 18 lists with the lowest levels of false recall (M_p(O?) = .29), we computed the mean complementarity ratios for critical distractors and list words separately for each group.

Taking critical distractors first, there was some weak evidence that complementarity is influenced by baseline levels of false recall. For critical distractors, the complementarity ratios were .45 and .56 for high and low lists, respectively. Neither of these ratios differed reliably from .5, and thus, complementarity was complete, regardless of baseline level of false memory. On the other hand, the complementarity ratio for low lists was reliably larger, and therefore more reality-consistent, than the ratio for high lists. For targets, there was no evidence that complementarity is influenced by baseline levels of false recall. The complementarity ratios were .87 and .83 for high and low lists, respectively. Both values were reliably larger than .5 but did not differ reliably from each other. Thus, the weak and reality-consistent complementarity that was observed for the list pool as a whole was also observed for the high and low halves of the pool.

Experiment 5

In this experiment and in Experiment 6, we take up the question of whether and how the complementarity illusion can be controlled by theoretically-motivated manipulations. According to Equations 1 and 2, the most direct way to decrease the level of complementarity that critical distractors exhibit (i.e., move the complementarity ratio away from .5) in either a reality-consistent or a reality-reversed direction is to drive target recollection (parameter R) up or down, respectively, relative to a baseline condition that exhibits strong complementarity. Here, remember that the relevant expressions are p_NS(O?) = (1−R)P + (1−R)(1− P)S_NS and p_NS(NS?) = R + (1− R)(1− P)S_NS. Suppose that these expressions refer to a baseline condition in which critical distractors display strong complementarity, and some manipulation A is introduced that increases R without affecting other processes. Obviously, p_NS(NS?) will increase and p_NS(O?) will decrease because the R term increases in the p_NS(NS?) expression, while the (1− R)P term decreases in the p_NS(O?) expression. The net effect is to decrease complementarity in the reality-consistent direction by forcing the complementarity ratio toward 1. On the other hand, suppose that some manipulation B is introduced that decreases R without affecting other processes, relative to the same baseline condition. Now, p_NS(O?) will increase and p_NS(NS?) will decrease because the (1−R)P term increases in the p_NS(O?) expression, while the R term decreases in the p_NS(NS?) expression. The net effect of manipulation B is to decrease complementarity in the reality-reversed direction by driving the complementarity ratio toward 0.

In Experiment 5, we investigated a familiar manipulation that ought to decrease complementarity by increasing target recollection, whereas in Experiment 6, we investigated another familiar manipulation that ought to decrease complementarity by decreasing target recollection. The manipulation in Experiment 5 was list repetition, which has often been shown not only to increase hit rates but to increase vivid recollection of list words, using indexes such as R judgments in the remember-know procedure and confidence ratings (for a review, see Yonelinas, 2002). Thus, repetition should increase the R parameter. We replicated the immediate phase of Experiment 3, with the addition of a repetition condition: For control subjects, the procedure was identical to Experiment 3, but for subjects in the repetition group, each DRM list was presented twice.

Method

Subjects

The subjects were 60 undergraduates, who participated to fulfill a course requirement. Half the subjects were randomly assigned to the control and repetition conditions, respectively.

Materials and Procedure

For the control group, the materials and procedures were identical to the immediate-testing phase of Experiment 3: Subjects listened to audio files of 16 DRM lists that had been randomly sampled from the Stadler et al. (1999) norms, followed by a recognition test for 8 randomly selected lists on which half the probes were O? and half were NS?. The test items were O, strong NS, and weak NS items for the eight lists, plus ND items. For the repetition group, the procedure was the same, except for one change—namely, that subjects listened to the audio file for each of eight DRM lists twice. Thus, the subjects in both groups listened to a total of 16 audio files of DRM lists. However, 8 randomly selected DRM lists were each presented twice in the repetition condition, whereas 16 randomly selected RM lists were each presented once in the control condition. As in Experiment 3, the order of list presentation was random, but in the repetition condition, it was subject to the constraint that the two presentations of a given DRM list were never consecutive.

Results and Discussion

In Figure 6, we display the bias-corrected acceptance probabilities for O? and NS? probes for strong NS, weak NS, and O items. The data for the control condition (Panel A) parallel the findings of the immediate testing conditions of Experiments 2 and 3 in that strong NS items displayed complete complementarity. However, so did weak NS items. O items displayed reality-consistent partial complementarity [i.e., p(O?) > p(NS?)]. The results for the repetition condition were quite different (Figure 6B). First, strong NS items now displayed only partial complementarity, which was reality-consistent [i.e., p(NS?) > p(O?), with a complementarity ratio of .62]. Second, weak NS items and O items displayed only moderate, reality-consistent complementarity that was roughly equivalent (complementarity ratios of .72 and .77, respectively). In short, as expected on theoretical grounds, a manipulation that should increase target recollection, produced across-the-board reductions in complementarity by increasing reality-consistent memory, as measured by p(NS?) for new-similar items and by p(O?) for list items, and decreasing reality-reversed memory, as measured by p(O?) for new-similar items and by p(NS?) for list items.

Figure 6.

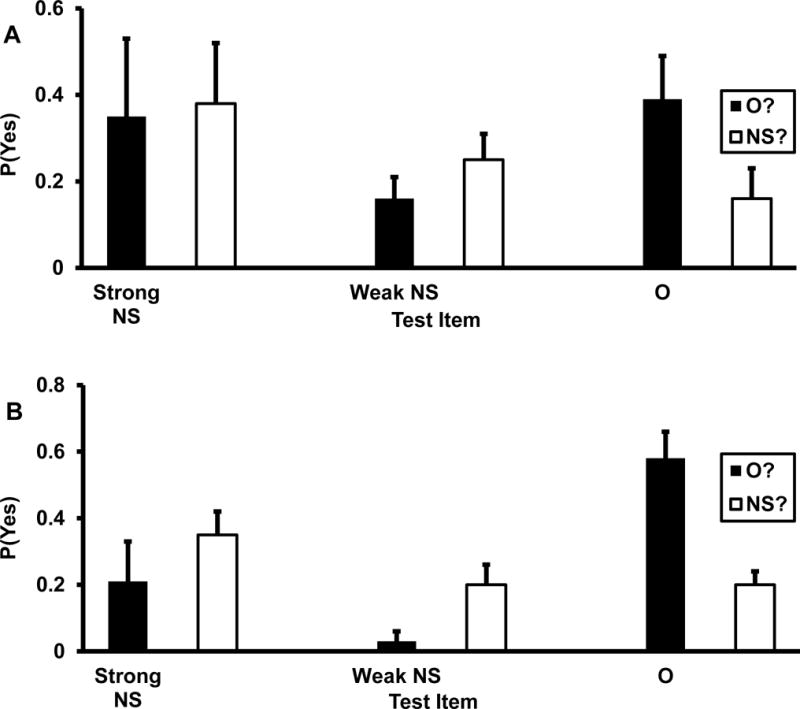
Means and variances of bias-corrected acceptance rates [P(Yes)] for NS (new-similar) and O (old) items. O? refers to old probes, and NS? refers to new-similar probes. These are the relations between p(O?) and p(NS?) for strong NS items, weak NS items, and O items in the control condition of Experiment 5 (Panel A) and in the repetition condition (Panel B). In Panel A, strong NS performance is completely complementary, whereas weak NS and O performance are both partially complementary and reality-consistent. In Panel B, performance for all items is partially complementary and reality-consistent.

The main statistical analysis was a 2 (repetition: control vs. repetition) X 2 (condition: O? vs. NS? probes) X 3 (item: strong NS vs. weak NS vs. O) ANOVA of the bias-corrected means of p(O?) and p(NS?) for the three types of items. There were two key results—namely, a Condition X Item interaction, F(2, 116) = 25.17, MSE = .05, η_p² = .30 and a Repetition X Condition X Item interaction, F(2, 116) = 6.06, MSE = .05, η_p² = .11. The reason for the Condition X Item interaction is that the order of overall acceptance probabilities for the three types of items was different for O? probes versus NS? probes. Post hoc tests showed that the order was O > strong NS > weak NS for O? probes, but was strong NS > weak NS = O for NS? probes. The reason for the Repetition X Condition X Item interaction is that although these two orderings were the same in the control and repetition conditions, for O? probes the differences between the acceptance probabilities for the three probes were greater in the repetition condition.

The important consequence of the latter result is the manner in which repetition affected the complementarity ratios for the three types of items. As mentioned, repetition’s overall effect was to drive all of the complementarity ratios toward 1. In the control condition, the ratios for O, strong NS, and weak NS items were .71, .52, and .61, respectively. The O ratio was reliably different from .5 [i.e., p(O?) > p(NS?); t(29) = 3.05], but the two NS ratios were not. In the repetition condition, the corresponding ratios for O, strong NS, and weak NS items were .71, .63, and .87, respectively. The O ratio was reliably different from .5 [i.e., p(O?) > p(NS?); t(29) = 6.64] and so were the strong NS ratio [i.e., p(NS?) > p(O?); t(29) = 2.05] and the weak NS ratio [i.e., p(NS?) > p(O?); t(29) = 3.79].

In short, the overall picture is that a manipulation that ought to increase target recollection by enhancing retrieval of verbatim traces of list words affected complementarity across-the-board and by driving the complementarity ratios for strong and weak NS items in the reality-consistent direction. In most conditions of prior experiments and in the control condition of this experiment, critical distractors have shown complete complementarity. In the present repetition condition, however, they exhibited partial complementary that was reality-consistent for the first time under theoretically predicted conditions; that is, critical distractors were more likely to be remembered as what they are than as what they are not.

Experiment 6

The manipulation that we studied in Experiment 6 should decrease target recollection. Theoretically, the effect on memory ought to be similar to Experiment 5 in one respect and different in another. Here, remember that repetition affected complementarity across-the-board, forcing the complementarity ratio in a reality-consistent direction for all items. If some other manipulation decreases target recollection, relative to a control condition like that in Experiment 5, the complementarity ratio for all items should now be forced toward 0, which is the reality-reversed direction. For NS items, that follows from the fact that for them, decreasing target recollection shrinks R/(1− R) relative to P, forcing complementarity ratios toward 0. For O items, the same effect follows because decreasing target recollection shrinks R_O and increases (1− R_O)S_O in the expression for p(O?) but simply increases (1− R_O)S_O in the expression for p(NS?). Thus, p(O?) will decrease, p(NS?) will increase, and the complementarity ratio is again forced toward 0. Notice, too, that when the ratio moves toward 0, the consequences for complementarity depend on where it starts. For critical distractors, the starting value is so close to .5 that movement toward 0 will mean decreased complementarity, as it did in Experiment 5 when the ratio moved toward 1. For weak NS items and O items, however, the fact that they start above .5 will mean increased complementarity as their respective ratios move toward 0.

The specific manipulation that we implemented, speeded testing, has a venerable history in memory research, and there is a literature in which its effects on false memory have been studied (for a review, see Brainerd & Reyna, 2005). In order to control the precise amount of retrieval time that subjects are permitted before they respond to memory probes, the relevant experiments used Dosher’s (1984) response-signal paradigm. A general conclusion that has emerged from that research, which makes speeded testing pertinent here, is that retrieval of the information that supports vivid recollection of O items is a slower process than retrieval of the information that supports false alarms to NS items. Two retrieval-time effects support that conclusion. First, false alarm rates for NS items are higher when the amount of retrieval time is short (e.g., ≤ 750 msec) rather than long (e.g., ≥ 1,500 msec). Second, hit rates for O items are lower when retrieval time is short, and importantly, hits are less often accompanied by realistic recollective phenomenology. The latter finding is obtained for both behavioral measures of recollective phenomenology (e.g., R judgments in remember/know; Brainerd & Reyna, 2005) and neurophysiological measures (e.g., the 400–800 msec parietal component of event-related potentials; Curran & Doyle, 2011). Because signal lag is manipulated after list presentation, these are retrieval effects. Taken together, they suggest that short retrieval times selectively impair target recollection. If so, short retrieval times should decrease the R and R_O parameters in Equations 1–4, producing the above-mentioned effects on complementarity.

We evaluated these predictions in a response-signal experiment. The design was a replication of Experiment 2, except with a response-signal manipulation. More specifically, instead of responding to self-paced O? and NS? probes, subjects responded following either short (500 msec) or long (1,500 msec) retrieval intervals.

Method

Subjects

The subjects were 100 undergraduates, who participated to fulfill a course requirement. Half of the subjects were randomly assigned to a 1,500 msec signal delay condition and half were assigned to a 500 msec signal delay condition.

Materials and Procedure

For both signal delay conditions, the materials and procedures for the study phase were identical to Experiment 2. Subjects listened to audio files of 16 DRM lists that had been randomly sampled from the Stadler et al. (1999) norms. However, the test phase differed from Experiment 2. Although the instructions about the types of test items and how to respond to O? and NS? probes were the same as before, responses to probes were no longer self-paced. Instead, subjects were required to respond within 350 msec after hearing an audio signal (tone), with the signal delay being 500 msec for half the subjects and 1,500 msec for the other half. The details of the response-signal procedure run as follows.

After completing the study phase, the subject read the same instructions as in Experiment 2, except for the addition of instructions about the response-signal procedure. The latter informed the subject that when a test item appeared on the computer screen, he/she should not respond until a tone sounded, after which he/she should respond immediately by pressing the Y(yes) or N(no) keys on the computer keyboard. After reading the instructions, the subject completed a practice test, on which the signal delay was 500 msec for the subjects in that condition and was 1,500 msec for the subjects in that condition. The deadline for responding was 350 msec following the tone. After each response, the subject’s response time appeared in the center of the screen, and when it exceeded 350 msec, the message “too slow – answer more quickly” also appeared on the screen.

Following the practice test, the subject proceeded to the actual test, which consisted of the same 144 items and probes as in Experiment 2. For subjects in the 500 msec condition, a probe question (old? or new-similar?) first appeared on the screen for 1,000 msec. Then, a test word (e.g., chair) appeared on the screen for 500 msec, disappeared, and the tone signaled the subject to respond immediately. After the Y or N response, the subject’s response time appeared in the center of the screen, and when it exceeded 350 msec, the message “too slow – answer more quickly” also appeared on the screen. Next, a fixation cross was displayed for 1,000 msec before presentation of the next probe and test item. The order of the 144 items and test probes was separately randomized for each subject. For subjects in the 1,500 msec condition, the procedure was identical, except that each test item remained on the screen for 1,500 msec before it disappeared and the tone signaled the subject to respond.

Results and Discussion

In Figure 7, we display the bias-corrected acceptance probabilities for O? and NS? probes for the three types of test items. The data for the 1,500 msec condition (Panel A) are roughly comparable to the control condition of Experiment 5. Strong NS items exhibited complete complementarity, and so did weak NS items. O items displayed partial complementarity, which was reality-consistent [i.e., p(O?) > p(NS?)]. The results for the 500 msec condition were notably different (Figure 7B). First, strong NS items now showed only partial complementarity that was reality-reversed [i.e., p(O?) > p(NS?)], with a complementarity ratio of .38. Second, weak NS items also displayed partial complementarity that was reality-reversed, but the degree of reversal was quite modest (a complementarity ratio of .44). Third, O items displayed partial complementarity that was reality-consistent, with a complementarity ration of .63 (in contrast to .82 in the 1,500 msec condition). Thus, as expected on theoretical grounds, a manipulation that should decrease target recollection, drove all three complementarity ratios toward 0. The absolute level of complementarity decreased for strong and weak NS items, whose complementarity ratios were close .5 in the 1,500 msec condition, but it increased for O items, whose complementarity ratio was close to .9 in the 1,500 msec condition.

Figure 7.

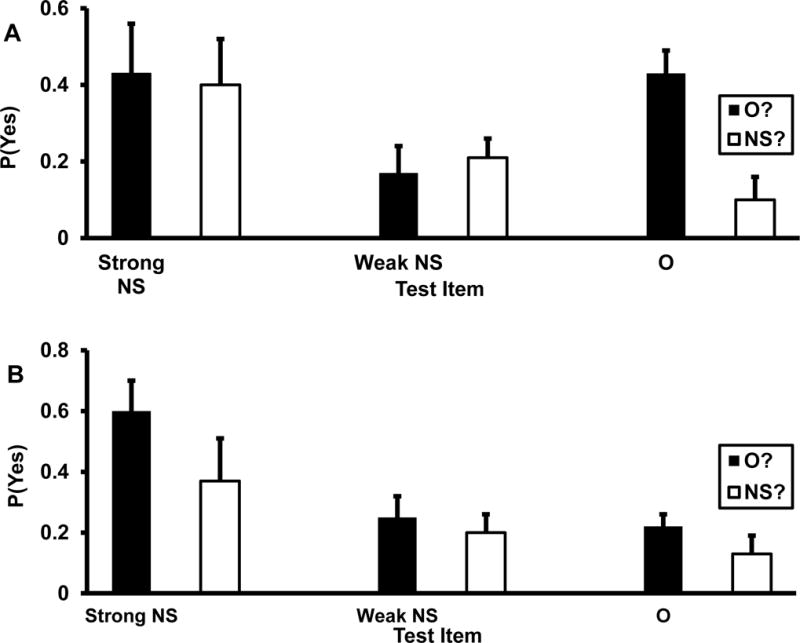
Means and variances of bias-corrected acceptance rates [P(Yes)] for NS (new-similar) and O (old) items. O? refers to old probes, and NS? refers to new-similar probes. These are the relations between p(O?) and p(NS?) for strong NS items, weak NS items, and O items in the 1,500 msec condition of Experiment 6 (Panel A) and in the 500 msec condition (Panel B). In Panel A, strong and weak NS performance are completely complementary, whereas O performance is partially complementary and reality-consistent. In Panel B, strong NS performance is partially complementary and reality-reversed, weak NS performance is completely complementary, and O performance is partially complementary and reality-consistent.

The main statistical analysis was a 2 (signal delay: 500 vs. 1,500 msec) X 2 (condition: O? vs. NS? probes) X 3 (item: strong NS vs. weak NS vs. O) ANOVA of the bias-corrected means of p(O?) and p(NS?) for the three types of items. As in Experiment 5, there were two key results, which in this case were a Condition X Item interaction, F(2, 196) = 8.32, MSE = .06, η_p² = .08 and a Signal Delay X Condition X Item interaction, F(2, 116) = 9.06, MSE = .06, η_p² = .09. Naturally, the Condition X Item interaction occurred because, as in all prior experiments, the order of overall acceptance probabilities for the three types of items was different for O? probes versus NS? probes. Post hoc tests showed that the order was strong NS > O > weak NS for O? probes but was strong NS > weak NS > O for NS? probes. The reason for the Signal Delay X Condition X Item interaction is that signal delay also affected these orderings. In the 1,500 msec condition, post hoc tests indicated that the order was strong NS = O > weak NS for O? probes and strong NS > weak NS > O for NS? probes. In the 500 msec condition, on the other hand, post hoc tests indicated that the order was strong NS > O = weak NS for O? probes and strong NS > weak NS > O for NS? probes. At the level of item response probabilities, signal delay changed the orders because it had two specific effects on O? probes: It substantially decreased the acceptance probability of list words while substantially increasing the acceptance probability of critical distractors.

As mentioned, the important effect of the signal delay manipulation was to drive all of the complementarity ratios toward 0 in the 500 msec condition. In the 1,500 msec condition, the ratios for O, strong NS, and weak NS items were .81, .48, and .55, respectively. The O ratio was reliably different from .5 [i.e., p(O?) > p(NS?); t(49) = 6.51], but the two NS ratios were not. In the 500 msec condition, the corresponding ratios for O, strong NS, and weak NS items were .63, .38, and .44, respectively. The O ratio was reliably different from .5 [i.e., p(O?) > p(NS?); t(49) = 2.18] and so was the strong NS ratio [i.e., p(NS?) > p(O?); t(49) = 3.56], but the weak NS ratio was not.

In short, the overall picture is that a manipulation that is thought to decrease target recollection by impairing retrieval of verbatim traces of list words affected complementarity across-the-board by driving all complementarity ratios toward 0. This contrasts with Experiment 5, in which a manipulation that is thought to increase target recollection by enhancing retrieval of verbatim traces of list words affected complementarity across-the-board by driving all complementarity ratios toward 1. Together, the two experiments indicate that in the DRM paradigm, the level and direction of complementarity for all three types of test items can be changed by manipulating subjects’ ability to access verbatim memories of the presentation of list words.

General Discussion

The research that we have reported revolved around a single question: Exactly what type of illusion is induced by the DRM paradigm? Is it a reality-reversal illusion, in which critical distractors are remembered as what they are not (old) at high levels and as what they are (new-similar) at low levels? Is it a complementarity illusion, in which critical distractors are remembered both as what they are and as what they are not at high levels? Reality reversal is the traditional interpretation, whereas complementarity has not been carefully evaluated. Certain findings seem especially supportive of reality reversal, but such evidence is limited by the fact that prior experiments provided subjects with the opportunity to remember whether items old but not with the opportunity to remember whether items were new-similar.

It is essential to measure both because episodic memory, like preference and some other forms of judgment and decision making, may be complementary over judgments about logically incompatible reality states (Brainerd et al., 2015). We filled in the missing design cell in our experiments and introduced a convenient performance statistic, the complementarity ratio, which delivers quantitative information about levels of complementarity and about whether performance is reality-reversed or reality-consistent. The weight of evidence from this metric fell on the side of DRM lists inducing complementarity illusions rather than reality-reversal illusions; that is, the proportions of critical distractors that were judged to be old and new-similar were roughly comparable.

In the present section, we briefly discuss three matters that bear on this conclusion and briefly present results from an additional experiment. First, we step back from the individual experiments and consider broad empirical patterns that cut across them, particularly trends that were predicted on theoretical grounds. Second, we evaluate the mathematical relation between measured levels of complementarity and estimates of the conjoint recognition model’s parameters. In that connection, we know that the model posits a specific relation between complementarity ratios for NS items and the parameters that measure its two recollective processes. The results of the last two experiments were consistent with that relation but did not directly test it. We do that below. Third, we evaluate a different approach to explaining high levels of complementarity for critical distractors, which assumes that items’ perceived reality states are strongly influenced by the types of memory judgments that are made about them. We report further data that provide differential tests of this judgment-dependency explanation.

Experiment-wide Patterns

Several results point to the conclusion that DRM lists induce complementary illusions, but four patterns are especially probative. The first is for list words versus critical distractors. A key finding that is taken to support reality reversal is that list items and critical distractors are often indistinguishable on recognition tests—hit and false alarm rates are approximately equal (e.g., Gallo, 2006). We found that this result is dependent on which reality state is tested. Under conditions that are common in the literature (Experiment 2, the immediate testing condition of Experiment 3, the control condition of Experiment 5, and the 1,500 msec condition of Experiment 6), NS? probes produced excellent separation between list words and critical distractors. The second pattern is for critical distractors per se. Under the same standard conditions, the modal finding for critical distractors was strong complementarity; that is, complementarity ratios that were in the neighborhood of .5. The third pattern is that strong complementarity was not confined to critical distractors, but to varying degrees, it spilled over to weak NS items. The modal finding for weak NS items was a mixture of reality-consistent partial complementarity and complete complementarity (e.g., in the control condition of Experiment 5 and the 1,500 msec condition of Experiment 6). As predicted theoretically, the contrasting finding for list items was weak, reality-consistent, complementarity, with complementarity ratios that often approached 1 (perfect compensation). The fourth pattern is that the despite reality reversal being the dominant view of the DRM illusion, there was very little evidence of it. Reality reversal corresponds to complementarity ratios for critical distractors that approach 0, but in the event, most were close to .5.

Beyond answering the core question of what type of illusion DRM lists induce, the most instructive thing about these patterns is their consistency with the theoretical distinctions that motivated the research. Remember that beyond explaining how complementarity can result from familiar memory processes, the implementation of those distinctions in the conjoint recognition model generated a series of parameter-free predictions. One group of predictions, on which all of the experiments supplied data, was concerned with the relative strengths of complementarity effects for different types of test items. The main predictions were that complementarity would be more marked for strong NS items than for weak NS or O items and that O items would exhibit far weaker complementarity than either type of NS item, leading to an overall complementarity ordering of strong NS > weak NS > O. Those predictions were borne out in most conditions of most experiments. To illustrate: Complementarity was always stronger for both types of NS items than for O items, except in two nonstandard conditions, one in Experiment 3 and one in Experiment 6; the most robust complementarity (ratios closest to .5) was always observed for strong NS items, except in two nonstandard conditions, one in Experiment 3 and one in Experiment 6; O items never displayed complete complementarity in any condition of any experiment; the order of complementarity was strong NS > weak NS > O, except in three nonstandard conditions, one in Experiment 3, one in Experiment 5, and one in Experiment 6.

A second group of predictions, which figured in Experiments 5 and 6, was concerned with the types of manipulations that should reduce the marked complementarity that strong NS items displayed under standard conditions, by forcing complementarity ratios away from .5, toward 1 or 0. The conjoint recognition model says that the simplest way to force complementarity ratios toward 1 is via manipulations that inflate target recollection, and the simplest way to force complementarity ratios toward 0 is via manipulations that deflate it. We studied a manipulation of the first type in Experiment 5, list repetition. We found that the complementarity ratio for strong NS items was reliably larger than .5 (i.e., reality-consistent) when DRM lists were presented twice rather than once. We studied a manipulation of the second type in Experiment 6, speeded testing. Now, the complementarity ratio for strong NS items was reliably smaller than .5 (i.e., reality-reversed) when subjects were permitted only a brief amount of retrieval time before they had to respond to memory probes.

Three conclusions follow. First, although complementarity troubles our intuition, the data show that it is a hallmark of the DRM illusion. Second, this fact seems less counterintuitive when we consider that complementarity is a consequence of familiar theoretical distinctions about the types of representations that are retrieved on memory probes. Third, those same distinctions point to successful ways to gain leverage on the amount and direction of complementarity.

Complementarity and Dual Recollection Processes

In the conjoint recollection model, there are two recollection processes that influence subjects’ responses to NS items in opposite ways—target recollection (parameter R) and context recollection (parameter P.). The mathematical relation between these processes controls the level of complementarity for NS items and whether it lies in the reality-reversed or the reality-consistent direction. We know that the level and direction of complementarity is captured by the difference between the empirical probabilities p_NS(O?) and p_NS(NS?): Memory is completely complementary, partially complementary and reality-reversed, or partially complementary and reality-consistent accordingly as p_NS(O?) − p_NS(NS?) is 0, > 0, or < 0. The model posits that this is controlled by the mix of target recollection and context recollection. In particular, p_NS(O?) − p_NS(NS?) is 0, > 0, or < 0 accordingly as R/(1−R) = P, R/(1−R) < P, or R/(1−R) > P because p_NS(O?) − p_NS(NS?) = R/(1−R) − P.

In our experiments, we exploited this hypothesized relation to identify manipulations that ought to drive complementarity in either a reality-reversed or reality-consistent direction, but we did not evaluate the relation itself. That is only possible with full conjoint recognition designs in which the model is fit to sample data and its parameters are estimated. Experiments 2–6 were not of that sort because only the O? and NS? conditions are needed to study complementarity. However, the corpus of data sets that were used in Experiment 1 involved full conjoint recognition designs, and thus, they are sufficient to test the model’s predicted relation between complementarity and the two recollection processes. Those data sets allowed us to evaluate the prediction for three different types of NS items—namely, strong NS items in the DRM sub-corpus, weak NS items in the DRM sub-corpus, and NS items in the non-DRM sub-corpus.

Recall that the bias-corrected expressions for accepting O? and NS? probes for NS items are p_NS(O?) = (1−R)P + (1−R)(1P)S_NS and p_NS(NS?) = R + (1− R)(1− P)S_NS, from which it follows that p_NS(O?) − p_NS(NS?) = (1−R)P − R. This means that performance (a) will be completely complementarity whenever P = R/(1−R), (b) will be partially complementary and reality-reversed whenever P > R/(1−R), and (c) will be partially complementary and reality-consistent whenever P < R/(1−R). More generally, over many experiments and conditions, variation in the empirical quantity p_NS(O?) − p_NS(NS?) should be a linear function of variation in the theoretical quantity R/(1−R) − P. In order to test that prediction, we estimated the model’s parameters separately for the strong NS data sets in the DRM sub-corpus of Experiment 1, for the weak NS data sets in the DRM sub-corpus, and for the data sets in the non-DRM sub-corpus. With respect to how the model’s parameters were estimated, details of its parameter estimation machinery are provided elsewhere (Brainerd et al., 2014). Briefly, the model’s parameter space is identifiable, and hence, its parameters can be estimated for any data set by expressing its equations (e.g., Equations 1–4) in a standard likelihood function, in which the data appear as observable states. The function is then maximized, yielding maximum likelihood estimates of the parameters for those data.

Using the parameter estimates, we computed the quantity R/(1−R) − P for each data set and fit it to the value of p_NS(O?) − p_NS(NS?) for that data set. The results appear in Figure 8, where Panel A displays the strong NS results for the DRM sub-corpus, Panel B displays the weak NS results for the DRM sub-corpus, and Panel C displays the results for the non-DRM sub-corpus.

Figure 8.

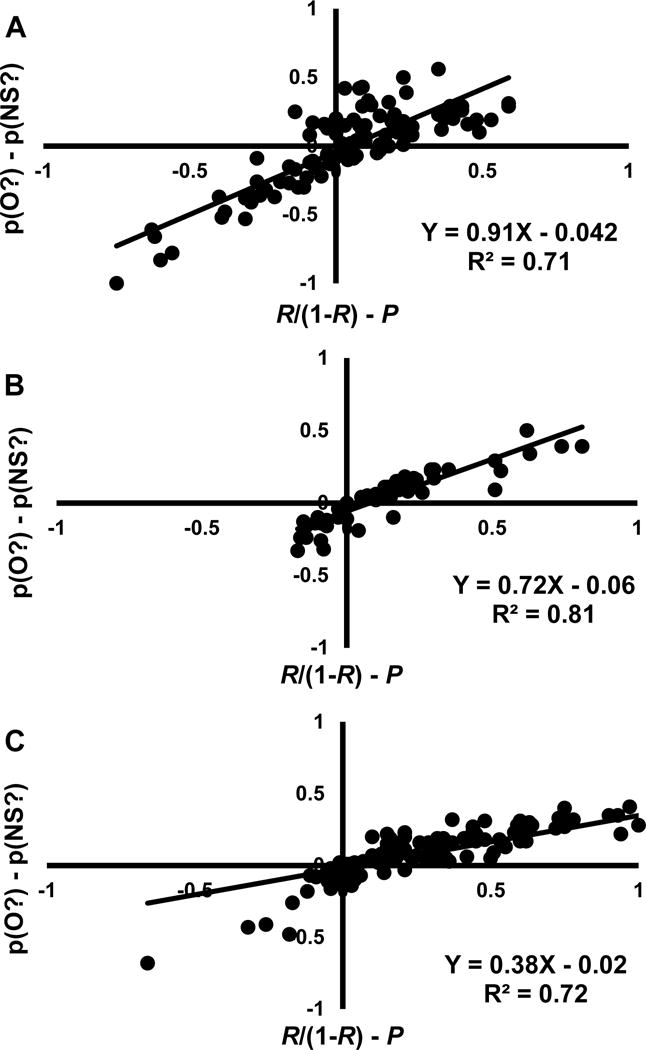
The ability of the target recollection and context recollection parameters (R and P) to predict levels of complementarity for new-similar items [p(O?) − p(NS?)] in the corpus of conjoint recognition data sets. p(O?) is the probability of accepting new-similar items on old probes, and p(NS?) is the probability of accepting them on new-similar probes. Panel A = strong NS items (critical distractors) in DRM experiments, Panel B = weak NS items in DRM experiments, Panel C = NS items in non-DRM experiments.

Three overall patterns are apparent. First, there is a strong linear relation between p_NS(O?) − p_NS(NS?) and R/(1−R) − P in all three fits, with individual fits for the strong NS DRM, weak NS DRM, and non-DRM data accounting for 71%, 81%, and 72% of the variance, respectively. Second, inspection of the point clouds reveals no obvious evidence of nonlinearity, and when standard two-parameter nonlinear functions (power, exponential, logarithmic) were fit to these data, none accounted for significantly more variance than the linear fits. It should perhaps be added that the first few entries in the point cloud for the non-DRM sub-corpus (Panel C) seem to suggest positive acceleration at the start of the function, but the suggestion is only that: There was no statistically reliable departure from linearity when nonlinear functions were fit to those data. Third, note that the intercept, the estimated point at which p_NS(O?) − p_NS(NS?) crosses the Y axis, is very close to 0 in all three panels of Figure 8. Therefore, we refit each of the functions with the intercept set at 0. Although the refits naturally accounted for less variance than the unconstrained fits (A = 68%, B = 73%, C = 70%), none of the reductions was statistically reliable. All of the intercepts were 0 to a statistically acceptable approximation, and hence, p_NS(O?) − p_NS(NS?) was a ratio scale transformation of R/(1−R) − P in all three fits.

Inspection of the best-fitting functions in Figure 8 reveals large differences in their respective slope parameters, which measure the rates at which p_NS(O?) − p_NS(NS?) increased as a function of increases in R/(1−R) − P. The increase was steepest for the strong NS DRM data sets, with a unit change in R/(1−R) − P producing approximately a unit (.91) change in p(O?) − p(NS?). The increase was moderately steep for the weak NS DRM data sets, with a unit change in R/(1−R) − P producing nearly three-quarters of a unit (.72) change in p(O?) − p(NS?). Last, the increase was shallower for non-DRM data sets, with a unit change in R/(1−R) − P producing roughly one-third of a unit (.38) change in p(O?) − p(NS?). The differences among these slope parameters were statistically reliable. When the three functions were refit under the constraint that their respective slope parameters were equal, that produced significant reductions in the variance that all three functions accounted for.

Finally, because estimates were available for P, R, and also for the semantic familiarity parameter S_NS, we were able to investigate two further questions of theoretical interest. The first concerns the two routes to complementarity that were discussed earlier: (a) Some NS items are perceived to occupy both the O and NS states, causing both O? and NS? probes to be accepted for such items, and (b) other items are perceived to occupy only the O state or only the NS state, causing the former to be accepted on O? probes but the latter to be accepted on NS? probes. The first route involves items that provoke semantic familiarity on memory tests, and its probability is given by the (1−R)(1− P)S_NS term in Equations 1 and 2. The second route involves items that provoke target recollection, with probability R in Equation 1, and items that provoke context recollection, with probability (1−R)P in Equation 2. Thus, estimates of these parameters can be used to calculate the extent to which complementarity is due to one or the other route in the sub-corpora of Experiment 1.

The results appear in Table 2. The mean estimates of P, R, and S_NS for strong and weak NS items in the DRM sub-corpus and for NS items in non-DRM sub-corpus appear in the upper half of the table. The mean estimates of the corresponding proportions of items that are perceived to occupy both states, only O, or only NS by virtue of semantic familiarity, context recollection, or target recollection, respectively, appear in the bottom half of the table 1. Three instructive patterns are apparent.

Table 2.

Mean Estimates of the Conjoint Recognition Model’s Parameters for New-Similar Items and Estimates of the Proportions of New-Similar Items that Occupy the Two Reality States

	Data sub-corpus
	DRM Strong	DRM Weak	Non-DRM
Parameter estimates:
R	.19	.16	.31
P	.23	.08	.20
SNS	32	.14	.19
Reality states:
O	.19	.07	.11
NS	.19	.16	.31
Both	.21	.11	.11

First, a distinguishing feature of critical distractors, relative to the other two types of NS items, is that memory superposes a high percentage of them on the incompatible O and NS states. The values are 21% for critical distractors versus 11% for both weak NS items in the DRM sub-corpus and NS items in the non-DRM sub-corpus. Second, complementarity for critical distractors is due to a roughly equal measure to (a) items that memory superposes on the two reality states (21%) and (b) the fact that the percentages of items that provoke target recollection or context recollection (19%) are equal. Third, complementarity is different and lower for each of the other two types of NS items because (c) the percentage of items that are perceived to belong to both of the O and NS states is so much lower, and (d) the percentage of items that provoke target recollection is so much higher than the percentage that provokes context recollection (16% vs. 7% for weak NS items and 31% vs. 14% for non-DRM NS items).

Item-Dependent versus Judgment-Dependent Retrieval

The probes in our experiments may be thought of as retrieval cues with two components. The components are (a) an item that belongs to an objective reality state (O, NS, or ND), together with (b) a hypothesized reality state that a judgment must be made about (O? NS?). The objective and hypothesized states may or may not agree. In order to make a judgment, subjects must implicitly identify the item’s reality state, using information that is retrieved from memory, or if that is not possible, rely on bias processes to generate a judgment. An important theoretical question is, which component of a probe controls the memories that are retrieved to identify the item’s reality state and which controls bias levels? The conjoint recognition model posits that the item controls memory retrieval, and the judgment controls bias levels (Brainerd, Reyna, & Mojardin, 1999). These assumptions are testable because they place two strong mathematical constraints on the model’s parameters.

One is that bias levels will be different for O? versus NS? judgments, and further, that they will higher for NS? judgments because identification of the NS state relies on negative memory evidence. Reported bias levels are higher for NS? judgments (e.g., Singer & Remillard, 2008; Singer & Spears, 2015). That is also true of the large data corpus in Experiment 1. There, the mean values of the model’s bias parameters for O? and NS? judgments were b_O? = .18 and b_NS? = .30 for the strong DRM sub-corpus, b_O? = .16 and b_NS? = .27 for the weak DRM sub-corpus, and b_O? = .14 and b_NS? = .28 for the non-DRM sub-corpus. In short, the judgment component a marked effect on bias, producing levels that were roughly 75% higher for NS? judgments.

The other constraint is on the memory parameters in Equations 1–4: If the item component but not the judgment component determines the memories that are retrieved to identify the item’s reality state, then the same parameters with the same values must appear in the model’s expressions for O? and NS? This is commonly known as a parameter invariance assumption (e.g., Graf & Komatsu, 1994; Klauer, Dittrich, Scholtes, & Voss, 2015), and it is of particular importance when interpreting our complementarity results. Suppose that the assumption is incorrect, and the judgment component, as well as the item component, determines the memories that are retrieved to identify reality states. If so, complementarity can occur in a different way, in which an item’s perceived reality state depends both on the item and on the type of judgment that must be made about it. To see how that could happen, assume that when the test item is held constant, the memories that it accesses are different when the judgment emphasizes oldness than when it emphasizes similarity. Explicitly, assume that (a) subjects selectively search for content that supports oldness with O? judgments, but (b) they selectively search for content that supports similarity with NS? judgments. That should produce significant complementarity because DRM lists and other semantically-related materials generate both types of memories.

Unlike the conjoint recognition account, which predicts complementarity, judgment dependency only explains it after the fact. Further, there are four considerations that run counter to this alternative explanation. The first is that the conjoint recognition account’s parameter invariance assumption is testable by goodness-of-fit statistics. The fit statistics for memory models are sensitive to violations of the parameter invariance assumption (see Brainerd et al., 1999), and in fact, violations of this assumption are among the most common reasons for fit failures (Klauer et al., 2015). We mentioned that the conjoint recognition model is known to fit DRM data well, and thus, the assumption that memory retrieval is controlled by the item component and not by the judgment component (O? vs. NS?) has been confirmed statistically.

The second consideration is that the judgment-dependency explanation does not differentiate between the levels of complementarity that are predicted for NS items versus O items. On the contrary, if the memory information that is accessed to identify an item’s reality state is controlled by whether the judgment emphasizes oldness or similarity, the straightforward prediction is that when strong complementarity is observed for one, it will be observed for the other. In contrast, the conjoint recognition account expects strong complementarity for NS items under certain combinations of parameter values, but rules it out for O items. The results of our experiments were consistent with that prediction. For the judgment-dependency account to explain those results, additional assumptions would have to be introduced that would, in some way, constrain judgment-dependent retrieval to operate for NS items but not for O items. There may be various assumptions that would deliver such constraints, but invoking such assumptions means that judgment-dependent retrieval becomes a less parsimonious route to complementarity.

The third consideration is that judgment dependency has an unfortunate consequence for the adaptiveness of retrieval. To the extent that the memory content that identifies an item’s reality state is controlled by whether a judgment emphasizes oldness versus similarity, then to that extent retrieval loses the adaptive property of consistently identifying an item as belonging to the same reality state in different testing contexts. This property is adaptive because, of course, an item’s objective reality state is invariant over testing contexts, but judgment dependency surrenders it in order to explain complementarity. The conjoint recognition account does not. For O items, target and context recollection cause them to be correctly perceived as old for both O? and NS? judgments. For NS items, on the other hand, target and context recollection also identify the same reality state for both O? and NS? judgments, but complementarity emerges because they identify different reality states.

The fourth consideration is that the judgment-dependency explanation can also be tested in a very simple way, without resorting to model fits. Consider the following modification to the memory tests that were administered in our experiments. Rather than administering one probe per item (O? or NS?), suppose that two probes are administered, which may be either the same (i.e., O₁? followed by O₂? or NS₁? followed by NS₂?) or different (i.e., O₁? followed by NS₂? or NS₁? followed by O₂?). Suppose that there is sufficient spacing between them that short-term memory for responses to the first probe is not an issue on the second. The judgment-dependency explanation posits that subjects selectively search their memories for information that favors the old state for O? judgments and for information that favors the new-similar state for NS? judgments. If so, an initial O? test provides practice at retrieving content that favors the old state, whereas an initial NS? test provides practice at retrieving content that favors the new-similar state.

This leads to three obvious predictions about the modified testing design, one about performance on Test 2 and the others about changes in performance between Test 1 and Test 2. The first prediction concerns how subjects should perform on Test 2 when they receive an O? probe for an O item or an NS? probe for an NS item. Clearly, performance on the O? probe should be better if Test 1 was also an O? probe, and performance on the NS? probe should be better if Test 1 was also an NS? probe: The first O? probe provides practice are retrieving memories that will support the old state on the second O? probe, and the first NS? probe provides practice at retrieving memories that will support the new-similar state on the second NS? probe. The other two predictions are about facilitation and inference effects between Test 1 and Test 2. Concerning facilitation, consider the situation that we just described in which a Test 2 O? probe for an O item is preceded by a Test 1 O? probe, and a Test 2 NS? probe for an NS item is preceded by a Test 1 NS? probe. The practice effect from selective retrieval on Test 1 should facilitate accuracy on Test 2, causing accuracy to increase between Test 1 and Test 2. Concerning interference, consider the situation in which we compare performance on Test 1 O? probes for old items to performance on Test 2 O? probes for old items that had a Test 1 NS? probe, and consider the situation in which we compare performance on Test 1 NS? probes for new-similar items to performance on Test 2 NS? probes for new-similar items that had a Test 1 O? probe. In both instances, accuracy should decline between Test 1 and Test 2 because the type of retrieval practice on Test 1 works against the information that needs to be retrieved on Test 2.

We conducted a simple experiment that tested all three judgment-dependency predictions. The subjects were 60 undergraduates who participated to fulfill a course requirement. The materials were drawn from a pool of 200 DRM lists, consisting of 4 list words plus a critical distractor per list. These types of lists were originally developed to induce the DRM illusion with very few words, by selecting only list words with high backward associative strength (BAS) to their critical distractors (e.g., Atkins & Reuter-Lorenz, 2011). The mean BAS of the 72 lists that were administered to the present subjects was .42. The design involved three study-test cycles, followed by a final recognition test. During each cycle, 24 of the 72 lists were presented (2 sec per word, with a 8 sec pause between consecutive lists), followed by test instructions like those in Experiment 2, followed by a 72-item recognition test [1 O item per list + 1 NS item per list (the critical distractor) + 24 ND items drawn from unpresented DRM lists]. For each of these three types of test items, half the probes were O? and half were NS?. Following the third study-test cycle, the subjects performed 5 min of buffer activity (solving arithmetic problems) and then received instructions for the final recognition test, which consisted of 144 items (48 O, 48 NS, 48 ND). The probes were for 48 lists that had been randomly selected from the 72 presented lists, and each item had been previously tested with either an O? or NS? probe. For each type of item, the probe was O? for 24 items and NS? for 24 items, and within each of these two groups the probe was either same as the earlier test or different. Thus, for the 48 items of each type (O, NS, ND) there were 12 items with each of the following probe pairs: O₁?−O₂?, NS₁? −O₂?, NS₁? −NS₂?, and O₁? −NS₂?

The key findings are displayed in Table 3, and they run against all of the judgment-dependency predictions. With respect to the first, note that the values of p(O₂?│O) were roughly the same regardless of whether the prior test was an O? probe on an NS? probe (.71 vs. .65), and note that the values of p(NS₂?│NS) were roughly the same regardless of whether the prior test was an O? probe or an NS? probe (.64 vs. .59). Neither difference was statistically reliable. Turning to the second prediction, the facilitation effect of selective search means that p(O₂?│O) > p(O₁?│O) and p(NS₂?│O) > p(NS₁?│O). However, it can be seen at the top of Table 3 that neither prediction was borne out. For O items, p(O₂?│O) = .71 versus p(O₁?│O) = .69, and for NS items, +p(NS₂?│NS) =.58 versus p(NS₁?│NS) = .59. Neither difference was statistically reliable. Finally, concerning the third prediction, the interference effect of selective search means that p(O₁?│O) > and p(O₂?│O) when the latter was preceded by a Test 1 NS? probe, and that p(NS₁?│NS) > and p(NS₂?│NS) when the latter was preceded by a Test 1 O? probe. It can be seen at the bottom of Table 3 (diagonal arrows) that neither of these predictions was borne out either. For O items, p(O1?│O) = .67 versus p(O₂?│O) = .65, and for NS items, p(NS₁?│NS) =.62 versus p(NS₂?│NS) = .64.

Table 3.

Mean Probabilities of Old and New-Similar Judgments on Test 1 and Test 2 for Items for which the Two Probes were the Same or Different

Item/probe	Test 1	Test 2
Same probe type (acceptance probabilities)
List items:
V	.69	.71
G	.44	.46
Critical distractors:
V	.47	.52
G	.58	.59
New-different items
V	.22	.41
G	.30	.35
Different probe type (acceptance probabilities)
List items;
V ➔ G
G ➔ V
Critical distractors:
V ➔ G
G ➔ V
New-different items
V ➔ G	.21	.38
G ➔ V	.31	.44

Note. V = probes that ask if the test item is old. G = probes that ask if the test item is new-similar.

Summing up, this simple experiment provided ample opportunity to secure evidence in support of the hypothesis that subjects selectively search memory for content that supports the type of judgment that they are asked to make about an item. This hypothesis predicts three different effects, and the power to detect them was excellent because the number of replications and subjects were both large. Because each effect had two parts, one for O items and one for NS items, there were actually six opportunities to detect an effect that is predicted by the hypothesis. None of those effects was detected, and hence, there was no evidence that subjects selectively search memory for content that supports the judgments they are asked to make.

Concluding Comments

To conclude, it is reasonable to ask about the larger theoretical significance of the results of Experiments 1–6. We briefly note three points in that connection. First and most obviously, the DRM illusion is not the type of distortion that we thought it was. This illusion has long been viewed as a reality reversal, in which new-similar items and old items are remembered in the same way, and that view has guided how the illusion has been used to understand episodic memory. It is not a reality reversal, however, because new-similar and old items are actually remembered in fundamentally different ways—compensatory memory for old items but complementary memory for new-similar items. The reason this pattern has not been previously identified is that it cannot be detected with traditional O? tests. The pattern’s larger significance is that, apparently, the DRM illusion is a powerful tool for studying noncompensatory memory processes; that is, processes that cause an item’s reality state to be perceived in mutually contradictory ways.

Second, our results provide a compelling demonstration of an unsuspected parallel between episodic memory and the well-known illusions and biases of judgment and decision making. In the latter, it is well established that reasoning violates the simple rule of logical exclusion inasmuch as humans often make judgments and decisions about medical treatment, investment, education, and so forth that are mutually contradictory (e.g., Tversky & Koehler, 1994). Experiments 1–6 generated considerable evidence that the same is true in the memory sphere. It appears that some types of memory content violate logical exclusion because they support mutually incompatible reality states for the same item. Semantic gist is the prime example. It is measured by the semantic familiarity parameter of conjoint recognition, and those measurements indicated that it was responsible for roughly half of the complementary that was observed for new-similar items.

Third, our results also provide a convincing demonstration that recollection is bivariate rather than univariate. That demonstration takes the form of a deeply paradoxical effect in which complementarity at the level of judgment emerges from compensation at the level of process. We saw that bivariate recollection operations are individually compensatory over mutually incompatible reality states: Target recollection causes NS items to be correctly perceived as NS on both O? and NS? probes, and context recollection causes the same items to be in correctly perceived as O on both types of probes. However, we also saw that the two recollections are jointly complementary, and that they will tend to produce complete complementarity when their impact on memory performance is roughly equivalent. Our data showed that this paradoxical effect was responsible for the other half of the complementarity that we observed for new-similar items.

Figure 5.

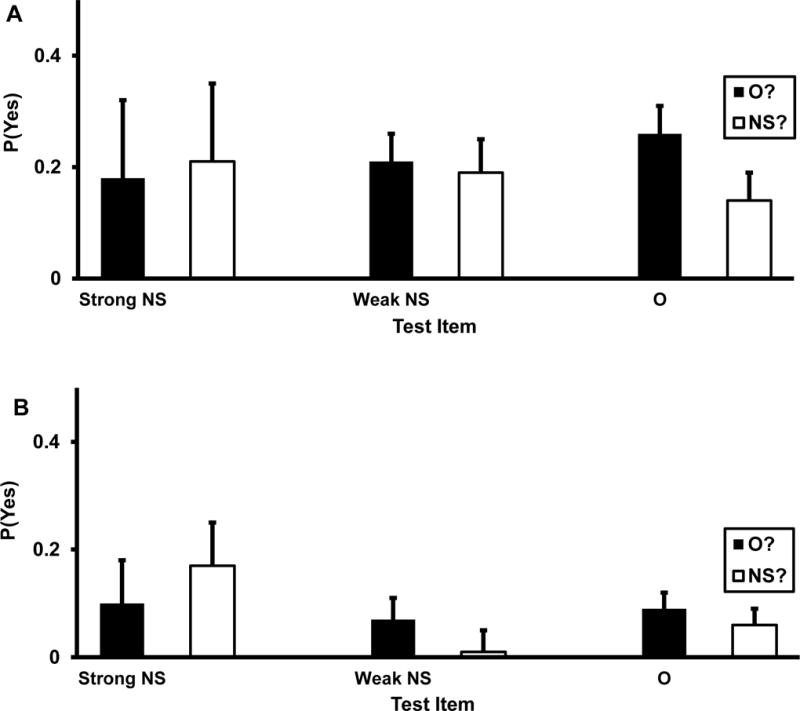
Means and variances of bias-corrected acceptance rates [P(Yes)] for NS (new-similar) and O (old) items. O? refers to old probes, and NS? refers to new-similar probes. These are the relations between p(O?) and p(NS?) for strong NS items, weak NS items, and O items in the delayed testing condition of Experiment 3 for items that were previously tested (Panel A) and for items that were not previously tested (Panel B). In Panel A, strong NS performance is partially complementary and reality-consistent because p(O?) < p(NS?), weak NS performance is partially complementary and reality-reversed because p(O?) > p(NS?), and O performance is weakly complementary and reality-consistent because p(O?) > p(NS?). In Panel B, strong NS performance is partially complementary and reality-consistent because p(O?) < p(NS?), weak NS performance is weakly complementary and reality-reversed because p(O?) > p(NS?), and O performance is partially complementary and reality-consistent because p(O?) > p(NS?).