Binding kinetics of ultrasmall gold nanoparticles with proteins

Abstract

Synthetic ultrasmall nanoparticles (NPs) can be designed to interact with biologically active proteins in a controlled manner. However, rational design of NPs requires a clear understanding of their interactions with proteins and the precise molecular mechanisms that leads to association/dissociation in biological media. Although much effort has been devoted to the study of the kinetics mechanism of the protein corona formation on large NPs, the nature of NP-protein interactions in the ultrasmall regime is radically different and poorly understood. Using a combination of experimental and computational approaches, we study the interactions of a model protein, CrataBL, with ultrasmall gold NPs passivated with p-mercaptobenzoic acid (AuMBA) and glutathione (AuGSH). We have identified this system as an ideal in vitro platform to understand the dependence of binding affinity and kinetics on NP surface chemistry. We find that the structural and chemical complexity of the passivating NP layer leads to quite different association kinetics, from slow and reaction-limited (AuGSH) to fast and diffusion-limited (AuMBA). We also find that the otherwise weak and slow AuGSH-protein interactions measured in buffer solution are enhanced in macromolecular crowded solutions. These findings advance our mechanistic understanding of biomimetic NP-protein interactions in the ultrasmall regime, and have implications for the design and use of NPs in the crowded conditions common to all biological media.

Graphical abstract

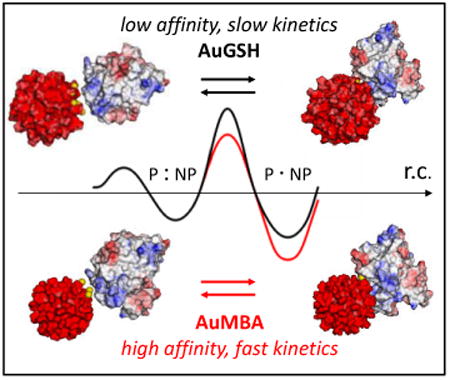
The kinetics of nanoparticle-protein interactions is modulated by nanoparticle surface chemistry.

1. Introduction

Gold nanoparticles and other nanomaterials can be engineered with similar sizes and surface chemistry to proteins and thus can be generally viewed as protein mimics^1-3. Such biomimetic nanostructures can interact reversibly with proteins via the same non-covalent forces responsible to bring and hold biomolecules together⁴. A thorough characterization study of nanoparticle (NP)-protein complexation is therefore of paramount importance to understand how NP structure relates to protein function and biological activity, potentiating novel applications in biomedicine^4-11.

Size is one of the key physicochemical parameters that can influence NP-biomolecular interactions. For example, protein binding onto large gold particles beyond the ultrasmall size regime (> 3 nm) can result in a stable adsorption layer, often referred to as the hard protein corona^12-15. For ultrasmall particles, however, it has been argued that a hard, persistent protein corona may not form^16-18. This may be partly a consequence of the reduced contact area for an ultrasmall NP-protein complex and the weaker interactions that ensue at the binding interface¹⁸.

Despite recent experimental work on ultrasmall NP-protein complexation, there is still limited quantitative knowledge about their interactions, particularly on their microscopic mechanisms of association. A quantitative characterization of NP-protein interactions typically includes determination of the binding affinity (K_D)^19-22. Whereas K_D is an important thermodynamic quantity to measure, it is dependent on the reaction rates of association (k_on) and dissociation (k_off) (K_D = k_off/k_on). Dissecting the individual contributions of the reaction rate constants to K_D can thus provide unique insights into the interaction mechanisms²³.

Herein we investigated the binding affinity and kinetics of two types of ultrasmall, uniform gold NPs, AuMBA and AuGSH, with a model protein, CrataBL²⁴. Ultrasmall AuMBA is passivated with p-mercaptobenzoic acid ligands, whereas AuGSH is coated with glutathione. Both types of NPs are negatively charged and have virtually identical size distributions and average core diameters (∼ 2 nm)^25-26. Ultrasmall AuGSH particles are being investigated in vivo as “non-interacting” renal clearable nanoformulations^27-29. Recent in vitro experiments have also shown that ultrasmall AuGSH displays weak binding affinity towards serum proteins, although this effect may depend critically on NP size, among other variables^{25, 30}. In contrast, ultrasmall AuMBA was previously found to interact more strongly with serum proteins both in vitro and in vivo^25,31. Ultrasmall AuMBA and AuGSH were therefore employed in this study as prototype NPs showing strong and weak binding affinities towards proteins.

The NP-CrataBL interactions were characterized by surface plasmon resonance (SPR)in combination with other biophysical techniques. SPR is an established technique for the study of biomolecular interactions^32-33, but only more recently has it been applied for the quantitative characterization of NP-protein interactions^34-39. The experimental data and results from computer simulations were used to provide mechanistic insights into NP-protein association. The paper closes with a brief outlook of the possible practical implications of binding kinetics in nanomedicine.

2. Results and Discussion

2.1. Nanoparticles and CrataBL

Characterization data for the NPs are displayed in Fig. 1. Quantitative dark-field scanning transmission electron microscopy (STEM) confirms that AuMBA and AuGSH are highly uniform with average core sizes around 2 nm. The UV-visible spectra show lack of a prominent surface plasmon peak around 500 nm, consistent with the small size of the particles. STEM in combination with analytical ultracentrifugation also reveal that AuMBA and AuGSH have virtually identical size distributions. The NPs are negatively charged, with a zeta potential in phosphate buffer of -22 ± 0.5 and -22.5 ± 0.7 mV, respectively.

Figure 1. Nanoparticles and CrataBL.

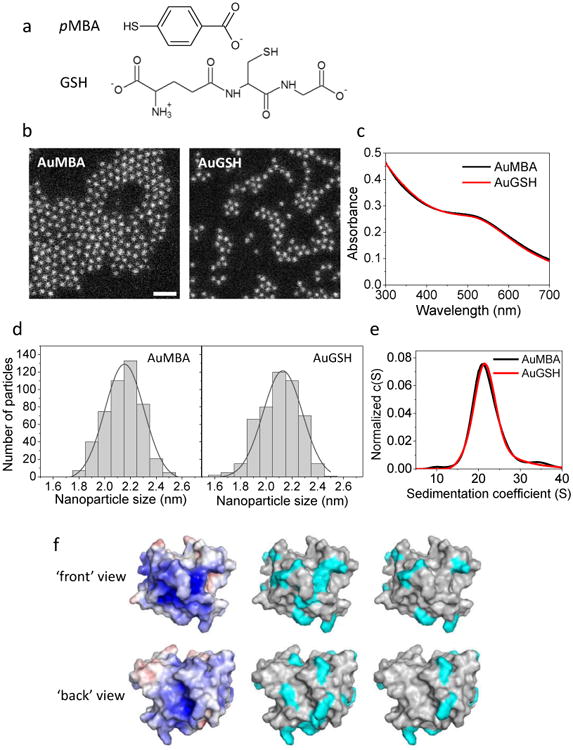
a, Structure of p-mercaptobenzoic acid (pMBA) and glutathione (GSH) passivating ligands. b, Characterization of NP size and uniformity by dark-field scanning transmission electron microscopy. NPs are approximately 2 nm in core diameter and highly uniform (2.1 ± 0.2 nm). Scale bar, 10 nm. c, UV-visible spectra of NPs. d, Histograms of STEM measurements of nanoparticle diameter. e, Characterization of NP size and uniformity by analytical ultracentrifugation. NPs are ∼ 2 nm in core diameter based on a sedimentation coefficient of ∼ 21 S (cf. ref. [25]). NPs appear reasonably uniform as judged from the widths of their sedimentation coefficient distributions (note these widths are also affected by NP diffusion). f, Left: Surface electrostatic potential of CrataBL scaled from -5 to +5 kT/e (red to blue; calculated with APBS). Middle: surface areas (cyan) corresponding to the 16 Arg⁺ and 5 Lys⁺ residues of the protein. Right: areas corresponding to the 8 Arg⁺ and 2 Lys⁺ residues deemed to be accessible to the solvent (calculated with GetArea).

CrataBL, a small glycosylated basic protein (21 kDa; theoretical pI = 10.5), was isolated from the bark of Crataeva tapia⁴⁰. We have identified CrataBL as an ideal protein to perform comparative kinetics measurements in strong- and weak-binding systems. In contrast, other candidate proteins with net positive charge at pH 7 (trypsin, chymotrypsin and lysozyme) were also tested but none produced measurable SPR signals with AuGSH (Fig. S1). CrataBL is characterized as both a Kunitz-type protease inhibitor and a lectin, with several biological properties demonstrated to date, including anti-thrombotic, anti-inflammatory and anti-tumor activities²⁴. CrataBL contains several solvent-exposed Arg⁺ and Lys⁺ residues, and its surface electrostatic potential shows clusters of positive field (Fig. 1f). CrataBL has been previously characterized as a heparin-binding protein⁴¹. Consistent with this, Fig. S2 shows that the protein does not elute from a heparin column until the salt concentration has reached 0.4 M. For comparison, lysozyme (14.3 kDa, pI = 11.3) elutes at much lower salt concentration (0.15 M) despite also being a small and highly basic protein. Absorption, emission and circular dichroism spectra of CrataBL as a function of NaCl concentration are displayed in Fig. S3.

2.2. Steady-state fluorescence quenching and circular dichroism spectroscopy

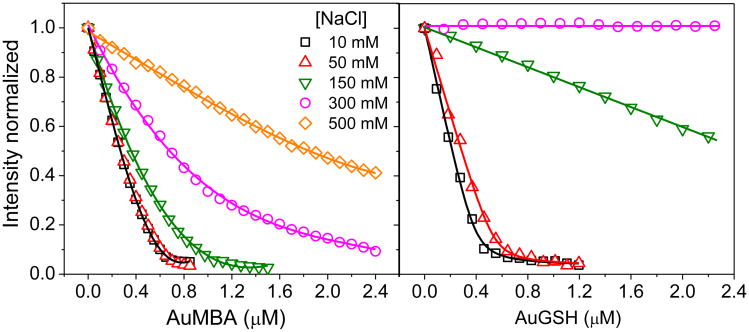
Figure 2 shows fluorescence titration quenching⁴² of CrataBL intrinsic fluorescence by the NPs as a function of salt concentration. (Control experiments showed that the NPs were colloidally stable at the salt concentrations utilized; Fig. S4a). The data enables a qualitative assessment of the relative binding strengths of AuMBA and AuGSH towards CrataBL, and the role played by electrostatics on the interactions. For both AuMBA and AuGSH, binding affinity becomes progressively weaker as the salt concentration is increased. This is consistent with interactions driven mainly by electrostatics. At 10 mM NaCl, the pattern of CrataBL fluorescence decay appears similar for AuMBA and AuGSH. This is expected considering the large value of the Debye length (κ) at 10 mM NaCl (κ ∼ 3 nm). Thus, charge interactions are screened only beyond 3 nm and a significant portion of the overall protein and NP charge densities contributes to the binding free energy⁴³. At higher salt concentrations, CrataBL undergoes much stronger interactions with AuMBA than with AuGSH. The shorter Debye length (κ ∼ 0.8 nm at 150 mM NaCl) presumably contributes to the observed binding selectivity, as ionic interactions are now more effectively screened, and NP-protein complexation depends more on local characteristics of the protein and NP surfaces^43-44, such as charge distribution, topography, conformational flexibility, and degree of hydration. Detailed quantitative analysis of the data in Fig. 2 is hindered by the multivalent nature of the interactions and CrataBL-induced aggregation of NPs (Supplementary Section S1 and Fig. S4b). Nonetheless, the results are in qualitative agreement with those obtained by SPR (see below).

Figure 2. Steady-state fluorescence quenching of CrataBL with AuMBA and AuGSH as a function of the NaCl concentration.

The CrataBL concentration was 2 μM. The lines are a guide to the eye.

Circular dichroism spectroscopy reveals changes in protein secondary structure upon NP binding at 150 mM NaCl (Fig. S5a,b). The changes observed are qualitatively like those induced by heparin binding (Fig. S5c). The conformational changes can be fully reversed at higher ionic strength (Fig. S5d), suggesting again that NP-CrataBL interactions are electrostatically driven.

2.3. Binding affinity and kinetics probed by surface plasmon resonance

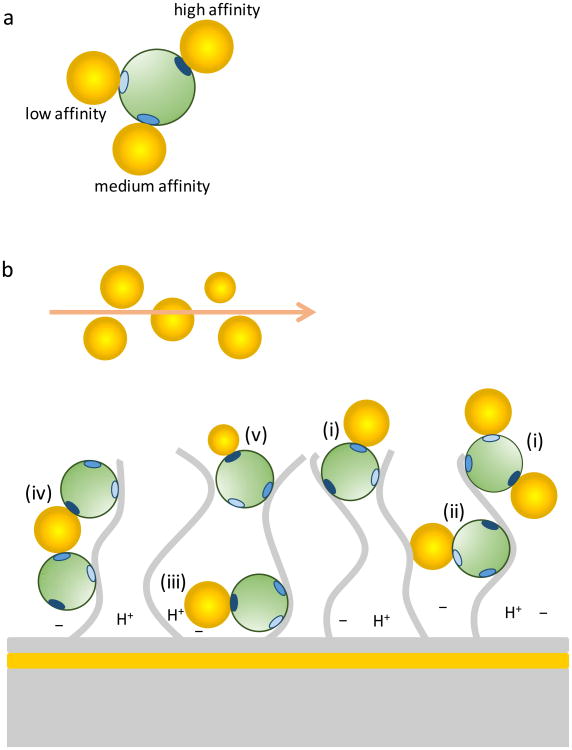
The NP-CrataBL interactions as measured by SPR show multi-phasic binding. Potential sources of binding heterogeneity are depicted in Fig. 3. These interactions therefore deviate from the simplest mechanism described by a single-site binding with pseudo-first-order kinetics, and so cannot be quantified using the discrete models of the commercial SPR software. Data analysis was therefore performed with a continuous surface-site distribution model (Fig. 4), which calculates the simplest possible distribution of subpopulations of affinities and rate constants that fit the data well^45-47.

Figure 3. Potential sources of heterogeneity of surface binding sites in surface plasmon resonance.

a, A protein (green) is represented with three positive charge clusters of different charge densities (shades of blue). The remaining protein surface is assumed to have a uniform distribution of charges. Negatively charged NPs are assumed to bind with different affinities to the different charge clusters. b, The proteins are immobilized in random orientation to a dextran matrix (extended gray lines) by amine coupling. (i) Depending on protein orientation, only certain charge clusters may be exposed to allow binding. (ii) Immobilization to different regions in the dextran matrix may produce different extent of steric hindrance. (iii) Chemical nonuniformity of the matrix may create sub-regions with different charge and pH, which could possibly affect binding. Also represented in (iii) is the fact that NP binding can take place close to the gold surface, leading to an increased signal response. (iv) Binding avidity may result from one NP binding two or more proteins simultaneously. (v) Heterogeneity in NP size and/or surface chemistry may contribute to polydispersity of the binding constants.

Figure 4. NP-protein interactions by surface plasmon resonance.

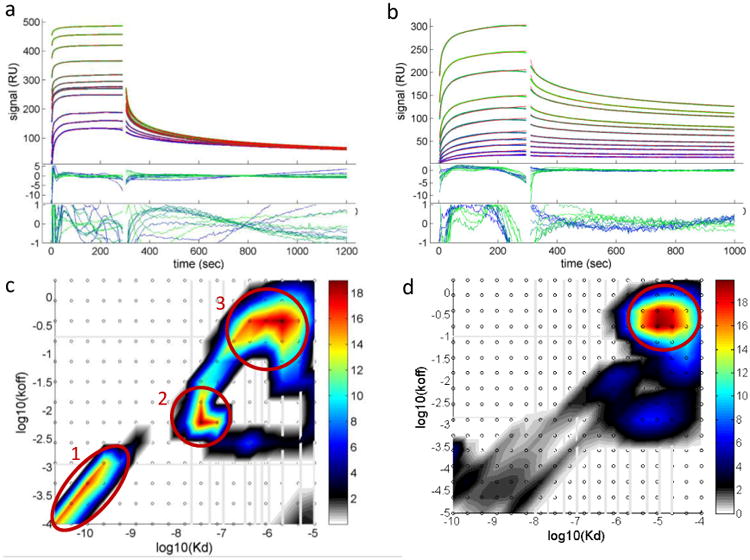
a, Analysis of AuMBA-CrataBL binding traces with the surface-site distribution model. b, The same for AuGSH-CrataBL. Phosphate buffer supplemented with 150 mM NaCl was used as running buffer. AuMBA was injected in the flow at the concentrations of 0.02, 0.05, 0.1, 0.3, 0.5 (2×), 0.7, 1, 2, 5, 10, 20 μM. For AuGSH the concentration range was 0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20 μM. Shown are the experimental traces (green and blue lines), best-fit curves (red lines), and fitting residuals. c, Calculated affinity and rate constant distributions for AuMBA-CrataBL. d, The same for AuGSH-CrataBL. Circled regions indicate the major peaks in the distributions. Integration of the peaks provides the binding parameters K_D, k_on and k_off.

The calculated rate and affinity constant distributions are shown in Fig. 4c-d. Circled areas indicate the positions of the major peaks in each of the distributions, and integration of these peaks provides the average binding parameters listed in Table 1. Standard deviations from replicate experiments are generally within a factor of two, which is common for protein interactions, and reasonable given that the measurements were performed using independent sensor surfaces and two independent batches of NPs.

Table 1.

Average affinity and kinetic parameters for AuMBA-CrataBL (n = 8) and AuGSH-CrataBL (n = 5) interactions.

Binding site	AuMBA-CrataBL			AuGSH-CrataBL
	1	2	3	-
KD(M)	(7.1 ± 1.4)×10-11	(3.5 ±1.2)×10-8	(1.7 ± 0.7)×10-6	(2.7 ± 2.0)×10-5
kon(M-1s-1)	(2.2 ± 1.1)×106	(4.4 ± 2.4)×105	(2.9 ± 2.5)×105	(1.7 ± 0.7)×104
koff (s-1)	(1.6 ± 1.1)×10-4	(1.5 ± 1.2)×10-2	(3.8 ± 2.2)×10-1	(3.8 ± 2.1)×10-1

The results initially revealed that AuMBA binds to three distinct sites on the CrataBL surface, with K_D of 71 pM, 35 nM and 1.7 μM, whereas AuGSH binds CrataBL with a single major K_D of 27 μM (Table 1). It is remarkable that two negatively charged NPs of essentially the same size and zeta potential bind the same oppositely charged protein with such widely different affinities. The calculated reaction rate constants are also displayed in Table 1. They reveal a larger association rate constant for AuMBA (∼ 10⁵–10⁶ M^-1s^-1) and longer residence times (1/k_off ∼ 66 sec for site #2) relative to AuGSH (∼ 10⁴ M^-1s^-1 and ∼ 3 s, respectively).

The affinity and rate constant distributions are remarkably similar among the different sensor surfaces utilized (cf. Figs. S6-S7 and Tables S1-S2). This is an important result, as marked dissimilarities in the distributions would render the SPR analysis unreliable. Nevertheless, we deemed necessary to check whether the picomolar binding affinity exhibited by AuMBA for CrataBL (site #1 from Table 1) could be corroborated by a set of additional experiments. Control experiments with fluorescence quenching, calorimetry and a dissociation assay revealed that site #1 was an artifact of the SPR assay, most likely due to multivalent surface binding events (see Section S2 for details and Figs. S8-S10). Therefore, site #2 (Table 1) was assigned instead as the binding site of highest affinity on CrataBL for AuMBA (K_D = 35 nM).

2.4. Association kinetics of NP-protein interactions in analogy with protein-protein complexation

To contextualize the SPR results, we consider the association kinetics of NP-protein interactions in analogy with the kinetics of protein-protein complexation, which can be described in terms of the following equilibrium⁴⁸:

$$A+B\underset{k_{-1}}{\overset{k_1}{\rightleftarrows }}A:B\underset{k_{-2}}{\overset{k_2}{\rightleftarrows }}A\cdot B$$ (1)

The isolated proteins (A and B) undergo random diffusion until their binding sites face each other to allow formation of an intermediate encounter complex (A ∶ B) with a second-order rate k₁. This complex might be held together by long-range electrostatic forces and maintain a mostly hydrated binding interface. From this first-encounter complex, the interacting proteins go through a transition state where desolvation of the interface and possible conformational changes take place, and the final bound complex (A · B) is formed with a first-order rate k₂.

If it is assumed that k₂ is fast and not rate-limiting, then the association reaction is characterized as diffusion-limited. In this case, a basal association rate constant can be estimated. First, the rate of collision of two uniform uncharged spheres in water at 25 °C is given by k_coll 7×10⁹ M⁻¹s⁻¹ (Smoluchowski limit)⁴⁸. For stereospecific association of proteins, however, stringent orientational constraints reduce this rate by a factor p_r (k_pr = p_rk_coll). This factor has been estimated by considering surface patches δα and δβ on the interacting proteins and a torsion angle χ of rotation of one protein relative to the other, so that p_r = (δα²/4)(δβ²/4δχ/π), which gives the probability that the surface patches face each other in the proper orientation for binding⁴⁹. Fixing each angular parameter at 5° yields p_r = 1×10^-7 and k_pr ∼ 7×10²M⁻¹s⁻¹, a drastic reduction from k_coll. The two interacting proteins may also undergo a series of microcollisions leading to a 10²–10³-fold increase in the association rate⁵⁰. The final basal association rate is then predicted to be k_basal ∼ 10⁵–10⁶ M⁻¹s⁻¹. In certain systems, long-range electrostatic forces can steer the proteins facilitating the mutual search for their binding interface, in which case k_on>k_basal⁵¹. Reactions with slow k₂ rates on the other hand imply a relatively large energy barrier between the first encounter and final complex, e.g., due to desolvation of polar/charged residues and/or major conformational changes, leading to a smaller k_on. Thus, k_on<k_basal is designated as the reaction-limited regime of association⁴⁸.

From these considerations and the insight gained from the computer simulations (see below), we propose that the association of proteins with NPs can be described similarly by:

$$A+NP\underset{k_{-1}}{\overset{k_1}{\rightleftarrows }}A:NP\underset{k_{-2}}{\overset{k_2}{\rightleftarrows }}A\cdot NP$$ (2)

A few points to notice are: (i) The above equilibrium equation is not strictly applicable to all NP systems. For example, binding of proteins to large naked NPs may be more properly viewed as an adsorption process, where proteins bind through an extended interface and undergo a series of slow conformational rearrangements at the particle surface to minimize their interfacial energy, resulting in a nearly irreversibly bound hard-protein corona^13-14,52. Here we deal instead with protein-mimetic ultrasmall NPs, which presumably follow an equilibrium reaction by binding proteins in a way that is more reminiscent of biomolecular complexation. (ii) Relative to a protein-protein complex, electrostatic forces are expected to play a more prominent role in stabilizing the final NP-CrataBL complexes through the k_-2 term; (iii) Because the NPs are spherical and uniform, the new expression for p_r incorporates only the orientational constraint imposed by the protein: p_r = (δα²/4). For δα = 5°, p_r = 1.9×10^-3 and k_pr ∼ 10⁷ M⁻¹s⁻¹; (iv) Microcollisions and long-range electrostatic forces presumably play now only a small role in speeding up association through k₁, since the interaction is not strongly stereospecific⁵³; (v) From (iii) and (iv), k_basal is predicted to fall in the 10⁸–10⁹ M⁻¹s⁻¹ range.

The SPR results (Table 1) indicate that the association rates are significantly smaller than 10⁸–10⁹ M⁻¹s⁻¹, suggesting the presence of an energy barrier between the first encounter and final states. However, SPR cannot reliably measure rates higher than ∼ 10⁶ M⁻¹s⁻¹. Nevertheless, considering that AuMBA-CrataBL association is at least ∼ 20 times faster relative to AuGSH-CrataBL, and given that AuGSH-CrataBL association rate falls well below the 10⁶ M⁻¹s⁻¹ SPR limit, we designate AuMBA-CrataBL interaction as mainly diffusion-limited and AuGSH-CrataBL as reaction-limited. The nature of the energy barrier that slows down association of AuGSH-CrataBL is addressed in Section 2.7 with the help of computer simulations.

2.5. Effect of NaCl concentration on NP-CrataBL interaction kinetics

The interaction kinetics were also measured by SPR at a higher NaCl concentration of 400 mM. Consistent with electrostatic-controlled complexation, the binding affinities are much weaker at 400 mM (Fig. S11). In addition, the increase in salt concentration shows disparate effects on the binding kinetics of the NPs: for AuMBA, k_on changed by only 2-fold whereas k_off increased 43-fold; for AuGSH on the other hand, k_off varied by only 2-fold whereas k_on decreased 21-fold (Fig. S11).

These results can be tentatively rationalized by considering the expressions for k_on and k_off in Eq. 2⁵⁴: k_on = k₁k₂/(k_-1 + k₂) and k_off = k_-1k_-2/(k_-1 + k₂). If AuMBA-CrataBL interaction is a diffusion-limited process (k₂≫k_-1), then

$$\begin{array}{ccc}{k}_{\text{on}}=k_1& \text{and}& k_{\text{off}}=k_{-1}{k}_{-2}/k_2\end{array}$$ (3)

and if AuGSH-CrataBL association is reaction-limited (k_-1≫k₂),

$$\begin{array}{ccc}{k}_{\text{on}}=k_1{k}_2/k_{-1}& \text{and}& k_{\text{off}}=k_{-2}\end{array}$$ (4)

It may be assumed that the energy levels of the encounter complex, transition state and final complex change by a similar magnitude as a function of ionic strength (Fig. S12). In this case k₂ and k_-2 would vary little with salt concentration. Similar considerations may explain the weak influence of ionic strength on k_off in the interactions between proteins⁵³. k₁ is also expected to remain mostly constant with changes in salt concentration, since the association of CrataBL to the NPs is not strongly stereospecific. This observation regarding k₁ contrasts with that for geometrically restricted interfaces in protein-protein complexes, where k₁ may depend strongly on the magnitude of long-range electrostatic forces⁵¹. Finally, per the adopted model (Eq. 2), k_-1 is expected to increase under higher ionic strengths, since the encounter complex would become energetically less stable. Based on these considerations, Eqs. 3 and 4 predict the correct trends in k_on and k_off for both AuMBA- and AuGSH-CrataBL interactions as the salt concentration is increased to 400 mM.

2.6. Effect of macromolecular crowding on NP-CrataBL interactions

Protein-protein interactions measured in dilute buffer might differ quantitatively from interactions measured in macromolecular crowded solutions⁵⁵. On the one hand, crowding can decrease the rate of association between proteins due to the increased solution viscosity and hydrodynamic interactions. On the other hand, crowding and depletion effects can promote the complexation between proteins. When considered in combination, these two opposing effects are predicted to affect diffusion- and reaction-limited associations differently⁵⁶. For proteins that interact with fast on-rates, crowding shows typically a minor impact on binding affinity because the effects of viscosity and depletion tend to cancel out⁵⁷. However, for proteins that interact with slow on-rates, crowding is predicted to increase binding affinity, because the already slow association is not significantly impacted by the higher solution viscosity.

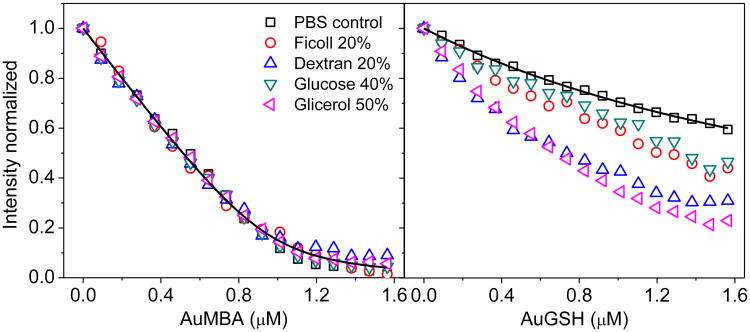
Based on these considerations, we hypothesized that AuMBA- and AuGSH-CrataBL interactions would be affected differently by macromolecular crowding. As a test, we performed fluorescence titration quenching of CrataBL with AuMBA and AuGSH in both PBS and PBS supplemented with different crowding agents (Fig. 5). For AuMBA, macromolecular crowding has no apparent influence on binding affinity, whereas stronger interactions are observed for AuGSH under crowding. These results are in accord with the notion that AuMBA- and AuGSH-CrataBL association kinetics follows diffusion- and reaction-limited processes.

Figure 5. Effect of macromolecular crowding on NP-CrataBL interactions.

Steady-state fluorescence quenching of CrataBL with AuMBA and AuGSH in PBS and PBS supplemented with different crowding agents (mass %). Black lines are a guide to the eye.

2.7. Computational modeling and NP-CrataBL interaction potentials

The interaction potentials between the NPs and CrataBL are shown in Fig. 6. Overall, CrataBL has a higher affinity for AuMBA than for AuGSH, and the energy barrier separating states 1 and 2 are due to the penalty required to remove ions from the interface; this barrier disappears in the absence of ions. The potentials justify the two-state binding mechanism proposed: association proceeds first through a rather loose first-encounter complex (pre-bound state 2) stabilized by long-range electrostatics mediated by ions; once interfacial ions are removed the complex becomes tightly bound (state 1). In state 1 the protein binds to both NPs through the same interface (inset Fig. 6c), but displays more variability in state 2. This situation is indeed akin to the current view of the protein complexation mechanism^58-59 (These simulations cannot fully represent the water desolvation barrier, which is modulated by liquid-structure forces and require atomic resolution; these forces would destabilize both potentials in Fig. 6 and introduce a barrier between state 1 and the dissociated state⁶⁰, but such modulations do not change the kinetics mechanism discussed.)

Figure 6. Molecular modeling and simulation of NP-protein complexation.

a, Molecular surface representations of the atom-based (left column) and coarse-graining (right) models of the NPs and protein. b, Molecular surface representations of the NPs (red: −CO₂^‒ groups; blue: −NH₃⁺); despite their identical Au core sizes and coating densities the NPs have slightly different overall diameters and differ substantially in surface chemistry, charge distribution, and topography. c, Potentials of mean force, V, driving NP-protein association (r is the distance between the centers of mass) showing the (loosely-held) pre-bound state 2 and the (tight) bound state 1; dotted line indicates the inferred change of the potential due to the CrataBL/AuGSH interfacial restructuring.

Two additional observations can be made by comparing the potentials. (i) the larger energy barrier for the 2 → 1 transition in AuGSH implies that k₂ is smaller for AuGSH than for AuMBA. This is due to the more complex nature of the counterions atmosphere and the larger number of ions surrounding AuGSH (Fig. 6b). This result is consistent with the experimental observation that binding of AuGSH should involve a mechanism that slows down association. (ii) State 2 is energetically more favorable than state 1 in AuGSH, which is inconsistent with the experimental observation that both NPs bind to CrataBL as stable complexes. This implies that there must be further reconfiguration of the AuGSH-CrataBL complex once it reaches state 1 that lowers its energy below that of state 2 (Fig. 6). The CD data (cf. Section 2.2) show indeed the occurrence of secondary structural changes on CrataBL upon NP binding. However, the global changes in secondary structure inferred from the CD spectra are similar for both types of NPs, so secondary structural changes are probably not responsible for the qualitative differences observed in the kinetics of both NP types. The relevant restructuring during AuGSH-CrataBL association probably occurs at the NP/protein interfaces and may include NP-protein H-bonds formation. Such conformational changes will increase the energy barrier separating states 1 and 2. Although such interfacial reconfigurations may also occur during AuMBA-CrataBL association, the simulations indicate that this is not required to stabilize a tight complex, consistent with the less demanding diffusion-limited mechanism proposed for AuMBA.

These observations suggest a three-state kinetic model for a general NP-protein system: formation of a loose complex separated by water and ions → a tighter complex stabilized upon desolvation of the interface by long-range electrostatic forces → a final tight complex stabilized upon conformational changes, including interfacial restructuring, by short-range NP-protein interactions.

3. Conclusions

We prepared two ultrasmall gold NPs having different passivating layers but nearly identical core sizes and overall negative charge (AuMBA and AuGSH). This simple NP system served as a platform to understand the dependence of binding affinity and kinetics on NP surface chemistry.

We found that AuMBA and AuGSH displayed strong and weak binding affinities (K_D ∼ 30 nM and 30 μM, respectively) and fast and slow association kinetics (k_on ∼ 10⁶ M^-1s^-1 and 10⁴ M^-1s^-1, respectively) towards the model protein CrataBL. A slow k_on was unexpected given the initial estimate of the rate of association in the 10⁸–10⁹ M⁻¹s⁻¹ range, i.e., near the diffusion limit. However, we found that, depending on the structural and chemical complexity of the passivating layer, desolvation of the interface can slow down the on-rate by up to 10⁵-fold. This stems from two energetically demanding mechanisms: removal of the NP hydration shells, which includes the counterions; and the interfacial structural changes that allows short-range interactions to develop. These results highlight that specific molecular events along the association pathway – i.e., events preceding formation of the final bound complex – must be considered explicitly to understand biomimetic interactions of NPs with proteins. Additional studies are needed to determine whether similar conclusions hold for other ultrasmall NP-protein systems.

Knowledge of binding kinetics has practical implications in biomedicine. Interactions that are long-lived (k_off< 10^-4 s^-1; t_1/2> 2h) may result in long-term exposure of cryptic epitopes when binding is accompanied by protein conformational changes; this, in turn, may trigger an immune response in vivo^61-62. In contrast, the formation of long-lasting NP-protein complexes may be desirable when NPs are engineered as nanopharmaceuticals for targeting cell surface receptors in the open in vivo system. This is analogous to the action of small drugs on target receptors, for which a slow k_off – and not simply a small K_D – has been proposed to improve pharmacological activity⁶³. On the other hand, interactions with a slow k_on rate (reaction-limited) are predicted to be enhanced by depletion forces in crowded solutions⁵⁶, as shown here for AuGSH. Thus, NPs that seem otherwise capable of resisting protein adsorption in buffer may become more “sticky” towards proteins in the crowded biological environment. We therefore propose that macromolecular crowding must be another variable to incorporate in the characterization of NP interactions.

4. Materials and Methods

4.1. Materials

HAuCl₄·3H₂O, NaBH₄, glutathione (GSH), glycerol, glucose and Dextran from Leuconostoc mesenteroides (∼40 kDa) were purchased from Sigma-Aldrich. Ficoll PM70 (∼70 kDa) was from GE Healthcare Life Sciences. p-mercaptobenzoic acid (pMBA) was obtained from TCI America. Streptavidin-coupled magnetic beads were obtained from Thermo Scientific. The peptide ECGK-biotin was synthesized by Peptide 2.0 (Chantilly, VA).

4.2. AuNPs and CrataBL

AuMBA was prepared by mixing HAuCl₄·3H₂O with pMBA ligands in the presence of a reducing agent (NaBH₄). The details of the synthesis have been described in previous publications^25-26,64. AuGSH was prepared from ligand exchange of the parent AuMBA particles with GSH as previously reported^25-26. NP size and uniformity were characterized by dark-field scanning transmission electron microscopy (STEM) and analytical ultracentrifugation as previously described^25-26. Zeta potential was recorded in phosphate buffer (pH = 7.4) without NaCl in a Malvern Zetasizer. NP concentration was estimated by UV-visible absorbance using an extinction coefficient of ε = 4.3 × 10⁵ M^-1cm^-1 at 510 nm. Isolation of the protein CrataBL from the bark of Crataeva tapia was performed as specified in Araujo et al⁴⁰. The surface electrostatic potential of CrataBL was calculated with APBS⁶⁵. Solvent-accessible residues X (here, Arg⁺ and Lys⁺) were identified with GetArea⁶⁶ as residues with a SASA of at least 50% of that in the Gly-X-Gly tripeptide; a probe radius of 1.4 Å was used in the calculations.

4.3. Fluorescence titration quenching and circular dichroism

Fluorescence measurements were performed on a Shimadzu spectrofluorimeter model RF-5301PC at 25°C. CrataBL was loaded into a quartz cuvette at a concentration of 2 μM and titrated with the NPs. The intrinsic CrataBL fluorescence signal (due to Trp and Tyr) was recorded following addition of each NP aliquot from a concentrated stock solution. The titration experiments were performed in phosphate buffer (10 mM) supplemented with NaCl (10, 50, 150, 300 and 500 mM), or in PBS (150 mM NaCl) supplemented with the crowding agents glycerol, glucose, Dextran (40 kDa) and Ficoll (70 kDa). The excitation wavelength was 280 nm and the slit width was set to 5 nm. To account for the inner-filter effect from the NPs, a solution of the amino acid tryptophan was titrated with NPs. Corrected quenching curves for CrataBL were generated by dividing the uncorrected data by the tryptophan reference curve. This inner-filter correction procedure has been validated as demonstrated in previous work⁴². CD measurements were carried out on a Jasco instrument model J-180. The scanning step size and scanning speed were set to 0.5 nm and 50 nm/min, respectively. CrataBL and NPs were used in the concentration ranges of 5-10 μM and 2-4 μM, respectively.

4.4. Surface plasmon resonance (SPR) biosensing

Experiments were carried out in a Biacore T-200 SPR instrument (GE Healthcare Life Sciences). CrataBL was immobilized using standard amine coupling onto CM3 and CM5 carboxy-methyl dextran-coated sensor chips. For the experiments with AuMBA, the following sensor surfaces were prepared (the values of RU refer to amount of immobilized CrataBL): 320, 950, 1280 and 2200 RU (CM5); 430 RU (CM3). Sensor surfaces used with AuGSH: 950, 2090 and 2200 RU (CM5). Two independent batches of AuMBA and AuGSH were used in the experiments. Phosphate buffer supplemented with either 150 or 400 mM NaCl was used as running buffer. AuMBA and AuGSH were injected in the flow typically at concentrations spanning 10 nM to 20 μM. The association and dissociation phases were recorded for 300 and 700 s, respectively, and the flow rate was 30 μL/min. Complete regeneration of the sensor surfaces was achieved using 0.005% sodium dodecyl sulfate followed by a solution of 2M NaCl; both solutions were injected for 30 s at a flow rate of 30 μL/min. Correction of bulk refractive index changes and NP nonspecific binding was performed by subtracting the responses from a reference surface from the raw SPR traces. Data analysis was carried out with the surface sites representing a continuous distribution of equilibrium constants and dissociation rate constants. This model is globally fit to the experimental data at different analyte concentrations using the software EVILFIT^45-46.

4.5. Dissociation assay for estimation of k_off

AuMBA was biotinylated for immobilization onto commercial streptavidin-coupled magnetic beads. Biotinylation was accomplished as previously reported³⁰. Next, streptavidin-coupled beads (50 μL) were mixed with AuMBA-biotin (1.5 μM) for 10 min. The amount of immobilized AuMBA (0.7 μM) was calculated by measuring the concentration of free NPs in solution before and after addition of the beads. The same procedure was repeated using non-derivatized NPs as control, in which case the NPs did not stick to the beads as expected. Next, CrataBL (2 μM) was incubated with the beads for 10 min, after which the solution containing excess protein was withdrawn with a pipette following application of a magnetic field to separate the beads. The beads were washed once with phosphate buffer without NaCl to remove remaining unbound CrataBL. Finally, the beads were resuspended in PBS and the dissociation of bound CrataBL was monitored over 3h at specific time intervals by recording the intrinsic CrataBL fluorescence in a fluorimeter.

4.6. Isothermal titration calorimetry

ITC measurements were performed with a Microcal VP-ITC instrument. CrataBL (100 μM) was loaded into the syringe and titrated (10 μL) into the calorimeter cell containing AuMBA (5 μM) in PBS at 25 °C. The thermogram data were integrated with the software NITPIC⁶⁷, followed by titration isotherm analysis in SEDPHAT⁶⁸ with a single-site model.

4.7. Molecular modeling

The interaction potentials of mean force, V(r), between the NPs and the protein were calculated in an aqueous solution containing 150 mM of NaCl at 25 °C. The NPs, both with a gold core of 2 nm in diameter and containing 144 Au atoms, were modeled as hardcore spheres of radii R = (3v/4π)^1/3, where v is the time-averaged molecular volume of the NPs calculated from molecular dynamics simulations using a fully atomistic model. This yielded R ∼ 1.5 nm for AuMBA and R ∼ 1.7 nm for AuGSH. Based on the experimental surfactant density, 64 –CO₂⁻ groups were randomly placed on the surface of AuMBA, whereas 128 –CO₂⁻ and 64 -NH₃⁺ were distributed on AuGSH. These groups were represented as spheres with effective radii of 2 Å and charges of ±e. To account for the shape and charge distribution of CrataBL, a coarse-grained model⁶⁹ was used with a total of 20 spherical domains (Fig. 6). Ions were represented explicitly, whereas the effects of water were modeled implicitly⁷⁰. The calculations were carried out with canonical Monte Carlo simulations in a biased potential η, so V(r) = − kT ln P(r) + η(r) + c, where P are the weighted probability distributions, and r is the distance between the centers of mass of the NP and the protein. A nonharmonic potential of the form⁶⁰η(r) = a₁(r² – r_i²) + a₂(r – r_i)² – a₃ln{[1 + exp(–a₄(r – r_i)²)]/2} was applied at intervals of 1 Å, where a₁ = −9×10⁻⁴; a₂ = 4×10⁻³; a₃ = 2; a₄ = 0.05 were determined in test simulations. A total of 10⁶ trial moves were performed for each r_i consisting of rotations and/or translations. The constants c's were determined by WHAM and the 4πr² contributions removed.