Abstract
Objective
The presence of interictal epileptiform discharges (IED) in the electroencephalogram (EEG) is a key finding in the medical workup of a patient with suspected epilepsy. However, inter-rater agreement (IRA) regarding the presence of IED is imperfect, leading to incorrect and delayed diagnoses. An improved understanding of which IED attributes mediate expert IRA might help in developing automatic methods for IED detection able to emulate the abilities of experts. Therefore, using a set of IED scored by a large number of experts, we set out to determine which attributes of IED predict expert agreement regarding the presence of IED.
Methods
IED were annotated on a 5-point scale by 18 clinical neurophysiologists within 200 30-s EEG segments from recordings of 200 patients. 5538 signal analysis features were extracted from the waveforms, including wavelet coefficients, morphological features, signal energy, nonlinear energy operator response, electrode location, and spectrogram features. Feature selection was performed by applying elastic net regression and support vector regression (SVR) was applied to predict expert opinion, with and without the feature selection procedure and with and without several types of signal normalization.
Results
Multiple types of features were useful for predicting expert annotations, but particular types of wavelet features performed best. Local EEG normalization also enhanced best model performance. As the size of the group of EEGers used to train the models was increased, the performance of the models leveled off at a group size of around 11.
Conclusions
The features that best predict inter-rater agreement among experts regarding the presence of IED are wavelet features, using locally standardized EEG. Our models for predicting expert opinion based on EEGer’s scores perform best with a large group of EEGers (more than 10).
Significance
By examining a large group of EEG signal analysis features we found that wavelet features with certain wavelet basis functions performed best to identify IEDs. Local normalization also improves predictability, suggesting the importance of IED morphology over amplitude-based features. Although most IED detection studies in the past have used opinion from three or fewer experts, our study suggests a “wisdom of the crowd” effect, such that pooling over a larger number of expert opinions produces a better correlation between expert opinion and objectively quantifiable features of the EEG.
Keywords: Epilepsy, Interictal epileptiform discharges, Spikes, EEG feature selection, Inter-rater agreement, Support vector regression
1. Introduction
The scalp electroencephalogram (EEG) comprises 20–30 min recording from about 20 scalp electrodes. Approximately 650,000 outpatient EEGs were performed in the United States in 2013 with a cost of around $480 million (Simpson KN. Unpublished data from Medicare 5% sample and Truven MarketScan 2013 data set. 2016. Personal communication.) Interictal epileptiform discharges (IEDs) include spikes and sharp waves, and are conventionally identified by an EEG expert. In patients with epilepsy, the EEG recording is usually distinguished by the presence of IEDs. It is important to detect IEDs, since their presence aids in the diagnosis of epilepsy (Fountain and Freeman, 2006), and predicts recurrence of seizure after a first seizure (van Donselaar et al., 1992). The main question in this task is whether any IEDs exist in a particular patient’s EEG, and to find their locations if the EEG contains IEDs (Webber and Lesser, 2017). However, it is challenging to detect IEDs, since their morphologies are of a huge variety, and they can be similar to waveforms that are considered to be part of normal background EEG activity as well as artifacts (Halford, 2009).
The majority of neurologists annotating EEGs do not have neurophysiology fellowship training; these neurologists often misinterpret EEGs (Benbadis, 2007). In addition, there is a substantial discrepancy in interpretations between board-certified academic clinical neurophysiologists (Halford et al., 2013, 2017).
There are currently no universally-accepted IED-detection systems available. Almost no study have compared the performance between different IED-detection methods as well (Halford, 2009). According to the few previous studies and the general opinion of academic EEG experts, existing IED-detection systems have a low sensitivity, which requires a neurologist to review the EEG to ensure that IEDs which are present in the EEG, are detected (Ver Hoef et al., 2010; Halford et al., 2013). Moreover, existing systems have a low specificity; the neurologist thus needs to look through the output detections, to determine which ones are false positive or true positive annotations (De Lucia et al., 2008; Indiradevi et al., 2008; Halford, 2009; Halford et al., 2013). In a recent study (Scheuer et al., 2017), the performance of an IED-detection software on a dataset consisting of 40 epileptic patients, was compared with IED detection by three skilled EEGers. They reported that the algorithm is noninferior to human experts who annotated the data. It is unclear how well these results might generalize to larger, more comprehensive sets of EEGs. Moreover, there was substantial disagreement among human experts marking the dataset. The factors underlying agreement and disagreement regarding IEDs among human experts has not been intensively studied.
IED-detection software could perhaps be improved if we understood more which features optimally characterize IEDs, and which features lead to disagreement between experts. In this study, we test a broad list of EEG features for their potential correlation with expert scored IEDs, test different approaches to EEG normalization before feature extraction for the purpose of predicting expert scores, and explore which features contribute to inter-rater agreement (IRA) and disagreement among experts.
2. Methods
2.1. EEG scoring and EEGnet software
EEG recordings were annotated by experts using EEGnet, a software system hosted at the School of Computing of Clemson University. By means of this software, users can view and annotate EEG datasets on a web browser with no local software installation required (Halford et al., 2013). EEGnet has been designed to create a user interface similar to commercially available software applied in clinical EEG interpretation. Ten seconds of EEG data are displayed at one time; it also shows channel labels along with one electrocardiogram channel. Channel gain can be adjusted for all channels or for individual channels, and users can scroll through the signal one or ten seconds at one time. Several conventional EEG montages which include: hatband montage, transverse bipolar, AP bipolar, Cz reference, ipsilateral ear reference, and common average reference can be considered for scoring (Halford et al., 2013).
2.2. EEG dataset description
A dataset of EEG segments has been formed by reviewing around 1000 EEG recordings performed during the years 2010–2011, at the Medical University of South Carolina (MUSC) Neurophysiology Laboratory, for clinical purposes. EEGs were recorded by applying the standard 10–20 electrode placement. 200 thirtysecond EEG segments from EEG recordings of 200 different patients were chosen by two experts (one of which was JJH). Fifty segments were selected from EEGs which contained IEDs. Fifty segments were from EEGs read as normal in the clinical report. Fifty segments were chosen due to containing IEDs from patients who were known to have epilepsy with difficult-to-interpret IEDs. Fifty were chosen because of containing benign paroxysmal activity; an inexperienced reviewer might misinterpret these segments to be epileptiform. Institutional Review Board (IRB) approval which allowed collection and retrospective review of de-identified clinical EEG data as well as sharing the dataset with researchers at other universities has been granted by MUSC and Clemson University. All 200 segments were randomly ordered and concatenated into one long 100-min recording.
2.3. Scoring the EEG dataset by experts
Annotation of IEDs by experts was conducted in three phases. During the first phase, 19 academic clinical neurophysiologists (EEGers) were instructed to label all IEDs on the channel in which they thought it was best represented. All of these experts had completed at least one year of fellowship training in EEG interpretation and were board certified by the American Board of Clinical Neurophysiology. A clustering algorithm was used to eliminate redundancy by merging labeled EEG segments that strongly overlap in time, as described in previous studies (Halford et al., 2013). If two labeled EEG segments overlapped in time by at least half of the duration of the shortest segment, they were placed into the same cluster. The representative EEG segment for a cluster was considered as the EEG segment which had maximum sum of correlations with all segments of the same cluster. A master list of EEG events was formed by adding all the representative EEG segments, to be considered in the second phase of scoring. The master list included a representative segment from each cluster which included at least two members (events which were marked by at least two EEGers).
Of the 19 EEGers who participated in phase one of the study, 18 EEGers took part in the second phase of EEG scoring. In this second phase, each EEGer was presented with the same EEG recording in which the master list of 235 events was labeled within it, presented as transparent yellow boxes superimposed over single channel EEG segments. The EEGers were guided to click on each highlighted segment and to score it on a 5-point Likert scale (using keyboard keys 1–5) as either (1) ‘definitely not an epileptiform discharge’, (2) ‘not likely an epileptiform discharge’, (3) ‘not sure, could go either way’, (4) ‘likely an epileptiform discharge’, and (5) ‘definitely an epileptiform discharge’.
In some cases, EEGers were inconsistent in their marking of IEDs between phase one and phase two scoring. For example, in some cases an EEGer marked an event as an IED in phase one scoring yet in phase two scoring labeled the same event with a score of 1–3, indicating that they thought the event was probably not an IED. In the third phase of scoring, each EEGer was presented with a unique list of events for which they were inconsistent between phase one and phase two scoring. Each EEGer was then asked to rescore this list of events in EEGnet using the phase two scoring method. This provided a third “tie breaker” opinion on these events. Further details about this method are published elsewhere (Halford et al., 2017).
2.4. Inter-rater agreement analysis
Marginal homogeneity was assessed using the Stuart-Maxwell test (Stuart, 1955; Maxwell, 1970). To quantify agreement among the experts, the IRA was measured using linearly weighted Gwet’s agreement coefficient (AC2) (Gwet, 2008, 2014). Kappa measures of IRA were not considered due to the “kappa paradox” which leads to lower IRA values for datasets with low marginal homogeneity (Wongpakaran et al., 2013). In order to interpret the agreement, AC2 can be interpreted as: 0.8–1.0 ‘very good’, 0.6–0.8 ‘Good’, 0.4–0.6 ‘Moderate’, 0.2–0.4 ‘Fair’, less than 0.2 ‘Poor’. Groups of EEGers of size 2–17 having highest AC2 among themselves were selected as groups of “top scorers”. The majority opinion of all EEGers and the top scorers groups were used for training machine learning models, as discussed in the following sections.
2.5. Signal analysis methods
2.5.1. EEG signal preparation
EEG records were resampled at the sampling frequency of 256 Hz, and high-pass filtered at 0.5 Hz. Since various events were annotated on one of seven montages, they were all re-montaged to common average referential montage in order to make the analysis uniform. Although the events were annotated with differing lengths, we analyzed them all as 0.5 s segments centered at the peak of the IED.
2.5.2. Feature extraction
All data processing and statistical analysis were performed offline using a commercial software package (MATLAB 2014a with the Statistical Analysis Toolbox, The Math Works Inc., Natick, MA, 2014). Many types of signal analysis features were evaluated: (1) morphological features, (2) nonlinear energy operator (NLEO), (3) wavelet analysis, (4) energy of the EEG signal, (5) power spectral density using spectrogram, and (6) scalp electrode location. Methods for feature extraction are explained below. A total of 5538 features were computed for the EEG signals.
2.5.2.1. Signal morphology features
These features are related to the shape and morphology of the EEG waveform. The features which are considered include: (a) peak voltage, (b) rising voltage and slope, (c) falling voltage and slope, (d) peak-to-peak voltage, (e) spike duration, and (f) line length. Feature extraction was performed on the signals which were in the frequency interval of 0.5–256 Hz, as well as 5 main EEG frequency bands and their combinations. The frequency band is divided as: < 4 Hz, 4—8 Hz, 8—12 Hz, 12—32 Hz, > 32 Hz, which are known as delta, Theta, Alpha, Beta, and Gamma bands, respectively (Nuwer et al., 1994). The definitions of morphological features are illustrated in Fig. 1.
Fig. 1.
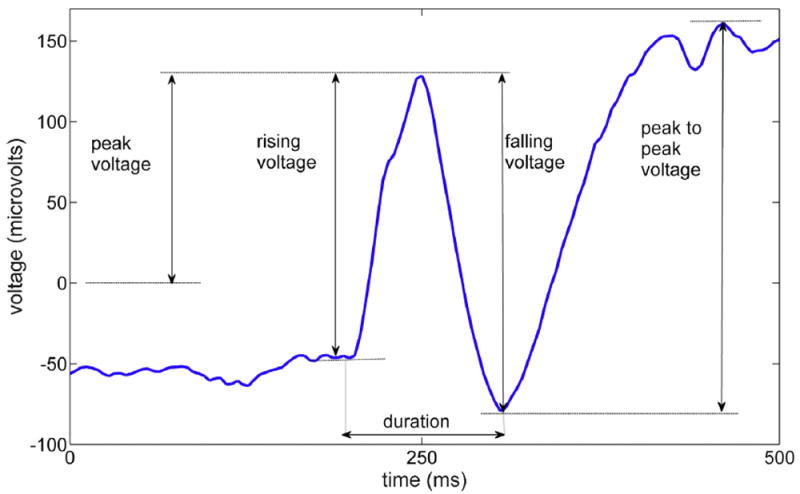
Morphological features of an interictal epileptiform discharge.
We first found the IED peak in each waveform. The neighboring troughs were then computed, and the desired voltages and slopes, as well as the spike duration, were calculated. Peak to peak voltage was defined as the difference between highest peak and lowest trough in the signal segment that is analyzed. Slopes were calculated based on the rising and falling edge voltages, and duration was defined as the total time in which the voltage goes up to the spike peak and falls down to the trough. The line length of signal x[n] with N samples was computed as (Esteller et al., 2001):
| (1) |
2.5.2.2. Nonlinear energy operator
Some previous studies have applied nonlinear energy operator (NLEO) for IED detection purposes (Mukhopadhyay and Ray, 1998; Liu et al., 2013; Bagheri et al., 2016). The NLEO is computed as:
| (2) |
where the resolution parameter k (Choi and Kim, 2002) is chosen to have values in the range of 1–40. We first calculated the NLEO value for every sample point of the EEG signal, before extracting the event segment, and then the NLEO features for each 0.5 s waveform were considered as the standard deviation, maximum, minimum, and maximum absolute NLEO value within the segment.
2.5.2.3. Wavelet analysis
The wavelet transform is useful for characterizing several aspects of EEG signals such as non-stationary transient events which makes it suitable for IED detection purpose (Halford, 2009). Many recent IED detection algorithms have applied wavelet analysis (Senhadji et al., 1995; Latka et al., 2003; Güler and Übeyli, 2005; Indiradevi et al., 2008; Bagheri et al., 2016). In this study, the discrete wavelet transform (DWT) was applied to decompose the signal into multiple scales based on wavelet basis functions. Since there is no consensus as to which wavelet basis function is best suited to characterize IEDs, multiple wavelet basis functions were applied to extract wavelet features. Hence, in this study we considered 53 wavelets including symlets (sym), coiflets (coif), Daubechies (db), biorthogonal (bior), reverse biorthogonal (rbio), and discrete approximation of Meyer (dmey) wavelet basis families with different degrees. 5 levels were considered for applying the DWT, and the wavelet decomposition was obtained for all levels (Mallat, 2008). The detail and approximation coefficients were then reconstructed for every level. The output of this step is a vector of same length as the input segment. Features were calculated based on the resulting detail and approximation coefficients; these features include standard deviation, maximum, minimum, and maximum absolute value of the detail and approximation coefficients at every level, within each segment for the transforms performed using each of the wavelet basis functions. Since the sampling rate is 256 Hz and a high-pass filter with 0.5 Hz cut-off frequency is applied, the filters applied in the wavelet transform for each of the decomposition scales include the frequency bands of d1 (64–128 Hz), d2 (32–64 Hz), d3 (16–32 Hz), d4 (8–16 Hz), d5 (4–8 Hz), a1 (0.5–64 Hz), a2 (0.5–32 Hz), a3 (0.5– 16 Hz), a4 (0.5–8 Hz), and a5 (0.5–4 Hz).
One potential disadvantage of the critically sampled discrete wavelet transform (DWT) for a one-dimensional signal is the lack of shift invariance; i.e., a small amount of shift in the signal can significantly perturb the wavelet coefficients. Since we need our method to generalize well for new data and signals which are shifted with respect to their peaks, we further investigated whether this can be problematic for this study or not. Complex wavelets provide a solution to this shortcoming of the DWT as they are known to be shift invariant. Therefore, in addition to the DWT features described above, we also evaluated the dual-tree complex wavelet transform (DT-CWT), in which two separate DWT decompositions are calculated providing real and imaginary coefficients, and using specifically designed filters (Kingsbury, 2001; Selesnick et al., 2005). We applied this method to decompose the signal into multiple scales in multiple levels. The filters ‘dtf1’, ‘dtf2’, ‘dtf3’, ‘dtf4’ were applied for the wavelet decomposition. Features were selected based on the resulting detail and approximation coefficients similar to the features extracted from DWT.
Because we extract summary statistics of DWT coefficients as features (e.g. maximum value within a brief window) rather than using the wavelet coefficients directly, it is possible that the effect of shifts will be negligible for this study. Therefore, we applied the DWT on the shifted signals in order to find out whether shifts adversely affect the prediction of expert scores. By evaluating the DT-CWT in addition to DWT on shifted signals, we determine which type of wavelet transform better suits our analysis and objectives.
2.5.2.4. Energy of the signal
The energy of the EEG signal was computed for all possible frequency bands spanning at least 4 Hz, starting at 1 Hz in steps of 2 Hz. The signal was first filtered by a linear phase FIR filter which was applied backward and forward to ensure zero-phase filtering, and then the energy was computed. Energy of a discrete signal x[n] with n samples was calculated as
| (3) |
2.5.2.5. Spectrogram and power spectral density
The spectrogram of the signal was derived by applying the short time Fourier Transform (STFT) with Hamming windowing (Oppenheim et al., 1989). Several STFT features were defined based on the matrix which consists of PSD values for each time segment of the signal, as follows: (1) mean of the PSD values, (2) maximum PSD value, (3) frequency and time of the maximum PSD value, (4) mean PSD value in neighborhoods of the maximum of the PSD in both time and frequency axes, considering all possible symmetric neighborhood lengths, (5) standard deviation of the mean PSD values along both frequency and time axes, as well as (6) mean of the standard deviation of these values.
2.5.2.6. Electrode location features
Several features were created to reflect the spatial location of IEDs on the scalp. Projecting the location of the EEG electrodes onto a two-dimensional scalp map, features were assigned to represent (1) anterior versus posterior location (2) temporal versus non-temporal location, (3) the lateralization (right versus left), and (4) the lateral distance from the midline (central versus lateral). The 2D location of each channel was represented by X (anterior-posterior) and Y (left-right) ranging from 1 to −1, respectively, based on the relative location of the electrode on the 2D scalp map. Temporal region versus nontemporal region is defined as |X|. Central versus non-central region is defined as |Y|.
2.5.3. Features versus expert scoring
The correlation between the extracted features and two aspects of the EEGer scores were analyzed. First, we analyzed the correlation between features and the average score of all experts (S̄), to find which features are present in EEG events which the EEGers thought were IEDs. Second, we analyzed the correlation between features and the standard deviation of expert scores (σs) to determine which features were associated with the most disagreement among the EEGers.
2.5.4. Feature selection: Elastic net regularization
Because of the large number of features which were generated in our analysis, a feature selection step utilizing elastic net regression was applied in order to select features which most significantly relate to the expert scores before predictive modeling analysis was applied. Elastic net is a regularized regression method which is a hybrid of ridge regression and LASSO (least absolute shrinkage and selection operator) regression. LASSO is a method for performing linear regression which is a shrinkage estimator, i.e. it estimates the coefficients such that they are biased to be small and sparse (small number of nonzero coefficient values). The elastic net method can outperform LASSO and overcome its limitations, especially for data having highly correlated predictors and high-dimensional data with few examples (Tibshirani, 1996; Zou and Hastie, 2005). In order to avoid overfitting and to evaluate the performance of our method on test data, a 10-fold crossvalidated elastic net feature selection procedure was applied to the feature sets. The feature selection was performed for each of the 10 cross-validation folds resulting in 10 selected feature sets which were applied to train and evaluate the machine learning model that will be explained in Section 2.5.6. In addition, a 10- fold cross-validation was applied to select the parameter a, which determines the relative contributions of LASSO versus ridge optimization. The value of a giving the least error was chosen and used to select the features to be included in the machine learning model.
2.5.5. EEG normalization
In order to determine whether normalizing the EEG data is a beneficial pre-processing step before feature extraction, the analysis was performed using multiple types of normalization procedures. Four different data representations were analyzed based on four different normalization procedures: (1) no normalization; (2) global standardization of each EEG channel X by z-scores, performed as follows:
| (4) |
| (5) |
| (6) |
where X represents each channel of the EEG signal, with standardization performed individually for each channel in the EEG record by subtracting its mean and dividing by its standard deviation, and N represents the total number of samples in each EEG channel; (3) local standardization using a z-score performed for each data segment rather than for each channel, by applying Eqs. 5 and 6 with X representing a 0.5 s waveform, and N representing the number of samples in each waveform (128 points); and (4) RMS (root mean squared) normalization Xm calculated for each channel (globally) as:
| (7) |
| (8) |
where Br[n] represents the 0.5 s background segments extracted by applying a sliding window for each channel of the EEG recording, and RMSBR is the RMS of these segments. Background was defined as all the data in each 30 s EEG segment which is not annotated as an IED, and which does not overlap with the annotations in any of the channels. L is the number of samples in each background segment (128 points). The signal of each channel X[n] was divided by the median of the RMS values of all background waveforms, yielding Xm.
2.5.6. Machine learning analysis
We trained machine learning regression models to predict the mean (S̄) and standard deviation (σs) of the EEGer scores for groups of scorers of various sizes. These groups included all EEGers and subsets of EEGers of various sizes selected based on having the highest AC2 IRA coefficient for that group size. This allowed us to investigate how well IED detection models performed with data from groups of EEGers of different sizes. Furthermore, different representations of the data were considered as inputs to fit the model including (a) the raw EEG data, (b) all extracted features, and (c) the features retained after feature selection with elastic net regression. We compute the root mean squared error (RMSE) and normalized root mean squared error (NRMSE) to assess the models. The RMSE is defined as:
| (9) |
where Xp and Xe represent variables that are predicted by the regression model and the actual value of the variable (mean or standard deviation of scores), respectively. The NRMSE is defined as:
| (10) |
If the NRMSE value is close to 0, there is a low error in prediction and the prediction is reliable, while the NRMSE value close to 1 suggests that the prediction is close to random guessing.
We trained support vector regression models to determine which combinations of features are present in the events with high S̄ or σs, and to predict the S̄ and σs by these features. Support Vector Regression (SVR) is a variant of Support Vector Machine (SVM). SVM are a group of machine learning algorithms in which small subset of the training examples are used to represent the decision boundary between classes; these training examples are called the support vectors (Schölkopf et al., 1995). In this study, a variant of SVM, ν-Support Vector Regression (ν-SVR) (Schölkopf et al., 2000) with a radial basis function kernel was applied to fit a regression model, which predicts the average expert score given to an EEG event. The Library for Support Vector Machines (LIBSVM) (Chang and Lin, 2011) was applied for this purpose. We applied 10-fold cross validation for training and testing the ν-SVR model. The cost parameter (c) was tuned by minimizing the crossvalidation error for each fold. SVR models were trained on 9 folds and the trained model was applied on the 10th (remaining) fold, resulting in one predicted score for each event in the 10th fold. We performed this process over all 10 folds, and computed the average RMSE and NRMSE over the 10 folds.
Throughout the analysis, including feature selection and regression, internal cross-validation was applied to select the model parameters. This helps tune model parameters while avoiding overfitting. In addition, since our dataset is relatively small, external cross-validation is important for evaluating the performance of the models and calculating error values on test data. Hence, we have applied nested cross-validation. In our use of nested cross-validation, we used internal cross-validation to select values for a α and then to train the model to obtain regression parameters giving least error on internal cross-validation. Then we applied external cross-validation to evaluate the performance of the regression model. A more detailed explanation of this procedure is included in Supplementary Material.
3. Results and discussion
3.1. Expert scoring results
19 EEGers used the EEGnet system to label a total of 1115 single-channel segments of the EEG as containing IEDs, in the first phase. The average number of IEDs labeled by the EEGers was 58.7 (range, 16–195). A clustering algorithm was used to create a master list of 235 segments to remove redundancy and to include only events which were marked by at least two EEGers, as described above. This phase 1 scoring task was completed by each EEGer within 1–2 h. In the phase 2 scoring task, the 19 EEGers were asked to categorize the events in the master list of EEG segments on the 5-point Likert scale described above and 18 EEGers completed this task, making a total of 4320 classification decisions. In phase 3 scoring, each EEGer was presented with a unique list of between 30 and 104 events to be rescored, if there was a difference between their phase 1 and phase 2 scoring opinion. The scoring results considered for analysis were the phase 2 results corrected for consistency with the phase 3 results.
The IRA for all EEGers was 0.31 based on Gwet’s AC2, indicating low to moderate agreement, as found in previous studies of IED detection (Hostetler et al., 1992; Webber et al., 1993; Wilson et al., 1996; Castellaro et al., 2002; Scheuer et al., 2017). In addition, there was a high degree of marginal inhomogeneity (mean pair-wise Stuart-Maxwell statistic: 76.7, range 1.7–176.6). For example, the average EEGer marked 19% of events with a score of 5 but this varied between 7 and 51% among EEGers.
We calculated the IRA of all possible groups of EEGers ranging in size between 2 and 17 expert scorers (262,124 groups). The AC2 IRA for the group with the highest agreement, as a function of group size, as well as the AC2 IRA of the remaining EEGers, are shown in Fig. 2. We observe that there are groups of EEGers of various sizes who agree most among themselves, while the rest of the EEGers have a low degree of agreement. It is observed from Fig. 2 that as the group size increases, the IRA of the group with the maximum agreement decreases. We call the subgroup of EEGers of size (n) having the highest AC2 IRA the “top scorers”.
Fig. 2.
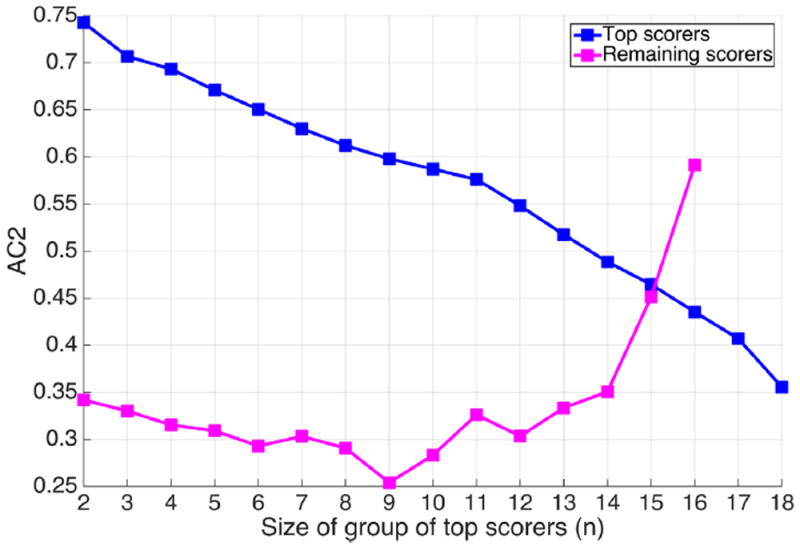
AC2 agreement coefficient among the groups of top scorers of size n.
3.1.1. Features versus expert scoring
We performed a correlation analysis on all the features which allowed us to compare feature categories based on how much they correlate with expert scores. This is important since a large number of features are considered in this analysis, and by applying elastic net feature selection, most of the redundant and highly correlated features are removed. Therefore, while feature selection output was considered for machine learning analysis, correlation analysis was also performed independent from feature selection, with the purpose of having an overall comparison between all considered features.
Fig. 3 demonstrate the Spearman correlation between each group of features with S̄ and σs. The correlation values correspond to the maximum correlation for a feature in each category, to provide an overall comparison between various feature types. We observe that wavelet coefficients as a category have the highest correlation with both average and standard deviation of scores.
Fig. 3.
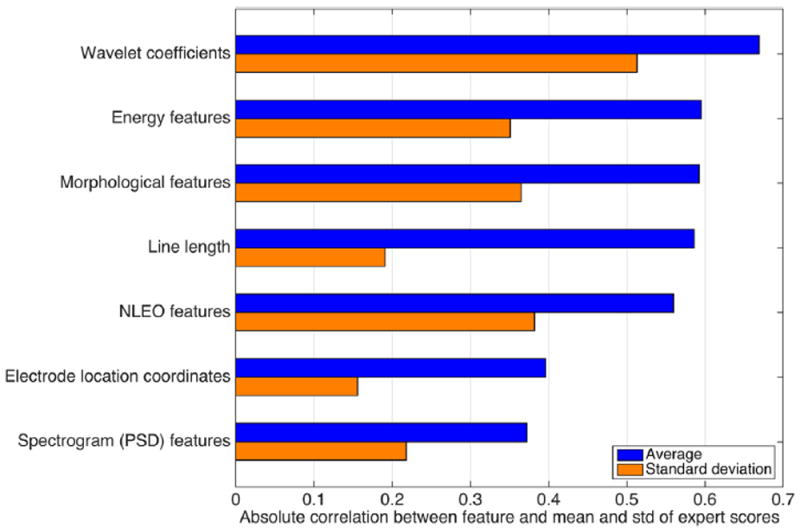
Feature categories and their maximum correlation with the average and standard deviation of the expert scores.
The top features of each category are listed in Tables 1 and 2 for S̄ and σs, respectively. Most of these correlate positively with the mean scores, including magnitude and standard deviation of wavelet coefficients and NLEO, energy, PSD, morphological features, and line length. An exception is waveform duration, which is inversely correlated with the average expert score. By contrast, most of the top features are inversely correlated with the standard deviation of expert scores, as shown in Table 2. The electrode location features will be discussed in 3.1.2.
Table 1.
Highest correlation between the features from each category with the mean expert scores. ψ represents wavelet basis function, and ϕk is the NLEO with resolution parameter (k). Subscripts ‘t’ and ‘f’ indicate the operation on PSD values along time or frequency axis, respectively.
| Wavelet coefficients | NLEO features | Morphological features | Energy | Spectrogram (PSD) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ψ = dmey, |min(d3)| | 0.669 | σ(Øk=6) | 0.559 | Peak to peak voltage | 0.593 | 12–20 Hz | 0.595 |
|
0.373 | |
| ψ = sym5, max(|d3|) | 0.667 | max(|Øk=6|) | 0.542 | Rising voltage | 0.587 | 12–30 Hz | 0.579 |
|
0.333 | |
| ψ = bior5.5, max(|d3|) | 0.666 | max(|Øk=11|) | 0.539 | Rising slope | 0.572 | 10–30 Hz | 0.569 |
|
0.317 | |
| ψ = rbio5.5, max(|d3|) | 0.665 | max(|Øk=16|) | 0.537 | Peak voltage | 0.570 | 10–42 Hz | 0.556 | Max(PSD) | 0.306 | |
| ψ = db8, max(|d3|) | 0.663 | σ(Øk=1) | 0.533 | Falling slope | 0.568 | 8–34 Hz | 0.547 | |||
| ψ = coif4, max(|d3|) | 0.660 | max(|Øk=21|) | 0.512 | Falling voltage | 0.566 | 6–40 Hz | 0.541 | |||
| ψ = rbio3.7, max(d3) | 0.659 | σ(Øk=16) | 0.501 | Duration | −0.204 | 4–38 Hz | 0.174 | |||
Table 2.
Highest correlation between the features from each category with standard deviation of expert scores. w represents wavelet basis function, and ϕk is the NLEO with resolution parameter (k). Subscripts ‘t’ and ‘f’ indicate the operation on PSD values along time or frequency axis, respectively.
| Wavelet coefficients | NLEO features | Morphological features | Energy | Spectrogram (PSD) features | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ψ = sym4,|min(d1)| | −0.513 | min(Øk=1) | 0.382 | Rising slope | −0.365 | 6–50 Hz | −0.351 |
|
−0.218 | |
| Ψ = sym5, max(d1) | −0.502 | σ(Øk=1) | −0.345 | Rising voltage | −0.364 | 4–50 Hz | −0.344 |
|
−0.217 | |
| Ψ = rbio5.5, max(d1) | −0.497 | max(Øk=1∣) | −0.267 | Peak to peak voltage | −0.295 | 6–32 Hz | −0.344 |
|
−0.212 | |
| Ψ = rbio4.4, max(|d1|) | −0.497 | min(Øk=16) | 0.250 | Falling voltage | −0.280 | 8–46 Hz | −0.315 | |||
| Ψ = coif2, max(|d1|) | −0.492 | max(|Øk=31|) | −0.244 | Peak voltage | −0.247 | 8–32 Hz | −0.312 | |||
| Ψ = rbio2.4, max(|d1|) | −0.491 | max(|Øk=26|) | 0.241 | Duration | 0.207 | 4–16 Hz | −0.308 | |||
| Ψ = db6, min(d1) | 0.491 | max(|Øk=21|) | 0.237 | Falling slope | −0.162 | 2–50 Hz | −0.265 | |||
From Table 1, we see that the wavelet basis functions most correlated with S̄ include dmey, sym5, bior5:5, rbio5:5, db8, coif 4, rbio3.7; and wavelet coefficients of d3 decomposition scale have the highest correlation with S̄. In addition to these features, scales of d4, d2, a2, d1, a1, and d5 come next, respectively. From Table 2, we observe that sym4, sym5, rbio5.5, rbio4.4, coif 2, rbio2.4, db6 have the highest correlation with σs. In addition, wavelet coefficient for decomposition scale of d1 have the highest correlation with σs, followed by d4, d2, a4, d5, a1, a2 and a3, respectively.
3.1.2. Electrode position on scalp
Spearman correlation of the electrode location coordinate features, based on a two-dimensional projection of the scalp electrode positions, demonstrated a weak correlation between expert scores and several electrode location features. The correlation coefficients between the scores and electrode location features are listed in Table 4. Experts’ scores are greater anteriorly than posteriorly (ρ = 0.32), indicating that the EEGers tended to label anterior events as more epileptiform than posterior events. Higher score events tend to be more in non-temporal regions (ρ = −0.35) and in the central versus lateral regions (ρ = −0.42). There is not a significant relation between electrode coordinates and the standard deviation of the scores (σs).
Table 4.
Correlation coefficient between electrode coordinates, and mean and standard deviation of expert scores.
| Electrode location comparison | Correlation with mean expert scores | Correlation with standard deviation of expert scores |
|---|---|---|
| Anterior vs. posterior | 0.32 | 0.07 |
| Lateralization (left vs. right side) | −0.31 | −0.09 |
| Temporal vs. non-temporal | −0.35 | −0.10 |
| Lateralized vs. central | −0.42 | −0.16 |
3.1.3. Feature selection
Features selected using elastic net regression which were highly predictive for S̄ and σs, are presented in Figs. 4 and 5, respectively. The parameter α = 0.8 for the feature selection was selected by cross-validation. In the figures, the features are rank-ordered based on their absolute coefficient in the elastic net feature selection. 10- fold cross validation was applied during feature selection; and all features presented in Figs. 4 and 5 were selected in all 10 cross validation folds. It is important to note that the selected features are not necessarily the only useful features for predicting expert scores. During feature selection, highly correlated features are eliminated; and by running feature selection multiple times, or by making slight changes to the signals such as shifting, the resulting set of features may be slightly different.
Fig. 4.
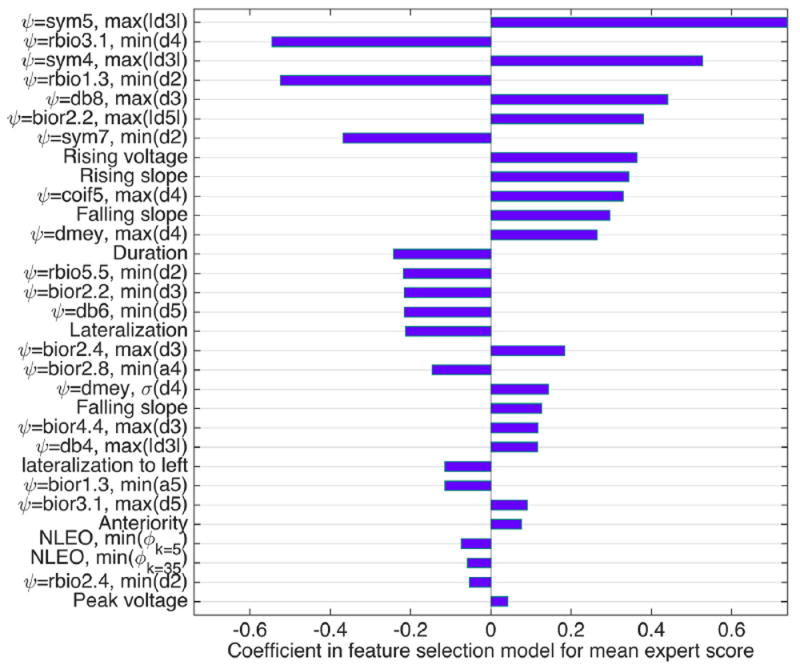
Features selected in feature selection step, which are more significant in predicting the average scores. ψ represents wavelet basis function,ϕk is the NLEO with resolution parameter (k).
Fig. 5.
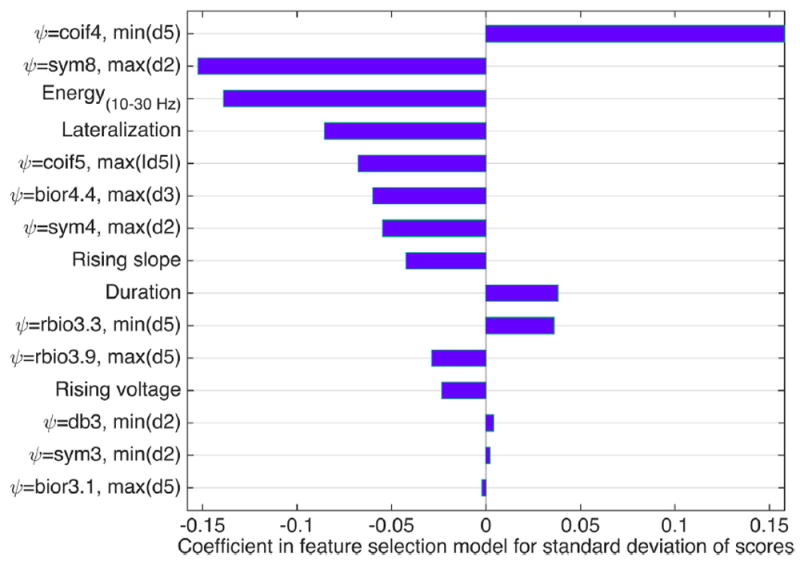
Features selected in feature selection step which are more significant in predicting standard deviation of the scores. ψ represents wavelet basis function.
From Fig. 4 we observe that mainly wavelet features are selected to predict mean expert scores. Morphological features such as rising and falling voltages and duration, electrode location (lateralization and anteriority), NLEO features, and peak voltage are also selected though they receive less weight. The features with negative coefficients correlate inversely with average scores, for which lower feature value corresponds to a higher score.
We also observe in Fig. 5 that most features selected as predictors of the standard deviation of scores are a different set of wavelet features, followed by energy in 10–30 Hz, electrode location (lateralization) and morphological features including rising voltage and slope, and duration. For these features also, negative coefficients indicates negative correlation, and higher values of the features with negative coefficients correspond predict lower standard deviations in expert scores.
It is observed from Fig. 3 and correlation values listed in Tables 1 and 2, that wavelet features have the highest correlation with both mean and standard deviation of expert scores. Moreover, among the selected features mentioned in Figs. 4 and 5, wavelet features have the largest coefficients. Hence, wavelet features are shown to be more beneficial in characterizing expert scores in IED interpretation. To make these results more tangible, we provide the morphology of the wavelet basis functions which are shown to be more useful in Supplementary Material. Nevertheless, other features such as morphological features are also seen to be highly correlated with the scores, thus may be helpful in IED interpretation.
It could be expected that wavelet features perform better than other features in this study. Analysis of electrical signals usually calls for some type of time-frequency analysis. Wavelet analysis is an efficient method for doing this and wavelet signal processing techniques have recently led to significant gains in critical signal processing tasks. In this method, data is split into different frequency components, and each component is studied with a resolution which matches its scale. If the analysis approach is wellmatched to the task, wavelets provide an extremely sparse and efficient representation for several types of signals appearing often in real world applications, but are not well matched by the Fourier basis, which is ideally meant for periodic signals. In particular, they provide an optimal representation for many signals containing singularities (jumps and spikes) (Selesnick et al., 2005), of which IEDs are a classic example.
3.1.4. Multivariate analysis of expert agreement
We fitted support vector regression (SVR) models to predict the expert scores using the features selected above and evaluated the performance by 10-fold cross-validation.
We fitted SVR models to the dataset for the scenario in which all scorers are included, and also for top scorers of various group sizes (17 groups in total). The target variable to be predicted by the model is the average score given to each event by each of the 17 expert groups (the group of all experts and the 16 “top scorer” groups). This was done separately for both S̄ and σs. The resulting RMSE values and the bars indicating ±1 standard deviation from the 10-fold cross-validated SVR models are shown in Fig. 6. We see that, as the number of top scorers increases, error in predicting expert agreement decreases. Performance is best when using the average score of all available 18 EEGers. The performance appears to level off when the top scorer group size increases to 12. We would not expect the SVR performance to improve much after 12 top scorers have been added, because the mean expert opinion in these large top scorer groups above size 12 does not change much as more EEGers are added (Halford et al., 2017). Nevertheless, because the group of all scorers produced the best overall performance, we choose “all experts” to be the optimum set of experts to be used in the further analysis presented below.
Fig. 6.
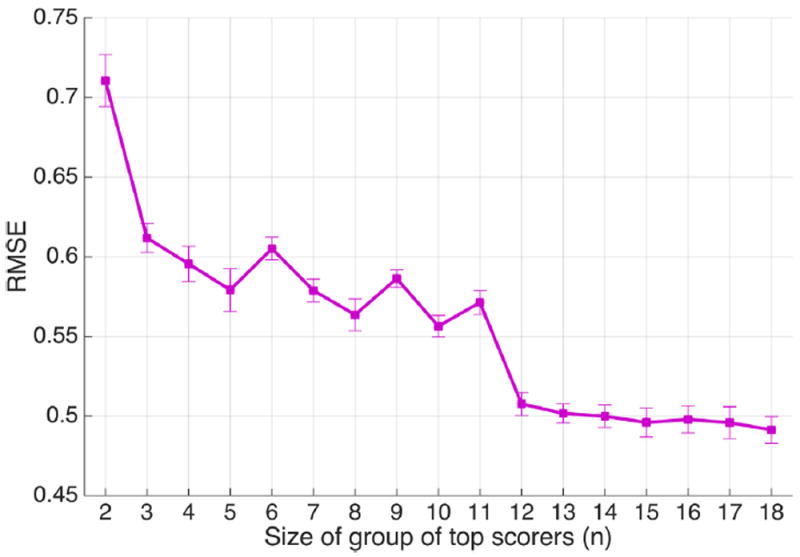
Root mean square errors resulted from SVR models fitted to the dataset, considering groups of top scorers of different sizes (n = 2–18); n = 18 indicates the group of all experts.
Three different sets of feature inputs were considered to train the models: (1) raw EEG waveforms, (2) all extracted features, (3) and selected features using elastic net regression. Furthermore, the models were compared using non-normalized and normalized data types. RMSE values for these SVR models are listed in Table 3. In addition to the waveforms centered on the peaks, the errors for waveforms shifted by a random number of samples ranging from 1 to 10 are included in Table 3. Table 3 also shows the errors for the SVR models trained on the feature set with DT-CWT. We observe that although shifting the EEG signal changes prediction errors, the effects on the prediction error are small when using the set of extracted wavelet statistics. This is probably because we do not use the wavelet transform coefficients directly; instead, we are considering statistics of the coefficients within a small neighborhood around the peak. Therefore, our features have some shift invariance built in. In addition, no significant change was observed in the feature values and set of selected features by shifting the signals. Moreover, the error values when considering the DT-CWT as an alternative to DWT, are higher than the feature set including the DWT. This may be because the four wavelet filters applied in DT-CWT are not appropriate for IED analysis. Consequently, we consider the DWT features to be a better choice of wavelet transform for our analysis.
Table 3.
RMSE values of SVR models based on average expert score for all EEGers for normalized and non-normalized data types, as well as various sets of inputs to the algorithm. The errors are calculated both for predictions made by peak-centered and shifted signals.
| Data type → Normalization Approach ↓ | Raw EEG waveforms | All features | Features selected with elastic net regression | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|||||||
| DWT Centered | DWT Shifted | DT-DWT Centered | DWT Centered | DWT Shifted | DT-DWT Centered | DWT Centered | DWT Shifted | DT-DWT Centered | |
| No normalization | 0.80 | 0.85 | 0.87 | 0.58 | 0.59 | 0.64 | 0.49 | 0.49 | 0.57 |
| Local standardization | 0.85 | 0.88 | 0.86 | 0.61 | 0.61 | 0.63 | 0.47 | 0.49 | 0.56 |
| Global standardization | 0.81 | 0.83 | 0.88 | 0.67 | 0.68 | 0.72 | 0.61 | 0.60 | 0.66 |
| Median background RMS normalization | 0.80 | 0.83 | 0.88 | 0.67 | 0.68 | 0.70 | 0.63 | 0.62 | 0.66 |
The smallest SVR error is achieved by utilizing the set of elastic net selected features on the data with local standardization. For this model, the predicted scores have a high correlation (rho = 0.87) with the mean expert scores, as shown in Fig. 7(a), with the RMSE and NRMSE performance values for the predictions 0.46 and 0.50, respectively. After fitting an SVR model to predict the standard deviation of scores using the selected features, the correlation coefficient is 0.62, whereas the predictions have RMSE and NRMSE of 0.21 and 0.79, respectively.
Fig. 7.
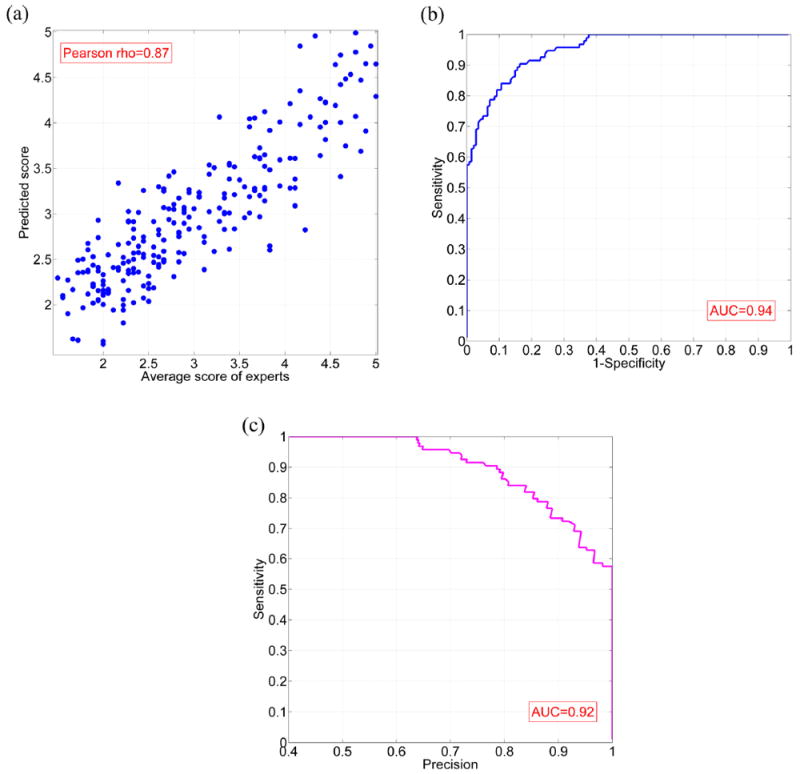
(a) Predicted scores produced by SVR trained using elastic net selected features versus original expert scores, using EEG signals normalized by local standardization; (b) ROC curve for classification based on the SVR output; (c) Precision-recall curve for classification based on the SVR output.
Fig. 7(b) shows a Receiver operating characteristic (ROC) curve for this model. In this figure, the ‘sensitivity’ (true positive rate) is plotted versus ‘1-specificity’ (false positive rate). ‘Precision’ versus ‘sensitivity (recall)’ is demonstrated in the precision-recall curve in Fig. 7(c). To create the ROC and precision-recall curves, we first set the ground truth. The events scored 4 or 5 by at least half of the experts (at least 9 experts) were considered as IED, while the other events were labeled as non-IED. Next, a threshold θ ranging from 1.5 to 5 was applied to the predicted scores of test waveforms. The events with scores of higher than h were classified as IED, and events with lower scores were classified as non-IED. The area under curve (AUC) equals to 0.94 for the ROC curve, and 0.92 for the precision-recall curve.
4. Conclusions
Identification of IEDs in EEG by experts is a cornerstone of the medical diagnosis of epilepsy, yet the features which mark an EEG waveform as “epileptiform” are difficult to specify with precision. The International Federation of Clinical Neurophysiology defines IEDs (Noachtar et al., 1999) as “distinctive waves or complexes, distinguished from background activity, and resembling those recorded in a proportion of human subjects suffering from epileptic disorders….” This highlights the fact that expert recognition of IEDs is based on experience rather than rigid definitions, and helps to explain imperfect agreement between experts scoring the same EEG. The present study evaluated numerous EEG features to determine which ones best predict whether a waveform will be judged by experts to be an IED, and which features best predict differences of opinion. We found that expert opinion regarding IEDs is predictable when the number of experts is large.
We also found that the most effective features to consider in models that predict higher expert scores were wavelet features (using certain wavelet basis functions, as listed in Fig. 4). Certain features (as listed in Fig. 5) were also associated with a high level of variance in scores, indicating disagreement among EEGers, although it was not possible to predict the variance among scorers as well as the mean score.
As expected, as the number of experts interpreting EEG increases, IRA decreases, as would be expected by chance. Although the overall IRA of the EEGers was only mild to moderate, there was a subset of EEGers with good IRA. We found groups of top scorers which have substantially higher IRA, which raised the question of whether using just a subset of top scorers rather than all scorers to train the SVR models might improve model performance. However, based on prediction error for subsets of top scorers with different sizes, we found that the consensus opinion of all available experts, rather than a subset with good IRA, resulted in the most accurate predictions. A “wisdom of the crowd” (WOC) effect seems a likely explanation of this observation: The aggregated answers of a large group are frequently better than the answer given by any individuals within the group (Surowiecki, 2005; Yi et al., 2012). WOC effects are observed when individual judgments can be thought of as “noisy” but are correlated with an underlying, true signal (as opposed to having no objective basis), such that averaging tends to cancel the noise. Nevertheless, the performance of our models levels off at a top scorer group size of around 12. This is consistent with a detailed analysis of our expert opinion published elsewhere which showed that the average opinion of our experts ceases to change significantly when the top scorer group gets to the size of 10–12 (Halford et al., 2017).
The FDA currently only requires three EEGers to annotate the location of IEDs in a testing dataset for approval of an IED detection algorithm. Most studies of IED detection algorithms in the past have expert opinion from five or fewer experts (Halford, 2009) and previous work by Wilson et al. suggested that probably only three EEGers were needed to annotate EEG datasets (Wilson et al., 1996). The present study suggests that using more than three EEGers will probably produce better results.
Since average amplitudes of EEG signal and artifacts vary between individuals, we hypothesized that it might be helpful to normalize EEG signals before feature extraction. We observed better prediction is achieved if normalization is performed by locally standardized EEG by z-scores. Globally normalizing each channel of EEG data did not improve the prediction error. This is a useful finding since it may inform best practices regarding preprocessing steps for future IED detection algorithms.
We also investigated the relationship between expert scores and the location of EEG events on the scalp. Our data suggests that experts tend to give higher (more epileptiform) scores to events which are: (1) anterior rather than posterior, (2) more in the non-temporal region rather than temporal regions, and (3) more central compared to lateralized. This result may not reflect a finding about IEDs in general since it may only be due to selection bias, since only part of our EEG dataset was selected randomly. But our finding of more non-epileptiform paroxysmal activity in the temporal region agrees with reports that benign epileptiformappearing events are frequently found in the temporal regions (Santoshkumar et al., 2009).
Our study is subject to several important limitations. First, the number of EEG events considered is probably quite a bit lower than the total number of EEG events necessary to completely encompass the variability found in epileptiform and benign epileptiform-appearing signals in all individuals. Future definitive studies will need to include larger EEG datasets and more subjects. Second, the IRA of our expert opinion was only low to moderate, calling into question the quality of the expert opinion considered to train the machine learning models of this study. IRA between experts might have been higher if the EEG segments from each subject had been longer than 30 s. It is known that IRA is higher if experts are interpreting 20-min routine EEG recordings than shorter EEG recordings (Black et al., 2000). It should be noted that the IRA was not uniformly low among our EEGers, since there was a large subset of EEGers with moderate to high IRA. This illustrates the importance of carefully selecting EEGers for IED annotation research projects. Third, the high degree of marginal inhomogeneity in the expert opinion of this study is a weakness and may have affected results. Hopefully, this can be decreased in future studies by providing more detailed instructions to EEGers. Fourth, although this study suggests certain features that may be beneficial in constructing IED detection algorithms, creating and testing an IED detection algorithm was beyond the scope of this study. In particular, the present study does not address how well our features might discriminate IEDs from background waveforms when large amounts of EEG are examined in a typical IED detection system, a situation in which non-IED background waveforms vastly outnumber IEDs.
In conclusion, the results of this study show that expert opinion regarding agreement or disagreement regarding the interpretation of IEDs is predictable. In addition, our analysis has identified preprocessing steps and particular features which are effective for training machine learning algorithms to predict expert agreement regarding IEDs, including local normalization of waveforms, and particular types of wavelet functions, among other features. Our analysis reveals that aggregated scores from a large number of experts are substantially more predictable than scores from small numbers of individuals. This finding suggests that despite studies finding that inter-rater agreement among experts is imperfect (a) there is an underlying objective and predictable reality that can be captured by machine learning algorithms, and (b) the common practice of seeking consensus by group review on difficult EEG cases may, in fact, be helpful in getting closer to the truth. It is our goal to create a large freely-available standardized testing and training database for the improvement of IED detection algorithms and work to improve IED detection algorithms themselves. In the future, we hope to collect expert opinion on longer EEG recordings and to develop a complete IED detection system.
Supplementary Material
Highlights.
Experts do not always agree on what transient waveforms are IEDs.
Wavelets are useful to predict expert agreement.
Pooling over many expert opinions yields more predictable scores.
Acknowledgments
We acknowledge the support of the Critical Care EEG Monitoring Research Consortium, since the Consortium allowed the authors to advertise for EEG expert scorers among its members.
Funding
E.B. is a PhD student in Nanyang Technological University, supported by the Singapore International Graduate Award (SINGA) scholarship funded by A*STAR. M.B.W. is supported by a grant from NIH-NINDS (1K23NS090900-01). J.J.H. is supported by a grant from NIH-NINDS (SBIR-IIB-2R44NS064647-05A1).
Footnotes
Appendix A. Supplementary material
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.clinph.2017.06.252.
Disclosures
The authors have no disclosures to report.
References
- Bagheri E, Jin J, Dauwels J, Cash S, Westover MB. Fast and efficient rejection of background waveforms in interictal EEG. 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); IEEE; 2016. pp. 744–748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benbadis SR. Errors in EEGs and the misdiagnosis of epilepsy: importance, causes, consequences, and proposed remedies. Epilepsy Behav. 2007;11:257–62. doi: 10.1016/j.yebeh.2007.05.013. [DOI] [PubMed] [Google Scholar]
- Black MA, Jones RD, Carroll GJ, Dingle AA, Donaldson IM, Parkin PJ. Real-time detection of epileptiform activity in the EEG: a blinded clinical trial. Clin EEG Neurosci. 2000;31:122–30. doi: 10.1177/155005940003100304. [DOI] [PubMed] [Google Scholar]
- Castellaro C, Favaro G, Castellaro A, Casagrande A, Castellaro S, Puthenparampil D, et al. An artificial intelligence approach to classify and analyse EEG traces. Neurophysiol Clin. 2002;32:193–214. doi: 10.1016/s0987-7053(02)00302-7. [DOI] [PubMed] [Google Scholar]
- Chang C-C, Lin C-J. LIBSVM: a library for support vector machines. ACM Trans Intell Syst Technol. 2011;2:27. [Google Scholar]
- Choi J, Kim T. Neural action potential detector using multi-resolution TEO. Electron Lett. 2002;38:541–3. [Google Scholar]
- De Lucia M, Fritschy J, Dayan P, Holder DS. A novel method for automated classification of epileptiform activity in the human electroencephalogrambased on independent component analysis. Med Biol Eng Comput. 2008;46:263–72. doi: 10.1007/s11517-007-0289-4. [DOI] [PubMed] [Google Scholar]
- Esteller R, Echauz J, Tcheng T, Litt B, Pless B. Line length: an efficient feature for seizure onset detection. Engineering in Medicine and Biology Society; 2001 Proceedings of the 23rd annual international conference of the IEEE; IEEE; 2001. pp. 1707–10. [Google Scholar]
- Fountain NB, Freeman JM. EEG is an essential clinical tool: pro and con. Epilepsia. 2006;47:23–5. doi: 10.1111/j.1528-1167.2006.00655.x. [DOI] [PubMed] [Google Scholar]
- Güler I, Übeyli ED. Adaptive neuro-fuzzy inference system for classification of EEG signals using wavelet coefficients. J Neurosci Meth. 2005;148:113–21. doi: 10.1016/j.jneumeth.2005.04.013. [DOI] [PubMed] [Google Scholar]
- Gwet KL. Computing inter-rater reliability and its variance in the presence of high agreement. Brit J Math Stat Psy. 2008;61:29–48. doi: 10.1348/000711006X126600. [DOI] [PubMed] [Google Scholar]
- Gwet KL. Handbook of inter-rater reliability: the definitive guide to measuring the extent of agreement among raters: advanced analytics. LLC; 2014. [Google Scholar]
- Halford JJ. Computerized epileptiform transient detection in the scalp electroencephalogram: obstacles to progress and the example of computerized ECG interpretation. Clin Neurophysiol. 2009;120:1909–15. doi: 10.1016/j.clinph.2009.08.007. [DOI] [PubMed] [Google Scholar]
- Halford JJ, Arain A, Kalamangalam GP, LaRoche SM, Leonardo B, Basha M, et al. Characteristics of EEG interpreters associated with higher interrater agreement. J Clin Neurophysiol. 2017;34:168–73. doi: 10.1097/WNP.0000000000000344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halford JJ, Schalkoff RJ, Zhou J, Benbadis SR, Tatum WO, Turner RP, et al. Standardized database development for EEG epileptiform transient detection: EEGnet scoring system and machine learning analysis. J Neurosci Meth. 2013;212:308–16. doi: 10.1016/j.jneumeth.2012.11.005. [DOI] [PubMed] [Google Scholar]
- Hostetler WE, Doller HJ, Homan RW. Assessment of a computer program to detect epileptiform spikes. Electroencephalogr Clin Neurophysiol. 1992;83:1–11. doi: 10.1016/0013-4694(92)90126-3. [DOI] [PubMed] [Google Scholar]
- Indiradevi K, Elias E, Sathidevi P, Nayak SD, Radhakrishnan K. A multi-level wavelet approach for automatic detection of epileptic spikes in the electroencephalogram. Comput Biol Med. 2008;38:805–16. doi: 10.1016/j.compbiomed.2008.04.010. [DOI] [PubMed] [Google Scholar]
- Kingsbury N. Complex wavelets for shift invariant analysis and filtering of signals. Appl Comput Harmon A. 2001;10:234–53. [Google Scholar]
- Latka M, Was Z, Kozik A, West BJ. Wavelet analysis of epileptic spikes. Phys Rev E. 2003;67:052902. doi: 10.1103/PhysRevE.67.052902. [DOI] [PubMed] [Google Scholar]
- Liu Y-C, Lin C-CK, Tsai J-J, Sun Y-N. Model-based spike detection of epileptic EEG data. Sensors. 2013;13:12536–47. doi: 10.3390/s130912536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallat S. A wavelet tour of signal processing: the sparse way. Academic Press; 2008. [Google Scholar]
- Maxwell AE. Comparing the classification of subjects by two independent judges. Brit J Psychiat. 1970;116:651–5. doi: 10.1192/bjp.116.535.651. [DOI] [PubMed] [Google Scholar]
- Mukhopadhyay S, Ray G. A new interpretation of nonlinear energy operator and its efficacy in spike detection. IEEE Trans Biomed Eng. 1998;45:180–7. doi: 10.1109/10.661266. [DOI] [PubMed] [Google Scholar]
- Noachtar S, Binnie C, Ebersole J, Mauguiere F, Sakamoto A, Westmoreland B. A glossary of terms most commonly used by clinical electroencephalographers and proposal for the report form for the EEG findings. The International Federation of Clinical Neurophysiology. Electroencephalogr Clin Neurophysiol Suppl. 1999;52:21. [PubMed] [Google Scholar]
- Nuwer MR, Lehmann D, da Silva FL, Matsuoka S, Sutherling W, Vibert J-F. IFCN guidelines for topographic and frequency analysis of EEGs and EPs. Report of an IFCN committee. Electroencephalogr Clin Neurophysiol. 1994;91:1–5. doi: 10.1016/0013-4694(94)90011-6. [DOI] [PubMed] [Google Scholar]
- Oppenheim AV, Schafer RW, Buck JR. Discrete-time signal processing. Prentice hall; Englewood Cliffs, NJ: 1989. [Google Scholar]
- Santoshkumar B, Chong JJ, Blume WT, McLachlan RS, Young GB, Diosy DC, et al. Prevalence of benign epileptiform variants. Clin Neurophysiol. 2009;120:856–61. doi: 10.1016/j.clinph.2009.03.005. [DOI] [PubMed] [Google Scholar]
- Scheuer ML, Bagic A, Wilson SB. Spike detection: inter-reader agreement and a statistical Turing test on a large data set. Clin Neurophysiol. 2017;128:243–50. doi: 10.1016/j.clinph.2016.11.005. [DOI] [PubMed] [Google Scholar]
- Schölkopf B, Burgest C, Vapnik V. Extracting support data for a given task. Proceedings of the 1st international conference on knowledge discovery & data mining; pp. 252–7. [Google Scholar]
- Schölkopf B, Smola AJ, Williamson RC, Bartlett PL. New support vector algorithms. Neural Comput. 2000;12:1207–45. doi: 10.1162/089976600300015565. [DOI] [PubMed] [Google Scholar]
- Selesnick IW, Baraniuk RG, Kingsbury NC. The dual-tree complex wavelet transform. IEEE Signal Proc Mag. 2005;22:123–51. [Google Scholar]
- Senhadji L, Dillenseger J-L, Wendling F, Rocha C, Kinie A. Wavelet analysis of EEG for three-dimensional mapping of epileptic events. Ann Biomed Eng. 1995;23:543–52. doi: 10.1007/BF02584454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart A. A test for homogeneity of the marginal distributions in a two-way classification. Biometrika. 1955;42:412–6. [Google Scholar]
- Surowiecki J. The wisdom of crowds. Anchor; 2005. [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. J Roy Stat Soc B Met. 1996;58:267–88. [Google Scholar]
- van Donselaar CA, Schimsheimer R-J, Geerts AT, Declerck AC. Value of the electroencephalogram in adult patients with untreated idiopathic first seizures. Arch Neurol. 1992;49:231–7. doi: 10.1001/archneur.1992.00530270045017. [DOI] [PubMed] [Google Scholar]
- Ver Hoef L, Elgavish R, Knowlton RC. Effect of detection parameters on automated electroencephalography spike detection sensitivity and false-positive rate. J Clin Neurophysiol. 2010;27:12–6. doi: 10.1097/WNP.0b013e3181cb4294. [DOI] [PubMed] [Google Scholar]
- Webber WRS, Lesser RP. Automated spike detection in EEG. Clin Neurophysiol. 2017;128:241–2. doi: 10.1016/j.clinph.2016.11.018. [DOI] [PubMed] [Google Scholar]
- Webber WRS, Litt B, Lesser R, Fisher R, Bankman I. Automatic EEG spike detection: what should the computer imitate? Electroencephalogr Clin Neurophysiol. 1993;87:364–73. doi: 10.1016/0013-4694(93)90149-p. [DOI] [PubMed] [Google Scholar]
- Wilson S, Harner R, Duffy F, Tharp B, Nuwer M, Sperling M. Spike detection. I. Correlation and reliability of human experts. Electroencephalogr Clin Neurophysiol. 1996;98:186–98. doi: 10.1016/0013-4694(95)00221-9. [DOI] [PubMed] [Google Scholar]
- Wongpakaran N, Wongpakaran T, Wedding D, Gwet KL. A comparison of Cohen’s Kappa and Gwet’s AC1 when calculating inter-rater reliability coefficients: a study conducted with personality disorder samples. BMC Med Res Methodol. 2013;13:1. doi: 10.1186/1471-2288-13-61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi SKM, Steyvers M, Lee MD, Dry MJ. The wisdom of the crowd in combinatorial problems. Cogn Sci. 2012;36:452–70. doi: 10.1111/j.1551-6709.2011.01223.x. [DOI] [PubMed] [Google Scholar]
- Zou H, Hastie T. Regularization and variable selection via the elastic net. J Roy Stat Soc B. 2005;67:301–20. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


