Radiobiological issues in proton therapy

Abstract

Background

The relative biological effectiveness (RBE) for particle therapy is a complex function of particle type, radiation dose, linear energy transfer (LET), cell type, endpoint, etc. In the clinical practice of proton therapy, the RBE is assumed to have a fixed value of 1.1. This assumption, along with the effects of physical uncertainties, may mean that the biologically effective dose distributions received by the patient may be significantly different from what is seen on treatment plans. This may contribute to unforeseen toxicities and/or failure to control the disease.

Variability of Proton RBE

It has been shown experimentally that proton RBE varies significantly along the beam path, especially near the end of the particle range. While there is now an increasing acceptance that proton RBE is variable, there is an ongoing debate about whether to change the current clinical practice.

Clinical Evidence

A rationale against the change is the uncertainty in the models of variable RBE. Secondly, so far there is no clear clinical evidence of the harm of assuming proton RBE to be 1.1. It is conceivable, however, that the evidence is masked partially by physical uncertainties. It is, therefore, plausible that reduction in uncertainties and their incorporation in the estimation of dose actually delivered may isolate and reveal the variability of RBE in clinical practice. Nevertheless, clinical evidence of RBE variability is slowly emerging as more patients are treated with protons and their response data are analyzed.

Modelling and Incorporation of RBE in the Optimization of Proton Therapy

The improvement in the knowledge of RBE could lead to better understanding of outcomes of proton therapy and in the improvement of models to predict RBE. Prospectively, the incorporation of such models in the optimization of intensity-modulated proton therapy could lead to improvements in the therapeutic ratio of proton therapy.

Introduction

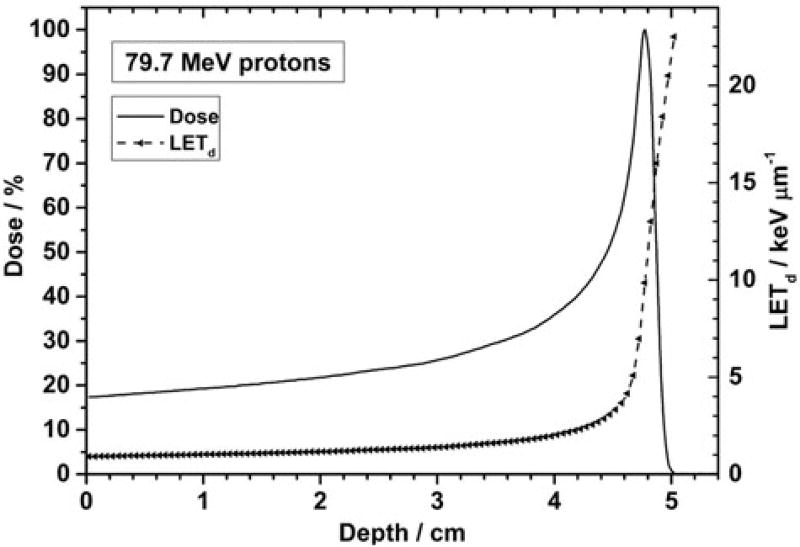
Biological properties of positively charged particles (ions) stem from their physical properties. As particles of a given energy of therapeutic interest traverse a medium, they lose energy continuously. The rate of energy loss per unit distance, i.e., the linear energy transfer (LET, defined mathematically as dE/dx), increases first slowly and linearly and then very sharply near the end of the particle range (Figure 1 [1]). Increasing LET also leads to increasing ionization density along the particle track, which, in turn, leads to increasing amount and complexity of biological damage. The relative biological effectiveness (RBE) of a particle is defined as the ratio of reference radiation dose to the particle dose required for the same biological damage. Most frequently, the reference radiation is chosen to be therapeutic photons; though there is some variability in biological effectiveness among photons of different nominal energies. (See publication by Paganetti [2] and references cited therein for additional details on proton RBE.)

Figure 1.

Depth-LET and depth-dose (Bragg) curves for a 79.7 MeV monoenergetic 20 cm × 20 cm scanned proton beam. The LET increases slowly up to about one cm before the Bragg peak and steeply at points beyond the peak. Reproduced from Guan et al. [1]

RBE is a complex function of numerous variables, which include radiation type, dose, fractionation, LET, tissue or cell type (alpha-beta ratio), biologic endpoint of interest, etc. While the RBE for radiotherapy with ions heavier than protons is accepted to have such functional dependence, for proton therapy the RBE has been, and still generally continues to be, assumed to have a fixed value of 1.1. This assumption is based on the average of data derived from historical experiments performed under limited conditions and almost entirely for clonogenic cell survival [3]. As described later in this article, recent experiments show that RBE may vary significantly along the proton beam path, especially near the end of the particle range [4]. RBE variability, along with other uncertainties in dose distributions, may mean that the biologically effective dose distributions received by the patient may be significantly different from what is seen on treatment plans and used to make treatment decisions. This may contribute to unforeseen toxicities [5,6] and/or failures to control the disease.

The following sections provide an overview of current thinking with regard to proton RBE giving examples of ongoing research, describing the need for future research and highlighting the need to improve our understanding of this important topic in order to translate the resulting new knowledge into the clinical practice of proton therapy.

Relative biological effectiveness of protons as a function of physical parameters

Paganetti has summarized the relationship between proton RBE vs. dose, LET and biological endpoints relevant to tumor control and normal tissue complications as well as cellular damage and repair [3]. Paganetti’s summary is based on the analyzes of large amounts of experimental in-vitro and in-vivo data and finds that, on average, RBE for cell survival at the center of a typical spread-out Bragg peak (SOBP) is ~1.15 at 2 Gy/fraction. The RBE increases with increasing dose-averaged LET (LET_d) in an SOBP from ~1.1 in the entrance region, to ~1.35 at the distal edge and to ~1.7 in the distal fall-off when averaged over all cell lines. Paganetti’s analyses also found that the RBE increases with decreasing α/β and, in general, with decreasing dose. Uncertainties in data were found to be large, leading to the conclusion that the best estimate of average proton RBE is 1.1.

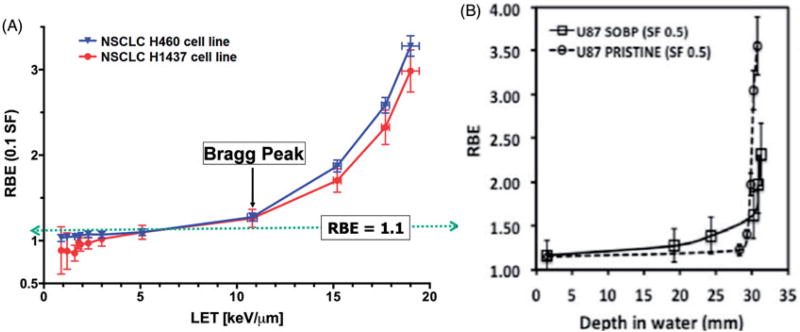
Recent high-precision in-vitro experiments, carried out using monoenergetic protons, confirm the variability of RBE and indicate that the RBE increases from approximately 1.0 at the entrance into the tissue to approximately 1.3 to 1.4 at the Bragg peak. As shown in Figure 2(A), substantially higher values of the order of 4 may occur in distal fall-off regions. Similarly high [4] values have been reported by Chaudhary et al., as shown in Figure 2(B) [7].

Figure 2.

(A) Measured RBE for 10% surviving fraction of non-small cell lung cancer (NSCLC) H460 and H1437 cells as a function of LET for a monoenergetic 79.7 MeV scanned proton beam. The RBE values are lower than 1.1 for low LET values at the entrance of the beam in the medium and increase linearly up to the Bragg peak, and then rapidly and non-linearly at points beyond the Bragg peak. Reproduced from Guan et al. [4] (B) Relative biological effectiveness as a function of depth along monoenergetic and modulated 62-MeV proton beams for the radioresistant glioma U87 cells. RBE values are relative to 225 kVp x-rays using proton alpha and beta values obtained by the linear quadratic model. Reproduced from Chaudhary et al. [7]

Large uncertainties in the past biological data are attributable to multiple factors. These include inconsistencies in experimental design; measurements in the SOBPs of different widths and maximum ranges, which meant that LET spectra were different for different experiments; differences in reference radiation; inconsistencies in the biological assays performed; etc. In fact, even in high precision experiments with monoenergetic beams, physical factors such as dose and LET values in high gradient regions are subject to uncertainty. These data are calculated using Monte Carlo simulations [8], but there is a dearth of accurate basic cross-sections data at low energies where the LET and RBE are high.

With regard to in-vivo data, the work of Slabbert et al. [9] is an excellent example. They conducted ex-vivo experiments by irradiating mice jejunum at multiple positions in an SOBP of 200 MeV protons and have shown that the RBE relative to Co-60 increases to 1.25 near the end of the SOBP. However, to our knowledge, there are no reports of high precision in-vivo experiments with monoenergetic beams and in the distal fall-off regions. Such experiments are challenging to perform in part due to the difficulty of positioning the tissues to be irradiated accurately in regions of high dose and LET gradients.

In general, it has not been practical to accumulate sufficient data for biological response endpoints of interest other than the clonogenic cell survival. Thus, there is substantial room for further study.

Clinical evidence

As mentioned earlier, an argument has been made that there is no definitive clinical evidence that the tradition of proton RBE of 1.1 should be abandoned. However, in clinical practice, out of concern for risk of injury to normal tissues just beyond the distal edge, certain beam directions are avoided or the beams are stopped just proximal to the normal tissue at risk. These approaches are adopted in part because of the uncertainty in the range of protons and in part due to uncertainty in RBE. However, such practices may limit the true potential of proton therapy.

Increasingly, however, there are reports of unforeseen recurrences and toxicities observed in the use of proton therapy. While there may be multiple contributing factors involved in such failures, the assumption of RBE of 1.1 may be among the most significant. As mentioned above, clear evidence of clinical consequences may often be obscured by physical sources of uncertainty. Such sources include inter- and intra-fractional anatomy and setup variations and approximations in computed dose distributions. Regardless, as the number of patients treated with protons increases, evidence of clinical consequences is accumulating [5,6,10,11]. Prompted by increasing concern that pediatric patients receiving proton therapy are at a higher than anticipated risk for radiation induced brain necrosis, a research workshop (Proton Radiation Therapy for Children: Caveats and Opportunities), co-hosted by the Children’s Oncology Group and the National Cancer Institute, was held in May 2016. It was noted that proton therapy practitioners, realizing the potential for increased adverse effects, namely radiation necrosis, which can have profound clinical consequences [10], have reduced prescription doses, opting to accept the potential for compromised disease control.

There are other examples of reports of significant serious neurological toxicities for patients treated with proton therapy. (See, for instance, Weber et al. [12] and Mizumoto et al. [13]). However, few have attempted to systematically characterize differences in outcomes between patients treated with proton and photon therapies.

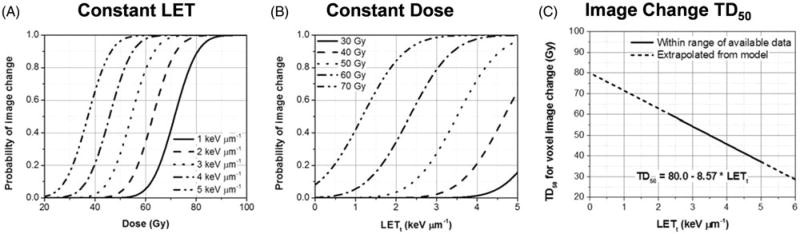
One of the few examples is that of Gunther, et al. [5], who compared rates of post-radiotherapy changes in MR images in pediatric ependymoma patients treated with photon and proton therapy. Imaging changes may serve as a biomarker of differential damage between protons and photons. Gunther, et al retrospectively analyzed the data for seventy-two patients with non-metastatic intracranial ependymoma who received postoperative radiotherapy (37 proton therapy, 35 intensity-modulated radiotherapy). Of the proton therapy patients, 43% developed post-radiation MRI changes at 3.8 months (median) with resolution by 6.1 months. In contrast, 17% of IMRT patients developed changes at 5.3 months (median) with 8.3 months to resolution. In general, the grade and incidence of image intensity changes was found to be greater for protons than for photons. Peeler, et al. [6] further analyzed the data for the same proton therapy cohort in order to determine if the image changes were associated with higher LET and hence higher biological effectiveness of protons compared to the assumed RBE of 1.1. Figure 3(A) shows the probability of image changes as a function of dose for a set of constant values of LET and 3(B) shows the changes as a function of LET for a set of constant dose values. Figure 3(C) depicts the dose for 50% probability of change in image voxel intensity (denoted as TD50) as a function of LET. These figures suggest that increased LET contributes to a higher incidence of imaging changes within the brain tissue, indicative of radiation damage and an increased biological effectiveness.

Figure 3.

Image change predictions of an analytical model fitted with clinical MR image response data. Voxel image change probability is displayed as a function of dose for constant LET values in panel A, and as a function of LET for constant dose values in panel B. Panel C shows physical dose that produces 50% probability of image change in voxels (“TD50”) as a function of LET calculated using the image change predictive model derived from clinical image response data. The equation for the fit of TD50 versus track-averaged LET (LET_t) is also shown. Reproduced from Peeler et al. [6]

Modelling of RBE

Predictive models of biological effect can be highly valuable for not only evaluating the potential clinical efficacy of proton dose distributions and for comparing competing dose distributions but also for use in the optimization of treatment plans. It is important that the predictions of such models be clinically useful even if they are only approximate and not absolute. Models are crucial for optimizing dose distributions to maximize the biological effect (cell kill) within the tumor target for the same physical dose and to minimize the biological damage outside (see next section).

Proton RBE models may be simple to very complex. In fact, for protons, RBE = 1.1 may be considered to be the simplest of the models. At the next level, Jones et al. have suggested using RBE of 1.0 for tumors and 1.2 (or higher) for late reacting normal tissues, implicitly offering higher biologically effective dose to the tumors and greater protection for critical normal tissues [14]. Furthermore, Unkelbach, et al have used a model of the type (A + B * dose * LET) as a surrogate of the proton biological effect [15].

Numerous analytical phenomenological models have also been developed for protons and heavier ions. Many of them were incorporated into a Monte Carlo simulation system by Polster, et al and are summarized in the reference cited [16]. Some of these models are based on the use of proton LET; whereas others are based on more fundamental quantities such as DNA double strand break induction, frequency-mean specific energy, lineal energy or track structure. Most of them rely on the linear quadratic (LQ) function of cell survival to define RBE as:

$$\mathit{\text{RBE}}(D_p,{\mathrm{\alpha }}_x,{\mathrm{\beta }}_x,{\mathrm{\alpha }}_p,{\mathrm{\beta }}_p)=\frac{D_x}{D_p}=\frac{\sqrt{{\mathrm{\alpha }}_x^2+4{\mathrm{\beta }}_x{D}_p({\mathrm{\alpha }}_p+{\mathrm{\beta }}_p{D}_p)}-{\mathrm{\alpha }}_x}{2{\mathrm{\beta }}_x{D}_p}$$

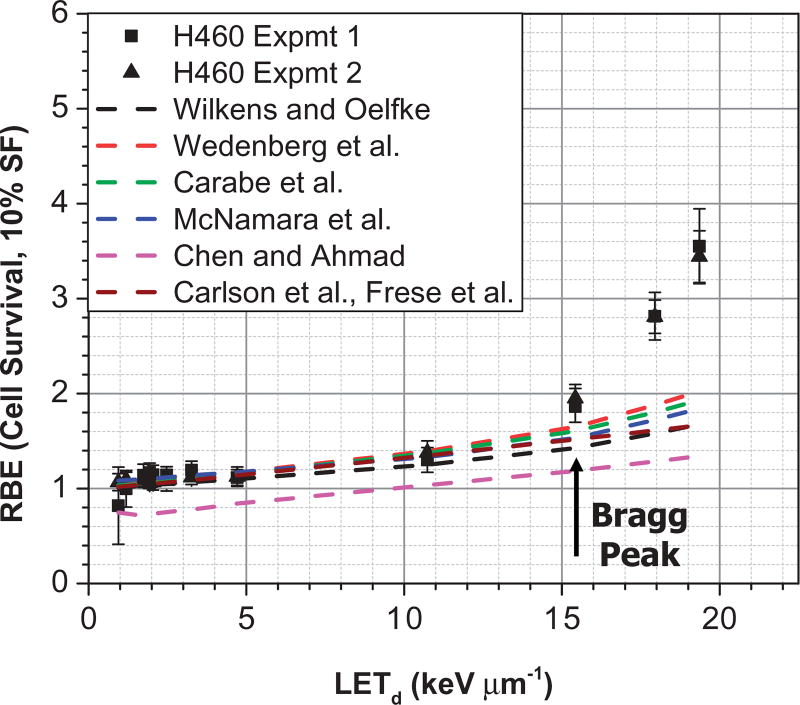
Where subscripts x and p denote reference x-ray and proton quantities respectively. These models express proton α_p and β_p parameters as functions of dose, LET, α_x and β_x. Figure 4 compares the measured H460 lung cancer cell survival data of Guan et al. [4] vs. calculations using seven different models (Wilkens and Oelfke [17], Wedenberg et al. [18], Carabe-Fernandez et al. [19], McNamara et al. [20], Chen and Ahmad [21], and RMF [16,22,23]). Although these models are more advanced in that proton RBE increases as a function of LET, they are not able to explain the high non-linearity of RBE that has been observed in pre-clinical studies at higher LET at points beyond the Bragg peak. Such non-linearity may be due to the increased complexity of double strand breaks at higher LETs. Research is in progress to ascertain if this, indeed, is the case, and efforts to develop novel models are ongoing. We note that in the field of heavy ion therapy, advanced models, such as the local effect model (LEM) [24,25] and the micro-dosimetric kinetic model (MKM) [26,27], have been developed. They are also being adapted and evaluated to explain the observed non-linearity of proton RBE in the distal edge.

Figure 4.

Comparison of measured and model-predicted RBE values as a function of LET_d for the H460 lung cancer cell line. Predicted RBE values were computed using seven models of Wilkens and Oelfke, Wedenberg et al., Carabe-Fernandez et al., McNamara et al., Chen and Ahmad, and RMF, which are cited in the text. All models predict RBE to be essentially a linear function of LET, especially up to the Bragg peak. (C. Peeler, MD Anderson Cancer Center, unpublished.).

A common criticism of all models is their associated uncertainties and the clinical relevance of their predictions. Some of this criticism is related to the biological effects while some other concerns are related to uncertainties in physical parameters. With regard to the latter, as mentioned above, calculating dose and LET values in the high gradient regions with sufficient accuracy is challenging. In addition, the biological effect depends on the LET spectrum not just the averaged LET (dose or track-averaged) [7,28]. The spectrum is asymmetric and becomes increasingly broad as a function of depth. Theoretically, the high LET portion of the LET spectrum would cause more damage than the low LET portion for the same dose deposited. It is plausible, therefore, that models that use averaging of the LET spectrum may underestimate the biological effect. This would especially be the case in regions in which high energy as well as very low energy protons each contribute substantial dose.

Incorporation of variable RBE and LET in the optimization of proton therapy

The central rationale for using protons (and heavier ions) is the characteristic Bragg curve. The low entrance dose and sharp distal falloff can be used to design treatment plans that have greater differential between the target dose and doses to the surrounding normal tissues than in photon treatments. Variable RBE-weighted dose at the Bragg peak may be additionally 30–40% higher than the entrance dose compared to the assumption of RBE of 1.1. Therefore, the incorporation of variable RBE in the treatment planning process should, in principle, lead to an even greater differential between target and normal tissue biologically effective doses. Intensity-modulated proton therapy (IMPT) is just the right tool to achieve such a differential. It is, by far, the most effective approach to optimize proton therapy dose distributions. Intensities of beamlets of each of a set of beams are optimized using sophisticated mathematical algorithms to optimally balance high tumoricidal dose while maintaining doses to normal tissues below tolerance limits. IMPT, with its ability to manipulate the intensities of individual beamlets, can tailor dose distributions in such a way as to direct protons with higher biological effectiveness into the tumor target and away from critical normal tissues. This is in sharp contrast to the most commonly used existing treatment planning techniques, including passively scattered proton therapy as well as scanning beam treatments employing single field uniform dose optimization. In these techniques, the high LET protons of the beams are invariably placed in normal tissues just distal to the target volume.

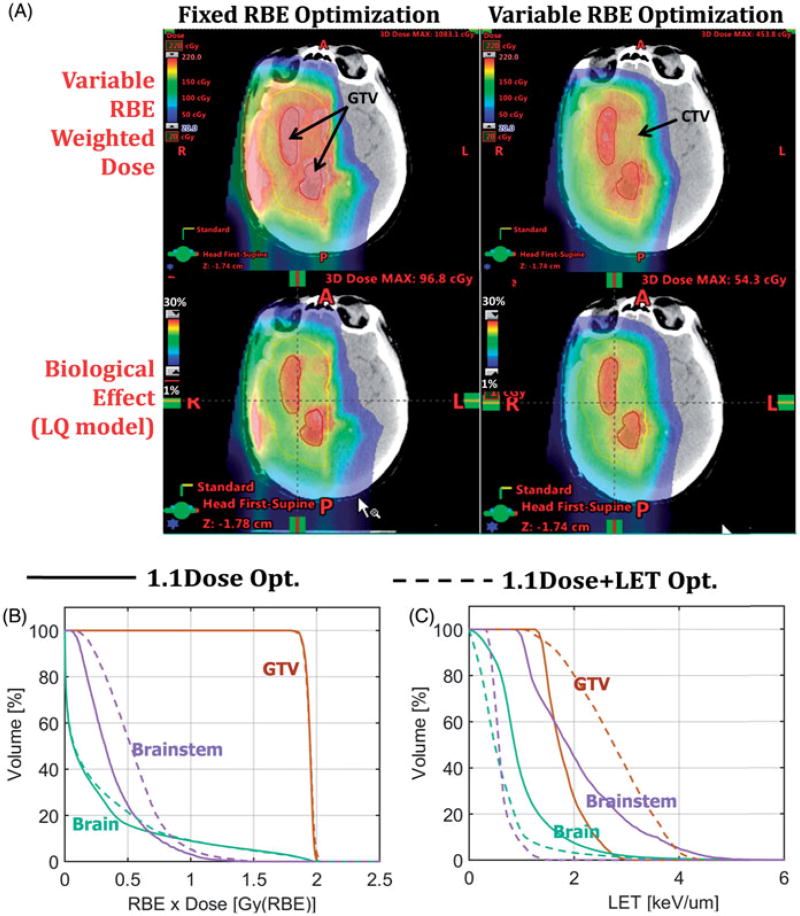
In order to achieve greater differential in biologically effective tumor and normal tissue doses, one strategy is to perform IMPT optimization based on criteria defined in terms of the biological effect as proposed by Wilkens and Oelfke [29]. The biological effect may be defined as the exponent of the LQ model. Figure 5(A) is an illustrative example. An alternative approach is to optimize RBE-weighted dose computed using a variable RBE model as proposed by Horcicka et al. [30] in carbon ion therapy optimization. Both these approaches have been shown to produce nearly identical results.

Figure 5.

(A) Comparison of a glioblastoma IMPT plan optimized using criteria defined in terms of fixed RBE (RBE = 1.1) vs. the plan optimized using criteria defined in terms of variable RBE. The variable RBE was computed using the Wilkens and Oelfke model [17]. The top two panels display dose distributions in terms of variable RBE-weighted dose whereas the bottom two panels display biological effect in terms of (1-surviving fraction) calculated using the linear-quadratic model. Panels (B) and (C) compare a pediatric brain tumor IMPT plan optimized based on criteria defined in terms of RBE 1.1-weighted dose vs. a plan based on the same criteria plus additional terms that control LET in the target and normal structures. Panel (B) compares the RBE 1.1-weighted DVHs for the GTV, brainstem and normal brain, whereas panel (C) compares the corresponding LET-volume histograms. This figure demonstrates that significant increases in LET values in the tumor and significant reduction in normal structures is possible. Of course, the achievable biological effect gain depends on the geometric configuration of anatomic structures and may necessitate tradeoffs. (W. Cao, MD Anderson Cancer Center, unpublished.).

Another strategy to maximize the biological effect differential is to base the optimization criteria defined in terms of dose*LET. This approach has been shown to reduce LET in critical normal tissues [15]. It is favored by some relative to the use of variable RBE models because of the high uncertainties in RBE and the importance of providing the physician with physical data that can be calculated accurately.

Yet another approach being investigated to explicitly control LET within the target and normal tissues is to define the optimization criteria in terms of RBE-weighted dose plus terms that can control LET in the target volume and individual normal tissues. The RBE may be 1.1 or variable. Relative weights of components of the criteria can be used to adjust the dose and LET tradeoffs among individual structures. Figures 5(B,C) show preliminary results illustrating the potential of this approach. We note that Bassler et al. [31,32] have shown that LET painting for heavy ions may lead to improved tumor control probability (TCP) for hypoxic tumors and lower normal tissue complication probabilities (NTCPs). However, the work of Malinen and Sovik [33] suggests that dose painting results in higher TCP than LET painting, especially for protons; but that combined dose and LET painting leads to a modest increase in TCP.

Regardless of how the IMPT is optimized, the dose distributions may be examined either in terms of RBE = 1.1 or using one or more of the variable RBE models. Since the current practice is RBE of 1.1, if the variable RBE or LET-based approach is found to produce a potentially beneficial dose distribution, it may be normalized so that the dose and dose-volume constraints are met in the RBE = 1.1 domain.

Summary

In contrast with the field of heavy ion therapy, where RBE variability is taken for granted and accounted for in clinical practice, for proton therapy there is a reluctance to adopt variable RBE for routine clinical treatments. In support of the use of a static RBE of 1.1, many cite uncertainties in biologic data along with a lack of clinical data supporting variable RBE. However, newly emerging in-vitro data along with preliminary clinical data increasingly support that RBE varies in a complex manner as a function of dose, LET and other factors.

We reiterate that improved understanding of biological effects of protons is essential for more effective interpretation of clinical response to proton therapy. Incorporating the improved knowledge in the optimization of IMPT plans is equally important to make this powerful technology truly effective. However, many challenges remain. There is a need to conduct a wide array of biology experiments to acquire additional in-vitro and in-vivo data for appropriate ranges of dose and LET values and to model the results. Moreover, the analyses of clinical response data with accurately estimated dose distributions delivered to the patients can produce additional clinically relevant biological effect information. Such information, combined with the laboratory data, should lead to the development of clinically relevant models, which are essential for increasing the biological effectiveness of protons.

The number of proton therapy centers is increasing seemingly exponentially. As such, the number of patients treated with proton therapy is expected to increase dramatically. If RBE in patients treated with proton therapy is, in fact, variable, using current treatment planning techniques we may see not only inferior disease control outcomes but higher rates of normal tissue toxicity. Conversely, if through the conduct of controlled, high accuracy experiments we are better able to describe and model the biologic effects of proton beams, we may be able to incorporate this into the treatment planning process, which should improve the therapeutic index. Remarkably, in contrast to the development of novel biologic agents, etc., for proton therapy this may be expected to occur on the time scale of years vs. decades.