Wavefront shaping with disorder-engineered metasurfaces

Abstract

Recently, wavefront shaping with disordered media has demonstrated optical manipulation capabilities beyond those of conventional optics, including extended volume, aberration-free focusing and subwavelength focusing. However, translating these capabilities to useful applications has remained challenging as the input-output characteristics of the disordered media (P variables) need to be exhaustively determined via O(P) measurements. Here, we propose a paradigm shift where the disorder is specifically designed so its exact input-output characteristics are known a priori and can be used with only a few alignment steps. We implement this concept with a disorder-engineered metasurface, which exhibits additional unique features for wavefront shaping such as a large optical memory effect range in combination with a wide angular scattering range, excellent stability, and a tailorable angular scattering profile. Using this designed metasurface with wavefront shaping, we demonstrate high numerical aperture (NA > 0.5) focusing and fluorescence imaging with an estimated ~2.2×10⁸ addressable points in an ~8 mm field of view.

Wavefront shaping can be best described as a class of methods that allow control of a very large number of optical degrees of freedom, ranging up to hundreds of thousands¹. This sets it apart from the regime of wavefront manipulation in adaptive optics where the corrections are typically performed for aberrations modeled by a relatively small number of Zernike orders². As a class of technologies, wavefront shaping is particularly well suited for applications involving disordered media. These applications can be broadly divided into two categories. In the first category, wavefront shaping works to overcome intrinsic limitations of the disordered media. Biological tissue is one such example where scattering is a problem, with wavefront shaping emerging as a solution to produce a shaped light beam that counteracts multiple scattering and enables imaging and focusing deep inside the tissue³.

In the second category, disordered media are intentionally introduced in conjunction with wavefront shaping to unlock an optical space with spatial extent (x) and spatial frequency content (ν) that is inaccessible using conventional optics^4–10. One of the first demonstrations of this ability was reported by Vellekoop et al.⁴, showing that the presence of a disordered medium (e.g. a scattering white paint layer) between a source and a desired focal plane can actually help render a sharper focus. In related efforts, researchers have also shown that wavefront shaping can make use of disordered media to couple propagating and evanescent modes, in turn enabling near-field focusing^6,7. Recently, there have been more extensive demonstrations combining disordered media with wavefront shaping to increase the flexibility of the optical system to, for example, significantly extend the volumetric range in which aberration-free focusing can be achieved^8–10 or generate co-localized, thin light sheets at several wavelengths¹¹.

Unfortunately, this class of methods is stymied by one overriding challenge – the optical input-output response of the disordered medium needs to be exhaustively characterized before use^10,12–15. Fundamentally, characterizing P input-output relationships of a disordered medium requires O(P) measurements. For most practical applications, P greater than 10¹² is highly desired to enable high fidelity access to the expanded optical space enabled by the disordered media with wavefront shaping. Unfortunately, the time-consuming nature of the measurements and the intrinsic instability of the vast majority of disordered media have limited the ability to achieve high values of P. To date, the best P quantification that has been achieved is ~10⁸ with a measurement time of 40 seconds¹². We also note, although there have been several computational imaging methods proposed to exploit disordered media for enhanced imaging resolution and field of view (FOV) without such characterization^16,17, their range of applications is much narrower as they do not enable active manipulation of the optical field.

In this paper, we report the use of a disorder-engineered metasurface (we call this a disordered metasurface for brevity) in place of a conventional disordered medium. The disordered metasurface provides the optical ‘randomness’ of conventional disordered media, but in a way that is fully known a priori. We note that this approach is conceptually different from previous techniques aimed at engineering disordered media^11,18–21 (e.g. Engineered Diffusers^™ from RPC Photonics) since the disordered metasurface enables the individual input-output responses rather than the statistical properties of the scattered light pattern to be engineered. With this approach, we reduce the system characterization to a simple alignment problem.

In addition to eliminating the need for extensive characterization measurements, the disordered metasurface has unique physical properties that make it useful for wavefront shaping. First, it should be emphasized that the scattering mechanism of the disordered metasurface is fundamentally different from that of a conventional disordered medium. In contrast to a conventional disordered medium (e.g. a several micron thick layer of Zinc Oxide particles or a ground glass diffuser) that has three-dimensional optical inhomogeneity (i.e. the thickness of the scattering medium is much larger than the optical wavelength), the disordered metasurface is composed of a two-dimensional array of subwavelength scatterers of uniform height. These subwavelength scatterers are realized by high refractive index contrast, dielectric nanoposts which act as truncated multimode waveguides²² supporting low quality factor Fabry-Perot resonances. Consequently, the metasurface platform exhibits useful properties for wavefront shaping such as high transmittance and a very large angular (tilt/tilt) correlation range due to the low angular sensitivity of the nanoposts’ resonances²³. The large transmittance and angular correlation range, which are typically coupled with the thickness and angular scattering profile of a scattering medium, are independent features in the metasurface platform. Moreover, the metasurface platform also offers excellent stability and the capability to tailor the light scattering profile.

Using this disorder-engineered metasurface platform, we demonstrate control over P = 1.1×10¹³ input-output relationships after a simple alignment procedure. To demonstrate this new paradigm for controllably exploiting optical ‘randomness’, we have implemented a disordered metasurface assisted focusing and imaging system that is capable of high NA focusing (NA ≈ 0.5) to ~2.2×10⁸ points in a FOV with a diameter of ~8 mm. In comparison, for the same FOV, a conventional optical system such as an objective lens can typically at most access one or two orders of magnitude fewer points.

Principles

The relationship between the input and output optical fields traveling through a disordered medium¹⁵ can be generally expressed in discretized form as

$$E_o=T{E}_i,$$ (1)

where E_i is the field vector at the input plane of the medium, E_o is the field vector at the output projection plane behind the medium, and T is the transmission matrix connecting the input field vector E_i with the output field vector E_o on the other side of the disordered medium. In the context of addressable focal spots with disordered medium assisted wavefront shaping, E_o is a desired focusing optical field, E_i is the linear combination of independent optical modes controlled by the spatial light modulator (SLM), and T is the transmission matrix, where each element describes the amplitude and phase relationship between a given input mode and output focal spot. In this scenario, E_i has a dimension of N, the number of degrees of freedom in the input field (i.e. the number of SLM pixels), E_o has a dimension of M given by the number of addressable spots on the projection plane, and T is a matrix which connects the input and output fields with P elements, where P = M × N (see Methods for computation details). We note that the following concepts and results can be generalized to other applications (e.g. beam steering or optical vortex generation) simply by switching E_o to an appropriate basis set.

One of the unique and most useful aspects of wavefront shaping with disordered media is that it allows access to a broader optical space in both spatial extent and spatial frequency content than the input optical field can conventionally access. For example, when an SLM is used alone, the generated optical field E_i contains a limited range of spatial frequencies due to the large pixel pitch of the SLM (ν_x or ν_y ≤ 1/(2d_SLM) where ν_x and ν_y are spatial frequency contents along the transverse axes of the SLM and d_SLM is the pixel pitch; typically ~10 μm). As a consequence, the number of addressable spots M is identical to the number of controllable degrees of freedom N. In contrast, when a disordered medium is placed in the optical path, its strongly scattering nature generates an output field E_o with much higher spatial frequencies given by $\sqrt{{\mathrm{\nu }}_x^2+{\mathrm{\nu }}_y^2}\le 1/\lambda$, where λ is the wavelength of the light. According to the space-bandwidth product formalism²⁴, this means that the number of addressable focal spots M within a given modulation area S is maximally improved to

$$M=S\times \frac{\pi }{{\lambda }^2}.$$ (2)

The scheme for focusing with disordered medium assisted wavefront shaping can be understood as the process of combining N independent optical modes to constructively interfere at a desired position on the projection plane^4,25,26. In general, due to the increased spatial frequency range of the output field, the number of addressable spots M is much larger than the number of degrees of freedom in the input, N, and therefore the accessible focal spots on the output plane are not independent optical modes (see Supplementary Note 1). Instead, because the transmission through the metasurface can be described as a linear transformation of N input basis vectors, the number of degrees of freedom at the output plane (i.e. the number of orthogonal patterns at the output plane) remains the same as at the input plane. More specifically, when the incident wavefronts for M different spots are transmitted through the metasurface, each focal spot exists on top of a background which contains the correlated contributions from the unoptimised optical modes in the output field, thus resulting in a maximum of N degrees of freedom at the output plane. Here the contrast η, the ratio between the intensity transmitted into the focal spot and the surrounding background, is dictated by the number of controlled optical modes in the input, N²⁵. In practical situations where, for instance, the addressable spots are used for imaging or photo-switching, the contrast η simply needs to be sufficiently high to ensure the energy leakage does not harmfully compromise the system performance. In such applications, the addressable spots can also be described as resolvable spots. Henceforth, we use these terms interchangeably, depending on whether we are discussing the physics or the specific imaging applications.

To maximize performance in imaging applications, we can see it is desirable to have as many resolvable spots as possible, each with high contrast. This means that both M and N, and in turn P, should be as high as possible. Practically, there are two ways to measure the elements of the transmission matrix – orthogonal input probing and output phase conjugation (see Supplementary Note 2). In each case, an individual measurement corresponds to a single element in the transmission matrix and is accomplished by determining the field relationship between an input mode and a location on the projection plane. Both still necessitate O(P) measurements which, when P is large, leads to a prohibitively long measurement time. As a point of reference, if the fast transmission matrix characterization method reported in ref. ¹² could be extended without complications, it would still require a measurement time of over 40 days to characterize a transmission matrix with P = 10¹³ elements. In comparison, the stability associated with most conventional disordered media is only several hours^25,27,28.

In contrast, our disordered metasurface avoids the measurement problem altogether since all elements of the transmission matrix are known a priori. This means that now the procedure to calibrate the system is simplified from the O(P) measurements needed to determine the transmission matrix to the small number of steps required to align the disordered metasurface and the SLM.

A schematic illustration of the technique is presented in Fig. 1 with the omission of a 4-f imaging system optically conjugating the SLM plane to the disordered metasurface. An SLM structures a collimated incident beam into an optimal wavefront which in turn generates a desired complex output wavefront through the disordered metasurface. Since the transmission matrix is known a priori, the process to focus to a desired location is a simple computation. The optimal incident pattern $E_i^{\text{opt}}$ that encodes the information for a target field $E_o^{\text{target}}$ is calculated using the concept of phase conjugation (see Methods). This approach enables us to access the maximum possible number of resolvable spots for wavefront shaping for a given modulation area S with the added benefit of control over the scattering properties of the metasurface.

Figure 1. Wavefront shaping assisted by a disorder-engineered metasurface.

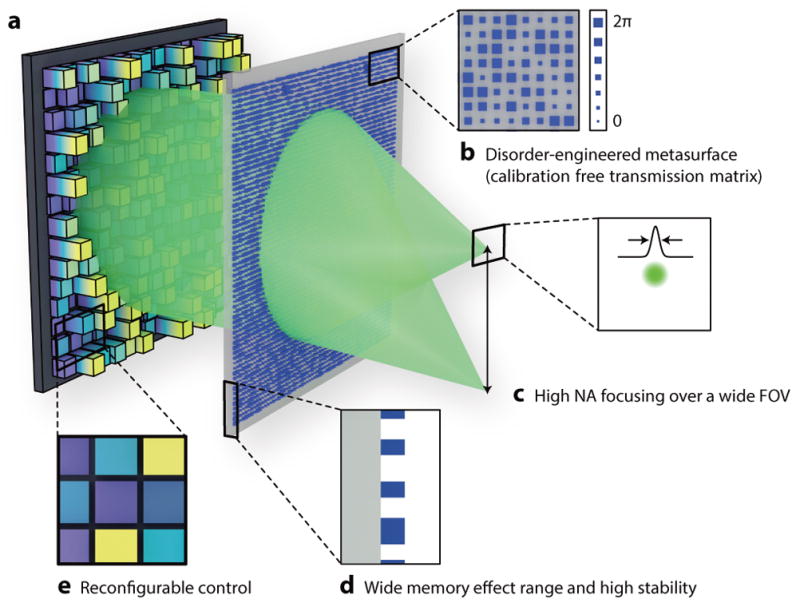
(a) The system setup consists of two planar components, an SLM and a disorder-engineered metasurface. (b) The disorder-engineered metasurface is implemented by fabricating the nanoposts with varying sizes, which correspond to different phase delays ϕ(x,y) on the metasurface. (c) The wide angular scattering range enables high NA focusing over a wide FOV. (d) The thin, planar nature of the disordered metasurface yields a large memory effect range and also makes the transmission matrix of the metasurface extraordinarily stable. (e) The SLM enables reconfigurable control of the expanded optical space available through the disordered metasurface.

Results

The disorder-engineered metasurface

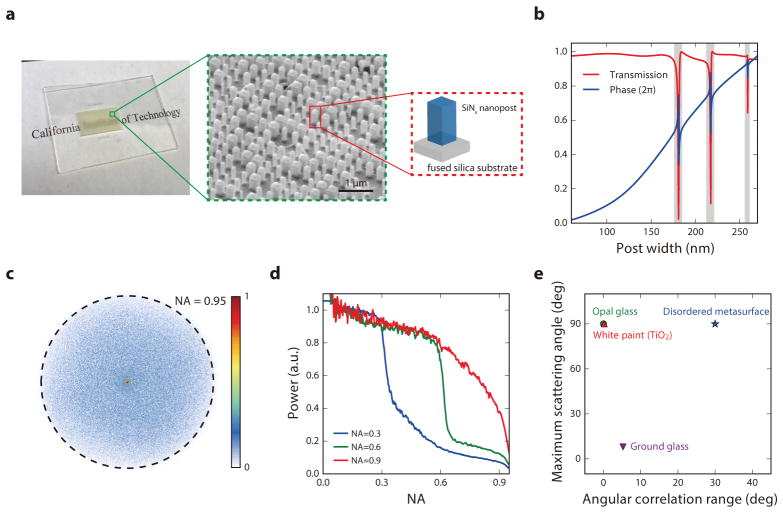
The disordered metasurface platform demonstrated in this study shares the same design principles as the conventional metasurfaces that have been previously reported to implement planar optical components^29–35: subwavelength scatterers or meta-atoms are arranged on a two-dimensional lattice to purposefully shape optical wavefronts with subwavelength resolution (Fig. 2a). The disordered metasurface, consisting of Silicon Nitride (SiN_x) nanoposts sitting on a fused silica substrate, imparts local and space-variant phase delays with high transmission for the designed wavelength of 532 nm. We constrained the design of the phase profile ϕ(x,y) of the metasurface in such a way that its angular scattering profile is isotropically distributed over the maximal possible spatial bandwidth of 1/λ in free space, and then chose the width of the individual nanoposts according to the look-up table shown in Fig. 2b (see Methods). The experimentally measured scattering profile confirms the nearly isotropic scattering property of the disordered metasurface, presenting a scattering profile that fully extends to the spatial frequency of 1/λ as shown in Fig. 2c. The measured transmittance was approximately 50% regardless of the incident pattern. In contrast, it is known that conventional three-dimensional disordered media in the diffusive regime present fluctuations in transmittance, depending on the incident field, because the transmittances of its fundamental transmitting eigenchannels are distributed over a wide range³⁶. The disordered metasurface platform also allows the scattering profile to be tailored, which can be potentially useful in conjunction with angle-selective optical behaviors such as total internal reflection. Figure 2c presents the measured scattering profiles of disordered metasurfaces designed to have different angular scattering ranges, corresponding to NAs of 0.3, 0.6, and 0.9 (see Supplementary Fig. 1 for 2D angular scattering profiles).

Figure 2. Characterization of disorder-engineered metasurfaces.

(a) Photograph and SEM image of a fabricated disorder-engineered metasurface. (b) Simulated transmission and phase of the SiN_x nanoposts as a function of their width at a wavelength of 532 nm. These data are used as a look-up table for the metasurface design. (c) Measured 2D angular scattering profile of the disordered metasurface, normalized to the strongest scattered field component. (d) Measured 1D angular scattering profile of the disordered metasurfaces that were specifically designed to scatter the incident light to certain angular ranges (NA = 0.3, 0.6, 0.9). (e) Memory effect range and angular scattering range of the disordered metasurface compared with conventional random media such as white paint, opal glass, and ground glass diffusers.

In addition to a highly isotropic scattering profile, the disordered metasurface also exhibits a very large angular (tilt/tilt) correlation range (also known as the optical memory effect³⁷). The correlation is larger than 0.5 even up to a tilting angle of 30 degrees (Fig. 2e). In conventional disordered media, the volumetric nature of the media makes it very difficult to achieve a wide angular scattering profile and a large memory effect at the same time due to the competing influence of the thickness of the scattering medium on both of these properties. In contrast, due to the low angular sensitivity of the nanoposts’ resonances²³, the disordered metasurface can simultaneously achieve a broad angular scattering profile and a wide memory effect range. For example, conventional scattering media commonly used for scattering lenses, such as opal glass and several micron-thick Titanium Dioxide (TiO₂) white paint layers, exhibit much narrower correlation ranges of less than 1 degree (Fig. 2e)³⁸. Although ground glass diffusers present a relatively larger correlation range of ~5 degrees, their limited angular scattering range makes them less attractive for wavefront shaping (see Supplementary Fig. 2 for angular tilt/tilt measurement setup and correlation profiles).

Moreover, the disordered metasurface is extraordinarily stable due to its fixed, two-dimensional fabricated structure¹¹. We were able to retain the ability to generate a high quality optical focus from the same metasurface without observable efficiency loss over a period of 75 days by making only minor corrections to the system alignment to compensate for mechanical drift (see Supplementary Fig. 3).

High NA optical focusing over an extended volume

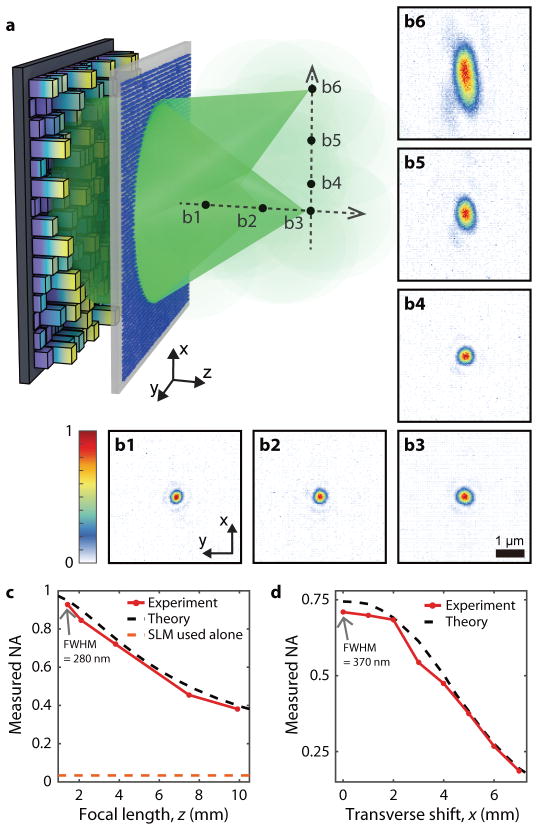
We experimentally tested our wavefront manipulation scheme in the context of disordered medium assisted focusing and imaging. First, we aligned the disordered metasurface to the SLM by displaying a known pattern on the SLM and correcting the shift and tilt of the metasurface to ensure high correlation between the computed and measured output fields (see Methods for details). Next, to demonstrate the flexibility of this approach, we reconstructed a converging spherical wave (see Methods for details) for a wide range of lateral and axial focus positions. Figure 3a presents the simplified schematic for optical focusing (see also Methods and Supplementary Fig. 4 for more details). Figure 3b1–b3 show the 2D intensity profiles for the foci reconstructed along the optical axis at z′ = 1.4, 2.1, and 3.8 mm, measured at their focal planes. The corresponding NAs are 0.95, 0.9, and 0.75, respectively. The full width at half maximum (FWHM) spot sizes of the reconstructed foci were 280, 330, 370 nm, which are nearly diffraction-limited as shown in Fig. 3c. The intensity profiles are highly symmetric, implying that the converging spherical wavefronts were reconstructed with high fidelity through the disordered metasurface. It is also remarkable that this technique can reliably control the high transverse wavevector components corresponding to an NA of 0.95, while the SLM used alone can control only those transverse wavevectors associated with an NA of 0.033, based on the Nyquist-Shannon sampling theorem.

Figure 3. Experimental demonstration of diffraction-limited focusing over an extended volume.

(a) Schematic of optical focusing assisted by the disordered metasurface. The incident light is polarized along the x direction. (b1–6) Measured 2D intensity profiles for the foci reconstructed at the positions indicated in (a). b1–b3 are the foci along the optical axis at z = 1.4, 2.1, and 3.8, mm, respectively, corresponding to NAs of 0.95, 0.9, and 0.75. b3–b6 are the foci at x = 0, 1, 4, and 7 mm scanned on the fixed focal plane of z = 3.8 mm. Scale bar: 1 μm. (c) Measured NA (along x-axis) of the foci created along the optical axis (red solid line) compared with theoretical values (black dotted line). When the SLM is used alone, the maximum accessible NA is 0.033 (orange dotted line), based on the Nyquist-Shannon sampling theorem. (d) Measured NA (along x-axis) of the foci created along x axis at z = 3.8 mm (red solid line) compared with theoretical values (black dotted line). The number of resolvable focusing points within the 14-mm diameter FOV was estimated to be 4.3×10⁸.

Figure 3b4–b6 show the 2D intensity profiles at x′ = 0, 1, 4, and 7 mm on the fixed focal plane of z′ = 3.8 mm (corresponding to an on-axis NA of 0.75). Because the disordered metasurface based scattering lens is a singlet lens scheme, the spot size along the x-axis increased from 370 to 1500 nm as the focus was shifted (summarized in Fig. 3d).

The total number of resolvable spots achievable with the disordered metasurface, M, was estimated to be ~4.3×10⁸ based on the plot in Fig. 3d, exceeding the number of controlled degrees of freedom on the SLM (N~10⁵) by over 3 orders of magnitude. This enables high-NA focusing over a large FOV without the mechanical scanning necessary using conventional objective lenses, demonstrating that the metasurface-assisted platform, as a fixed optical system, can access a wider optical space (represented by x and ν) compared to conventional optics. For the disordered metasurface, an NA of ~0.5 was maintained in a lateral FOV with a diameter of ~8 mm, resulting in an estimated 2.2×10⁸ resolvable focal spots. For the sake of comparison, a high-quality objective lens with an NA of 0.5 typically has ~10⁷ resolvable spots³⁹, an order of magnitude smaller than the number of the spots demonstrated with the disordered metasurface. We note that although the resolvable spots for the objective lens have the additional property that they are independent, as long as the contrast η is high enough to enable a sufficient signal-to-noise ratio, the number of resolvable spots is the appropriate metric of interest, regardless of whether or not they are independent.

With our disordered metasurface platform we control a transmission matrix with a number of elements P given by the product of the number of resolvable focal spots on the output plane and the number of controllable modes in the input. The P we can achieve with our system was 1.1×10¹³ which enabled us to address an estimated ~4.3×10⁸ focal spots with a contrast factor η of ~2.5×10⁴. This value of P is 5 orders of magnitude higher than what has previously been reported¹². These findings testify to the paradigm-shifting advantage that this engineered ‘randomness’ approach brings.

We also experimentally confirmed that even with reduced control over the number of input modes, we can still access the same number of addressable spots on the output projection plane, albeit with a reduced contrast. By binning pixels on the SLM, we reduced the number of controlled degrees of freedom on the SLM by up to three orders of magnitude, from ~10⁵ to ~10², and verified that the capability of diffraction-limited focusing over a wide FOV is maintained (see Supplementary Fig. 5). Although the same number of focal spots can be addressed, the contrast factor η is sacrificed when the number of degrees of control is reduced. Using ~10² degrees of freedom in the input, we achieved a contrast factor of ~70. This validates that the complex wavefront manipulation scheme assisted by the disordered metasurface can greatly improve the number of addressable focal spots for wavefront shaping regardless of the number of degrees of freedom in the input.

Wide FOV fluorescence imaging

Finally, we implemented a scanning fluorescence microscope for high-resolution, wide FOV fluorescence imaging (see Methods, Supplementary Figs 4 and 6 for detailed procedure). Figure 4a presents the wide FOV, low-resolution fluorescence image of immunofluorescence-labeled parasites (Giardia lamblia cysts; see Methods for sample preparation procedures) captured through the 4× objective lens. As shown in the magnified view in Fig. 4b3, a typical fluorescence image directly captured with the 4× objective lens was significantly blurred, so that the shape and number of parasites was not discernible from the image. Figure 4b1, c, and d present the fluorescence images obtained with our scanning microscope. The scanned images resolve the fine features of parasites both near the center and the boundary of the 5-mm wide FOV (Fig. 4d). Our platform provides the capability for high NA focusing (NA ≈ 0.5) within a FOV with a diameter of ~8 mm, as shown in Fig. 3. In addition, the large memory effect range of the metasurface allows us to use galvanometer mirrors to scan the focus without having to refresh the pattern displayed on the SLM, improving acquisition speed compared to using the SLM alone (see Methods for details). To validate the performance of our imaging system, we compared it to conventional 20× and 4× objectives. The captured images in Fig. 4 demonstrate that we can achieve the resolution of the 20× objective over the FOV of the 4× objective.

Figure 4. Demonstration of disordered metasurface assisted microscope for high resolution wide-FOV fluorescence imaging of giardia lamblia cysts.

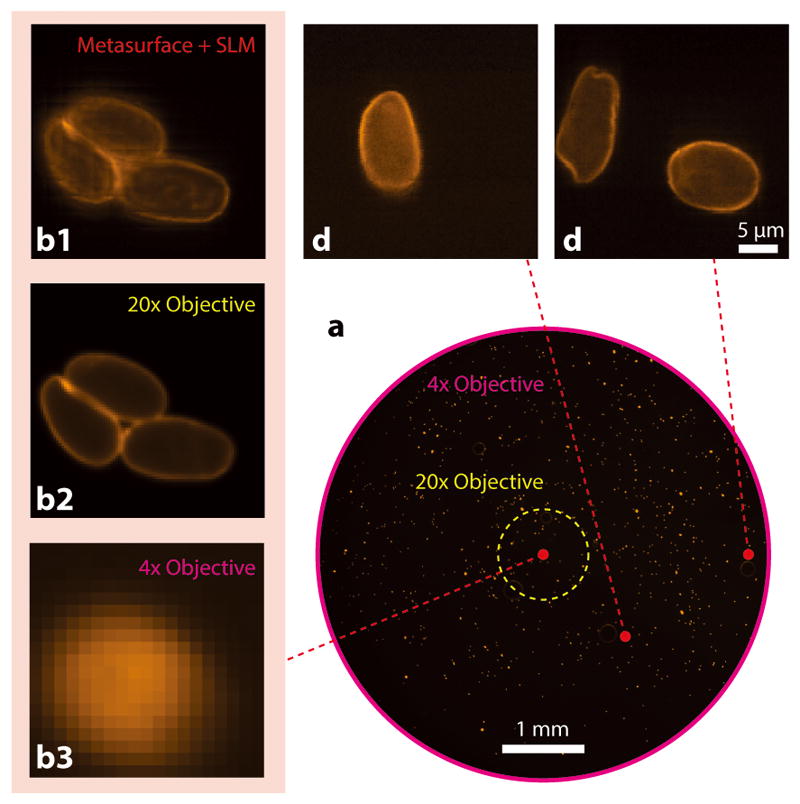
(a) Low resolution bright field image captured by a conventional fluorescence microscope with a 4× objective lens (NA = 0.1). Scale bar: 1 mm. (b1–3) Fluorescence images captured at the center of the FOV. (b1) Scanned image obtained with a disordered metasurface lens. (b2) Ground truth fluorescence image captured with a 20× objective lens (NA = 0.5). (b3) Magnified low-resolution fluorescence image captured with the 4× objective. (c, d) Images obtained with the disorder metasurface-assisted microscope at (x, y) = (1, 1) and (2.5, 0) mm, respectively. This demonstrates that we can indeed use the system for high resolution and wide FOV imaging.

Discussion

Here we have implemented a disorder-engineered medium using a metasurface platform and demonstrated the benefit of using it for wavefront shaping. Our study is the first to propose engineering the entire input-output response of an optical disordered medium, presenting a new approach to disordered media in optics. Allowing complete control of the transmission matrix a priori, the disorder-engineered metasurface fundamentally changes the way we can employ disordered media for wavefront shaping. Prior to this study, to control P input-output relationships through a disordered medium, O(P) calibration measurements were required. In contrast, the disorder-engineered metasurface allows for a transmission matrix with P elements to be fully employed with only a simple alignment procedure.

Although we only demonstrate the reconstruction of spherical wavefronts in this study, our method is, in principle, generally applicable to produce arbitrary wavefronts for applications such as beam steering, vector beam generation, multiple foci, or even random pattern generation (see Supplementary Fig. 7 for experimental demonstrations). We anticipate that the large gain in the number of addressable optical focal spots (or equivalently angles or patterns) enabled by our method could potentially be used to improve existing optical techniques such as fluorescence imaging, optical stimulation/lithography^40,41, free space coupling among photonic chips/optical networks^42,43, and optical encryption/decryption⁴⁴. However, because the metasurface does not fundamentally improve the number of degrees of freedom (N < M), our method is not well suited for applications in which a large fraction of the addressable spots are used simultaneously such as holographic displays. In this scenario, as the contrast η decreases in proportion to the number of target modes in the output plane, the nonzero background would obscure the target pattern.

In the specific application of focal spot scanning, our basic system consisting of two planar components, a metasurface phase mask and a conventional SLM, offers several advantages. The system is highly scalable and versatile, bypassing the limitations and complexities of using conventional objective lenses. The scalability of the metasurface could be especially useful in achieving ultra-long working distances for high NA focusing. The scheme could also be implemented as a vertically integrated optical device together with electronics⁴⁵ (e.g. a metasurface phase mask on top of a transmissive LCD), providing a compact and robust solution to render a large number of diffraction-limited spots. Furthermore, the concept is potentially applicable over a wide range of the electromagnetic spectrum with the proper choice of low-loss materials for the meta-atoms (e.g. SiN_x or TiO₂ for entire visible^33,46 and Si for near infrared wavelengths^31,47–49), which allows for multiplexing different colors, useful for multicolor fluorescence microscopy and multiphoton excitation microscopy. Finally, the planar design provides a platform to potentially achieve ultra-high NA solid-immersion lenses⁵⁰ or total internal reflection fluorescence (TIRF) excitation⁵¹, suitable for super-resolution imaging and single-molecule biophysics experiments.

More broadly speaking, we anticipate the ability to customize the design of the disordered metasurface for a particular application will prove highly useful. For example, we could potentially tailor the scattering profile of the disordered metasurface to act as an efficient spatial frequency mixer or to be exploited for novel optical detection strategies^19,52,53. The disordered metasurface could also potentially serve as a collection lens, analogous to the results obtained for light manipulation, providing an enhanced resolving power and extended view field. Additionally, while the disordered metasurface in our demonstration was designed to be insensitive to the polarization of the incident optical field (see Supplementary Fig. 8), the metasurface platform could be designed independently for orthogonal polarization states, which provides additional avenues for control in wavefront shaping⁵⁴. Together, the engineering flexibility provided by these parameters offers unprecedented control over complex patterned illumination, which offers the potential to directly benefit emerging imaging methods that rely on complex structured illumination^17,55.

To conclude, we explored the use of a disorder-engineered metasurface in wavefront shaping, challenging a prevailing view of the ‘randomness’ of disordered media by programmatically designing its ‘randomness’. The presented technology has the potential to provide a game-changing shift that unlocks the benefits of wavefront shaping, opening new avenues for the design of optical systems and enabling new techniques for exploring complex biological systems.

Methods

Design of disordered metasurface

The disordered metasurface consisted of Silicon Nitride (SiN_x) nanoposts arranged on a subwavelength square lattice with a periodicity of 350 nm as shown in Fig. 2a. The width of each SiN_x nanopost was precisely controlled within a range from 60 nm to 275 nm, correspondingly imparting local and space-variant phase delays covering a full range of 2π with close to unity transmittance for an incident wavefront at the design wavelength of 532 nm (Fig. 2b). The widths of the nanoposts corresponding to the grayed regions in Fig. 2b correspond to high quality factor resonances and are excluded in the design of the disordered metasurface. The phase profile ϕ(x,y) of the disordered metasurface was designed to yield an isotropic scattering profile over the desired angular range using the Gerchberg-Saxton (GS) algorithm. The initial phase profile of the far-field was randomly chosen from a uniform distribution between 0 and 2π radians. After several iterations, the phase profile converged such that the far-field pattern had isotropic scattering over the target angular ranges. This approach helps to minimize undiffracted light and evenly distribute the input energy over the whole angular range.

Fabrication of disordered metasurface

A SiN_x thin film of 630 nm was deposited using plasma enhanced chemical vapor deposition (PECVD) on a fused silica substrate. The metasurface pattern was first defined in ZEP520A positive resist using an electron beam lithography system. After developing the resist, the pattern was transferred onto a 60 nm-thick aluminum oxide (Al₂O₃) layer deposited by electron beam evaporation using the lift-off technique. The patterned Al₂O₃ served as a hard mask for the dry etching of the 630 nm-thick SiN_x layer in a mixture of C₄F₈ and SF₆ plasma and was finally removed by a mixture of ammonium hydroxide and hydrogen peroxide at 80°C.

Alignment procedure

The alignment procedure consisted of two steps to ensure the proper mapping of the SLM pixels onto the intended coordinates of the disordered metasurface. Cross-shaped markers engraved at the four corners of the metasurface were used to guide rough alignment. Then, the marginal misalignments (e.g. translation and tip-tilt) and aberrations induced by the 4-f system were corrected. For this purpose, a collimated laser beam (Spectra-Physics, Excelsior 532) was tuned to be incident on the metasurface and the resulting field was measured with phase shifting holography. The residual misalignments and aberrations were then calibrated by comparing the measured complex field with the calculated one and digitally compensating for the misalignment by adding appropriate correction patterns on the SLM.

Procedure to compute a transmission matrix for optical focusing

The transmission matrix model in our experiments describes the amplitude and phase relationship between each controllable input mode, given as each SLM pixel, and each desired focusing optical field. The calculation of T was carried out in a row by row manner, based on the intrinsic phase profile of the disordered metasurface ϕ(x, y). Setting the position of the focal spot corresponding to m-th row vector as ${\mathit{r}}_m^{\prime }=(x_m^{\prime },y_m^{\prime },z^{\prime })$, the converging spherical wavefront on the plane of metasurface is given as:

$$S_m(x,y)=exp\left[-i\frac{2\pi }{\lambda }\sqrt{{(x-x_m^{\prime })}^2+{(y-y_m^{\prime })}^2+{z^{\prime }}^2}\right],$$

where z′ is the focal length. Then, the corresponding input field on the plane of metasurface was simply given as the product of the spherical wavefront S_m(x, y) and the transmission phase profile of the disordered metasurface (see Design of disordered metasurface in Methods for details):

$$E_m^{\text{meta}}(x,y)=S_m(x,y)\times exp(i\varphi (x,y)).$$

Next, to calculate the input field on the plane of SLM that corresponds to the input field on the plane of metasurface $E_m^{\text{meta}}(x,y)$, a low-pass spatial frequency filter ℒ was applied to $E_m^{\text{meta}}(x,y)$ using a fast Fourier transform algorithm:

$$E_m^{\text{SLM}}(x,y)=\mathcal{L}[E_m^{\text{meta}}(x,y)].$$

Finally, $E_m^{\text{SLM}}(x,y)$ was sampled at positions corresponding to N SLM pixels for discretization, yielding N matrix elements. That is, the discretized complex field composes a row of the transmission matrix T that relates all controllable input modes to a given focal spot on the projection plane.

The optimal incident field $E_i^{\text{opt}}$ that reconstructs the target field $E_o^{\text{target}}$ (either of a single spot or a pattern composed of multiple spots) was calculated using

$$E_i^{\text{opt}}=T^{†}{E}_o^{\text{target}}$$

where † represents the conjugate transpose. In the actual experiment, we used an SLM (Pluto, Holoeye) for phase-only reconstruction of the optimal field $E_i^{\text{opt}}$ within a circular aperture with a 4.3 mm radius. In order to measure the focal spot, we used a custom-built microscope setup consisting of a 100× objective lens (Olympus, UMPlanFl) with an NA of 0.95, a tube lens (Nikon, 2×, Plan Apo), and a CCD camera (Imaging Source, DFK 23UP031).

Procedure for scanning fluorescence imaging

The setup of our scanning microscope is shown in Supplementary Fig. 5c. For the collection of the scanned fluorescent signal, an imaging system consisting of a 4× objective lens (Olympus, 0.1NA, Plan N) and tube lens (Thorlabs, AC508-100-A-ML) was used to cover most of the FOV of the scanning microscope. We scanned the focal spot created behind the metasurface across the region of interest with a 10 ms pixel dwell time. A pair of galvanometric mirrors were used to scan a 2×2 μm patche with a step size of 200 nm, and the neighboring patches were successively scanned by adding a compensation map on the SLM to correct coma aberrations, instead of exhaustively calculating and refreshing the $E_i^{\text{opt}}$ for every spot. Each image in Figs. 4b–4d consists of 15x15 patches. The fluorescence signal was detected by the sCMOS camera (PCO, PCO.edge 5.5) with an exposure time of 7 ms. The fluorescence signal was extracted from the camera pixels corresponding to the scanned focus position. The imaging time for a 30×30 μm² area was 5 min, which can be easily improved by two orders of magnitude using a high-power laser and resonant scanning mirrors.

Immunofluorescence-labeled sample preparation

As a biological sample, we used microscopic parasites, Giardia lamblia cysts (Waterborne, Inc.). Before labeling the Giardia, we first prepared (a) the sample of 10⁵ Giardia in 10 μL phosphate buffered solution (PBS) in a centrifuge tube, (b) 1 μg of Giardia lamblia cysts antibody (Invitrogen, MA1-7441) in 100 μL PBS, and (c) 2 μg of Goat anti-Mouse IgG (H+L) Secondary Antibody conjugated with Alexa Fluor® 532 fluorescent dye (Life Technologies, A-11002) in 100 μL of PBS. The sample (a) was incubated with a blocking buffer. After the blocking buffer was removed, the sample was again incubated with the Giardia antibody solution (b). The sample was rinsed twice with PBS to remove the Giardia antibody solution. The sample was then incubated with the secondary antibody solution with fluorescent dye (c). Finally, the sample was rinsed twice with PBS to remove the secondary antibody solution. All incubations were carried out for 30 min at 37°C. The sample in 10 μL PBS was prepared on a slide with Prolong® Gold antifade reagent with DAPI (Life Technologies, P36935) to protect the labeled sample from fading and covered with a coverslip.

Data availability

The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.