Measurement of Murine Single-Kidney Glomerular Filtration Rate using Dynamic Contrast-Enhanced MRI

Abstract

Purpose

To develop and validate a method for measuring murine single-kidney glomerular filtration rate (GFR) using dynamic contrast-enhanced MRI (DCE-MRI).

Methods

This prospective study was approved by the Institutional Animal Care and Use Committee. A fast T₁ measurement method was implemented to capture gadolinium dynamics (1s/scan), and a modified two-compartment model developed to quantify GFR as well as renal perfusion using 16.4T MRI in mice two weeks after unilateral renal artery stenosis (RAS, n=6) or sham (n=8) surgeries. This approach was validated by comparing model-derived GFR and perfusion to those obtained by FITC-inulin clearance and arterial spin labeling (ASL), respectively, using the Pearson’s and Spearman’s rank correlations and Bland-Altman analysis.

Results

The compartmental model provided a good fitting to measured gadolinium dynamics in both normal and RAS kidneys. The proposed DCE-MRI method offered assessment of single-kidney GFR and perfusion, comparable to the FITC-inulin clearance (Pearson’s correlation coefficient r=0.95 and Spearman’s correlation coefficient ρ=0.94, P<0.0001, and mean difference −7.0 ± 11.0 μl/min) and ASL (r=0.92 and ρ=0.84, P<0.0001, and mean difference 4.4 ± 66.1 ml/100g/min) methods.

Conclusion

The proposed DCE-MRI method may be useful for reliable noninvasive measurements of single-kidney GFR and perfusion in mice.

INTRODUCTION

Glomerular filtration rate (GFR) and renal perfusion are fundamental indices for detection of kidney diseases and monitoring of treatment interventions. Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) has emerged as a promising tool that enables simultaneous measurements of GFR and renal perfusion (1–3). By following the passage of gadolinium contrast from input arteries through the renal parenchyma, renal functional parameters can be quantified based on mathematical models.

Renal dynamic MR imaging typically involves acquisition of T₁-weighted images, from which gadolinium dynamics are quantified by relative signal enhancement (4), analytical calculation (5), or phantom calibration (6). However, these methods are either limited by inaccuracies or require additional phantom calibration, and may become problematic at high/ultrahigh field strengths due to B₁/B₀ field inhomogeneity (7). Alternatively, rapid T₁ measurement can provide a more direct measurement of gadolinium concentration, which can be indexed as changes in R₁ (1/T₁) based on the linear relationship between gadolinium concentration and R₁ (8). For subsequent quantification of renal functional parameters from gadolinium dynamics, several useful mathematical models have been developed, such as the Baumann–Rudin (5), Patlak–Rutland (9), and two/three compartment (10–13) models. Among these, the two/three compartment models provide simultaneous measurements of GFR and renal perfusion, and have been widely used experimentally in clinical and preclinical studies.

Successful implementation of DCE-MRI for measuring renal functional parameters has been demonstrated in humans (4,12–15) and animals, including rats (5,16–18) and rabbits (11,19,20). However, either no validation studies were performed or significant underestimations of GFR by DCE-MRI were reported in these studies. Therefore, an accurate and robust MRI method for data acquisition and analysis is still needed. Moreover, the applicability and accuracy of GFR measurement by DCE-MRI in mice have not been fully explored. Given that surgical and transgenic mouse models of kidney diseases are playing an increasing important role in renal research, a reliable and accurate DCE-MRI technique for measurements of gadolinium dynamics and a suitable model to analyze them could be useful for assessing and monitoring murine renal function in vivo. Importantly, a sufficiently high temporal resolution during dynamic imaging is required for precise assessment of renal function, and has been shown to be 4s in humans (21), but remains to be determined in mice.

In this study, we tested the hypothesis that DCE-MRI could provide reliable assessments of murine single-kidney GFR and perfusion. Our aims included (1) implementation of a fast T₁ measurement method for dynamic imaging and development of a suitable compartment model for accurate and robust measurement of renal functional parameters in mice; (2) validation of GFR measurement by FITC-inulin clearance (22) and perfusion by arterial spin labeling (ASL) (23); (3) estimation of the minimal temporal resolution required for these measurements in mice.

METHODS

Animals

The Institutional Animal Care and Use Committee approved this prospective study. To validate the proposed DCE-MRI technique over a wide range of renal function, fourteen 129S1 mice were studied two weeks after sham (n=8) or unilateral renal artery stenosis (RAS, n=6) surgeries.

The surgery procedures have been described previously (24,25). Briefly, animals were anesthetized with 1.5% isoflurane and placed prone on a warm (~37°C) heating pad. The right kidney was exposed by a flank incision of ~1cm, after which the right renal artery was dissected from the renal vein. To induce RAS, a 0.20 mm ID × 0.5 mm length cuff (made from a polytetrafluoroethylene tubing, Braintree Scientific, Braintree, MA) was placed around the right renal artery and tied with 10-0 nylon sutures (Surgical Specialties, Reading, PA). Sham surgery included isolation of the renal artery, but without placement of a cuff. Kidneys were returned to their original positions and the incisions sutured. Animals were weighed and their blood pressure measured by tail-cuff (XBP1000, Kent Scientific, Torrington, CT) one day before MRI.

MRI Study

MRI studies were performed on a vertical 16.4T scanner (Bruker, Billerica, MA) equipped with a 38-mm inner diameter birdcage coil. Mice were anesthetized with 2% isoflurane in a mouse chamber and maintained with 1 to 2% isoflurane in an animal holder in supine position. A homemade catheter with a fine needle (30G) was placed and secured in the tail-vein for injection of contrast agent. Warm air was blown on the mice to maintain the body temperature at ~36°C. Respiration and body temperature were monitored and recorded by a physiological monitoring system (SA Instruments, Stony Brook, NY).

Kidney volume and perfusion were measured using non-contrast-enhanced MRI (25). Renal volume was quantified from coronal images acquired using a respiration-gated 3D Fast Imaging with Steady Precession (3D-FISP) sequence with the following parameters: TR 14ms; TE 2.1ms; flip-angle 20°; FOV 5.12×2.56×1.28cm³; matrix size 256×128×64; number of averages 2. Renal perfusion was measured using ASL with a Flow-sensitive Alternating Inversion Recovery sequence with Rapid Acquisition with Relaxation Enhancement (FAIR-RARE) with the following parameters: TR 18000ms; TE 4.88ms; slice number 1; slice thickness 2mm; inversion slab thickness 2mm; inversion pulse 8-ms hyperbolic secant pulse; FOV 2.56×2.56cm²; matrix size 128×128; RARE factor 8; number of averages 1. The central encoding scheme was used to ensure sensitivity to perfusion. A total of 12 images were acquired with inversion delays at 23.4, 500, 1000, 2000, 3000, and 18000ms. The FAIR-RARE scan was performed right before the DCE-MRI scans to ensure consistent measurements of renal perfusion.

In DCE-MRI, a fast T₁ measurement method saturation recovery snapshot fast low-angle shot (Snapshot-FLASH) was implemented to trace gadolinium dynamics. T₁ measurement consisted of acquisition of one proton density (M₀) and one T₁-weighted (M_t) image after saturation recovery. The magnetization saturation module contained three 0.1-ms nonselective 90° radiofrequency pulses, each followed by spoil gradients (26,27). During MRI, ten M₀ images for each slice were first acquired (repetition time of 18s). Then ten M_t images were acquired at baseline, immediately followed by the injection of 37.5mM gadodiamide (0.03mmol/kg) through tail-vein over 2s, with M_t images continuously acquired. To increase signal-to-noise ratio (SNR), a central encoding scheme was used. One slice was prescribed at the center of each of the two kidneys, with their saturation recovery times at 0.25 and 0.57s. The longer saturation recovery time of the second slice was caused by the Snapshot-FLASH readout of the first slice in approximately 0.32s. Other imaging parameters were: TR 4.92ms; TE 0.8ms; flip angle 15°; slice thickness 2mm; FOV 2.56×2.56cm²; matrix size 128×128; number of repetitions 150. The temporal resolution was 1s/scan.

The reliability of T₁ measurement using a mere two points (M₀ and M_t) is dependent on saturation efficiency, SNR, and TD. When the averaged T₁ from hundreds of pixels in the renal parenchyma is used, as in our studies, the accuracy of T₁ estimation is dominated by saturation efficiency at our current SNR level (>100 in the M₀ image). To investigate the impact of saturation efficiency on R₁ estimation with different TDs we performed a theoretical analysis (Supporting Information), and tested it in vitro and in vivo. Preliminary studies on a multi-compartment MnCl₂ phantom and mouse kidneys showed saturation efficiency over 98% with TD at 0.25 and 0.57 s, with a corresponding error in estimated T₁ within 5% (Supporting Information). These preliminary studies support the use of our T₁ measurement method to delineate Gd dynamics in mouse kidneys.

Compartmental Model

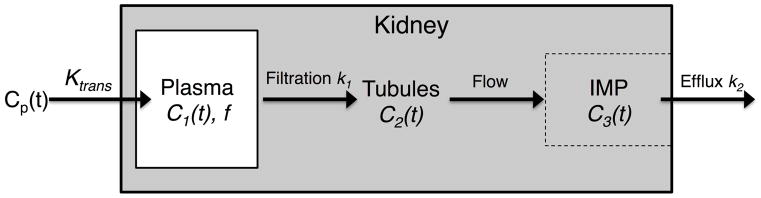
A modified two-compartmental model (Fig. 1) was derived from the one proposed by Annet and colleagues in rabbits (11). The kidney is compartmentalized into blood vessels (plasma) and tubules (glomerular filtrate). In this model, C₁(t) is the gadolinium concentration in renal plasma, C₂(t) in the tubular compartment and expressed per unit volume of the whole renal parenchyma, and C₃(t) in the inner medullary papilla (IMP), in which the outflow converges. An important advance of our model is inclusion of the kidney outflow function (C₃(t)), which may allow a more complete depiction of renal functional parameters. Changes in C₁(t) and C₂(t) can be described by the kinetic equations:

$$\frac{d{C}_1(t)}{dt}=K_{\mathit{trans}}(C_p(t)-C_1(t))$$ [1]

$$\frac{d{C}_2(t)}{dt}=k_1{C}_1(t)-k_2{C}_3^{\prime }(t)$$ [2]

where K_trans is the perfusion rate constant, k₁ normalized GFR, and k₂ gadolinium efflux rate constant. C_p(t) is the arterial input function (AIF), calculated from gadolinium concentration in the abdominal aorta plasma as C_a(t)/(1-Hct), where C_a(t) and Hct are the gadolinium concentration in abdominal aorta blood and the hematocrit, respectively. C₃′(t) is the gadolinium concentration in the IMP deriving from glomerular filtration. Total gadolinium concentration in IMP (C₃(t)) is derived from both its perfusion (C_3p(t)) and tubular transit (C₃′(t)). Based on Eq. 1, the IMP perfusion coefficient can be fitted from the early (20 to 40s) phase that precedes tubular gadolinium arrival, after which the whole C_3p(t) curve is derived. Then C₃′(t) is calculated as C₃(t)-C_3p(t) (Fig. 2d).

Figure 1. The compartmental model.

The kidney is compartmentalized into blood vessels (plasma) and tubules (containing the glomerular filtrate). Gadolinium from the abdominal aorta enters renal plasma and is filtered by glomeruli, after which it arrives in the inner medullary papilla (IMP) following tubular flow, and then outflows from the kidney. C_p(t) is the arterial input function; K_trans is the perfusion rate constant; C₁(t) is the gadolinium concentration in renal plasma space; f is the volume fraction of renal plasma space; k₁ is the normalized GFR; C₂(t) is the gadolinium concentration in the tubules distributed over the whole kidney; C₃(t) is the gadolinium concentration in the IMP space; k₂ is the gadolinium efflux rate constant.

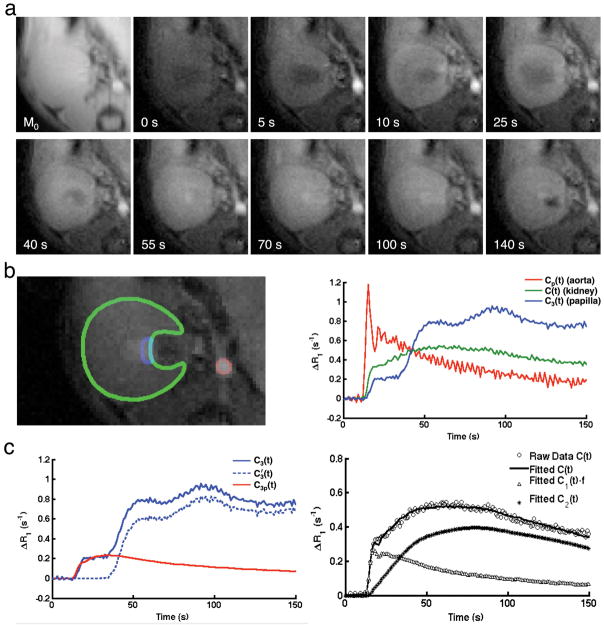
Figure 2. Dynamic imaging and model fitting.

a. Representative M₀ and M_t images acquired at baseline, and 5, 10, 25, 40, 55, 70, 100, 140 s post-gadolinium injection. b. Manually selected ROIs (left) on abdominal aorta (red), renal parenchyma (green), and IMP (blue), and the gadolinium dynamics in all three ROIs (right). c. Decomposition of the gadolinium concentration in IMP into perfusion and filtration components (left), and experimentally-measured and model-fitted gadolinium dynamics in the renal parenchyma, as well as model-fitted dynamics in the renal plasma and tubules (right).

Total gadolinium concentration in the kidney is C(t)=C₁(t)×f+C₂(t), where f is the volume fraction of renal plasma and interstitial (12) spaces. There are four unknown parameters: K_trans, f, k₁ and k₂. Dynamic curves were fitted with the least-squares algorithm, and GFR (μl/min) calculated as:

$$\mathit{GFR}=k_1·V·\mathit{60}$$ [3]

where V is the effective kidney volume. Renal perfusion (ml/100ml/min) is calculated as:

$$\mathit{Perfusion}=K_{\mathit{trans}}·f·\mathit{60}·\mathit{100}/(1-\mathit{Hct})$$ [4]

Image Analysis

Renal volumes were quantified from the 3D-FISP images using Analyze^™ (version 12.0, Biomedical Imaging Resource, Mayo Clinic, MN). Renal regions of interest (ROIs) were manually traced on all frames where kidney was observed, from which the total renal volume was calculated. The effective kidney volume was calculated from the MRI-measured kidney volume and the renal parenchyma used for quantification of C(t) (excluding the renal sinus).

All other images were analyzed using Matlab^® (Mathworks, Natick, MA) modules developed in-house. Renal perfusion was quantified from the FAIR-RARE images (25). The magnitude images were used to generate the global (T₁^gl) and slice-selective (T₁^sl) T₁ maps by pixel-wise mono-exponential fitting with two unknown parameters (inversion efficiency and T₁). The perfusion was quantified as (23)

$$P=\lambda ·\frac{T_1^{gl}}{T_1^b}(\frac{1}{T_1^{sl}}-\frac{1}{T_1^{gl}})$$ [5]

where λ is the blood/tissue partition coefficient for water (0.9ml/g) (28). $T_1^b$ is the T₁ of blood, which is 2.0s at 16.4T in the 129S1 strain (24). The same renal parenchyma ROI selected in the DCE-MRI analysis was used for measurement of renal perfusion by ASL. Renal blood flow was calculated as the multiplication of renal perfusion and kidney volume.

In DCE-MRI analysis, M₀ and M_t images with obvious motion artifacts were excluded, and remaining M₀ images averaged to increase SNR. T₁ maps were generated pixel-wise by a simple exponential fitting (8). Baseline T₁ maps were averaged for calculation of change in R₁ (ΔR₁) post-injection. ROIs were selected on the abdominal aorta (4–9 pixels depending on its size), renal parenchyma, and IMP for measurement of C_a(t), C(t), and C₃(t), respectively. The renal ROI encompassed most of the kidney, excluding areas with gadolinium blooming effects. A thin IMP ROI was prescribed at the tip of the inner medulla (Fig. 2b). Single-kidney GFR and renal perfusion were quantified by model fitting of the dynamics, and total renal mass GFR was summing single-kidney GFRs.

GFR by FITC-inulin Clearance

One day after MRI, GFR was measured in each mouse by the reference standard FITC-inulin clearance and assigned to kidneys by their renal blood flow. The procedures for GFR measurement using FITC-inulin clearance has been shown previously (22). Briefly, 3.5% FITC-inulin at 3.74μl/g was injected retro-orbitally, after which ~20μl blood was repeatedly collected via the saphenous vein at around 3, 7, 10, 15, 35, 55, and 75 minutes. The concentration of FITC-inulin in isolated plasma was measured using fluorescence, with 485 nm excitation and 538 nm emission. A two-compartment model was used for curve fitting, in which the concentration of FITC-inulin was described by A·e^−at + B·e^−bt, with the first and second term represents redistribution and clearance, respectively. GFR was then calculated as I/(A/a+B/b), where I is the total amount of injected FITC-inulin. Single-kidney GFR was assessed by partitioning the total renal mass GFR based on the fractional blood flow (perfusion × volume) of each kidney.

Simulation Study

To evaluate the effect of temporal resolution in dynamic imaging on the accuracy of perfusion and GFR estimation in mouse kidneys, a Monte-Carlo simulation study was performed in a separate group of normal 129S1 mice (n=5). In DCE-MRI, only one slice was imaged, resulting in a temporal resolution of 0.65s/scan. This sub-second temporal resolution was assumed to be sufficient in capture the dynamics of gadolinium concentration in all ROIs, and therefore provide a reliable measurement of renal perfusion and GFR. The measured curves were linearly interpolated with an interval of 0.01s, from which data was resampled with temporal resolutions ranging from 0.2 to 3.0s/scan (at 0.2s steps). The resampled curves were then model-fitted to quantify renal perfusion and GFR values, which were normalized by those obtained with the sampling interval of 0.2s.

Statistical Analysis

All statistical analysis was performed using JMP 10.0 (SAS Institute, Cary, NC). Normality of data was assessed using Shapiro-Wilk test. Results were expressed as means±standard deviations for normally distributed data, or medians with interquartile ranges (IQR) for non-normally distributed data. One-way analysis of variance was followed by Student’s unpaired t-test for statistical comparisons of normally-distributed data. The Kruskal-Wallis test was used to assess differences among non-normally-distributed data, followed by the Wilcoxon rank-sum or signed-rank test, as appropriate. Pearson’s and Spearman’s rank correlations as well as Bland-Altman analysis were used to compare the GFR and perfusion among different methods. p≤0.05 was considered statistically significant.

RESULTS

Representative proton density (M₀) and T₁-weighted (M_t) images acquired at baseline and 5, 10, 25, 40, 55, 70, 100, and 140 sec post gadolinium-injection are shown in Fig. 2a. The murine renal cortex shows initial signal enhancement due to perfusion, followed by renal filtration and tubular flow, which subsequently intensify the outer and inner medulla. Manually traced ROIs for the abdominal aorta (red), kidney (green), and IMP (blue) are shown in Fig. 2b (left). Distinctive gadolinium dynamics in these ROIs are indicated by the time course of ΔR₁ changes (Fig. 2b, right) that are comparable to those shown before (11,15,29). The AIF (C_p(t)) shows a transient increase after the bolus injection, followed by a gradual decrease. In the renal parenchyma, gadolinium concentration shows a initial sharp increase as a result of perfusion, followed by a steady rise due to glomerular filtration and tubular transit, and then a gradual decrease due to outflow. In IMP, a similar increase due to renal perfusion is observed, followed by a plateau (representing a time-lag between vascular and tubular flow), and then two peaks, possibly due to tubular transit of gadolinium through short and long nephrons (30,31), and finally a steady fall due to elimination from the kidney.

Fig. 2c (left) shows representative decomposition of IMP gadolinium concentration (C₃(t)) into the perfusion (C_3p(t)) and filtration (C₃′(t)) components. Fig. 2c (right) shows the representative raw and model-fitted gadolinium dynamics in the renal parenchyma, vascular (C₁(t)^·f), and tubular (C₂(t)) compartments. A good fit of the raw data C(t) was achieved, suggesting the proposed compartment model provides a faithful delineation of renal gadolinium dynamics in mice.

RAS mice showed decreased body weight as well as elevated systolic, diastolic, and mean arterial pressures two weeks post-surgery (Table 1). The stenotic kidneys had a decrease in volume compared to the control (P=0.0006) and contralateral (P=0.0082) kidneys (Table 2). Representative model-fitted gadolinium dynamics in the control and stenotic kidneys are shown in Fig. 3a (left), and the model-fitted parameters in Table 2. Compared to control kidney, K_trans (P=0.0011), k₁ (P=0.0005), and k₂ (P=0.0017) all fell significantly in the stenotic kidney. In the contralateral kidney, K_trans was also decreased (P=0.0082), whereas no change was observed in k₁ and k₂. No difference was found in f.

Table 1.

Characteristics of mice two weeks after renal artery stenosis (RAS) surgery

	Control (n=8)	RAS (n=6)	P Value
Body Weight (g)	25.6 ± 1.7	21.4 ± 1.7	0.001
Blood Pressure (mmHg)
Systolic	119.9 ± 4.5	170.7 ± 18.3	0.006
Diastolic	78.3 ± 4.6	122.2 ± 28.0	0.003
MAP	92.2 ± 2.7	138.4 ± 24.3	0.003

Data are means ± standard deviations. MAP=mean arterial pressure.

Table 2.

Kidney volume and model-fitted parameters in control, stenotic, and contralateral kidneys

	Control Kidney	Stenotic Kidney	Contralateral Kidney
Volume (μl)	255 (244–276)	177 (174–184)*	234 (221–249)†
Ktrans (s−1)	0.35 (0.32–0.38)	0.18 (0.14–0.19)*	0.14 (0.13–0.18)*
f	0.16 (0.15–0.18)	0.19 (0.14–0.20)	0.15 (0.13–0.17)
k1 (s−1)	0.011 (0.010–0.012)	0.006 (0.005–0.007)*	0.012 (0.011–0.012)†
k2 (s−1)	0.011 (0.009–0.016)	0.005 (0.004–0.006)*	0.010 (0.006–0.017)†

Data are medians with interquartile ranges in parentheses.

^*P<0.05 compared to control kidney,

^†P<0.05 compared to stenotic kidney.

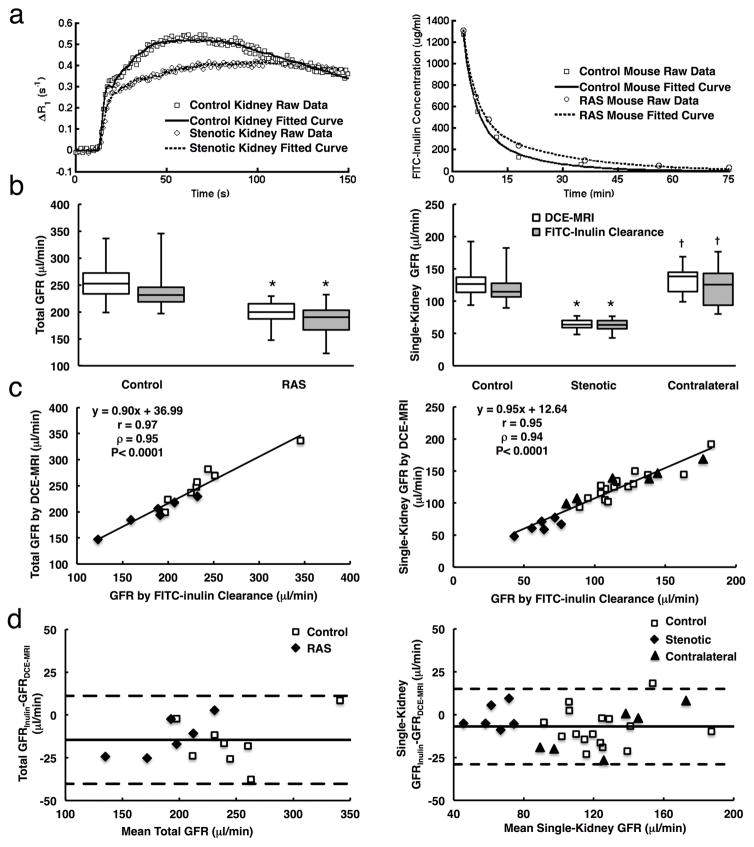
Figure 3. Validation of GFR measurement by DCE-MRI using FITC-inulin clearance.

a. Representative experimentally measured and model-fitted gadolinium dynamics in control and stenotic kidneys, and dynamics of FITC-inulin clearance from plasma in control (blue) and RAS (red) mice. b. Total (left) and single-kidney (right) GFRs measured by DCE-MRI and FITC-inulin clearance in control and RAS mice. c. Correlation between DCE-MRI and FITC-inulin clearance in measuring total (left) and single-kidney (right) GFRs. d. Bland-Altman analysis of total (left) and single-kidney (right) GFR measurements by DCE-MRI and FITC-inulin clearance. ^*P<0.05 compared to control kidney, ^†P<0.05 compared to stenotic kidney.

Representative curves of plasma clearance of FITC-inulin in control and RAS mice are shown in Fig. 3a (right). In both groups, total renal mass GFRs measured from DCE-MRI were comparable to those measured using FITC-inulin clearance (Fig. 3b, left) and showed a good correlation (Fig. 3c left, Pearson’s correlation coefficient r=0.97 and Spearman’s correlation coefficient ρ=0.95, P<0.0001). Bland-Altman analysis (Fig. 3d, left) showed a good consistent agreement between total GFR measured by Inulin clearance and DCE-MRI (mean difference, −14.6 ± 12.8 μl/min). The stenotic kidneys showed a 49.5% decrease in DCE-MRI-measured GFR (63.9 (59.3–70.2) vs. 126.6 (113.7–137.0) μl/min), as compared to controls (Fig. 3b, right). No change was observed in the contralateral kidney GFR. The single-kidney GFRs measured using these two methods were also similar in control, stenotic, and contralateral kidneys, as indicated by the strong correlation (Fig. 3c right, r=0.95 and ρ=0.94, P<0.0001). Bland-Altman analysis also revealed a close agreement between single-kidney GFR measured by Inulin clearance and DCE-MRI (mean difference, −7.0 ± 11.0 μl/min).

Renal perfusion measured by DCE-MRI and ASL also showed a good agreement in all kidneys (Fig. 4a–b). A good correlation was found between ASL and DCE-MRI measured renal perfusion values (Fig. 4a, r=0.92 and ρ=0.84, P<0.0001), between which a minimal difference (Fig. 4b, mean difference, 4.4 ± 66.1 ml/100g/min) was found by the Bland-Altman analysis. Renal perfusion by DCE-MRI was found decreased by 60.8% in the stenotic as compared to control kidneys (227.8 (199.9–276.8) vs. 581.2 (555.1–613.4) ml/100g/min, P=0.0005).

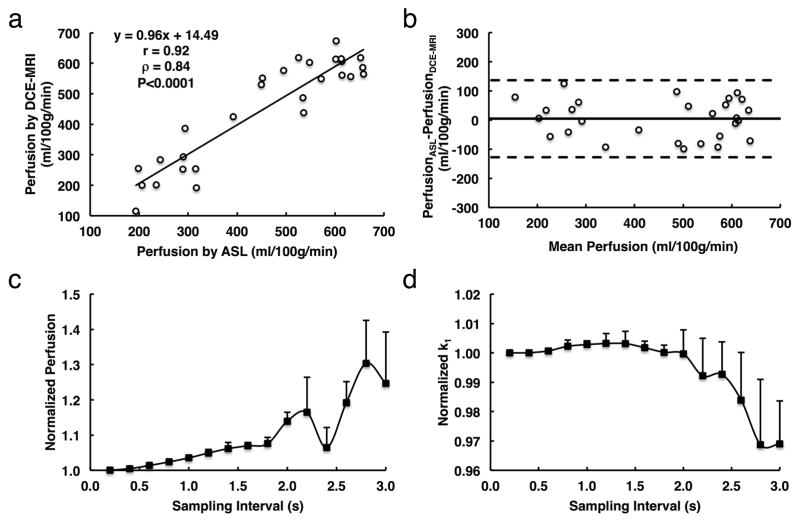
Figure 4. Validation of perfusion measurement by DCE-MRI and the impact of sampling interval on measurement of GFR and renal perfusion.

a. Correlation between renal perfusion by DCE-MRI and arterial spin labeling (ASL). b. Bland-Altman analysis of the same data. c and d. Monte-Carlo simulation of the impact of sampling interval on measurement of renal perfusion (c) and GFR (d). Large variations in estimated GFR and renal perfusion are observed when the sampling interval is larger than 1.8 and 2.0s, respectively.

The impact of sampling interval on assessment of perfusion and GFR is shown in Fig. 4c and d, respectively. A larger sampling interval tended to lead to overestimation of renal perfusion, which was within 10% at a sampling interval up to 1.8s (Fig. 4c). In contrast, GFR measurement was less affected by sampling interval and required a sampling interval equal or less than 2s, after which large fluctuations were observed (Fig. 4d). Therefore, accurate measurements of murine GFR and renal perfusion require a minimal temporal resolution of 1.8s/scan.

DISCUSSION

This study introduces a DCE-MRI method that allows noninvasive assessment of murine single-kidney GFR in vivo. We implemented a fast T₁ measurement method for dynamic imaging at 1s/scan and proposed a modified two-compartment model for estimation of GFR and renal perfusion. Our validation studies show that this DCE-MRI method offers measurements of both GFR and renal perfusion that agree well with the FITC-inulin clearance and ASL methods. In addition, a temporal resolution no lower than 1.8s/scan was found necessary for reliable estimation of GFR and renal perfusion in mice.

Single-kidney GFR assessment is critical in diagnosis and evaluation of unilateral kidney disorders, such as ureteral obstruction or RAS. Conventional estimation of GFR based on the serum level of endogenous or exogenous markers cannot assess single-kidney function, and is complicated by factors other than GFR (32), or limited by the need for collections of blood or urine samples. In contrast, DCE-MRI provides the opportunity for noninvasive measurement of single-kidney GFR. Previously, Sadick et al. demonstrated the feasibility of GFR measurement in mice at 3T (33). Nevertheless, image resolution was limited and no validation studies were performed. Validation studies of DCE-MRI in other animal models or humans showed under- (11–13) or over-estimation (10) compared to reference techniques. In this study, we proposed a DCE-MRI method for reliable estimation of mouse GFR.

Several strategies were used in our study to ensure accurate measurements of gadolinium dynamics. First, instead of T₁-weighed imaging we used a rapid T₁ measurement method, which is less susceptible to B₀/B₁ inhomogeneity at high/ultra-high field strength (26), and provides a more direct measurement of gadolinium concentration, which can be indexed as ΔR₁ (7). However, a separate scan is needed to acquire the proton density image, which prolongs the total scan time. Second, nonselective 90° pulses and spoil gradients were applied for whole-body magnetization saturation to eliminate the blood inflow effect in the aorta, increasing the accuracy of the AIF measurement. Finally, a small volume of contrast media (0.8μl/g) was injected through tail-vein to minimize the effect of the bolus on renal hemodynamics.

The modified two-compartment model provided good fits to gadolinium dynamics in both normal and diseased kidneys, suggesting that it faithfully depicted the biological process of renal perfusion, filtration, and tubular flow. An important advance over some previous models (9,11,12,14) is that the outflow function from the IMP is quantified. Consequently, the delay between gadolinium filtration and outflow from kidney is inherently accounted for during curve fitting. As opposed to the three-compartment models, which may nonetheless provide useful tubular parameters in addition to GFR and renal perfusion (12,13), no corticomedullary segmentation is needed in our model.

We were able to test the applicability and accuracy of the proposed DCE-MRI in measuring GFR over a wide range of values. The DCE-MRI measured GFR showed a good agreement with the inulin clearance method, a reference standard for measurements of GFR. Although ASL is not a gold standard for perfusion measurement, DCE-MRI notably provided similar renal perfusion values as ASL. In addition, our measured renal perfusion and GFR values in control mice also closely matched those reported in the literature (22,34–36). Overall, the good agreement with reference techniques suggests that our DCE-MRI method provides a reliable measurement of murine GFR and renal perfusion. In addition, we observed a decrease in contralateral kidney perfusion. Presumably, this might be due to a transient response at early RAS or a species-specific phenomenon. Moreover, the fall in renal perfusion might be secondary to scanning the mice in an erect posture, which may decrease renal blood flow (37,38).

An accurate measurement of gadolinium dynamics requires sufficient imaging temporal resolution, especially for delineation of the AIF. Previously, Michaely et al have shown that a temporal resolution of 4s is required to achieve 10% precision in estimates of renal perfusion and filtration rates in humans (21). In this study, given the smaller circulation volume and higher heart rates in mice, we found that a temporal resolution of 1.8s/scan is needed for accurate and robust measurement of murine GFR and renal perfusion, which may be useful for future study designs.

There are several limitations in our study. First, 2D imaging was performed to ensure high temporal resolution. A 3D coverage of kidneys can provide a more complete assessment of renal function, especially for kidneys with focal abnormalities. Techniques such as parallel imaging (39) or non-Cartesian sampling (40) may expedite data acquisition and realize fast 3D DCE-MRI. Second, kidney regions with gadolinium blooming effects were excluded during data analysis, which might introduce subtle inaccuracies in measured renal parameters. Future studies may employ quantitative susceptibility mapping (41) to measure the gadolinium concentration in those regions. Third, the measurement of GFR might be biased by the vertical position of mice in the MRI bore. Human GFR is slightly higher in erect than supine position (42,43), but whether this also occurs in mice is unknown.

In conclusion, the proposed DCE-MRI method provided accurate and robust measurements of single-kidney GFR and perfusion in normal and RAS mice. The fast T₁ measurement method saturation recovery Snapshot-FLASH can capture gadolinium dynamics at a temporal resolution of 1s/scan and the modified two-compartment model provides a close fit to gadolinium dynamics in renal parenchyma. This technique may therefore provide a valuable tool for assessment of renal function and evaluation of therapeutic strategies for renal diseases in patients.

Supplementary Material

Supp info. Supporting Figure S1. Reliability of the two-point method in T₁ estimation by theoretical analysis and experimental studies.

a.Overestimation in R₁ at different saturation efficiencies with TD at 0.25 and 0.57 s. b–c. The fitted T₁ maps (b) and measured T₁ values (c) of the two slices by the multi-point and single-point methods in the MnCl₂ phantom study. d–e. Representative T₁ maps (d) and the measured T₁ values (e) of the two slices by the multi-point and single-point methods in the in vivo study.