Rapid Dual Echo Ramped Hybrid Encoding MR-Based Attenuation Correction (dRHE-MRAC) for PET/MR

Abstract

Purpose

In this study, we propose a rapid acquisition for MR-based attenuation correction (MRAC) in PET/MR imaging, where an ultrashort echo time (UTE) image and an out-of-phase echo image are obtained within a single rapid scan (35sec) at high spatial resolution (1mm³), which allows accurate estimation of a pseudo CT image utilizing 4 class tissue classification (discrete bone, discrete air, and continuous fat and water).

Methods

In dual echo ramped hybrid encoding (dRHE), a UTE echo is directly followed by a second, out-of-phase echo where hybrid spatial encoding combining single-point imaging and 3D radial frequency encoding is utilized to improve the quality of both images. Two-point Dixon reconstruction is used to estimate fat and water separated images, and UTE images are used to estimate bone. Air and bone segmentation is improved by utilizing multiple UTE images with an advanced hybrid encoding scheme that allows reconstruction of multiple UTE images. To evaluate the proposed method, dRHE-MRAC, PET/MR brain imaging was performed in 10 subjects. Dice coefficients and PET reconstruction errors relative to CT-based attenuation correction were compared to existing system MRAC approaches.

Result

In dRHE-MRAC, the Dice coefficients for soft tissue, air, and bone were respectively 0.95±0.01, 0.62±0.06, and 0.78±0.05, which was a significantly improved result compared to existing approaches. In most brain regions, dRHE-MRAC showed significantly reduced PET error (less than 1%) with p-values less than 0.05.

Conclusion

dRHE enables rapid and robust imaging for MRAC with a very rapid acquisition.

INTRODUCTION

Simultaneous PET/MR systems have been developed to complement the features of each individual imaging modality, that is, providing highly sensitive molecular-specific contrast with PET and rich soft tissue contrast and anatomical information with MRI. For example, PET/MR can be utilized to simultaneously acquire images of glucose metabolism (FDG PET) with anatomical information (T1-weighted, T2-weighted, or proton density-weighted imaging in MRI) or tissue micro-structure (diffusion weighted imaging in MRI) in a single simultaneous imaging session. Moreover, combining PET with functional imaging, such as functional MRI or cardiac/flow imaging in MRI, can provide orthogonal biomarkers for more accurate diagnosis. In spite of the promises and benefits of simultaneous PET/MR imaging, it remains challenging to obtain a reliable photon attenuation correction map necessary for accurate PET quantitation.

Many MR-based attenuation correction (MRAC) approaches have been proposed to overcome this limitation, such as atlas registration-based or image segmentation-based methods. Atlas registration-based methods perform indirect estimation of CT contrast using a template based on a database of attenuation maps of similar subjects (1–5). The atlas registration method does not directly consider the uniqueness of an individual’s anatomy, and hence it can mislead estimation of the attenuation map if anatomy deviates significantly from normal cases. Image segmentation-based methods can potentially allow more direct and precise estimation of CT contrast based upon MR images with specialized imaging schemes or parameters (e.g., images acquired at different TEs to obtain fat and water separated images) (6–13). However, it is still difficult to directly image bone due to MRI’s fundamental limitations in imaging short T2* species, which has high photon attenuation relative to soft tissues.

Recent reports in the literature have demonstrated that ultrashort echo time (UTE) or zero echo time (ZTE) imaging can be successfully utilized for MRAC owing to its capability to resolve objects with short T2* decay (i.e., bone)(14–19). Unfortunately, UTE/ZTE techniques can take several minutes of acquisition time, particularly for multi-echo approaches, and are thus likely to impede PET/MR workflow. This is especially true for whole body PET/MR where only 3–5 minutes may be available for MRI at each bed position. Using faster imaging schemes (<3 min) in ZTE/UTE based MRAC often compromises spatial resolution (18), which complicates pixel intensity based tissue segmentation due to exacerbated partial volume effect. Moreover, in ZTE/UTE imaging additional scan time is required to obtain information to segment fat and water tissues (e.g., images at different TEs), which further slows down MRAC acquisition.

In this study, we propose a new set of techniques for rapid MRAC acquisition in the brain based on dual echo ramped hybrid encoding (20), termed dRHE-MRAC. In dRHE-MRAC, UTE and out-of-phase echo images with high spatial resolution (1 mm³) are obtained within a single 35-second acquisition. Hybrid single point imaging is utilized to improve reconstruction quality and enable acquisition of multiple UTE images to improve air and bone detection. Selective excitation using Shinnar-La Roux (SLR) RF pulses is utilized to improve imaging performance relative to non-selective excitation techniques (which are challenged in UTE techniques due to undesirable detection of plastic components in RF coils and other system components) (21). With multiple UTE images and an out-of-phase image, a fully-automated, histogram-based tissue segmentation is performed to estimate bone, air, water, fat components, and the resultant pseudo CT image. To evaluate the proposed dRHE-MRAC, phantom and in vivo head imaging was performed using an integrated 3T PET/MR system. For in vivo brain imaging performed on 10 patients, dRHE-MRAC showed significantly improved PET error (less than 1%) compared to existing MRAC approaches.

METHODS

Dual echo RHE

Dual echo RHE (dRHE) is based on ramped hybrid encoding (RHE) as previously described (20). In RHE, pure phase encoding, or single point imaging (SPI) (22), is used to acquire the central region of k-space, while radial frequency encoding is used to acquire data in outer k-space. In dRHE-MRAC, the following strategies are used to achieve fast, multi-echo image acquisition. First, ramp sampling is performed with the fastest possible encoding gradient (i.e., at the maximum slewrate and gradient amplitude). Second, dual echo imaging is performed using two gradients with opposite polarity to minimize a per-TR scan time, where UTE and out-of-phase images are acquired in each gradient blip. Third, radial spokes are undersampled to minimize the total scan time.

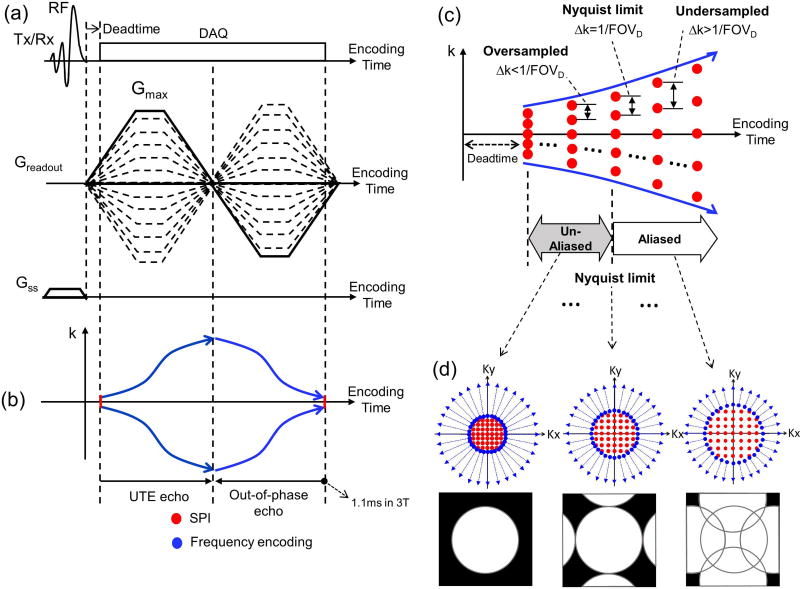
Figure 1-a shows the pulse sequence diagram (PSD) of dRHE, which utilizes RHE to minimize the per-excitation encoding time and minimize blurriness in short T2* components (i.e., bone). For the UTE acquisition in dRHE, frequency encoding is performed in a center-out direction with the fast and large encoding gradient turned on before RF coil deadtime (solid line in Figure 1-a) to rapidly encode k-space (blue lines in Figure 1-b). Cartesian SPI (dotted lines in Figure 1-a) is used to encode the central k-space region missing from frequency encoding as a result of RF coil deadtime (red lines in Figure 1-b). The UTE encoding (in-phase, TE<0.1ms) is immediately followed by encoding an out-of-phase echo (TE = ~1.1ms at 3T), and is used to perform fat and water separation based on a two-point Dixon reconstruction (23). Note that data acquired during the fly-back to the center of k-space is used to reconstruct an out-of-phase image instead of prescribing another center-out readout gradient as in conventional fly-back gradient echo imaging to reduce scan time. The out-of-phase image is also reconstructed using SPI data for the central k-space region and radial frequency encoded data in outer k-space to benefit from reduced eddy current effects in SPI and a subsequent reduction in reconstruction errors such as ringing artifacts. Note that in SPI encoding, the sampling positions spread out in the first encoding gradient, and come back to central k-space in the end of the second encoding gradient, as in frequency encoding. To attain a proton density weighted (PDW) image, a small flip angle is applied (≤1 degree).

Figure 1.

Dual echo RHE imaging using a fly-back echo to acquire a UTE echo and an out-of-phase image at approximately TE=1.1ms. By slightly oversampling the SPI region, multiple UTE images are obtained without aliasing artifact. (a) Pulse sequence diagram, (b) k-space trajectory, (c) oversampled SPI to obtain multiple UTE images, and (d) 2D examples of hybrid k-space trajectory and images.

We improve upon the original RHE by incorporating an SLR pulse with minimum phase (24) to selectively excite a 3D slab and suppress streaking and aliasing artifact due to undersampling and fast encoding, which can be exacerbated by signals originating in the RF coil or non-imaged region in body (e.g., shoulder in head/neck imaging or legs in pelvis imaging). In conventional implementations of hybrid encoding (20,25), SPI encoding is performed to acquire just a single point in k-space (at TE) within a TR, while radial frequency encoding acquires multiple samples in center-out or out-in radial direction. In this work, we show feasibility of incorporating “dynamic” SPI (26) in hybrid encoding to secure data at multiple TEs in a TR. To achieve this, SPI is slightly oversampled to allow acquisition of multiple UTE images as in (27), which can later be used to improve air and bone detection. Figure 1-c illustrates the time-spreading k-space sampling pattern in SPI over multiple TEs. If SPI is oversampled at the first TE after RF coil deadtime, multiple SPI data without aliasing can be acquired at subsequent TEs until the k-space sampling density violates the Nyquist limit (Δk=1/FOV_D, where FOV_D is a desired FOV). Figure 1-d shows a 2D example of the acquisition of multiple k-spaces and images using oversampled, dynamic SPI. An example for combining SPI and radial spokes us shown in Supporting Figure S1.

Dual echo RHE allows fast encoding by performing ramp sampling with fast and high amplitude readout gradients; however, strong eddy currents are generated by such rapidly changing gradients. The eddy current distorts gradient the shape and deviates the k-space trajectory from the nominal trajectory, which results in imaging artifacts such as blurring, ringing, scaling, and phase errors (leading to inaccurate water and fat separation). Therefore, it is crucial to estimate the gradient distortion when calculating k-space trajectory for artifact-free image reconstruction. In this study, a dynamic SPI-based gradient measurement technique was used to estimate the actual k-space trajectory and utilize it for reconstruction (28). Note that measurements of the gradient trajectory can be performed in a phantom scan on a separate day from the in vivo imaging experiment and appear to stable over many months, thus requiring no additional time for the in vivo experiment.

SPI data acquired at a desired TE and frequency encoding data acquired from the TE to the end of readout are combined and input to a gridding process, which was implemented based on (29,30), to yield a 3D Cartesian k-space matrix. The resultant 3D image at each TE is reconstructed by performing inverse discrete Fourier transform.

Modeling tissue distributions

Once dRHE images have been acquired, images are passed through a series of post-processing steps to segment them into individual tissue components to generate a pseudo CT suitable for use in PET image reconstruction. First, signal bias in UTE images is corrected in the inverse log domain similar to (19), where a mean intensity of soft tissue of neighboring pixels is used to determine the DC bias. Knowledge of the expected tissue distribution is prerequisite to automatically determine thresholds to detect air and bone. In a PDW-UTE image, it is expected that the pixel intensity for air (or noise) is darkest, and that of soft tissue is brightest, while bone shows an intermediate intensity. After bias correction, the tissue distribution is determined empirically based on the histogram of pixel intensities within the object region (i.e., head). The distribution of air is approximated to a Gaussian distribution, which is a valid assumption when the SNR is sufficiently high (e.g., larger than 2) (31). The distribution of soft tissue is more difficult to model with a Gaussian distribution since it is composed of different types of tissue with contrasts dependent upon the imaging scheme. In a PDW-UTE brain image, gray matter exhibits higher pixel intensity than white matter. To simplify soft tissue modeling, only the gray matter distribution is considered, and thus the right side of the soft tissue peak (gray matter only) is mirrored to the left side, and the soft tissue distribution is estimated as following equation.

$$f(x)=u(x_p-x)h(s(x_p-x)+x_p)+u(x-x_p)h(x)$$ (1)

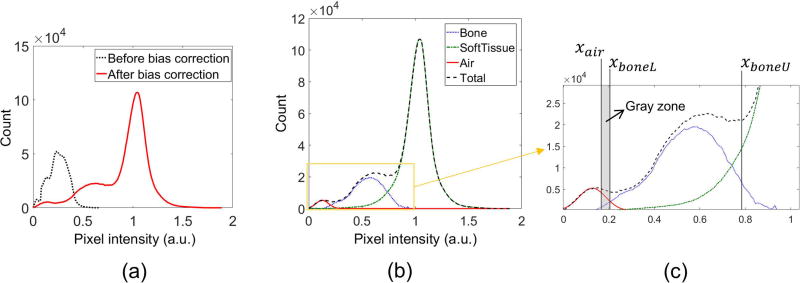
, where h(x) is an intensity histogram corresponding to a pixel intensity, x, u(x) is a unit step function (returning 1 when x is positive, and 0 otherwise), x_p is the pixel intensity of the peak value in the histogram, and s is a stretching factor to deal with the case that left half of soft tissue distribution is skewed due to imperfect bias-correction. The stretching factor, s, is determined by minimizing error between f(x) and h(x). The Nelder-Mead simplex algorithm with l2-norm as error function was used to automatically find the stretching factor in this study. The bone distribution is indirectly estimated by subtracting the estimated air and soft tissue distribution from the total histogram. Figure 2-a and b show an example of the histogram before and after bias correction and estimated tissue distributions.

Figure 2.

Bias correction and threshold setup. The air distribution is fitted with a Gaussian model, and the soft tissue distribution is empirically found based on the symmetry of a soft tissue (gray matter) peak. The bone distribution is found by subtracting the estimated air and soft tissue distribution from the total histogram. (a) Histogram before and after bias correction, (b) estimation of tissue distribution, and (c) threshold setup.

Threshold setup for bone/air detection

Tissue segmentation is performed based on relative scaling of the histogram of pixel intensity between air (inside subject), bone, and soft tissue in the bias-corrected, unscaled (not log scaled) image. The threshold for air detection, x_air, is computed utilizing the following equation.

$$x_{\mathit{\text{air}}}={\mathit{\text{argmin}}}_x|\frac{h_{\mathit{\text{air}}}(x)}{h_{\mathit{\text{bone}}}(x)}-k_1|$$ (2)

, where h_air and h_bone are the estimated air and bone distribution, respectively. Pixels with intensity below x_air are classified as air. The lower and upper threshold for bone detection, respectively x_boneL and x_boneU, are determined as follows.

$$x_{\mathit{\text{boneL}}}={\mathit{\text{argmin}}}_x|\frac{h_{\mathit{\text{bone}}}(x)}{h_{\mathit{\text{air}}}(x)}-k_2|$$

$$x_{\mathit{\text{boneU}}}={\mathit{\text{argmin}}}_x|\frac{h_{\mathit{\text{bone}}}(x)}{h_{\mathit{\text{soft}}}(x)}-k_3|$$ (3)

, where h_soft is the estimated soft tissue distribution. k₁, k₂, and k₃ are system dependent parameters that need to be adjusted with respect to different imaging parameters (e.g., flip angle, field strength). In this study, k₁, k₂, and k₃ were empirically determined as 5, 1, and 0.5, and fixed for all in vivo experiments. Figure 2-c shows an example of threshold setup. Pixels with intensity between x_boneL and x_boneU are classified as bone. Note that pixels in the gray zone with intensity between x_air and x_boneL remain unresolved to remove the risk of overestimating air or bone. Note futher that x_boneU is loosely set to comprehensively detect bone in the gray zone between bone and soft tissue distributions by which darker soft tissues (e.g., white matter) can also be classified as bone, which is refined using the edge information.

Air and bone detection with multiple UTE images

For air and bone detection, multiple UTE images obtained as previously described are utilized. Pixelwise air/bone segmentation is performed across all UTE images (14 as utilized herein), and the detected air/bone maps are combined by logical summation (OR operation). This improves air/bone detection since different UTE images exhibit a time-varying noise pattern in the air/bone region, and some pixels in this gray zone that are not detected for a single UTE image can be detected in other UTE images. Additionally, the background region is added to the air map.

Edge-based bone refinement

After initial segmentation of bone, misclassified bone pixels in gray zone between bone and soft tissue can be removed using edge information of a UTE image owing to the PDW contrast where no strong edge appears in soft tissue. First, an edge image is obtained using Canny edge detection on a UTE image, where 2D edge detection is performed in each of the three slice directions and combined by logical summation. A refinement map for bone detection is obtained by applying dilation process with a spherical structuring element with radius of 4 pixels, with the assumption that bone resides near strong edges. Next, the initial bone segmentation is refined by logical multiplication (AND operation) with the obtained refinement map.

Morphological image processing

Small islands of bone or air are removed from the segmented image using morphological processing. The detected air map is subdivided into smaller segments, where 8-connected pixels are grouped together in a 2D slice. Segments with a number of elements less than 10 are removed in the slice. This process is repeated in each slice direction (axial, sagittal, coronal) and the refined maps are combined by logical summation. To remove falsely detected bone inside the sinus (which is a particularly difficult region due to partial volume effects) bone pixels detected in-between air pixels are removed. To accomplish this, the air map is processed with a closing operation utilizing a spherical structuring element with a radius of 10 pixels. Finally, any bone pixels present inside the closed air map are removed.

Pseudo CT generation

Pseudo CT maps are generated using the detected bone map, air map, and fat/water separated images. First, a CT image for soft tissue is generated based on fat fraction as follows:

$${\mathit{\text{CT}}}_{\mathit{\text{softTissue}}}=(1-f_{\mathit{\text{fat}}}){\mathit{\text{HU}}}_{\mathit{\text{water}}}+f_{\mathit{\text{fat}}}{\mathit{\text{HU}}}_{\mathit{\text{fat}}}$$ (4)

, where f_fat is a fat fraction (in the range [0, 1]) image obtained by two point Dixon, and HU_water and HU_fat are Hounsfield unit values (HU) for water and fat, respectively. To add air and bone regions as computed above, a 4-class pseudo CT image is composed as follows:

$${\mathit{\text{CT}}}_{\mathit{\text{dRHE}}}=(1-{\mathit{\text{BW}}}_{\mathit{\text{bone}}}-{\mathit{\text{BW}}}_{\mathit{\text{air}}}){\mathit{\text{ CT}}}_{\mathit{\text{softTissue}}}+{\mathit{\text{BW}}}_{\mathit{\text{bone}}}{\mathit{\text{ HU}}}_{\mathit{\text{bone}}}+{\mathit{\text{BW}}}_{\mathit{\text{air}}}{\mathit{\text{HU}}}_{\mathit{\text{air}}}$$ (5)

, where BW_bone is a binary map of the detected bone, HU_bone is a representative value for HU of bone, BW_air is a binary map of the detected air, and HU_air is HU of air in CT. The generated CT image is then smoothed by spatial Gaussian filter with standard deviation of 2 pixel (2-mm).

Experimental setup

To evaluate the proposed method, phantom and in vivo experiments were performed using a head and neck coil (HNU) on a 3T PET/MR system (GE Healthcare, Waukesha, WI, USA). Imaging parameters are as follows: Gmax=33mT/m, slew rate=118mT/m/ms, desired FOV=350mm³, nominal voxel size=1mm³, TR=4.2ms TE=52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, and 78 µs for UTE images, TE=1172 µs for an out-of-phase image, readout duration for each echo=0.56ms, scan time=35sec, sampling bandwidth=250Hz, FA=1degree, # of radial spokes=7442, and # of SPI encoding=925.

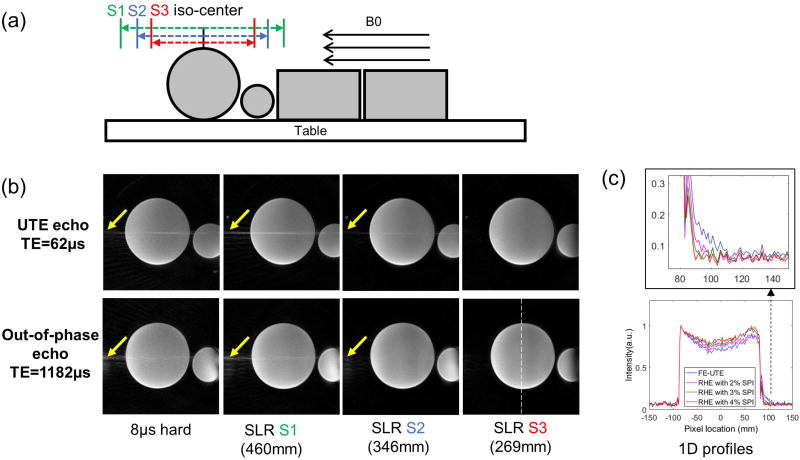
In the phantom experiment, data acquisition and image reconstruction for dRHE were tested using manufacturer-provided phantoms. Four phantoms were placed on the MR table as shown in Figure 3-a to mimic a human subject in size to evaluate streaking artifacts utilizing different slab selection strategies. Four different cases were tested: no slab selection (using a non-selective 8µs hard pulse), slab selection (using a 628µs SLR pulse with minimum phase) with slab size of 460 mm, 346 mm, and 269 mm. In addition to dRHE, conventional frequency encoding based UTE (FE-UTE) was obtained for comparison.

Figure 3.

Phantom experiment. (a) Experimental setup, (b) UTE and out-of-phase images with different slab selection, and (c) 1D profiles in out-of-phase images reconstructed with different sizes of SPI regions. Three different slab sizes were tested (S1=460mm, S2=346mm, S3=269mm) as in (a), where the smallest slab size (S3) showed the best image quality with minimal aliasing/streaking artifact in the S-I direction as shown in (b). (c) shows efficacy of SPI in reducing ringing artifacts in the out-of-phase echo image as shown in 1D profiles.

In vivo brain imaging was performed with 10 subjects in an IRB-compliant study. Patients undergoing clinical ¹⁸F-FDG PET/CT imaging were recruited to undergo additional simultaneous PET/MR imaging on a 3T PET/MR scanner (Signa PET/MR, GE Healthcare, Waukesha, WI). MR imaging consisted of the system-default MRAC scan and the proposed 35-second dRHE-MRAC acquisition during a 10-minute PET acquisition. In dRHE-MRAC acquisition, the slab size in S-I direction was adapted to individual patients to cover the whole skull of a patient (around 280–300mm), avoiding the shoulders. The CT image (from either a Discovery 710 or Discovery VCT PET/CT scanner [GE Healthcare]) was used as a ground truth comparison to quantitatively evaluate the accuracy of the proposed MRAC technique.

Data processing and analysis

To reconstruct MR images, convolution gridding (29) using kernel size=5, oversampling ratio=1.5 was applied, and phase-arrayed coil images were combined (32). Images were reconstructed with matrix size of 301×301×301, FOV=300mm, and nominal voxel size of 1 mm³. After image reconstruction, fat and water separated images were obtained using a 2-point Dixon reconstruction (Flex) from within the GE Healthcare Orchestra SDK. For bias correction, a 3D block of size 21×21×21 was used. For generation of the pseudo CT, assigned HU values were −1000, −42, 42, and 939 for air, fat, water, and bone, respectively, which is consistent with values used in other studies (5,33–35).

To evaluate the accuracy of pseudo CT generation, Dice coefficients for soft tissue, air, and bone were calculated using system available MRAC methods (soft tissue only [MRAC-1], atlas-based [MRAC-2]), the proposed dRHE-MRAC, and CT-based attenuation correction (CTAC) (a CT image spatially co-registered to the in-phase LAVA-Flex image [a two-point Dixon sequence] used for MRAC-1 and MRAC-2 using Elastix (36)) as the gold standard. To evaluate the efficacy of using multiple UTE images in dRHE for improved air/bone detection, two pseudo CT images were generated without and with multiple UTEs, and the Dice coefficient was calculated in each case. The reference CT images, which are continuously-valued, were thresholded to obtain tissue labels to calculate the Dice coefficient as follows: HU > 400 for bone, HU < −300 for air, otherwise soft tissue.

To evaluate PET quantitative accuracy, an offline PET reconstruction (PET Toolbox, GE Healthcare) was performed using MRAC-1, MRAC-2, dRHE-MRAC, and CTAC. PET reconstruction parameters were: 256×256 matrix, 300×300 mm² field of view, TOF-OSEM reconstruction algorithm, 28 subsets, 4 iterations, SharpIR, and 4 mm post filter.

PET images reconstructed from MRAC-1, MRAC-2, and dRHE-MRAC were compared to those reconstructed using CTAC. Pixelwise error maps were obtained by calculating the percentage error in image intensity relative to CTAC. Region-of-interest (ROI) analysis was performed using the IBASPM parcellation software (37). Repeated-measures one-way ANOVA were first used to compare absolute errors within each ROI for MRAC-1, MRAC-2 and dRHE-MRAC. Paired-sample t-tests were used for pairwise comparison between dRHE-MRAC and MRAC-1 and between dRHE-MRAC and MRAC-2. Statistical analysis was performed with statistical significance defined as a p < 0.05 after Holm-Bonferroni correction for minimizing type-I error(38). All image reconstructions and data analysis were performed in Matlab (2013a, MathWorks, Natick, MA, USA) using a computer equipped with an Opteron 6134 CPU.

RESULTS

Phantom experiment

Figure 3-b shows that the aliasing/streaking artifact in the S-I direction at UTE echo times is suppressed by utilizing selective excitation with an SLR pulse. The images using a non-selective 8µs hard pulse or larger slab selection exhibit objectionable streaking artifact due to the strong readout gradients utilized and the undersampled number of radial spokes necessary for fast imaging. Therefore, it is beneficial to use a selective SLR pulse with a slab matched to the S-I coverage of the PET detector (~25 cm). Figure 3-c shows the efficacy of hybrid encoding (with SPI) in reducing the ringing artifact in the fly-back echo (out-of-phase) image, owing to the SPI encoded central k-space that is more robust to errors in k-space trajectory relative to FE-UTE. As shown in the 1D profile (white dotted line), images with SPI encoding (magenta, green, and red) better suppress ringing artifact at object boundaries compared to FE-UTE without SPI encoding (blue).

In vivo - air and bone detection

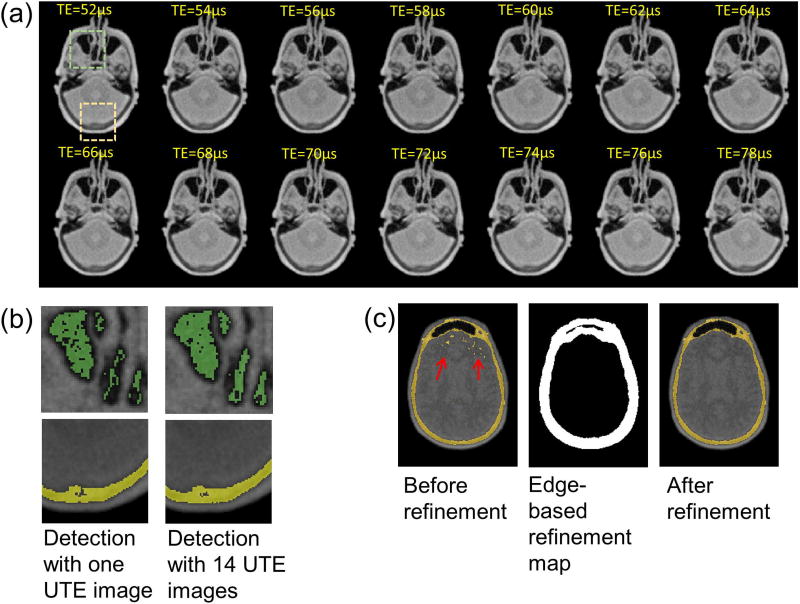
Figure 4-a shows 14 UTE images from the single 35 second dRHE scan, and Figure b shows a zoomed in view of the detected air (green) and bone (yellow) with one UTE image at 52µs or UTE images from 52µs to 78µs. As seen, an improved air map is detected using 14 UTE images. Bone detection also shows improvement by using multiple UTE images. Individual air and bone maps for each TE are shown in Supporting Figure S2. Figure 4-c shows the initially detected bone map before refinement, refinement map based on edge detection, and the resultant refined bone map. An edge map obtained by Canny edge detection was dilated to yield the refinement map, which was used to remove falsely detected bone within soft tissue (mostly white matter showing darker contrast) as indicated by the red arrows.

Figure 4.

Air and bone detection. Utilization of multiple UTE echoes (requiring only 2.5 seconds of additional scan time) improves the estimation of air and bone. (a) 14 UTE images, (b) air and bone detected with one UTE image or 14 UTE images, (c) refinement of the bone map using edge information.

In vivo - pseudo CT

Figure 5 shows 3 different slices from a single subject of a UTE image at TE=52µs before and after bias correction (Figure 5-a,b), an out-of-phase echo image at TE=1172µs (Figure 5-c), a water and fat image (Figure 5-d,e), a segmented bone and air (Figure 5-f,g) and the resultant pseudo CT image (Figure 5-h). dRHE-MRAC exhibits more accurate pseudo CT estimation relative to the real CT image (Figure 5-k) compared to MRAC-1 (Figure 5-i) and MRAC-2 (Figure 5-j). More 2D slices of the pseudo CT image are shown in Supporting Figure S3. Dice coefficients calculated in total 10 subjects for soft tissue, air, and bone in MRAC-1 were 0.89±0.01, 0.15±0.17, and 0±0, respectively. In MRAC-2, the Dice coefficients for soft tissue, air, and bone were 0.88±0.02, 0.31±0.11, and 0.59±0.05, respectively. In dRHE-MRAC, the Dice coefficients for soft tissue, air, and bone were respectively 0.95±0.01, 0.56±0.07, and 0.77±0.06 when only one UTE image (TE=52µs) was used for air/bone detection. Using multiple UTE images improved Dice coefficients for soft tissue, air, and bone to 0.95±0.01, 0.62±0.06, and 0.78±0.05, respectively, which shows the efficacy of using multiple UTE images (with no additional scan time) for air/bone detection. Compared with other approaches, dRHE-MRAC showed significantly improved detection rate in all tissue segments. Compared to the state-of-the-art MRACs reported in the literature, where the Dice coefficients for bone and air (inside subject) were reported as 0.75~0.81 and 0.60, respectively (16,39–41), the proposed dRHE-MRAC approach showed comparably robust bone and air detection despite the short scan time.

Figure 5.

Input images to dRHE-MRAC and resulting pseudo CT images. Relative to MRAC-1 and MRAC-2, dRHE-MRAC shows improved pseudo CT estimation. Three 2D slices of (a) a UTE image without bias correction, (b) a UTE image with bias correction, (c) an out-of-phase image, (d) a water image, (e) a fat image, (f) a segmented air image, (g) a segmented bone image, (h) a dRHE-MRAC pseudo CT image, (i) a MRAC-1 pseudo CT image, (j) a MRAC-2 pseudo CT image, and (k) a CTAC image used as ground truth.

In vivo - PET reconstruction

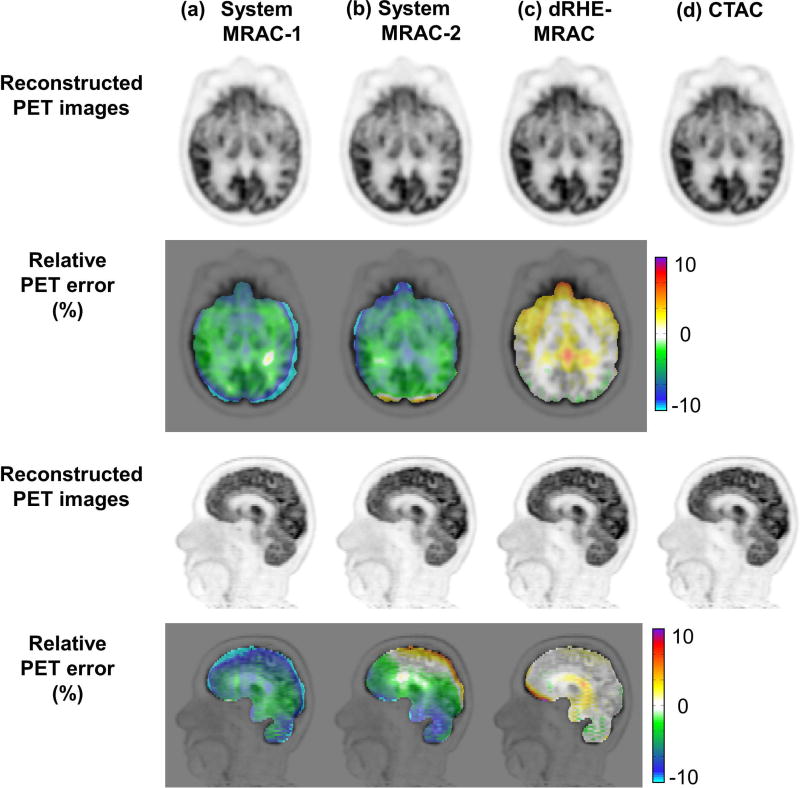
Figure 6 shows reconstructed PET images and the relative PET error in brain. MRAC-1 shows errors larger than 5% in most brain regions. MRAC-2 shows errors below 5% in the parietal lobe where the template for the upper brain case is expected to match well to individual patients, but in the other brain regions that are more individually unique, such as cerebellum, nasal cavities, and facial bones, errors larger than 5% are observed. dRHE-MRAC shows error rate less than 1% over most brain regions. In this study, there was a special case in which MRAC-2 (atlas-based method) failed due to incorrect registration, which is shown in Supporting Figure S4.

Figure 6.

PET reconstruction quality where dRHE-MRAC shows accurate PET reconstruction with percent error less than 1% in most brain areas. Reconstructed PET images and relative PET error maps with (a) MRAC-1, (b) MRAC-2, (c) dRHE-MRAC, and (d) CTAC.

Table 1 provides average error and standard deviation from three approaches within different brain regions. There was a significant difference between the average error of MRAC-1, MRAC-2 and dRHE-MRAC in all brain ROIs with p ranging from 4.5e-9 to 0.038 except for brainstem (p=0.055), right thalamus (p=0.063), and right subthalamic nucleus (p=0.069). Within all brain ROIs, dRHE-MRAC provides significantly lower absolute errors than MRAC-1 with p ranging from 7.9e-8 to 0.04 except for brainstem (p=0.098) and right subthalamic nucleus (p=0.058). dRHE-MRAC provides significantly lower absolute errors than MRAC-2 with p ranging from 5.3e-4 to 0.048 except for right frontal lobe (p=0.13) and right occipital lobe(p=0.068).

Table 1.

Image error (mean ± standard deviation) relative to CTAC for PET images reconstructed utilizing dRHE-MRAC, MRAC-1, and MRAC-2 in various brain regions of ten subjects.

Brain Regions	MRAC-1 error [%]	MRAC-2 error [%]	dRHE- MRAC error [%]
Frontal Lobe Left	−9.1 ± 3.8	−0.1 ± 5.2	−1.2 ± 1.3
Frontal Lobe Right	−10.7 ± 4.0	2.0 ± 6.2	−1.4 ± 1.4
Temporal Lobe Left	−2.3 ± 4.1	−5.6 ± 2.6	0.6 ± 1.2
Temporal Lobe Right	−5.7 ± 4.6	−4.2 ± 3.3	0.3 ± 1.3
Parietal Lobe Left	−9.1 ± 5.4	2.2 ± 4.5	−0.5 ± 1.3
Parietal Lobe Right	−9.8 ± 5.9	3.6 ± 5.1	−0.5 ± 1.5
Occipital Lobe Left	−10.1 ± 1.8	−2.7 ± 3.5	−1.0 ± 1.0
Occipital Lobe Right	−12.3 ± 2.0	−1.0 ± 4.2	−1.1 ± 1.0
Cerebellum Left	−4.5 ± 6.0	−7.0 ± 2.1	−1.9 ± 1.9
Cerebellum Right	−4.4 ± 6.3	−6.6 ± 1.8	−1.6 ± 2.1
Brainstem	−1.1 ± 5.4	−4.6 ± 2.8	0.5 ± 1.8
Caudate Nucleus Left	−2.7 ± 2.3	−1.2 ± 2.7	0.2 ± 1.0
Caudate Nucleus Right	−2.7 ± 2.0	−0.9 ± 3.0	0.1 ± 1.1
Putamen Left	−2.3 ± 3.0	−2.0 ± 2.6	0.2 ± 1.0
Putamen Right	−1.8 ± 2.9	−1.7 ± 2.7	0.3 ± 0.9
Thalamus Left	−2.3 ± 2.6	−1.3 ± 2.7	1.0 ± 1.1
Thalamus Right	−2.1 ± 2.3	−1.1 ± 2.9	0.9 ± 1.0
Subthalamic Nucleus Left	−2.2 ± 3.5	−1.8 ± 2.8	1.1 ± 1.2
Subthalamic Nucleus Right	−1.6 ± 3.3	−2.3 ± 2.3	0.9 ± 0.9
Globus Pallidus Left	−2.9 ± 3.6	−2.0 ± 2.8	0.3 ± 1.1
Globus Pallidus Right	−2.2 ± 3.1	−2.2 ± 2.5	0.2 ± 1.0
Cingulate Region Left	−4.5 ± 1.6	−0.3 ± 3.7	−0.6 ± 1.2
Cingulate Region Right	−4.5 ± 1.4	−0.1 ± 3.8	−0.7 ± 1.2
All	−4.8 ± 3.5	−1.8 ± 2.6	−0.2 ± 1.5

DISCUSSION

In this study, we proposed a new UTE-based MRAC approach that allows UTE and out-of-phase images to be obtained with high spatial resolution (1 mm) and a clinically feasible scan time (35 sec), by utilizing a dual echo RHE acquisition with notable improvements from the hybrid encoding approach and selective excitation of the SLR pulse. We have shown the efficacy of dRHE-MRAC for in vivo head imaging in 10 subjects. Because this method does not rely on atlas registration and is fast, it is expected to be adaptable to whole-body simultaneous PET/MR imaging where MRAC imaging must be performed at each bed position. Moreover, compared to approaches that utilize hybrid ZTE and Dixon approaches (18), dRHE-MRAC does not require additional fat/water imaging (Dixon or IDEAL) owing to the dual echo acquisition, which not only reduces scan time, but reduces the likelihood patient motion between UTE and fat/water imaging when acquired in multiple scans.

dRHE-MRAC reduces a total scan time in two ways: minimization of length of sequence and undersampling of radial spokes (to reduce the total number of TRs). To minimize length of sequence, a UTE echo (52 µs) is utilized as the in-phase echo with the following out-of-phase echo (around 1.1 ms), which shortens the pulse sequence length by 60% compared with conventional bipolar gradient echo acquisitions where two echoes are acquired at approximately 1.1ms and 2.2ms for 3T. To further shorten the pulse sequence, fly-back (bipolar) echoes were utilized, which reduces length of sequence by 33% relative to monopolar gradient echo imaging. Moreover, dRHE benefits from operation at the system hardware maximum slewrate and gradient amplitude. To reduce the number of TRs, 5.2% of all radial spokes were acquired relative to fully-sampled 3D radial imaging. To reduce the streaking/aliasing artifact caused by undersampled radial spokes and fast readout (high readout bandwidth) with a large FOV, slab selection was applied using an SLR pulse with minimum phase and successfully reducing the effective FOV in the S-I direction. Note that while good performance was obtained in spite of a high degree of radial undersampling using a straightforward gridding approach, the application of parallel imaging and compressed sensing reconstruction (42) is likely to improve image quality for future applications.

Because SPI encoding (pure phase encoding) is more robust to eddy currents that distort the k-space trajectory, we were able to reconstruct an image acquired during fly-in with no imaging artifacts. Moreover, by slightly over-sampling the SPI region (Nyquist sampling requires approximately 300 SPI encodings, whereas 925 were utilized), which requires an additional scan time of only 2.5 seconds, it was possible to obtain multiple UTE images. With the ability to obtain multiple UTE echoes, it may be possible to improve the reconstruction further, utilizing model-constrained approaches (43) or to directly estimate the T2* of bone by additional SPI oversampling to secure a wider range of TEs, which could be used to assign continuous HU values based on the T2* of bone (16) or contrast of PDW UTE image (19). In this study, we have shown the efficacy of utilizing multiple UTE images to improve air and bone detection. In addition, it has been reported that SPI can be utilized for imaging near metal owing to its robustness to magnetic susceptibility (44). In future work, we will explore the efficacy of SPI in dRHE in relation to image artifacts to achieve more reliable pseudo CT estimation near metallic implants.

Another strategy to leverage multiple UTE images is by simple averaging. This approach was tried, but only resulted in a slight improvement in SNR (10%) as shown in Supporting Figure S5. Note that the improvement in the air region was more noticeable. However, there were some issues for this approach. First, there is no simple way to average raw SPI-encoded k-space data between different TEs since they are sampled in different location in k-space (time-spreading sampling patterns). Alternatively, magnitude UTE images can be combined after gridding, but the Gaussian distribution of the histogram cannot be guaranteed. Averaging of the data in complex value domain (real and imaginary) is also challenging due to B₀-related phase change with TE. For the data obtained herein, the use of individual UTE images for bone and air detection with combined labeling empirically provided the best results.

Compared with ZTE-based MRAC methods (18,19), dRHE-MRAC is expected to achieve better image quality with reduced chemical shift artifact and blurriness in bone owing to the faster encoding. The encoding speed in ZTE imaging is inherently limited due to selective excitation effects related to minimum RF pulse width limitations, where the readout gradient amplitude must be kept low to avoid unwanted slice selectivity artifacts (45). Utilization of gradients with low amplitude requires a longer readout (e.g., readout duration=1.36 ms to achieve 2 mm³ spatial resolution in (18)), which can result in chemical shift artifacts and blurriness within short T2* tissues (e.g., bone) (20). dRHE-MRAC operates at the maximum slewrate and readout gradient to minimize the readout duration (readout duration=0.56ms to achieve 1mm³ spatial resolution), where encoding is more than 4 times shorter than ZTE, which improves image quality for bone (which has an expected T2* of 300–400 microseconds (46)).

dRHE-MRAC is based on reproducible image processing methods such as histogram-based thresholding, morphological processing, and edge detection. Therefore, processing time is very short compared with other methods such as atlas-based approaches where high computational complexity is imposed by registering template to image. In dRHE-MRAC, the processing time to generate a pseudo CT image was approximately 5 minutes using a MATLAB script, where the most computationally complex processes were bias correction (<100sec) and post processing (<90sec), which are both highly parallelizable tasks. However, various algorithm parameters required manual tuning such as thresholds for air/bone detection and Canny edge detection. In future work, we expect to incorporate a deep learning based segmentation framework to dRHE-MRAC to realize more generalizable and reliable postprocessing workflow (47,48).

CONCLUSION

In this study, we have proposed a rapid dual echo RHE-based MRAC technique, dRHE-MRAC, that benefits from dual echo acquisition and hybrid encoding to acquire UTE and out-of-phase images within a single scan (35 sec). The utilization of SPI encoding along with slab selection improved image quality, while still allowing fast image acquisition. Moreover, slightly oversampled SPI encoding enabled acquisition of multiple UTE images which was used to improve air and bone detection. Compared to existing MRAC approaches, dRHE-MRAC enabled the generation pseudo CT images with improved air, bone, and soft tissue detection with significantly reduced relative error in reconstructed PET images.

Supplementary Material

Supp info

Figure S1. Reconstruction of multiple UTE images. This shows how SPI data and radial frequency encoded data are combined to yield multiple UTE images. For example, let’s assume that there are 7442 radial spokes and 925 SPIs acquired in dRHE, and 250 data points are acquired with sampling interval of 2µs from TE1 to the end of readout for UTE in each TR. The 1st UTE image is reconstructed with 925 SPI data acquired at TE1 and 7442(250-1) radial data from TE1. The 2nd UTE image is reconstructed with 925 SPI data acquired at TE2=TE1+2µs and 7442(250-2) radial data from TE2. The n-th UTE image is reconstructed with 925 SPI data acquired at TEn=TE1+2(n−1) µs and 7442(250-n) radial data from TEn. The combined individual datasets are individually gridded to Cartesian grid and inverse Fourier transformed.

Figure S2. Air or bone detection using multiple UTE images. Air or bone maps are initially detected using individual UTE images, and then combined by logical summation to yield one air or bone map.

Figure S3. Pseudo CT image. Nine 2D slices of (a) a UTE image without bias correction, (b) a UTE image with bias correction, (c) an out-of-phase image, (d) a water image, (e) a fat image, (f) a segmented air, (g) a segmented bone, (h) a dRHE-MRAC pseudo CT image, (i) a MRAC-1 pseudo CT, (j) a MRAC-2 pseudo CT image, and (k) a CTAC image used as a ground truth. dRHE-MRAC shows improved pseudo CT estimation relative to MRAC-1 and MRAC-2.

Figure S4. In this study, there was one case in which MRAC-2 (atlas-based method) failed due to incorrect registration. Note that MRAC-1 in (a) failed to detect soft tissues around chin due to strong metallic dental implants as indicated by red arrow. MRAC-2 in (b) failed completely due to mis-registration of template. dRHE in (c) shows much improved detection of the soft tissues and most of bone, but is challenged by the susceptibility effects in bone regions near the dental implant.

Figure S5. A UTE image vs. an averaged UTE image. An averaged UTE image shows slightly improved SNR by 10% in this example. The improvement in air region was more noticeable as shown in a zoom-in view.