Abstract
Purpose
Estimation of brain metabolite concentrations by MR spectroscopic imaging (MRSI) is complicated by partial volume contributions from different tissues. This study evaluates a method for increasing tissue specificity that incorporates prior knowledge of tissue distributions.
Methods
A spectral decomposition technique was evaluated for separation of spectra from white-matter and gray-matter and for measurements in small brain regions using whole-brain MRSI. Simulation and in vivo studies compare results of metabolite quantifications obtained using the spectral decomposition technique to those obtained by spectral fitting of individual voxels, using mean values and linear regression against tissue fractions, and spectral fitting of regionally integrated spectra.
Results
Simulation studies showed that for gray-matter and the putamen, the spectral decomposition method offers <2% and 3.5% error, respectively, in metabolite estimates. These errors are considerably reduced in comparison to methods that do not account for partial volume effects or use regressions against tissue fractions. In an analysis of data from 197 studies, significant differences in mean metabolite values, and changes with age were found. Spectral decomposition resulted in significantly better linewidth, SNR and spectral fitting quality as compared to individual spectral analysis. Moreover, significant partial volume effects were seen on correlations of neurometabolite estimates with age.
Conclusion
The spectral decomposition analysis approach is of considerable value in studies of pathologies that may preferentially affect white or gray-matter, and smaller brain regions significantly affected by partial volume effects.
Keywords: magnetic resonance spectroscopic imaging (MRSI), partial volume effects, spectral decomposition, white-matter, gray-matter
INTRODUCTION
Proton Magnetic Resonance Spectroscopic Imaging (MRSI) enables non-invasive measurement of tissue metabolite distributions, which is of considerable value for studying neurological disease or injury (1,2). Clinical studies commonly rely on measurements of the relative metabolite concentrations and comparisons with normative values at the corresponding brain region or tissue. For this purpose, a previous study estimated regional distributions of brain metabolites in normal subjects at 3T using a data analysis approach that used spatial averaging of multiple MRSI voxels to obtain high-quality spectra from multiple atlas-registered anatomic regions of interest (ROIs) (3). However, regional estimation of brain metabolites is complicated by partial volume effects due to variations in tissue composition within an ROI and the relatively broad spatial response function of the MRSI acquisition. These partial volume effects can be particularly notable for measurements from gray-matter or smaller brain regions.
Tissue-specific metabolite concentrations for gray-matter (GM) and white-matter (WM) can be determined by regressing MRS measurements at multiple locations against MRI-derived tissue fractions for each location. Hetherington et al. demonstrated the application of this method to MRSI data to estimate metabolite concentrations in pure GM and WM by regressing against tissue fractions derived from segmentation of T1-weighted MRI (4). An alternative approach described by Tal et al. is to describe the signal at each voxel as the sum of two tissue compartments, leading to an over-determined system of equations that can be solved with least-squares optimization (5). Similarly, Spectral localization by imaging (SLIM) has been shown to be valuable method towards estimation of metabolite concentration from homogenous ROIs while accounting for partial volume effects (6,7). SLIM reconstructs compartmental spectra by solving an over-estimated system using the tissue information from high resolution MR images. Partial volume effects in MRSI can also be accounted for by modeling the spectrum from a voxel as a linear mixture of constituent spectra from the individual tissue regions. The linear mixture model can be represented as a superposition of the constituent spectra with the partial volume fraction used as weighting factors. Mandl et al. presented a linear model to estimate the metabolite concentration in the cingulum bundle using tissue fractions derived from segmentation of gray and white-matter from T1-weighted images, and the cingulum from diffusion tensor imaging (8). Statistical analysis methods, such as principal component analysis (PCA) (9) and independent component analysis (ICA) (10), perform the spectral factorization by exploiting statistical properties of covariance and independence. Nonnegative matrix factorization method has also been proposed for blind recovery of constituent spectra (11). This iterative method assumes that both the partial volume fraction and the constituent spectra can only take on non-negative values, and estimates simultaneously the partial volume fractions of the underlying tissue and the set of constituent spectra that result in the least error in the model.
The aims of this study are to evaluate the accuracy of a spectral decomposition technique that uses anatomical MR based tissue fractions as weighting factors. The technique is evaluated for separation of spectra corresponding to 100% WM and GM regions using a whole-brain MRSI measurement, and for analysis of a specific brain region that is subject to partial volume contributions from surrounding tissue. Results of metabolite quantifications obtained using the spectral decomposition technique are compared to those obtained by spectral fitting of individual voxels, using mean values and linear regression against tissue fractions, and spectral fitting of regionally integrated spectra (3). These methods are compared using simulation studies and volumetric MRSI data obtained from healthy subjects. Finally, we demonstrate the utility of the spectral decomposition technique towards estimation of metabolite concentrations in small anatomical regions such as thalamus and putamen, which are of value in various neurological conditions (12,13).
METHODS
Simulated MRSI Data
Simulated spectroscopic data were created to determine the accuracy of the spectral decomposition technique in estimating metabolite concentrations in volumes containing a mixture of GM and WM and for a region simulating the putamen. Evaluations were carried out for varying conditions of noise and spatial smoothing.
MRSI data sets were simulated using methods available in the MIDAS package (14,15), based on the BrainWeb structural images (16). The BrainWeb data consisted of a 1 mm isotropic T1-weighted image with segmentations of WM and GM, cerebrospinal fluid (CSF), skull, and a lipid layer. Additionally, maps for putamen were created by manually segmenting this region in the T1 image. The spectrum for each segmentation region was defined as a combination of single resonances for each simulated metabolite, using a Gaussian lineshape for all resonances with a linewidth of 5.0 Hz and for a field strength of 1.5 T.
Different spectral signatures were simulated in the WM, GM, CSF, and putamen to enable the accuracy of regional analyses to be determined. For WM and GM, the spectra were simulated with N-acetylaspartate (NAA) at 2.0 ppm, Creatine (Cr) at 3.0 ppm, Choline (Cho) at 3.2 ppm, and water at 4.7 ppm. Spectral amplitudes for the simulated spectra in the different tissue regions relative to H2O are given in Table 1. To provide a unique spectral pattern for the putamen, the spectra were simulated without Cr at 3.0 ppm but with an additional simulated peak at 2.5 ppm, referred to as pseudocreatine (psCr), since the simulated properties of this peak were similar to that of Cr in GM.
Table 1.
Simulated spectral amplitudes in different tissue regions.
| ppm | Tissue Regions | |||||
|---|---|---|---|---|---|---|
| WM | GM | CSF | Putamen | |||
| Simulated Metabolites | H2O | 4.7 | 1.0 | 1.0 | 1.0 | 1.0 |
| Cho | 3.2 | 0.9 | 1.0 | 0.0 | 1.0 | |
| Cr | 3.0 | 1.0 | 1.0 | 0.0 | 0.0 | |
| NAA | 2.0 | 1.2 | 1.0 | 0.0 | 1.0 | |
| psCr | 2.5 | 0.0 | 0.0 | 0.0 | 1.0 | |
Abbreviations: Cho = Choline; Cr = Creatine; CSF = cerebrospinal fluid; GM = gray-matter; NAA = N-acetylaspartate; psCr = pseudocreatine; WM = white-matter.
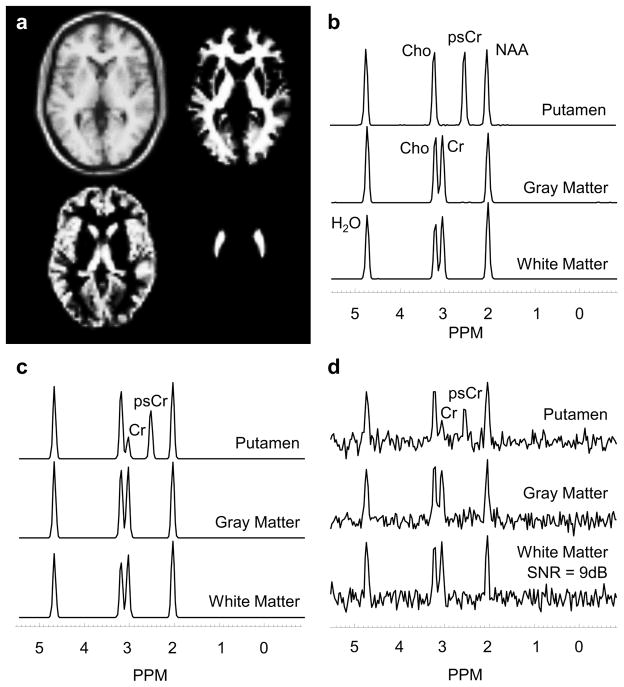
Each data set was simulated with a matrix size of 64 x 64 with 32 slices resulting in a simulated voxel size of 4 x 4 mm in-plane and a slice thickness of 6 mm. The resultant field of view was 256 x 256 x 192 mm3. Spectra were simulated with 256 spectral points and a sweep width of 1000 Hz. Random Gaussian spectral noise was simulated in time-domain and spatial smoothing was applied as a post-processing option. Five levels of spectral noise (0 – 4) were simulated that cover a range of signal-to-noise ratios (SNR) typical for human MRSI. To examine the effect of changes in the spatial response function a range of spatial smoothing was applied in k-space, from none to a value of σ = 2.0 using a Gaussian filter function expressed as exp(−σ*(2k/K)2), for −K/2 ≤ k ≤ K/2, where K is the number of k-space points. The combined effect of different noise and spatial smoothing levels represents a mean WM SNR range of 5 dB (noise level 4, no spatial smoothing) to 41 dB (noise level 0, spatial smoothing of σ = 2.0). SNR is estimated as the ratio of the height of the NAA peak to the standard deviation of the noise signal estimated between 0 to 1.2 ppm (3). SNR is expressed in decibels (dB) as 10*log10 (SNR). In Figure 1 are shown the simulated ROIs and the spectral signatures of each region for different noise and smoothing levels. T1 images and the segmented regions of WM, GM and putamen and the corresponding spectra are shown in Figure 1a and 1b. Partial volume effects are illustrated in Figures 1c and 1d for single voxel spectra from the putamen region, which is indicated by the reduced psCr and presence of Cr.
Figure 1.
a) Simulated brain model showing white and gray-matter regions and the putamen. Simulated spectral signatures are shown for each region, with b) zero noise and no spatial smoothing, c) zero noise and a spatial smoothing of σ = 2.0 and d) a noise level of 4 and a spatial smoothing of σ = 2.0.
Human MRSI Data
To examine the effect of the different methods on the evaluation of regional GM and WM metabolite concentrations and changes of these values with age, data were obtained from an existing database (17) for 197 normal subjects, 111 female and 86 male, with a mean age of 37.2 ± 14.2 years (median 35 years). Subjects completed a self-reporting questionnaire to indicate the absence of neurological or psychological disease or injury and all MRIs were confirmed to be without any structural abnormalities via visual inspection. Informed consent was acquired from each subject, and all studies were approved by the institutional review boards. Subjects underwent an MR study at 3T (Siemens Medical Solutions, Erlangen, Germany) that included a T1-weighted MRI and volumetric MRSI.
T1-weighted imaging was carried out using a 3D Magnetization Prepared Rapid Acquisition Gradient Echo (MPRAGE) sequence with 1.0 mm isotropic resolution; TR/TE/TI=2150/4.38/1100 ms; FA, 8°; NEX, 1; image matrix, 256 x 256 x 144. Whole-brain MRSI was acquired using echo-planar acquisition with spin-echo excitation; TR/TE = 1710/70 ms; non-selective lipid inversion-nulling with TI = 198 ms; a FOV of 280 x 280 x 180 mm3; k-space matrix size of 50x50x18 points; echo train length of 1000 points; bandwidth of 2500 Hz; and acquisition time of 26 min. The acquisition included a water reference measurement interleaved with the metabolite signal acquisition.
Preprocessing for in vivo MRSI data included corrections for B0 shifts (3), lipid k-space extrapolation (18), and linear registration between T1-weighted MR and whole-brain MRSI (14,19). Metabolite maps were interpolated to 64x64x32 points, for an interpolated voxel volume of 0.107 cc. Following spatial smoothing, the effective voxel volume was 1.55 cc.
Spectral Decomposition
A set of spectra from all voxels within an ROI can be represented as a system of linear equations that describe the fractional contributions from WM and GM as D ≈ WS ; where D(n x m) is a matrix of n voxel spectra with m points each, W(n x 2) is the fractional WM and GM content for each voxel, and S(2 x m) are the representative spectra for WM and GM each with m points. This system of linear equations can be solved for S as S = ((W)−1 WTD, where WT is the transpose of W.
For human studies, the tissue content in each SI voxel was estimated by downsampling the tissue segmentation maps obtained using FSL/FAST algorithm (20), using the spatial response function of the MRSI acquisition, to generate partial volume maps for WM, GM, and CSF. To remove the effect of CSF, which contributes no metabolite signal, the fractional tissue content for WM, fWM, was then derived as fWM = pWM/(pWM + pGM), where pWM and pGM are the fractions of WM and GM, respectively, as obtained from FAST. Similarly, fGM was estimated as fGM = pGM/(pWM + pGM). Before performing spectral decomposition, quality criteria were applied to remove spectra with a linewidth of >12 Hz or a CSF fraction >20%.
To demonstrate the utility of the spectral decomposition technique for estimation of relative metabolite concentrations in small anatomical regions, partial volume maps of the thalamus and putamen were created at SI resolution. For simulation studies, partial volume maps were created by manual segmentation of putamen followed by downsampling to the SI resolution, whereas, for in vivo studies, partial volume maps were derived by inverse transforming the AAL atlas (21) to the subject space at MRSI resolution (22). Contribution of partial volume fractions was accounted for by updating the WM and GM fractional tissue contents respectively as fWM = pWM/(pWM + pGM + pSub) and fGM = pGM/(pWM + pGM + pSub), and by incorporating an additional tissue fraction fSub = pSub/(pWM + pGM + pSub) in the linear system. Here, fSub and pSub are the fractional tissue content and partial volumes calculated for the sub-cortical region under consideration (putamen or thalamus).
Comparative Analysis
The relative metabolite concentrations estimated for WM and GM by the spectral decomposition technique (sDec) were compared to those obtained by (i) fitting of a spectrum obtained by integrating all spectra within an ROI (M-Int) (3); (ii) averaging the results from fitting individual voxels within a ROI (vAvg); and (iii) linear regression of values obtained by fitting individual spectra against tissue fractions (vReg) (15). M-Int spectra for WM and GM regions were created by averaging voxels with >80% of WM and GM tissue fraction respectively. The vReg method used the metabolite estimates obtained by fitting of a single voxel, which is the same employed in the vAvg method, with the addition of linear regression-based correction for partial volume effects (4,15).
Spectral analysis was carried out using the FITT program (23), which included estimation of H2O, NAA, Cho, Cr and psCr for simulation data; and NAA, Cho, and Cr for the human data. Depending on the estimation method, spectral analysis was either carried out on individual voxels (vAvg and vReg) or the calculated high SNR spectra (M-Int and sDec) for each ROI independently. For all methods, fitted spectra with a linewidth of >12 Hz, CSF fraction >20%, and Cramer-Rao Lower Bounds (CRLB) > 10% for the fitting of NAA, Cho, or Cr were excluded from any further analysis. Additionally, for the vAvg and vReg methods, voxels with outlying data values were also excluded using a threshold based on the mean value and standard deviation of all voxels within the ROI, with values ≥3 times the standard deviation (SD) away from the mean being omitted from the analysis.
For simulation data, the ratios of NAA, Cho, Cr, and psCr to H2O were calculated for different noise values and spatial smoothing settings, and the percent absolute error in estimation of NAA/H2O, Cho/H2O, and Cr/H2O were calculated for GM and WM and NAA/H2O, Cho/H2O, and psCr/H2O were calculated for the putamen.
For in vivo studies, the metabolite maps were spatially registered to a reference MRI, defined in MNI space, and a lobar level atlas (14) was used to estimate lobar mean values of NAA/Cr and Cho/Cr for WM and GM. A partial fraction of 50% was used to assign a voxel to a particular lobe of the brain in the reference atlas. Two-tailed paired t-tests were carried out to identify if estimated metabolite ratios obtained by the M-Int, vAvg, and vReg methods were significantly different from those estimated using the sDec method. A False Discovery Rate (FDR) corrected p-value less than 0.05 was considered significant for the differences. Additionally, mean lobar SNR was also reported. For spectral decomposition and M-Int methods, the SNR of the resultant spectrum is reported whereas for the vAvg (and consequently vReg) the mean SNR of the constituent spectra of the ROI is reported. For assessment of spectral quality, whole-brain WM and GM linewidth and CRLBs of spectral fitting of NAA, Cr, and Cho are reported.
General linear models were used to evaluate correlations of lobar NAA/Cr and Cho/Cr with age, controlling for the effect of gender. In the case that gender effects were found insignificant, associations of metabolites with age were assessed using linear regression analysis. An FDR corrected p-value less than 0.05 was considered significant for the correlations.
RESULTS
Simulation Results
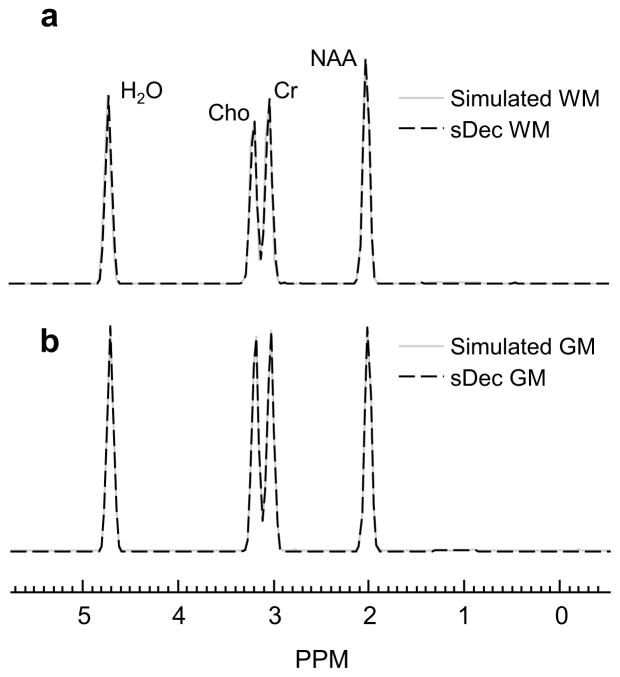
In Figure 2 are shown the simulated spectra and the resultant spectrum using the SDec method for parietal WM and GM lobar regions under no noise and no spatial smoothing conditions. The simulated and the sDec derived spectra are qualitatively identical in the absence of noise and spatial smoothing with small errors in the estimation of NAA/H2O (0.32%), Cho/H2O (0.24%), and Cr/H2O (0.23%).
Figure 2.
Comparison of simulated spectra and sDec derived spectrum in parietal (a) WM and (b) GM for zero noise and no spatial smoothing.
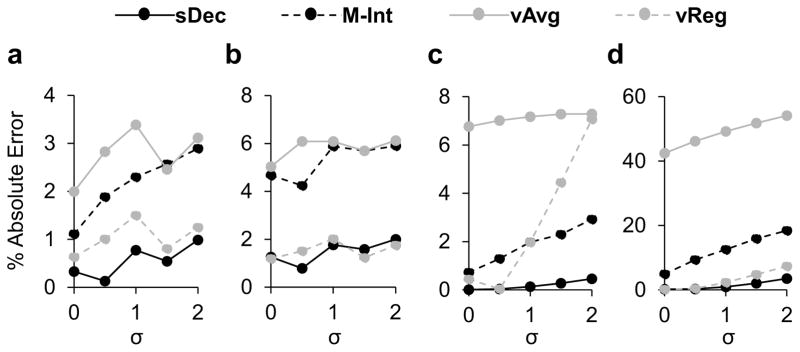
In Figure 3a and 3b are shown the results for the quantification of NAA/H2O in GM and WM, and in Figure 3c and 3d are shown NAA/H2O, and psCr/H2O in the putamen, respectively. The graphs show the percent absolute errors in the estimation of metabolite ratios for zero noise conditions with different spatial smoothing to examine the performance of the different methods with increasing partial volume effects. Results demonstrate that for WM (Figure 3a), a considerably homogeneous region, M-Int, vAvg, and vReg show on average 2.12 ± 0.67%, 2.75 ± 0.54% and 1.04 ± 0.34% across different smoothing levels for the NAA/H2O ratio with the sDec method performing the best showing 0.60 ± 0.36% error. For GM regions (Figure 3b), there is a clear difference between the performance of methods that account for partial fractions, sDec and vReg, which show an error <2%, and those that do not, M-Int and vAvg, which show an average error of approximately 6% for NAA/H2O and 8% for Cho/H2O and Cr/H2O (results not shown).
Figure 3.
Results for quantification of NAA/H2O in white-matter (a), gray-matter (b), and putamen (c), and psCr/H2O in the putamen (d) for zero noise condition and a varying spatial smoothing σ.
The results for metabolite ratio estimation in the putamen show that the sDec method outperforms the other approaches, with an error of <1% for the estimation of NAA/H2O (Figure 3c). The M-Int method also performed well, with errors in the range of 2–3%. However, methods that rely on spectral fitting of individual spectra (vAvg and vReg) show a worse performance with increasing errors with higher smoothing. Results for the estimation of psCr/H2O in the putamen (Figure 3d) show the considerable advantage of spectral decomposition. In the worst case, the sDec method showed an error of 3.5% while vReg, M-Int, and vAvg showed errors of 7.4%, 18.4%, and 54.1%, respectively, in psCr/H2O estimation for a smoothing of σ = 2.0.
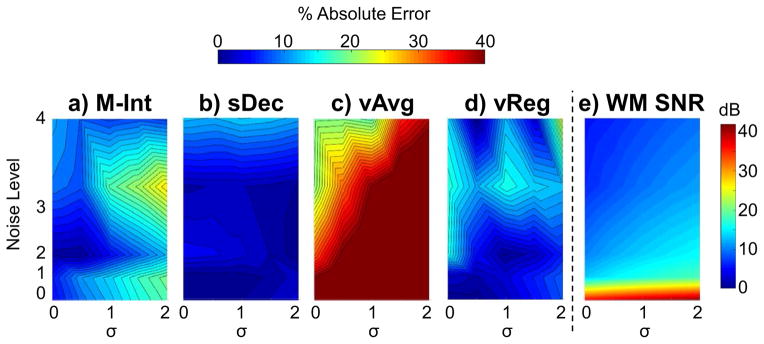
Quantitative analysis for estimation of psCr/H2O in the putamen under various noise and smoothing conditions is shown in Figure 4. The estimated SNR for WM NAA is also shown, as a function of noise and smoothing. The maps in Figure 4 show that the percent absolute error in estimated psCr/H2O increases with larger noise values. As would be anticipated for a small ROI and measurements from noisy single-voxel spectra, the volume averaging method shows a considerable error, reaching a maximum value of 54%. By spectral averaging, the fitting errors can be reduced and the maximum error for the M-Int method is reduced to 25%. The maximum error values for the sDec and vReg methods were much smaller at 13% and 17%, respectively, and showed a flatter error map than the others. The sDec showed slightly improved performance at larger spatial smoothing (σ > 1.0).
Figure 4.
Maps showing the percent absolute error in the estimation of psCr/H2O in the simulated putamen area using M-Int (a), sDec (b), vAvg (c), and vReg (d) methods along with the WM SNR (e) as a function of noise and spatial smoothing, σ.
In simulation studies, the average number of voxels analyzed across different noise and spatial smoothing combinations in WM ROIs were 701 ± 147 (frontal lobe), 169 ± 42 (temporal lobe), 353 ± 67 (parietal lobe), 122 ± 41 (occipital lobe), and 121 ± 54 (cerebellum). GM ROIs had 190 ± 179 (frontal lobe), 164 ± 122 (temporal lobe), 81 ± 83 (parietal lobe), 53 ± 55 (occipital lobe), and 912 ± 104 (cerebellum) voxels in lobar regions. On the other hand, putamen ROIs had 46 ± 17 voxels.
Finally, simulation results showed that both M-Int and sDec methods, due to their inherent spectral averaging property, showed an average improvement of 319% and 270% in lobar WM SNR, respectively, relative to single voxel spectra.
In Vivo Results
In Table 2 are shown the results for mean lobar measures for Cho/Cr in WM and GM using the four estimation methods. Along with lobar ratios, absolute percent differences are also reported. These percent differences report the deviation that the M-Int, vAvg, and vReg methods show from the developed sDec method for estimation of Cho/Cr in WM and GM. In WM, there were no significant differences for the M-Int and sDec results, whereas the vAvg and vReg methods showed significant differences in multiple regions across the brain. Whole-brain Cho/Cr maps showed an average difference of 1.9%, 4.3%, and 4.0% for M-Int, vAvg, and vReg methods, respectively, in the WM. GM analysis indicated a greater number of brain regions with significant differences between the results from the different methods compared to the WM results. On comparing other methods to sDec, vReg methods showed the best agreement, though still reported differences of up to 18% for Cho/Cr. Considerably larger differences were seen for Cho/Cr with M-Int and vAvg methods. For NAA/Cr, the analysis showed a mean difference of 1.0%, 2.5%, and 1.72% for NAA/Cr in WM for M-Int, vAvg and vReg methods, respectively (Supporting Table S1).
Table 2.
Measures of Cho/Cr calculated in lobar WM and GM, thalamus, and putamen using sDec, M-Int, vAvg, and vReg methods. The percent absolute differences calculated using M-Int, vAvg, and vReg methods as compared to sDec methods are also shown. Significant differences from the sDec method are shown with asterisks with FDR corrected p<0.05, p<0.01, and p<0.001 denoted by *, **, and ***, respectively. Results are shown for the right and left frontal (RF and LF), temporal (RT and LT), parietal (RP and LP), and occipital (RO and LO) lobes, and the cerebellum (C).
| WM | Cho/Cr (Mean ± Std. Dev.) | % Absolute Difference from sDec | |||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Region | sDec | M-Int | vAvg | vReg | M-Int | vAvg | vReg |
| RF | 0.302 ± 0.031 | 0.299 ± 0.031 | 0.309 ± 0.035 | 0.313 ± 0.036 | 1.151 | 2.120 | 3.324 (*) |
| LF | 0.298 ± 0.032 | 0.295 ± 0.031 | 0.306 ± 0.036 | 0.31 ± 0.037 | 0.891 | 2.664 (*) | 3.982 (**) |
| RT | 0.309 ± 0.034 | 0.301 ± 0.033 | 0.318 ± 0.034 | 0.319 ± 0.036 | 2.703 | 3.088 (*) | 3.108 (*) |
| LT | 0.288 ± 0.031 | 0.284 ± 0.031 | 0.3 ± 0.03 | 0.297 ± 0.033 | 1.511 | 4.378 (***) | 3.124 (*) |
| RP | 0.285 ± 0.032 | 0.282 ± 0.031 | 0.295 ± 0.033 | 0.303 ± 0.036 | 1.081 | 3.382 (**) | 6.257 (***) |
| LP | 0.282 ± 0.03 | 0.279 ± 0.029 | 0.289 ± 0.03 | 0.301 ± 0.034 | 0.958 | 2.438 (*) | 6.764 (***) |
| RO | 0.215 ± 0.03 | 0.215 ± 0.027 | 0.222 ± 0.028 | 0.224 ± 0.031 | 0.084 | 3.479 (*) | 4.32 (**) |
| LO | 0.216 ± 0.031 | 0.213 ± 0.028 | 0.229 ± 0.029 | 0.225 ± 0.035 | 1.444 | 6.21 (***) | 4.261 (*) |
| C | 0.279 ± 0.065 | 0.298 ± 0.052 | 0.309 ± 0.049 | 0.281 ± 0.055 | 6.806 | 10.745 (***) | 0.896 |
| GM | Cho/Cr (Mean ± Std. Dev.) | % Absolute Difference from sDec | |||||
|
| |||||||
| Region | sDec | M-Int | vAvg | vReg | M-Int | vAvg | vReg |
| RF | 0.197 ± 0.027 | 0.269 ± 0.04 | 0.262 ± 0.037 | 0.214 ± 0.031 | 36.499 (***) | 32.823 (***) | 8.556 (***) |
| LF | 0.193 ± 0.027 | 0.254 ± 0.044 | 0.256 ± 0.039 | 0.228 ± 0.032 | 31.54 (***) | 32.345 (***) | 18.224 (***) |
| RT | 0.162 ± 0.025 | 0.223 ± 0.067 | 0.215 ± 0.042 | 0.139 ± 0.025 | 37.699 (***) | 33.023 (***) | 14.306 (***) |
| LT | 0.161 ± 0.028 | 0.232 ± 0.045 | 0.229 ± 0.045 | 0.176 ± 0.025 | 44.576 (***) | 42.361 (***) | 9.529 (***) |
| RP | 0.135 ± 0.024 | 0.181 ± 0.024 | 0.181 ± 0.024 | 0.146 ± 0.028 | 34.512 (***) | 34.526 (***) | 8.164 (***) |
| LP | 0.137 ± 0.023 | 0.182 ± 0.028 | 0.185 ± 0.025 | 0.163 ± 0.024 | 32.376 (***) | 34.852 (***) | 18.845 (***) |
| RO | 0.122 ± 0.025 | 0.176 ± 0.04 | 0.167 ± 0.025 | 0.124 ± 0.023 | 43.925 (***) | 36.083 (***) | 1.158 |
| LO | 0.134 ± 0.024 | 0.176 ± 0.026 | 0.172 ± 0.025 | 0.15 ± 0.024 | 31.097 (***) | 27.697 (***) | 11.791 (***) |
| C | 0.179 ± 0.03 | 0.213 ± 0.037 | 0.196 ± 0.036 | 0.172 ± 0.026 | 19.597 (***) | 9.97 (***) | 3.685 (*) |
| Cho/Cr (Mean ± Std. Dev.) | % Absolute Difference from sDec | ||||||
|
| |||||||
| Region | sDec | M-Int | vAvg | M-Int | vAvg | vReg | |
| Thalamus | 0.289 ± 0.034 | 0.291 ± 0.033 | 0.303 ± 0.037 | 0.567 | 4.813 (***) | 4.798 (***) | |
| Putamen | 0.263 ± 0.033 | 0.266 ± 0.031 | 0.267 ± 0.032 | 1.223 | 1.847 | 1.598 | |
In vivo results show that for WM regions M-Int and sDec (average difference of 1.9%) show slightly better agreement in quantification of Cho/Cr than vReg and sDec (average difference of 4.0%), whereas vReg and sDec methods show better agreement in GM regions (average difference of 10.5% for vReg vs. 34.6% for M-Int). At noise levels comparable to in vivo data (Noise level = 3) similar trend was seen in simulated data. In Figure 5 are shown the percent absolute errors in measurement of Cho/H2O in simulated data at noise level 3 (9.3±4.0 dB). Results show that in WM lobar regions M-Int (3.75%) shows similar (p = 0.729) performance as vReg (3.92%) across different spatial smoothing levels, but in GM regions vReg shows significantly improved (p< 0.01) performance as compared to the M-Int method. Moreover, the sDec method shows significantly improved (p<0.01) performance than both M-Int and vReg methods in GM regions.
Figure 5.
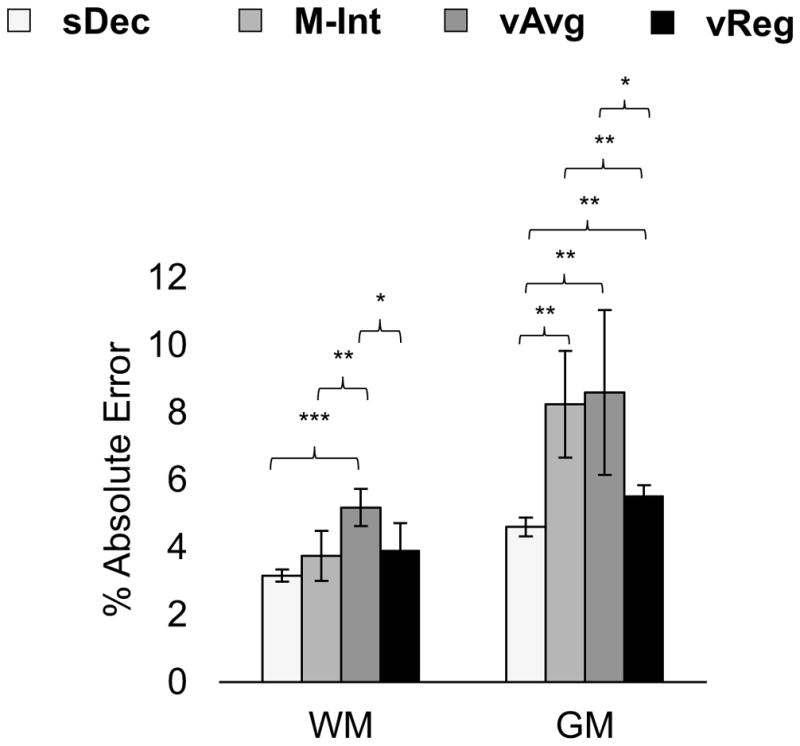
Errors in estimation of Cho/H2O in (a) WM and (b) GM averaged across spatial smoothing levels using sDec, M-Int, vAvg, and vReg methods in simulation data with noise comparable to in vivo data. Significant differences using two-sample t-test with p<0.05, p<0.01, and p<0.001 are denoted by *, **, and ***, respectively.
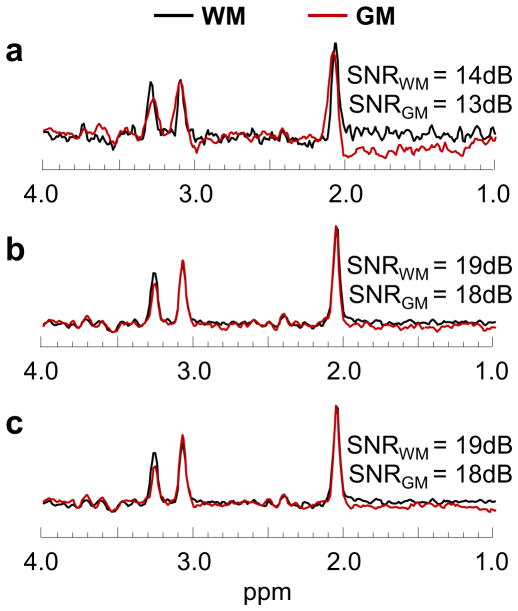
In Figure 6 are shown typical WM and GM spectra from the parietal lobe for a) single voxels, as used in the vAvg and vReg methods; b) obtained using the M-Int method; and c) derived using the sDec method. The sDec and M-Int methods show an average improvement of 175% and 190% in lobar WM SNR and a 145% and 139% improvement in lobar GM SNR, respectively, as compared to the single voxel spectra that are used for the spectral fitting with the vAvg and vReg methods. However, sDec and M-Int methods do not show significant differences (p>0.05) in SNR from each other. The sDec derived WM and GM spectra for an individual from all lobar regions has been provided in Supporting Figure S1.
Figure 6.
Typical single voxel WM and GM spectra in parietal lobe used in vAvg and vReg methods (a), WM and GM spectra using spectral averaging (M-Int) over the parietal lobe (b), and representative WM and GM spectra using the spectral decomposition (sDec) method (c).
The number of voxels analyzed in WM ROIs for in vivo studies was 651 ± 54 in the frontal lobe, 195 ± 20 in the temporal lobe, 417 ± 33 in the parietal lobe, 135 ± 20 in the occipital lobe, and 138 ± 58 in the cerebellum. In contrast, GM ROIs had fewer voxels analyzed with frontal, temporal, parietal, and occipital lobar regions comprising of 102 ± 31, 51 ± 16, 54 +12, and 28 ± 6 respectively.
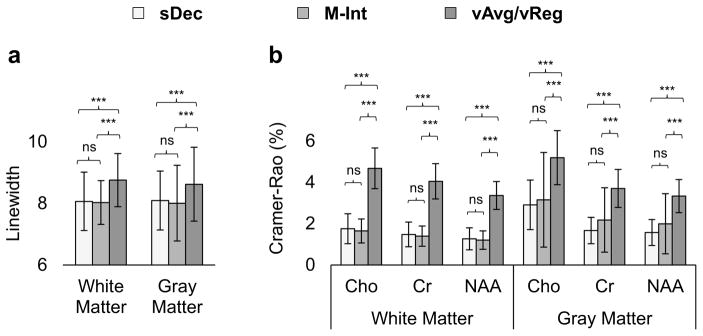
The average whole-brain spectral linewidth and the CRLB of the spectral fitting assessed using the four methods are shown in Figure 7. sDec and M-Int methods show a significant (p < 0.001) improvement in linewidth as compared to individual voxel. Additionally, significantly (p <0.001) lower CRLB were seen for M-Int and sDec methods as compared to vAvg or vReg methods. sDec and M-Int methods do not show significant (p > 0.05 ) differences from each other in terms of linewidth or CRLB.
Figure 7.
Whole-brain linewidth (a) and CRLB (b) for spectra evaluated using sDec, M-Int, vAvg, and vReg methods. CRLBs for the spectral fitting of Cho, Cr, and NAA in WM and GM are reported. Significant differences with p<0.05, p<0.01, and p<0.001 are denoted by *, **, and ***, respectively, with ns = not significant.
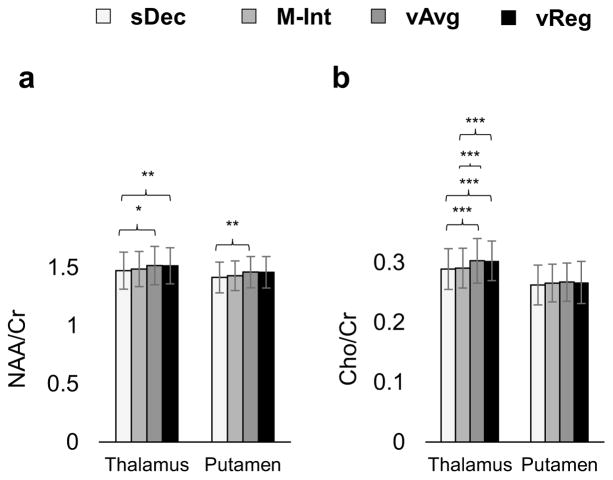
In Figure 8 are shown the mean metabolite estimates for the thalamus and putamen for all subjects. NAA/Cr and Cho/Cr in thalamus calculated using sDec were significantly (p < 0.05) lower than that calculated using vAvg and vReg methods. M-Int method shows a significant difference from vAvg and VReg method only in the estimation of Cho/Cr. The vAvg method shows a 3.0%, and 4.8% over-estimation of NAA/Cr and Cho/Cr, respectively, as compared to the sDec method. Similar findings are seen in the putamen with significant (p < 0.05) variations in NAA/Cr between the sDec and vAvg methods. vAvg and vReg methods did not show significant (p > 0.05) differences in estimation of either metabolite in thalamus or putamen. Over-estimation in NAA/Cr using the vAvg method seen in the thalamus and putamen can be attributed to bleeding from surrounding white-matter regions due to partial volume effects. This finding is consistent with other reports that indicate higher NAA/Cr in surrounding WM as compared to the thalamus (24).
Figure 8.
NAA/Cr (a) and Cho/Cr (b) calculated in the thalamus and putamen using the sDec, M-Int, and vAvg methods. Significant differences in metabolite ratios are shown with asterisks. FDR corrected probabilities p<0.05, p<0.01, and p<0.001 are denoted by *, **, and ***, respectively.
Impact of Estimation Techniques on Age and Gender Correlations
Age- and gender- dependent regression of lobar metabolite ratios, NAA/Cr and Cho/Cr, showed that gender was not significant in regression models (FDR p>0.05), therefore results using linear regression with age are reported. The slopes of regressions were compared using Student t-tests (25). Regression of NAA/Cr as estimated by the sDec method showed a −3.1% change per decade in right frontal WM. In comparison, the M-Int, vAvg, and vReg methods showed significantly (p < 0.05) lower values of −2.3%, −2.2%, and −2.3% change per decade, respectively. For Cho/Cr, the sDec method indicated a 3.0% increment per decade, whereas the vAvg, vReg, and M-Int methods returned values of 1.7%, 3.0%, and 2.6%, respectively, although only the M-Int method show a significant difference compared to the sDec method (p < 0.05). Detailed results of regressions in WM and GM regions can be found in Supporting Tables S2 and S3 respectively.
DISCUSSION
This study has evaluated a spectral decomposition technique to quantify mean values of tissue-specific metabolites using MRSI measurements that account for partial volume effects. Comparisons with other methods commonly used for regional analysis of MRSI studies demonstrate that the spectral decomposition technique provides increased accuracy for estimation of metabolite concentrations over a range of SNRs and spatial resolutions. The sDec method was also applied to the analysis of MRSI data from a large cohort of human subjects to examine how the analysis method may impact measurements in the relatively small volumes of the thalamus and putamen, as well as the associations of regional metabolite ratios with age and gender. The findings of this study indicate that significant differences in the measured metabolite ratios are obtained when partial volume effects are accounted for.
Simulation results showed that the spectral decomposition method showed little value in large homogeneous regions, such as lobar WM; however, in regions where partial volume effects are more pronounced the sDec and vReg methods clearly show significant improvement in the estimation of relative metabolite concentrations (Figure 3). While both the sDec and vReg methods account for partial volume effects, the vReg method can have larger errors as a result of fitting single voxel spectra with lower SNR. In addition to the increased spectral SNR obtained by the sDec method, this commonly generates spectra with better baselines as compared to individual spectra, as seen from Figure 6, which can benefit the spectral analysis. Moreover, individual spectra fitting is affected due to the presence of residual lipid signals and unsuppressed water artifacts which are generally reduced due to the inherent averaging property of the sDec method.
Comparison of the M-Int and vReg methods showed that for WM regions both methods performed similarly, however in GM regions vReg method performed significantly better than M-Int. In WM regions which are comparatively more homogenous than GM, the M-Int spectrum is similar to sDec spectrum, whereas the significant partial volume effects in GM result in quantification errors when simple averaging is employed. In principle, the sDec and vReg methods are inherently weighted averaging techniques that work with spectra and fit results, respectively, accounting for tissue fraction and show improved performance over simple averaging in GM regions.
Several studies have presented techniques to account for partial volume effects in MR spectroscopic imaging studies. Tal et al. (5) showed a theoretical 10% error for measurement of Cr in WM due to partial volume effects assuming a 20% contamination of WM voxels from the GM. In this study, the simulation found a 6–8% error for the vAvg method in quantifying Cr/H2O for GM, which was similar to that offered theoretically (5). However, human studies showed that a variation of 31.5% was seen using vAvg methods in the estimation of GM Cho/Cr as compared to the sDec method. The larger errors in human data as compared to simulation (or theoretical) can be attributed to errors in the fitting of individual voxels and in the tissue segmentation. Additionally, for vAvg and vReg methods that analyze individual spectra outliers may impact the accuracy of the estimations, especially in small regions with few voxels. The effect of the outliers was reduced by imposing a standard deviation based threshold and limiting the analyses to ROIs with at least 25 voxels.
Sajda et al. demonstrated the use of a nonnegative matrix factorization approach to derive constituent MRSI spectra and showed the utility of the technique towards estimating spectra in lesions (11,26). Mandl et al. have used the spectral decomposition technique to analyze 2D MRSI data based on voxel selection using diffusion tensor fiber tracking to estimate a single spectrum for the cingulum bundle while accounting for partial volume effects from WM and GM (8). Maudsley et. al. mapped metabolite concentrations in WM and GM using regression to tissue fractions to account for partial volume effects, which has been replicated in this study in the vReg method (15). The current study, not only presented an effective non-iterative method for spectral decomposition but provided the most comprehensive analysis to date of errors in relative metabolite estimation due to partial volume effects in various tissue compartments.
For a lobar analysis, the sDec technique showed a 270% improvement in the SNR of the spectra obtained after decomposition compared to individual voxels. Su et. al. showed that a minimum individual voxel spectrum SNR of 4dB was required for accurate estimation of constituent spectra using the nonnegative matrix factorization scheme (26). For this study, lobar spectra derived using sDec method showed an average WM and GM SNR of 19dB and 18dB, respectively. This increased SNR as a result of the inherent averaging property of the sDec method while accounting for partial fractions offers significant improvement in fitting quality and reliability of metabolite estimates.
The simulation study indicated that for estimation of metabolites in small ROIs, such as the putamen, the simple voxel averaging approach can result in errors of 40 to 55% (Fig. 2c). However, in the good SNR situation, the sDec and M-Int methods showed similar performance, suggesting that the advantage of the sDec method is seen most clearly where partial volume effects are even larger, as in measurements in the cortical GM.
The regression analyses indicated strong associations with age for NAA/Cr, in both lobar WM and GM regions, and for Cho/Cr in WM, similar to those previously reported (15,27–29), but also that significant differences in the findings were found between the analysis methods. A previous study that applied the vReg analysis method to a sub-sample of the data analyzed in this study, showed that NAA/Cr reduced at the rate of −3.68%/decade in frontal WM regions (15). This study showed an average change of −3.12%/decade in frontal WM (averaged over left and right hemisphere) using the sDec method. Differences of the reported values, which are on the order of 10–15% in the cerebrum and 23% in the cerebellum for WM NAA/Cr, may be attributed to the additional subjects included, better spectral fitting of high SNR spectra (Figure 7) and different quality control criteria used in this study. To account for the different sample sizes between this study and (15), a regression analysis performed using a reduced sample of 88 subjects showed that NAA/Cr calculated using the sDec method in frontal WM reduced at the rate of −3.23%/decade. The differences found for the associations of the metabolite ratios with age with the different analysis methods are impacted by errors due to spectral fitting making it difficult to estimate the direct effect of partial volumes on these correlations.
An obvious limitation of all the ROI-based analysis approaches used in this study is the inability to account for variations across the ROI or tissue type. In the case of diseases that show focal changes, such as the presence of lesions or white-matter abnormalities, the assumption of uniformity across an ROI or tissue type may not hold true and the methods presented would only be sensitive to the average change over the ROI. Moreover, the simulated data are simplified to have a constant linewidth, lineshape, and a homogenous bias field rendering any heterogeneity across an ROI muted. The presented technique assumes homogenous relaxation rates, bias field, and linewidth across an ROI. Preprocessing for in vivo MRSI data included corrections for B0 shifts but variations in linewidth were not accounted for. This study was also limited to metabolite ratios, to reduce the effects of receive and transmit bias fields (30) and CSF partial volume contribution. Finally, the methods that aim to account for tissue content are limited by the accuracy of the tissue segmentation algorithms, which differ in their approaches to assign partial tissue fractions based on MRI images and can be affected by motion and field inhomogeneity (31).
In summary, this study indicates that the spectral decomposition analysis approach is of considerable value in studies of pathologies that may preferentially affect either WM or GM, and also provides increased accuracy for measurements in smaller brain regions that are subject to significant partial volume effects.
Supplementary Material
Supporting Figure S1: The sDec derived WM and GM spectra for an individual from all studied lobar regions. Results are shown for the right and left frontal (RF and LF), temporal (RT and LT), parietal (RP and LP), and occipital (RO and LO) lobes, and the cerebellum (C).
Supporting Table S1: Lobar measures of NAA/Cr calculated in WM and GM using sDec, M-Int, vAvg, and vReg methods. The percent absolute differences calculated using M-Int, vAvg, and vReg methods as compared to sDec methods are also shown. Significant differences from the sDec method are shown with asterisks with FDR corrected p<0.05, p<0.01, and p<0.001 denoted by *, **, and ***, respectively.
Supporting Table S2. Regression equations for associations of NAA/Cr and Cho/Cr with Age in WM regions. The table reports the R2 and False Discovery Rate (FDR) corrected p-values for the lobar regression.
Supporting Table S3. Regression equations for associations of NAA/Cr and Cho/Cr with Age in GM regions. The table reports the R2 and False Discovery Rate (FDR) corrected p-values for the lobar regression.
Acknowledgments
This work was supported by National Institute of Health (NIH) grants R01CA172210 and R01EB016064.
References
- 1.Ross B, Michaelis T. Clinical applications of magnetic resonance spectroscopy. Magn Reson Q. 1994;10(4):191–247. [PubMed] [Google Scholar]
- 2.Soares DP, Law M. Magnetic resonance spectroscopy of the brain: review of metabolites and clinical applications. Clin Radiol. 2009;64(1):12–21. doi: 10.1016/j.crad.2008.07.002. [DOI] [PubMed] [Google Scholar]
- 3.Goryawala MZ, Sheriff S, Maudsley AA. Regional distributions of brain glutamate and glutamine in normal subjects. NMR Biomed. 2016;29(8):1108–1116. doi: 10.1002/nbm.3575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hetherington HP, Pan JW, Mason GF, Adams D, Vaughn MJ, Twieg DB, Pohost GM. Quantitative H-1 spectroscopic imaging of human brain at 4. 1 T using image segmentation. Magn Reson Med. 1996;36(1):21–29. doi: 10.1002/mrm.1910360106. [DOI] [PubMed] [Google Scholar]
- 5.Tal A, Kirov II, Grossman RI, Gonen O. The role of gray and white matter segmentation in quantitative proton MR spectroscopic imaging. NMR Biomed. 2012;25(12):1392–1400. doi: 10.1002/nbm.2812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Adany P, Choi IY, Lee P. B0-adjusted and sensitivity-encoded spectral localization by imaging (BASE-SLIM) in the human brain in vivo. Neuroimage. 2016;134:355–364. doi: 10.1016/j.neuroimage.2016.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hu X, Levin DN, Lauterbur PC, Spraggins T. SLIM: spectral localization by imaging. Magn Reson Med. 1988;8(3):314–322. doi: 10.1002/mrm.1910080308. [DOI] [PubMed] [Google Scholar]
- 8.Mandl RC, van den Heuvel MP, Klomp DW, Boer VO, Siero JC, Luijten PR, Hulshoff Pol HE. Tract-based magnetic resonance spectroscopy of the cingulum bundles at 7 T. Hum Brain Mapp. 2012;33(7):1503–1511. doi: 10.1002/hbm.21302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nuzillard D, Bourg S, Nuzillard J. Model-free analysis of mixtures by NMR using blind source separation. J Magn Reson. 1998;133(2):358–363. doi: 10.1006/jmre.1998.1481. [DOI] [PubMed] [Google Scholar]
- 10.Ladroue C, Howe FA, Griffiths JR, Tate AR. Independent component analysis for automated decomposition of in vivo magnetic resonance spectra. Magn Reson Med. 2003;50(4):697–703. doi: 10.1002/mrm.10595. [DOI] [PubMed] [Google Scholar]
- 11.Sajda P, Du S, Brown TR, Stoyanova R, Shungu DC, Mao X, Parra LC. Nonnegative matrix factorization for rapid recovery of constituent spectra in magnetic resonance chemical shift imaging of the brain. IEEE Trans Med Imaging. 2004;23(12):1453–1465. doi: 10.1109/TMI.2004.834626. [DOI] [PubMed] [Google Scholar]
- 12.Bernasconi A, Bernasconi N, Natsume J, Antel SB, Andermann F, Arnold DL. Magnetic resonance spectroscopy and imaging of the thalamus in idiopathic generalized epilepsy. Brain. 2003;126(Pt 11):2447–2454. doi: 10.1093/brain/awg249. [DOI] [PubMed] [Google Scholar]
- 13.Ende G, Braus DF, Walter S, Weber-Fahr W, Henn FA. Multiregional 1H-MRSI of the hippocampus, thalamus, and basal ganglia in schizophrenia. Eur Arch Psychiatry Clin Neurosci. 2003;253(1):9–15. doi: 10.1007/s00406-003-0398-5. [DOI] [PubMed] [Google Scholar]
- 14.Maudsley AA, Darkazanli A, Alger JR, Hall LO, Schuff N, Studholme C, Yu Y, Ebel A, Frew A, Goldgof D, Gu Y, Pagare R, Rousseau F, Sivasankaran K, Soher BJ, Weber P, Young K, Zhu X. Comprehensive processing, display and analysis for in vivo MR spectroscopic imaging. NMR Biomed. 2006;19(4):492–503. doi: 10.1002/nbm.1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Maudsley AA, Domenig C, Govind V, Darkazanli A, Studholme C, Arheart K, Bloomer C. Mapping of brain metabolite distributions by volumetric proton MR spectroscopic imaging (MRSI) Magn Reson Med. 2009;61(3):548–559. doi: 10.1002/mrm.21875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Collins DL, Zijdenbos AP, Kollokian V, Sled JG, Kabani NJ, Holmes CJ, Evans AC. Design and construction of a realistic digital brain phantom. IEEE Trans Med Imag. 1998;17:463–468. doi: 10.1109/42.712135. [DOI] [PubMed] [Google Scholar]
- 17.Maudsley AA, Domenig C, Govind V, Darkazanli A, Studholme C, Arheart K, Bloomer C. Mapping of brain metabolite distributions by volumetric proton MR spectroscopic imaging (MRSI) Magn Reson Med. 2009;61(3):548–559. doi: 10.1002/mrm.21875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Haupt CI, Schuff N, Weiner MW, Maudsley AA. Removal of lipid artifacts in 1H spectroscopic imaging by data extrapolation. Magn Reson Med. 1996;35(5):678–687. doi: 10.1002/mrm.1910350509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Studholme C, Hill DLG, Hawkes DJ. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recogn. 1999;32(1):71–86. [Google Scholar]
- 20.Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imag. 2001;20(1):45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]
- 21.Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage. 2002;15(1):273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- 22.Studholme C, Hill DL, Hawkes DJ. Automated three-dimensional registration of magnetic resonance and positron emission tomography brain images by multiresolution optimization of voxel similarity measures. Med Phys. 1997;24(1):25–35. doi: 10.1118/1.598130. [DOI] [PubMed] [Google Scholar]
- 23.Soher BJ, Young K, Govindaraju V, Maudsley AA. Automated spectral analysis III: Application to in vivo proton MR spectroscopy and spectroscopic imaging. Magn Reson Med. 1998;40(6):822–831. doi: 10.1002/mrm.1910400607. [DOI] [PubMed] [Google Scholar]
- 24.Hattingen E, Luckerath C, Pellikan S, Vronski D, Roth C, Knake S, Kieslich M, Pilatus U. Frontal and thalamic changes of GABA concentration indicate dysfunction of thalamofrontal networks in juvenile myoclonic epilepsy. Epilepsia. 2014;55(7):1030–1037. doi: 10.1111/epi.12656. [DOI] [PubMed] [Google Scholar]
- 25.Andrade JM, Estevez-Perez MG. Statistical comparison of the slopes of two regression lines: A tutorial. Anal Chim Acta. 2014;838:1–12. doi: 10.1016/j.aca.2014.04.057. [DOI] [PubMed] [Google Scholar]
- 26.Su Y, Thakur SB, Karimi S, Du S, Sajda P, Huang W, Parra LC. Spectrum separation resolves partial-volume effect of MRSI as demonstrated on brain tumor scans. NMR Biomed. 2008;21(10):1030–1042. doi: 10.1002/nbm.1271. [DOI] [PubMed] [Google Scholar]
- 27.Angelie E, Bonmartin A, Boudraa A, Gonnaud PM, Mallet JJ, Sappey-Marinier D. Regional differences and metabolic changes in normal aging of the human brain: proton MR spectroscopic imaging study. AJNR American journal of neuroradiology. 2001;22(1):119–127. [PMC free article] [PubMed] [Google Scholar]
- 28.Bozgeyik Z, Burakgazi G, Sen Y, Ogur E. Age-related metabolic changes in the corpus callosum: assessment with MR spectroscopy. Diagn Interv Radiol. 2008;14(4):173–176. [PubMed] [Google Scholar]
- 29.Schuff N, Ezekiel F, Gamst AC, Amend DL, Capizzano AA, Maudsley AA, Weiner MW. Region and Tissue Differences of Metabolites in Normally Aged Brain Using Multislice 1H Magnetic Resonance Spectroscopic Imaging. Magn Reson Med. 2001;45(5):899–907. doi: 10.1002/mrm.1119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Barker PB, Bizzi A, De Stefano N, Gullapalli R, Lin DDM. Clinical MR spectroscopy: Techniques and applications. Cambridge: Cambridge University Press; 2009. [Google Scholar]
- 31.Kazemi K, Noorizadeh N. Quantitative Comparison of SPM, FSL, and Brainsuite for Brain MR Image Segmentation. J Biomed Phys Eng. 2014;4(1):13–26. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Figure S1: The sDec derived WM and GM spectra for an individual from all studied lobar regions. Results are shown for the right and left frontal (RF and LF), temporal (RT and LT), parietal (RP and LP), and occipital (RO and LO) lobes, and the cerebellum (C).
Supporting Table S1: Lobar measures of NAA/Cr calculated in WM and GM using sDec, M-Int, vAvg, and vReg methods. The percent absolute differences calculated using M-Int, vAvg, and vReg methods as compared to sDec methods are also shown. Significant differences from the sDec method are shown with asterisks with FDR corrected p<0.05, p<0.01, and p<0.001 denoted by *, **, and ***, respectively.
Supporting Table S2. Regression equations for associations of NAA/Cr and Cho/Cr with Age in WM regions. The table reports the R2 and False Discovery Rate (FDR) corrected p-values for the lobar regression.
Supporting Table S3. Regression equations for associations of NAA/Cr and Cho/Cr with Age in GM regions. The table reports the R2 and False Discovery Rate (FDR) corrected p-values for the lobar regression.