Experimental design and analysis and their reporting II: updated and simplified guidance for authors and peer reviewers

Abstract

This article updates the guidance published in 2015 for authors submitting papers to British Journal of Pharmacology (Curtis et al., 2015) and is intended to provide the rubric for peer review. Thus, it is directed towards authors, reviewers and editors. Explanations for many of the requirements were outlined previously and are not restated here. The new guidelines are intended to replace those published previously. The guidelines have been simplified for ease of understanding by authors, to make it more straightforward for peer reviewers to check compliance and to facilitate the curation of the journal's efforts to improve standards.

Abbreviations

ANOVA

analysis of variance

BJP

British Journal of Pharmacology

SEM

standard error of the mean

Introduction

The aim of this update is to

• share lessons learnt during the two years since the implementation of our guidelines;

• update guidance on requirements for design and analysis where our views have changed/advanced since 2015;

• include advice and guidance on additional areas of design and analysis pertinent to pharmacology research not discussed in the previous version; and

• make the journal requirements clearer and easier to curate.

The main lesson learnt (from internal journal audit) that we may now share is that the guidelines that have been journal requirements since 2015 are not being routinely followed by authors and this is being missed during the peer review process. This ‘non‐compliance’ is not unique to British Journal of Pharmacology (BJP) and is a phenomenon experienced by many other journals. Indeed, Nature recently reported that when guidelines are introduced, ‘author compliance can be an issue’ (Anonymous, 2017). There are certain topics that continue to be particularly problematic (e.g. normalization, transformation and inappropriate use of parametric statistics). Our solution is to make two key changes. We have updated and simplified our list of requirements for authors, and we have created a flow chart explaining how peer review may be accomplished efficiently. We also include figures to illustrate key aspects of good and inappropriate practice in data acquisition and processing. In doing this, we facilitate one of the key aims of the British Pharmacological Society which is to support the improved reporting and ‘transparency’ of experimental work. Finally, we provide new guidance on certain more nuanced matters, including the handling of outliers in datasets.

We note that this new guidance is entirely focused on design and analysis. Previous guidance in our journal discussed requirements for design and analysis with other important, but distinct, issues concerning the use of animals and experimental ethics (e.g. ARRIVE). In hindsight, we feel that our discussion of the two separate issues together may have resulted in a lack of clarity, contributing to the inadequate compliance. Guidance on ethical animal experimentation is published elsewhere (McGrath and Lilley 2015) and will be updated separately in 2018.

In order to facilitate implementation of the guidelines, journal instructions now require that every paper should contain a data and statistical analysis sub‐section within the Methods and full detail of design within each protocol described.

Key points of the updated guidance

1. Group sizes should be sufficient to permit any statistical analysis to be meaningful. BJP has set 5 as the minimum ‘n’ required for datasets subjected to statistical analysis. Designing a study to compare groups with n < 5 is permissible if carefully justified (e.g. shortage of sample availability), but any data set containing groups of n < 5 must not be subjected to statistical analysis, and findings must be labelled as ‘exploratory’ or ‘preliminary’. Any such data should constitute only a small proportion of the paper. We note that group size is the number of independent values, so one sample run five times is n = 1, not n = 5. We note that it is common for authors to run three samples ‘in quintuplicate’ then analyse the data with statistical analysis as if it were n = 15 rather than n = 3. This is not acceptable for publication in BJP.

2. Studies should be designed to generate groups of equal size, using randomization and blinded analysis where possible (with credible justification if not possible). If group sizes become unequal during a study owing to technical failure this must be explained in the Results. However, we encourage replacement of lost values according to defined criteria. Clear statements on all these features must be made in the Methods.

3. After ANOVA, post hoc tests may be run only if F achieves the necessary level of statistical significance (i.e. P < 0.05) and there is no significant variance inhomogeneity. Adherence must be stated in the Methods (‘data were analysed by ANOVA followed by Tukey's test’ is not sufficient). If these criteria are not met, a post hoc test should not be run (even if the software permits this, which it may).

4. In Methods, approaches used to reduce unwanted sources of variation by data normalization (which means the correction of test values to baseline or control group values) or to generate normal (Gaussian) data (e.g. by log‐transformation) must be justifiable and explained. Normalization or transformation can affect the appropriateness of the chosen statistical method. For example, normalization to matched controls will generate a control mean of 1 and no SEM, meaning that parametric tests (ANOVA, etc.) cannot be used (only non‐parametric analysis is acceptable). Any dataset where one group has no SEM (common in Western blot analysis) must be analysed by non‐parametric statistics. Following data transformation, the Y axis is often labelled incorrectly (it should be ‘fold matched control values’ or ‘fold of the control mean’, and not ‘fold control’).

5. When comparing groups, a level of probability (P) deemed to constitute the threshold for statistical significance (typically in pharmacology this is P < 0.05) should be defined in Methods and not varied later in Results (by presentation of multiple levels of significance).

6. Outliers are data values that diverge from the central tendency. An outlier may be a rogue value or part of the innate data distribution. Several aspects of the data distribution may need to be considered before an investigator can decide how to deal with outliers. It is possible to define an outlier in a control population, but only if a large number of control values are available for evaluation. Outliers should therefore be included in data analysis and presentation unless a predefined and defensible set of exclusion criteria can be generated and applied.

The peer review process

We expect BJP papers to be written in such a way that the basic requirements of design and analysis are described clearly by authors and can be checked in peer review. To improve this process, we have prepared a summary flow chart of how peer reviewers may quickly triage the key areas and check for compliance with BJP's core requirements. At the same time this flow chart explains to authors what BJP expects from them. The triage scheme (Figure 1) should be used by authors and those involved in peer review, with the more detailed updated guidance (above) used as a reference to clarify any uncertainty.

Figure 1.

This flow chart describes how triage of the design and analysis aspects of a paper may be checked by authors and by peer reviewers.

Areas of particular concern that require renewed vigilance

Many of the key issues in the flowchart (Figure 1) will be simple to address. Authors must make statements about each listed item in their Methods. In recently submitted studies that do not currently comply with our requirements, it is often the case that we find all of the following: a lack of randomization and blinding, unequal group sizes, and statistical analysis applied when n is <5. Together, these render a paper fundamentally flawed, and, as Figure 1 indicates, this will now result in triage rejection. In view of this, we conducted an audit of the present general compliance with the guidance introduced in 2015. Table 1 illustrates that the outcome has not been as successful as we had hoped.

Table 1.

Many papers published in BJP do not adhere to all the journal's guidance

	All n = 5+	Equal n	Randomization statement	Blinding statement	P constant	Correct Y axis label	Correct post hoc test
	0	0	0	0	0	0	1
	0	0	0	0	1	1	1
	0	0	0	0	1	0	1
	1	0	0	0	1	1	1
	0	1	0	0	1	1	1
	1	0	1	1	1	0	1
	1	1	1	1	1	1	1
	1	0	1	1	1	1	1
	1	0	1	0	1	0	1
	1	1	1	0	1	1	1
	0	0	0	0	1	1	1
	1	0	0	0	1	1	1
	1	0	0	1	0	1	1
	1	0	0	0	0	1	0
	1	1	0	0	0	1	1
	1	1	1	0	1	1	1
	1	0	1	1	1	0	1
	1	0	1	1	1	1	1
	1	1	0	1	1	0	0
	1	0	1	1	1	0	0
	1	0	0	0	1	0	0
	1	1	0	0	1	0	0
	0	0	1	1	1	0	0
	1	0	0	0	1	0	0
	1	0	0	0	1	0	0
	0	1	0	0	1	0	1
% compliance	73	31	38	35	85	50	69

The data above summarizes papers in three issues of BJP published at least 6 months after the publication of the journal's original guidance on design and analysis. The issues analysed were selected at random and are representative. The articles are the entire set of original research papers published in each of the three issues sampled. Papers were judged compliant (1) or not (0). Papers not stating whether the study was blinded or randomized or not were assumed to be non‐compliant. ‘Correct Y axis label’ means that for normalized data, if the control mean is 1 with no SEM, the label should be ‘fold matched controls’, whereas if the control mean has an SEM, the Y axis label should be ‘fold control mean’ (especially relevant to Western blot and qRT‐PCR data).

‘Correct post hoc test’ means that parametric tests were used only when the control mean has a variance, or there is no obvious violation of ANOVA (e.g. post hoc tests done when the controls have no variance or a sequence of groups' SEMs that are proportional to the mean). Given that all the papers were found to cite the previous guidance document, and in doing so made a declaration of concordance with the guidelines, we would expect the % compliance for each item to be 100%. The fact that it is not 100% explains why we have written this article.

Below, we discuss specific matters illustrated in Table 1.

Data normalization, transformation, statistical analysis and presentation

One important matter concerns normalization (e.g. correction of values to baseline to reduce variation) and data transformation to generate data necessary for the application of statistics that depend upon a ‘normal’ (Gaussian) distribution. With respect to normalization, Figure 2, as an example, shows two different acceptable ways of analysing and presenting data that, for reasons the author should explain in Methods, are normalized to control (a common procedure in Western blot analysis and electrophysiology studies). It is interesting, and not well recognized, that the data normalization approach in panel B is not actually a true normalization and is, in fact, simply a rescaling of the Y axis of the raw data (see legend). The important difference between the two approaches, however, is that the control in panel B has a standard error whilst the control in panel A does not. Both are acceptable forms of data presentation for BJP; however, the Y axis label and the statistical tests that should be applied are different.

Figure 2.

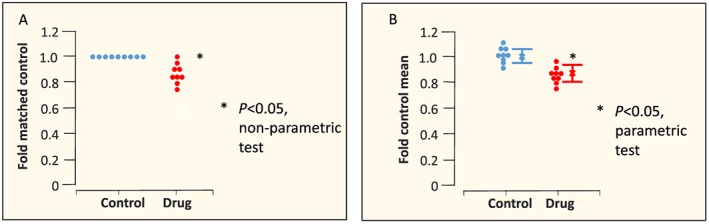
Parametric versus non‐parametric. Individual data points (circles), mean values (x) and SEM values are shown. In panel A, two datasets derived from an analysis (e.g. Western blotting) where each drug experiment included a matched (contemporaneous) control. A common practice is for each drug value to be normalized to each matched control value. This means that the control mean is 1, and there is no variance in the control. The correct way to analyse these data is using a non‐parametric statistical test, and the correct label for the Y axis is ‘fold matched control’. Because analysis is non‐parametric, it is misleading to show the parameter SEM. In panel B, each control and each drug value has been ‘normalized’ to the mean value of the control group (mean values shown as x). In other words, each raw value has been divided by the value of the mean of the control values. This generates a Gaussian dataset that can be analysed by parametric statistics (provided the variance is similar in the two groups ‐ a t‐test may falsely identify a nonsignificant difference if the two SEM values differ greatly ‐ see Figure 3), and if so, it is appropriate to show the SEM (error bars in the figure). However, there is actually no benefit in making this transformation since the ratio between each mean and each SEM is the same as the equivalent ratios for the raw data. In other words, this ‘transformation’ is identical to a relabelling or rescaling of the Y axis from the absolute raw values to new values for which the control mean value is relabelled as ‘1’. This has no effect on the ability of the parametric statistical test to detect a significant difference. However, readers have a tendency to make ‘eyeball’ comparisons between normalized datasets in the same paper or indeed from one paper to the next, and this may lead to false inferences. Thus, use of the normalization shown in panel A or presentation of the raw data (in units that may be arbitrary if this is the case) is preferred, although we acknowledge that for quantitative PCR, the ‘transformation’ depicted in panel B represents common practice at the present time. We also remind authors to ensure that whatever normalization is chosen, the Y axis is labelled correctly (fold control is not correct) and the appropriate type of statistical test is used.

With respect to data transformation, our audit has revealed two key issues:

• The first is that data that are not Gaussian distributed are often subjected to parametric statistical analysis (t‐tests, ANOVA and post hoc tests that account for multiple groups such as Tukey). This should not happen, and such data should be subjected to non‐parametric tests such as the Mann–Whitney U‐test.

• The second key point is that data transformation is underused. It can be helpful for analysis because it can convert data to fit a Gaussian distribution. In this context, in pharmacology, we are familiar with log‐Gaussian datasets and recommend log transformation when it can be justified. The need is much easier to identify than one might imagine: if the SEM increases in size in proportion to the size of the mean, the data are likely to be log‐Gaussian distributed, and the benefits (and indeed the necessity) of log transformation are shown in Figure 3.

Figure 3.

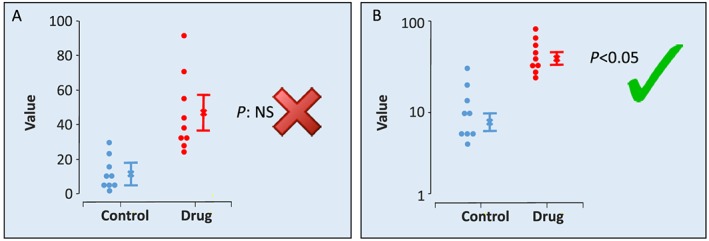
Data transformation. Individual data points (circles), mean values (x) and SEM values are shown. In panel A, owing to the large variance in the drug group, a t‐test identifies the two groups as not significantly different. However, closer examination shows this to be a false inference. The individual data values are not equally distributed around the arithmetic mean, and an arithmetic SEM should not be used to summarize the distribution. It is possible to analyse the data shown in panel A using a nonparametric statistical test (such as a U‐test), but nonparametric tests are less powerful than parametric tests, and their use can result in false negative findings. In panel B, the same data are log transformed, and the Y axis uses the log scale. Here, the SEM is no longer proportional to the mean, and the values are Gaussian distributed. It is appropriate to show the SEM. A t‐test correctly identifies a statistically significant difference between groups. This transformation unsettles some investigators as it appears to be a manipulation of data. However, in nature, many variables are log‐Gaussian distributed. Sound (decibels) and acidity (pH) are units on a log scale, used because the distribution is log Gaussian. In pharmacology, the pA₂ and even the relationship between a response and a drug concentration are log‐Gaussian. This is why we express agonist and antagonist ‘affinity’ values as pK_A and pK_B, respectively, not K _A and K _B, and similarly so for EC₅₀ or IC₅₀ that should be expressed as pEC50 and pIC50. It should be no surprise that many other variables in biology are log‐Gaussian distributed (e.g. the number of ectopic beats occurring in experimental myocardial infarction). The key issue here is that authors and peer reviewers should look at figures to ensure that data like those in the left‐hand part of the figure are not included in a paper ‐ if they are the data should be re‐analysed.

What is a group and what is a group size?

We have become aware of inconsistencies in how authors analyse data in terms of how the group and its size are defined. The first question to address is ‘what is a group’? We alluded above to a group being comprised of independent samples. But what is an independent sample? For BJP, ‘independent’ signifies that the sample represents a bias‐free representation of the population. Thus, five cells from one mouse given the same treatment is not n = 5, and these five cells should be regarded as technical replicates, with n = 1 consensus value taken forward into statistical analysis. Studies may include technical replicates when it is quick and easy to do so because it helps provide confidence that the technique and equipment are working. In summary, we expect statistical analysis to be undertaken on groups whose size is defined by the number of samples that are demonstrably independent, that is, generated from a study with a randomized design.

BJP has rules on minimum group sizes (stated above), but determination of the precise group size sufficient to permit statistical analysis is normally undertaken using approaches such as power analysis that take into account the anticipated ‘spread’ of the data. These approaches identify the minimum group size that will allow detection of a difference at a predefined P value, and therefore if this minimum value is selected there is a high risk of ‘false negative’ findings. To reduce this risk we encourage investigators to acknowledge this and add 50% to the calculated minimum group sizes.

Experimental outliers

We have introduced new guidelines on how to manage experimental outliers, which are defined as values that digress from the central tendency (or ‘central location’). There are several issues that need to be considered before an investigator can decide how to deal with outliers. First, how does one identify an outlier? With small group sizes (n < 12) this may be impossible. It is feasible to define an outlier in a control population as a value that lies outside a defined range, but only if the distribution of values is well defined. This requires a very large group size.

If it is possible to define an outlier, then the next question to address is: why is a value an outlier? The reason may be that the value is false, contaminated or in some other way incorrect. On the other hand, it may be correct, and the result of a natural wide spread of data, or even a bimodal distribution of data. The latter would arise, for example, if one were to analyse readouts in a population that expresses a polymorphism, such as a deficiency in acetylcholinesterase in a small section of the human population. Excluding such outlier values or subjects is justified only in an experiment defined to be relevant only to the larger population, for instance, in the acetylcholinesterase example, those with typical enzyme activity. It is therefore essential to know what the explanation is for an outlier, since it is inappropriate to exclude correct values just because they alter the data distribution.

Genuinely false values should be excluded from a sample, but this must be done using predefined criteria. Using a formula based on the standard deviation is one. A number of others are available in routinely used statistical packages, but their use can be problematic (Leys et al., 2013). Alternatively, one may use an arbitrary limit of acceptability (e.g. to exclude animals whose surgery has lowered blood pressure to below a value appropriate for testing drug effects especially, in this example, effects on blood pressure). This approach is acceptable to BJP, but exclusion criteria should be defined beforehand and applied on blinded data to avoid bias. Exclusion criteria should be fully described in Methods.

With a novel type of study (i.e. where there are no historical controls and database of records with which to consult), it is essential to ensure unbiased quality control, which means undertaking preliminary studies in order to allow generation of arbitrary exclusion criteria, keeping in mind that the justification cannot be ‘scientific’, merely pragmatic (to ensure that data can be analysed statistically without the need for onerously large group sizes). It is wise to revisit any criteria as new data emerge. We encourage authors to include in the manuscript any data that updates their previous exclusion criteria.

When it is impossible to justify reasons for exclusion of data, the best solution is to include all data including any apparent ‘outliers’ and ensure group sizes are large (increased by 50% from the value determined by power analysis is advisable). When inclusion of outliers is decided to be the best option, this may generate non‐Gaussian datasets. These can be modified by use of transformations or processed using non‐parametric statistical tests, as discussed above.

In summary, outliers should be included in a data set unless a predefined and defensible set of exclusion criteria can be generated and applied.

Statistical significance

The majority of papers published in BJP contain data sets where several test groups are compared with a control group in order to examine whether a drug has ‘an effect’. In this context, statistics are used to inform a binary decision about whether there is an effect or not. BJP continues with the policy that authors must define what level of P they consider to constitute statistical significance within the Methods section of the paper. Authors may choose a more stringent P threshold than the current norm of P < 0.05, but this must not be changed from one part of a manuscript to another.

Statistical analysis does not guarantee that a finding is necessarily correct, and we will allow an author the right to argue that a false positive or a false negative finding may have been generated. This issue is particularly relevant to variables of secondary interest. Clearly, group size should be determined a priori such that an expected effect on the variable of primary interest can easily be detected using the predefined P threshold (we refer readers to our advice on determining group sizes). However, such group sizes may be insufficient for reliable detection of effects on secondary and subsidiary variables. It is the responsibility of the author to explain this in the paper, especially if they wish to argue that an apparent lack of effect was due to a type 2 error (false negative). We additionally encourage authors to be aware that the calculated P value is almost always bigger than it seems (‘less significant’) owing to the false discovery rate which is one reason why some investigators argue that most (rather than just some) research findings are false (Colquhoun 2014; Begley 2013; Begley & Ioannidis 2015).

Flexibility and pilot data

An unreplacable sample may be lost due to a technical problem, and blinding the data analysis may be impossible owing to a very large and unmistakable effect in one group, that cannot be ‘blinded’ by inclusion of an equally effective positive control. In such scenarios, authors may easily explain why group sizes were not all equal, or blinding was compromised, and we expect editors to accept this. Separately, it may be useful to include a small amount of pilot data (e.g. the high throughput data on tens or hundreds of compounds used in selecting candidates for full investigation) derived from experiments that may not be blinded, randomized or fit for statistical analysis, and we encourage authors to do so, with the data presented (without P values) in Methods in a sub‐section headed Pilot Study.

Conclusions

Here, we have updated and simplified the requirements of BJP for experimental design and analysis. The objective is to facilitate manuscript preparation and help peer review become more consistent and transparent, generating research articles whose data are more likely to be reproducible.

The caveat is that there is no panacea, as implementation of any process is entirely dependent on stakeholders engaging with it. If guidance is too onerous, too detailed or ambiguous, or presented as optional (‘best practice’), it is likely to fail. If authors ignore the guidance, and peer review fails to recognize this, we will make no progress. Keeping guidance and the process of its implementation simple has a better chance of success than elaboration of complex and detailed guidance on every nuance. We will revisit the guidance in 2020 but will also conduct six‐monthly audits, in order to monitor its effects, and will introduce new guidance as appropriate.

In summary, this update describes a modified approach to concerns that have arisen from our experiences following the publication in 2015 of our design and analysis guidelines. The areas of focus have been selected from our internal audits as issues requiring reconsideration and aspects of experimentation that we did not consider in the first iteration. Our intention is to continue to support the Pharmacology community in identifying strategies that support and enable transparency and reproducibility. As we stated previously (Curtis et al. 2015), some of our guidance is arbitrary, and some will change. We will make progress, but it will need clear requirements and constant vigilance with progress made in stages. This is our stage II.

Author contributions

The article originated from discussions at the regular meetings of the Senior Editors of BJP during 2016 and 2017. M.J.C. coordinated the writing of the manuscript with contributions and edits from all of the other authors.

Curtis, M. J. , Alexander, S. , Cirino, G. , Docherty, J. R. , George, C. H. , Giembycz, M. A. , Hoyer, D. , Insel, P. A. , Izzo, A. A. , Ji, Y. , MacEwan, D. J. , Sobey, C. G. , Stanford, S. C. , Teixeira, M. M. , Wonnacott, S. , and Ahluwalia, A. (2018) Experimental design and analysis and their reporting II: updated and simplified guidance for authors and peer reviewers. British Journal of Pharmacology, 175: 987–993. doi: 10.1111/bph.14153.