Time-dependent pharmacokinetics of dexamethasone and its efficacy in human breast cancer xenograft mice: a semi-mechanism-based pharmacokinetic/pharmacodynamic model

Abstract

Dexamethasone (DEX) is the substrate of CYP3A. However, the activity of CYP3A could be induced by DEX when DEX was persistently administered, resulting in auto-induction and time-dependent pharmacokinetics (pharmacokinetics with time-dependent clearance) of DEX. In this study we investigated the pharmacokinetic profiles of DEX after single or multiple doses in human breast cancer xenograft nude mice and established a semi-mechanism-based pharmacokinetic/pharmacodynamic (PK/PD) model for characterizing the time-dependent PK of DEX as well as its anti-cancer effect. The mice were orally given a single or multiple doses (8 mg/kg) of DEX, and the plasma concentrations of DEX were assessed using LC-MS/MS. Tumor volumes were recorded daily. Based on the experimental data, a two-compartment model with first order absorption and time-dependent clearance was established, and the time-dependence of clearance was modeled by a sigmoid E_max equation. Moreover, a semi-mechanism-based PK/PD model was developed, in which the auto-induction effect of DEX on its metabolizing enzyme CYP3A was integrated and drug potency was described using an E_max equation. The PK/PD model was further used to predict the drug efficacy when the auto-induction effect was or was not considered, which further revealed the necessity of adding the auto-induction effect into the final PK/PD model. This study established a semi-mechanism-based PK/PD model for characterizing the time-dependent pharmacokinetics of DEX and its anti-cancer effect in breast cancer xenograft mice. The model may serve as a reference for DEX dose adjustments or optimization in future preclinical or clinical studies.

Introduction

Breast cancer has been considered the most common malignancy and second leading cause of mortality among women around the world¹. Endocrine therapy, targeted therapy, cytotoxic chemotherapy and radiotherapy are the most commonly used therapeutic strategies for breast cancer patients, and they can be administered either before or after surgery².

Dexamethasone (DEX) is a type of synthetic glucocorticoid that is widely used in the clinical setting. Several previous studies have demonstrated the anti-cancer efficacy of DEX in xenograft breast tumor or other tumor models based on its inhibitory effect on active estrogens in the circulation and regulation of anti-inflammatory cytokines or other factors related to tumor progression^{3,4,5,6,7,8,9}. In our previous studies, DEX had a greater suppression effect than general chemotherapeutic drugs, such as epirubicin and gemcitabine, in breast cancer treatment^4,10. Therefore, it may be of great significance to study the pharmacokinetic and pharmacodynamic processes of DEX in xenograft breast tumor models in detail.

As widely reported, DEX is the substrate of cytochrome P450 3A (CYP3A)^11,12. However, the activity of CYP3A could be induced by DEX when DEX was persistently administered, resulting in auto-induction and time-dependent pharmacokinetics (pharmacokinetics with time-dependent clearance) of DEX^12,13. It is well-known that the auto-induction effect of DEX may increase its clearance and decrease its bioavailability and drug efficacy after long-term used¹². Therefore, it is of great importance to study the time-course of pharmacokinetics and anti-cancer effect of DEX for long-term use.

Pharmacokinetic-pharmacodynamic (PK/PD) modeling and simulation has been widely applied in drug research and development. The model could appropriately quantify the process of drug behaviors and actions in vivo, and it could help people better understand the time-course of drug efficacy and safety. In addition, a mechanism- or semi-mechanism-based PK/PD model has more reliability and predictability than a traditional model¹⁴. Regarding to the PK/PD relationship of DEX in a breast tumor xenograft model, Yuan et al established the PK/PD model of DEX, but the time-dependence of the pharmacokinetics was not considered. Additionally, the drug effect was modeled as a linear relationship with the drug concentration in their study, which was somewhat defective and did not sufficiently account for the drug mechanisms¹⁰. To the best of our knowledge, there is no report referring to the PK/PD model for characterizing the time-dependent pharmacokinetics of DEX and its anti-cancer effect. Therefore, the aim of this study was to investigate the pharmacokinetic profiles of DEX after single or multiple doses as well as to establish a semi-mechanism-based PK/PD model for characterizing the time-dependent clearance of DEX and its anti-cancer effect in a breast cancer xenograft model.

Materials and methods

Reagents and chemicals

Dexamethasone (purity >99%) and testosterone, which was used as an internal standard (IS) in the pharmacokinetic study, were purchased from Sigma-Aldrich (St Louis, MO, USA). RPMI-1640 medium and fetal bovine serum (FBS) were purchased from Macgene Biotech Co, Ltd (Beijing, China) and Gibco (Grand Island, NY, USA), respectively. Other chemicals were purchased from Beijing Chemical Works (Beijing, China).

Cell line and animals

The human breast cancer cell line, MCF-7/Adr, was obtained from the Institute of Materia Medica, Academy of Medical Sciences, China, and cultured in RPMI-1640 medium supplemented with 10% FBS at 37 °C in a 5% CO₂ atmosphere.

Female nu/nu nude mice (4–5 weeks old, 20±4 g) were obtained from Vital River (Beijing, China) and maintained in standard conditions of 50%–60% humidity at 22–24 °C with 12 h/12 h light/dark cycles. The mice were given free access to food and water, except for 12 h before administration, which is when the food supply was stopped. All animal studies were approved by the Institutional Animal Care and Use Committee of Peking University Health Science Center.

Pharmacokinetic study

The plasma concentrations of DEX after single or multiple doses in nude mice were determined by the LC-MS/MS method that was previously published by our group¹⁵. The range of the calibration curve was 2.5–500 ng/mL, and the selectivity, linearity, precision, accuracy, recovery, stability, matrix effect and dilution effect of the method were eligible. Samples with a DEX concentration greater than 500 ng/mL were diluted to the concentration within the calibration range.

During the study, 33 nude mice were given DEX by gavage at 8 mg/kg for a single dose, and the plasma samples were collected via extracting eyeballs at 20 min, 30 min, 40 min, 1 h, 1.5 h, 2 h, 3 h, 5 h, 8 h, 12 h and 16 h after administration. In addition, DEX was given daily at 8 mg/kg in another 27 mice for multiple doses; in this group, plasma samples of 18 mice were collected after the 9^th dose at 20 min, 30 min, 40 min, 2 h, 5 h and 8 h and those from the other 9 mice were collected at 5 h after the 3^rd, 6^th and 13^th doses. Three nude mice were euthanized per time point, and the two batches of PK studies after single or multiple doses were performed separately.

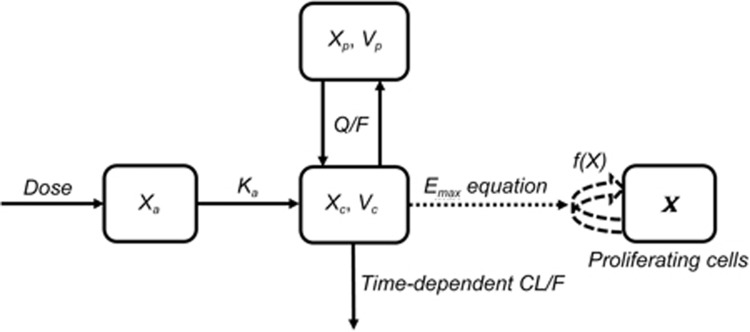
A two-compartment model with first order absorption and time-dependent clearance was used to characterize the PK of DEX (Figure 1). Time-dependent clearance was modelled with a sigmoid E_max equation. The differential equations of the PK model are as follows:

Figure 1.

Schematic representation of the established PK/PD model of DEX in nude mice. X_a, X_c and X_p represent the level of DEX in the absorption, central and peripheral compartments of the PK model, respectively; X represents the tumor size with proliferating tumor cells in the tumor compartment; K_a represents the first order absorption rate; CL represents the systemic clearance, which was time-dependent; Q represents the clearance between compartments; V_c and V_p are the apparent volumes of distribution in the central and peripheral compartments, respectively; and F is the bioavailability.

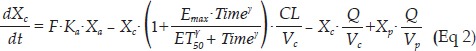where X_a, X_c and X_p represent the amount of DEX in the absorption, central and peripheral compartments, respectively; V_c and V_p are the apparent volumes of distribution in the central and peripheral compartments, respectively; C_c and C_p represent the drug concentrations in the central and peripheral compartments, respectively; CL represents the systemic clearance; Q represents the clearance between compartments; F is the bioavailability; Time indicates the time after the first dose of DEX; E_max and ET₅₀ represent the maximal effect of auto-induction and the time when half of the maximal induction effect was achieved, respectively; and γ is the shape factor.

Because the PK studies after a single or multiple dose(s) were conducted separately in two different batches, inter-occasion variability (IOV) of PK parameters was considered. The IOV was initially added to K_a, CL, Q, V_c, V_p, E_max or ET₅₀, but the IOV on K_a was finally selected based on the model fitting results and rationality of the estimated parameters. The equation is as follows:

where η₁ represents the inter-individual variability (IIV) and η₂, η₃ represent the IOV of the first (OCC₁, single dose) and second (OCC₂, multiple dose) occasions, respectively. The IIV and IOV were modelled by assuming that the individual PK parameters followed a logarithmic normal distribution around the population values as follows: P_i = P_pop·e^η.

Pharmacodynamic study

The detailed PD study was published earlier⁴. In terms of methods, 2×10⁶ MCF-7/Adr cells were suspended in 200 μL of FBS-free medium and subcutaneously injected into the right flanks of mice to establish an orthotopic breast cancer xenograft model. At approximately d 5 after injection, the mice were randomly divided into 4 groups (n=5 per group) and orally administered vehicle or 1 mg/kg, 2 mg/kg or 8 mg/kg of DEX daily. The DEX was dissolved in corn oil. The tumor length and width were measured using an electronic vernier caliper, and the tumor volumes were calculated according to the following formula¹⁶: tumor volume (mm³)=0.5×length×width². The tumor volumes were recorded daily for 18 d during this study.

PK/PD model

The natural growth of xenograft tumor in this study was described by the non-linear growth model suggested by Koch et al¹⁷. In Koch's model, tumor growth is characterized by an exponential growth phase followed by a linear growth phase, and the transition process is smooth instead of having a threshold tumor mass between the two phases proposed by Simeoni et al¹⁸. The differential equation is as follows:

where X represents the tumor size, ω₀ is the initial tumor value before administration, and λ₀ and λ₁ represent the exponential and linear growth rates, respectively. In this model, it was assumed that all tumor cells in the vehicle group continue proliferating during the study.

When DEX was administered, the tumor growth was significantly perturbed. As previously reported, DEX exerts its anti-cancer effect through inactivating estrogens in the circulation or by regulating the anti-inflammatory cytokines or other factors related to tumor progressions. These factors were closely correlated with the proliferation of tumor cells^3,19,20. Based on these main mechanisms, we assumed that DEX suppresses tumor growth by inhibiting the proliferation of tumor cells rather than stimulating their eradication¹⁰. Thus, the PK/PD model of DEX was developed by multiplying the natural growth function with an inhibitory function, which was characterized by an E_max equation. The integrated PK/PD model structure is shown in Figure 1, and the differential equation is as follows:

where C_dex represents the DEX concentration in the central compartment, and EC₅₀ represents the DEX concentration when half of the maximal drug effect, which was assumed as 100% of inhibition, was achieved. The other parameters were defined as above.

Modeling constructions, evaluations and simulations

All modeling and simulations in this study were performed using NONMEM 7.2 (ICON Development Solutions, Ellicott City, MD, USA) and PsN 4.2.0 (Uppsala University, Uppsala, Sweden) with a first order conditional estimation with interaction (FOCEI) method. It was assumed that the IIV and IOV of parameters, as well as the residual error variabilities, followed a logarithmic normal distribution. The 95% confidence intervals (95% CI) or relative standard errors (RSE) were provided to assess the precision and reliability of the estimated parameters. A mixed error model was selected as the residual error model for both the PK model and integrated PK/PD model. Model evaluation and selection depended on the rationality of the estimated parameters, decline of the objective function value (OFV), diagnostic plots and visual predictive check (VPC) based on 1000 times of simulation. Tumor growth curves with or without the auto-induction effect were simulated by fixing the parameters estimated by the final integrated model (Eq 2 was changed to Eq 9 for the model without an auto-induction effect of DEX on metabolizing enzymes in the process of simulation), revealing the necessity of considering the auto-induction effect while modeling the drug effect of DEX after multiple doses. In addition, tumor growth rates under different DEX dose regimens were further simulated by the final PK/PD model with auto-induction effect.

Statistical analysis

The PK and PD results were presented as the mean±SD, and statistical analyses were performed using GraphPad Prism 5.0 software (GraphPad Software, Inc, La Jolla, USA). One-way ANOVA was used to determine the significance among different groups followed by post hoc tests with Bonferroni's correction. Difference at a level of P<0.05 was considered statistically significant.

Results

Pharmacokinetic results and anti-cancer effects of DEX

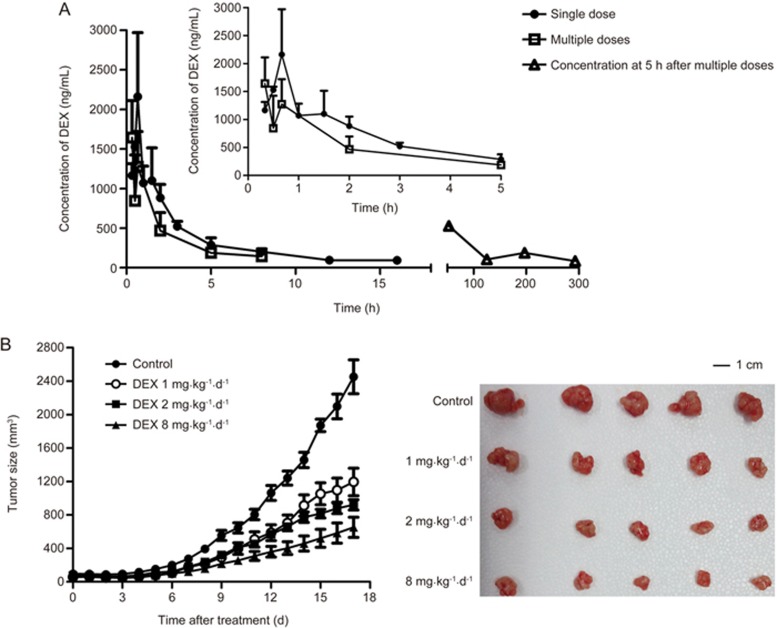
The concentration-time curves of DEX after single or multiple doses at 8 mg/kg are shown in Figure 2A. Both DEX concentrations and the area under the curve (AUC) after the 9^th dose were obviously lower than that of a single dose, and the concentrations at 5 h after the 3^rd, 6^th, 9^th and 13^th dose gradually trended to decline, which is consistent with previously reported PK results for DEX in rats¹². Multiple studies have demonstrated that DEX is the substrate and inducer of CYP3A^11,12,13. Therefore, the time-dependent changes of DEX concentration in nude mice might be considered to result from auto-induction of CYP3A by DEX after multiple doses.

Figure 2.

The pharmacokinetic and tumor growth data used for developing the PK/PD model. (A) Concentration-time curves of DEX after single or multiple doses at 8 mg/kg in nude mice (n=3). (B) Anti-cancer effects after different doses of DEX in MCF-7/Adr xenograft nude mice (n=5).

The detailed inhibitory effects of DEX on a MCF-7/Adr xenograft tumor was published elsewhere⁴. Tumor growth after different dose regimens is shown in Figure 2B. It can be clearly identified that DEX significantly suppressed the tumor growth in a dose-dependent manner.

The PK and tumor growth data after different DEX regimens were utilized to establish time-dependent PK and integrated PK/PD models.

Time-dependent pharmacokinetic model of DEX

The PK profile of DEX in nude mice was characterized by a two-compartment model with first order absorption and time-dependent clearance. The estimated PK parameters are summarized in Table 1. The precisions of all parameters were acceptable, suggesting the reliability of the established model. The typical value of E_max was 1.09, indicating that the systemic clearance might be induced to more than twofold the initial value along with persistent dosing, which somewhat suggests the importance of considering the auto-induction effect with persistent DEX use.

Table 1. Estimated pharmacokinetic parameters of DEX in nude mice at 8 mg·kg⁻¹·d⁻¹.

Parameters	Typical estimates	95% CI	IIV
Ka (h−1)	1.95	0.47–2.48	0 FIX
CL/F (L/kg·h−1)	1.28	1.03–1.41	0 FIX
Vc/F (L/kg)	2.47	1.08–2.93	0 FIX
Vp/F (L/kg)	4.87	−0.46–10.85	0 FIX
Q/F (L/kg·h−1)	1.34	0.68–1.59	0 FIX
Emax	1.09	0.97–1.84	0 FIX
ET50 (h)	81.3	71.68–151.54	0 FIX
γ	4.38	1.25–6.48	0 FIX
ωIOV1 (CV%)	26.8%
ωIOV2 (CV%)	217.7%
Residual errors
σprop (%)	33%
σadd (ng/mL)	0.01

CI, confidence interval; IOV, inter-occasion variability; IIV, inter-individual variability; CV, coefficient variation.

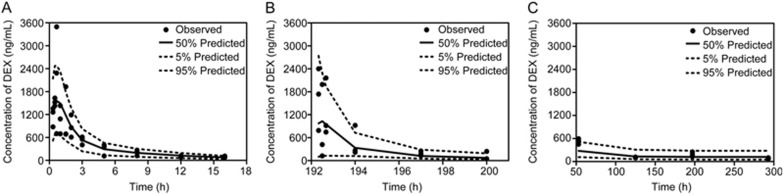
The VPCs of the concentration-time profiles after single and multiple doses were evaluated by the final PK model, and the results are presented in Figure 3. Most of the observed concentration data were within the 90% confidence interval of the predictions, implying that the established PK model could fit the current data very well and had good predictability. Moreover, Supplementary Figure S1 presents the goodness-of-fit (GOF) plots of the model, which also demonstrated the fitness of the established PK model.

Figure 3.

Visual predictive check (VPC) of the concentration-time profiles after a single dose (A); the 9^th dose (B); and at 5 h after the 3^rd, 6^th, 9^th and 13^th doses (C), which was evaluated by the final time-dependent PK model.

PK/PD model

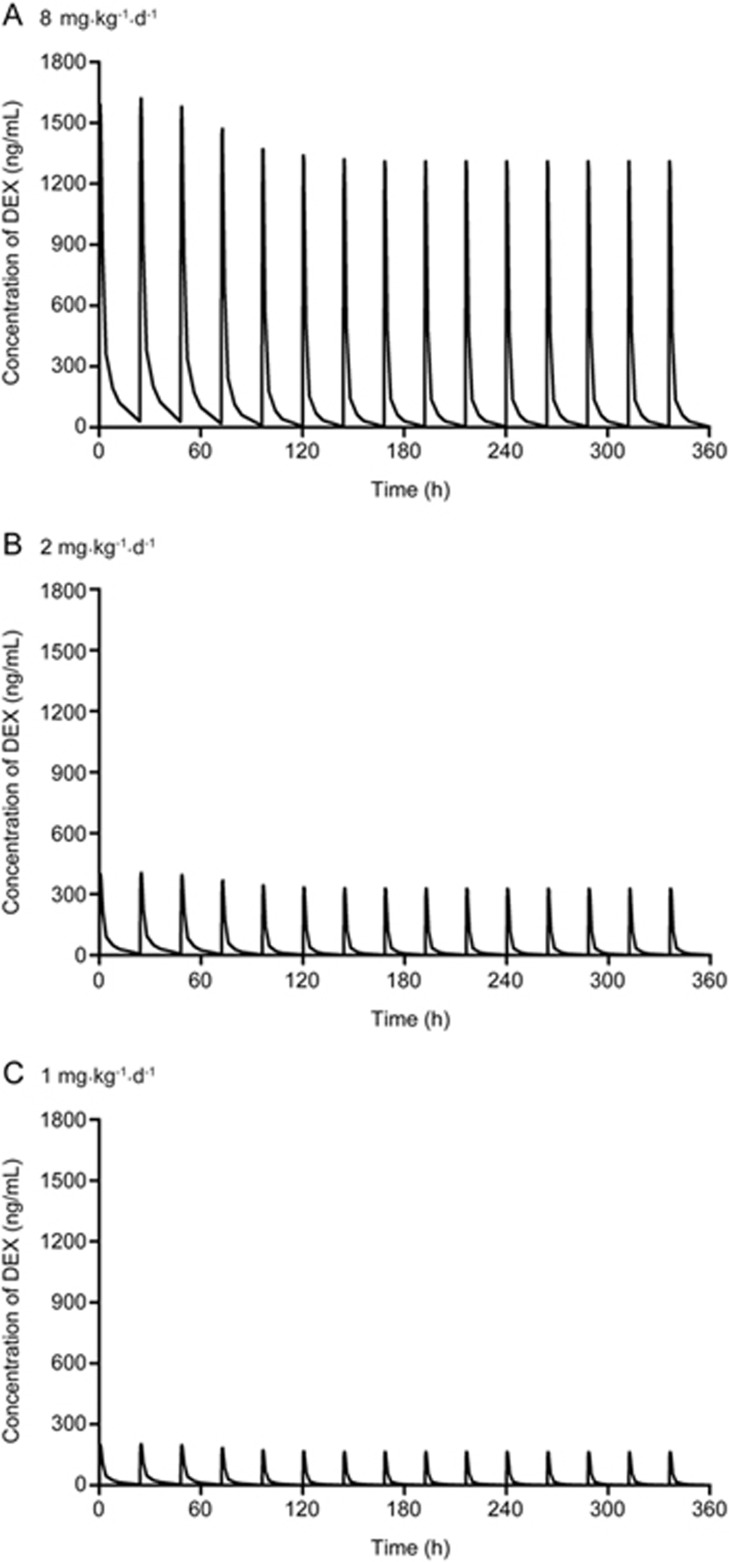
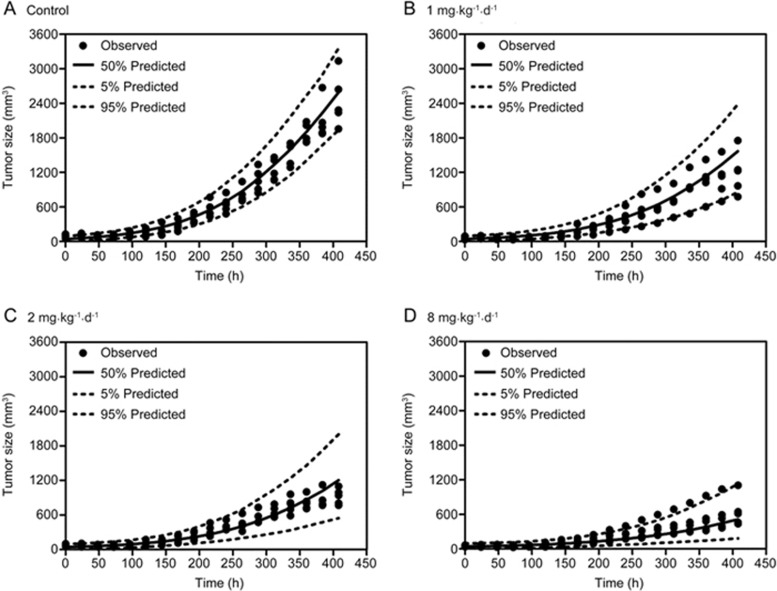
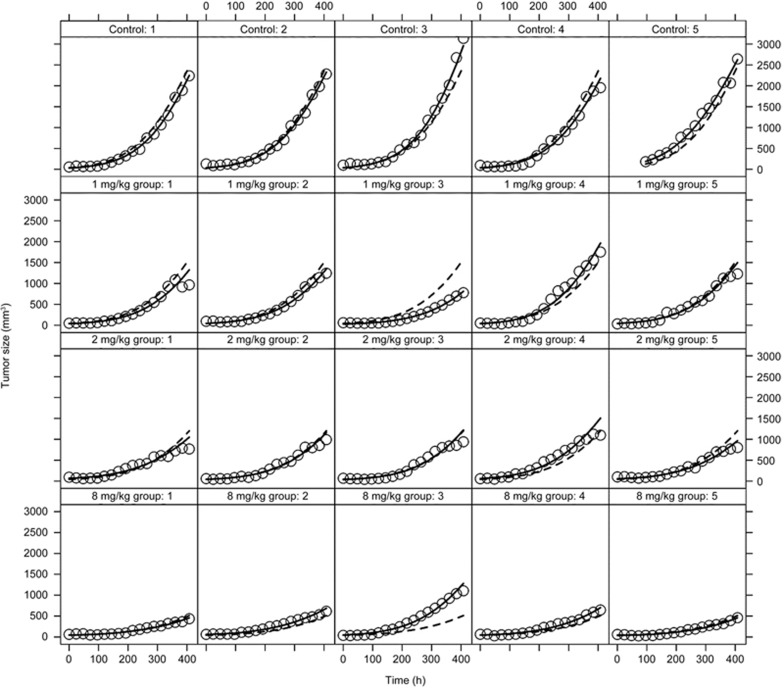
Pharmacokinetic profiles of DEX at different doses were simulated based on the established time-dependent PK model by fixing the PK parameters (Figure 4). The natural tumor growth was modelled well by the nonlinear growth model introduced by Koch et al¹⁷, and the anti-cancer effect of DEX was successfully characterized by an E_max equation. The estimated parameters of the integrated PK/PD model are shown in Table 2. The RSE of all parameters was less than 30%, suggesting the reliability of the established model. The VPCs of the tumor growth curves in the vehicle group and different treatment groups were generated by the final integrated PK/PD model (Figure 5). Most of the observed tumor size data were within the 90% confidence interval of the predictions, suggesting that the established integrated PK/PD model could adequately characterize the natural tumor growth and inhibitory effect of DEX at different doses as well as that the model had high predictability. In addition, Figure 6 shows the individual and population predictions, as well as observed values, of the tumor size dynamics in each group, which were derived from the integrated PK/PD model. The individual predictions in each group nearly corresponded to the observed data, showing that the model could predict individual data very well. Moreover, Supplementary Figure S2 shows the GOF plots of the integrated PK/PD model, which also supported the fitness of the established model.

Figure 4.

The simulated pharmacokinetic profiles of DEX at 8 mg·kg⁻¹·d⁻¹ (A), 2 mg·kg⁻¹·d⁻¹ (B) and 1 mg·kg⁻¹·d⁻¹ (C) based on the established time-dependent PK model.

Table 2. Estimated pharmacodynamic parameters of the integrated PK/PD model.

Parameters	Typical estimates	RES%	IIV (CV%)
λ0 (h−1)	0.0065	8.9	0 FIX
λ1 (mm3·h−1)	28.1	28.6	21.1
ω0 (mm3)	42	7.1	26.3
EC50 (ng/mL)	48.5	22.1	70.1
Residual errors
σprop (%)	10.9%
σadd (mm3)	27.0

RSE, relative standard error; IIV, inter-individual variability; CV, coefficient variation.

Figure 5.

VPC of the tumor growth curves in the vehicle group (A) and different treatment groups (B-D) based on the integrated PK/PD model.

Figure 6.

The individual tumor growth curves in each group. The dots represent the observed tumor sizes; the solid and broken lines represent the individual and population predictions, respectively.

Model simulations

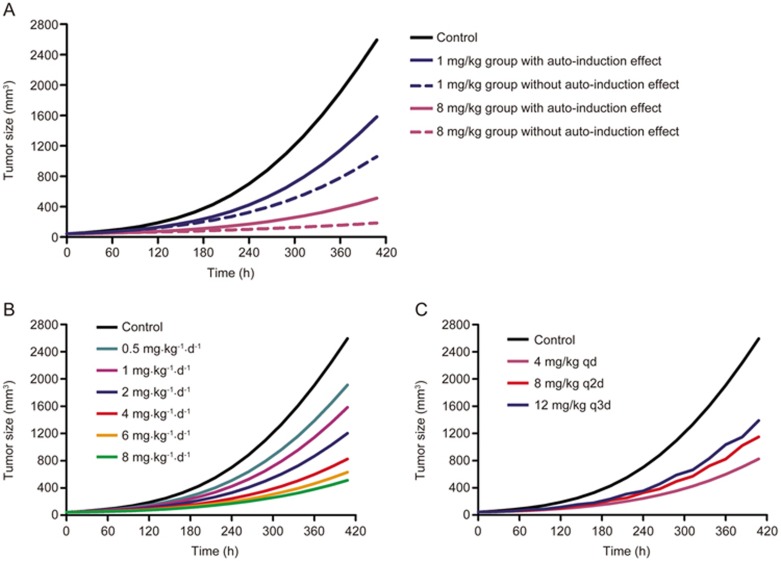
To compare the differences of model predicted tumor growth when the auto-induction effect of DEX on CYP3A was or was not considered, tumor size-time profiles were simulated by fixing the PK and PD parameters (Figure 7A). Tumor growth rates predicted by the model with the auto-induction effect are obviously higher than that without the auto-induction effect, which may be due to the greater systemic clearance and resulting lower exposure and bioavailability of DEX after multiple doses in a model with an auto-induction effect¹². These results further confirmed the significance and necessity of adding the auto-induction effect into the PK/PD model when DEX was persistently administered in a breast cancer xenograft model.

Figure 7.

The simulated tumor growth curves based on the integrated PK/PD model when the auto-induction effect was or was not considered (A) and the tumor growth rates under different DEX dose regimens simulated by the final PK/PD model with the auto-induction effect (B and C).

Additionally, tumor growth curves under different DEX dose regimens were simulated by the final PK/PD model with the auto-induction effect. Figure 7B shows that the tumor growth rates could be significantly suppressed by DEX in a dose-dependent manner. Moreover, the tumor inhibitory efficacy of DEX at 4 mg/kg daily was greater than that at 8 mg/kg every other day, which was further greater than that at 12 mg/kg every three days (Figure 7C), indicating that the anti-cancer effect of DEX may increase when it was administered more frequently at the same total dose.

Discussion

The time-dependence of the DEX PK profile was discovered much earlier than this study¹², and several studies have reported on PK models of DEX in animals or humans^13,15,21,22. However, neither the auto-induction nor auto-inhibition effect of DEX on metabolizing enzymes was usually assumed in those models, which does not agree with the real drug mechanisms. In this study, the time-dependence of the DEX PK profile was further discovered in nude mice, and a time-dependent PK model, as well as an integrated semi-mechanism-based PK/PD model, in breast cancer xenograft mice was established, which may be considered as an improvement in the DEX PK/PD model field. In addition, significant differences in the tumor growth curves, simulated by models with or without an auto-induction effect, were observed, which could be considered solid evidence for the need to consider the auto-induction effect while modeling the drug efficacy of DEX after multiple doses.

The PK profile of DEX in nude mice was described by a two-compartment model with a first order absorption rate, which is consistent with a previously published study¹⁵. In previously reported PK models of other drugs with auto-induction characteristics, the time-dependent function was generally added to the parameter of systemic clearance based on the mechanism that the auto-induction effect may increase the activity of metabolizing enzymes as well as the metabolic rates^23,24,25,26. Therefore, time-dependent clearance was also used in this study.

Because the PK studies after single or multiple doses were conducted separately in two different batches, the IOV of the various PK parameters were initially tried to be modeled. However, only K_a was finally modeled with the IOV based on the model fitting results and rationality of the estimated parameters. In addition, the PK model without IOV was also attempted in this study. The time-dependence of clearance could only be characterized by a linear equation and not by the E_max equation for the current data if no IOV was considered. It is well-known that extrapolation of the model by a linear equation continues to have many limitations. Hence, the model with the IOV on K_a was ultimately selected as the final PK model. The coefficient variation value of the IOV for the second occasion was relative large (Table 1), which may be from large variations in the multiple dose group resulting from the long study time and multiple administration times.

Since the growth of the xenograft breast tumor observed in this study showed a smooth transition from the exponential growth phase to the linear growth phase, the tumor growth was well characterized by the non-linear growth model suggested by Koch et al¹⁷ and not by that of Simeoni et al¹⁸, which is consistent with Yuan et al's study¹⁰. We did not try any three-phase models (such as the Logistic model or Gompertz model)²⁷ because no obvious S-shape curve of tumor growth was observed in this study.

The integrated PK/PD model of DEX was developed on the assumption that DEX exerted its tumor inhibitory efficacy through suppressing the proliferation of tumor cells rather than stimulating their eradication, which was based on its main mechanisms of inactivating estrogens in the circulation or regulating the anti-inflammatory cytokines or other factors related to tumor progression^{3,4,5,6,7,8,9}. The drug potency of DEX was characterized by an E_max equation, and the E_max value was assumed as 1, which does not agree with Yuan et al's study in which the drug effect was modeled as a linear correlation to the concentration of DEX¹⁰. Theoretically, the extrapolating ability of E_max model may be somewhat better than that of the linear model, and the E_max model may preferentially follow the biological mechanisms²⁸.

In summary, this study established a semi-mechanism-based PK/PD model for characterizing the time-dependent pharmacokinetics of DEX and its anti-cancer effect in breast cancer xenograft mice. The integrated PK/PD model enabled the quantitative description of the relationship between the DEX plasma concentration and its anti-cancer efficacy based on the real drug mechanisms and may be considered to be a great improvement from previously published models. The established preclinical PK/PD model may provide references for dosage adjustments or optimization of DEX when it is used for long-term medication in future preclinical or clinical studies.

Abbreviations

DEX, dexamethasone; CYP3A, cytochrome P450 3A; PK/PD, pharmacokinetic/pharmacodynamic; NONMEM, non-linear mixed effect modeling; FOCEI, first order conditional estimation with interaction; OFV, objective function value; VPC, visual predictive check; GOF, goodness-of-fit; RSE, relative standard error; IOV, inter-occasion variability; IIV, inter-individual variability.

Author contribution

Tian-yan ZHOU, Wei LU and Jian LI designed the research; Jian LI, Qing-yu YAO, Chun-yi HAO and Xiu-yun TIAN performed the research; Jian LI, Rong CHEN, Sheng-jun LIU, Tian-yan ZHOU and Wei LU analyzed the data; and Jian LI wrote the manuscript.

Supplementary Information

Supplementary Figure S1

The goodness-of-fit plots of the time-dependent PK model.

Supplementary Figure S2

The goodness-of-fit plots of the integrated PK/PD model.