Using genomics data to reconstruct transmission trees during disease outbreaks

Summary

Genetic sequence data from pathogens presents a novel means to investigate the spread of infectious disease between infected hosts, or infected premises, complementing traditional contact-tracing approaches, and much recent work has gone into the development of methods for this purpose. The objective is to recover the epidemic transmission tree, which identifies who infected whom. This paper reviews the various approaches that have been taken. The first step is to define a measure of difference between sequences, and factors such as recombination and convergent evolution must be taken into account. Three broad categories of method, of increasing complexity, exist: those that assume no within-host genetic diversity or mutation, those that assume no within-host diversity but allow mutation, and those which allow both. Until recently, the assumption was usually made that every host in the epidemic could be identified, but this is now being relaxed, and some methods are intended for sparsely sampled data, concentrating on the identification of pairs of sequences that are likely to be the result of direct transmission rather than inferring the complete transmission tree. Many of the procedures described here are available to researchers as free software.

3. Introduction

A key objective when investigating and controlling infectious disease outbreaks is to be able trace to the spread of a pathogen through a host population. The ultimate target of such investigations is the recovery of the transmission tree of the epidemic, a diagram of who infected whom for all hosts that experience an infection, sometimes combined with information on the time that each became, and ceased to be, infected or infectious. Traditional methods for investigation of the transmission tree have relied upon contact tracing, a labour-intensive procedure that must deal with many unknowns. With technological advances opening up the possibility of rapid DNA and RNA sequencing on a massive scale, genetic data now offers a promising new source of information to infer paths of infection. Pathogens experience mutation as an outbreak unfolds, resulting in changes to their genetic code, and if the rate of mutation is sufficiently fast, genome sequences for viruses, bacteria or other infectious agents taken from different hosts will be distinct from each other. There is a positive relationship between the similarity of two sequences taken from pathogen isolates and the closeness of the ancestral relationship between the isolates; if two sequences are very similar then less time will have elapsed since they shared a common ancestor. Intuitively, this notion can be extended to the relationship between the hosts that the isolates came from: a close relationship between pathogens implies that the hosts were close to each other in the transmission tree. This principle opens up the possibility that the tree can be reconstructed using a new type of data that was previously invisible to the naked eye, so long as isolates can be acquired from enough hosts (and, if this is to be conducted while the outbreak is ongoing, quickly enough) to make inference useful. Traditional epidemiological data from contact-tracing or other sources could also be used to augment the procedure.

Ideally, samples would be taken from every host, a natural prerequisite being that all hosts can be identified in the first place. This is more likely for some pathogens, and some host populations, than others; promising situations are those in which all potential hosts will be closely monitored. This is one reason why work on this topic has often been undertaken on outbreaks occurring in farmed animals. The “host”, the infected unit, is taken to be a farm rather than an individual animal, as it is generally of more interest to determine which farms infected which others than how the disease spread from animal to animal. As considerable resources will often be expended to stamp out the disease, at least in high-income countries, identification of all infected farms is quite likely. Work has been published reconstructing the tree for outbreaks of foot-and-mouth disease virus (1, 2, 3, 4), avian influenza (5, 6), and salmon infectious anaemia virus (7). However, as perfect sampling is unlikely in most circumstances, many of the most up-to-date methods are appropriate for imperfect and even quite sparse isolate collection (8, 9). The motivation for such work is often to design procedures to reconstruct the tree for endemic disease, but they are also appropriate for poorly-sampled outbreaks. Nevertheless, it will always be true that the transmission tree will be only very partially revealed if a small fraction of the population of hosts provides any data.

There is, in practice, little difference between a method to reconstruct the spread of a pathogen between infected individuals, be they humans or animals, or between locations within which a number of infected individuals are present, except that the latter situation makes it straightforward to include a geographical component to the analysis. As a result, this review will not confine itself solely to discussing work dealing with pathogens of animals, but will also refer to work that has been conducted on human disease. However, the methods described here are not suitable for inference of transmission between locations where the chances of multiple introductions are high and the concept of a single infection affecting the entire area is not meaningful; analysis of spread between, for example, cities or countries are better conducted using more general phylogeographical methods (10, 11).

The tools developed for analyses of this sort have the potential to be used in real time as an outbreak is occurring, but such an application has not yet been demonstrated in the literature and, as yet, all published studies have conducted analyses using a sequence dataset completed after the event is concluded, or else have focussed on endemic pathogens. If they were indeed to be used in real time as an epidemic unfolded, a centralised process to acquire and sequence isolates as fast as possible would be essential.

The power of the procedures outlined here should not be overstated. Perfect reconstruction of the transmission tree using genetic data alone would be possible only if pathogen mutation rates were much faster than they actually are; in practice the genetic diversity that accumulates over the relatively short timescale of an outbreak is limited, some isolates taken from different hosts may be found to have identical sequences, and uncertainty regarding transmission routes will never be entirely eliminated. The output of more sophisticated methods will assign a score to inferred links in the transmission tree designating how well-supported the relationship between the hosts is by the data. Due to the lack of resolution that is frequently seen when inference uses genetic data alone, authors regularly stress the importance of including data from traditional epidemiological investigations and prior knowledge about the pathogens and hosts involved in an analysis (12, 13, 6). Geographical data or estimates of dates of infection can be used to improve the reconstruction, or contact tracing can be used to rule out some transmission trees. The emergence of a new way to infer pathogen spread should not be taken as a reason to entirely abandon all the old ones.

4. Definition of difference between isolates

The fundamental principle of any kind of molecular epidemiological analysis is that the more similar the genetic sequences for two pathogens are, the more recently they shared a common ancestor, which must have been present in a single host. Closeness of genetic sequences therefore indicates closeness in the transmission chain. The first thing that is needed is some measure by which sequences can be compared. As it is important to capture as much genetic diversity as possible, this is usually done at the nucleotide level, and on the full genome if possible. While some studies have used the simple genetic distance (the number of differing sites) as a measure of distance, this approach does not take into account the nature of the mutation process (such the possibility of back-mutation, and differing probabilities of occurrence for different mutations) and using the distance matrix from a nucleotide substitution model (for example (14, 15)), is more suitable, although in practice the differences may be small, given the limited amount of mutation that is expected to occur over outbreak timeframes.

Care should be taken in situations where the similarity between sequences in fact cannot be taken simply as a proxy for the closeness of the ancestral relationship between the corresponding isolates. There are two major causes for concern. The first is situations of reassortment or recombination, where two pathogens may have a closer ancestral relationship in some parts of their genomes than in others. In an outbreak situation, and presuming that even if more than one genetic variant is introduced to a host upon infection the difference between them is not large, this is only likely to be a serious problem in cases of superinfection; if recombination or reassortment takes place within a host, all the resulting variants are still descendants of the strain that caused the infection and have the same ancestral relationship to it, even if they have exchanged genetic material with each other. If, on the other hand, a host is infected twice by quite divergent strains, mixing of genetic information could have a seriously distorting effect on the picture. It is recommended that datasets be checked for recombination or reassortment using a tool developed for this purpose (16), though no approaches have yet been proposed if it is found. A starting point might be to conduct separate analyses of the parts of the sequence on either side of any identified breakpoint.

The second concerning situation revolves around convergent evolution. While the assumption in methods of this type is that mutation is a neutral process, it frequently is not, and some variations may be selected for. If this is so, then genetic similarity between isolates at some sites may not be the result of a close historical relationship, but instead because of the similar environments that they find themselves in. Software exists to identify such sites (17), and if this is suspected for certain sites, those should simply be excluded from the analysis.

The problem of reconstructing a transmission tree given a measure of the genetic distance between two sequences is closely related to the problem of reconstructing a phylogeny, and similar approaches have been used: simpler ones attempt to find the single tree which keeps the amount of mutation required to a minimum, whereas the more complex construct an ancestry by fitting models of transmission and mutation to the sequence data and include some measure of uncertainty in the output. The phylogeny itself, which depicts the ancestral relationship between the pathogen isolates without reference to the host structure, is of relevance, because internal nodes in it correspond to points at which a lineage was present in one host and subsequently split; if descendant nodes are sampled from more than one host, at least one transmission is implied.

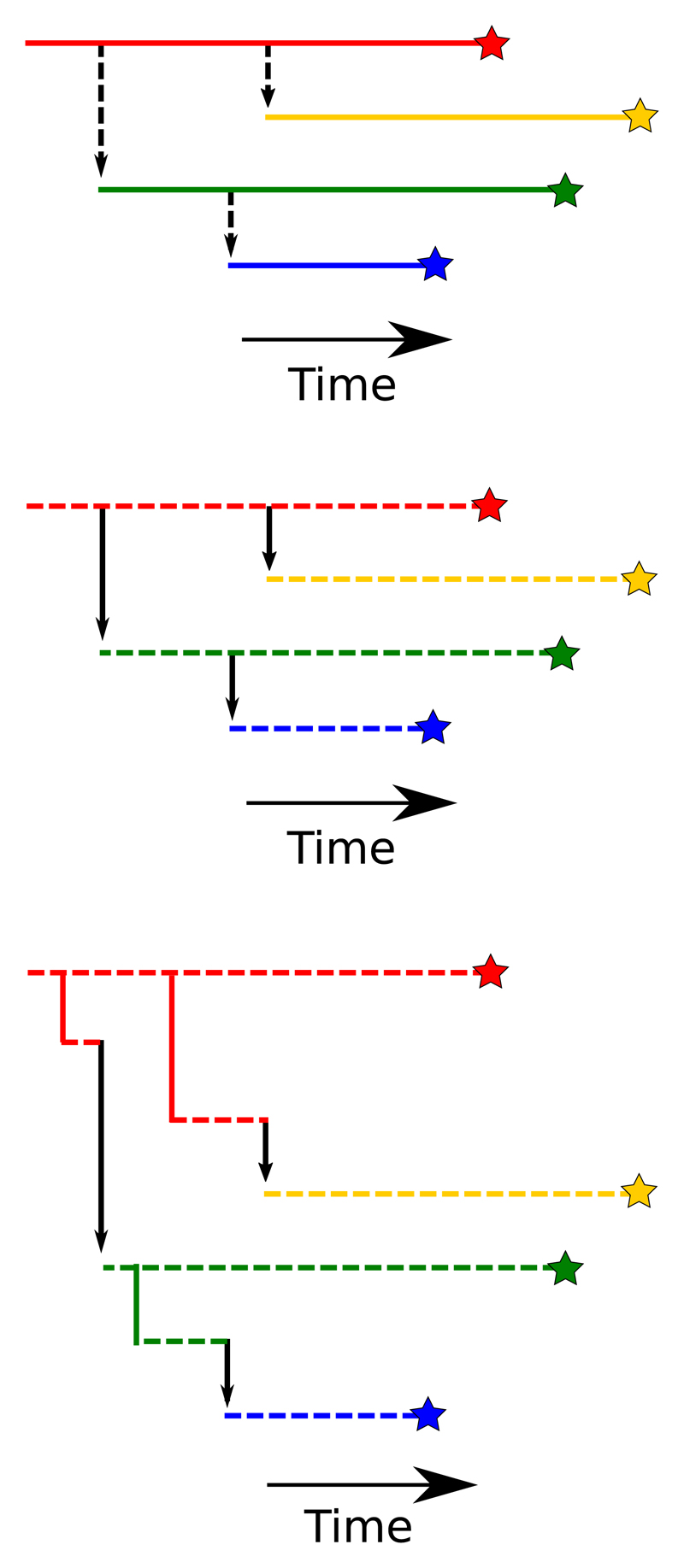
There are broadly three classes of transmission tree reconstruction method, of increasing complexity. The simplest assume that a sampled sequence is entirely representative of the strain which infected the corresponding host over the full period of its infection. The intermediate group still assume that each host was infected by one lineage, but allow for mutation of that lineage; any sequence is taken to be entirely representative of the pathogen population in the host at the time of sampling. The most complex class acknowledge that multiple, genetically distinct, lineages can co-exist within a host at the same time. Figure 1 provides an illustration of the three approaches. The most complex model is not necessarily the most appropriate to the problem; the assumptions made in the simpler versions have enabled recent work on the detection of unsampled cases, and more basic models may also be preferred for reasons of computational time.

Figure 1.

Illustration of the three basic approaches to transmission tree reconstruction using genetic data. Stars represent the sampling of isolates from hosts; each horizontal line is a distinct pathogen lineage and is coloured by the host it is present in. Black vertical arrows represent transmissions between hosts, and dashed lines are undergoing mutation. Top: Mutation is a consequence of transmission and only one lineage is present in each host. Middle: Mutation occurs within-host but only one lineage is present in each. Bottom: multiple lineages per host.

5. Within-host genetic uniformity

The most rudimentary way to infer a transmission network from a set of genetic isolates is to construct a tree that minimises the total genetic distance between them, under the assumption that as few mutations as possible were responsible for the observed sequences (18). Each sequence is taken to be uniquely representative of the pathogen strain infecting each host, and the transmission process is not modelled in any way. This tree is in a mathematical concept known as the minimal spanning tree, and it has similarities to the maximum parsimony method for phylogeny reconstruction. However, it is not identical, because maximum-parsimony phylogenetics reconstructs a tree with sequences assigned only to leaf nodes, whereas every node in the minimal spanning tree corresponds to a sequence. This approach has the advantage of simplicity; as no assumption of direct transmission is made, links in the network can corresponding to any number of intervening hosts and, in fact, this approach is often used to infer transmission histories between epidemiologically unrelated samples (19, 20). However, it has many inadequacies (21). It outputs only a single transmission tree, even if large numbers fit the distance matrix equally well, and gives no indication of whether particular ancestral relationships are highly supported by the data or more likely to be spurious. There is also no temporal component to the analysis; the direction along the tree that the pathogens travelled can be at best inferred post-hoc using data about the order of infection, with no guarantee that this approach will be consistent between every pair of isolates.

To deal with the issue of uncertainty, a bootstrapping procedure to overcome the first of these limitations was proposed by Salipante and Hall (21). A procedure to find the transmission tree that minimises genetic distance while maintaining the order in which sequences were sampled is the SeqTrack algorithm developed by Jombart et al. (22); this also introduces epidemiological data (such as spatial locations) as a means to discriminate between ancestries that are equally likely according to genetic distances.

The SeqTrack approach can be improved to accommodate uncertainty by, instead of searching out the single “best” transmission tree, using a Bayesian Monte Carlo Markov Chain (MCMC) procedure to sample from the probability distribution of trees, given the sequences and potentially also epidemiological data (such as spatial locations). The output is not one but many, potentially thousands, of transmission trees; this set can then be analysed to identify likely pathways of infection. Ypma et al. (5), applied such a procedure to data from the 2003 H7N7 avian influenza outbreak in the Netherlands, incorporating a spatial component defined by a transmission kernel function. The effective assumption, when within-host genetic diversity is ignored, is that mutation is a consequence of transmission. The mutation rate will be expressed in units of mutations per generation, rather than the more common mutations per unit time. While this is certainly a simplification, it can be a useful one; for example it allows for quantification of the number of unsampled links in the transmission chain if the distribution of the serial interval (the time between successive infections in the chain) of the infection is known. If it is likely that two hosts are adjacent in the transmission tree of known hosts, but the number of mutations between them is larger than expected for a single transmission, it would suggest the presence of an unsampled intervening host. This is the principle by which the outbreaker algorithm by Jombart et al (13), another Bayesian MCMC method, can estimate the number of unsampled cases in the transmission chain between those that sequences have been obtained from. It also includes a procedure to identify situations where there is likely to be more than one independent introduction to the population of hosts.

6. Within-host mutation

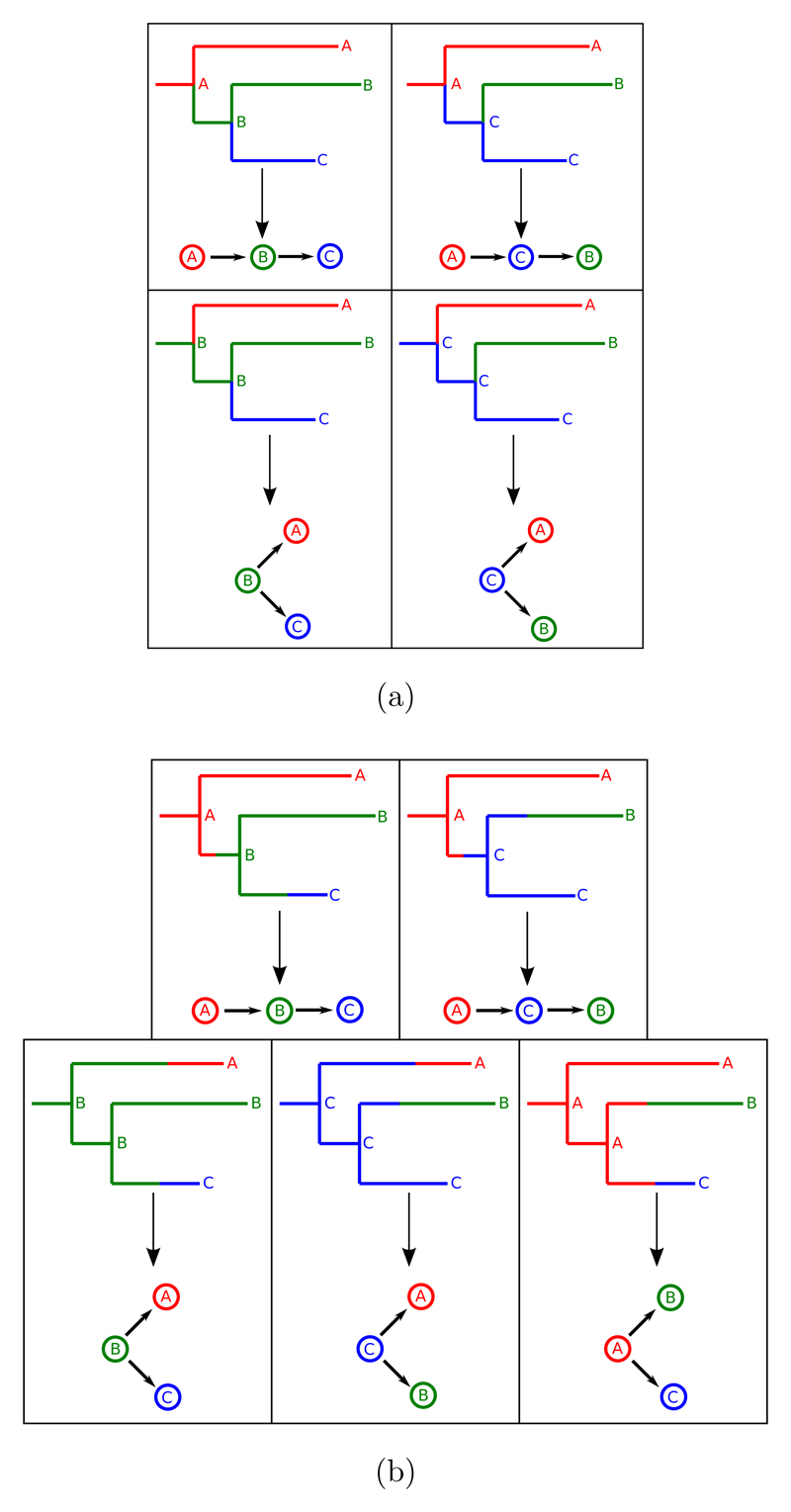
If mutations are assumed to occur over the lifetime of a pathogen’s presence in a host, but no two genetic variants are allowed to occupy the same host at the same time, the implicit assumption is that lineages split only at transmission. This is a simplification but is unlikely to be a major one if few mutations are expected to be observed during a host’s infection, or if the rate backwards in time at which two lineages “coalesce” to a common ancestor is much faster than the transmission rate of the pathogen between hosts (23). If one draws a phylogeny, an internal node represents an infection of one host by another, in addition to a common ancestor of pathogen isolates. The work of Cottam et al (1) explored this by mapping possible transmission histories onto a pre-generated phylogeny for the 2001 UK foot and mouth disease virus (FMDV) epidemic. This is illustrated in figure 2a; if we assume that each host was sampled, then each internal node in the phylogeny corresponds to an ancestor of the samples that was present in one of these hosts and by exploring different assignments of nodes to hosts we are in fact exploring different transmission trees. Each internal node must be assigned to the same host as one of its child nodes; a branch whose terminal node is assigned to a particular host corresponds to a lineage existing solely in that host. Cottam et al. then calculated the probability of each possible assignment of these nodes based on epidemiological information about the location of the host farms and their probable infection dates.

Figure 2.

Examples of the annotation of the internal nodes of a phylogeny and the correspondence to transmission trees, if one sequence is taken per host in an outbreak amongst three cases. In a), internal nodes represent transmissions, but in b) they do not represent transmissions.

The Cottam et al. approach had the limitation that it took a fixed phylogeny as input, and as a result genetic uncertainty was not taken into account. Their dataset was also sufficiently small that they could do calculations by exhaustively assigning the internal nodes of the phylogeny to every possible configuration of hosts. For larger datasets this would prove prohibitive in terms of computational time. The latter limitation can be overcome by use of Bayesian MCMC, which provides a representative sample from the probability distribution of transmission trees without the having to examine every single one. This is the approach taken by Morelli et al. (3), whose method was also the first of this type to not employ an underlying fixed phylogeny. As with Cottam et al., they were working on the 2001 FMDV outbreak and were able to include farm locations in the analysis. The work was extended by Mollentze et al. (8), working instead on rabies samples from South Africa; this second paper extended the procedure to a situation of less consistent sampling by, as with outbreaker, allowing for multiple introductions to a study population and for the path of infection between two sampled individuals to pass through unsampled ones, although unlike outbreaker the procedure only indicates the presence of such indirect infections and does not enumerate them.

7. Within-host diversity

Usually, methods allowing for within-host diversity have assumed that only a single genetic variant is passed from one host to another during transmission (in other words, that transmission is a complete bottleneck), but that this single variant is then the source of a large, freely-mutating population. If one were to consider the ancestry of the pathogens within this population that are sampled and sequenced, or are subsequently transmitted to other hosts, it can be represented as a phylogenetic tree. The time of most recent common ancestor of all these sampled or transmitted pathogens is any time after the infection of the host. Each host in the outbreak has such a within-host phylogeny and, if one for each is joined up according to the transmission tree, the result is once again a single phylogeny tracing the ancestry of the samples taken from the entire event. However, no longer is there a temporal correspondence between internal nodes and transmission events.

The methods of the previous two sections have required that two processes be modelled: the spread of the pathogen between hosts, and mutation. If within-host diversity is to be considered then a model may be required for a third process, which is that occurring within each host. If the “host” is an organism, this will be a model of the dynamics of the population of pathogens infecting it; if is instead a location, it can instead be a model of the infection as it spreads through the organisms present. In either case, all approaches to date have employed a coalescent process as this model of within-host dynamics, with the population assuming to be freely mixing and its size changing according to a deterministic function. This function may assume an invariant population size (12), or that it obeys exponential (4) or logistic (6) growth, or that it grows to a peak and then declines (4).

A great advantage of allowing for within-host genetic diversity is that this makes it easy for an analysis to include more than one distinct sequence taken from the same host. A method that assumes that all isolates taken from the same individual or location at the same time are identical obviously cannot deal with data that contradicts this. This is a useful enhancement, as it has been shown in simulation studies that the acquisition of multiple sequences per host can greatly improves the accuracy of inference of the transmission tree (24).

As in the previous two categories, most methods of this type utilise Bayesian MCMC. The first was developed by Ypma et al. (4), who treated every within-host phylogeny as a separate entity. An alternative approach, introduced by Didelot et al. (12) is to modify Cottam et al’s procedure of annotating the nodes of a single phylogeny with host information. Since internal nodes no longer represent transmissions, a modification must be made; a node must be assigned to the same host as at least one of three nodes: its two children and its parent (see figure 2b). This allows for situations in which a lineage in a given host was not the ancestor of any isolate sampled from that host, which is essential in a framework with within-host diversity; e.g. in figure 2b, in the bottom right, the common ancestor of the lineages sampled from hosts B and C was actually present in host A, but is not the ancestor of the lineage sampled from A. The node annotation procedure is convenient because is highly compatible with existing methods for phylogenetic reconstruction; trees need merely to be annotated with assignments of internal nodes to hosts and infection dates. Didelot et al. applied this to a fixed overall phylogeny, and it was recently extended by Hall et al. (6) to simultaneously account for variation in the overall phylogeny and the transmission tree structure.

A radically different framework, which eschews Bayesian MCMC in favour of an importance sampling approach with similarities to approximate Bayesian computation, was recently published by Numminen et al (9), and avoids modelling within-host dynamics at all, instead simulating a representative set of transmission trees and isolate TMRCAs, generated by models of transmission and mutation, that conform to a fixed phylogenetic structure. The key advantage of the approach is that it relies on an explicit model of the sampling process, and is therefore of use in situations where sampling is extremely sparse.

8. Pairwise methods

Some methods eschew any attempt to reconstruct the full transmission tree and instead concentrate on, given any two sequences, attempting to infer the probability that one was the infector of the other. In situations of sparse sampling, this may be the only useful inference that can be drawn in any case. Volz and Frost (23) take this approach, assuming that internal phylogeny nodes correspond to transmissions, and then outlining a method that uses the phylogeny to estimate probabilities of direct transmissions between sampled hosts in a very general framework allowing for complex disease dynamics. Worby et al. (25), while requiring complete sampling, is the first method to incorporate within-host genetic diversity while using a coalescent process for the within-host population which does not assume that transmission is a complete bottleneck, allowing for the transmission of multiple genetic variants at the same time. Basing inference entirely on pairwise genetic distance, it also is much less computationally intensive than many of the MCMC approaches outlined above. A similarly fast method was presented by Famulare and Hu (26), who identify likely direct transmissions by using a likelihood ratio test of the hypothesis that the time of common ancestor between sequences taken from each case being equal to the sampling date of the earlier one (implicitly assuming no within-host mutation). Where this procedure suggests several potential infectors for a case, a pruning algorithm can be employed to pick a single one, based on, for example, the pair that minimises the time between sampling.

9. Other approaches

Some investigations have used genetic data as a means to augment traditional contact tracing procedures, without using a combined methodology incorporating both sequences and traditional epidemiological data. For example, Gardy et al (27) investigated a Mycobacterium tuberculosis outbreak using contact tracing and subsequently showed that whole-genome genetic analysis could be used to improve the inference by ruling out connections between cases who were epidemiologically linked but whose pathogen strains, when sequenced, proved to be only distantly related.

An unusual approach was taken by Aldrin et al (7), who eschewed phylogenetic reconstruction or a model of mutation of any kind entirely, and instead treated the genetic distance between isolates in the same way as geographical distance between locations is treated in spatial models of disease transmission. The probability that one host infected another declines as the genetic difference between their respective sequences increases, according to a transmission kernel function. This was, in fact, combined with a geographical transmission kernel to calculate the probability of transmission across two landscapes, geographical and genetic. With the parameters of the kernels fit using a maximum-likelihood approach, the probability of each transmission route can be calculated.

10. Conclusions

It must be acknowledged that rigorous testing of these methods on outbreaks in animal populations (and indeed also in human populations, as outbreaks in which it is possible to identify a large proportion of cases are unusual) is hindered by the fact that such events are rare in locations where the resources for comprehensive sampling would be available. The most suitable real datasets are from 2001 (1, 3) and 2003 (5, 6), long before any of these procedures began development and also before it would have been possible to rapidly acquire sequences even if they had been available. While the tools now exist to begin to analyse an outbreak as soon as it is detected, it remains to be seen how quickly the infrastructure of an affected country would be able to provide sequences in such an event. Scope exists for a simulation study on the performance of these methods in inferring transmission links under emergency conditions when the outbreak is only partially revealed, and how short the period from detection of infection to the availability of a sequence would need to be for them to be useful. In any case, however, these tools would be available for a retrospective analysis once the emergency is over, in order to aid forensic investigation of what happened.

The lack of comprehensive genetic datasets from actual outbreaks has not hindered development of these methods, however, as many of the most recently-published papers on this subject have concentrated on endemic disease (8, 9). This is an important development for epidemic analysis as well, because the testing of methods on real data of any sort is essential if inference is to be relied upon in an emergency situation, and because the problems involved in applying such procedures to endemic pathogens where the infected population is not well revealed are similar to those involved in handling epidemic sampling which is less than comprehensive. This can enable transmission tree reconstruction for epidemics occurring in resource-poor settings, or in richer settings before the full extent of the event becomes clear.

In summary, sequencing technology is now advanced to the point that genetic data can add an important new element to the epidemiological investigation of outbreaks of infectious diseases. Many different approaches have been taken, of varying complexity and appropriate to a variety of different scenarios. With the theoretical basis and computational methods in place, the utility of these procedures in dealing with a genuine emergency is ready to be tested.

For publicly available implementations of the various procedures, SeqTrack is available as part of the adegenet R package, and outbreaker is its own R package. The method outlined by Didelot et al is available as the standalone Objective-C application transphylo, and that of Hall et al is implemented as part of the phylogenetics package BEAST (28).