ADAPTIVE METHODS FOR STOCHASTIC DIFFERENTIAL EQUATIONS VIA NATURAL EMBEDDINGS AND REJECTION SAMPLING WITH MEMORY

Abstract

Adaptive time-stepping with high-order embedded Runge-Kutta pairs and rejection sampling provides efficient approaches for solving differential equations. While many such methods exist for solving deterministic systems, little progress has been made for stochastic variants. One challenge in developing adaptive methods for stochastic differential equations (SDEs) is the construction of embedded schemes with direct error estimates. We present a new class of embedded stochastic Runge-Kutta (SRK) methods with strong order 1.5 which have a natural embedding of strong order 1.0 methods. This allows for the derivation of an error estimate which requires no additional function evaluations. Next we derive a general method to reject the time steps without losing information about the future Brownian path termed Rejection Sampling with Memory (RSwM). This method utilizes a stack data structure to do rejection sampling, costing only a few floating point calculations. We show numerically that the methods generate statistically-correct and tolerance-controlled solutions. Lastly, we show that this form of adaptivity can be applied to systems of equations, and demonstrate that it solves a stiff biological model 12.28x faster than common fixed timestep algorithms. Our approach only requires the solution to a bridging problem and thus lends itself to natural generalizations beyond SDEs.

1. Introduction

Explicit methods for solving Ordinary Differential Equations (ODEs) with adaptive time-stepping algorithms, such as the Dormand-Prince and Cash-Karp algorithms, have become efficient and popular solvers for numerical simulations of ODEs due to their ease of use and accuracy [8, 24, 6]. These algorithms consist of two major components: an embedded higher-order and lower-order pair of temporal integrators to allow for estimating the local error (i.e. the error indicator), and an adaptive time-stepping algorithm for choosing the next stepsize and performing the update [21, 1]. Together, the algorithm is able to effectively solve most equations by automatically adapting to the solutions by adjusting the timestep.

To derive adaptive algorithms for stochastic ordinary differential equations (SODEs) of the form

$$d{X}_t=f(t,X_t)dt+g(t,X_t)d{W}_t,$$ (1)

where f is the drift coefficient and g is the diffusion coefficient, a natural choice is to use embedded Stochastic Runge-Kutta (SRK) methods. Kloeden and Platen developed a set of stochastic Taylor expansions which allowed for the derivation of higher order (greater than order 1.0) SRK methods [15, 13]. One interesting feature of this class of algorithms is that, since no analytical solution exists for iterated stochastic integrals, they are usually replaced by sufficiently exact approximations due to Wiktorsson [25, 23]. While strong order 2.0 SRK methods have been studied [3, 15], existing works mainly focus on strong order 1.5 Stochastic Runge-Kutta methods, such as a series of methods for Stratanovich SDEs [4, 2] and for Ito SDEs [14].

One recent advance in SRK methods is Rößler’s methods for Ito SDEs [22]. This class of methods was shown to be efficient by reducing the number of function evaluations required per step. Their format via extended Butcher tableaus allows them to be easily amendable. However, these methods have not been used for adaptive algorithms. Here, we will show that for certain Rößler-SRK methods, there exists a naturally embedded order 1.0 method such that no extra function evaluations are needed in order to evaluate its difference from the order 1.5 method, presenting an efficient way to both perform the steps and approximate the error.

With the embedded SRK methods, the next challenge is to deal with the choice of time steps. For ODEs, one usually performs a trial step in order to calculate an error estimate and, using this estimate, either choose to step or reject the step and try again with a smaller timestep. The problem with such an approach for SODEs is that when performing the trial step, one takes a random number to simulate the future Brownian path, and if one rejects the timestep, this will change the sample properties of the Brownian path [5]. This is particularly an issue because larger variations in the Brownian path are correlated with more numerical error and thus such an algorithm would have a strong tendency to reduce the variance of the noise process. Lastly, it ‘s not clear how to effectively sub-sample a solution along a Brownian path after one decides it’s too coarse.

Most of the current approaches for adaptive time steps attempt to perform error calculations before stepping in order circumvent rejection sampling. One approach [9] utilizes an order 1.0 algorithm with a Brownian path stored at the h, $\frac{h}{2},\frac{h}{4}$ time-points, etc. stored as a tree. The algorithm solves for an error equation using a stochastic Taylor series and then utilizes this new equation to solve a linearization backwards in time in order to produce an error estimate for a future timestep without having to do rejection sampling. This method requires using halving/doubling of stepsizes and, since it’s not able to account for which timesteps the Brownian path has the largest future jumps, has to be conservative in order to achieve its chosen error estimate. It also requires the user to provide many derivatives of the drift and diffusion functions f and g, or alternatively perform a numerical estimation of these derivatives at each timestep. Lastly, in their paper they proved that any variable stepsize implementation must use a numerical method which has strong order of at least 1, meaning that any variable stepsize method must go beyond Euler-type methods.

Another algorithm may be limited to low-order methods due to its requirement of having a small “fixed number of observations”, and requires the calculation of derivatives of both f and g [19]. Lamba [16] presented an order 1.0 algorithm which used properties of the Brownian bridge restricted to a grid of multiples of $\frac{1}{3}$. It included the novel property of having separate error estimators for deterministic and noise induced error for finer control of the solution. There is one adaptive stepping algorithm which does not have restrictions on the stepsize and utilizes embedded strong order 1.0/1.5 SRK methods for Stratanovich SDEs [5]. Their embedded method requires two additional function evaluations in order to derive an error estimate, and requires solving for a dense matrix and performing a matrix multiplication each time an interval is subdivided. Their results show that general time-stepping tends to be vastly more efficient than grid-based methods from before.

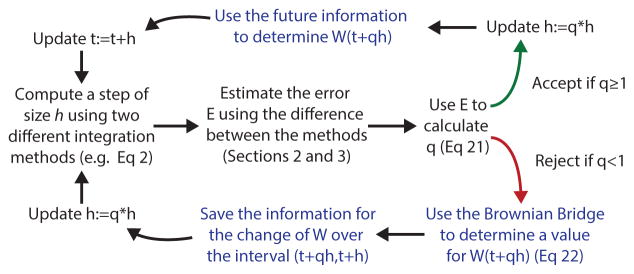
The main results of the paper are the development of strong order 1.0/1.5 embedded Runge-Kutta pairs for error estimation and a new adaptive time-stepping algorithm termed Rejection Sampling with Memory (RSwM). This extension to the rejection sampling algorithm is diagrammed in Figure 1 and gives an overview of how the various developments come together to form one complete algorithm.

Figure 1.

Outline of the adaptive SODE algorithm based on Rejection Sampling with Memory. This depicts the general schema for the Rejection Sampling with Memory algorithm (RSwM). The green arrow depicts the path taken when the step is rejected, whereas the red arrow depicts the path that is taken when the step is accepted. The blue text denotes steps which are specific to the stochastic systems in order to ensure correct sampling properties which are developed in section 4.

In section 2 we construct the method ESRK1 which is a strong order 1.0/1.5 embedded pair of algorithms which allows for high-order solving and error estimation. In section 3 we prove the existence of a natural order 1.0/1.5 embedded pair of Rößler SRK algorithms that allows for the efficient calculation of an error estimate for high-order SRK methods with no additional function evaluations. Using this error estimate, we construct the rejection sampling methods for SDEs which allows for efficient general adaptive time-stepping with almost no extra floating point operations. In section 4 we first elucidate a simple solution to general adaptive time-stepping, discuss how one could attempt to improve the efficiency of the algorithms, and then develop more efficient adaptive stepping algorithms.

Lastly, we perform numerical experiments to show the effectiveness of the algorithms. In section 5, we show that our methods are able to reproduce the proper sample statistics for the stochastic differential equations and the user chosen local error parameter ε is able to control the global error. Then in section 6, we demonstrate the ability for the adaptive parameters to control for the coarseness of the solution to nonlinear systems of equations, and show that when applied to a large stiff system derived from biology, our method is able to stability solve a Monte Carlo experiment of 10000 simulations without diverging 12.28x faster than a few popular fixed timestep methods. We conclude by discussing how these algorithms can be generalized to other problems like Stratanovich SDEs, jump diffusions, and SPDEs.

2. Construction of an order 1.0/1.5 embedded pair

Using a colored root tree analysis, Rößler developed a set of strong order 1.5 stochastic Runge-Kutta schemes [22]. This multi-step method resulted in less computational steps than the KPS schemes, and the number of steps grows much slower as the Ito dimension increases than in the KPS schemes [15]. The structure of Rößler methods are relatively simple, making the method both easy to implement and fast in runtime. For simplicity, we describe the equations for a single Ito dimension, though the results generalize to the case of multiple Ito dimensions.

The Runge-Kutta methods are strong order 1.5 if they satisfy a set of order conditions in A, taking the following form:

$$U_{n+1}=U_n+\sum _{i=1}^s{\alpha }_{i}f\left(t_n+c_i^{(0)}\mathrm{\Delta }t,H_i^{(0)}\right)\mathrm{\Delta }t+\sum _{i=1}^s\left({\beta }_i^{(1)}{I}_{(1)}+{\beta }_i^{(2)}\frac{I_{(1,1)}}{\sqrt{\mathrm{\Delta }t}}+{\beta }_i^{(3)}\frac{I_{(1,0)}}{\mathrm{\Delta }t}+{\beta }_i^{(4)}\frac{I_{(1,1,1)}}{\mathrm{\Delta }t}\right)g\left(t_n+c_i^{(1)}\mathrm{\Delta }t,H_i^{(1)}\right),$$ (2)

with stages

$$H_i^{(0)}=U_n+\sum _{j=1}^s{A}_{ij}^{(0)}f\left(t_n+c_j^{(0)}\mathrm{\Delta }t,H_j^{(0)}\right)\mathrm{\Delta }t+\sum _{j=1}^s{B}_{ij}^{(0)}g\left(t_n+c_j^{(1)}\mathrm{\Delta }t,H_j^{(1)}\right)\frac{I_{(1,0)}}{\mathrm{\Delta }t},$$ (3)

$$H_i^{(1)}=U_n+\sum _{j=1}^s{A}_{ij}^{(1)}f\left(t_n+c_j^{(0)}\mathrm{\Delta }t,H_j^{(0)}\right)\mathrm{\Delta }t+\sum _{j=1}^s{B}_{ij}^{(1)}g\left(t_n+c_j^{(1)}\mathrm{\Delta }t,H_j^{(1)}\right)\sqrt{\mathrm{\Delta }t}.$$ (4)

The iterated stochastic integrals I_(1,1), I_(1,0), and I_(1,1,1) are evaluated via the approximations due to Wiktorsson as noted in C. These methods are referred to as the SRI algorithms and are indicated by the tuple of 44 coefficients (A⁽ⁱ⁾, B⁽ⁱ⁾, β⁽ⁱ⁾, α). Similarly, for additive noise the Runge-Kutta methods are strong order 1.5 if they satisfy the order conditions contained B, taking the form

$$U_{n+1}=U_n+\sum _{i=1}^s{\alpha }_{i}f\left(t_n+c_i^{(0)}\mathrm{\Delta }t,H_i^{(0)}\right)\mathrm{\Delta }t+\sum _{i=1}^s\left({\beta }_i^{(1)}{I}_{(1)}+{\beta }_i^{(2)}\frac{I_{(1,0)}}{\mathrm{\Delta }t}\right)g(t_n+c_i^{(1)}\mathrm{\Delta }t),$$ (5)

with stages

$$H_i^{(0)}=U_n+\sum _{j=1}^s{A}_{ij}^{(0)}f\left(t_n+c_j^{(0)}\mathrm{\Delta }t,H_j^{(0)}\right)\mathrm{\Delta }t+\sum _{j=1}^s{B}_{ij}^{(0)}g\left(t_n+c_j^{(1)}\mathrm{\Delta }t\right)\frac{I_{(1,0)}}{\mathrm{\Delta }t}.$$ (6)

Given the efficiency of order 1.5 SRK methods for stochastic problems, we will develop Runge-Kutta-Fehlburg-like embedded algorithms [1], which step along an order 1.5 path using error estimates from an order 1.0 path.

We start with the order 1.5 method SRIW1 [22] denoted by coefficients (A⁽ⁱ⁾, B⁽ⁱ⁾, β⁽ⁱ⁾, α). Notice that the order 1.0 conditions from A only enforce β^(3)T B⁽¹⁾e = 0 on and β^(4)T B⁽¹⁾e = 0 on β⁽³⁾ and β⁽⁴⁾. Thus let β̃⁽³⁾ = β̃⁽⁴⁾ = 0. This gives an order 1.0 method (A⁽ⁱ⁾, B⁽ⁱ⁾, β̃⁽ⁱ⁾, α).

Let X̄ be the numerical solution of SRIW1 on the general SODE Equation 1, and X̃ be the numerical solution from the algorithm with coefficients (A⁽ⁱ⁾, B⁽ⁱ⁾, β̃⁽ⁱ⁾, α). By Equation 2, the difference between the numerical solutions on the next step is

$$\overline{X}-\stackrel{\sim }{X}=\sum _{i=1}^s\left({\beta }_i^{(3)}\frac{I_{(1,0)}}{\mathrm{\Delta }t}+{\beta }_i^{(4)}\frac{I_{(1,1,1)}}{\mathrm{\Delta }t}\right)g\left(t_n+c_i^{(1)}\mathrm{\Delta }t,H_i^{(1)}\right).$$ (7)

Note that we could keep β⁽³⁾ not equal to zero and still have an order 1.0 method, but zeroing β⁽³⁾ gives an estimate for the size of ΔZ (the second Brownian path used to estimate I_(1,0) as noted in C) which may need to be controlled as well.

However, this error estimate does not take into account stiffness in the drift coefficient f. Notice that the only condition on the coefficients α is Σ α_i = 1. Thus let $\stackrel{\sim }{\alpha }=(\frac{1}{2},\frac{1}{2},0,0)$. This gives another order 1.0 Method (A₀, B₀, β_i, α̃). If we let X̂ be the numerical solution to Equation 1 using the coefficients (A₀, B₀, β_i, α̃), then by Equation 2 notice

$$\overline{X}-\widehat{X}=-\frac{\mathrm{\Delta }t}{6}f\left(t_n+c_1^{(0)}\mathrm{\Delta }t,H_1^{(0)}\right)+\frac{\mathrm{\Delta }t}{6}f\left(t_n+c_2^{(0)}\mathrm{\Delta }t,H_2^{(0)}\right).$$ (8)

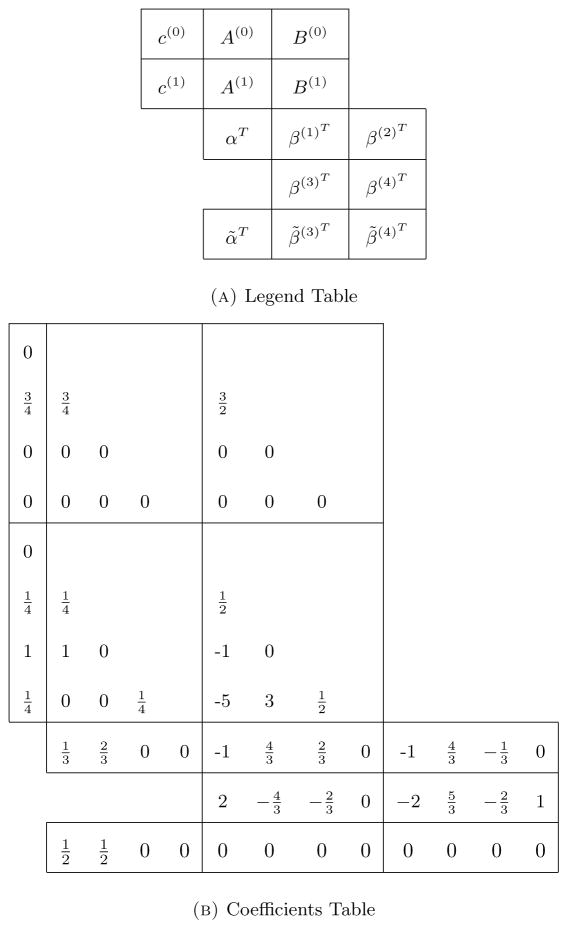
Notice that for this algorithm the difference is only due to the stiffness of the drift coefficient. Using both the β and the α changes together gives a pair of strong order 1.0/order 1.5 methods which is robust to errors in both coefficients. We designate this algorithm Embedded SRK 1 (ESRK1) as the set of coefficients defined in Table 1 for which steps are taken according to Equation 2, Equation 3, Equation 4.

Table 3.

qmax determination tests. Equation 31, Equation 33, and Equation 35 were solved using the ESRK+RSwM3 algorithm with a relative tolerance of 0 and absolute tolerance of 2⁻¹⁴. The elapsed time to solve a Monte Carlo simulation of 100,000 simulations to T = 1 was saved and the mean error at T = 1 was calculated. The final column shows timing results for using ESRK+RSwM3 on the stochastic cell model from F solved with the same tolerance settings as in subsection 6.2 to solve a Monte Carlo simulation of 10,000 simulations.

	Example 1		Example 2		Example 3		Cell Model
qmax	Time (s)	Error	Time (s)	Error	Time (s)	Error	Time (s)
1 + 2−5	37.00	2.57e-8	60.87	2.27e-7	67.71	3.42e-9	229.83
1 + 2−4	34.73	2.82e-8	32.40	3.10e-7	66.68	3.43e-9	196.36
1 + 2−3	49.14	3.14e-8	132.33	8.85e-7	65.94	3.44e-9	186.81
1 + 2−2	39.33	3.59e-8	33.90	1.73e-6	66.33	3.44e-9	205.57
1 + 2−1	38.22	3.82e-8	159.94	2.58e-6	68.16	3.44e-9	249.77
1 + 20	82.76	4.41e-8	34.41	3.58e-6	568.22	3.44e-9	337.99
1 + 21	68.16	9.63e-8	33.98	6.06e-6	87.50	3.22e-9	418.78
1 + 22	48.23	1.01e-7	33.97	9.74e-6	69.78	3.44e-9	571.59

Adding the two previous error equations Equation 7 and Equation 8, gives E, the error estimation via the difference between the order 1.5 and order 1.0 method, as

$$E=-\frac{\mathrm{\Delta }t}{6}f\left(t_n+c_1^{(0)}\mathrm{\Delta }t,H_1^{(0)}\right)+\frac{\mathrm{\Delta }t}{6}f\left(t_n+c_2^{(0)}\mathrm{\Delta }t,H_2^{(0)}\right)+\sum _{i=1}^s\left({\beta }_i^{(3)}\frac{I_{(1,0)}}{\mathrm{\Delta }t}+{\beta }_i^{(4)}\frac{I_{(1,1,1)}}{\mathrm{\Delta }t}\right)g\left(t_n+c_i^{(1)}\mathrm{\Delta }t,H_i^{(1)}\right).$$ (9)

Thus ESRK1 is a pair of order 1.0/order 1.5 embedded algorithms. Notice that every term in the error calculation Equation 9 is also part of the calculation for the order 1.5 timestep from Equation 2 and thus no additional function evaluations are required for this error estimate. Thus ESRK1 is an extension to the order 1.5 algorithm which allows for an efficient error estimation.

3. Error estimation via natural embeddings

The construction from section 2 is part of a more general construction which we call natural embeddings in Rößler SRK methods. Take a Rößler SRK method determined by coefficients (A⁽ⁱ⁾, B⁽ⁱ⁾, β⁽ⁱ⁾, α). For this method, we can generate an embedded order 1.0 method via a parameter δ by changing α to α̃ where we subtract δ from two coefficients and add δ to two coefficients. Thus by Equation 2, this gives the deterministic error estimate

$$E_D=\mathrm{\Delta }t\left(f\left(t_n+c_{k_1}^{(0)}\mathrm{\Delta }t,H_{k_1}^{(0)}\right)+f\left(t_n+c_{k_2}^{(0)}\mathrm{\Delta }t,H_{k_2}^{(0)}\right)\right)-\left(f\left(t_n+c_{k_3}^{(0)}\mathrm{\Delta }t,H_{k_3}^{(0)}\right)+f\left(t_n+c_{k_4}^{(0)}\mathrm{\Delta }t,H_{k_4}^{(0)}\right)\right),$$ (10)

If we then change β⁽³⁾ and β⁽⁴⁾ to zero on the indices in the index set I₂, then this gives the noise error estimate

$$E_N\left|\sum _{i\in I_2}\left({\beta }_i^{(3)}\frac{I_{(1,0)}}{\mathrm{\Delta }t}+{\beta }_i^{(4)}\frac{I_{(1,1,1)}}{\mathrm{\Delta }t}\right)g\left(t_n+c_i^{(1)}\mathrm{\Delta }t,H_i^{(1)}\right)\right|.$$ (11)

By the order conditions of A, these coefficient changes together give an order 1.0 method whose difference from the order 1.5 method (A⁽ⁱ⁾, B⁽ⁱ⁾, β⁽ⁱ⁾, α) is a bounded error estimate which is calculated directly from the coefficients of the order 1.5 method. This result is summarized in the following theorem:

Theorem 3.1 (Natural Embedding)

For any order 1.5 SRK method with coefficients (A⁽ⁱ⁾, B⁽ⁱ⁾, β_i, α), there exists a δ ∈ ℝ such that (A⁽ⁱ⁾, B⁽ⁱ⁾, β̃⁽ⁱ⁾, α̃ defines a natural order 1.0 embedded SRK method, where β̃⁽³⁾ and β̃⁽⁴⁾ are equivalent to β⁽³⁾ and β⁽⁴⁾ respectively except the indices in I₂ are zeroed, and α̃ differs from α by δ at each coefficient in I₁ by a sign difference of (−1)^σ(i) (σ(i) = 1 for at least one i and σ(i) = 2 for at least one i), and |I₁| even. The one-step difference between the methods (A⁽ⁱ⁾, B⁽ⁱ⁾, β⁽ⁱ⁾, α) and (A⁽ⁱ⁾, B⁽ⁱ⁾, β̃⁽ⁱ⁾, α̃ is bounded by

$$E=\delta E_D+E_N,$$ (12)

where

$$E_D=\left|\mathrm{\Delta }t\sum _{i\in I_1}{(-1)}^{\sigma (i)}f\left(t_n+c_i^{(0)}\mathrm{\Delta }t,H_i^{(0)}\right)\right|\le \mathrm{\Delta }t\sum _{i\in I_1}\left|f\left(t_n+c_i^{(0)}\mathrm{\Delta }t,H_i^{(0)}\right)\right|,$$ (13)

$$E_N=\left|\sum _{i\in I_2}\left({\beta }_i^{(3)}\frac{I_{(1,0)}}{\mathrm{\Delta }t}+{\beta }_i^{(4)}\frac{I_{(1,1,1)}}{\mathrm{\Delta }t}\right)g\left(t_n+c_i^{(1)}\mathrm{\Delta }t,H_i^{(1)}\right)\right|.$$ (14)

Notice that from this theorem if we take the coefficients from the SRIW1 method and let $\delta =\frac{1}{6}$ then we arrive at the ESRK1 method from section 2. Also, note that this theorem be extended to the case where |I₁| = 3 by letting α̃ differ from α by δ in one coefficient and $\frac{\delta }{2}$ in the two others. However, in order to satisfy the Order 0.5 constraint Σ α_i = 1, we cannot simply modify a single component.

This implies that there is no need to specifically derive embedded pairs of methods. Instead, for any order 1.5 Rößler SRK method that one constructs, there exists a naturally embedded order 1.0 method such that E is an error estimate, and thus the error estimator can be utilized without ever explicitly constructing the order 1.0 method. In addition, the calculation of E only uses values found in the order 1.5 timestep from Equation 2. As a result, the error estimate is naturally obtained without any additional function evaluations. Lastly, the equation Equation 12 also has a adjustable parameter δ, which allows the user to scale the relative contributions of the deterministic and noise terms to the overall error estimate.

We note that all of these equations generalize to systems by considering the variables and functions as vectors and vector functions respectively, with the absolute value generalizing to an appropriate norm. This result also generalizes to multiple Ito dimensions, i.e., SODEs of the form

$$d{X}_t=f(X_t,t)dt+\sum _k^d{g}_k(X_t,t)d{W}_t,$$ (15)

in the case where the noise function g is diagonal by a similar construction on the Rößler SRID, giving the error estimates

$$E_D=\left|\mathrm{\Delta }t\sum _{i\in I_1}{(-1)}^{\sigma (i)}f\left(t_n+c_i^{(0)}\mathrm{\Delta }t,H_i^{(0)}\right)\right|\le \mathrm{\Delta }t\sum _{i\in I_1}\left|f\left(t_n+c_i^{(0)}\mathrm{\Delta }t,H_i^{(0)}\right)\right|,$$ (16)

$$E_N=\left|\sum _k^d\sum _{i\in I_2}\left({\beta }_i^{(3)}\frac{I_{(1,0)}}{\mathrm{\Delta }t}+{\beta }_i^{(4)}\frac{I_{(1,1,1)}}{\mathrm{\Delta }t}\right)g_k\left(t_n+c_i^{(1)}\mathrm{\Delta }t,H_i^{(1)}\right)\right|.$$ (17)

Note that in the case of SRA-type methods (additive noise), a similar theorem also holds. By Equation 5 on the multiple Ito dimension SDE Equation 15 we utilize the same construction and receive a natural embedding with the error estimation Equation 12 containing the same deterministic error estimation Equation 13, with a new noise-error estimation:

$$E_N=\left|\sum _k^d\sum _{i=1}^s{\beta }_i^{(2)}\frac{I_{(1,0)}}{\mathrm{\Delta }t}{g}_k(t_n+c_i^{(1)}\mathrm{\Delta }t)\right|.$$ (18)

4. Three algorithms for rejection sampling with memory

4.1. Rejection sampling for stochastic differential equations

As in deterministic rejection sampling algorithms [1, 21, 11], define

$$e=\sqrt{\frac{1}{n}\sum _i^n\left(\frac{E_i}{s{c}_i}\right)},$$ (19)

where

$$s{c}_i={\epsilon }_{\mathit{abs}}+X_t^{(i)}{\epsilon }_{\mathit{rel}},$$ (20)

is the absolute/relative mixed error with ε is the user-chosen error absolute and relative tolerances respectively, E_i is the error estimation of the ith element computed with the methods from section 3, and n is the size of the system. Using this measure of the system error with respect to tolerance, it is common in deterministic systems to define

$$q={\left(\frac{1}{\gamma e}\right)}^{1/(\mathcal{O}+1)},$$ (21)

where γ is a penalty factor (in deterministic methods it is often taken as γ = 2) and 𝒪 is the minimum order of the numerical methods used in the error estimators. For solving deterministic equations, the rejection sampling method for adaptive time-stepping can be summarized as:

1. If q < 1, reject the initial choice of h and repeat the calculation with qh

2. If q ≥ 1, then accept the computed step and change h to min (h_max, qh) where h_max is chosen by the user.

For solving SODEs, this approach needs to be modified since rejection of future steps involves throwing away information about the future Wiener process which biases the sample statistics for the path. Our solution is to change rejection sampling so that all information about the future path is kept, and adapt the sampling of the Brownian path to accommodate for this information. This is summarized as follows:

1. If q < 1, reject the initial choice of h, store the values for the future steps of the Wiener process ΔW_t, and repeat the calculation with qh.

2. If q ≥ 1, then accept the computed step and change h to min (h_max, qh) where h_max is chosen by the user. Use future information to determine the next step.

The algorithm for adapting the random number sampling to account for future information is as follows. As noted in C, due to the term I_(1,0) in the SRK algorithm, we must consider two Brownian paths: W_t, the path from the SODE, and Z_t, an independent Brownian path for the approximation. First, propose a step with ΔW^P and ΔZ^P for a timestep h. If these are rejected, change the step size to qh. Thus we need to sample a new value at W(t_n + qh) using the known values of W(t_n) and W(t_n + h). By the properties of the Brownian Bridge [20, 17], if W(0) = 0, W(h) = L, and q ∈ (0, 1), then

$$W(qh)~N(qL,(1-q)qh).$$ (22)

Thus propose a step of size qh and take the random numbers ΔW = W(qh) and ΔZ = Z(qh) from the distribution Equation 22.

Notice that by the Markov property of Brownian motion, the immediate future and current timestep values fully characterize the distribution of the Brownian Bridge, and using the Brownian Bridge we can interpolate the Brownian process to whatever time-point we deem necessary. Thus if the every time we take a sample of the future Brownian process (i.e. take a random number) we save the random number (even if rejecting the step), we can recover the correct distribution for interpolations of the Brownian process using Equation 22, giving all of the necessary information for computing a step of size qh.

4.2. Computational issues

First we deduce the proper form to save the future information upon rejection and the necessary details to save. Assume that we are at a time t and the Brownian process changed by an amount ΔW^P in the timestep of size h. If there was no future information, this would be the value given by a random number generator with the distribution N(0, h). When a step is rejected, a new stepsize is chosen as qh where q < 1. Knowing the Brownian process’ value at t and t+h, we can determine a value for W(t+qh) using Equation 22. Labeling ΔW as the change in W over our new step of size qh, we have future knowledge that the Brownian path changes over the interval (t+qh, t+h) by $\overline{\mathrm{\Delta }W}=\mathrm{\Delta }{W}^P-\mathrm{\Delta }W$ (note that for the same reasons, we have that the secondary Brownian motion Z used as part of the high-order integrator must also satisfy $\overline{\mathrm{\Delta }Z}=\mathrm{\Delta }{Z}^P-\mathrm{\Delta }Z$). To store this future information, we save the 3-tuple ( $\overline{\mathrm{\Delta }W},\overline{\mathrm{\Delta }Z}$, (1 − q)h). The first two values denote how much the Brownian motions changed and the last denotes the length of the time interval over which the changes occurred. From these values we have the information necessary for to use Equation 22 in order to interpolate the change in Brownian motion from t+qh to any value in [t+qh, t+h]. Since we know the value of the Brownian motions at t+qh, we can perform rejections using this algorithm recursively to see that we can re-reject to any value in [t, t+qh] and still accurately re-create the Brownian motions at any point in the full [t, t + h]. Therefore saving this 3-tuple at each rejection suffices for the full reconstruction of the Brownian processes. Since this algorithm requires very few floating point operations, this algorithm has a good potential for efficiency.

At this point a naive implementation runs into many practical computational issues. The first implementation which comes to mind is to store this 3-tuple of future information into an array. The storage must be a mutable multi-valued data structure because it is possible for consecutive rejections to occur, meaning that we may have to store many pieces of future information. However, when using general stepsizes, it is possible for a step to go past some values of future information, and if this step is then rejected and the future information is added to the end of the array, the array is no longer necessarily in time order. The naive approach to solve this problem is to expand to saving a 4-tuple which also includes the timepoint, and at every timestep either search the array or re-sort the array given new inputs. While the search can be made 𝒪(log n) by using bisection (where n is the number of future information points), insertion into an arbitrary point in an array still constitutes 𝒪(n) operations since the other elements in the array must be moved. Since this is the cost per insertion and many insertions can required before accepting a timestep, it is essential to the efficiency of the algorithm to make this process more performant.

Knowing that we will need to insert arbitrary values into the middle of the array, one may then propose using a linked list data structure. However, if the search is done on a linked list data structure, then the bisection still constitutes 𝒪(n) operations due to the traversal structure. To alleviate these problems, we propose an algorithm using stacks. Stacks are computationally efficient data structures which allow for 𝒪(1) insertion and retrieval, but with the restriction that only the value at the top of the stack is readily available. By achieving this complexity, we minimize the computational cost of rejections, allowing for one to not have to be overly conservative with the choice of stepsize. In the following subsection we will show how to achieve general timestepping with 𝒪(1) information insertions and retrievals while only requiring the necessary floating point operations and ordering the data in a manner which is efficient for caching.

4.3. The RSwM algorithms

Due to the LIFO (last in, first out) structure of the stack data structure, if the algorithm iteratively adds the future portions to the stack, then the tuple at the top of the stack always denotes the values for the time interval of the immediate future. Thus, after a successful step, if the stack is non-empty, we use the values from the top of the stack to propose our next step. If the stack is ever empty, then this indicates that the algorithm currently has no future information. In this case, take new random numbers and propose a new step in the same manner as the non-adaptive algorithm. By using the stack in such a manner, we are able to perform all of the memory operations in 𝒪(1) with the only additional floating point operations due to adaptation being the few operations to calculate the L_i, resulting in a computationally efficient algorithm.

A psudocode version of the algorithm is given as Algorithm 1. While intuitive, RSwM1 is not the most efficient since it does not always use the estimated “best stepsize” qh. If the stack is non-empty, then the step size is taken to be the first component from the tuple on the top of the stack (L₁) which may be significantly less than qh. This constrains the algorithm to step to any timepoint t which was the value of a previously rejected timestep. Thus, RSwM1 is not an entirely general stepping algorithm.

Algorithm 1.

RSwM1

1:	Set the values ε, hmax, T
2:	Set t = 0, W = 0, Z = 0, X = X0
3:	Take an initial h, ΔZ, ΔW ~ N(0, h)
4:	while t < T do
5:	Attempt a step with h, ΔW, ΔZ to calculate Xtemp according to (2)
6:	Calculate E according to (9)
7:	Update q using (21)
8:	if (q < 1) then	▷ % Reject the Step
9:	Take ΔW̃ ~ N (qΔW, (1 − q)qh) and ΔZ̃ ~ N (qΔZ, (1 − q)qh)
10:	Calculate $\overline{\mathrm{\Delta }W}=\mathrm{\Delta }W-\mathrm{\Delta }\stackrel{\sim }{W}$ and $\overline{\mathrm{\Delta }Z}=\mathrm{\Delta }Z-\mathrm{\Delta }\stackrel{\sim }{Z}$
11:	Push ((1 − q) h, $\overline{\mathrm{\Delta }W},\overline{\mathrm{\Delta }Z}$) into stack S
12:	Update h := qh
13:	Update ΔW := ΔW̃, ΔZ := ΔZ̃
14:	else	▷ % Accept the Step
15:	Update t := t + h, W := W +ΔW, Z := Z +ΔZ, X = X + Xtemp
16:	if (S is empty) then
17:	Update c := min(hmax, qh), h := min(c, T − t)
18:	Take ΔW, ΔZ ~ N(0, h)
19:	else
20:	Pop the top of S as L
21:	Update h := L1, ΔW := L2, ΔZ := L3
22:	end if
23:	end if
24:	end while

To extend the previous algorithm, we wish to change the stepping algorithm when the stack is not empty to allow for unraveling the stack multiple times per step. To do so, let the algorithm take enough items off the stack so that the total length is close to the proposed timestep qh, and adjust for the difference.

A psudocode version of the algorithm is given as Algorithm 4 in Appendix D. The resulting algorithm, RSwM2, is more complex than RSwM1. However, the advantage of this algorithm is that if we propose a step of size h_new = qh, we will always step with a size h_new regardless of the number of items on the stack. In the example simulations in section 5, this algorithm is shown to be more efficient.

However, RSwM2 is not correct. The problem comes from “re-rejections”. If the algorithm pops a more than one item off the stack and then rejects the step, these elements are lost. Thus when it tries to re-step with the proposed qh, it does not properly recreate our Brownian path since we will have lost some of the future information. In section 5 we see that this case is rare enough that the results are usually statistically correct, though we wish to extend this algorithm to a truly correct algorithm.

To ensure correctness we need to save the popped elements until an accepted step passes the point which they encode. The idea is to use a deque where future information is added to the back and re-popped information is added to the front. However, whenever a step is accepted, we will wish to drop all of the elements added from the front. This means that the most natural algorithm would be similar to the common decomposition of the deque into two stacks. Instead of utilizing a deque directly, we will use one stack S₁ for the future information and another S₂ for the re-popped information. Whenever a value is popped from the future information stack S₁, it will be placed into S₂. If the step is rejected, those values will be popped back over to S₁, and if the step is accepted they will be discarded.

The algorithm RSwM3 is explained in more detail by example. Assume we reject a timestep which uses the first n elements from the stack, and that the new proposed timestep qh uses what would have only been the first k. The fix would be to add the last n − k − 1 tuples of future information back to the stack (in reverse time order), solve the Brownian bridge problem with the k and k + 1st items straddling the proposed step qh, and add the future information from qh to the k + 1st items to the stack. The algorithm should then only “discard” items after they have been passed by a successful step.

If we saved the n tuples as they popped from the stack S₁ into a different stack S₂, then we can think of S₂ as the stack which contains all future information that is currently being used in a proposed timestep. Since this will add the elements to S₂ in chronological order, the elements of stack S₂ will pop out in reverse time order. Thus after rejecting the timestep, the n − k elements we wish to save will be the first n − k elements of the stack S₂. Therefore, after a rejection, the algorithm should pop off the first n − k − 1 elements of S₂, re-add them to S₁, and pop one more element to solve a Brownian Bridge problem. Then after any successful timestep, the algorithm can simply discard all of the information in S₂.

A psudocode version of the algorithm is given as Algorithm 2. The resulting algorithm, RSwM3, is an extension to RSwM2 which keeps the property of always using the estimated “best timestep” qh but is now able to ensure correctness.

5. Numerical verification of correctness and efficiency

In order to evaluate the efficiency of the adaptive methods, we implemented ESRK1 with the three rejection sampling with memory algorithms RSwM1, RSwM2, and RSwM3. We chose the three example equations Equation 31, Equation 33, and Equation 35 defined in E.

These three examples cover a variety of behaviors seen in SODEs. Example 1 is a linear stochastic differential equation. Since α > 0, the solution tends to infinity and thus presents a case where the algorithms must decrease the timesteps in order to ensure the accuracy. Example 2 has a periodic solution and will be used to show that the error of our method decreases even in cases where the process is stable. Example 3 will be used to test the algorithm’s ability to handle additive noise. For all of the tests, the relative tolerance was set to 0 and the absolute tolerance was adjusted in order to test various algorithm behaviors.

5.1. Correctness

We first checked for the correctness of the algorithm. In order to study the correctness of each implementation, we ran RSwM1, RSwM2, and RSwM3 200 times on Equation 31, and tested the distribution of W₂. For Brownian motion, W_t ~ N(0, t) and thus $\frac{W_2}{\sqrt{2}}~N(0,1)$ should be a standard normal random variable. In order to test that our rejection sampling algorithms did not change the distributions for the underlying Brownian processes, we used the Kolmogorov-Smirnov Test. The 1-Sample Kolmogorov-Smirnov test is a standard non-parametric test of distributions which is known for being very sensitive and easily rejecting the null-hypothesis of standard normality [10]. A plot of the p-values for the Kolmogorov-Smirnov test on 20 trials tolerances of 10⁻¹, 10⁻³, 10⁻⁵ is shown in Figure 2. We note that due to multiple sampling issues, one would expect 1/20 tests to fail at a p-value of .05. Indeed, for the RSwM1 and RSwM3 algorithms our results have around the expected number of failures. We see that RSwM2 has 6 failures, which shows that it also generally passes the tests even though there is no guarantee for its correctness. However, it is clear that the issue magnifies at lower tolerances. These results indicate that the normalized Brownian process’s distribution was standard normal and thus were not significantly altered by the RSwM sampling algorithms. Therefore RSwM algorithms generate statistically correct results.

Figure 2.

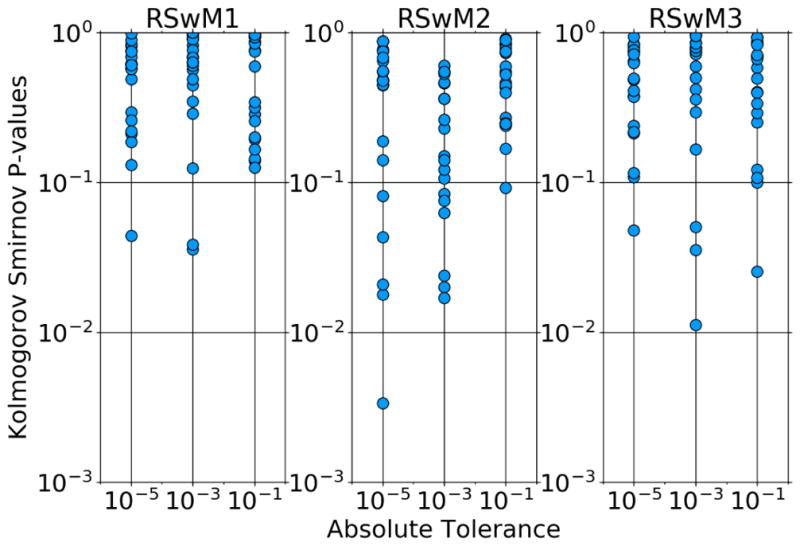
Adaptive algorithm Kolmogorov-Smirnov Tests. Equation 31 was solved from t = 0 to t = 2. Scatter plots of the p-values from Kolmogorov-Smirnov tests against the normal distribution. At the end of each run, a Kolmogorov-Smirnov test was performed on the values at end of the Brownian path for 200 simulations. The x-axis is the absolute tolerance (with relative tolerance set to zero) and the y-axis is the p-value of the Kolmogorov Smirnov tests.

Algorithm 2.

RSwM3

1:	Set the values ε, hmax, T
2:	Set t = 0, W = 0, Z = 0, X = X0
3:	Take an initial h, ΔZ, ΔW ~ N(0, h)
4:	while t < T do
5:	Attempt a step with h, ΔW, ΔZ to calculate Xtemp according to (2)
6:	Calculate E according to (9)
7:	Update q using (21)
8:	if (q < 1) then	▷ % Reject the Step
9:	Set hs = 0, ΔW = 0, ΔZ = 0
10:	while S2 is not empty do
11:	Pop the top of S2 as L
12:	if hs + L1 < (1 − q)h then
13:	Update hs := hs + L1
14:	Update ΔWtmp := ΔWtmp + L2, ΔZtmp := ΔZtmp + L3
15:	else
16:	Push L onto S2 and break
17:	end if
18:	end while
19:	Set hK = h − hs, K2 = ΔW − ΔWtmp, K3 = ΔZ − ΔZtmp
20:	Set $q_K=\frac{qh}{h_K}$
21:	Take ΔW̃ ~ N(qKK2, (1 − qK)qKL1)
22:	Take ΔZ̃ ~ N(qKK3, (1 − qK)qKL1)
23:	Pop ((1 − qK)hK,K2 − ΔW̃,K3 − ΔZ̃) onto S1
24:	Pop (qKL1,ΔW̃, ΔZ̃) onto S2
25:	Update ΔW = ΔW̃, ΔZ = ΔZ̃, h = qh
26:	else	▷ % Accept the Step
27:	Update t := t + h, W := W + ΔW, Z := Z + ΔZ, X = X + Xtemp
28:	Empty S2
29:	Update c := min(hmax, qh), h := min(c, T − t)
30:	Set hs = 0, ΔW = 0, ΔZ = 0
31:	while S is not empty do
32:	Pop the top of S1 as L
33:	if (hs + L1 < h) then	▷ % Temporary not far enough
34:	Update hs := hs + L1, ΔW := ΔW + L2, ΔZ := ΔZ + L3
35:	Push a copy of L onto S2
36:	else	▷ % Final part of step from stack
37:	Set $q_{\mathit{tmp}}=\frac{h-h_s}{L_1}$
38:	Let ΔW̃ ~ N(qtmpL2, (1 − qtmp)qtmpL1)
39:	Let ΔZ̃ ~ N(qtmpL3, (1 − qtmp)qtmpL1)
40:	Push ((1 − qtmp)L1, L2 − ΔW̃, L3 − ΔZ̃) onto S1
41:	Update ΔW := ΔW +ΔW̃, ΔZ := ΔZ +ΔZ̃
42:	end if
43:	end while
		▷ % Update for last portion to step. Note zero if final part is from stack
44:	if (h − hs is not zero) then
45:	Let ηW, ηZ ~ N(0, h − hs)
46:	Update ΔW = ΔW + ηW, ΔZ = ΔZ + ηZ
47:	Push (h − hs, ηW, ηZ) onto S2
48:	end if
49:	end if
50:	end while

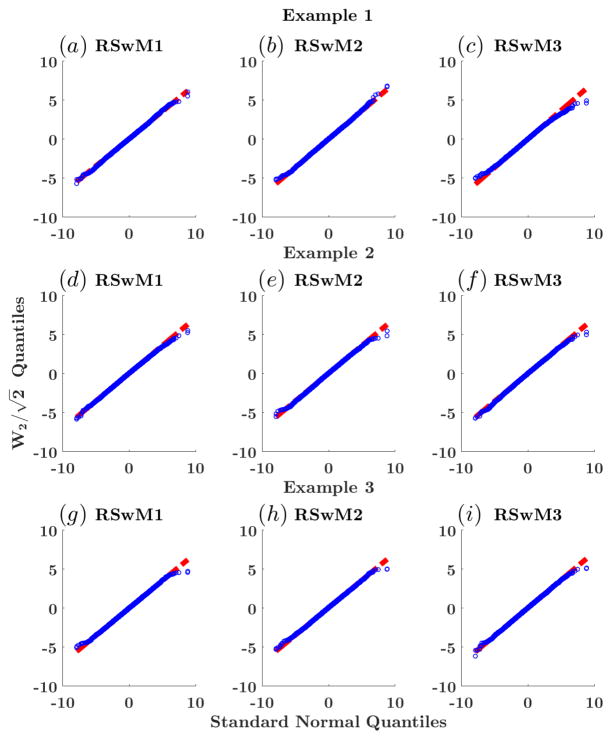
As an additional verification, we included a Quantile-Quantile Plot (QQplot) of $\frac{W_2}{\sqrt{2}}$ against 10,000 standard normal random variables generated via MATLAB’s randn command. The simulation results are shown in Figure 3. The estimated quantiles for $\frac{W_2}{\sqrt{2}}$ as generated by RSwM 1 through 3 line up on the x = y axis, indicating that $\frac{W_2}{\sqrt{2}}$ follows a standard normal distribution. To test for edge effects, we ran the same calculation with higher/lower numbers of paths. This shows that as the number of paths increases, the number of quantiles which align also increases. These results show that although we cannot guarantee the correctness of the RSwM2, its sample statistics cannot be distinguished from the correct algorithms. This indicates that the edge case that the algorithm omits is a rare occurrence.

Figure 3.

Adaptive algorithm correctness checks. QQplots of the distribution of the Brownian path at the end time T = 2 over 10,000 paths. The x-axis is the quantiles of the standard normal distribution while the y-axis is the estimated quantiles for the distribution of $W_2/\sqrt{2}$. Each row is for a example equation for Examples 1–3 respectively, and each column is for the algorithm RSwM1–3 respectively. ε = 10⁻⁴. The red dashed line represents x = y, meaning the quantiles of a 10,000 standard normal random variables equate with the quantiles of the sample. The blue circles represent the quantile estimates for $W(2)/\sqrt{2}$ which should be distributed as a standard normal.

5.2. Accuracy and efficiency

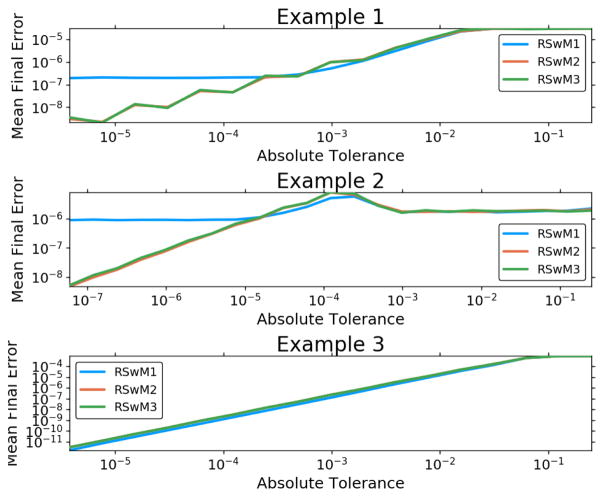
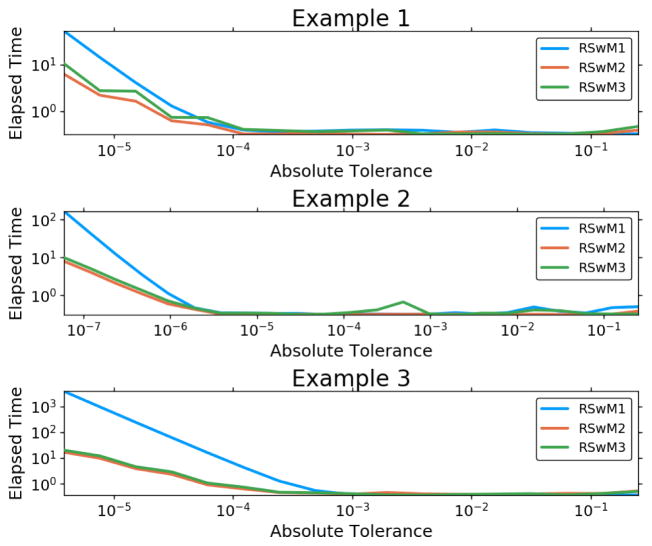
Next we tested the accuracy and efficiency of the three algorithms RSwM1, RSwM2, RSwM3 on the three example SDEs Equation 31, Equation 33, and Equation 35. The results, as summarized in Figure 4 and Figure 5, show that in almost every case, the improved algorithms RSwM2 and RSwM3 tend to have lower runtimes and better convergence of the error at the final timepoint. Notice that the RSwM2 and RSwM3 algorithms tend to have error convergences much closer to log-linear, whereas RSwM1 tends to flatten out at lower tolerances. Also notice how in all cases, the RSwM2 and RSwM3 algorithms have comparable runtimes which are much smaller than those of RSwM1. This suggests that, while RSwM1 is vastly simpler to implement, the more complex RSwM2 and RSwM3 are more efficient.

Figure 4.

Adaptive Algorithm Error Comparison on Equation 31, Equation 33, and Equation 35. Comparison of the rejection sampling with memory algorithms on examples 1–3. Along the x-axis is ε which is the user chosen local error tolerance. The y-axis is the average l² error along the path. These values are taken as the mean for 100 runs. Both axes are log-scaled.

Figure 5.

Adaptive Algorithm Timing Comparison. Comparison of the rejection sampling with memory algorithms. Along the xaxis is ε which is the user chosen local error tolerance. In the y-axis time is plotted (in seconds). The values are the elapsed time for a 1000 Both axes are log-scaled.

5.3. Summary of numerical correctness and efficiency

The results of the numerical experiments can be summarized as follows. From subsection 5.1 we see that by simulating Equation 31 Equation 33, and Equation 35 by ESRK1 with the time-stepping algorithms RSwM1, RSwM2, and RSwM3, the resulting Brownain paths have the appropriate sample statistics. This indicates that in all of these cases the algorithms produce the correct results. Notably, this shows that RSwM2, whose correctness we could not guarantee from its derivation, generates results which are can be statistically correct at low tolerances. Given that the Kolmogorov-Smirnov test is a stringent test for normality, this indicates that the edge case not appropriately dealt with in RSwM2 is a rare enough occurrence that the algorithm can likely be statistically indistinguishable from being correct in non demanding circumstances.

From subsection 5.2 we see that the RSwM2 and RSwM3 algorithms are the most efficient on the test equations Equation 31 and Equation 33 in terms of run-time and accuracy. Together, the results show that the three algorithms are correct and that there exists a tradeoff between them. The simplest algorithm to implement is RSwM1, but on some classes of problems it can perform slower than the other algorithms. RSwM2 is by a slight margin the fastest algorithm but is only psudo-correct. RSwM3 is an extension of RSwM2 which, at the cost of adding correctness, adds complexity in the implementation and runs with only slightly decreased efficiency.

6. Numerical experiments with systems of SDEs

Next we wished to show the applicability of the adaptive algorithms for solving large systems of nonlinear equations. These examples better match user cases, though no analytical solution exists for the error analysis. Instead, we wish to show how the error tolerance parameters allow for specifying the granularity of the numerical approximation, and demonstrate that this algorithm can be used to solve problem which would be computationally intractable without the adaptivity.

6.1. Control of numerical granularity

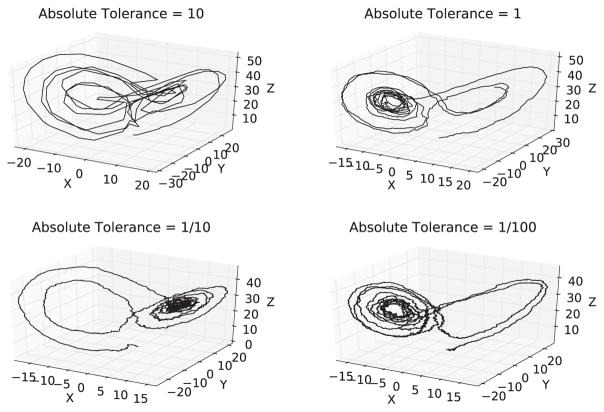
To test the ability for the error tolerance parameters to control the granularity of the solution, the ESRK1 algorithm with RSwM3 was used to solve the well-known Lorenz system with additive noise. The parameters were chosen so the deterministic solution is chaotic and generates the well-known Lorenz attractor. The relative tolerance was fixed at zero and equation was solved at a variety of absolute tolerances. The solution was plotted as Figure 6. One can see that as the tolerance is decreased, the solution becomes more exact. Thus the RSwM tolerance parameters allow the users to adjust the trade-off between the exactness of the numerical approximation and computational time on nonlinear systems of equations.

Figure 6.

Solution to the Lorenz system Equation 39 on t ∈ [0, 10] with additive noise and parameters α = 10, ρ = 28, σ = 3, and β = 8/3 at varying tolerances. The system was solved using ESRK+RSwM3 with the relative tolerance fixed at zero and varying absolute tolerances.

6.2. Large nonlinear system on cell differentiation

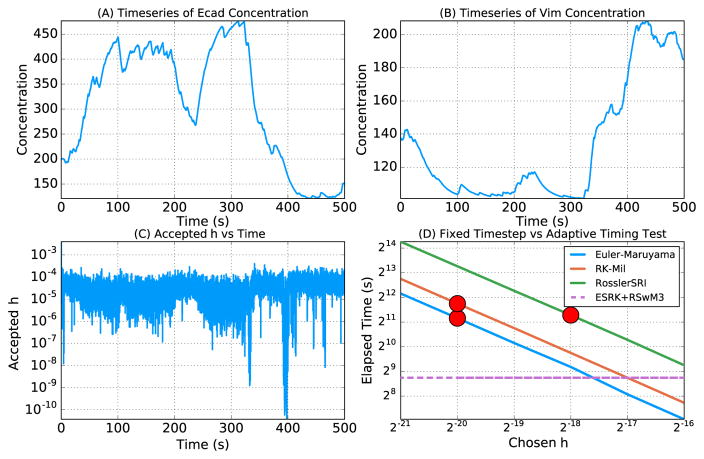
Next we demonstrated the ability of the ESRK+RSwM algorithms to allow for solving large systems of nonlinear equations. As a test, we chose a model of stochastic cell differentiation in the epithelial-to-mesenchymal transitions of somatic cells. The system of 19 equations is given in Appendix F. This system serves as an ideal test case for adaptive algorithms since the stochastic switches give large intervals of relative stability with small intervals of extreme stiffness. Thus the ability to be able to automatically adjust the timestep depending on whether a stochastic transition is occurring is fundamental for making the system computationally tractable. In Figure 7 we show the solution on a time interval from 0 to 500 for two indicators of the cell states, Ecad and Vim, and the corresponding stepsizes the ESRK+RSwM algorithm used to solve the equations throughout the simulation. This figure shows that the ESRK+RSwM algorithm is able to reproduce the scientific results, and that the adaptive algorithm is able to adjust the timestep between 10⁻⁴ and 10⁻¹¹ to ensure accuracy and stability.

Figure 7.

Stochastic cell differentiation model solutions. (A) Timeseries of the concentration of [Ecad]. The solution is plotted once every 100 accepted steps due to memory limitations. (B) Timeseries of the concentration of [Vim]. The solution is plotted once every 100 accepted steps due to memory limitations. (C) Accepted h over time. The h values were taken every 100 accepted steps due to memory limitations. (D) Elapsed time of the Euler-Maruyama and ESRK+RSwM3 algorithms on the stochastic cell model. Each algorithm was used to solve the model on t ∈ [0, 1] 10,000 times. The elapsed time for the fixed timestep methods for given h’s are shown as the filled lines, while the dashed line is the elapsed time for the adaptive method. The red circles denote the minimal h and times for which the method did not show numerical instability in the ensemble.

Unlike the deterministic case, whether a given solution is numerically stable for a given stepsize is dependent on the random Brownian trajectory and thus one cannot as easily classify the methods as stable for a given stepsize on a given problem. Instead, we define a method as sufficiently stable at a stepsize h if the method has no unstable trajectories in a sufficiently large ensemble. The reason for this choice is because it gives a measure for how fast a Monte Carlo simulation can correctly be computed. The condition that no trajectories can fail is because if the noisiest (and thus most unstable) trajectories are always discarded from the ensemble, the resulting Monte Carlo solution would be biased. This is a major concern for many models in practice. For example, the chosen epithelial-to-mesenchymal transition model has the most numerical instability during the stochastic switching events, but these events are the quality of interest and thus must be accurate in the resulting simulations.

Therefore, to test how efficiently the algorithms could produce statistically correct results on a stiff system, we solved cell model from Appendix F 10,000 times via the Euler-Maruyama, Runge-Kutta Milstein (RK-Mil) [15], and Rößler SRI methods using increments of h = 2⁻ⁱ and calculated the number of runs which diverged (failed) and the elapsed time for the 10,000 runs (note that the algorithm exited and denoted a run as diverged when encountering a NaN). These results are compared to the adaptive algorithm in Table 2. The adaptive algorithm solved 10,000 simulations with no failures in 187 seconds. The comparable value for fixed timestep methods, the shortest time for which there were no failures, was the Euler-Maruyama algorithm with h = 2⁻²⁰ which took 2286 seconds. This shows that the adaptive algorithm performed 12.28x as fast as the fastest fixed time-stepping algorithm, indicating that the advantages of adaptive time-stepping far out-weighted the overheads of the adaptive algorithm. Note that this testing method also far underestimates the advantages of the adaptive method: from Figure 7 we see that the most stiff portions are during the middle of stochastic transition events which would not happen during 1 second simulations. However, testing multiple solutions of the non-adaptive algorithms at such a low h in order to converge on the full t ∈ [0, 500] was not computationally feasible. Indeed, one large advantage of the adaptive method is that the tests to determine the appropriate h are computationally expensive themselves. Also note that the tolerance for the adaptivity had to be set low in order to ensure stability. The advantage of the adaptive method could be made even larger by using a numerical method with a larger stability region. The application of the RSwM algorithms to more stable solvers for stiff systems and higher weak order solvers is a subject for future research.

Table 1.

ESRK1. Table (a) shows the legend for how the numbers in Table (b) correspond to the coefficient arrays/matrices c⁽ⁱ⁾, A⁽ⁱ⁾, B⁽ⁱ⁾, α, β⁽ⁱ⁾, α̃, and β̃⁽ⁱ⁾. For example, these tables show that ${\alpha }^T=(\frac{1}{3},\frac{2}{3},0,0)$. Note that the matrices A⁽ⁱ⁾ and B⁽ⁱ⁾ lower triangular since the method is explicit.

7. Implementation issues

For deploying these algorithms, there are a few extra implementation issues that should be addressed. First of all, the choice of q is due to calculations for the optimal stepsize for deterministic equations [7] and thus does not directly apply to stochastic systems. We instead use the deterministic q as a guideline. We heuristically modify it by noting that due to the extra overhead of the stack implementations, it may be wise to over-accelerate the stepsize changes and thus choose a higher power. In practice, we found

$$q={\left(\frac{1}{\gamma e}\right)}^2,$$ (23)

to be an efficient choice. Future research should investigate this issue in more detail.

In addition, it is wise in practice to ensure that q takes acceptable values [11]. We found that the following tends to work well in practice:

$$q=min(\mathit{qmax},max(q,\mathit{qmin})),$$ (24)

where qmax and qmin are parameters set by the user. While for deterministic systems it’s suggested that qmax is between 4 and 10 [11], we note that our algorithm has a higher overhead than in the deterministic case, and thus further restricting q to reduce the number of rejections had the potential to increase the efficiency to of the algorithm. This was tested in Table 3 where we found a suitable value qmax = 1.125 which we used as the default throughout this paper (except in subsection 5.2 where qmax = 10 was used in order to better evaluate the ability to accurately unravel the stack). Further research should look into the usage of PI-controlled stepsize choices to further reduce the number of rejections.

Table 2.

Fixed timestep method fails and runtimes. The fixed timestep algorithms and ESRK+RSwM3 algorithms were used to solve the stochastic cell model on t ∈ [0, 1] 10,000 times. Failures were detected by checking if the solution contained any NaN values. During a run, if any NaNs were detected, the solver would instantly end the simulations and declare a failure. The runtime for the adaptive algorithm (with no failures) was 186.81 seconds.

	Euler-Maruyama		Runge-Kutta Milstein		Rößler SRI
Δt	Fails (/10,000)	Time (s)	Fails (/10,000)	Time (s)	Fails (/10,000)	Time (s)
2−16	137	133.35	131	211.92	78	609.27
2−17	39	269.09	26	428.28	17	1244.06
2−18	3	580.14	6	861.01	0	2491.37
2−19	1	1138.41	1	1727.91	0	4932.70
2−20	0	2286.35	0	3439.90	0	9827.16
2−21	0	4562.20	0	6891.35	0	19564.16

Also, one should note that elements entering the stack should be sanitized in order to eliminate issues due to round-off error. In some cases the mathematical algorithm may specify very small intervals to go on the stack. This is particularly the case when q,q_tmp, or q_K are close to 1 when the step size is very small. When this item from the stack is eventually used to calculate q_tmp, there is the possibility of overflow which can lead to NaNs and stall the algorithm. To avoid this issue, it is wise to discard any interval smaller than some size. We found 10⁻¹⁴ to be a good cutoff.

Lastly, it is common for many adaptive implementations to give a heuristic determination of an initial stepsize. Using the simple approximation that with 99% probability a N(0, σ) random variable is in the interval ( $-3\sqrt{\sigma },3\sqrt{\sigma }$), we adapt the scheme from [11] to take in account this a priori estimate, adjust due to the symmetry of the normal distribution, assume the next error power is $\frac{1}{2}$ larger, and arrive at the following 3.

Algorithm 3.

Initial h Determination

1:	Let d0 = ||X0||
2:	Calculate f0 = f(X0, t) and σ0 = 3g(X0, t)
3:	Let d1 = ||max(|f0 + σ0|, |f0 − σ0|)||
4:	if d0 < 10−5 or d1 < 10−5 then
5:	Let h0 = 10−6
6:	else
7:	Let h0 = 0.01(d0/d1)
8:	end if
9:	Calculate an Euler step: X1 = X0 + h0f0
10:	Calculate new estimates: f1 = f(X1, t) and σ0 = 3g(X1, t)
11:	Determine ${\sigma }_1^M=max(\mid {\sigma }_0+{\sigma }_1\mid ),\mid {\sigma }_0-{\sigma }_1\mid )$
12:	Let $d_2=\Vert max(\mid f_1-f_0+{\sigma }_1^M\mid ,\mid f_1-f_0-{\sigma }_1^M\mid )\Vert /h_0$
13:	if max(d1, d2) < 10−15 then
14:	Let h1 = max(10−6, 10−3h0)
15:	else
16:	Let h1 = 10−(2+log1 0(max(d1,d2))/(order+0.5)
17:	end if

Note that ||·|| is the norm as defined in Equation 19 with Equation 20. In practice we found this to be a conservative estimate which would “converge” to some approximate stepsize in < 10 steps, making it useful in practice.

8. Conclusion and discussion

In this paper we have developed a class of adaptive time-stepping methods for solving stochastic differential equations. The approach is based on a natural creation of high Strong-order embedded algorithms (with implicit error calculations) and generalized rejection sampling techniques. These algorithms are highly efficient: the error estimators require no extra evaluations of the drift and diffusion terms, while the rejection sampling with memory algorithms are 𝒪(1) for rejecting and interpolating the Brownian motion, with RSwM2 and RSwM3 allowing for an unconstrained choice of timestep. Through numerical testing, we demonstrated the algorithm’s ability to adapt the error to the user-chosen parameter ε, the prescribed local error threshold. We also have shown the efficiency of the algorithms and their ability to scale to efficiently solve large stiff systems of equations.

Our results show that rejection sampling with memory can be used to speed up the solution of large systems of equations, particularly those coming from biological models. Many of these models are created to show interesting behavior which is dependent on the stochasticity, such as stochastic switching, but can be difficult to simulate due to the stiffness associated with these properties. Using such an adaptive algorithm allows the simulation to focus its computational time to accurately capture the rare but important events. Further research into the application of these methods with stiff solvers could further improve the effectiveness. Also, the adaptive methods reduce the practical amount of time to conduct such experiments since one major time-consuming activity can be finding a small enough stepsize so that large Monte Carlo simulations can run without any path diverging and biasing the result. Further research should look into using rejection sampling with memory combined with higher order weak convergence methods to improve the computational efficiency when investigating moment properties from Monte Carlo experiments.

One of the unique features of the adaptive methods is that the embedded algorithm does not require an explicit construction of the order 1.0 method. It also does not have any extra requirements on the order 1.5 algorithm. This allows one to use any order 1.5 Rößler SRK algorithm, and thus as new coefficients for these algorithms are found to have “better” properties, such as improved stability or lower highest-order truncation error, our construction shows the existence of embedded versions for adaptive algorithms by default.

There are many implementation details that can be examined in order to more efficiency utilize these algorithms. For example, in the algorithm RSwM3, one could simulate discarding the second stack S₂ by explicitly controlling the pointer on an array and thus not have to deallocate memory every accepted timestep. Further research can investigate such implementation details for even more computationally efficient versions. Note that the calculation of the tuple for the stack requires only 3 floating point calculations and the generation of the new random numbers requires only 3x2 floating point calculations. Thus in total the algorithm requires only ≈ 10 floating point operations per rejection. Therefore the adaptive time-stepping algorithms require a minimal number of floating point operations, making them have a theoretically small impact on the computational effort.

The time-stepping method can be easily extended to other types of equations. Notice that as stated this algorithm controls the strong or pathwise error. There are many cases where one may be interested in the weak or average error of a Monte Carlo simulation. Our algorithm can be used to create a weak error estimate as well. To do so, instead of solving N independent size n systems, combine the systems into an equivalent system of size nN. Notice that by the definition of e, the error estimate obtained by this algorithm will be an average error over all simulations, and thus give a weak estimate. Using this weak estimate along with the RSwM algorithms on high weak order methods could be a path of future research.

At its core, the time-stepping algorithms are methods to sub-sample a continuous-time stochastic process as needed and effectively reproduce the sample properties at every point. Thus for any continuous-time martingale which defines a type of differential equation, this method can be applied by simply knowing the sample statistics of a bridge-type problem. Thus no part of the derivation required that the underlying process was an Ito process. Therefore, if one uses an embedded pair of methods for Stratonovich SODEs, the adaptive time-stepping algorithms still apply. Also, this includes problems like stochastic partial differential equations (SPDEs). For example, for SPDEs with space-time white noise, if one imposes a space-discretization then one arrives at a system of SODEs for which the Brownian bridge statistics are the same as any standard system of SODEs and thus our methods apply. If one needs to adapt the spatial discretization, then this also follows the sample properties of the Brownian bridge and thus one can upsample the process along space until the desired error is met. For a Hilbert space valued Brownian motion like a Q-Wiener process, a Brownian bridge-like problem will need to be solved but the same general algorithm holds.

Notice that since the stepping algorithms only require the values on the stack, the RSwM form of adaptivity allows one to solve an equation while only storing the current values and the Brownian stack values. This is important for solving large systems of SPDEs which become memory-bound if one attempts to store the solution of the Brownain path at every timepoint. During our study of the implementation we saw the stack reaching maximum sizes of 20, and thus only used a modest amount of memory. For problems which are more memory bound, one can effectively decrease the maximum stack size by changing around some of the parameters, for example lowering the q exponent or decreasing qmax.

This method also provides an effective way to develop adaptive algorithms for variable-rate Markovian switching and jumps [18]. These problems are usually difficult to numerically simulate because one must effectively estimate the times for switching or else incur a large penalty due to the discontinuity. One can normally estimate whether a jump has occurred in an interval to a certain degree of accuracy, and using our adaptive algorithm one can hone in on the time at which the jump occurred, effectively solve the continuous problem to that time, and apply the jump. Therefore, the embedded time-stepping method along with the new rejection sampling algorithm developed in this work provides a general framework which one could build on for adaptive algorithms in solving many other stochastic problems.

Lastly, we wish to note that implementations of these algorithms are being released as part of a package DifferentialEquations.jl. DifferentialEquations.jl is a Julia library for solving ODEs, SDEs, DDEs, DAEs, and certain classes of PDEs and SPDEs, using efficient solvers in an easy-to-use scripting language. This package, developed by the authors, is freely available and includes additional functionalities such as parallelizing Monte Carlo experiments using the discussed methods on HPCs.

Appendix

A. Order conditions for Rößler-SRI methods

The coefficients (A⁽ⁱ⁾, B⁽ⁱ⁾, β⁽ⁱ⁾, α) must satisfy the following order conditions to achieve order .5:

1. αTe = 1	3. β(2)Te = 0	5. β(4)Te = 0
2. β(1)Te = 1	4. β(3)Te = 0

additionally, for order 1:

1. β(1)TB(1)e = 0	3. β(3)TB(1)e = 0
2. β(2)TB(1)e = 1	4. β(4)TB(1)e = 0

and lastly for order 1.5:

1. ${\alpha }^T{A}^{(0)}e=\frac{1}{2}$	9. β(2)T(B(1)e)2 = 0
2. αTB(0)e = 1	10. β(3)T(B(1)e)2 = −1
3. ${\alpha }^T{(B^{(0)}e)}^2=\frac{3}{2}$
4. β(1)TA(1)e = 1	11. β(4)T(B(1)e)2 = 2
5. β(2)TA(1)e = 0	12. β(1)T(B(1) (B(1)e)) = 0
6. β(3)TA(1)e = −1	13. β(2)T (B(1) (B(1)e)) = 0
7. β(4)TA(1)e = 0	14. β(3)T (B(1) (B(1)e)) = 0
8. β(1)T(B(1)e)2 = 1	15. β(4)T (B(1) (B(1)e)) = 1
16. $\frac{1}{2}{\beta }^{{(1)}^T}\left(A^{(1)}\left(B^{(0)}e\right)\right)+\frac{1}{3}{\beta }^{{(3)}^T}\left(A^{(1)}\left(B^{(0)}e\right)\right)=0$

where f, g ∈ C^1,2(ℐ × ℝ^d,ℝ^d), c⁽ⁱ⁾ = A⁽ⁱ⁾e, e = (1, 1, 1, 1)^T [22].

B. Order conditions for Rößler-SRA methods

The coefficients (A⁽ⁱ⁾, B⁽ⁱ⁾, β⁽ⁱ⁾, α) must satisfy the conditions for order 1:

1. αTe = 1

2. β(1)Te = 1

3. β(2)Te = 0

and the additional conditions for order 1.5:

1. αTB(0)e = 1	3. ${\alpha }^T{\left(B^{(0)}e\right)}^2=\frac{3}{2}$	4. β(1)T c(1) = 1
2. ${\alpha }^T{A}^{(0)}e=\frac{1}{2}$		5. β(2)T c(1) = −1

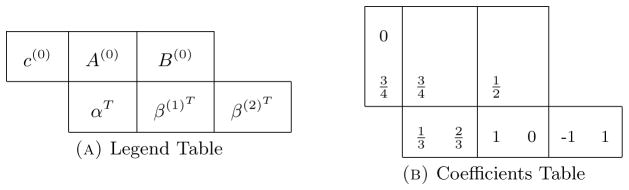
where c⁽⁰⁾ = A⁽⁰⁾e with f ∈ C^1,3(ℐ × ℝ^d, ℝ^d) and g ∈ C¹(ℐ,ℝ^d) [22]. From these conditions he proposed the following strong order 1.5 scheme found in Table 4 known as SRA1.

Table 4.

SRA1. Table (a) shows the legend for how the numbers in in Table (b) correspond to the coefficient arrays/matrices c⁽ⁱ⁾,A⁽ⁱ⁾,B⁽ⁱ⁾, α, and β⁽ⁱ⁾. Note that the matrices A⁽ⁱ⁾ and B⁽ⁱ⁾ are lower triangular since the method is explicit.

C. Wiktorsson iterated stochastic integral approximations

In the Ito expansions for the derivation of SRK methods of order greater than 1.0, iterated stochastic integrals appear. We denote these as:

$$I_{(1)}={\int }_{t_n}^{t_{n+1}}d{W}_s,$$ (25)

$$I_{(1,1)}={\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s}d{W}_{u}d{W}_s,$$ (26)

$$I_{(1,1,\dots ,1_k)}={\int }_{t_n}^{t_{n+1}}\int \dots {\int }_{t_n}^{s}d{W}_{u_1}\dots d{W}_s.$$ (27)

Note that for our purposes we are using a single Brownian path, though this extends to multiple Ito dimensions. For a timestep h = t_n+1−t_n, the approximation due to Wiktorsson [25, 22] is as follows:

$$I_{(1,1)}=\frac{1}{2}(I_{(1)}^2-h),$$ (28)

$$I_{(1,1,1)}=\frac{1}{6}(I_{(1)}^3-3h{I}_{(1)}),$$ (29)

$$I_{(1,0)}=\frac{1}{2}h\left(I_{(1)}+\frac{1}{\sqrt{3}}\zeta \right).$$ (30)

I₍₁₎ is one timestep of the Brownian path W_t, which is referred to as ΔW ~ N(0, h). ζ ~ N(0, h) is a standard normal random variable which is independent of ΔW. If we collect all of the ζ from [0, T], then its cumulative sum is itself an approximation to a Brownian path which we denote Z_t with discrete steps ΔZ = ζ. Z_t is independent of W_t and is the second Brownian path considered in the RSwM algorithms.

D. RSwM2 algorithm specification

The algorithm for RSwM2 is specified as Algorithm 4.

Algorithm 4.

RSwM2

1:	Set the values ε, hmax, T
2:	Set t = 0, W = 0, Z = 0, X = X0
3:	Take an initial h, ΔZ,ΔW ~ N(0, h)
4:	while t < T do
5:	Attempt a step with h, ΔW, ΔZ to calculate Xtemp according to (2)
6:	Calculate E according to (9)
7:	Update q using (21)
8:	if (q < 1) then	▷ % Reject the Step
9:	Take ΔW̃ ~ N (qΔW, (1 − q)qh) and ΔZ̃ ~ N (qΔZ, (1 − q)qh)
10:	Calculate $\overline{\mathrm{\Delta }W}=\mathrm{\Delta }W-\mathrm{\Delta }\stackrel{\sim }{W}$ and $\overline{\mathrm{\Delta }Z}=\mathrm{\Delta }Z-\mathrm{\Delta }\stackrel{\sim }{Z}$
11:	Push ((1 − q) h, $\overline{\mathrm{\Delta }W},\overline{\mathrm{\Delta }Z}$) into stack S
12:	Update h := qh
13:	Update ΔW := ΔW̃, ΔZ := ΔZ̃
14:	else	▷ % Accept the Step
15:	Update t := t + h, W := W +ΔW, Z := Z +ΔZ, X = X + Xtemp
16:	Update c := min(hmax, qh), h := min(c, T − tn)
17:	Set hs = 0, ΔW = 0, ΔZ = 0
18:	while S is not empty do
19:	Pop the top of S as L
20:	if (hs + L1 < h) then	▷ % Temporary not far enough
21:	Update hs := hs + L1, ΔW := ΔW + L2, ΔZ := ΔZ + L3
22:	else	▷ % Final part of step from stack
23:	Set $q_{\mathit{tmp}}=\frac{h-h_s}{L_1}$
24:	Let ΔW̃ ~ N(qtmpL2, (1 − qtmp)qtmpL1)
25:	Let ΔZ̃ ~ N(qtmpL3, (1 − qtmp)qtmpL1)
26:	Push ((1 − qtmp)L1, L2 − ΔW̃, L3 − ΔZ̃) onto S
27:	Update ΔW := ΔW +ΔW̃, ΔZ := ΔZ̃
28:	end if
29:	end while
	▷ % Update for last portion to step. Note zero if final part is from stack
30:	if (h − hs is not zero) then
31:	Let ηW, ηZ ~ N(0, h − hs)
32:	Update ΔW = ΔW + ηW, ΔZ = ΔZ + ηZ
33:	end if
34:	end if
35:	end while

E. Example equations

The three example equations are:

Example 1

$$d{X}_t=\alpha X_{t}dt+\beta X_{t}d{W}_t,X_0=\frac{1}{2},$$ (31)

where $\alpha =\frac{1}{10}$ and $\beta =\frac{1}{20}$. Actual Solution:

$$X_t=X_0{e}^{\left(\beta -\frac{{\alpha }^2}{2}\right)t+\alpha W_t}.$$ (32)

Example 2

$$d{X}_t=-{\left(\frac{1}{10}\right)}^2\text{sin}(X_t){cos}^3(X_t)dt+\frac{1}{10}{cos}^2(X_t)d{W}_t,X_0=\frac{1}{2},$$ (33)

Actual Solution:

$$X_t=arctan\left(\frac{1}{10}{W}_t+tan(X_0)\right).$$ (34)

Example 3

$$d{X}_t=\left(\frac{\beta }{\sqrt{1+t}}-\frac{1}{2(1+t)}{X}_t\right)dt+\frac{\alpha \beta }{\sqrt{1+t}}d{W}_t,X_0=\frac{1}{2},$$ (35)

where $\alpha =\frac{1}{10}$ and $\beta =\frac{1}{20}$. Actual Solution:

$$X_t=\frac{1}{\sqrt{1+t}}{X}_0+\frac{\beta }{\sqrt{1+t}}(t+\alpha W_t).$$ (36)

Example 4

$$d{X}_t=\alpha (Y_t-X_t)+\sigma d{W}_t,$$ (37)

$$d{Y}_t=X_t(\rho -Z_t)-Y_t+\sigma d{W}_t,$$ (38)

$$d{Z}_t=X_t{Y}_t-\beta Z_t+\sigma d{W}_t,$$ (39)

where X₀ = Y₀ = Z₀ = 0, α = 10, ρ = 28, σ = 3, and β = 8/3.

F. Stochastic cell differentiation model

The stochastic cell differentiation model is given by the following system of SDEs which correspond to a chemical reaction network modeled via mass-action kinetics with Hill functions for the feedbacks. This model was introduced in [12] to model stochastic transitions between Epithelial and Mesenchymal states.

$$\begin{gathered} A={(([\mathit{TGF}]+[\mathit{TGF}0])/J{0}_{\mathit{snail}})}^{n{0}_{\mathit{snail}}}+{([\mathit{OVOL}2]/J{1}_{\mathit{snail}})}^{n{1}_{\mathit{snail}}} \\ \frac{d{[\mathit{snail}1]}_t}{dt}=k{0}_{\mathit{snail}}+k_{\mathit{snail}}\frac{{(([\mathit{TGF}]+[\mathit{TGF}0])/J{0}_{\mathit{snail}})}^{n{0}_{\mathit{snail}}}}{(1+A)(1+[\mathit{SNAIL}]/J{2}_{\mathit{snail}})}-k{d}_{\mathit{snail}}([\mathit{snail}1]-[SR])-k{d}_{SR}[SR] \\ \frac{d[\mathit{SNAIL}]}{dt}=k_{\mathit{SNAIL}}([\mathit{snail}1]-[SR])-k{d}_{\mathit{SNAIL}}[\mathit{SNAIL}] \\ \frac{d[\mathit{miR}34]}{dt}=k{O}_{34}+\frac{k_{34}}{1+{([\mathit{SNAIL}]/J{1}_{34})}^{n{1}_{34}}+{([\mathit{ZEB}]/J{2}_{34})}^{n{2}_{34}}}-k{d}_{34}([\mathit{miR}34]-[SR])-(1-{\lambda }_{SR})k{d}_{SR}[SR] \\ \frac{d[SR]}{dt}=Tk(K_{SR}([\mathit{snail}1]-[SR])([\mathit{miR}34]-[SR])-[SR]) \\ \frac{d[\mathit{zeb}]}{dt}=k{0}_{\mathit{zeb}}+k_{\mathit{zeb}}\frac{{([\mathit{SNAIL}]/J{1}_{\mathit{zeb}})}^{n{1}_{\mathit{zeb}}}}{1+{([\mathit{SNAIL}]/J{1}_{\mathit{zeb}})}^{n{1}_{\mathit{zeb}}}+{([\mathit{OVOL}2]/J{2}_{\mathit{zeb}})}^{n{2}_{\mathit{zeb}}}}-k{d}_{\mathit{zeb}}\left([\mathit{zeb}]-\sum _{i=1}^5{C}_5^i[ZR]\right)-\sum _{i=1}^{5}k{d}_{Z{R}_i}{C}_5^i[Z{R}_i] \\ \frac{d[\mathit{ZEB}]}{dt}=k_{\mathit{ZEB}}\left([\mathit{zeb}]-\sum _{i=1}^5{C}_5^i[Z{R}_i]\right)-k{d}_{\mathit{ZEB}}[\mathit{ZEB}] \\ \frac{d[\mathit{miR}200]}{dt}=k{0}_{200}+\frac{k_{200}}{1+{([\mathit{SNAIL}]/J{1}_{200})}^{n{1}_{200}}+{([\mathit{ZEB}]/J{2}_{200})}^{n{2}_{200}}}-k{d}_{200}\left([\mathit{miR}200]-\sum _{i=1}^{5}i{C}_5^i[Z{R}_i]-[TR]\right)-\sum _{i=1}^5(1-{\lambda }_i)k{d}_{Z{R}_i}{C}_5^{i}i[Z{R}_i]-(1-{\lambda }_{TR})k{d}_{TR}[TR] \\ \frac{d[Z{R}_1]}{dt}=Tk\left(K_1\left([\mathit{miR}200]-\sum _{i=1}^{5}i{C}_5^i[Z{R}_i]-[TR]\right)\left([\mathit{zeb}]-\sum _{i=1}^5{C}_5^i[Z{R}_i]\right)-[Z{R}_1]\right) \\ \frac{d[Z{R}_2]}{dt}=Tk\left(K_2\left([\mathit{miR}200]-\sum _{i=1}^{5}i{C}_5^i[Z{R}_i]-[TR]\right)[Z{R}_1]-[Z{R}_2]\right) \\ \frac{d[Z{R}_3]}{dt}=Tk\left(K_3\left([\mathit{miR}200]-\sum _{i=1}^{5}i{C}_5^i[Z{R}_i]-[TR]\right)[Z{R}_1]-[Z{R}_3]\right) \\ \frac{d[Z{R}_4]}{dt}=Tk\left(K_4\left([\mathit{miR}200]-\sum _{i=1}^{5}i{C}_5^i[Z{R}_i]-[TR]\right)[Z{R}_1]-[Z{R}_4]\right) \\ \frac{d[Z{R}_5]}{dt}=Tk\left(K_5\left([\mathit{miR}200]-\sum _{i=1}^{5}i{C}_5^i[Z{R}_i]-[TR]\right)[Z{R}_1]-[Z{R}_5]\right) \\ \frac{d[\mathit{tgf}]}{dt}=k_{\mathit{tgf}}-k{d}_{\mathit{tgf}}([\mathit{tgf}]-[TR])-k{d}_{TR}[TR] \\ \frac{d[\mathit{TGF}]}{dt}=k{0}_{\mathit{TGF}}+k_{\mathit{TGF}}([\mathit{tgf}]-[TR])-k{d}_{\mathit{TGF}}[\mathit{TGF}] \\ \frac{d[TR]}{dt}=Tk\left(K_{TR}\left([\mathit{miR}200]-\sum _{i=1}^{5}i{C}_5^i[Z{R}_i]-[TR]\right)([\mathit{tgf}]-[TR])-[TR]\right) \\ \frac{d[\mathit{Ecad}]}{dt}=k{0}_E+\frac{k_{E1}}{1+{([\mathit{SNAIL}]/J{1}_E)}^{n{1}_E}}+\frac{k_{E2}}{1+{([\mathit{ZEB}]/J{2}_E)}^{n{2}_E}}-k{d}_E[\mathit{Ecad}] \\ B=k_{V1}\frac{{([\mathit{SNAIL}]/J{1}_V)}^{n{1}_V}}{1+{([\mathit{SNAIL}]/J{1}_V)}^{n{1}_V}}+k_{V2}\frac{{([\mathit{ZEB}]/J{2}_V)}^{n_{2}V}}{1+{([\mathit{ZEB}]/J{2}_V)}^{n{2}_V}} \\ \frac{d[\mathit{Vim}]}{dt}=k{0}_V+\frac{B}{(1+[\mathit{OVOL}2]/J{3}_V)}-k{d}_V[\mathit{Vim}] \\ \frac{d[\mathit{OVOL}2]}{dt}=k{0}_0+k_0\frac{1}{1+{([\mathit{ZEB}]/J_0)}^{n_0}}-k{d}_O[\mathit{OVOL}2] \end{gathered}$$

where

$$\begin{gathered} \sum _{i=1}^{5}i{C}_5^i[Z{R}_i]=5[Z{R}_1]+20[Z{R}_2]++30[Z{R}_3]+20[Z{R}_4]+5[Z{R}_5], \\ \sum _{i=1}^5{C}_5^i[Z{R}_i]=5[Z{R}_1]+10[Z{R}_2]+10[Z{R}_3]+5[Z{R}_4]+[Z{R}_5]. \end{gathered}$$

The parameter values are given in Table 5.

Table 5.

Table of Parameter Values for the Stochastic Cell Model.

Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
J1200	3	J1E	0.1	K2	1	k0O	0.35
J2200	0.2	J2E	0.3	K3	1	kO200	0.0002
J134	0.15	J1V	0.4	K4	1	kO34	0.001
J234	0.35	J2V	0.4	K5	1	kdsnail	0.09
JO	0.9	J3V	2	KTR	20	kdtgf	0.1
J0snail	0.6	J1zeb	3.5	KSR	100	kdzeb	0.1
J1snail	0.5	J2zeb	0.9	TGF0	0	kdTGF	0.9
J2snail	1.8	K1	1	Tk	1000	kdZEB	1.66
k0snail	0.0005	k0zeb	0.003	λ1	0.5	k0TGF	1.1
n1200	3	n1snail	2	λ2	0.5	k0E	5
n2200	2	n1E	2	λ3	0.5	k0V	5
n134	2	n2E	2	λ4	0.5	kE1	15
n234	2	n1V	2	λ5	0.5	kE2	5
nO	2	n2V	2	λSR	0.5	kV1	2
n0snail	2	n2zeb	6	λTR	0.5	kV2	5
kO	1.2	k200	0.02	k34	0.01	ktgf	0.05
kzeb	0.06	kTGF	1.5	kSNAIL	16	kZEB	16
kdZR1	0.5	kdZR2	0.5	kdZR3	0.5	kdZR4	0.5
kdZR5	0.5	kdO	1.0	kd200	0.035	kd34	0.035
kdSR	0.9	kdE	0.05	kdV	0.05