Design of a Continuous Blood Pressure Measurement System Based on Pulse Wave and ECG Signals

Abstract

With increasingly fierce competition for jobs, the pressures on people have risen in recent years, leading to lifestyle and diet disorders that result in significantly higher risks of cardiovascular disease. Hypertension is one of the common chronic cardiovascular diseases; however, mainstream blood pressure measurement devices are relatively heavy. When multiple measurements are required, the user experience and the measurement results may be unsatisfactory. In this paper, we describe the design of a signal collection module that collects pulse waves and electrocardiograph (ECG) signals. The collected signals are input into a signal processing module to filter the noise and amplify the useful physiological signals. Then, we use a wavelet transform to eliminate baseline drift noise and detect the feature points of the pulse waves and ECG signals. We propose the concept of detecting the wave shape associated with an instance, an approach that minimizes the impact of atypical pulse waves on blood pressure measurements. Finally, we propose an improved method for measuring blood pressure based on pulse wave velocity that improves the accuracy of blood pressure measurements by 58%. Moreover, the results meet the american medical instrument promotion association standards, which demonstrate the feasibility of our measurement system.

In this paper, based on the analysis of the original method of measuring blood pressure during pulse conduction time, a new continuous blood pressure detection system based on pulse wave is proposed. The system integrates important physiological indexes such as pulse wave conduction time, pulse wave characteristics and waveform characteristics to overcome the issues with pulse conduction time measurement of diastolic blood pressure.

I. Introduction

As the economy has developed, people’s diets and lifestyle habits have become worse, indirectly raising the risks of cardiovascular disease. Most importantly, hypertension is a direct factor in developing this disease. The most recent medical approach is to monitor the hypertension. Monitoring is currently undergoing a major shift, gradually transforming from manual measurements to machine measurements. Importantly, machine measurements can accurately acquire both blood pressure and other related data. In recent years, the development of industrial internet [1], Internet of Things is also used in health care such as in [2] and [3]. Moreover, it can make precise judgments as described in [4].

Currently, however, there is a problem in the processing of the machine-acquired data. At present, the main forms of noninvasive blood pressure measurement are divided into intermittent and continuous blood pressure measurements. The intermittent blood pressure measurements include both auscultation and oscillographic methods, while currently, the continuous blood pressure measurement method primarily involves pulse wave characteristics, pulse wave velocity, tension measurement, and the volume compensation law [5].

The main advantage of the auscultation method is that it is simple and convenient, but it has many drawbacks. For example, the accuracy of the results are related to the experience and hearing of the person taking the measurement and are highly dependent on the measurement environment. The oscillographic method improves these two shortcomings, but tends to make the measured person uncomfortable and increase the cuff pressure error [6]. The principle behind measuring pulse wave characteristics involves an analysis of the pulse wave parameters and arterial blood pressure results to establish a corresponding mathematical model of blood pressure measurement [7].

The pulse wave velocity measurement method, also known as the pulse wave conduction time measurement method, is based on the blood pressure of the artery and can be calculated indirectly by measuring the velocity of the pulse wave. A large number of studies have shown a positive correlation between arterial pulse wave velocity and blood pressure.

In 1957, the American medical scientist Landowne suggested that a certain linear relationship exists between the pulse wave conduction time (PTT) and blood pressure [8]. In 1995, Hu Zhang and others in the blood pressure field extracted the characteristic values of the pulse wave to establish the pulse wave characteristics for diastolic and systolic blood pressure using a regression equation and used this method successfully to detect the blood pressure of pregnant women [9].

In 2006, Payne et al. [10], extended the previous pulse wave measurement of blood pressure by adding ECG signals as a reference to calculate the pulse wave conduction time. Experimental results have shown that systolic blood pressure changes and pulse wave conduction velocity have a good positive correlation; however, the correlation between diastolic blood pressure and blood pressure is not as high as that of systolic blood pressure. Li et al. [11], at Zhejiang University, proposed a normalized pulse wave model in 2008 and established a measurement model for the relationship between cardiovascular system parameters and blood pressure. Experimental results showed that the model is consistent with the AAMI (American Medical Instrument Promotion Association) measurement standards and can be used for noninvasive continuous measurement [11].

In 2016, the American scientist Chenxi Yang placed a custom wearable sensor at the auricle. This sensor included an acoustic device and a three-axis MEMS accelerometer. The device successfully collected the pulse signals and ECG signals and then used the pulse conduction time to obtain a blood pressure measurement. Experimental results revealed that pulse wave conduction time and blood pressure have a strong relation [12].

This paper describes the design of a continuous blood pressure measurement system based on pulse waves. The system hardware is small and unobtrusive. It can comprehensively collect the body’s pulse wave signals and ECG signals, effectively filter the noise, and complete eigenvalue detection. In this paper, the evaluating indicator and diagnostic criteria of the pulse wave waveform are proposed for the first time, overcoming the shortcomings of blood pressure measurements using the original pulse wave velocity method. The experimental results show that this new blood pressure measurement model is more accurate than the original pulse wave velocity measurement model. We also show that our measurements are highly feasible. The main contributions in this paper are as follows.

• •A hardware circuit is designed based on medical theory concerning blood pressure pulse wave velocity measurements.
• •Second, for pulse wave analysis, this paper presents both a pulse wave waveform evaluating indicator and a pulse wave waveform diagnosis standard, and combines these in an example of pulse wave waveform analysis and diagnosis.
• •Finally, to overcome the shortcomings of pulse wave velocity blood pressure measurements, this paper proposes a new blood pressure measurement model that uses a stepwise regression equation combined with the experimental data. The accuracy of the new blood pressure measurement model was improved by 58% compared with the original pulse wave velocity measurement method. The error range meets the AAMI standard, demonstrating the system’s high feasibility for continuous blood pressure measurements.

The rest of this paper is organized as follows: Section II describes the medical principles and measurement systems. Section III introduces the analysis and processing of the physiological signals. Section IV explains the blood pressure diagnosis algorithm, and Section V suggests future works and concludes this paper.

II. Medical Principles and Measurement System

A. Pulse Signal

In the heart, when the ventricle contracts, blood from the ventricle passes into the aorta. However, because of vascular wall resistance, the blood cannot immediately flow into the artery; instead, the blood temporarily remains in the proximal aorta and vascular wall pressure increases. When the ventricle is diastolic, the blood stops being injected into the aorta, and the pressure on the vessel wall decreases. This pressure reduction begins at the proximal end of the aorta, and pressure waves spread to the distal aorta and the main arteries of the various branches, forming a pulse wave [13].

Fig. 1 shows a common radial artery pulse wave waveform:

FIGURE 1.

Typical pulse wave.

Point A is the starting point of the pulse wave and the lowest point of the whole pulse wave. B is the highest point of the pulse wave, called the “main peak height” by medical professionals. The waveform between point C and point D is called a tidal wave, E is called the lower gorge, and the F points represent the height of the bow wave [14], [15]. In addition to these pulse wave feature points, there are some typical pulse wave eigenvalues, such as the K value. The K value refers to the complete wavefront area of the pulse wave and contains all the information carried by the pulse wave, which is highly important in clinical trials [14].

B. ECG Signal

As the heart pulses, the cardiac muscle will be excited. The weak current produced in this process is called the ECG signal [16], which is extremely weak, and when directly collected includes considerable noise. Subsequent circuit amplifications also amplify the noise in the ECG signal. Fig. 2 shows some typical ECG signals, which are mainly divided into P, Q, R, S, T and U waves. The most important of these is the QRS wave group or complex, which is also the focus of this system. QRS waves are the most important feature of ECG signals. The ECG signal amplitude changes dramatically over a brief time period, and the differences between the highest and lowest points of the ECG signal amplitude are very large. Where the Q wave is a “trough” before the peak, the R wave is ECG signal peak amplitude, and the S wave is the band in the lowest point of the ECG signal amplitude [17].

FIGURE 2.

A complete circle of typical pulse wave.

C. Measurement System Framework

The hardware system primarily involves the use of the HK2000B pulse wave sensor to collect the pulse wave analog signal. It uses a silver chloride-based flexible electrode to collect the ECG analog signal, then performs filtering, amplification, AD conversion and other preprocessing steps. Finally, a smooth digital signal is output for subsequent processing. Because the pulse wave signal frequency is low, and the signal amplitude is small, the measurement is highly susceptible to interference from external electromagnetic noise. The ECG signal strength is weak. The ECG signal collected by the ECG electrode ranges from approximately 50uV 5mV, and its frequency range is 0.05Hz–100Hz. Influences from external factors interfere with the subsequent signal analysis and processing. Interference commonly stems from noise sources such as power frequency, EMG interference and baseline drift. Therefore, after collecting the pulse wave and ECG signals, signal amplification and denoising are necessary. The hardware system includes a signal amplification circuit, a pre-class buffer circuit, a notch filter and a band-pass filter, which perform initial hardware-based signal filtering. The overall system framework is shown in Fig. 3.

FIGURE 3.

Measurement system framework.

D. Pulse Wave Signal Acquisition

The pulse wave propagates in wave form to the aorta and its branch vessels as the blood travels. Therefore, the pulse wave can be measured in the shallow surfaces of multiple arteries; however, the pulse wave waveforms are different in different positions. The radial artery located at the wrist is easy to detect, relatively close to the heart, and is suitable for determining a wealth of physiological information about the cardiovascular system. This system uses the pulse wave at the radial artery as the signal acquisition source. The system’s signal acquisition device is the HK-2000B pulse sensor. The sensitivity of this sensor is 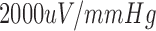, the corresponding blood pressure range is −50 +300 mmHg, and the sensor can output a complete pulse wave voltage signal.

E. ECG Signal Acquisition

The system consists of a flexible silver chloride electrode attached to the surface of the human body to collect the ECG signal. The system involves some other hardware devices as well; the entire system performs initial filtering and amplification processing of the collected signal, which, overall, functions a a good preparation for the subsequent signal processing and analysis.

The pulse wave and ECG signals collected from the sensor first undergo the relevant hardware processing in the circuit module. These operations amplify the weak physiological signals, and filter out some noise, but do not achieve the expected result. Consequently, a further filtering algorithm is required, all of these are described in the next section.

III. Analysis and Treatment of Physiological Signals

With the goal of collecting the pulse wave and ECG signal data, using the STM32 interrupt function at a certain frequency can achieve the desired effect. Then, the data must undergo some in-depth data processing, including digital filtering, pulse wave and ECG signal feature detection, and waveform detection. Based on these operations, mathematical modeling is performed based on the conduction time of the pulse wave, the characteristic point of the pulse wave and the waveform characteristics of the pulse wave. The relevant flow chart is shown in Fig. 4.

FIGURE 4.

Software system signal processing.

A. Wavelet Transform

Traditional signal analysis is based on the Fourier transform. A Fourier transform is a global transformation that has some limitations regarding time domain signal information [18]. Thus, the wavelet transform method was proposed by the French engineer J.Morlet. This method inherits and was developed on the basis of the Fourier transform, which is an emerging branch of mathematics. Wavelet transform plays an important role in signal processing, image processing, voice processing and other fields. The wavelet transform inherits and extends the idea of Short-time Fourier Transform (SIFT) localization, and overcomes its shortcomings. Compared with a Fourier transform, a wavelet transform can effectively extract valid information from both the time domain and the frequency domain. Through expansion, translation and other computing operations, wavelet transforms can solve many of the remaining problems in analyzing signal functions in multi-scale refinement analysis. Wavelet transforms can be applied to both time windows and frequency windows. The signal resolution is higher in the low frequency part of the signal; in contrast, the time resolution is higher in the high frequency part of the signal. Therefore, it is suitable for detecting the details of transient anomalies entrained in the detection signal. For this reason, we use the continuous wavelet transform to detect extreme and abnormal signal points [19]. In wavelet analysis, the continuous wavelet transform of the signal is defined as in [11]:

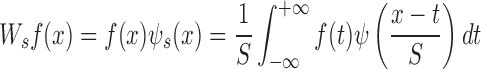In the preceding formula, S is the scale of the signal, also known as the expansion factor, T is called the translation factor, and 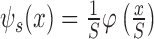is the expansion and contraction of the mother wavelet on the S scale.

The reconstruction formula (wavelet transform inverse transformation) is as follows:

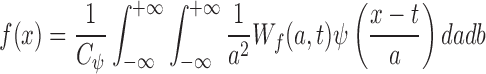Because the wavelet 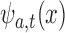generated by the mother wavelet during the wavelet transform must conform to the analysis signal, the mother wavelet also needs to satisfy the general function of the constraint:

Therefore, the mother wavelet is a continuous function. To satisfy the full reconstruction condition, , the origin must be equal to zero. Thus, we have the following condition:

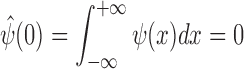To ensure that the signal reconstruction implementation is numerically stable, in addition to signal reconstruction, it is required that the Fourier transform of the wavelet 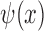satisfies the following conditions:

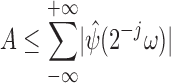In the formula 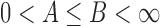, the signal frequency is .

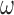Wavelet filtering with time-frequency localization and multi-resolution allows the choice of the wavelet base to be both flexible and diverse, and is a suitable approach for signal denoising because it not only removes noise but also retains the signal details. Also useful in other industries such as in [20] and [21]. We selected the method called Modulus Maximum Reconstruction Based on Signal Singularity, which was proposed by Mallat. The main idea is that signal and noise propagation show different characteristics at different wavelet transform scales. Based on this method, to obtain the effect of baseline drift in the filtered signal, the coefficient closest to the baseline drift is removed from the original signal by dividing the physiological signal into separate components.

The baseline drift of the general frequency is relatively low, generally within an approximate range of 0.15–0.6Hz, while the pulse wave signal frequency mainly lies between 0.4 and 40Hz, and the normal frequency of the pulse wave is concentrated in the 1–20Hz. Therefore, we can use the wavelet transform method to filter out the baseline drift.

The main steps of wavelet transform to remove baseline drift are as follows [22]:

• (1)read the physiological signal data;
• (2)perform wavelet decomposition of the physiological signals;
• (3)Extract the scale and wavelet coefficients of the layers after decomposing the physiological signals;
• (4)remove the coefficient closest to the baseline drift from the original signal;
• (5)perform waveform reconstruction.

The wavelet transform removes the baseline drift of the pulse wave. The original collected pulse wave signal is shown in Fig. 5. As shown, this group of pulse wave waveforms exhibits a clear baseline drift.

FIGURE 5.

Pulse wave signal spectrum.

The wavelet transform is used to eliminate the effects of baseline drift. The first step breaks down the pulse wave. The system uses the sym6 wavelet.

The low-frequency approximation coefficients of the original pulse wave signal after wavelet decomposition are shown in Fig. 6, while the high frequency approximation coefficients are shown in Fig. 7.

FIGURE 6.

Low frequency approximation of a pulse wave.

FIGURE 7.

High frequency detail factors for a pulse wave.

The wavelet decomposition needs to be performed on several layers that need to be determined based on the signal situation. The hardware provides a pulse wave divided into six layers. as can be seen from Fig. 6. The approximate coefficients of the first to third layers are similar to the third. When the pulse wave is a low-frequency signal, we cannot find any obvious effect, but as the number of layers increases, the frequency of the lower baseline drift gradually becomes apparent by the sixth (bottom) layer. The sixth layer of the low-frequency approximation coefficients is most similar to the baseline drift shown in Fig. 7; consequently, we only need to filter the approximate value of the sixth layer from the original signal. Based on the above conclusions, we only need to set the original sixth layer of the approximate coefficient of the array set to a zero-based array in the program design to achieve the desired effect of filtering the baseline drift.

The effect of filtering the baseline drift is shown in Fig. 8, which shows the pulse wave after the wavelet analysis signal processing, The original signal waveform information is no longer distorted, and the wavelet processing largely eliminates the effects of the original baseline drift. This provides a good basis for the subsequent detection of the characteristic pulse wave points, especially the starting points of the pulse waves.

FIGURE 8.

Filter the pulse wave after baseline drift.

Using the same approach, we can also perform wavelet filtering on the ECG signal to remove baseline drift interference. However, due to the particular characteristics of ECG signals, the ECG signal amplitude is small; after the circuit performs signal amplification, the original weak interference will also be amplified. Specifically, the result is that there are more blurred edges in the signal. Therefore, in addition to removing the interference after baseline drift, we also need to perform simple ECG signal denoising. For this system, we selected a relatively simple smooth denoising operation.

B. Detection of Pulse Wave Characteristic Points Based on Wavelets

In this system, the main role of the ECG signal is to calculate the pulse wave conduction time based on a reference point; therefore, we need to calculate only the peak values. Because of the nature of the ECG signal itself, the R wave is prominent in the full ECG signal wave group; consequently, there is no need to analyze the ECG signal using wavelet transforms; we can obtain the peak values simply by setting a threshold and comparing the values at the peaks of the ECG signal. However, for the wave pulse signal, in addition to the peak value, we also need to obtain the starting value, the tidal wave height value, the lower gorge height value, the value of the wave height, and so on. Detecting these pulse wave feature points is the key to the system.

Feature point detection is performed on the pulse wave and ECG signal waveforms to discover some of the special points, such as the waveform signal at its extreme points (maximum and minimum), inflection points, crests, and troughs, These feature points are usually physiologically significant, and they have a large influence on the subsequent waveform diagnosis.

While many methods exist for detecting the characteristic pulse wave points, considering the subsequent waveform detection used here, there are three main approaches [14]. The first approach is the differential method. Generally, feature points exist primarily at extreme points and inflection points; therefore, signal derivation can find these characteristic features. This method is simple, involves less computation and is easy to implement. However, it also has severe limitations and works well only in the case of an ideal waveform. Noises in the signal often form the extreme points; when using the differential method, we cannot eliminate interference from such noise points. The second approach is the computational intelligence method, which uses a neural network. This method can find the point positions of features and, compared with other methods, this approach has been better researched, works at large scales, is more advantageous, and produces results suitable for the subsequent waveform analysis. However, this approach is also time-consuming and requires a large number of samples for training to obtain good results; therefore, the development process is more difficult. The third approach uses wavelet transforms. This approach is both accurate and is robust to interference. Its calculation time is moderate, but its development is difficult.

Compared with other methods, the wavelet transform method can meet the accuracy requirements for detecting feature points and also meets the time consumption constraints of the system. Therefore, wavelet analysis was adopted in this study to detect the feature points.

When the wavelet function is regarded as the first derivative of a smoothing function, the extreme point of the wavelet transform of the signal corresponds to a sudden change in the signal. When the wavelet function is regarded as the second derivative of a function, the zero-crossing of the wavelet transform also corresponds to the sudden point of the signal. Therefore, we can use the wavelet transform system model of the zero-crossing and local extreme points as a method to detect the pulse wave signal feature points [23], [24].

There are three main steps involved in detecting pulse wave characteristic points using the wavelet transform approach:

• (1)perform wavelet decomposition of the pulse wave signal;
• (2)find the extremum and zero-crossing of the modulus of the layer coefficients at different levels;
• (3)find the signal value of the extreme value of the die and the zero-crossing point.

Based on the waveform characteristics of the pulse wave and the results of experiments with different wavelet bases, for this system, we use the first derivative and the second derivative of the Gaussian function as the wavelet basis.

After using wavelet analysis to eliminate the baseline drift due to AC, we need to detect the characteristics of the pulse wave. To recognize the starting point of the pulse wave, the wavelet basis used in this system is the Gaussian wavelet gaus1. The wavelet signal is decomposed at the same time as the pulse wave signal. Some examples of the result of Gaussian wavelet decomposition are shown in Fig. 9:

FIGURE 9.

Removing the pulse wave after baseline drift.

As shown in Fig. 9, the starting point (trough) of the pulse wave is located at the zero point of the wavelet transform coefficient. As shown in Fig. 10, the wavelet transform coefficient is zero, and the zero-crossing point also represents the extreme value of the pulse wave signal, that is, the main wave height, including the pulse wave at the height of the wave.

FIGURE 10.

Wavelet Coefficient Zero-crossing and its corresponding pulse wave signal.

To accurately locate the trough corresponding to the zero-crossing, you need to find a rule. By observing, we can see that the beginning of the pulse wave start point corresponds to the zero crossing before the minimum value of the wavelet coefficients. Therefore, we need to find the minimum value of the pulse wave corresponding to those coordinates, and then search for the wavelet coefficient modulus corresponding to the previous zero-crossing, which can be zero. Therefore, the first step in finding the pulse wave valley is to find the minimum value of the wavelet transform coefficients. Finding the minimum value involves these specific steps. First, find the wavelet transform coefficient of the smallest value. Then, using that as a threshold, the modulus can be found by multiplying the threshold value. Consequently, by finding the minimum value of the wavelet transform coefficient and then the minimum value of the abscissa corresponding to the original pulse wave signal, you can find the minimum value of the corresponding pulse wave signal point. The results are shown in Fig. 11.

FIGURE 11.

Wavelet modulus minimum and its corresponding pulse wave signal.

As shown in Fig. 11, the minimum value of the wavelet coefficients corresponds to the maximum slope of the pulse wave signal, and the wavelet signal modulus corresponds to the first zero-crossing corresponding to the pulse wave signal, then the pulse wave starting point (trough) occurs. In the program design, the minimum value of the wavelet coefficients and the zero-crossing of the wavelet coefficients are stored in an array. The minimum value of the corresponding array index before the wavelet coefficient of the zero-crossing array subscript is the starting point of the pulse wave of the abscissa, through which the abscissa can be found in the corresponding pulse wave trough. The results are shown in Fig. 12.

FIGURE 12.

Pulse wave starting point and corresponding wavelet coefficient zero-crossing.

Similar to the method for finding the starting point of the pulse wave, it is necessary to identify the main wave and the beat of the pulse wave through the zero-crossing of the wavelet coefficients.

C. Pulse Waveform Detection

The pulse wave waveform can be measured by a number of indicators. In addition to characteristic pulse wave points such as the starting point, the main peak, the peak of the tidal wave, the height of the lower gorge, and the peak value of the hit wave, there are several other important waveform evaluation indicators.

• (1)
  The kurtosis coefficient mainly reflects how sharp or flat the top of the curves are in a digital waveform sequence. In statistics, the second-order central moment represents the variance of the data and can reflect the kurtosis of the data sequence waveform to a certain extent. However, for a digital sequence with the same variance and its own kurtosis, the second-order central moment is not sufficient. For example, a fourth order center moment is required to describe the sharpness of the top of the curves in a digital waveform sequence.

  

  In the preceding formula, K represents the kurtosis coefficient, N represents the number of samples, represents the standard deviation of the fourth power, M represents the number of types of each frequency component in the sample, 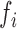represents the number of occurrences of each frequency component, represents the value of each type, and represents the average of the samples.

  Because the kurtosis coefficient of the normal distribution is 3, the waveform is considered to be at a peak when the kurtosis coefficient K of the waveform exceeds 3, and when the crest factor K of the waveform is less than 3, the waveform is considered to be flat.

• (2)
  The skewness coefficient is a characteristic number (asymmetry of time) describing the deviation of a number sequence distribution from symmetry. The formula for calculating the skewness coefficient is shown in Equation 7.

  

  When a waveform is symmetrical, the skewness coefficient T of the waveform is 0; when the skewness coefficient T is greater than 0, the waveform has a positive skew; consequently, the right end of the waveform is thicker. When the skewness coefficient T is less than 0, the waveform has a negative skew and the left end of the waveform is thicker.

• (3)
  The pulse coefficient represents the ratio between the peak and the mean of the signal and is calculated as shown in Equation 8.

  

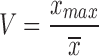
The larger the kurtosis coefficient V is, the more obvious the shock in the waveform is. In a pulse wave, this value denotes that the heart ventricle has a greater ability to pump blood.

In this system, the kurtosis coefficient of the evaluation index is used as a primary metric. Specifically, the kurtosis coefficient refers to the kurtosis coefficient of the waveform between the starting point of the pulse wave and the descending gorge. A normal pulse wave kurtosis coefficient is large, has a sharp peak, the rise time is very short, and the decline period is relatively flat. The kurtosis coefficient of a normal distribution is 3; the kurtosis of the pulse wave is steeper than a normal distribution. Therefore, the kurtosis coefficient of the pulse wave is greater than 3.

The skewness coefficient refers to the skewness coefficient over the entire pulse wave period. A normal person’s pulse wave has a steep front and a slow descent. The skewness of a normalized distribution is 0; the pulse wave descending period is significantly longer than the listing period. Therefore, the pulse wave skew coefficient is greater than zero: under normal circumstances the it exceeds 0.5.

The pulse coefficient consists of two items, one is the pulse coefficient of the main wave and the other is the pulse coefficient of the red wave in Fig. 15. The height of the normal pulse wave is between 1 / 3–1 / 4 the height of the main wave, The main wave pulse coefficient of the wave is greater than the pulse coefficient of the pulse wave.

FIGURE 15.

The PTT pulse wave conduction time.

D. Pulse Wave Waveform Detection Results and Analysis

This experiment was developed on the basis of the previous pulse wave eigenvalue detection and extends it. The unit cycle of the pulse wave (the period from the starting point of the pulse wave to the starting point of the next pulse wave period is the unit cycle) is the research objective. Two representative sets of pulse wave data were selected, and the test results are shown in Fig. 13 and Fig. 14.

• (1)Normal pulse wave waveform detection results

  This group of data was acquired directly from the system hardware sensors. After removing baseline drift and detecting feature points, from Fig. 13 it can be seen that the set of pulse wave eigenvalues are complete and that the kurtosis coefficient, skew coefficient, main wave pulse coefficient and pulse wave coefficient are all at normal levels; therefore, the diagnosis results are also normal. This set of data is suitable for subsequent diagnosis of blood pressure values.

• (2)Abnormal pulse wave waveform detection results

FIGURE 13.

Normal pulse wave waveform detection results.

FIGURE 14.

Atypical pulse wave waveform detection results.

Due to limitations of the experimental setup, the sample data available from our system included no information about hypertension or aortal sclerosis. Therefore, the abnormal pulse wave of the system comes from a publicly available database from MIT-BIH, led by the Massachusetts Institute of Technology [25], and derived from the Beth Israel Hospital in Boston, USA. This database contains extensive physiological information, including pulse and ECG signals. We downloaded the MIT-BIH database of abnormal pulse wave files and extracted the data according to the BIT-BIH format to obtain the pulse wave information. The results are shown in Fig. 14.

In Fig. 14, the pulse wave is missing from the typical wave, the kurtosis coefficient and the re-wave coefficient are low, the crest is flat, and the bounce wave is low; therefore, the initial diagnosis of this pulse wave is not Normal. It would be recommended that the subject be re-measured or go to the hospital for further testing.

IV. Blood Pressure Diagnosis Algorithm

After the initial filtering and the digital filtering performed by the hardware, noise is suppressed in the pulse wave signal and the ECG signal. Then, after the signal has undergone wavelet transform, the number of extreme points, the largest point and the maximum value of the ECG signal are obtained. Next, the sampling frequency is used to derive the PTT pulse wave velocity. Then, based on the pulse wave velocity and blood pressure measurement statistical model recognized by eh medical community, a new blood pressure measurement model is proposed. Finally, we verify the pulse wave based real-time blood pressure measurement system by comparing it with the actual situation.

A. Pulse Wave Conduction Time Measurement

Pulse wave velocity and blood pressure have a very close relationship. The pulse wave velocity is the pulse wave conduction time. The pulse wave signal and ECG signal are combined to measure the pulse wave conduction time. The pulse wave signal includes a number of harmonic syntheses and is highly impacted by the surrounding environment [26]. However, the ECG signal acquisition device is a flexible electrode, which adheres tightly to the human body and is easy to relocate. Therefore, the ECG signal pulse signal is a more suitable reference point than the pulse signal.

The pulse wave signal and the ECG signal are recorded at the same time, and the maximum values of the pulse wave and the ECG signal over a single cycle are determined as a reference point. These are the peak value of the pulse wave signal in a single cycle, and the vertex of the R wave of the ECG signal in a single cycle. After calculating the characteristic points of these two signals, because the sampling frequency of the two signals is the same, the sample time difference between the two feature points can be deduced to calculate the PTT pulse conduction time.

The PTT is the time difference between the two signals. PTT is calculated as shown in Fig. 15, where 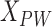represents the sequence number of the sampling point of the pulse signal feature point in the cycle, indicates the characteristic point of the ECG signal, and 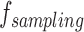is a serial number indicating the sampling frequency.

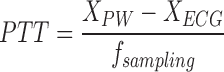B. Pulse Wave Conduction Time Estimation of Blood Pressure

In 1957, the American physician Landowne [8] suggested that if the elasticity of blood vessels remained constant, there is a positive correlation between the conduction time of the pulse wave and the blood pressure within a certain range. The specific relationship is:

Therefore, blood pressure BP and pulse wave conduction time PTT have the following approximate relationship:

In the preceding equation, a and b are undetermined coefficients that can be determined by regression analysis. Based on the analysis of the sample data, an improved blood pressure model based on pulse wave conduction time is proposed based on the pulse wave conduction time method of blood pressure measurement. However, before proposing a new blood pressure measurement model, it is necessary to verify the relationship between the pulse wave conduction time and blood pressure.

C. Establishment of New Blood Pressure Measurement Model by Regression Equation

The relationship between the pulse wave conduction time and blood pressure are verified through an experiment. First, the pulse wave signal and ECG signal of the subject are collected by the system. Then, the pulse wave conduction time, the pulse wave characteristic value, and the pulse wave waveform are calculated. At the same time, the blood pressure of the subjects was measured again using a mercury sphygmomanometer and an Aurora 2006-2 arm-type electronic sphygmomanometer. Finally, we can propose a new blood pressure measurement model based on the regression equation we established.

D. Experiment

The human subjects experiments were performed under the approval of the Shenzhen University IRB. The human subjects gave their informed consent before participating in the trial. The subjects consisted of 10 young men, 2 young women, and 3 middle-aged men. From each group, we collected 10 sets of data: 5 before exercise, 5 after exercise. These measurements were collected five times per day. In addition, we collected continuous measurements over 3 days. There were a total of 1800 data measurements.

The purpose of these experiments was to establish a new type of blood pressure measurement using the regression equation; thus, we needed to capture the data in different scenarios. Similar experimental models and experimental data processing reference articles [27] and [28]. The selected test times were after breakfast, before lunch, after lunch, before dinner and after dinner: five time periods. The experiment lasted two days. There were two test scenarios: resting state and post-motion state. Excluding interference data (waveform abnormal data), there were 800 number of valid sample data was 800 group, part of the data are list in the Table 1.

TABLE 1. Part of the Pulse Wave Signal and ECG Signal Data.

R	A	B	C	D	E	F	F/B	K	T	V1	V2	PTTS	SP	DP
98	83	160	129	122	82	95	0.59	2.37	0.75	1.44	1.08	26	110	67
97	81	158	124	120	92	100	0.63	2.42	0.74	1.42	1.07	27	111	69
104	71	225	205	180	93	104	0.46	3.31	1.24	2.34	1.31	20	128	74
91	76	135	117	107	89	97	0.72	2.74	0.83	1.31	1.04	27	109	73
136	98	155	134	112	96	108	0.70	3.89	1.82	1.46	1.09	28	118	73
106	94	253	194	173	104	113	0.45	3.97	1.41	2.41	1.61	18	135	79
106	63	244	151	116	93	106	0.43	3.68	1.26	2.24	1.35	22	125	70
137	90	154	130	113	101	108	0.70	3.97	1.74	1.46	1.08	27	119	72
106	79	141	120	110	98	102	0.72	4.67	1.59	1.43	1.03	27	126	78
94	75	195	130	123	97	102	0.52	4.27	1.43	1.91	1.05	28	119	74
103	89	151	112	103	90	98	0.65	4.45	1.50	1.42	1.02	26	129	76
117	87	158	117	111	103	110	0.70	4.34	1.45	1.47	1.15	29	113	60
106	63	244	151	116	93	106	0.43	3.62	1.25	2.21	1.31	21	127	71
99	87	153	113	96	92	102	0.67	4.32	1.46	1.47	1.14	28	116	60
95	79	213	130	128	96	99	0.47	4.10	1.41	1.87	1.29	29	117	70
88	86	130	110	97	87	104	0.80	2.71	0.87	1.29	1.03	28	108	72
134	91	155	132	113	101	108	0.70	3.94	1.76	1.51	1.08	28	118	71
101	65	216	170	133	100	109	0.50	3.33	1.28	2.39	1.26	26	120	77
95	81	164	115	114	95	97	0.59	4.08	1.45	1.59	1.06	26	114	67
95	72	162	115	107	96	102	0.62	4.10	1.42	1.48	1.03	26	116	70
104	80	154	116	109	103	106	0.88	4.09	1.30	1.44	1.06	31	104	66
98	98	133	124	117	105	116	0.87	3.04	1.02	1.24	1.01	29	106	66
114	83	159	122	118	82	95	0.60	2.78	0.88	1.47	1.03	21	110	69
109	92	136	114	102	97	102	0.75	3.15	1.12	1.25	1.05	26	124	87

The source of the sample signal was collected mainly from the pulse wave and ECG signals. After processing the signal as described previously, we obtain the related statistics, including the peak value of the ECG signal (R), the height of the pulse wave starting point (A), the main wave height (B) of the pulse wave, the starting point of the waveform of the pulse wave, the end of the waveform of the pulse wave (Point D), the pulse wave drop height (G), the height of the pulse wave (F), the pulse wave conduction time sampling coordinate difference (PTTS), the kurtosis coefficient (K), the skew coefficient (T), the main wave pulse coefficient (V1), and the buoy wave pulse coefficient (V2). Meanwhile, we used third-party blood pressure measurement instruments to measure systolic blood pressure (SP) and diastolic blood pressure (DP).

According to Landowne [8], pulse wave conduction time and blood pressure have the linear relationship 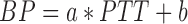. Therefore, we first analyzed the relationship between the pulse sampling time difference and the systolic blood pressure (SP) and then linearly fit the measured data.

For a linear one-time fitting, the coefficients can be estimated by the least squares estimation method. The least squares method is a mathematical optimization technique that minimizes the square of the error and finds the best matching function of the data. Using the least squares method, the unknown values can be easily obtained by minimizing the squared sum of the errors between the obtained data and the actual data. In this system when , the relationship between the systolic and pulse wave conduction time sampling coordinates is as follows:

In linear correlation analysis, the correlation coefficient between the two variables is generally described by the correlation coefficient R [29]. When the trend change of the two variables is the same, their relationship is called a linear positive correlation, and when the two variables have opposite trends, their relationship is called a linear negative correlation. The mathematical expression of the correlation coefficient is shown in Equation 13:

In Equation 13, R represents the correlation coefficient, which lies in the range: , and 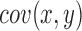is the covariance of two variables, , which represent the standard deviations of the x and y variables, respectively. When the correlation coefficient R is closer to 1, the degree of correlation between the two variables is larger. In the linear regression equation, in addition to the correlation coefficient R, a more commonly used evaluation index is the coefficient of determination, 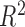, which is the square of the correlation coefficient. The range of values is: . As with the correlation coefficient R, the closer the coefficient of determination is to 1, the greater the degree of correlation is between the two variables.

The calculated coefficient, , between the two sets of PTTS variables, calculated from systolic pressure SP and pulse wave conduction time, demonstrates a very good correlation between the systolic pressure SP and the coordinate difference PTTS of the pulse wave conduction time.

The relationship between the pulse sampling time difference and diastolic blood pressure (DP) was analyzed, and the measured data were linearly fitted. The results of the linear fitting are: .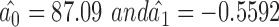

Similarly, the coefficient of determination of difference between the two variables diastolic blood pressure DP and the pulse wave conduction time difference PTTS is ; there is not a large correlation between the two. In contrast, the relationship between diastolic blood pressure and pulse wave conduction time is not particularly close either. As the pulse wave conduction time increases, the change in diastolic blood pressure is very small. It is also known from the literature [11] that the correlation between pulse wave conduction time and diastolic blood pressure is relatively small. Thus, in this system, the PTT pulse wave conduction time is used to estimate systolic blood pressure, while diastolic blood pressure requires more pulse wave parameters to be estimated.

Next, to perform further analysis, we calculated the correlation between the parameters of the pulse wave and the diastolic blood pressure DP to determine whether the correlation coefficient R and the coefficient of determination show a correlation between the partial parameters and diastolic blood pressure. In cardiovascular system theory, in addition to pulse wave conduction time to estimate blood pressure, the pulse wave parameters can also be used to estimate blood pressure [11]–[13]. In the previous section, we calculated the parameters of the pulse wave using wavelet filtering and wavelet transform. Next, we need to analyze the relationships between the pulse wave parameters and the blood pressure.

The process of analyzing all dependent variables, y, to determine whether they significantly affect an independent variable, x, is often referred to as regression analysis. Stepwise regression analysis is based on multiple linear regressions. The main idea is to find the size of the effect of a dependent variable y on the independent variable x by gradually introducing the dependent variable to the regression equation [29].

The general expression of a stepwise regression equation is defined as follows:

The main idea behind stepwise regression analysis is that the variables are gradually introduced into the model. After each introduction of an explanatory variable, it is necessary to carry out an F test. When the new explanatory variable is introduced by the explanatory variable, and becomes no longer significant, then remove it. In this system, we gradually introduce the characteristic parameters related to the pulse wave signal to explore the relationship between these characteristic parameters and blood pressure.

The purpose of an F test is to calculate the significance of the variable test. Taking the regression equation as an example, in Equation 15, to test the relationship between x and y, we need only test whether is established.

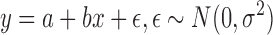In probability statistics, it is generally assumed that , which shows that the linear regression model is reasonable. We construct the sum of the squares of the variance of the variable y:

Decomposing formula 16, we obtain

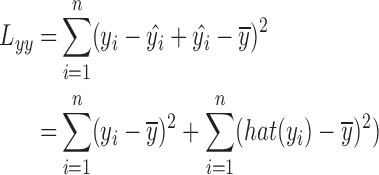Let 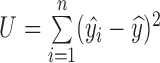, where U is the sum of the squared deviations of the regression value 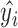from its mean , and can be regarded as a change in the y value due to the change in x, and is called the regression square sum.

Let 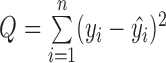, which reflects the sum of the squares of the deviations between the observed and the regression values and reflects all the factors other than the linear effect of x to y, the change in the y value, which is called the sum of the squares of errors, or residual squares.

When is true, there are

When the test level is , the inspection rule is: if the sample is calculated by , then accept ; otherwise, reject .

The smaller the value of the general test level 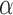is, the more stringent the criteria for selecting the variable are. In regression analysis, there are two test levels; one is and the other is . For this system, .

It is more convenient to establish a stepwise regression equation using PASW Statistics 18 software. The regression coefficients of the pulse wave are analyzed by stepwise regression analysis. Thus, the model is derived as a binary primary equation for diastolic pressure as follows: .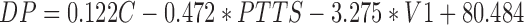

Through the previous analysis, we used the pulse wave conduction time and pulse wave characteristic parameters to establish the systolic and diastolic pressure measurement equation. Systolic blood pressure is mainly calculated by the pulse wave conduction time. According to the characteristics of pulse wave conduction time and diastolic blood pressure, a regression equation is established by stepwise regression based on the theory of the correlation between pulse wave eigenvalues and blood pressure. This method is a good solution to the problem that the original pulse wave conduction time measurement of diastolic blood pressure is not accurate. The systolic and diastolic blood pressure measurement equations are as follows:

E. Comparative Experiments and Results

The comparative experimental devices used here was an AiOuYue 2006-2 type arm electronic sphygmomanometer, which meets the GB3053 standard, a Yuyao mercury sphygmomanometer, and the device we designed. Subjects in the experiments were divided into two groups, blood pressure data was collected from one group of subjects under a resting state. These data were mainly used to compared the difference between blood pressure values measured by the traditional mercury sphygmomanometer, the electronic sphygmomanometer and our own device. Data from the other group were used to compare the pulse wave velocity measurements based on blood pressure and the new blood pressure measurement proposed by this paper. The test subjects consisted of 4 young men, 2 young women, and 2 mid-age men.

Results analysis

• (1)For the first experimental group we compared the three different measurements collected by the different instruments as shown in Table 2.

  In Table 2, C and D respectively represent the systolic and diastolic blood pressure measured by the mercury sphygmomanometer meter; E and F respectively represent the systolic and diastolic blood pressure measured by the electronic sphygmomanometer, and G and H represent the mean diastolic blood pressure and mean diastolic blood pressure. I and J represent the proposed system’s measured systolic and diastolic blood pressure, K is the diastolic pressure single error, and L is the average diastolic pressure error.

  The results of the first group of experiments showed that the results of the proposed continuous blood pressure measurement system were more accurate. Compared with the results of the electronic and mercury sphygmomanometers, the systolic blood pressure error ranged from 3±2.5 mmHg, and the diastolic pressure error ranged from 4 ± 3mmHg, This error range meets the United States Medical Instrument Association’s AAMI standards of control within an 8mmHg range.

• (2)Based on the pulse wave velocity measurement of blood pressure and the system’s improved pulse wave velocity blood pressure measurement results, in the comparison shown in Table 3, B SP represents the systolic blood pressure measured by the mercury sphygmomanometer, C DP is the diastolic pressure measured by the mercury sphygmomanometer, D is the starting point of the tidal wave of the pulse wave, V1 is the pulse wave coefficient of the pulse wave, F represents the sampling slope of the pulse wave velocity conduction time, and G and H SP respectively represent the systolic blood pressure and diastolic pressure estimated by the designed continuous blood pressure system. K DP2 indicates the diastolic pressure estimated by the original pulse wave velocity method, and L DP2 is the deviation between a method and the measured value of the mercury sphygmomanometer. When L DP2 is negative, the estimated value is smaller than the measured value, and when it is positive, the estimated value is larger than the measured value.

TABLE 2. Blood Pressure Measurements From Three Different Instruments.

number	times	C	D	E	F	G	H	I	J	K	L
		SP	DP	SP	DP	SP	DP	SP	DP	SP	DP
1	1	116	62	113	64	114.5	63	113.2	69.2	−1.3	5.2
	2	115	64	114	62	114.5	63	116.4	68.2	1.9	5.2
2	1	122	72	125	69	123.5	70.5	125.9	71.8	2.4	1.3
	2	120	70	123	70	121.5	70	125.9	68.8	4.4	−1.2
3	1	104	66	102	73	103	69.5	108.4	67.7	5.4	−1.8
	2	104	68	103	70	103.5	69	106.8	71.8	3.3	2.8
4	1	105	67	106	65	105.5	66	106.8	71.1	1.3	5.1
	2	107	69	104	67	105.5	68	108.4	70.6	2.9	2.6
5	1	117	72	115	73	116	72.5	116.4	71.8	0.4	−0.7
	2	116	71	114	72	115	71.5	114.8	70.6	−0.2	−0.9
6	1	124	80	122	81	123	80.5	125.9	76.8	2.9	−3.7
	2	126	81	121	84	123.5	82.5	125.9	76.8	2.4	−5.7
7	1	110	67	112	69	111	68	114.8	67.7	3.8	−0.3
	2	111	68	113	67	112	67.5	116.4	68.2	4.4	0.7
8	1	134	83	134	83	134	83	129.1	78.4	−4.9	−4.6
	2	135	81	132	82	133.5	81.5	129.1	76.8	−4.4	−4.7

TABLE 3. Parts of the Pulse Wave Signal and ECG Signal Data.

Number	B	C	D	V1	F	G	H	I	J	K	L
	SP	DP				SP	SP	DP1	DP1	DP2	DP2
1	119	71	132	1.91	26	114.8	−4.2	68.0	−3	72.5	1.5
2	127	71	151	2.21	21	125.9	−1.1	71.8	0.8	75.3	4.3
3	104	61	116	1.44	25	119.6	5.6	68.1	7.1	73.1	12.1
4	125	70	151	2.24	22	124.3	−0.7	71.2	1.2	74.8	4.8
5	112	69	124	1.42	27	116.4	4.4	68.2	−1.2	72.0	3
6	116	61	113	1.47	28	113.2	−2.8	66.5	4.5	70.8	9.8
7	132	79	194	2.41	20	127.5	−4.5	76.8	−2.2	75.9	−3.1
8	118	71	132	1.51	28	114.8	−3.2	68.4	−2.6	71.4	0.4
9	105	66	116	1.44	25	119.6	4.6	68.1	2.2	73.1	7.1
10	115	69	124	1.42	27	116.4	1.4	68.2	−0.8	72.0	3
11	140	84	212	2.31	15	135.4	−4.6	81.7	−2.3	78.7	−5.3
12	108	70	110	1.29	29	113.2	5.2	66.0	−4	70.9	0.9
13	114	71	122	1.47	25	117.9	3.9	69.8	−1.2	72.5	1.5
14	128	74	205	2.34	20	125.9	−2.1	77.9	3.9	75.4	1.4
15	116	70	115	1.48	26	119.6	3.6	67.4	−2.6	72.6	2.6
16	116	60	113	1.47	28	114.8	−1.2	66.2	6.2	71.4	11.4

From the Table 3, our system clearly achieves better accuracy than the original pulse wave velocity measurement method. The mean of the absolute value of diastolic pressure errors in this system is shown by the formula . The mean measured the other way is shown by 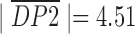. Therefore, accuracy was improved by 58%, indicating that the parameters C, PTTS and V1 introduced by the system are helpful in improving the measurement accuracy of diastolic blood pressure and that the new blood pressure scheme proposed by this system is feasible within a certain range.

V. Conclusions

As concern about cardiovascular disease rises in communities, companies have increasingly invested in research for this field. This system is a realization of the exploration of portable continuous blood pressure measurement systems; it includes the design for a portable hardware circuit and using a series of hardware and software operations on the collected pulse wave signal and the ECG signal, performs signal processing, analysis and diagnosis, and obtains good results. The main innovations of this system are summarized in the following three points:

• (1)Compared with an inflatable blood pressure measuring device, our designed hardware system is compact, portable, and has better accuracy; it acquires, amplifies, and filters the physiological signals.
• (2)We propose the concept of pulse wave waveform detection for the first time, then propose diagnostic criteria using the pulse wave waveform. Combined with the analysis and diagnosis of the experimental data, this approach provides a good foundation for the subsequent blood pressure calculation.
• (3)In view of the shortcomings of pulse wave velocity measurements, we proposed a new blood pressure measurement model, which is based on a stepwise regression equation. In the experiments, this model improved the accuracy of blood pressure measurement. The result meets the AAMI standard, suggesting that the continuous blood pressure measurement system has good feasibility.