Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Mar 21.
Published in final edited form as: J Biomech. 2017 Oct 6;70:82–87. doi: 10.1016/j.jbiomech.2017.09.024

A Model-based Approach for Estimation of Changes in Lumbar Segmental Kinematics Associated with Alterations in Trunk Muscle Forces

Iman Shojaei 1, Navid Arjmand 2, Judith R Meakin 3, Babak Bazrgari 1
PMCID: PMC5844798  NIHMSID: NIHMS912878  PMID: 29029957

Abstract

The kinematics information from imaging, if combined with optimization-based biomechanical models, may provide a unique platform for personalized assessment of trunk muscle forces (TMFs). Such a method, however, is feasible only if differences in lumbar spine kinematics due to differences in TMFs can be captured by the current imaging techniques. A finite element model of the spine within an optimization procedure was used to estimate segmental kinematics of lumbar spine associated with five different sets of TMFs. Each set of TMFs was associated with a hypothetical trunk neuromuscular strategy that optimized one aspect of lower back biomechanics. For each set of TMFs, the segmental kinematics of lumbar spine was estimated for a single static trunk flexed posture involving, respectively, 40° and 10° of thoracic and pelvic rotations. Minimum changes in the angular and translational deformations of a motion segment with alterations in TMFs ranged from 0° to 0.7° and 0 mm to 0.04 mm, respectively. Maximum changes in the angular and translational deformations of a motion segment with alterations in TMFs ranged from 2.4° to 7.6° and 0.11 mm to 0.39 mm, respectively. The differences in kinematics of lumbar segments between each combination of two sets of TMFs in 97% of cases for angular deformation and 55% of cases for translational deformation were within the reported accuracy of current imaging techniques. Therefore, it might be possible to use image-based kinematics of lumbar segments along with computational modeling for personalized assessment of TMFs.

Keywords: Trunk muscle forces, Finite element analysis, Optimization procedures, Trunk neuromuscular strategies, Lumbar segmental kinematics, Image-based modeling

Introduction

Neuromuscular control of spinal equilibrium and stability changes in the presence of pain or following exposure to known risk factors for low back pain (LBP) (Muslim et al., 2013; Radebold et al., 2000; Radebold et al., 2001; Toosizadeh et al., 2013). Such alterations may cause deformations and/or forces in lower back tissues such that exceed injury/pain thresholds instantaneously or cumulatively (Adams et al., 2013; Coenen et al., 2014; Marras et al., 2001; Panjabi, 1992a, b). Despite such a significant role, the current methods for personalized assessment of trunk muscle forces (TMFs) are limited. Kinematic measures of lumbo-pelvic coordination, though capable of distinguishing patients with LBP from controls (Vazirian et al., 2016), do not provide much information about individual muscle forces. Specifically, neuromuscular redundancy in control of lumbo-pelvic motion as well as individual variability in mechanical behavior of passive lumbar tissues hinder relating measured kinematics data to TMFs. The commonly used surface electromyography (EMG)-based methods for the assessment of TMFs, on the other hand, can only provide information about the activity of superficial trunk muscles. Further, the relationship between EMG measures of muscle activity and actual muscle force is still unclear (Staudenmann et al., 2010). Finite element and multi-joint biomechanical models of the spine with detailed musculature have also been developed and used for general assessment of TMFs (Arjmand and Shirazi-Adl, 2006a, b; Dreischarf et al., 2014; Ezquerro et al., 2004; Hughes, 2000; Stokes and Gardner-Morse, 2001). These models often implemented optimization procedures to estimate TMFs (Arjmand and Shirazi-Adl, 2006b; Daniel, 2011; Hughes, 2000; Stokes and Gardner-Morse, 2001) and are not suitable for personalized assessment of TMFs due to assumptions made related to lumbar segmental rotations and the requirement for a priori knowledge of trunk neuromuscular strategy (e.g., a strategy that minimizes stress in muscles).

Currently, imaging is used to detect structural and geometrical/kinematics abnormalities in the lumbar spine (Fujii et al., 2007; Iwata et al., 2013; Keller et al., 2003; Kjaer et al., 2005; Ochia et al., 2006). The image-based geometrical/kinematics information have also been used for development of geometrically personalized biomechanical models of normal and scoliotic spine (Eskandari et al., 2017; Ghezelbash et al., 2016; Lafon et al., 2010; Petit et al., 2004), biomechanical comparison of healthy and metastatically involved vertebrae (O’Reilly and Whyne, 2008), material sensitivity analysis of intervertebral disc (Fagan et al., 2002), indirect estimation of spinal loads (Shymon et al., 2014), and estimation of elastic modulus of cancellous bone (Diamant et al., 2005). The geometrical information from imaging if combined with optimization-based biomechanical models may provide a unique platform for personalized assessment of TMFs. Particularly, it will be possible to use an optimization-based biomechanical model to search for a set of muscle forces that results in lumbar kinematics similar to those obtained from imaging. Such a method, however, is reliable only if differences in lumbar spine kinematics due to differences in TMFs can be captured by the current imaging techniques.

Recently, we have used our finite element model of the spine within an optimization procedure to estimate TMFs and kinematics of lumbar segments resulting from a trunk neuromuscular strategy that minimized sum of squared stress across all trunk muscles (Shojaei et al., 2015). The resultant kinematics were consistent with image-based reports of lumbar spine kinematics of asymptomatic individuals. Using the proposed algorithm, estimation of TMFs and lumbar segmental kinematics for other hypothetical trunk neuromuscular strategies that optimize other aspects of lower back biomechanics is possible. As a first step toward testing the feasibility of using image-based kinematics of lumbar segments for personalized assessment of TMFs, therefore, the objectives of this short communication are to determine changes in lumbar segmental kinematics due to alterations in trunk neuromuscular strategy and the associated TMFs and to verify if such changes are within the reported precision of current imaging techniques.

Methods

To address our research questions, TMFs and lumbar segmental kinematics were estimated for five different trunk neuromuscular strategies. In our approach each neuromuscular strategy was represented by a distinct cost function for the optimization procedure and assumed to either represent the trunk neuromuscular strategy of asymptomatic persons or a neuromuscular abnormality that minimizes loading on a specific aspect of lower back tissues (i.e., muscles, ligaments, intervertebral discs, and facet joints). As noted earlier, a neuromuscular strategy associated with the minimum value of sum of squared muscle stresses across the entire trunk muscles resulted in lumbar segmental kinematics consistent with image-based reports of lumbar spine kinematics of asymptomatic individuals, hence, was regarded to represent a normal trunk neuromuscular strategy (Shojaei et al., 2015). On the other hand, abnormal neuromuscular strategies that minimize loads in muscles, ligaments, intervertebral discs, and facet joints were represented by cost functions that respectively minimize sum of squared muscle forces across the entire trunk muscles, passive moment, compression, and shearing force at the L5-S1 intervertebral disc. For each neuromuscular strategy, the associated TMFs and lumbar segmental kinematics for a single static trunk flexed posture involving, respectively, 40° and 10° of thoracic and pelvic rotations (i.e., equal to a total lumbar flexion of 40° − 10° = 30°) in the sagittal plane were estimated using our kinematics-driven finite element approach. Specifically, the changes in distance between centers of two vertebrae of each motion segment (i.e., translational deformation) as well as changes in their relative angular orientations with respect to each other (i.e., angular deformation) with alterations in TMFs were considered as changes in lumbar segmental kinematics. Forward trunk bending is a common posture used for X-ray imaging of patients with LBP and the specific thoracic and pelvic rotations considered here are the same rotations we used in a recent study for validation of our method (Shojaei et al., 2015).

In our approach, rather than implementing a force-driven approach for estimation of lumbar segmental kinematics resulting from TMFs that are associated with a given neuromuscular strategy, we used our kinematics-driven methods. Such a methodological choice was mainly because of the lower computational cost of kinematics-driven approach. Specifically, the potential TMFs that are searched in the optimization procedure, where a kinematics-driven approach is used, readily satisfy spine equilibrium. Hence, the solution space that is searched by the optimization search engine is much smaller than the case when a force-driven approach is implemented. Therefore, in our approach, from all possible sets of lumbar segmental kinematics that can be distributed across lumbar vertebrae and generate the total 30° lumbar flexion, we will search (i.e., through optimization procedures) for a set of lumbar segmental rotations where the associated biomechanical outcomes from the kinematics-driven approach minimize the desired cost function. Such a methodological choice (i.e., kinematics- versus force-driven), however, does not affect the outcomes. In the following subsections, we first elaborate on the kinematics-driven approach that uses lumbar segmental kinematics to estimate TMFs and other biomechanical outcomes (e.g., the L5-S1 passive moment) and subsequently present the structure of the optimization algorithm that finds the lumbar segmental rotations that optimize its cost function (i.e., representing a given neuromuscular strategy).

1. Estimating trunk muscle forces using the kinematics-driven approach

A nonlinear finite element (FE) model of spine, developed in the ABAQUS software (Version 6.13, Dassault Systémes Simulia, Providence, RI), is used in the kinematics-driven approach to estimate the moment at each lumbar vertebra to be balanced by muscles attached to that same vertebra (Arjmand et al., 2009; Bazrgari et al., 2007). In the FE model of spine, the thoracic region and lumbar spine vertebrae are simulated by rigid elements and intervertebral discs are simulated by nonlinear flexible beam elements (Fig. 1). Inputs to the FE model include sagittal plane rotational boundary conditions at the T12 to the S1 spinal levels along with the ~50% of total body weight distributed across the entire spine (Arjmand and Shirazi-Adl, 2006b). A muscle architecture including 56 muscles attached to the spine from lumbar and thorax to pelvis is considered for estimation of TMFs required to balance moments at lumbar vertebrae. Since the attached muscles to each level (i.e., 10 muscles in each level from T12 to L4 and 6 muscles in the level L5) outnumbers the moment equilibrium equations, an optimization procedure, hereafter called force optimization procedure, is used to estimate muscle forces at each level as follows:

{VarFCost function=g(F)Minimize(cost function)Subject to∑i=1mri×Fi=M (1)

where Fi and ri denote the force and the moment arm of the ith muscle, respectively and m is the number of muscles attached to that level and M is the output (reaction) moment. Where applicable, the cost function g(F) was set to be the same as the cost function representing trunk neuromuscular strategy (see the following section). However, if such a selected cost function is independent of muscle forces in force optimization (i.e., only when neuromuscular strategy minimizes the passive moment at the L5-S1), g(F) is set to minimize the sum of squared muscle stress at that level. A classic optimization technique (i.e., Lagrange Multiplier Method) is used to solve the force optimizations. Given the nonlinearity of FE model, the impact of estimated TMFs on mechanical response of the model is also considered by application of the estimated TMFs to the model as external loads and accounting for any residual moment estimated at each lumbar level in calculation of TMFs. Such iterative procedure is stopped when the residual moments estimated at each lumbar level become negligible (i.e., < 0.1 Nm).

Figure 1.

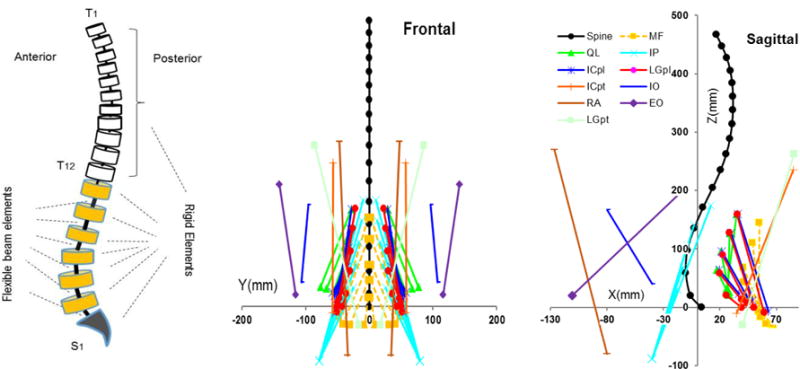
Figure 1

Open in a new tab

A schematic model of the spine and its components (left), the musculatures in the sagittal (right) and frontal (middle) planes in upright posture. ICpl: iliocostalislumborum pars lumborum, ICpt: iliocostalislumbroum pars thoracis, IP: iliopsoas, LGpl: longissimusthoracis pars lumborum, LGpt: longissimusthoracis pars thoracis, MF: multifidus, QL: quadratuslumborum, IO: internal oblique, EO: external oblique and RA: rectus abdominus.

2. Finding the lumbar segmental rotations that is associated with a given neuromuscular strategy

An optimization procedure (hereafter called neuromuscular optimization) was developed to minimize values of cost functions representing the trunk neuromuscular strategies. (Shojaei et al., 2015). The decision variables of the optimization procedure were angular kinematics of lumbar spine that were input to the kinematics-driven model. Predictions of the kinematics-driven model, including TMFs, were then used to calculate the cost function of the optimization procedure. The optimization procedure uses a genetic algorithm that involves 100 generations and 30 individuals in each generation (i.e., a total number of 3000 individuals/iterations), and the stop criterion is considered as the tolerance of 10−3 for both values of decision variables and cost function. The neuromuscular optimization procedure was formulated as:

{Varθ=[θL1θL2θL3θL4θL5]Cost function=g(F)(1+α∑i=1n=62Max[0,k])Minimize(cost function)Subject to0≤Fi≤σmax×PCSAi−9.6°≤θT12−θL1≤6°−9.6°≤θT1−θL2≤6°−12°≤θT2−θL3≤3.6°−14.4°≤θT3−θL4≤1.2°−15.6°≤θL4−θL5≤2.4°−10.8°≤θL5−θS1≤6° (2)

where θL1 to θL5 are vertebral kinematics from the L1 to the L5 respectively and are decision variables of the neuromuscular optimization procedure. n = 62 denotes the number of optimization constraints including 56 constraints for muscle forces and 6 rotational constraints. Fi and PCSAi denote the force and the physiological cross section area of ith trunk muscle respectively, k is the number of estimated muscle forces that exceed the muscle force boundaries plus the number of violated rotational constraints, α is a penalizing value, and σmax is the maximum allowable stress in the muscle (i.e., assumed to be 1.0 MPa). θT12 and θS1 are inputs of the neuromuscular optimization representing the rotations of the T12 and the S1 vertebrae. The rotational inequality constraints denote modified sagittal plane range of motion of lumbar motion segments with negative sign denoting flexion. These were obtained by adding a 20% increase to the mean reported values in Adams et al., (2013) to account for individuals’ variability.

The flowchart of the procedure for finding the lumbar segmental kinematics and TMFs that are associated with a given trunk neuromuscular strategy is presented in Fig. 2.

Figure 2.

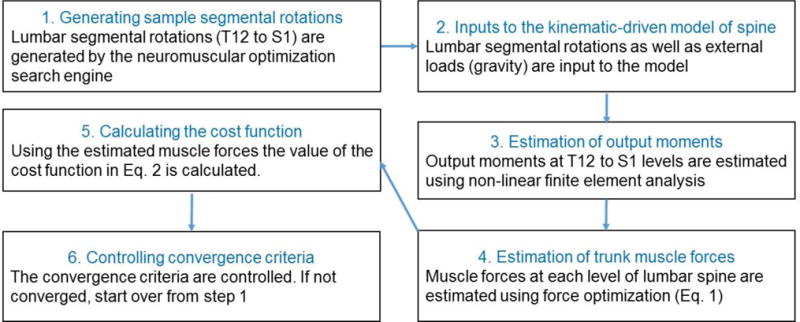
Figure 2

Open in a new tab

The algorithm used for finding a set of lumbar segmental rotations whose associated biomechanical pedictions from the kinematics-driven approach minimizes a cost function.

Results

The estimated angular and translational deformations of lumbar motion segments in the sagittal plan under TMFs associated with the five trunk neuromuscular strategies studied here are presented in the Table 1. Minimum changes in the angular and translational deformations of a motion segment with alterations in TMFs ranged from 0° (L2-L3 segment) to 0.7° (L4-L5 segment) and from 0 mm (L1-L2 and L2-L3) to 0.04 mm (L4-L5), respectively (Table 1). Similarly, maximum changes in the angular and translational deformations of a motion segment with alterations in TMFs ranged from 2.4° (L2-L3 segment) to 7.6° (L5-S1 segment) and from 0.11 mm (L2-L3) to 0.39 mm (L3-L4), respectively (Table 1). For each set of TMFs, the values of cost functions of other neuromuscular strategies were also calculated using the biomechanical predictions of the kinematics-driven approach (Table 2). As expected, the minimum value of a cost function was associated with predictions of kinematics-driven approach that were estimated to minimize that cost function.

Table 1.

The estimated angular (°) and translational (mm) deformations of lumbar motion segments in the sagittal plane under muscle forces of trunk neuromuscular strategies that minimize 1) sum of squared muscle stresses, 2) sum of squared muscles forces, 3) L5-S1 compression force, 4) L5-S1 anterior-posterior shearing force, and 5) L5-S1 passive moment.

Angular deformations translational deformations
T12-L1 L1-2 L2-3 L3-4 L4-5 L5-S1 T12-L1 L1-L2 L2-L3 L3-L4 L4-L5 L5-S1
ΣStress2 3.1 5.2 4.8 3.6 5.7 7.6 0.70 1.10 1.22 1.24 1.48 0.75
ΣForce2 7.8 7.6 4.8 1.6 2.5 5.7 0.97 1.19 1.22 1.09 1.20 0.70
Compression force 7.9 6.8 5.9 2.1 1.8 5.5 0.97 1.10 1.24 1.07 1.15 0.69
Shearing force 5.6 3.3 5.0 7.5 7.7 0.9 0.89 0.96 1.21 1.37 1.52 0.81
L5-S1 passive moment 4.2 6.6 7.2 7.8 4.2 0.0 0.87 1.18 1.32 1.46 1.44 0.86
Minimum change 0.1 0.2 0.0 0.3 0.7 0.2 0.02 0.0 0.0 0.02 0.04 0.01
Maximum change 4.8 4.3 2.4 6.2 5.9 7.6 0.27 0.23 0.11 0.39 0.37 0.17
Open in a new tab

Minimum and maximum changes in each column were, respectively, the smallest and largest value of difference between the deformations of any two trunk neuromuscular strategies.

Table 2.

The value of cost functions (horizontal top) under the five sets of muscle forces associated with neuromuscular strategies (vertical left) studied here.

ΣStress2 ΣForce2 Compression force (N) Shearing force (N) L5-S1 passive moment (Nm)
ΣStress2 8.39e+11 1.53e+05 1.49e+03 622.9 16.0
ΣForce2 2.28e+12 6.37e+04 1.34e+03 626.2 12.1
Compression force 3.02e+12 7.02e+04 1.32e+03 601.8 12.1
Shearing force 7.10e+12 1.73e+05 1.84e+03 518.0 2.7
L5-S1 passive moment 2.86e+12 1.92e+5 1.78e+03 610.5 0.0
Open in a new tab

Discussion

Lumbar segmental kinematics and TMFs resulting from neuromuscular strategies that optimize specific aspects of lower back biomechanics were calculated using a finite element model of the spine within an optimization procedure. The precision of current imaging techniques (e.g., computed tomography, magnetic resonance, fluoroscopy) have been reported to be ~ 0.1 mm and ~ 0.1° (Iwata et al., 2013; Keller et al., 2003; Ochia et al., 2006; Shymon et al., 2014; Breen and Breen, 2016; Zanjani-Pour et al., 2016) with repeatability errors of up to ~ 0.7 mm and ~ 1.3° (Breen et al., 2012). The differences in at least five (out of twelve: i.e., six angular and six translational deformations) kinematics outcome measures between each two sets of TMFs appear to be within the reported accuracy of current imaging techniques. Particularly, the differences in kinematics of lumbar segments between each combination of two different sets of TMFs (10 possible combinations) are detectable in 97% of cases for angular deformation and 55% of cases for translational deformation. Therefore, it might be possible to use image-based kinematics of lumbar segments along with computational modeling for personalized assessment of TMFs.

While image-based information have been used for development of subject-specific mechanical models of spine (Diamant et al., 2005; Eskandari et al., 2017; Fagan et al., 2002; Ghezelbash et al., 2016; Lafon et al., 2010; O’Reilly and Whyne, 2008; Petit et al., 2004; Shymon et al., 2014), previous studies have primarily used image-based information to personalize geometry (e.g., vertebra/disc dimensions, muscles cross-sectional areas and insertion points) and/or mechanical property of spine models (Diamant et al., 2005; Eskandari et al., 2017; Fagan et al., 2002; Ghezelbash et al., 2016; Lafon et al., 2010; O’Reilly and Whyne, 2008; Petit et al., 2004). Furthermore, some of these studies have been conducted in tissue level (Diamant et al., 2005; Fagan et al., 2002), have been designed for specific group of patients (Lafon et al., 2010; Petit et al., 2004), and have oversimplified the spine model by disregarding the effects of muscle forces when calibrating using experimental measures (Lafon et al., 2010; Petit et al., 2004). Although potentially feasible according to the results of current study, the personalized assessment of TMFs using geometrical information from imaging combined with optimization-based modeling, to the best of our knowledge, has not yet been reported.

The value of cost function of each neuromuscular strategy, as expected, increased when calculated using predictions of the kinematics-driven approach associated with the other cost functions (Table 2). However, what is notable in results presented in Table 2 is that alterations in TMFs, for example due to an abnormal trunk neuromuscular strategy, could result in loads and/or deformations in some areas of lower back that are larger than what is normally resisted by those areas. For instance, TMFs associated with the hypothetical neuromuscular strategy that minimized shearing force at the L5-S1 intervertebral disc resulted in an increase of ~ 350N in compression force when compared to TMFs that were associated with the a strategy that was considered normal in this study (i.e., the strategy that minimizes sum of squared muscle stresses). Similarly, a strategy that minimized compression force or muscle forces, compared to the normal strategy, led to large muscle stresses. Although the short term effect of a specific trunk neuromuscular strategy can be beneficial, for instance by protecting the injured tissues, the long term consequences of altered trunk neuromuscular strategy could be an injury to other lumbar tissues due to compensatory resisted larger than normal loads (Hodges and Smeets, 2015).

In the present study, we postulate that trunk neuromuscular strategies optimize some aspects of lower back biomechanics. Though alterations in neuromuscular strategy have been reported in the literature, our assumption might not be accurate and was merely made for the purpose of this feasibility study (i.e., to demonstrate changes in lumbar segmental kinematics with alterations in TMFs are within the reported accuracy of current imaging techniques). Furthermore, in all cases, the abnormal neuromuscular strategy that minimized loads in a tissue was represented by a single-force cost function which was a simplified assumption. For example, minimizing the loads on the facet joint involves reducing both shearing and compression forces, though shearing is the dominant force in characterizing facet joint environment. Whether there are one-on-one relationships between sets of TMFs (or the resultant kinematics) and neuromuscular strategies or whether all differences in trunk neuromuscular strategies result in detectable change in TMFs remains to be investigated in future. The availability of personalized assessment of TMFs, as proposed in this short communication, should, however, facilitate such future research efforts.

In conclusion, results of this feasibility study, support the idea of image-based personalized assessment of TMFs using computational models. Specifically, a geometrically and materially subject-specified model of the spine can be used in future to obtain a set of TMFs, as individualized TMFs, that generates the closest lumbar kinematics to those measured from imaging. The accuracy of such assessment strategy can further be improved by implementing dynamic rather than static assessment tasks. However, immediate research question to be addressed will be the reliability and validity of such an image-based method for personalized assessment of TMFs.

Acknowledgments

This work was supported, in part, by an award (5R03HD086512-02) from the National Center for Medical Rehabilitation Research (NIH-NICHD) and the Office of the Assistant Secretary of Defense for Health Affairs, through the Peer Reviewed Orthopaedic Research Program (award #W81XWH-14-2-0144).

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of interest statement

We declare that all authors have no financial or personal relationships with other persons or organizations that might inappropriately influence our work presented therein.

References

  1. Adams MA, Burton K, Bogduk N. The biomechanics of back pain. Elsevier; Health Sciences: 2013. [Google Scholar]
  2. Arjmand N, Gagnon D, Plamondon A, Shirazi-Adl A, Lariviere C. Comparison of trunk muscle forces and spinal loads estimated by two biomechanical models. Clinical Biomechanics. 2009;24:533–541. doi: 10.1016/j.clinbiomech.2009.05.008. [DOI] [PubMed] [Google Scholar]
  3. Arjmand N, Shirazi-Adl A. Model and in vivo studies on human trunk load partitioning and stability in isometric forward flexions. J Biomech. 2006a;39:510–521. doi: 10.1016/j.jbiomech.2004.11.030. [DOI] [PubMed] [Google Scholar]
  4. Arjmand N, Shirazi-Adl A. Sensitivity of kinematics-based model predictions to optimization criteria in static lifting tasks. Med Eng Phys. 2006b;28:504–514. doi: 10.1016/j.medengphy.2005.10.001. [DOI] [PubMed] [Google Scholar]
  5. Bazrgari B, Shirazi-Adl A, Arjmand N. Analysis of squat and stoop dynamic liftings: muscle forces and internal spinal loads. Eur Spine J. 2007;16:687–699. doi: 10.1007/s00586-006-0240-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Breen A, Breen A. Accuracy and repeatability of quantitative fluoroscopy for the measurement of sagittal plane translation and finite centre of rotation in the lumbar spine. Med Eng Phys. 2016;38:607–614. doi: 10.1016/j.medengphy.2016.03.009. [DOI] [PubMed] [Google Scholar]
  7. Breen AC, Teyhen DS, Mellor FE, Breen AC, Wong KW, Deitz A. Measurement of intervertebral motion using quantitative fluoroscopy: report of an international forum and proposal for use in the assessment of degenerative disc disease in the lumbar spine. Adv Orthop. 2012;2012 doi: 10.1155/2012/802350. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Coenen P, Kingma I, Boot CR, Bongers PM, van Dieën JH. Cumulative mechanical low-back load at work is a determinant of low-back pain. Occup Environ Med. 2014;71:332–337. doi: 10.1136/oemed-2013-101862. [DOI] [PubMed] [Google Scholar]
  9. Daniel M. Role of optimization criterion in static asymmetric analysis of lumbar spine load. WMW Wiener Medizinische Wochenschrift. 2011;161:477–485. doi: 10.1007/s10354-011-0904-8. [DOI] [PubMed] [Google Scholar]
  10. Diamant I, Shahar R, Gefen A. How to select the elastic modulus for cancellous bone in patient-specific continuum models of the spine. Med Biol Eng Comput. 2005;43:465–472. doi: 10.1007/BF02344727. [DOI] [PubMed] [Google Scholar]
  11. Dreischarf M, Zander T, Shirazi-Adl A, Puttlitz C, Adam C, Chen C, Goel V, Kiapour A, Kim Y, Labus K. Comparison of eight published static finite element models of the intact lumbar spine: predictive power of models improves when combined together. J Biomech. 2014;47:1757–1766. doi: 10.1016/j.jbiomech.2014.04.002. [DOI] [PubMed] [Google Scholar]
  12. Eskandari A, Arjmand N, Shirazi-Adl A, Farahmand F. Subject-specific 2D/3D image registration and kinematics-driven musculoskeletal model of the spine. J Biomech. 2017 doi: 10.1016/j.jbiomech.2017.03.011. [DOI] [PubMed] [Google Scholar]
  13. Ezquerro F, Simón A, Prado M, Pérez A. Combination of finite element modeling and optimization for the study of lumbar spine biomechanics considering the 3D thorax–pelvis orientation. Med Eng Phys. 2004;26:11–22. doi: 10.1016/s1350-4533(03)00128-0. [DOI] [PubMed] [Google Scholar]
  14. Fagan M, Julian S, Siddall D, Mohsen A. Patient-specific spine models. Part 1: Finite element analysis of the lumbar intervertebral disc—a material sensitivity study Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine. 2002;216:299–314. doi: 10.1243/09544110260216577. [DOI] [PubMed] [Google Scholar]
  15. Fujii R, Sakaura H, Mukai Y, Hosono N, Ishii T, Iwasaki M, Yoshikawa H, Sugamoto K. Kinematics of the lumbar spine in trunk rotation: in vivo three-dimensional analysis using magnetic resonance imaging. Eur Spine J. 2007;16:1867–1874. doi: 10.1007/s00586-007-0373-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Ghezelbash F, Shirazi-Adl A, Arjmand N, El-Ouaaid Z, Plamondon A. Subject-specific biomechanics of trunk: musculoskeletal scaling, internal loads and intradiscal pressure estimation. Biomechanics and modeling in mechanobiology. 2016;15:1699–1712. doi: 10.1007/s10237-016-0792-3. [DOI] [PubMed] [Google Scholar]
  17. Hodges PW, Smeets RJ. Interaction between pain, movement, and physical activity: short-term benefits, long-term consequences, and targets for treatment. The Clinical journal of pain. 2015;31:97–107. doi: 10.1097/AJP.0000000000000098. [DOI] [PubMed] [Google Scholar]
  18. Hughes RE. Effect of optimization criterion on spinal force estimates during asymmetric lifting. J Biomech. 2000;33:225–229. doi: 10.1016/s0021-9290(99)00153-0. [DOI] [PubMed] [Google Scholar]
  19. Iwata T, Miyamoto K, Hioki A, Ohashi M, Inoue N, Shimizu K. In vivo measurement of lumbar foramen during axial loading using a compression device and computed tomography. Clinical Spine Surgery. 2013;26:E177–E182. doi: 10.1097/BSD.0b013e318286f635. [DOI] [PubMed] [Google Scholar]
  20. Keller TS, Harrison DE, Colloca CJ, Harrison DD, Janik TJ. Prediction of osteoporotic spinal deformity. Spine (Phila Pa 1976) 2003;28:455–462. doi: 10.1097/01.BRS.0000048651.92777.30. [DOI] [PubMed] [Google Scholar]
  21. Kjaer P, Leboeuf-Yde C, Korsholm L, Sorensen JS, Bendix T. Magnetic resonance imaging and low back pain in adults: a diagnostic imaging study of 40-year-old men and women. Spine (Phila Pa 1976) 2005;30:1173–1180. doi: 10.1097/01.brs.0000162396.97739.76. [DOI] [PubMed] [Google Scholar]
  22. Lafon Y, Lafage V, Steib JP, Dubousset J, Skalli W. In vivo distribution of spinal intervertebral stiffness based on clinical flexibility tests. Spine (Phila Pa 1976) 2010;35:186–193. doi: 10.1097/BRS.0b013e3181b664b1. [DOI] [PubMed] [Google Scholar]
  23. Marras WS, Davis KG, Ferguson SA, Lucas BR, Gupta P. Spine loading characteristics of patients with low back pain compared with asymptomatic individuals. Spine (Phila Pa 1976) 2001;26:2566–2574. doi: 10.1097/00007632-200112010-00009. [DOI] [PubMed] [Google Scholar]
  24. Muslim K, Bazrgari B, Hendershot B, Toosizadeh N, Nussbaum MA, Madigan ML. Disturbance and recovery of trunk mechanical and neuromuscular behaviors following repeated static trunk flexion: influences of duration and duty cycle on creep-induced effects. Appl Ergon. 2013;44:643–651. doi: 10.1016/j.apergo.2012.12.004. [DOI] [PubMed] [Google Scholar]
  25. O’Reilly MA, Whyne CM. Comparison of computed tomography based parametric and patient-specific finite element models of the healthy and metastatic spine using a mesh-morphing algorithm. Spine (Phila Pa 1976) 2008;33:1876–1881. doi: 10.1097/BRS.0b013e31817d9ce5. [DOI] [PubMed] [Google Scholar]
  26. Ochia RS, Inoue N, Renner SM, Lorenz EP, Lim TH, Andersson GB, An HS. Three-dimensional in vivo measurement of lumbar spine segmental motion. Spine (Phila Pa 1976) 2006;31:2073–2078. doi: 10.1097/01.brs.0000231435.55842.9e. [DOI] [PubMed] [Google Scholar]
  27. Panjabi MM. The stabilizing system of the spine. Part I Function, dysfunction, adaptation, and enhancement. Journal of spinal disorders & techniques. 1992a;5:383–389. doi: 10.1097/00002517-199212000-00001. [DOI] [PubMed] [Google Scholar]
  28. Panjabi MM. The stabilizing system of the spine. Part II Neutral zone and instability hypothesis. Journal of spinal disorders & techniques. 1992b;5:390–397. doi: 10.1097/00002517-199212000-00002. [DOI] [PubMed] [Google Scholar]
  29. Petit Y, Aubin C-É, Labelle H. Patient-specific mechanical properties of a flexible multi-body model of the scoliotic spine. Med Biol Eng Comput. 2004;42:55–60. doi: 10.1007/BF02351011. [DOI] [PubMed] [Google Scholar]
  30. Radebold A, Cholewicki J, Panjabi MM, Patel TC. Muscle response pattern to sudden trunk loading in healthy individuals and in patients with chronic low back pain. Spine (Phila Pa 1976) 2000;25:947–954. doi: 10.1097/00007632-200004150-00009. [DOI] [PubMed] [Google Scholar]
  31. Radebold A, Cholewicki J, Polzhofer GK, Greene HS. Impaired postural control of the lumbar spine is associated with delayed muscle response times in patients with chronic idiopathic low back pain. Spine (Phila Pa 1976) 2001;26:724–730. doi: 10.1097/00007632-200104010-00004. [DOI] [PubMed] [Google Scholar]
  32. Shojaei I, Arjmand N, Bazrgari B. An optimization-based method for prediction of lumbar spine segmental kinematics from the measurements of thorax and pelvic kinematics. International journal for numerical methods in biomedical engineering. 2015;31 doi: 10.1002/cnm.2729. [DOI] [PubMed] [Google Scholar]
  33. Shymon SJ, Yaszay B, Dwek JR, Proudfoot JA, Donohue M, Hargens AR. Altered disc compression in children with idiopathic low back pain: An upright MRI backpack study. Spine (Phila Pa 1976) 2014;39:243. doi: 10.1097/BRS.0000000000000114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Staudenmann D, Roeleveld K, Stegeman DF, Van Dieën JH. Methodological aspects of SEMG recordings for force estimation–a tutorial and review. J Electromyogr Kinesiol. 2010;20:375–387. doi: 10.1016/j.jelekin.2009.08.005. [DOI] [PubMed] [Google Scholar]
  35. Stokes IA, Gardner-Morse M. Lumbar spinal muscle activation synergies predicted by multi-criteria cost function. J Biomech. 2001;34:733–740. doi: 10.1016/s0021-9290(01)00034-3. [DOI] [PubMed] [Google Scholar]
  36. Toosizadeh N, Bazrgari B, Hendershot B, Muslim K, Nussbaum MA, Madigan ML. Disturbance and recovery of trunk mechanical and neuromuscular behaviours following repetitive lifting: influences of flexion angle and lift rate on creep-induced effects. Ergonomics. 2013;56:954–963. doi: 10.1080/00140139.2013.785601. [DOI] [PubMed] [Google Scholar]
  37. Vazirian M, Van Dillen LR, Bazrgari B. Lumbopelvic rhythm in the sagittal plane: A review of the effects of participants and task characteristics. Int Musculoskelet Med. 2016;38:51–58. doi: 10.1080/17536146.2016.1241525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Zanjani-Pour S, Winlove CP, Smith CW, Meakin JR. Image driven subject-specific finite element models of spinal biomechanics. J Biomech. 2016;49:919–925. doi: 10.1016/j.jbiomech.2016.02.025. [DOI] [PubMed] [Google Scholar]

RESOURCES