Rotamer Libraries for the High-Resolution Design of β-Amino Acid Foldamers

SUMMARY

β-Amino acids offer attractive opportunities to develop biologically active peptidomimetics, either employed alone or in conjunction with natural α-amino acids. Owing to their potential for unique conformational preferences that deviate considerably from α-peptide geometries, β-amino acids greatly expand the possible chemistries and physical properties available to polyamide foldamers. Complete in silico support for designing new molecules incorporating non-natural amino acids typically requires representing their side-chain conformations as sets of discrete rotamers for model refinement and sequence optimization. Such rotamer libraries are key components of several state-of-the-art design frameworks. Here we report the development, incorporation in to the Rosetta macromolecular modeling suite, and validation of rotamer libraries for β³-amino acids.

INTRODUCTION

The explicit treatment of the conformation of side-chain atoms distinguishes low- and high-resolution models of protein structure (Renfrew et al., 2014). A common low-resolution approach is to instead approximate the side chain with a single pseudoatom located at the center of mass (Levitt, 1976); such methods require less physically realistic energy functions (Kussell et al., 2002; Feig et al., 2000) but permit faster sampling over a smoother energy landscape (Simons et al., 1999; Bonneau et al., 2001). Explicit (all atom) side-chain conformations may instead be efficiently sampled using a rotameric approximation, where discrete sets of side-chain χ angles are chosen from well-validated conformations that are meant, ideally, to correspond to the conformational energy minima for the side chain in question (Dunbrack, 2002). These sets of side-chain conformations are called ‘‘rotamer libraries.’’ Sampling side-chain conformations from rotamer libraries is especially efficient when there is substantial interdependence between side-chain degrees of freedom, and when only a small fraction of the plausible local minima are near the global minimum. Rotamer sampling requires rotamer libraries from which to sample conformations and recent works have demonstrated that these rotamer libraries should be dependent (to further improve computational efficiency) on backbone conformation (Kothiwale et al., 2015).

Prior development of non-canonical rotamer libraries for use in Rosetta has employed side-chain coordinate scans and energy optimization, either through quantum mechanics software or a molecular mechanics force field, followed by k-means clustering to generate rotamer libraries for non-canonical amino acids (NCAAs) and peptoids (Renfrew et al., 2012). For canonical 03b1-branched amino acids, the Dunbrack and Richardson labs have curated the most widely used rotamer libraries. In both cases, these libraries are derived from a statistical treatment of high-quality experimental structures (Lovell et al., 2000; Hintze et al., 2016; Shapovalov and Dunbrack, 2011; Dunbrack and Karplus, 1993; Bower et al., 1997; Dunbrack, 2002). The Daggett lab has recently taken an alternate approach and employed molecular dynamics simulations (Scouras and Daggett, 2011; Towse et al., 2016). Work on these molecular dynamics-based rotamer libraries points to several limitations to statistics-derived rotamers, and also demonstrates that simulations can model side-chain configurational clusters and minima when statistical methods are not applicable, as in the case of NCAAs (Jacobson et al., 2002; Renfrew et al., 2008).

Both this work and prior work by Kuhlman and Renfrew suggest that there exists a valuable role for rotamer libraries derived from simulations as well as experimental structures. Furthermore, since structural data on non-natural residues is very limited, general rotamer libraries for these moieties must be simulation derived. Peptides entirely composed of or containing β-amino acids (Figure 1) possess useful pharmacological properties, particularly slow proteolytic degradation and a curbed immune response (Cheloha et al., 2015). Such molecules have been used to mimic apolipoprotein (Werder et al., 1999) and as antimicrobial compounds (Raguse et al., 2003); they may target mdm2 (Kritzer et al., 2004), the GLP-1 receptor (Denton et al., 2013), or HIV fusion (Bautista et al., 2009). Detailed efforts to target BCL-2 family proteins (Smith et al., 2013) and GLP-1 (Johnson et al., 2014) have been described.

Figure 1. Schemes of Chemical Species Referred to in the Text.

(A) The α- and β-amino acids are marked with two main-chain torsions that were considered equivalent in prior representations of β-amino acids in Rosetta. While this work only considers rotamer libraries for β³-amino acids, the expansions to the Rosetta code enables representation of any β-amino acid or, indeed, any polyamide, using the same framework.

(B) The 20 β³-amino acid side chains, 18 of which are described with rotamer libraries developed in this study. β³-Glycine and β³-alanine do not possess side-chain degrees of freedom.

(C) The g⁺, g⁻, and a conformations described here, for χ¹: N-Cβ-Cγ-X dihedrals of 60°, −60°, and 180°.

These biological applications are enabled by the conformational preferences of β-amino acids. Their two backbone carbons provide four stereoisomers and six disubstituted isomers, leading to considerable conformational diversity. Helical structures achievable by β³-amino acids have been extensively studied. These include either the 3₁₄ or 14 helix, characterized by a helical axis opposite the α helix, and a 14-atom hydrogen bonding macrocycle, and the 2.5₁₂ or 12 helix, whose handedness is like the α helix (Seebach et al., 1996; Appella et al., 1996). Helical bundles similar to α-helical α-amino acid coiled coils are accessible to 3₁₄helices as well (Qiu et al., 2006), and one has been designed to have catalytic activity (Wang et al., 2014). β-Amino acids also form local structures that are ideal for mimicking parallel (Seebach et al., 1999, 2002; Langenhan et al., 2003) or antiparallel sheets (Seebach and Gardiner, 2008; Chung et al., 2000; Gademann and Seebach, 1999; Cheng et al., 2001). Such extended conformations may be adopted by cyclic β-peptide oligomers, but steric effects from multiple substitutions can provide a similar conformational bias. For example, similar extended conformations are favored by trans-^2,3-disubstituted residues by encouraging an anti θ. In contrast, ^2,3-disubstituted cyclic sidechains stabilize gauche θ conformers that favor turns and helices (Cheng et al., 2001), while achiral β^2,2- or β^3,3-disubstituted residues stabilize reverse turns (Seebach et al., 1998).

Although β-amino acids can form diverse conformations on their own, the accessible chemical space may be expanded further by using them in chimeric peptides, i.e., in combination with α-amino acids. Replacing an α-amino acid with a β-amino acid on both strands of a β hairpin extends the length of the hairpin by one methylene unit but maintains the hydrogen bond network and so only tertiary contacts must adjust to accommodate the perturbation (Lengyel et al., 2011; Haase et al., 2012).

Chimeric α/β-peptides can adopt helical conformations (Hayen et al., 2004; Schmitt et al., 2004, 2006; Sadowsky et al., 2005; Price et al., 2007). Optimized compositions ultimately involved organizing all the β residues on a single helical face by employing β³-amino acids every third or fourth position (Horne et al., 2007). Due to the high therapeutic value of mimicking an α helix (Modell et al., 2016; Moon and Lim, 2015; Cromm et al., 2015) and the conceptual simplicity of homo-oligomers, peptides composed of or containing β-amino acids have been applied primarily as α helix mimetics (Johnson and Gellman, 2013). Consequently, β-amino acid rotamer libraries have been developed only for all-β conformations that form helical folds. There are high-resolution rotamer libraries for β³- and β²-amino acids available for individual backbone conformations: those of 3₁₄ and 3₁₂ helices (Shandler et al., 2010). Such rotamer libraries, while valuable, are not suited to a general peptidomimetic context in two ways. First, they do not cover backbone conformations that are entirely favorable for β-amino acids, but do not form homopolymer secondary structures, and so they are limited in application. Second, rotamer libraries fit to the rotamers assumed by an entire secondary structure element do not necessarily apply to other polymeric contexts. For example, the dihedrals assumed by a β-amino acid in a 3₁₄ helix are only 20° from those assumed by a β-amino acid in an α3β helix, but the α3β helix has an opposite dipole moment and each β-residue is flanked by two α-residues. The resulting bias on rotamer libraries can be substantial; long-range effects from adjacent helical turns are known to bias PDB-based rotamer libraries for at least valine, leucine, and isoleucine (Renfrew et al., 2008). As a concrete example, the (a, g⁺) rotamer common in α-helical α-leucine residues creates no clashes in the all-β 3₁₄ helix depicted in Figure 2, but is incompatible with a common conformation of the chimeric α3β helix. Thus, to apply to a general peptidomimetic context, rotamer libraries must be constructed independent of non-local influences. These prior rotamer libraries have not been available for use in macromolecular modeling programs such as Rosetta, which has long assumed that rotamer libraries were dependent only on two main-chain dihedrals (Watkins and Arora, 2016). Prior work that attempted to model β³-peptides in Rosetta instead employed a limiting approximation: that the first two main-chain torsions of a β³-amino acid could be treated analogously to the φ and ψ torsions of an α-amino acid (Figure 1) (Molski et al., 2013). Backbone dihedral angles typical for a 3₁₄ helix such as (−140°, 60°, −120°) are described by a high-energy of Ramachandran space such as (−140°, 60°) and as a result are drastically undersampled.

Figure 2. Rotamer Steric Compatibility Depends Not Just on the Local Backbone Dihedrals but on the Entire Polymer Context.

The (a, g⁺) rotamer imposed on every fourth residue (a leucine) in the 3₁₄ helix (A) and the α3β helix (B). Molprobity clash analysis reveals that the 3₁₄ helix is free of clashes (C), while the α3β helix (D) has a clash score of 114, far worse, in 12 residues, than low-quality electron microscopy structures of hundreds of residues. The distinct clash, shown in red dots, is with the i + 3 alanine methyl group.

Here, we have developed and incorporated into Rosetta backbone-dependent rotamer libraries for β³-amino acids (Figure 3). Furthermore, we generalized Rosetta’s treatment of rotamers and rotamer libraries such that it can create and use rotamer libraries with any number of backbone dihedral angles. We validated this approach both computationally and experimentally. Our results are in good agreement with quantum mechanical calculations on several side chains, which demonstrate that we recover the rotamer wells and their approximate populations. Our results also recover the rotamers found in high-quality crystal structures in the PDB. Furthermore, use of these rotamer libraries in conjunction with Rosetta recovers trends in experimental binding affinity in experiments with β-peptide helices. We anticipate that this rotamer library system will constitute an important step toward the direct, accurate rotamer-based design of structures containing arbitrary oligomers in Rosetta.

Figure 3. The Process by Which Rotamer Libraries Are Constructed.

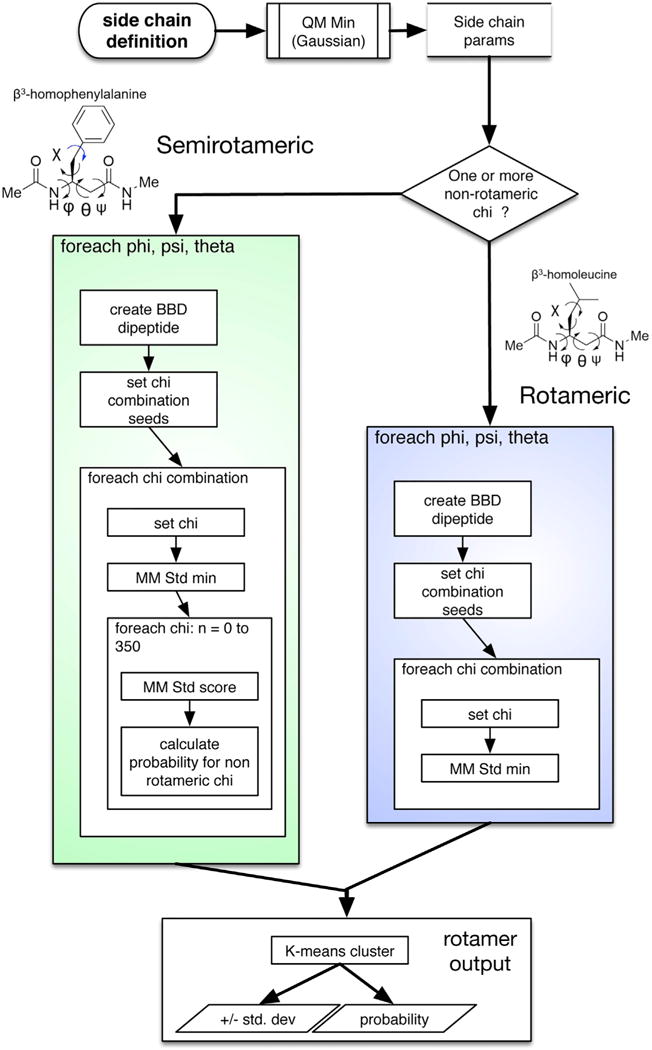
To construct rotamer libraries for β-amino acids, we create parameters for the residue by geometry optimization and charge fitting by quantum mechanics, as described previously. We seed backbone conformations and, for each one, we create hundreds or thousands of χ-combination seed conformations (omitting the final non-rotameric χ for semi rotameric amino acids). We minimize each χ combination (and, for semirotameric residues, obtain a probability distribution for the terminal χ). Finally, we cluster, obtain an SD in each dimension for each resulting rotamer well, and convert the minimized energies to probabilities via the Boltzmann distribution.

RESULTS

β-Amino Acids Exhibit Diverse Backbone Conformations

To quantify the need for a general, fully backbone-dependent rotamer library for β³-amino acids, we explored the backbone conformations that they can adopt. Rather than setting an energetic threshold and exploring candidate energy functions, we simply sought out conformations that lacked intramolecular clashes. Table 1 compares the volume of backbone dihedral space that each β side chain may adopt without clashes versus its α-amino acid equivalent. The volume within 40° of the 3₁₄ helix or α3β helix dihedral angles is only 1.1% of the total backbone dihedral space of a β³-amino acid, illustrating that β³-amino acids may adopt far more than the two homopolymer conformations that have received most attention. The generous standard of clash-free conformations is useful to assess the intrinsic flexiblity of β-amino acids, in contrast to homopolymer-preferred conformations, which might require regular, repeating stabilizing interactions. These conformations are important to multiple β-amino acid use cases, such as the design of substituted macrocycles, where the cyclic constraint enforces the local conformation and there is no requirement for regularity. In addition to the well-studied helical conformations, in the process of this investigation we found a range of extended conformations available to β-amino acids, which have not been previously investigated in any systematic way. Such extended conformations possess φ between −130° and −180°, with θ and ψ positive and summing to 30° −50° less than |φ|.

Table 1.

Proportion of Backbone Dihedral Space (‘‘Ramachandran Space’’ for α-amino Acids) that Does Not Result in Any Clashes

AA	α Torsion (%)	β3 Torsion (%)	AA	α Torsion (%)	β3 Torsion (%)
ALA	19.9	21.5	MET	18.5	22.7
CYS	19.1	28.9	ASN	18.4	23.1
ASP	18.5	25.3	PROa	8.7	17.7
GLU	18.7	22.4	GLN	18.3	22.5
PHE	18.0	21.4	ARG	18.0	19.1
GLY	46.6	47.2	SER	19.3	30.2
HIS	18.7	24.3	THR	17.1	24.0
ILE	12.3	13.7	VAL	11.8	18.9
LYS	14.0	19.4	TRP	18.2	20.3
LEU	16.2	19.6	TYR	18.2	21.4

A clash is defined by atoms closer than 60% of their summed van der Waals radii.

^aFor proline, only dihedral space that kept the pyrrolidine ring closed was considered.

The Molecular Mechanics Energy Function Reproduces the Energy Wells of Quantum Mechanics Studies

The molecular mechanics scoring function employed in Rosetta, which we used to generate these rotamer libraries, reproduces the minima identified by quantum mechanical calculations. We evaluated four common β³-amino acid side chains, β³W, β³L, β³I, and β³S, restrained to two backbone conformations: a helical conformation reminiscent of both the 3₁₄ helix (−140°, 60°, −120°), and the α3β helix and an extended conformation that would form a pleated sheet (−140°, 75°, 65°). We conducted constrained geometry optimization followed by single-point energy calculation at the B3LYP level of theory on side-chain conformations sampled every 10°. The resulting energy surface as a function of χ¹ and χ² compares favorably to the molecular mechanics-derived energy surfaces for each residue type, showing that we capture the same rotamers as the considerably more computationally expensive method (Figure 4). To quantify the accuracy with which the two heatmaps agree, we computed the Bhattacharyya distance for each residue and backbone conformation (Table 2; STAR Methods). The results verify the significant similarity of the energy landscapes, improving confidence in our results.

Figure 4. Side-Chain Probability Distributions as Computed by Quantum Mechanics and Molecular Mechanics.

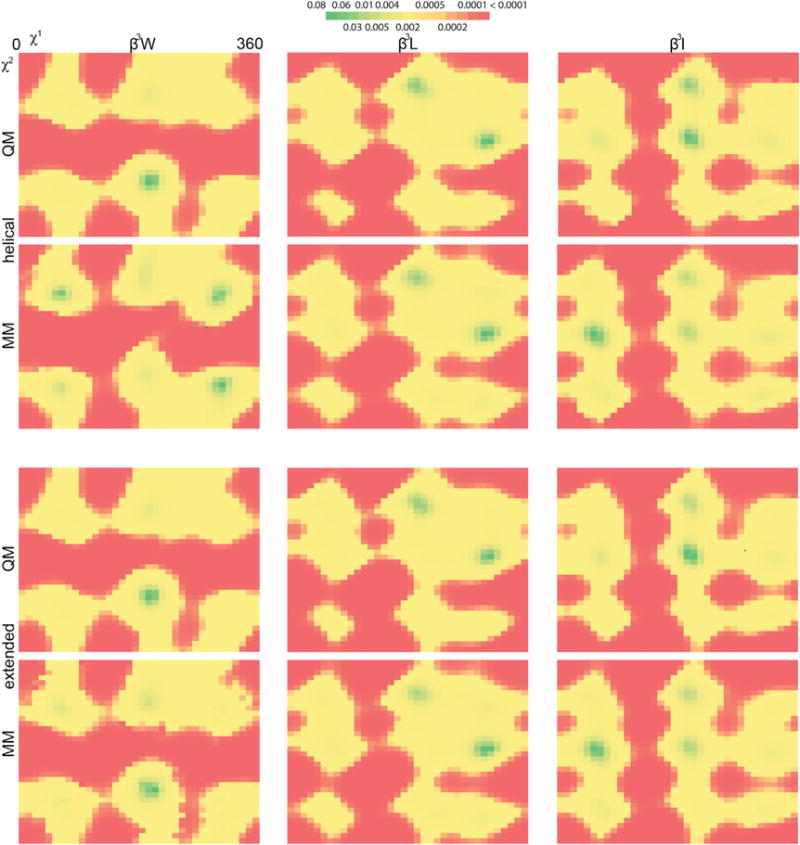
Two dimensional probability distributions for three residues (β³I, β³L, and β³W; columns) were determined by quantum mechanics (B3LYP optimization followed by Hartree-Fock energy; first and third row) and molecular mechanics (the energy function employed in the rotamer library protocol; second and fourth row). These distributions were generated for two distinct backbone conformations: one for a conformation common to the 3₁₄ and α3β helix (first and second rows) and one for an extended conformation (third and fourth rows). QM, quantum mechanical; MM, molecular mechanics.

Table 2.

The Bhattacharyya Distance for Each of Eight Pairs of Probability Distributions, Representing the Side-Chain Conformational Preferences of Four β³-Amino Acids in Two Conformations, Evaluated Either at the Quantum Mechanical or Molecular Mechanics Level of Theory

AA	QM-MM Distance
	Helical	Extended
β3I	0.155	0.163
β3L	0.048	0.069
β3S	0.237	0.233
β3W	0.261	0.074

QM, quantum mechanical; MM, molecular mechanics.

The New β³-Amino Acid Rotamer Libraries Reproduce Observed PDB Rotamers

A considerable number of structures containing β³-amino acids already exist in the PDB, although all but one is in a mixed α/βor 3₁₄ helix. To gauge the performance of these rotamer libraries against experimental data, we built the same rotamer set as employed in Rosetta’s packing algorithm, by performing tricubic interpolation between adjacent backbone dihedral bins (i.e., the eight vertices of the cube of backbone torsion space grid points for which explicit rotamers samples appear in the library). The resulting rotamer sets possess a rotamer within 15.5° of the experimental rotamer or better, with many closer than 10° (Figure 5).

Figure 5. Rotamer Libraries Accurately Capture Experimentally Determined Rotamers.

root-mean-square error in degrees for the nearest rotamer across all resolved β³-amino acid samples in the PDB. The number of examples of that β-amino acid are above each bar. No data exist on β³-homocysteine or β³-homohistidine, and rotamer libraries do not apply to β³-homoalanine or β³-homoglycine. Errors are comparable with those found in prior work on fitting peptoid and non-canonical amino acid rotamer libraries (Renfrew et al., 2012, 2014) and to the effective uncertainty of Dunbrack rotamer libraries (see the STAR Methods).

This performance in native rotamer recovery is comparable with the performance of the Dunbrack libraries on the equivalent α-amino acid side chain (see the STAR Methods; especially considering the narrow scope of the test data only one region of backbone torsion space) against the general model employed here, we find this result very encouraging. In the process of assessing the errors in PDB rotamer recovery, we found that several of the native rotamers we had been treating as ‘‘gold standards’’ inhabited structurally improbable conformations. Since they were not forming tightly packed interactions in a hydrophobic core, nor with a binding partner, nor with a crystal contact, we suspected that they might constitute structural errors. We examined several representative structures that possessed high-energy native rotamers and built maps from the publicly available structure factors; in doing so, we found that many β-amino acid residues with very little electron density supporting any particular side-chain conformation; for example, we highlight four examples from PDB: 3G7A and 4BPI in Figure 6, but others are found in PDB: 4KGR, 3O42, and more. We strongly suspect that many of the deviations observed here are due to rotamers that were built poorly in the absence of electron density constraints; these experimental samples are thus a poor reflection of physical ground truth. Since the total number of β-amino acid rotamers in the PDB is so small, we cannot perform this analysis on only those rotamers with sufficiently high-quality structural data supporting their conformations. Rather, we propose that, with the recent development of new structural refinement tools within Rosetta (Park et al., 2015; Chou et al., 2013), these and other β-amino acid containing structures may be further refined, particularly now that there exist general, backbone-dependent rotamer libraries for the task.

Figure 6. Many Crystal Structures Possess Poorly Resolved Density for β-Amino Acid Residues.

Many native side chains ‘‘missed’’ by these rotamer libraries are in very unlikely conformations in the crystal structure. Due to the challenges of fitting atomic coordinates to electron density, and due to the additional challenge of phasing diffraction data for novel heteropolymers, structural data might be particularly uninformative for these molecules. Indeed, maps frequently provided minimal density near β-amino acid residues, as in the four examples above (PDB: 3G7A and 4BPI).

The New Rotamer Libraries Improve Modeling of 3₁₄ Helix Ligands

Encouraged by the agreement with higher levels of theory and the recovery of native rotamers, we undertook a retroactive binding affinity prediction. We rewrote a substantial part of Rosetta’s core libraries so that rotamer libraries might possess any number of dihedral angles, and so that these rotamer libraries may be employed in the packer, Rosetta’s algorithm for concurrent side-chain optimization. To test the ability of this new code and these new libraries to deliver scientifically useful results, we revisited an effort to design improved 3₁₄ helix p53 mimetics from the Schepartz lab. Their dataset included computational predictions via Monte Carlo free-energy perturbation (Zwanzig, 1954) (MC/ FEP) in the OPLS-AA force field (Jorgensen and Tirado-Rives, 2005), as well as experimentally measured binding energies (Michel et al., 2009). We sought to reproduce the trend in point mutation energies (ΔΔG) versus the base sequence. We compared the original MC/FEP result (R² = 0.79) to a simple, standard “relaxation” simulation carried out in Rosetta, using either the new or old rotamer libraries. Our rotamer libraries deliver comparable results (R² = 0.80), without requiring any fit parameters. In contrast, with the prior rotamer libraries, which possessed the erroneous α-peptide-like dependence on only φ and θ, performed quite poorly in comparison (R² = 0.40) (Figure 7). This improvement suggests that a dependence on all three backbone angles is likely necessary for useful binding simulations.

Figure 7. The Fully Backbone-Dependent Rotamer Libraries Perform Considerably Better than the Old Model in Real Applications.

We compared experimental ΔΔ G values (kcal/mol) for mutations in a series of 3₁₄ helical p53 mimetics, which were assayed against the proteins mdm2 and mdm4, to computational predictions. The original predictions made by Schepartz (A) provided a standard of comparison; our Rosetta protocol performed poorly with the old (B) rotamer libraries but quite well using the rotamer libraries developed in this work (C).

Relative Rotamer Prevalence across β³-Leucine Backbone Cross-Sections

To visualize three-dimensional rotamer libraries in a useful way, we suggest plotting rotamer probability against two of the dependent main-chain dihedral angles, holding the third fixed. Three of these plots can be analyzed in combination to understand the neighborhood surrounding a backbone configuration of interest (Figure S1). To make comparable plots, one may employ the following Mathematica code:

1. anti_gaucheplus = Import[‘‘B3L_a_gp.txt’’, ‘‘Table’’];

2. gaucheminus_anti = Import[‘‘B3L_gm_a.txt’’, ‘‘Table’’];

3. interpolated_a_gp = Interpolation[anti_gaucheplus];

4. interpolated_gm_a = Interpolation[gaucheminus_anti];

5. Plot3D[{interpolated_a_gp[phi, psi], interpolated_gm_a[phi, psi]}, {phi, −180, 180}, {psi, −180, 180}, AxesLabel –> {‘‘phi’’, ‘‘psi’’}, AspectRatio –> 1, Ticks –> {{−180, −120, −60, 0, 60, 120, 180}, {−180, −120, −60, 0, 60, 120, 180}, {0.2, 0.4, 0.6, 0.8, 1.0}}]

The above code imports text files containing the probability of the (a, g⁺) and (g⁻, a) rotamers, respectively, as a function of φ and ψ, holding θ fixed at −60°. Those three-column text files are imported as tables (lines 1 and 2), then interpolated as functions of two variables (lines 3 and 4), then finally plotted over the full range of φ and ψ.

Detailed Rotamer Recovery for a Structure of Interest

To provide some context about the methods employed, we provide a worked example of rotamer recovery for two particular PDB structures: PDB: 4BPI, a complex between a Puma BH3 α/β-peptide mimetic with Mcl-1, and PDB: 3G7A, an HIV gp41 bundle with an α/β-peptide mimic of the CHR domain. Neither was an example of particularly good performance; rather, both illustrate the challenges of working with relatively sparse native structural data.

The former structure contains four β³ residues: β³D, β³R, β³Q, and β³E; while the latter contains two β³-homoglutamate residues. First, we had to revise atom and residue names in Rosetta to match Rosetta’s nomenclature, to make sure that no atoms were wrongly detected as missing, which would have resulted in coordinates being built from ideal. In fact, we discard the β³E residue from PDB: 4BPI on these grounds, as it is involved in binding a cadmium atom in the native structure, and one of the β³E residues from PDB: 3G7A, as its Cγ and Oδ atoms are missing. Second, we built rotamer sets for each residue. The closest interpolated rotamers to each experimental rotamer are given in Table S1.

Native conformations so far from the theoretical sp³-sp³ optimum, especially in mostly surface-exposed positions, seem surprising. Reproducing them perfectly would be an inappropriate burden for a rotamer library; this library’s attempts to do so largely hinge on very low-probability rotamers, which would likely be rebuilt in most simulations. Indeed, their distance from optima suggests that they could reflect structural errors that remain un-corrected simply because of the limited knowledge surrounding the preferred side-chain conformations of β-amino acids. The B factors for each β³ residue in these structures are quite high, from 45 to 70. Examining maps derived from the deposited structure factors, experimental evidence for these particular conformations seems either weak or absent entirely (Figure 6). Ironically, more side-chain electron density is present for the lower-resolution structure (PDB: 3G7A, at 2.8 Å, at least able to secure the relative position of the α and γ carbon atoms) than for the higher-resolution structure (PDB: 4BPI, at 1.98 Å).

Distinguishing Features of β-Amino Acid Rotamer Libraries versus Corresponding α-Amino Acid Rotamer Libraries

More than any other feature, rotamers for α- and β-amino acids are distinguished by steric clashes. As described throughout, many common rotamers compatible with an α-amino acid backbone are sterically incompatible with any β-amino acid backbone that shares φ and θ. A more minor influence is the absence of particular attractive interactions. For example, α-serine is well-known to form a hydrogen bond between its γ-H and its carbonyl oxygen in some backbone conformations, while that feature is largely absent in β³-serine: the six-membered hydrogen bonding ‘‘macrocycle’’ is replaced with a much less-favored seven-membered ‘‘ring.’’ In principle, β²-serine rotamer libraries would retain this backbone-dependent bias.

DISCUSSION

We developed and tested a model of backbone-dependent libraries of β-amino acid side-chain conformations. This model showed excellent agreement to simulations conducted at a higher level of theory as well as accurate recovery of experimental data, especially compared with previous models that borrowed α-amino acid conformations, without fitting additional scoring function parameters. We incorporated new code and new residue parameters into the Rosetta software suite. Integration with Rosetta enables our contributions to open up new possibilities in design, modeling, and structure determination protocols. Furthermore, users of the software may parameterize new β-amino acid side chains of interest and obtain their rotamer libraries. We anticipate an eventual need for higher-resolution rotamer libraries (with more backbone bins, especially in highly populated regions). Doing so demands particular attention for β-amino acids because their backbone-dependent libraries are dramatically larger, in both memory and on disk. To this end, superior β-amino acid rotamer libraries will require more sophisticated interpolation methods. Further efforts to create a framework suited for general heteropolymer modeling and design will include scoring function optimization to include alternative solvation and electrostatics models (Haberthur and Caflisch, 2008; Bazzoli et al., 2015), reference energies for design, and better methods for modeling hydrogen and halogen bonds. Re-refinement of structures containing β-amino acids will provide an experimental basis against which that scoring function might be optimized. Taken together, these efforts will create the groundwork for designing arbitrary polymers of α- and β-amino acids.

STAR★METHODS

Detailed methods are provided in the online version of this paper and include the following:

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
Gaussian 09 Revision D.01	Frisch et al., 2009	https://gaussian.com
Open Babel	O’Boyle et al., 2011	https://openbabel.org
PyMOL Molecular Graphics System, Version 1.8	Schrödinger, LLC	https://pymol.org
Rosetta	Leaver-Fay et al., 2011	https://rosettacommons.org

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Rich Bonneau (rb133@nyu.edu).

METHOD DETAILS

β-peptide Rotamer Library Creation

β-peptide rotamer libraries were created using the MakeRotLib protocol in Rosetta (Figure 3). For each backbone bin (from −150° to 180°, i.e. 12³ = 1728 combinations), acetylated and methylamidated amino acid structures were initialized with varied side chain conformations. Residues with one χ(β³Ser, β³Thr, β³Val) were sampled every degree; residues with two χ were sampled every 10° (1296 samples); residues with three (β³Met; β³Glu, β³Gln) every 15° (13824 samples) and four (β³Arg, β³Lys) χ angles every 30° (20736 samples).

The resulting conformations were minimized, holding all backbone bond geometry fixed but allowing all sidechain geometry, including bond lengths and angles, to vary, using a linear, monotone mini-mizer. The force field employed was the pre-existing mm_std energy function (Renfrew et al., 2012) augmented with previously developed terms to score bond lengths and angles. All bonded andnonbonded parameters employed in the mm_std energy function are derived from CHARMM; like in the standard Rosetta energy functions employed for canonical amino acids, mm_std uses the Lazaridis-Karplus solvation model (Lazaridis and Karplus, 1999). We clustered the resulting conformations using k-means clustering, with initial cluster centroids chosen to correspond to physical intuition and to the choices made by the 2010 Dunbrack rotamer libraries where possible (Shapovalov and Dunbrack, 2011) Specifically, every rotameric χ was given a centroid initialized to g^-, a, or g⁺, while nonrotameric χ angles had centroids every 30°. (Symmetric nonrotameric χ angles such as aspartate’s second χ had six wells, 0° through 150°, while asymmetric nonrotameric χ angles such as asparagine’s second χ had twelve.) For each cluster, the energies for the rotamer sample closest to the cluster center are converted to Boltzmann factors and thereby to probabilities.

To provide complete support for scoring and sampling, each rotamer well is approximated as a Gaussian, as in the Dunbrack rotamer libraries. The dimensions of the cluster that results from optimizing these conformations are quite small and not particularly physically meaningful. Rather, we manually search around each rotamer center to find the angle deviation necessary to increase the conformational energy by 0.5 Rosetta energy units (Renfrew et al., 2012), which produces physically realistic rotamer wells with standard deviations on the same scale as the Dunbrack libraries. We also implemented functionality to provide a continuous treatment of terminal nonrotameric χ angles, as is possible in the 2010 Dunbrack libraries, thus permitting a smoother surface for energy minimization. In such rotamer libraries, created for β³D, β³E, β³F, β³H, β³N, β³Q, β³W, and β³Y, only the rotameric χ angles are clustered, while the final χ is sampled at 36 evenly spaced positions (5° increments for symmetric χ; 10° increments otherwise) and the energies in question are converted to probabilities similarly. These rotamer libraries may be visualized to evaluate how well the major rotamers preferred at familiar backbone conformations correspond to physical intuition (Supplemental Information, Figure S1).

Evaluation of Clash-Free Conformations

We sampled each amino acid at 5° intervals for every backbone dihedral angle. We minimized the sidechain degrees of freedom to ensure that the sidechain was not making any unavoidable clashes (For a fair comparison to residues with one or more χ angles, we provided alanine and β³A with a ‘fake’ χ to model the rotation of their methyl sidechains.) Then, we evaluated the distance between every pair of atoms and determined whether they were making a severe clash by comparing to 0.6 times the sum of the two atoms’ van der Waals radii. For proline, we also disqualified conformations whose five-membered rings had been broken. Thus, the value for α-amino acids represents a percentage, area-over-area, while for β-amino acids, the corresponding value is a percentage, volume-over-volume.

Structure Optimization via Gaussian and Comparison to the Molecular Mechanics Scoring Function

Using Gaussian09 revision D, we initialized acetylated and N-methylamidated structures of β³Trp, β³Leu, β³Ile, and β³Ser to two distinct and structurally valuable backbone conformations: (−140°, 60°, −120°), intended to be near stable conformations for the 3₁₄ helix and the chimeric α3β-helix, and (65°, 75°, −140°), an extended state that can form pleated sheets like anα-amino acid forms β-sheets. We initialized a 10° grid of side chain conformations (i.e. 1296 points per two-χ residue; 36 points for β³Ser) and carried out energy optimization at the HF/6-311+G(2d,p) level of theory, followed by single point energy calculation at B3LYP/6-311+G(2d,p). Subsequently, we used OpenBabel to generate PDB format files from the resulting Gaussian output and scored each structure using the molecular mechanics scoring function within Rosetta. To analyze the similarity of the probability distributions, we evaluated the Bhattacharyya distance (see STAR Methods). Some deviations are, in fact, desirable and expected, as gas-phase quantum mechanics ought to deviate from molecular mechanics models that include solvation terms. The worst fit is for the helical conformation of β³Trp, where the MM scoring function appears to favor a g^- χ¹ dihedral. This result may partially result from Rosetta’s smaller van der Waals radii for hydrogen, as the g^- rotamer may feature some minor clashes. The next worst fit is for β³Ser, whose affinity for the g^- rotamer in both backbone conformations relies in part upon a seven-membered intramolecular hydrogen bond that mm_std does not score and that the QM method may over-value due to the vacuum state. Importantly, even in the cases where there is disagreement, the best QM rotamers are always represented in the MM rotamer set and therefore will be sampled in simulations.

Comparison to PDB Rotamers

For each crystal structure rotamer, we apply Rosetta’s tricubic interpolation to the nearest back-bone bins to obtain an interpolated set of rotamers for the exact backbone dihedrals from the crystal structure. We measure the minimum RMS distance in degrees from a rotamer built for that position to the rotamer in the crystal structure and average that value for each residue type. Figures from PDB structures are ray-traced in PyMOL. Electron density is generated from structure factors using phenix.maps or downloaded from the Uppsala Electron Density Server and visualized in PyMOL using the isomesh command at two standard deviations within 1.6Å of atoms.

Rosetta Simulations to Predict Binding Affinity

We conducted simulations of the 3₁₄ helices studied experimentally beginning with the same crystal structures of mdm2 and mdm4 as employed in the original computational study (PDB codes 2GV2 and 2Z5T, respectively). We generated point mutant structures of each 3₁₄ helix ligand by mutating a position then repacking and minimizing an 8Å shell around the mutated residue. We conducted a simple relaxation simulation, generating 1000 structures, to diversify the ensemble of β-peptide/protein complex structures, followed by interface scoring using the dGcross score term computed by the InterfaceAnalyzerMover. Separate sets of simulations were conducted with the old rotamer libraries (the canonicalα-amino acid rotamers applied to the first two mainchain torsions) and with those developed in this work.

QUANTIFICATION AND STATISTICAL ANALYSIS

Comparing MM- and QM-derived Probability Distributions by Evaluating the Bhattacharyya Distance

The Bhattacharyya distance

$$D_B\left(p,q\right)=-\ln \left({\displaystyle \sum _{x\in X}\sqrt{p\left(x\right)q\left(x\right)}}\right)$$

where p and q are two probability distributions and X is their domain (Bhattacharyya, 1943) is a generalization of the Mahalanobis distance that does not assume equal standard deviations; its range is [0, ∞), where zero reflects identical distributions and where entirely distinct distributions (two different delta functions, for example) have unbounded distance. Values from 0.04 to 0.27, as observed for these rotamer libraries, represent extremely similar distributions.

Comparing the Accuracy of These Rotamer Libraries to Dunbrack Rotamer Libraries for the α-amino Acids

It is challenging to directly compare two rotamer library models of different methodology and generality. This challenge, however, does not preclude the assessment of the fits of Figure 5. The Dunbrack libraries model rotamer wells as Gaussians with some standard deviation. We can employ these standard deviations to provide a natural scale for our observed average RMS errors. Let us assume that a Dunbrack rotamer is exactly centered on the ‘‘true’’ rotamer centroid for each χ angle. A typical standard deviation for such a Gaussian rotamer well is 8°. The expected RMS deviation from that rotamer well for one to four χ angles is 6.4°, 10°, 12.8°, and 15.1°. The standard deviation for this RMS deviation statistic is around 5° in each case. Thus, the performance we observe reflects the same underlying variability of protein and peptide structures that the Dunbrack libraries do.

Please describe here all of the statistical analysis and software used. We ask authors to indicate in this section where all of the statistical details of experiments can be found (e.g., in the figure legends, figures, Results, etc.), including the statistical tests used, exact value of n, what n represents (e.g., number of animals, number of cells, etc.), definition of center, and dispersion and precision measures (e.g., mean, median, SD, SEM, confidence intervals). Also please summarize in this section how significance was defined, the statistical methods used to determine strategies for randomization and/or stratification, sample size estimation, and inclusion and exclusion of any data or subjects, as well as any methods used to determine whether the data met assumptions of the statistical approach.

DATA AND SOFTWARE AVAILABILITY

Applications to create amino acid rotamer parameter files and rotamer libraries, as well as the resulting rotamer libraries, are distributed as part of the Rosetta software suite, which is free for academic use (https://rosettacommons.org).

The rotamer libraries generated are available as supplemental data (Data S1).

Highlights.

• Constructed rotamer libraries for β-amino acids

• Validated against quantum mechanical calculations

• Good reproduction of experimental side-chain conformations

• Compatible with the Rosetta software suite