MULTI-RESOLUTION GEOMETRIC MODELING OF THE MITRAL HEART VALVE LEAFLETS

Abstract

An essential element of the heart function, the mitral valve (MV) ensures proper directional blood flow between the left heart chambers. Over the past two decades, computational simulations have made marked advancements towards providing powerful predictive tools to better understand valvular function and improve treatments for MV disease. However, challenges remain in the development of robust means for the quantification and representation of MV leaflet geometry. In this study, we present a novel modeling pipeline to quantitatively characterize and represent MV leaflet surface geometry. Our methodology utilized a two-part additive decomposition of the MV geometric features to decouple the macro-level general leaflet shape descriptors from the leaflet fine-scale features. First, the general shapes of five ovine MV leaflets were modeled using superquadric surfaces. Second, the finer-scale geometric details were captured, quantified, and reconstructed via a 2D Fourier analysis with an additional sparsity constraint. This spectral approach allowed us to easily control the level of geometric details in the reconstructed geometry. The results revealed that our methodology provided a robust and accurate approach to develop MV-specific models with an adjustable level of spatial resolution and geometric detail. Such fully customizable models provide the necessary means to perform computational simulations of the MV at a range of geometric accuracies in order to identify the level of complexity required to achieve predictive MV simulations.

1. Introduction

1.1 Clinical context

Valvular heart disease is becoming a cardiac epidemic in developed nations with a current prevalence rate of 2.5% (Iung and Vahanian 2014) and worsening due to an aging population (d’Arcy et al. 2011). In particular, mitral valve regurgitation (MVR) (Thom et al. 2006) can cause serious complications like heart failure (Deja et al. 2012), stroke (Enriquez-Sarano et al. 2009), and in severe cases death (Enriquez-Sarano and Sundt 2010). MVR occurs when blood leaks back to the left atrium during ventricular contraction due to the incomplete closure of the mitral valve (MV). Interestingly, all forms of MVR are characterized by morphological alterations in the normal configuration of the MV apparatus (Tibayan et al. 2003). Thus, surgical procedures to treat MVR seek to restore the MV to a functional geometric state (Fedak et al. 2008). Over the past few decades, there has been substantial debate on whether MV valve repair is the most effective strategy to treat MVR (Braunberger et al. 2001; Kheradvar et al. 2015). Originally, early outcome assessments predicted excellent long-term results for the Carpentier’s technique to repair regurgitant MVs by the mitral annuloplasty technique (David et al. 2013). In this procedure, a prosthetic ring is surgically sutured on the MV annulus to shrink the dilated atrioventricular orifice, so that the leaflet coaptation can completely cover the valve opening (Rausch et al. 2012). While some recent studies strongly suggest that the MV repair is the “gold standard” treatment strategy (Kaneko and Cohn 2014; Rankin et al. 2013), other follow-up investigations have revealed an undesirable high rate of failure and regurgitation recurrence for repaired MVs (Acker et al. 2014). Furthermore, there remains an uncertainty over the optimal shape of annuloplasty rings for successful repair of regurgitant valves (Bothe et al. 2013). Thus, in spite of the ever-increasing rate of MVR incidence, the available treatment options still need to be greatly improved.

1.2 The role of computational biomechanics

In silico models of the MV have proven to provide powerful prediction tools to build insight into the valvular physiology (Lim et al. 2005), design medical prosthetics (Chandran 2010), and optimize surgical treatments (Choi et al. 2014). In a pioneering study, Kunzelman and colleagues (Kunzelman et al. 1993) developed the first 3D finite element (FE) model of the MV apparatus and performed numerical simulations of the MV function. Subsequently, several research studies focused on improving heart valve computational simulations by enhancing geometric models (Pouch et al. 2014), constitutive models (Rego and Sacks 2017; Zhang et al. 2015), and simulation frameworks (Fan and Sacks 2014; Sun and Sacks 2005; Weinberg and Kaazempur-Mofrad 2006). However, while valvular geometry and structure remain vital to mechanical simulations, acquiring accurate information about the MV shape and physical properties is by no means trivial. This is a direct result of the fact that the MV apparatus has a complex anatomic structure (McCarthy et al. 2010), comprised of various constituents—leaflets, annulus, chordae tendineae, and papillary muscles—that are dissimilar in terms of both shape and scale (Figure 1). These components are characterized by multi-layered internal structures (Millington-Sanders et al. 1998; Rausch et al. 2013) and heterogeneous fiber architectures (Cochran et al. 1991) which play a significant role in the valvular mechanical behavior (Ayoub et al. 2016). Moreover, all these properties are known to change in response to both pathological (e.g. myocardial infarction, myxomatous disease) and non-pathological (e.g. exercise, pregnancy) alterations to cardiac function (Rego et al. 2016). Consequently, developing anatomically accurate models of the MV apparatus to faithfully predict valvular function remains a hefty but important challenge. Moreover, to ultimately utilize computational simulations in clinical applications, the geometric fidelity and structural precision of the models used must be substantially improved, such as to increase predictive power.

Figure 1.

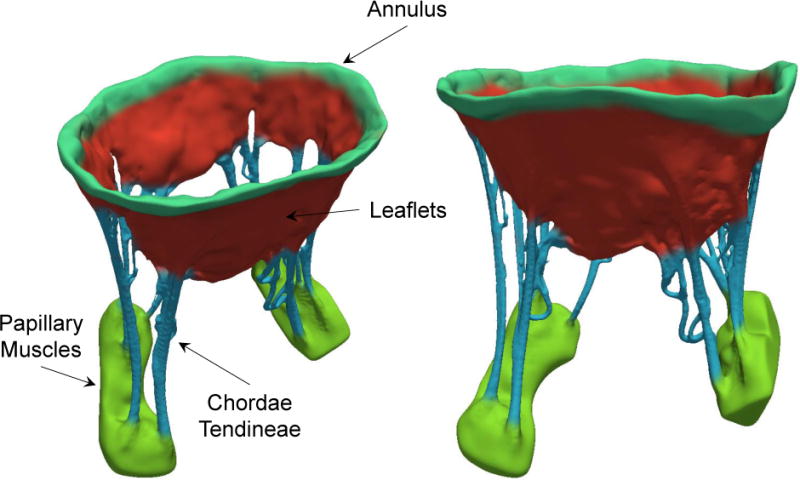
schematic representation of the mitral heart valve from two views. As illustrated, MV constituents are different shape and scale

1.3 Image-based modeling

Earlier MV modeling studies relied on the extensive idealizations of the MV geometry based on ex vivo measurements (Maisano et al. 2005). Recently, more realistic models have been developed using various imaging modalities such as ultrasound (US) (Skallerud et al. 2011), magnetic resonance (MR) (Stevanella et al. 2011), and computed tomography (CT) (Wang and Sun 2013). With all the development in imaging technologies, higher quality data can now be collected to build better biomechanical models based on the high-resolution imaging information (Desai et al. 2015). Two imaging modalities have been extensively used in recent years to develop anatomically accurate computational models of the MV: (1) transesophageal echocardiograms (TEE) and (2) micron-resolution CT (micro-CT). For instance, in several investigations, Pouch et al. studied 3D TEE images (Pouch et al. 2015; Pouch et al. 2012) to acquire MV geometric models and further applied their framework to perform biomechanical simulations (Pouch et al. 2012). In our previous studies, we have extensively used micro-CT images acquired ex vivo (Drach et al. 2015; Khalighi 2015; Khalighi et al. 2017; Khalighi et al. 2015) to build FE models of the MV for computational simulations (Lee et al. 2015). Interestingly, in spite of all the advanced MV imaging technologies that are becoming more prevalent, adequate geometric modeling techniques have yet to be developed in order to fully exploit the high-resolution MV imaging data. Moreover, there still remains the need for a thorough analysis of the MV geometry to answer the following questions: (1) what features of the MV leaflet geometry govern its overall shape? (2) how can we build MV models with an adjusted level of detail and in turn quantify the extent to which these details impact the fidelity of biomechanical simulations?

1.4 Contributions

Geometry remains the sin quo non in performing computational simulations of biomechanical systems. In the present study, we have developed a robust pipeline to build highly accurate geometric models of the MV in a multi-resolution framework. In particular, we present a geometry modeling methodology that allows building anatomically accurate MV geometries at various length scales. We applied our methods on extant high-resolution in vitro 3D geometry from five ovine MVs to develop models with multiple levels of geometric detail. Ultimately, these “multi-resolution” models provide the basis to robustly analyze the MV structure-function relation and in turn identify the level of geometric complexity required to achieve high fidelity in MV computational modeling.

2. Materials and Methods

2.1 Data acquisition

We utilized extant 3D high spatial resolution imaging data from prior studies (Khalighi et al. 2015; Lee et al. 2015), where details of the experimental setup used to image MV in the end-diastolic (open) state were extensively reported (Rabbah et al. 2013; Siefert et al. 2013). In brief, five fresh male Dorset sheep hearts were obtained from a USDA-approved abattoir (Superior Farms, CA, USA) and the MV apparatus was excised from each heart. Extracted MVs were then sutured to a morphable annulus holder (Bloodworth et al. 2016) to simulate the fully open state of the valve. Next, a Siemens Inveon micro-CT scanner (Siemens Medical Solutions USA Inc., PA, USA) was used to acquire high-resolution images, with the settings optimized for soft tissue imaging (80 kV energy, 500 μA intensity, 650 ms integration time). The Imaging time per valve was approximately seven minutes and the resulting imaging data comprised of 43.29-micron isotropic voxels.

2.2 Image processing

The acquired 3D datasets were loaded in the ScanIP software suite (Synopsys Inc., CA, USA) to process the images and build geometric representations (Figure 2). Each DICOM dataset consisted of 32-bit gray-scale intensity values of X-ray absorption, stored as stacks of orthogonal 2D images. Prior to image segmentation, a two-step filtering procedure was applied to attenuate the random noise polluting MV images. In short, an isotropic median filter and an anisotropic diffusion based filter (Malladi and Sethian 1995) were applied consecutively with a calibrated set of parameters for all datasets (100 iterations, time step=0.000125). Then, the MV structure was segmented from the image background using threshold values that were set empirically based on the intensity fields of each image (Figure 1B), so as to extract the MV leaflet geometry from input images with the highest possible level of detail.

Figure 2.

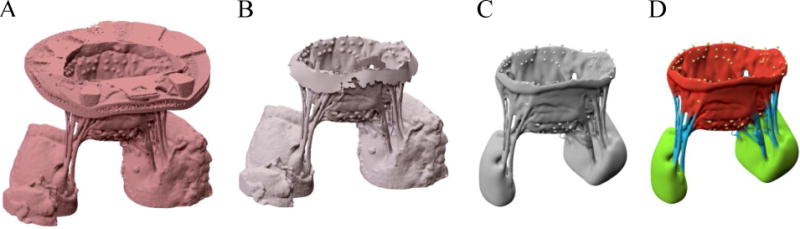
(A) shows the micro-CT image of an ovine MV. We used physical markers that we placed on the MV annulus to trim the image and remove the annulus holder, as shown in (B). (C) represents a geometric representation constructed from segmented images. Finally, the MV constituent parts were labeled as shown in (D).

Next, we applied a marching cube algorithm (Lorensen and Cline 1987) to create a triangulated boundary surface representation of each valve. The constructed mesh files were then imported in Zbrush sculpting software (Pixologic Inc., CA, USA) and the leaflets, chordae tendineae, and papillary muscles were manually labeled (Figure 2D). We processed five valves following the described pipeline (Figure 3) and developed discrete geometric representations that were further analyzed to characterize and reconstruct the MV leaflet geometry.

Figure 3.

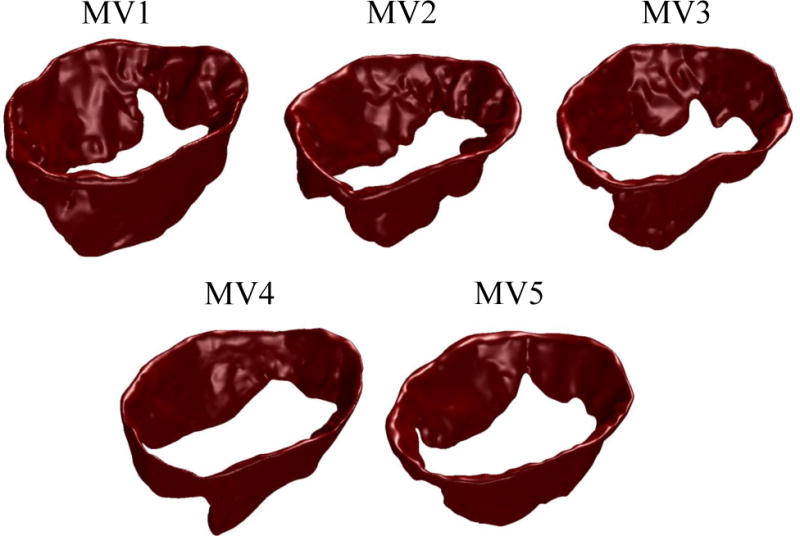
five ovine MV leaflets used for this study are shown.

2.3 Geometry modeling

2.3.1 General considerations

In our analysis, the multiscale image-based geometry of each studied MV was decomposed into two models: (1) a parametric model that approximated the general valvular shape, and (2) a fine-detail model that captured the geometric details as a set of discrete deviation fields from the primary model. The main rationale behind this additive decomposition of the shape (large-scale geometry) and features (fine-scale geometric details) was to decouple the physical dimensions and pose of the MV leaflets from their anatomical variations in geometry. The geometric details can then be reconstructed and incorporated with the parametric model to develop multi-resolution models for high-fidelity computational modeling. Moreover, the hierarchical representation facilitates registration of different MVs in a population to study inter-subject variations and ultimately develop a population-averaged model, which preserves the fine-scale details.

For the parametric model we used superquadrics (Jaklic et al. 2013) to describe the general MV geometry. Superquadric surfaces are powerful parametric shape descriptors, acquired by the generalization of quadric surfaces (spheres, ellipses, and hyperboloids) in terms of asymmetry, curvature, and singularities (Barr 1981). They have been successfully used to model manmade and anatomical shapes (Bardinet et al. 1996; Park et al. 1996; Terzopoulos and Metaxas 1990), and allow complex shapes to be represented with few physically meaningful parameters. To analyze the geometric details, we then reconstructed the residual fields of the differences between the fitted superquadric surface and the segmented surface of the MV using spectral approaches. In particular, we implemented a sparse Fourier transform algorithm to build a spectral model of the fine-scale features as deviations from the superquadric surface. Below, we thoroughly describe the proposed modeling pipeline.

2.3.2 Parametric large-scale model (Superquadric model)

To capture the general MV geometry, we computed a superquadric model for each valve by solving a non-linear minimization problem. In Cartesian coordinates, a superquadric surface can be represented using a function of the form

$$\mathbf{F}(\mathbf{x},\mathbf{y},\mathbf{z}|{\mathbf{a}}_1,{\mathbf{a}}_2,{\mathbf{a}}_3,{\mathrm{\epsilon }}_1,{\mathrm{\epsilon }}_2,\mathrm{\theta },{\mathbf{x}}_0,{\mathbf{y}}_0,{\mathbf{z}}_0)={\left(\frac{\mathit{z}-{\mathbf{z}}_0}{{\mathbf{a}}_3}\right)}^{\frac{2}{{\mathrm{\epsilon }}_1}}+{[{\left(\frac{\mathbf{cos}\mathrm{\theta }(\mathbf{x}-{\mathbf{x}}_0)-\mathbf{sin}\mathrm{\theta }(\mathbf{y}-{\mathbf{y}}_0)}{{\mathbf{a}}_1}\right)}^{\frac{2}{{\mathrm{\epsilon }}_2}}+{\left(\frac{\mathbf{sin}\mathrm{\theta }(\mathbf{x}-{\mathbf{x}}_0)+\mathbf{cos}\mathrm{\theta }(y-{\mathbf{y}}_0)}{{\mathbf{a}}_2}\right)}^{\frac{2}{{\mathrm{\epsilon }}_2}}]}^{\frac{{\mathrm{\epsilon }}_2}{{\mathrm{\epsilon }}_1}}$$ (1)

where parameters a₁, a₂, and a₃ are shape parameters that control the size of the superquadric shape along x, y, and z directions, respectively. The parameters ε₁ and ε₂ are the so-called squareness factors which respectively regulate the surface curvature in the xy-plane and along the z-axis. To center the coordinate system, we introduced the parameters x₀, y₀, and z₀ which denote the location of global origin. In addition, the parameter θ adjusts the pose of the superquadric shape about the z-axis. Using Eq. (1), the superquadric surface defined by a parameter set can be simply described using the implicit equation

$$\mathbf{F}(\mathbf{x},\mathbf{y},\mathbf{z}|{\mathbf{a}}_1,{\mathbf{a}}_2,{\mathbf{a}}_3,{\mathrm{\epsilon }}_1,{\mathrm{\epsilon }}_2,\mathrm{\theta },{\mathbf{x}}_0,{\mathbf{y}}_0,{\mathbf{z}}_0)-1=0$$ (2)

To fit superquadric geometries, there are several cost functions suggested in the literature (Solina and Bajcsy 1990). However, most of these objective functions were designed to fit shapes which are topologically equivalent to a sphere (genus-0), while the MV geometry has toroidal topology (genus-1) (Figure 4). Thus, we developed a novel objective function to capture the complex MV geometry using superquadric models. Briefly, we penalized the implicit equation that denotes a superquadric model, Eq. (2), to restrict the in-plane area and curvature-adjusted out-of-plane length using

$$\mathbf{R}({\mathbf{a}}_1,{\mathbf{a}}_2,{\mathbf{a}}_3,{\mathrm{\epsilon }}_1,{\mathrm{\epsilon }}_2,\mathrm{\theta },{\mathbf{x}}_0,{\mathbf{y}}_0,{\mathbf{z}}_0)=\sqrt{{\mathbf{a}}_1{\mathbf{a}}_2}\sqrt[{\mathrm{\epsilon }}_1]{{\mathbf{a}}_3}{\displaystyle \sum _{\mathrm{i}}({\mathbf{F}}_{\mathrm{i}}^{{\mathrm{\epsilon }}_1}({\mathbf{x}}_{\mathrm{i}},{\mathbf{y}}_{\mathrm{i}},{\mathbf{z}}_{\mathrm{i}})-1)}$$ (3)

In Eq. (3), the summation is over the point cloud we want to model using superquadrics. Then, we used a trust-region algorithm (Yuan 2015) to minimize the objective function R and determine the best-fit parameters (a₁,a₂,a₃, ε₁, ε₂,θ,x₀,y₀,z₀) to represent the shape of MV leaflets. In this procedure, we defined semi-empirical bounds to constrain the parameter set in our optimization problem. To make the shape physically meaningful, the size parameters (a₁,a₂,a₃) and shape parameters (ε₁,ε₂) were restricted to being positive values. For the angle parameter θ, we set the [0,π] interval as the search space instead of [−π,π] due to the rotational symmetry of the superquadric shapes. The origin location (x₀,y₀,z₀) was constrained to be along the z-axis by enforcing x₀ = y₀ = 0. The rationale behind this constraint is the fact that all valves were aligned with the central axis of the imaging chamber at the data acquisition step and thus the location of z-axis for all of them was pre-set. We solved the described nonlinear optimization problem to find superquadric surfaces with the convergence criteria of $\frac{1}{\mathbf{N}}\left|\frac{{\mathbf{R}}_{\mathrm{n}+1}-{\mathbf{R}}_{\mathrm{n}}}{{\mathbf{R}}_{\mathrm{n}}}\right|<\mathbf{1}\times {\mathbf{10}}^{-15}$, where N denotes the number of iterations.

Figure 4.

(A) shows the 3-D view of the MV leaflets (B) illustrates a representative torus. The MV leaflet structure belongs to the family of torus-like (genus-1) topologies.

2.3.3 Fine-scale spectral model (deviations from the superquadric surface)

Intuitively, the fitting residuals in computing a superquadric model for the MV geometry denote the surface details, which were not fully captured by the superquadric approximation (Figure 5). Thus, the difference between the original MV geometry and the superquadric model carries information on the deviations of natural MV geometries from idealized superquadric models (Figure 5C). However, computing the field of local distance between the two objects is very challenging as it requires proper bijective registration between the two geometries.

Figure 5.

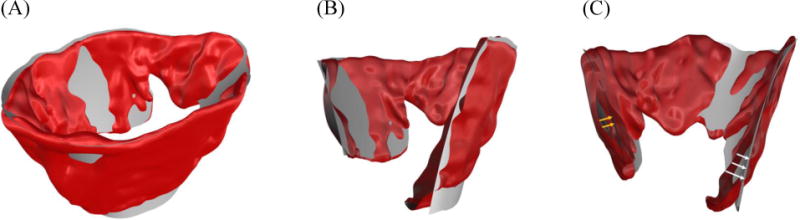
(A) shows a representative MV geometry and a superquadric model that approximates the MV shape; in (B) a cross sectional view of the MV leaflet structure and the computed superquadric model are shown. (C) illustrates that the deviation of MV atrial (white arrows) and ventricular (yellow arrow) sides from the original geometry can be evaluated to model the geometric details of the MV surface.

To evaluate the geometric details of MV surface, we computed the pointwise normally projected distances of the original MV geometry and the computed superquadric model. First, the original geometry was orthogonally projected on the computed superquadric model by solving the following nonlinear optimization problem

$$\text{minimize}\Vert \mathbf{r}-\mathbf{p}\Vert \text{subject}\text{to}1)\mathrm{F}(\mathbf{p})-1=02)\mathrm{\nabla }\mathrm{F}(\mathbf{p})\mathbf{·}(\mathbf{r}-\mathbf{p})=0$$ (4)

Formulation (4) aims to find the closest point p to each point r from the original geometry that satisfies the two following conditions simultaneously: (1) p sits on the superquadric surface, and (2) the line that connects r and p is normal to the superquadric surface at p. To solve this optimization problem, we developed a heuristic algorithm based on the bisection method (Khalighi 2015) and in turn built a correspondence between the original geometry and superquadric surface. Then, we evaluated the signed distance fields between the atrial and ventricular sides of the MV mesh, r_A and r_V respectively, and their corresponding points on the fitted superquadric surface p_A and p_V. Finally, we parameterized the scalar fields according to the following representation

$$\{\begin{array}{c}\mathrm{\eta }=\left[{\mathbf{\text{sin}}}^{-1}\right({\left|\frac{\mathbf{z}}{{\mathbf{a}}_3}\right|}^{\frac{1}{{\mathrm{\epsilon }}_1}}\left)\right]\mathbf{sgn}\left(\frac{\mathbf{z}}{{\mathbf{a}}_3}\right)\\ \mathrm{\omega }={\mathbf{\text{tan}}}^{-1}\left(\frac{{\left|\frac{\mathbf{y}}{{\mathbf{a}}_2}\right|}^{\frac{1}{{\mathrm{\epsilon }}_2}}\mathbf{sgn}\left(\frac{\mathbf{y}}{{\mathbf{a}}_2}\right)}{{\left|\frac{\mathbf{x}}{{\mathbf{a}}_1}\right|}^{\frac{1}{{\mathrm{\epsilon }}_2}}\mathbf{sgn}\left(\frac{\mathbf{x}}{{\mathbf{a}}_1}\right)}\right)\end{array}$$ (5)

Herein, the Cartesian coordinates of the MV mesh points projected on the superquadric p were transformed to the 2D parametric domain of the superquadric surface (η,ω). This parametrization is in fact a conformal map from the 3D Cartesian space, onto the 2D periodic domain of the superquadric surface. Ultimately, the mesh projection together with the subsequent parametrization enabled us to model the geometric details as scalar functions f_A and f_V defined on the superquadrics parametric domain (Figure 6).

Figure 6.

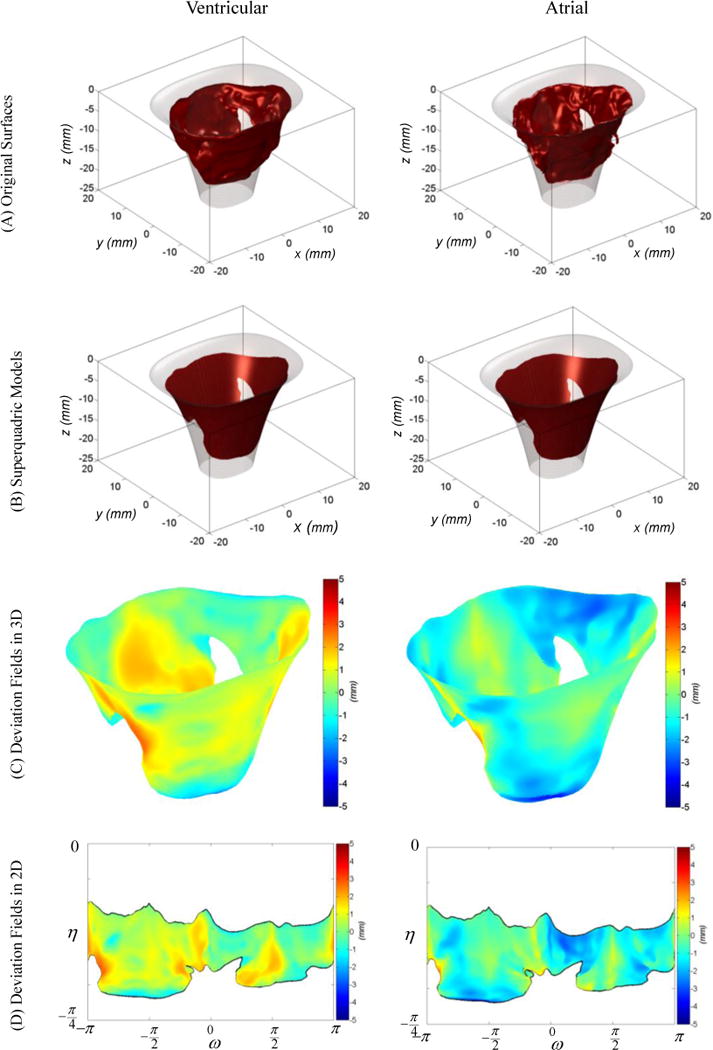
the two mappings required to model the geometric details of the MV leaflet are represented. The ventricular side is represented on the left and the atrial side on the right. The surface mesh (A) is normally projected on the superquadric fit to acquire (B). Shown in (C), the signed L₂ distance between these two meshes in (A) and (B) indicates the deviation of MV actual surface from the superquadric model. Then, the deviation fields evaluated on 3D Cartesian meshes are projected on the superquadric parametric domain as shown in (D).

1.5 Spectral analysis

1.5.1 Overview

We relied on spectral analysis to model the fine-scale features of the MV geometry. Specifically, signed-distance fields denoting the atrial and ventricular surfaces were reconstructed using a discrete Fourier series defined by

$${\mathbf{f}}_{\mathrm{A}}(\mathrm{\eta },\mathrm{\omega })={\displaystyle \sum _{\mathrm{m}=-{\mathrm{N}}_{\mathrm{\omega }}}^{{\mathrm{N}}_{\mathrm{\omega }}-1}{\displaystyle \sum _{\mathrm{n}=-{\mathrm{N}}_{\mathrm{\eta }}}^{{\mathrm{N}}_{\mathrm{\eta }}-1}{\mathrm{\beta }}_{\mathrm{A}}(\mathbf{n},\mathbf{m}){\mathbf{e}}^{2\mathrm{\pi }\mathrm{i}(\mathrm{n}\mathrm{\eta }+\mathrm{m}\mathrm{\omega })}}}{\mathbf{f}}_{\mathrm{V}}(\mathrm{\eta },\mathrm{\omega })={\displaystyle \sum _{\mathrm{m}=-{\mathrm{N}}_{\mathrm{\omega }}}^{N_{\mathrm{\omega }}-1}{\displaystyle \sum _{\mathrm{n}=-{\mathrm{N}}_{\mathrm{\eta }}}^{{\mathrm{N}}_{\mathrm{\eta }}-1}{\mathrm{\beta }}_{\mathrm{V}}(\mathbf{n},\mathbf{m}){\mathbf{e}}^{2\mathrm{\pi }\mathrm{i}(\mathrm{n}\mathrm{\eta }+\mathrm{m}\mathrm{\omega })}}}$$ (6)

where f_A (η,ω) and f_V (η,ω) correspond to the atrial and ventricular scalar deviation fields respectively which model the fine-scale surface details of the MV geometry. In this formulation, the MV attributes are modeled in the frequency domain by calculating the Fourier coefficients β_A (n,m) and β_V (n,m), then reconstructed back in the spatial domain according to Eq. (6). However, performing spectral reconstruction of scalar fields defined on unstructured triangulated meshes is challenging for two reasons: (1) the non-uniform structure of the tessellated mesh representation, (2) the free-form shape of the domain boundaries. Standard Fourier analysis techniques like DFT require periodic data, tabulated on rectangular grids. Thus, such approaches cannot be applied to perform spectral analysis on triangulated data with free-form non-periodic boundaries. In Appendix B, we have specified how these issues affect the spectral analysis and the details of our approach to overcome these challenges.

1.5.2 Sparse spectral analysis

To reconstruct the atrial and ventricular surfaces, we implemented a least squares spectral analysis method with an additional constraint to enforce sparsity of the reconstructed spectrum. Our methodology can also be viewed as a least absolute shrinkage and selection operator (LASSO) optimization formulation (Tibshirani 1996) that simultaneously solves for a faithful function reconstruction enforced by a parsimonious model selection criterion. In this framework, the objective function has the following form

$$\mathrm{\Psi }={\Vert \mathbf{f}-\mathrm{H}\mathrm{\beta }\Vert }_2^2+\mathrm{\lambda }{\displaystyle \sum _{\mathrm{m}=-{\mathrm{N}}_{\mathrm{\omega }}}^{{\mathrm{N}}_{\mathrm{\omega }}-1}{\displaystyle \sum _{\mathrm{n}=-{\mathrm{N}}_{\mathrm{\eta }}}^{{\mathrm{N}}_{\mathrm{\eta }}-1}|\mathrm{\beta }(\mathbf{n},\mathbf{m})|}}$$ (7)

where the term ${\Vert \widehat{\mathbf{f}}-\mathrm{H}\mathrm{\beta }\Vert }_2^2$ is an L₂ measure of the differences between the Fourier reconstruction and the original data, thus optimizing the coefficients β to closely reconstruct the known function values f (i.e. geometric details) in the spatial domain. The operator H is an inverse non-uniform fast Fourier transform (NUFFT) (Greengard and Lee 2004) operator which allows the reconstruction of the function values defined on the irregularly spaced (unstructured grid) spatial locations (η,ω). The second term ${\displaystyle \sum _{\mathrm{m}=-{\mathrm{N}}_{\mathrm{\omega }}}^{{\mathrm{N}}_{\mathrm{\omega }}-1}{\displaystyle \sum _{\mathrm{n}=-{\mathrm{N}}_{\mathrm{\eta }}}^{{\mathrm{N}}_{\mathrm{\eta }}-1}|\mathrm{\beta }(\mathbf{n},\mathbf{m})|}}$ imposes a sparsity constraint on the Fourier coefficients β(n,m). This penalization was added to attenuate the under-fitting problem related to the mismatch between the MV physical boundaries and the bounds of the superquadric parametric domain.

To solve the optimization problem and find the Fourier coefficients β(n,m), we implemented an accelerated proximal gradient method (Parikh and Boyd 2013) to iteratively resolve the Fourier representation of geometric details. With the Fourier basis functions being orthonormal, applying the proximal gradient method leads to the well-known fast iterative soft thresholding technique (Beck and Teboulle 2009). We further improved the convergence behavior of our optimization algorithm by adaptive restart of the acceleration term (Becker et al. 2011; O’Donoghue and Candes 2015). The convergence criterion used was set to $\left|\frac{{\mathrm{\Psi }}_{\mathrm{n}+1}-{\mathrm{\Psi }}_{\mathrm{n}}}{{\mathrm{\Psi }}_{\mathrm{n}}}\right|<1\times {10}^{-3}$, which took typically around 1000 iterations. Finally, to balance between the fidelity and sparsity criteria, the regularization ratio was set to λ = 1×10⁻⁴ by empirically exploring the optimal trade-off curves (L-curves) of all valves.

1.5.3 Geometry reconstruction

To reconstruct the full detailed MV model, we superimposed the MV geometric details on the smooth superquadric approximation of the MV shape

$${\mathbf{r}}_{\mathbf{A}}(\mathrm{\eta },\mathrm{\omega })=\mathbf{p}(\mathrm{\eta },\mathrm{\omega })+{\mathbf{f}}_{\mathrm{A}}(\mathrm{\eta },\mathrm{\omega }){\mathbf{e}}_{\mathbf{N}}(\mathrm{\eta },\mathrm{\omega }){\mathbf{r}}_{\mathbf{V}}(\mathrm{\eta },\mathrm{\omega })=\mathbf{p}(\mathrm{\eta },\mathrm{\omega })+{\mathbf{f}}_{\mathrm{V}}(\mathrm{\eta },\mathrm{\omega }){\mathbf{e}}_{\mathbf{N}}(\mathrm{\eta },\mathrm{\omega })$$ (8)

where r_A (η,ω) and r_V (η,ω) denote the location of MV atrial or ventricular sides respectively. Further, p(η,ω) refers to the superquadric model of the full MV geometry given by

$$\mathbf{p}(\mathrm{\eta },\mathrm{\omega })=\left[\begin{array}{c}{\mathrm{a}}_1{\cos }^{{\mathrm{\epsilon }}_1}(\mathrm{\eta }){\cos }^{{\mathrm{\epsilon }}_2}(\mathrm{\omega })\\ {\mathrm{a}}_2{\cos }^{{\mathrm{\epsilon }}_1}(\mathrm{\eta }){\sin }^{{\mathrm{\epsilon }}_2}(\mathrm{\omega })\\ {\mathrm{a}}_3{\sin }^{{\mathrm{\epsilon }}_1}(\mathrm{\eta })\end{array}\right],\begin{array}{c}-\frac{\mathrm{\pi }}{2}<\mathrm{\eta }<\frac{\mathrm{\pi }}{2}\\ -\mathrm{\pi }<\mathrm{\omega }<\mathrm{\pi }\end{array}$$ (9)

Herein, f (η,ω) corresponds to the reconstructed field of geometric details. Following Eq. (8), a parametric model of each MV side (atrial and ventricular) is reconstructed by deforming the superquadric surface in the direction of unit normal vector of the superquadric surface e_N (η,ω). This normal vector is computed simply by normalizing the gradient of the superquadric implicit form (Eq. (1)). The superposition relation for geometry recovery follows directly from the additive decomposition of the input geometry, as described in the section “Computing Surface Details”.

1.5.4 Medial representation

The parametric reconstruction of the MV geometry instantly provides a means to build a medial representation of the MV with regional thickness (Figure 7) which is required for the MV computational modeling using thin shell theory. To approximate a medial model, we averaged the geometric models of the MV atrial and ventricular sides (Figure 8) following the definition of medial representations (Choi et al. 1997). Next, we extracted the local thickness field by processing the distance of the atrial and ventricular sides of the MV from the superquadric model (Figure 9).

Figure 7.

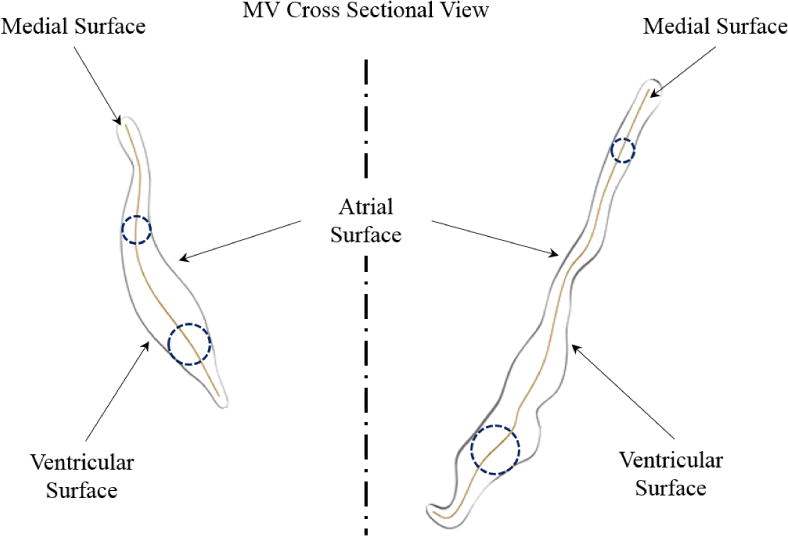
A cross-sectional value of MV leaflet structure is shown. The MV leaflet local thickness can be defined as the diameter of the spheres that are centered at the medial surface and tangent to the atrial and ventricular boundaries.

Figure 8.

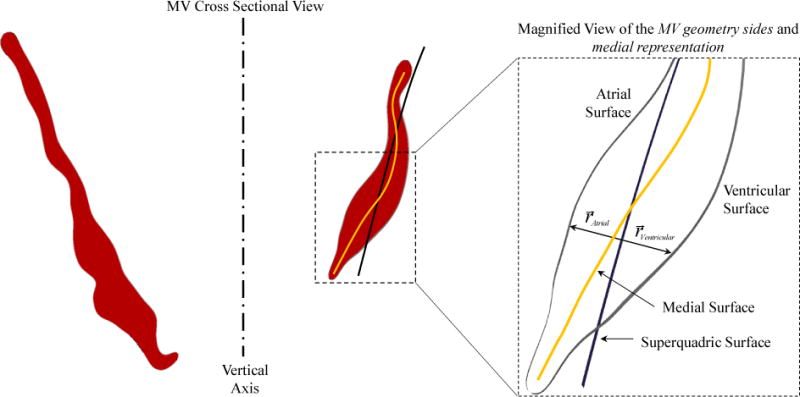
The medial surface location can be approximated by averaging the distance of atrial and ventricular surfaces from the superquadric model.

Figure 9.

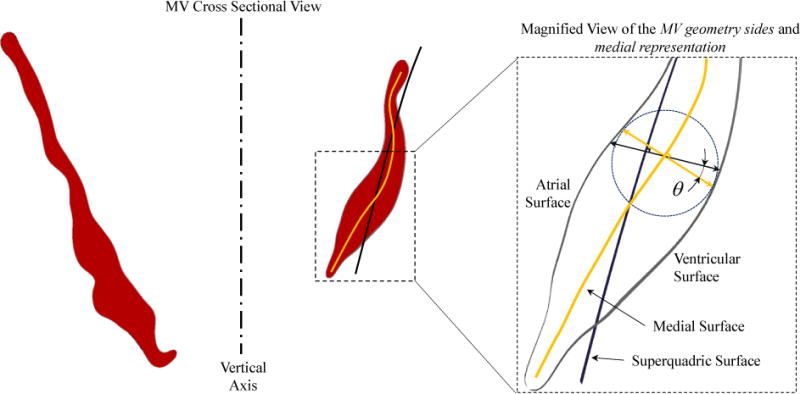
The normal to the superquadric surface is not necessarily in the same direction as the normal to the medial surface, shown as angle θ. The thickness field computed by using spectral reconstruction of the geometric details needs to be projected on the normal to the medial surface. This is done by multiplying the reconstructed thickness fields by cos(θ) that is evaluated pointwise on the medial surface.

3 Results

3.1 Geometry reconstruction

We applied our framework to five ovine MV datasets that were acquired using micron-resolution in vitro images. As analytic approximations of the MV leaflet geometry, valve-specific superquadric models were computed (Figure 10) which showed that superquadric surfaces can adequately approximate the geometry of MV leaflets based only on a small set of parameters (c.f. Eq. (2)). Essentially, superquadric models capture the 3D orientation, size scales, and characteristic curvatures of the MV leaflets in the fully open state (Table 1). The results suggest that superquadric models can also provide a basis to compare and combine different valves to ultimately develop population-representative models of the MV leaflets. Further, superquadric surfaces can potentially provide biomechanically adequate templates to build MV models based on clinical images which have low spatial resolution and suboptimal signal-to-noise ratio.

Figure 10.

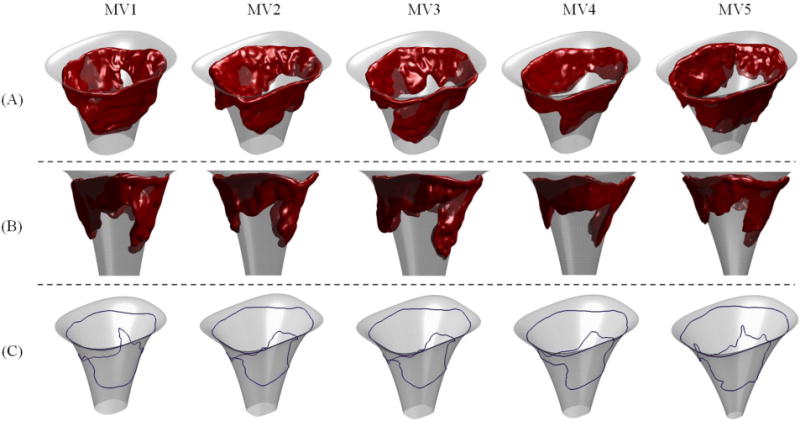
Computed superquadrics for five MVs are shown from two views in the Panels (A) and (B). For all valves, computed superquadric models are relatively similar and belong to the same family of superquadric shapes, shown in Panel (C).

Table 1.

superquadric parameters computed for the studied valves.

Valve ID	a1	a2	a3	ε1	ε2
MV1	16.8998	13.2680	92.7388	3.4354	0.7657
MV2	17.5733	13.4920	80.2733	3.3977	0.5866
MV3	17.8651	15.2902	81.1095	3.3742	0.6942
MV4	18.1185	13.5838	60.6123	3.0739	0.6905
MV5	18.2589	13.2078	40.9553	2.6806	0.7214

3.2 Detailed modeling

We also reconstructed the fine features of MV surface in the spectral domain (Figure 11). In the reconstructions, average absolute L₂ error in surface modeling was smaller than 5 μm, which indicates the high accuracy of spectral analysis to recover surface details. It should be noted that even this small reconstruction error is localized in the regions where the MV surface folds on itself which corresponds to the artifacts of imaging MV in air using in vitro setups (Bloodworth et al. 2016).

Figure 11.

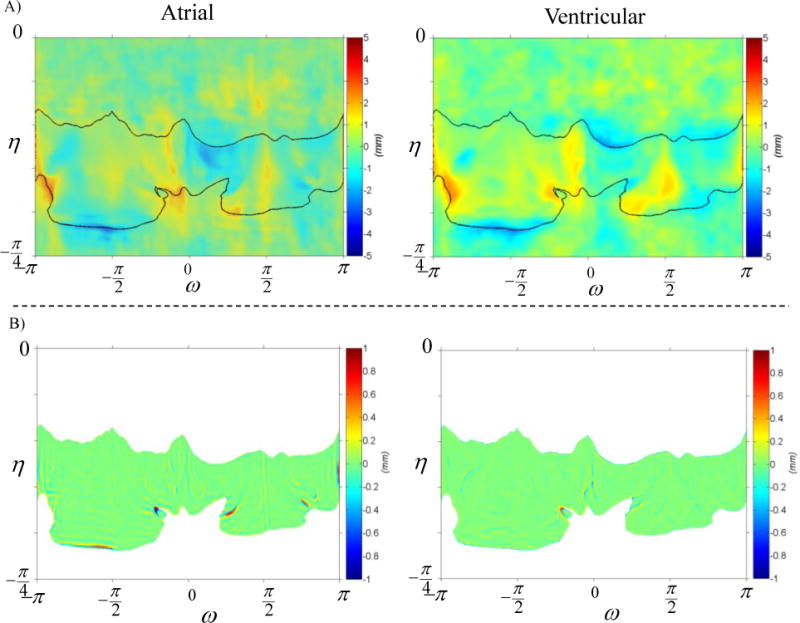
The reconstruction of MV geometric details for one of the studied valves, is demonstrated. Panel (A) shows the reconstruction of ventricular and atrial sides on the left and right figures respectively. The reconstruction error for both sides is illustrated in Panel (B) in the same order. Remarkably, the surface reconstruction is highly accurate, with local errors only exceeding 0.5 mm in regions where the leaflet free edge folds.

Upon modeling the MV features in the 2D spectral domain, we readily built 3D parametric models of the MV leaflet surfaces with very high precision (Figure 12). Remarkably, the reconstruction results for atrial and ventricular MV surfaces agree with the original 3D valvular geometry up to sub-millimeter accuracy. This strongly suggests that our pipeline provides a robust toolkit to characterize, quantify, and reconstruct the 3D MV leaflet geometry in a purely parametric form (c.f. Eq. (8)).

Figure 12.

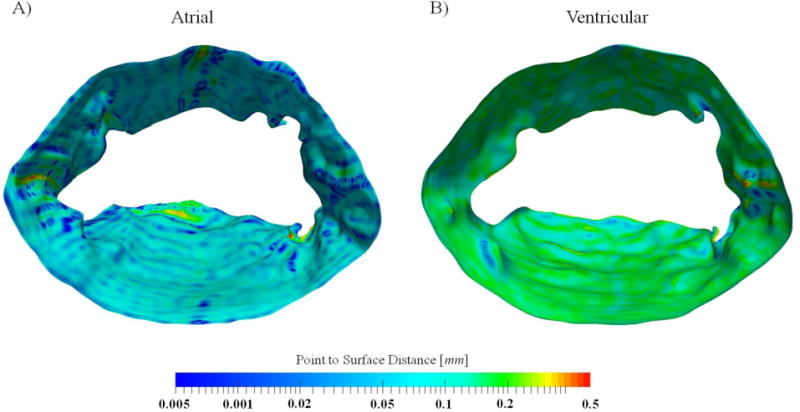
a representative, reconstructed MV atrial and ventricular surface are shown. The colormap corresponds to the quality of reconstruction and shows the sub-millimeter accuracy of models. Further, even this small error is concentrated in regions that valve tissue folds on itself.

3.3 Medial Model

Originally, building a medial representation for the MV geometry was challenging due to the genus-1 (toroidal) topology and multitude of physical protrusions on the surface. Nonetheless, our pipeline provided a stable approach to constructing an approximate medial representation of the MV geometry (Figure 13). The acquired medial model is enriched with the continuous field of symmetric thickness values, which can be directly used for finite element simulations of the MV using shell structural elements.

Figure 13.

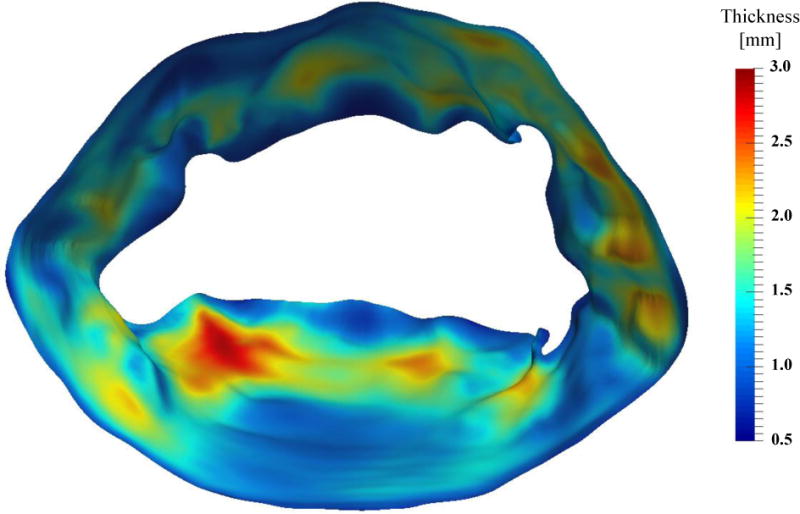
The medial representation of the MV leaflet structure is shown with colormap denoting the local thickness field

3.4 Multi-resolution representations

The sparse spectral analysis also enabled us to characterize the geometric details of the MV in the frequency domain (Figure 14). The computed power spectrum is concentrated around the zero frequency (analogous to the DC frequency in FFT) showing that a low frequency ensemble is sufficient to reconstruct the MV geometric details with high fidelity. Furthermore, the power spectrum is fairly sparse, suggesting that a small set of frequencies contain the information required to obtain a detailed geometric model by enriching the superquadric approximation. In particular, our study suggests that the full 3D MV geometry can be reconstructed up to sub-millimeter accuracy only with less than 10 percent of the entire frequency bandwidth (Figure 15). These results indicate limited aliasing in the spectral analysis, which then allows filtering the MV geometric details in the spectral domain and in turn control the complexity of reconstructed models.

Figure 14.

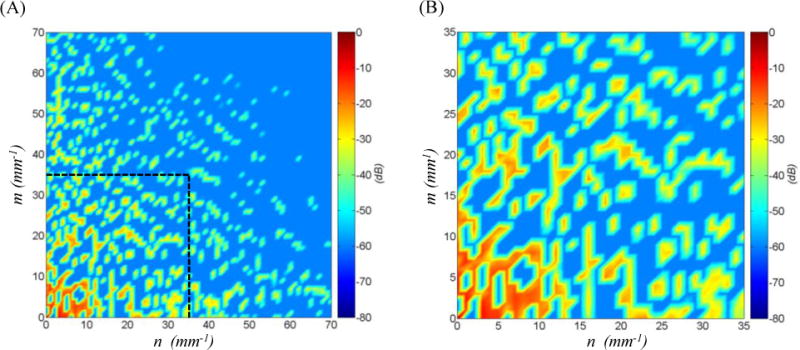
the spectral representation of the MV geometric details for the ventricular side for one of the studied MVs is shown in decibel. Plot (A) illustrates that the frequency spectrum is sparse and mostly concentrated at low frequencies. The horizontal axis n represents the frequencies along ω and the vertical axis m denotes the frequencies along η directions, Eq. (6). The low-frequency ensemble which contains more than 99% of the power spectrum density is shown in plot (B). This result indicates that we can reconstruct the MV geometric details using a relatively low number of frequencies.

Figure 15.

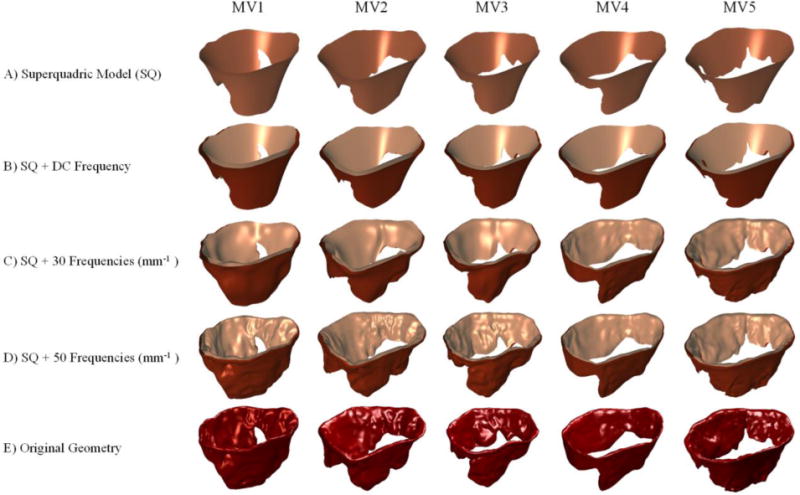
The results of multi-resolution reconstruction are shown for five MVs. The simplistic superquadric model (A) is enhanced by adding the DC frequency to reconstruct a basic model of the atrial and ventricular surfaces in (B). Integrating more frequencies in the reconstruction recovers more geometric details as shown in (C) and (D). The original geometry that is input to our pipeline is shown in (E) for comparison. In overall, the results show that spectral analysis of geometric attributes allows controlling the level of detail in model development.

4 Discussion

4.1 General overview

One labor-intensive and time-consuming task in developing image-based anatomic models for simulations is the development of computationally amenable geometric meshes. In the specific context of the MV, building accurate geometric models is notoriously challenging due the particular anatomic complexities of the leaflets and chordae tendineae (Bloodworth et al. 2016). In this work, we developed a novel 3D high-resolution image-based approach to process and create high-fidelity detailed geometric models of the MV leaflet. Our methodology has no direct limitations in processing other imaging modalities, however, further studies need to be performed to assess how accurately our methodology performs on MR or ultrasound data.

In contrast to the existing geometric models of the MV, we performed a multi-resolution analysis of the MV leaflet, with major emphasis on consistent parameterization within an objective modeling framework. This approach allowed us to perform accurate quantification and reconstruction of subject-specific geometric features. Moreover, by analyzing the fine-scale features in the spectral domain, we preserved (1) high levels of detail in model development along with (2) the ability to adjust the resolution in the reconstructed geometric representations and in turn fully control the quality of developed models. It is worth mentioning that multi-resolution geometry analysis methods generally exploit the use of wavelets and subdivision algorithms for mesh analysis (Eck et al. 1995; Lounsbery et al. 1997). In the current study, we have pursued a similar approach and developed a geometry processing pipeline that allows controlling the level of detail in the final model reconstruction. However, we replaced the “base mesh” with a parametric shape primitive (superquadrics) and the “wavelet coefficients” with discrete harmonic (Fourier) basis functions.

Another key advantage of our approach is the decoupling of general shape parameters (superquadric model) from the fine-scale features (spectral analysis). This decomposition allows to reconstruct patient-specific MV geometries with high accuracy while controlling the level of complexity in model reconstruction. Essentially, for a single a specimen, we can now build a spectrum of models ranging from clinical quality precision to micron-resolution, Figure 15. By integrating these geometric models into a computational framework, we are now performing sensitivity studies to identify the level of geometric accuracy required to build predictive MV models from clinical imaging data (Drach et al. 2017). Moreover, we believe our multi-resolution methodology can be further extended to other soft tissue imaging data (Ban et al. 2017) and in turn build anatomically accurate image-based models (Zarei et al. 2017; Zhang et al. 2017) for high fidelity soft tissue simulations.

In overall, we believe that our methodology allows developing optimally detailed geometric models of the MV leaflets. These models can then be integrated with simplified or stochastic models of chordae tendineae (Khalighi et al. 2016) to build complete computational models of the MV for repair simulations. Our framework also provides a basis for reconstructing MV physical attributes (e.g. mechanical properties, fiber architecture) and incorporating them into computational models in the same way that we modeled the thickness field of MV medial models. Specifically, scalar functions denoting other physical properties can be reconstructed, then registered and integrated with geometric models, using the superquadric parametric space (Eq. 9), to build high-resolution isoparametric models for high-fidelity computational simulations.

4.2 Limitations

In this study, we analyzed the leaflet geometry of five ovine MVs that were pre-selected to meet the size specifications of the imaging setup. Thus, all the studied samples were within a specific range of chosen sizes, and may not necessarily represent the entire ovine population. Our methodology relied on the premise that a superquadric shape can competently capture the generic geometry of the MV leaflets of any size range. While differences exist in the specific shape of the MV between species, the flexibility of this approach suggests that our modeling pipeline is directly applicable to MVs in various disease states and from other species.

4.3 Conclusion

We have presented a novel modeling pipeline to quantitatively characterize and represent the multiscale geometry of MV leaflets derived from imaging data. Our methodology provides a robust and accurate image-based approach to develop MV models with a customizable degree of geometric detail for advanced surgical simulations. Not only does our framework provide a streamlined approach to build high-fidelity MV computational models, it may also be applied to the other heart valves. Most notably, we believe that our approach provided a basis to incorporate in vivo gross anatomic information with high-resolution and attribute-rich in vitro data. Such approaches will facilitate the development of multi-resolution models of the MV for detailed exploration of the resolution required in high-fidelity computational simulations.

7 Nomenclature

MV

Mitral Valve

MVR

Mitral Valve Regurgitation

TEE

Trans-Esophageal Echocardiograms

Micro-CT

Micro Computed Tomography

US

Ultrasound

CLHS

Cylindrical Left Heart Simulator

PM

Papillary Muscle

FFT

Fast Fourier Transform

NUFFT

Non-Uniform Fast Fourier Transform

LASSO

Least Absolute Shrinkage And Selection Operator

‖ ‖₂

L₂ Norm

8 Appendix

8.1 Non-uniform data structure

We used an NUFFT algorithm that first interpolates (oversamples) the data on a dense Cartesian grid using truncated Gaussian kernels and then applies a standard FFT (Greengard and Lee 2004). This approach is a subset of NUFFT algorithms known as gridding algorithms. It has been shown that the effect of Gaussian kernels to interpolate the data on a regular grid can be removed using the convolution theorem. Thus, applying Gaussian gridding to perform Fourier analysis does not introduce interpolation errors if the data is uniformly distributed over a rectangular domain (one 2-D period). However, because MV attributes like the scalar fields representing geometric details are defined over irregular domains, gridding-based NUFFT algorithms fail unless the shape of the domain is accounted for.

8.2 Irregular domains

The deviation fields denoting the MV geometric details have the free-form top and bottom boundaries (Figure 16). These boundaries, corresponding to the MV annulus and free edge respectively, do not coincide with the top and bottom boundaries of the superquadric parametric domain. While the gridding step in the NUFFT algorithm oversamples the known function values on a periodic Cartesian grid, the data for deviation fields is defined on a subdomain of the entire periodic domain (Figure 16A). This results in the implicit zero-padding of the function values (Figure 16B).

Figure 16.

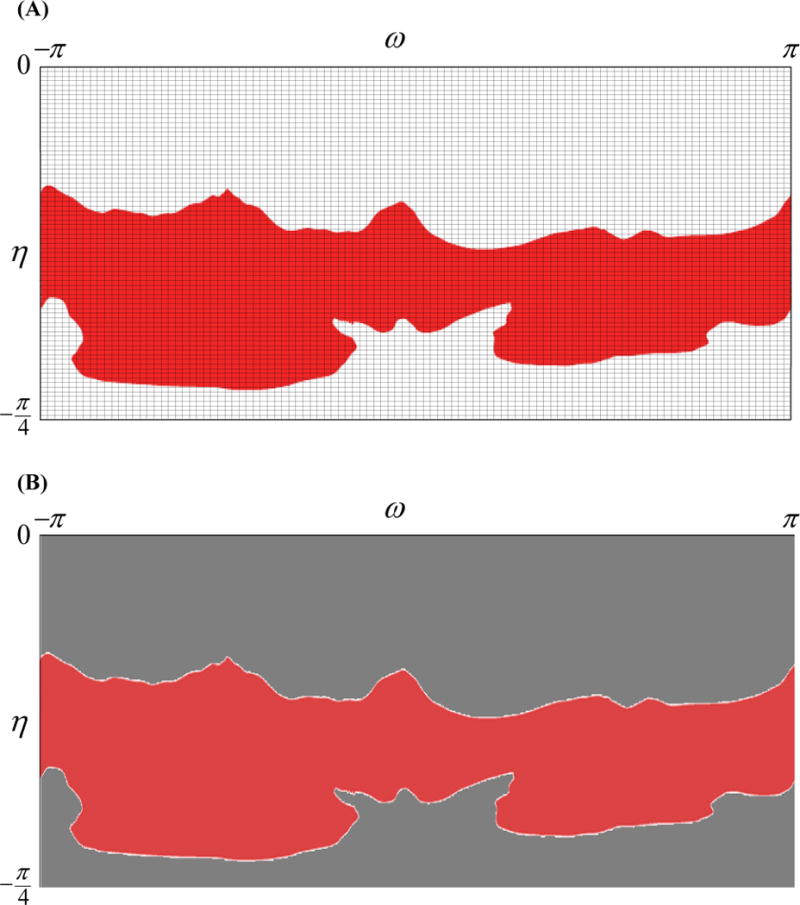
The Gaussian gridding approach for NUFFT interpolates the data on a super-sampled Cartesian grid shown in (A). For the MV attributes this results in zero-padding the data in subdomains of the parametric space where the MV domain is not defined, shown as grey in (B). Applying FFT for computing the Fourier transform of the interpolated function fails due to the discontinuity of data on the MV irregular boundaries, highlighted in (B).

Applying FFT on the zero-padded data results in a Fourier analysis that is drastically different from the actual frequency content of the MV geometric details. This is due to the Gibbs phenomenon (Gottlieb and Shu 1997), which can pollute the entire spectrum with noise, which is a direct artifact of a a discontinuity (jump from actual function values to zero) at MV boundaries. Following this, all the high-frequency pollution in the reconstruction of geometric details can be attributed to the spectral leakage caused by the effect of windowing (Bernstein et al. 2001), which in our case models the MV boundaries. Expanding the bandwidth to attenuate the Gibbs phenomenon (Gottlieb and Shu 1997) causes two problems: (1) the computational cost of the 2-D Fourier analysis process increases quadratically with the number of frequencies; and (2) faithful reconstruction of the geometric details becomes intractable as a result of the high-frequency components polluting the power spectrum. The addressed the latter issue by imposing sparsity penalization to the objective function for recovering the Fourier coefficients. Consequently, we were able to eliminate the spurious frequency components caused by the irregular boundaries and recover a clean spectrum through the implementation of iterative NUFFT penalized with the sparsity constraint Eq. (7).