An eFTD-VP framework for efficiently generating patient-specific anatomically detailed facial soft tissue FE mesh for craniomaxillofacial surgery simulation

Abstract

Accurate surgical planning and prediction of craniomaxillofacial surgery outcome requires simulation of soft tissue changes following osteotomy. This can only be achieved by using an anatomically detailed facial soft tissue model. The current state-of-the-art of model generation is not appropriate to clinical applications due to the time-intensive nature of manual segmentation and volumetric mesh generation. The conventional patient-specific finite element (FE) mesh generation methods are to deform a template FE mesh to match the shape of a patient based on registration. However, these methods commonly produce element distortion. Additionally, the mesh density for patients depends on that of the template model. It could not be adjusted to conduct mesh density sensitivity analysis. In this study, we propose a new framework of patient-specific facial soft tissue FE mesh generation. The goal of the developed method is to efficiently generate a high-quality patient-specific hexahedral FE mesh with adjustable mesh density while preserving the accuracy in anatomical structure correspondence. Our FE mesh is generated by eFace template deformation followed by volumetric parametrization. First, the patient-specific anatomically detailed facial soft tissue model (including skin, mucosa, and muscles) is generated by deforming an eFace template model. The adaptation of the eFace template model is achieved by using a hybrid landmark-based morphing and dense surface fitting approach followed by a thin-plate spline interpolation. Then, high-quality hexahedral mesh is constructed by using volumetric parameterization. The user can control the resolution of hexahedron mesh to best reflect clinicians’ need. Our approach was validated using 30 patient models and 4 visible human datasets. The generated patient-specific FE mesh showed high surface matching accuracy, element quality, and internal structure matching accuracy. They can be directly and effectively used for clinical simulation of facial soft tissue change.

1 Introduction

Craniomaxillofacial (CMF) deformities include acquired and congenital abnormalities of the head and face. CMF surgery is designed to restore both function and esthetics of patients. A successful CMF surgery depends not only on surgical expertise but also on accurate pre-surgical planning. CMF surgery involves osteotomies that cut the jaws into pieces and then reposition them to a desired (planned) position. Facial soft tissues are automatically changed following the bone movement. A good surgical planning requires precise simulation of bony segment movements (osteotomy) and accurate prediction of facial soft tissue changes. However, due to the complexity of facial soft tissue anatomy, accurate post-surgical predications are challenging even with precise osteotomy simulations (McCormick and Drew 2011; Hsu et al. 2013; Xia et al. 2015; Bobek et al. 2015).

The most widely used techniques for simulation of soft tissue changes are the finite element method (FEM), mass spring model (MSM), and mass tensor model (MTM). Comparing these three techniques, it is reported that FEM shows stronger biomechanical roots and more accurate results (Mollemans et al. 2007). FEM allows incorporating highly complex and nonlinear biomechanical tissues behavior, and it is based on a volumetric discretization of the tissue structure through the definition of 3D meshes. The success of FEM simulation depends on the geometrical fidelity of the FE mesh that represents the anatomy of interest (Freutel et al. 2014; Wu 2014; Luboz et al. 2014; Marchi and Arruda 2017), the accuracy of constitutive properties used to characterize the tissue mechanical behavior, and also realistic boundary conditions. In the FE mesh generation, there are two main challenges. First, the segmentation of anatomical facial soft tissue structures is very labor-intensive and time-consuming. Secondly, the process of generating a valid 3D mesh is also extensive and complex. 3D meshes can be constructed of tetrahedral or hexahedral finite elements. Historically, hexahedral element mesh was reported to be superior to tetrahedral element mesh in accuracy and efficiency in various simulation conditions and the usage of tetrahedral element mesh should be limited to specific conditions (Benzley et al 1995; Zienkiewicz and Taylor 1989; Ramos and Simoes 2006; Tadepalli et al. 2011; Burkhart et al. 2013; Warburton and Maddock 2013). However, nowadays, tetrahedral element mesh can also achieve acceptable stability, efficiency, and accuracy by solving large FE model (large number of elements and nodes) thanks to the advancement in computing power. In this study, we opt for using hexahedral meshes for simplicity of our analytical tools for mesh of varying density in post-processing. However, it can take days to generate a high-quality 3D hexahedral mesh for geometrically complex object such as the human face (Li et al. 2012). Thus, the overall time constraints significantly hinder the usability of FEM for surgical simulations in a clinical setting. This paper addresses current problem of 3D hexahedral mesh generation by proving fast and semi-automatic anatomically detailed patient-specific FE mesh generation.

A number of published reports have tried to overcome the aforementioned barriers in FE mesh generation and to increase the adoption of patient-specific soft tissue FE modeling in CMF surgical simulations. One approach aims to construct an anatomically detailed FE mesh template that adapts to match each patient (Chabanas et al. 2003; Bucki et al. 2010; Lou et al. 2012; Hung et al. 2015; Zhang et al. 2016). Although this approach is efficient, distorted elements are produced during superimposition and mesh quality is hard to be preserved after adaptation. Mesh repair is often required as a post-processing step. This procedure is algorithmically complex and time-consuming. Additionally, the mesh density for patients is determined by that of the template model. It could not be adjusted for sensitivity analysis. Instead of directly morphing a template FE model, there is an approach using predefined template Truegrid script (Ji et al. 2011). The script automatically generates patient-specific FE meshes by mapping between template and patient using image registration. Difficulties in script development for complex soft tissue models and lack of accuracy in image registration present limitations for this approach (Ren et al. 2014; Li et al. 2013; Yang et al. 2013). Hexahedral mesh transferring method by volumetric parameterization is another technique used to generate patient-specific facial soft tissue FE mesh (Li et al. 2011). This method, however, requires manual generation of a template facial soft tissue model with high-quality hexahedral mesh. Additionally, the hexahedral mesh quality can decrease during the transforming procedure. Even though these previous techniques have made advancements in facial soft-tissue-change simulation, their limitations in elemental quality distortion and registration accuracy still make patient-specific facial soft tissue FE modeling impractical for clinical use.

In this study, we propose to efficiently generate FE mesh with high-quality hexahedra and high-fidelity anatomical structure correspondence for patients. The resolution of the hexahedral mesh can also be controlled to best reflect individual need and conduct mesh density sensitivity analysis. Our FE mesh is intended for passive mechanics simulations of facial soft tissue change following craniomaxillofacial surgery, not for active facial simulations (e.g., facial expression simulation). In the passive mechanics simulation, the facial change is simulated according to the given osteotomy and surgical planning (bone repositioning). Our mesh is developed considering previously developed general methods for facial soft tissue prediction following craniomaxillofacial surgery (Koch et al. 1996; Keeve et al. 1998; Kim et al. 2010). In these studies, facial change following surgery is simulated by assigning appropriate boundary condition and tissue properties for corresponding mesh nodes and elements, respectively. The nodes on mesh inner surface are given nodal displacement boundary condition based on the movement of the contacting bony segments. Generally, the amount of bone movement according to the surgical planning is assigned as nodal displacement for the corresponding node. Finally, the soft tissue deformation is simulated by FEM according to the given simulation condition. Quality of FE mesh plays an important role for the accurate prediction of facial change. Therefore, in this study, we focus on generating quality mesh with high geometrical accuracy for usage of FE mesh for general facial soft tissue change simulation. As reported in previous research, the anatomical structure is necessary for achieving higher accuracy in facial soft tissue change prediction (Kim et al. 2012). Therefore, anatomical structure (including skin, mucosa, muscles, and filler (i.e., fat)) assignment is included in our FE mesh generation.

A new approach for generation of patient-specific facial soft tissue FE mesh has been developed using eFace template deformation and volumetric parameterization (eFTD-VP). The patient-specific facial soft tissue model is first generated by deforming the predefined eFace template. Then, hexahedral mesh for the patient-specific facial soft tissue model is created by using volumetric parameterization. Our eFTD-VP approach efficiently produces high-fidelity facial soft tissue FE mesh (including skin, mucosa, muscles, and filler (i.e., fat)) with adjustable mesh density. Our method was validated with 30 patient datasets and 4 visible human datasets through comparison with previous published techniques. The generated patient-specific FE mesh showed high surface matching accuracy, element quality, and internal structure matching accuracy. The clinical contribution of this project is that the resulted patient-specific facial soft tissue FE mesh can be directly and effectively used to simulate soft tissue changes following the osteotomy. The technical advancement of our approach is the generation of resolution-adjustable hexahedral FE mesh without sacrificing the quality of elemental shapes and registration accuracy.

2 The eFace template model

In our previous study, the anatomically detailed eFace template has been generated from CT data and color gross anatomical cross-sectional images of the Chinese Visible Female (CVF) (Zhang et al. 2016). The eFace template is a facial soft tissue model generated by forming a closed soft tissue surface (facial soft tissue envelope) that connects the skin (outer) surface and the mucosa (inner) surface adjacent to the skull. The eFace template also includes geometrical information of muscles (muscle surface). Eleven muscles are included in the template. They consist of: masseter (Ma), buccinator (Bu), orbicularis oris (Oo), depressor anguli oris (Dao), depressor labii (Dl), mentalis (Me), levator anguli oris (Lao), levator labii (Ll), levator labii alaeque nasi (Llan), zygomaticus major (Zma), and zygomaticus minor (Zmi) (Pan et al. 2012). The closed soft tissue surface (facial soft tissue envelope) and muscle surfaces are represented in triangular mesh. The eFace template model is shown in Fig. 1. In addition to the eFace template, a triangular skin surface (7586 vertices) and a skull surface (15,444 vertices) of the CVF are also constructed form the CT data for the surface registration between the template and patient dataset.

Fig. 1.

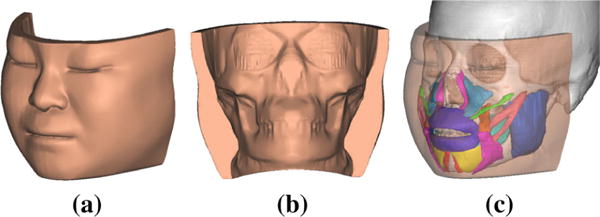
The eFace template model. a and b are the frontal and back views of the template facial soft tissue envelope. c The anatomical structure of the template model with highlighted musculature

3 The eFTD-VP approach

The framework of our eFTD-VP approach is shown in Fig. 2. It consists of two main steps. In the first step, the closed soft tissue surface (facial soft tissue envelope) and 11 muscle surfaces for the patient are generated by deforming the eFace template. They compose the patient-specific facial soft tissue model. They are presented in triangular mesh. In the second step, hexahedral mesh is generated from the patient-specific facial soft tissue model using volumetric parameterization. Both steps are described in detail below.

Fig. 2.

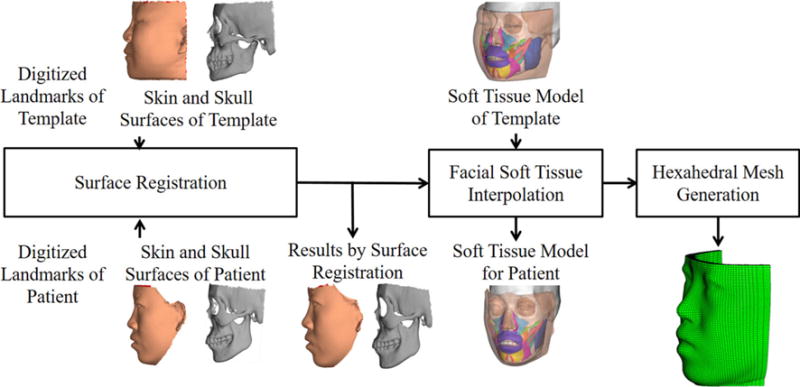
Framework of the eFTD-VP approach

3.1 Patient-specific facial soft tissue model generation

The patient-specific facial soft tissue model is generated based on the registration of the skin and skull surfaces of the eFace template to the skin and skull surfaces of the patient. The skin and skull surfaces of the patient are prerequisite data and are generated from the CT data of the patient. First, landmark-based thin-plate splines (TPS) are applied to align the template skin and skull surfaces to the patient skin and skull surfaces. A previously validated group of easily identifiable anatomical landmarks (Zhang et al. 2016) (45 on the skin, 26 on the maxilla, and 22 on the mandible) are manually digitized to guide the surface registration. TPS is used because it can generate smooth and non-rigid deformations simultaneously based on multiple landmarks (Chui and Rangarajan 2000). However, because vertex deformation is interpolated based on its distance to the closest landmarks, deformation of non-landmark vertices away from the landmarks decreases in accuracy. Therefore, we develop a dense surface fitting registration method to further refine the initial result from TPS.

In dense surface fitting registration, increased surface matching accuracy is achieved through projection of vertices from the initially registered eFace template surface onto the patient surface, which results in a better geometrical match. However, projection procedure can also result in partial mesh distortions due to the generation of intersecting triangles and distorted shapes. To overcome this mesh distortion problem, a smoothing term is integrated into the dense surface registration function. During both smoothing and projection, the correspondence of landmarks must be preserved. Therefore, an optimization function is developed to keep a balance among the degree of smoothness, the accuracy of surface fitting, and the landmark correspondence. The optimization function is as follows:

$$E={\displaystyle \sum _{p\in B}{\Vert v_p^{\prime }-v_p\Vert }^2+{\displaystyle \sum _{k\in C}{\Vert v_k^t-v_k\Vert }^2+\alpha {\displaystyle \sum _{i=1}^M{\Vert v_i-{\displaystyle \sum _{j\in i^C}\frac{v_j}{n_i}}\Vert }^2}}}$$ (1)

The first term represents the dense surface projection. B is the set of indices of the rest of vertices except landmark vertices, $B=\{p_1,\dots ,p_{N_B}\}$. For the soft tissue surface with M vertices and N landmarks, N_B = M − N. $v_p^{\prime }$ is the projected vertex of v_p. The projected vertex on the target patient surface is found by calculating the closest point with the minimum distance between the vertex and the target surface. The second term accounts for the landmark correspondence preservation. C is the set of indices of landmark vertices, C = {k₁, …, k_N}. The third term is the smoothing constraint. It is used to relocate each vertex of the mesh to the centroid of its neighboring vertices. The smoothing definition is $v_i={\displaystyle {\sum }_{j\in i^C}\frac{v_j}{n_i}}$, where i^c is the index set of neighborhood vertices to vertex v_i in the vertex set {v_i, i = 1, …, M}, and n_i is the number of neighborhood vertices to the vertex v_i. This term is used to avoid generation of poor-quality mesh resulted from the intersecting triangles and distorted shapes. α is a scale constant to control the degree of smoothness. The minima of Eq. (1) can be determined by taking its partial derivatives, which results in a linear system. The linear system can be solved in the sense of least square method. More details about the minimization of Eq. (1) can be found in the work of Zhang et al. (2016).

Based on the deformation of surface vertices (skin and skull), deformation of the eFace template facial soft tissue model (including closed facial soft tissue surface and muscles) can be interpolated using TPS. Thus, the whole eFace template facial soft tissue model is deformed while still preserving the accuracy of landmark correspondence between the eFace template to the patient data. This strategy performs well, even when large deformations exist between the template and the patient data.

3.2 Patient-specific 3D hexahedral mesh generation

The 3D hexahedral mesh is generated from the patient-specific facial soft tissue model using volumetric parameterization. Volumetric parameterization is the process of computing a mapping from the volumetric tetrahedral mesh in R³ to a parametric domain that is defined as a unit cube domain in R³. The unit cube is easily divided into hexahedra with predefined mesh density. The volumetric parameterization is usually implemented using the volumetric harmonic fields.

Facial soft tissue volume can be considered as a 3D shell structure, where compared to the other two dimensions (width and height), the dimension of thickness is smaller and not uniform. The traditional volumetric parameterization generates hexahedral mesh for shell structure by calculating the volumetric harmonic field from the outer to inner surface direction (Han et al. 2010). This method is prone to error because it requires a homeomorphic map between outer surfaces of the shell object and a polycube. Triple volumetric harmonic fields (i.e., from outer to inner surface, from right to left, and from bottom to top) are also used for hexahedral mesh transferring from a template model to patient-specific model (Li et al. 2011). However, the results are unstable for thin shell objects such as a facial soft tissue volume. Additionally, this method needs to manually create a template facial soft tissue model with high-quality hexahedral mesh. In order to avoid the aforementioned problems, our eFTD-VP approach constructs volumetric parameterization (mapping from patient-specific facial soft tissue model in tetrahedral mesh to a unite cube in hexahedral mesh) by calculating only two volumetric harmonic fields (i.e., from right to left, and bottom to top). Harmonic field from outer to inner surfaces is generated by uniform distribution (Fig. 3). Each boundary (top, bottom, left, and right) of the patient facial soft tissue model is projected on a flat plane for efficient boundary condition definition in the calculation of the harmonic fields (Fig. 3). The calculation of a volumetric harmonic field is performed on the tetrahedral mesh of the facial soft tissue model. The volumetric tetrahedral mesh is generated from the closed patient-specific facial soft tissue surface using Tetgen (Si 2015). Tetgen is a compact and fast quality 3D tetrahedral mesh generator. For a given closed facial soft tissue surface in triangular mesh, a three-step mesh generation algorithm is used to generate the tetrahedral mesh (including Delaunay tetrahedralization, constrained mesh generation, and quality mesh generation) in Tetgen. Then, we construct volumetric parameterization for the tetrahedral mesh of the patient-specific facial soft tissue model. By reversing the volumetric parameterization, we create the volumetric mapping from the hexahedral mesh of a cube to the patient-specific facial soft tissue model. The main framework of the hexahedral mesh generation is shown in Fig. 3.

Fig. 3.

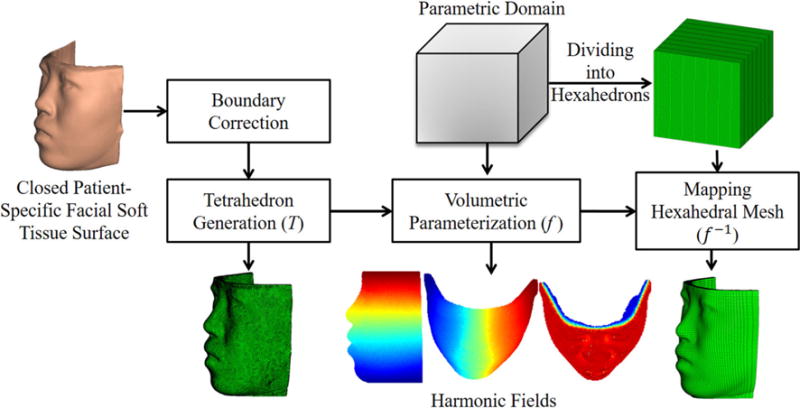
Framework of hexahedral mesh generation

3.2.1 Volumetric parameterization

Given the tetrahedralized patient-specific facial soft tissue model V, each vertex p_i ∈ V is with a triple coordinates (x_i, y_i, z_i). Given the parametric domain R, volumetric parameterization is equivalent to compute real valued parameter function (Xia et al. 2010):

$$f:V\to R$$ (2)

Let f_i = f (p_i), p_i ∈ V, f is harmonic if and only if it satisfies the following discrete Laplace equation:

$${\displaystyle \sum _{j\in N(i)}{w}_{ij}(f_i-f_j)=0}$$ (3)

where N(i) is the set of vertices adjacent to vertex i, and w_ij is a weight assigned to edge e_ij of tetrahedral mesh, which can be defined as $w_{ij}=\frac{1}{6}{\displaystyle {\sum }_{k=1}^m{l}_k}\cot {\theta }_k$ (Liao et al. 2009). Parameter l_k = l_pq is the length of the edge e_pq, which is the edge having no sharing nodes with edge e_ij in a tetrahedron. Parameter m is the number of adjacent tetrahedrons sharing edge e_ij, and θ_k is the dihedral angle. A harmonic field is a solution to the Laplace equation Eq. (3). It is solved based on specified Dirichlet boundary conditions, f (p_a) = 0,∀p_a ∈ B₀, f (p_b) = 1,∀p_b ∈ B₁, where B₀ and B₁ are two shape end boundaries.

By defining shape end boundaries B₀ and B₁ for right to left and bottom to top directions, the two harmonic fields, f_rl for right to left direction and f_bt for bottom to top direction, are calculated. Given the gradient vector fields of f_rl and f_bt as g_rl and g_bt, respectively, g_rl is corrected to be orthogonal with g_bt by the following function, which makes the two harmonic fields mutually orthogonal.

$${\stackrel{\sim }{\mathbf{g}}}_{\text{rl}}=[({\mathbf{g}}_{\text{bt}}\times {\mathbf{g}}_{\text{rl}})\times {\mathbf{g}}_{\text{rl}}]\cdot {\mathbf{g}}_{\text{rl}}\frac{({\mathbf{g}}_{\text{bt}}\times {\mathbf{g}}_{\text{rl}})\times {\mathbf{g}}_{\text{bt}}}{\Vert ({\mathbf{g}}_{\text{bt}}\times {\mathbf{g}}_{\text{rl}})\times {\mathbf{g}}_{\text{bt}}\Vert }$$ (4)

Based on the corrected gradient vector field ${\stackrel{\sim }{\mathbf{g}}}_{\text{rl}}$, a new harmonic field in the direction from right to left is restored. The details of the gradient vector field calculation and harmonic field restoration from gradient vector fields can be found in the work of Liao et al. (2009) and Li et al. (2011). This harmonic field restoration brings the parameterization closer to conformal, which preserves the angles and local shapes during the hexahedral mesh mapping (Cartade et al. 2013). Based on the harmonic fields from right to left and bottom to top, the harmonic fields from inner to outer are uniformly scaled by defining the value in harmonic field of the outer surface as 1 and the inner surface as 0. Given a node p_in on the inner surface having harmonic field values from right to left u₀ and from bottom to top w₀, there is a corresponding node p_ot on the outer surface having the same harmonic field values. The harmonic field from outer to inner on the trace of p_ot to p_in is uniformly changing from 1 to 0.

3.2.2 Hexahedral mesh mapping

After constructing the volumetric parameterization for the patient-specific facial soft tissue model, the mapping of the hexahedral mesh from the unit cube domain to the patient-specific facial soft tissue model is achieved by applying the reversed map, f⁻¹. First, hexahedral mesh is generated by dividing the unit cube according to the desired mesh resolution. Then, hexahedral mesh mapping from the cube to patient-specific facial soft tissue model is created by mapping the following vertices: (1) hexahedral mesh vertices on the frontal boundary of the unit cube to the skin surface of the patient-specific facial soft tissue model, (2) hexahedral mesh vertices on the back boundary of the unit cube to the mucosa surface of the patient-specific facial soft tissue model, and (3) hexahedral mesh vertices inside the frontal and back boundaries of the unit cube to the vertices insider the skin and mucosa surfaces of the patient-specific facial soft tissue model.

A corresponding parameterized triangle on the boundary of the patient-specific facial soft tissue model is identified for each of the hexahedron vertex on the frontal and back boundaries of the unit cube. Additionally, a corresponding parameterized tetrahedron on patient-specific facial soft tissue model is identified for each of the hexahedron vertex inside the frontal and back boundaries of the unit cube. Then, the mapped hexahedra vertex in the patient model is interpolated by a linear combination of the vertex coordinates of the identified triangle or tetrahedron with corresponding barycentric coordinates. For a hexahedral mesh vertex h on the boundary surfaces (frontal and back surfaces) of the unit cube and its corresponding parameterized triangle with vertices r₁, r₂, r₃ in the parametric domain, the barycentric coordinates of h in this triangle are λ₁, λ₂ and λ₃, where h = λ₁r₁+λ₂r₂+λ₃r₃. Based on the barycentric coordinates, the Cartesian coordinate of the mapped vertex of h on the patient model can be calculated by v_h = λ₁v₁+λ₂v₂+λ₃v₃, where v₁, v₂ and v₃ are the corresponding vertices of the triangle in original domain V. Similarly, for a hexahedral mesh vertex between the boundary surfaces of the unit cube, its corresponding parameterized tetrahedron with vertices r₁, r₂, r₃, r₄, with the barycentric coordinates λ₁, λ₂, λ₃, λ₄, the Cartesian coordinate of the mapped vertex of h on the patient model can be calculated by v_h = λ₁v₁+λ₂v₂+λ₃v₃+λ₄v₄, where v₁, v₂, v₃ and v₄ are the corresponding vertices of the tetrahedron in original domain V.

3.2.3 Anatomical structure information

For accurate simulation of the anatomical structure of the facial soft tissue, the generated patient-specific hexahedral mesh should have at least 3 layers (representing skin, muscles, and mucosa) from frontal to back boundaries. To achieve the best anatomical representation, anatomical structure information is integrated into the patient-specific hexahedral mesh. First, to better represent anatomical structures such as the skin and mucosa, tissue thickness is adjusted in the model. After hexahedral mesh mapping, the patient-specific hexahedral mesh has approximately equal thickness in all layers from inside to outside. However, the thickness of the real skin and mucosa is generally limited to within 2 mm each (Barbarino et al. 2009). Therefore, the thickness of the most inside and outside layers of the hexahedral mesh model, which represent mucosa and skin, respectively, are adjusted to be limited to within 2 mm. For the FE mesh with more than 3 layers, the layer between the inside and outside layers will be very thin for soft tissue of less than 6 mm of thickness (e.g., area above eyes). In order to preserve the shape regularity of hexahedra, all mesh layers in the thin soft tissue area (less than 6 mm) are divided into the same thickness. As these areas are mainly around the eyes and forehead, they have negligible effect on the soft tissue change simulation.

Secondly, muscle volume assignment in the hexahedral mesh model closely reflects real muscle volume. When the hexahedral mesh is generated, hexahedral elements will fall into one of two categories: elements overlapping with muscle or elements not overlapping with muscle. Muscle volume of the hexahedral mesh is then determined by a cutoff fraction. When the overlap ratio of a hexahedral element with the muscle region of the patient is larger than the cutoff fraction, this element is assigned as a muscle element. Using a minimization scheme to reduce partial volume effects, the cutoff fraction threshold that represents the real volume of the muscle the best is selected. The other elements except those for skin, mucosa, and muscles are assigned as filler elements. Lastly, elements between the upper and lower lips are deleted to replicate the open mouth of the patients.

The soft tissue layers in this study are tied together through sharing edges and nodes. The adjoining anatomical structures (skin, mucosa, muscles, or filler) are fully tied based on element connectivity. Tied contact without sliding between soft tissue layers is considered as a valid representation of the physiological interaction between the layers for its stability (Barbarino et al. 2009). A highly detailed description of interaction between layers can lead to excessive computational time and affect convergence (due to the high number of degrees of freedom of the numerical model) (Barbarino et al. 2009).

4 Validation and results

Two validations were completed to evaluate the efficiency of our eFTD-VP approach. In the first validation, the surface fitting accuracy of our eFTD-VP approach was evaluated using 30 patient datasets. Then, the mesh quality (element shape and regularity) of our approach was compared with two other published methods. In the second validation, the accuracy of the internal anatomical structure correspondence generated with our approach was assessed using four visible human datasets. During both validations, parameter α in the surface registration Eq. (1) was set as 1, which produced a good balance between surface mesh quality and registration accuracy (Zhang et al. 2016). It achieves registration error within 1 mm in average and produces triangular surface suitable for tetrahedral mesh generation using Tetgen (Si 2015). The algorithms were implemented in MATLAB using a regular office PC with a 3.4 GHz CPU and 16 GB RAM. The protocol was approved by our Institutional Review Board prior to the study (IRB0413-0045).

Computational power can be a limiting factor in FE mesh generation. Meshes with higher resolution may better reflect anatomical structures; however, they also demand greater computational resources for FEM processing. With the eFTD-VP approach, mesh resolution can be adjusted by controlling the density of the hexahedra as described in Sect. 3.2.2. We tested three different resolutions of patient-specific FE meshes for each dataset in both validations. The resolutions used were high (118 × 8 × 116 elements), medium (78 × 8 × 78 elements), and low (48 × 5 × 48 elements). The meshes in the three resolutions of a patient are shown in Fig. 4. Furthermore, different cutoff fractions for muscle elements were assigned to meshes of different resolutions. The cutoff fractions of 52, 50, and 45% were assigned, respectively, to the high-, medium-, and low-resolution meshes. These cutoff fractions were selected to ensure that the volume of muscle elements closely reflected the real muscle volume as identified by studying the 30 patient datasets. This always yielded the best representation of muscles at each mesh resolution. Lower-resolution meshes have lower cutoff fractions because larger elements lead to more coarsely defined muscles. Higher-resolution meshes require higher partial cutoff fractions to accurately reflect muscle volume. This is because in higher resolutions, the anatomical shape of muscles is represented in more intricacies and detail. The mesh qualities in different resolutions were analyzed and subsequently compared to each other.

Fig. 4.

Hexahedral meshes in three resolutions. Left: low resolution in 48 × 5 × 48 elements; middle: medium resolution in 78 × 8 × 78 elements; right: high resolution in 118 × 8 × 116 elements. The cutting plane in d crosses the middle of lower lip. In d, skin is in brown, mucosa is in yellow, and muscles are in red. a Hexahedral mesh in side view. b Close-up view of the mesh in the red box of a. c Hexahedral mesh in back view. d Cut view showing inner structure

4.1 Validation #1: surface fitting accuracy and mesh quality analysis

Datasets of 30 patients with Class I, II, or III dentofacial deformity were used in this validation. For each patient, an axial CT scan of the head (512 × 512 scanning matrix, 1.25-mm-thickness slice, and 250 mm field of view, captured in 120 kV and 250 mAs) and a 3D facial soft tissue photograph (3dMD, Atlanta, GA) were used. 3D CT soft tissue was replaced by the 3dMD soft tissue by registering the 3dMD photograph to the CT model. This was done to prevent any possible facial soft tissue strain during the CT scanning (Zhang et al. 2016). All patient-specific models needed in the validations were successfully generated using our eFTD-VP approach, regardless of the class of their deformity. Figure 5 shows four representative deformities.

Fig. 5.

Generated soft tissue models for 4 representative deformities (a Class III; b Class III with anterior open bite; c Class II; and d Class II with strained lip and anterior open bite) using our eFTD-VP approach. Each patient shows an original 3dMD skin surface, a generated tissue model with visible muscles, and a volume mesh (from left to right in both front and left views)

4.1.1 Surface fitting accuracy

Surface fitting accuracy of our eFTD-VP approach was evaluated between the boundary surfaces (skin and mucosa) of the eFTD-VP-generated hexahedral mesh to that of the original patient skin and skull surfaces. The surface fitting error was measured as the shortest distance from the surface nodes of the hexahedral mesh to the target surface.

The mean, standard deviation (SD), maximum, and minimum of the surface fitting errors in the resolution of high are presented in Table 1. The fitting error of skin surface was 0.20 mm/0.35 mm (mean/SD), and for the skull surface, the fitting error was 0.49 mm/0.52 mm. For hexahedral meshes in medium and low resolutions, the surface fitting error was similar to that of the hexahedral mesh in resolution of high. The difference was approximately 0.01 mm. The acceptable error in 3D surface registration and surgery navigation for clinical use in oral and maxillofacial surgery was reported to be less than 1 mm (Maal et al. 2010; Austin and Antonyshyn 2012; Grauvogel et al. 2017). Therefore, the eFTD-VP approach’s surface fitting accuracies of all three resolutions were better than the acceptable errors for surgical navigation. Consequently, this will allow us to use the proposed technique as adjunct with surgical planning in maxillofacial surgery.

Table 1.

The mean, SD, maximum, and minimum of the surface fitting errors between the boundary surfaces of the hexahedral mesh in resolution of high (118 × 8 × 116) and original skin and skull surfaces for the 30 test patients (mm)

	Mean	Maximum	Minimum	SD
Skin	0.20	1.97	0.0026	0.35
Skull	0.49	2.38	0.0036	0.52

Table 1 also shows that the maximum fitting error can be large as around 2 mm. In order to deeply analyze the fitting error, surface fitting accuracy was analyzed using error distribution and then visualized on a color-coded deviation map. Color-coded deviation maps of a randomly selected example patient from the 30 patients are shown in Fig. 6. The deviation maps indicated that the majority of the vertices on the skin boundary of the hexahedral mesh to patient skin surface displayed an error less than 0.2 mm (Fig. 6b). Only small regions around the lips, eyes, and cheeks had errors larger than 0.3 mm. For errors from the mucosa boundary of the hexahedral mesh to patient skull surface, some regions around the teeth, chin, and boundary of skull surface had errors larger than 0.8 mm (see Fig. 6c). The source of these larger errors of the mucosa surface stemmed from the simplification and smoothing during the preparation of the eFace template facial soft tissue model. The surface deviation between the boundary surfaces of the hexahedral mesh and outer surface of the generated patient-specific facial soft tissue model was less than 0.01 mm on average with a maximum error of around 0.5 mm, as shown in Fig. 6d, e. This is much smaller than the error between the boundary surfaces of the hexahedral mesh to the original patient skin and skull surfaces. Therefore, this indicates that the main source of surface fitting error is resulted from the generation of the patient-specific facial soft tissue model using the method in Sect. 3.1.

Fig. 6.

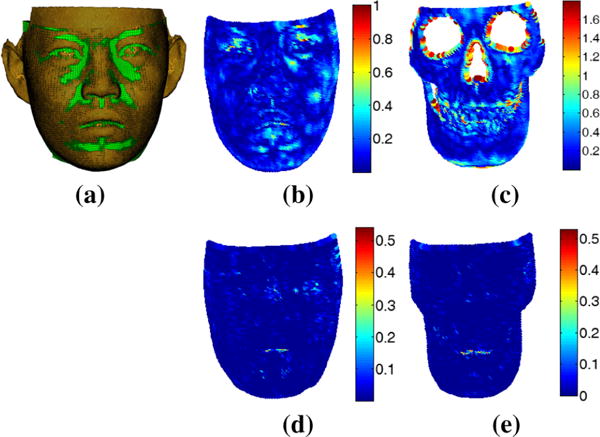
Distance measure for boundary surfaces (skin and mucosa) of the hexahedral mesh. a Overlay of original skin surface with the hexahedral mesh, b color code of distance to original patient skin surface, c color code of distance to original patient skull surface, d and e color codes of distance to generated closed patient-specific facial soft tissue surfaces by using proposed surface registration method in Sect. 3.1

4.1.2 Mesh generation accuracy compared with prior published methods

To evaluate the improvements of eFTD-VP-generated FE meshes, they were compared to FE meshes generated from two previously published methods. The related publications include our hybrid method (Zhang et al. 2016) and the hexahedral mesh transferring method (HMT method) (Li et al. 2011). These two methods generated patient-specific facial soft tissue FE mesh model by deforming a template FE mesh model. As reported, the hybrid method outperformed related methods of Chabanas et al. (2003), Lou et al. (2012). The hybrid method first performed a surface morphing. Then, the template hexahedral FE mesh model was deformed by TPS based on surface morphing to generate the patient-specific facial soft tissue FE mesh model. Differently, our eFTD-VP approach generated the patient-specific facial soft tissue FE mesh model directly from the patient-specific facial soft tissue surface. HMT method also used volumetric parameterization for generating patient-specific facial soft tissue FE mesh model. A triple harmonic fields (i.e., from outer to inner, right to left, bottom to top) were calculated to construct the volumetric parameterization from a template FE mesh model to a patient-specific facial soft tissue tetrahedral mesh model. Differently, our eFTD-VP approach only calculated two harmonic fields (i.e., from right to left, bottom to top) and generated a uniform scaled harmonic field from outer to inner. Additionally, our eFTD-VP approach constructed the volumetric parameterization from a unite cube with hexahedral mesh to a patient-specific tetrahedral mesh model. In order to comparable with our eFTD-VP method, the patient-specific facial soft tissue tetrahedral mesh model used by the HMT method was generated using our approach. The definition of the shape end boundaries was also defined the same way as our eFTD-VP approach.

The mesh quality of each method was evaluated. The mesh quality was measured by scaled Jacobian (SJ) (Zhang and Bajaj 2006), hexahedron shape skew (SS) (Knupp 2003), and the number of invalid elements (InE). SJ was evaluated for each node of a hexahedron and measured between −1 and 1. A higher value indicated a less distorted hexahedron. Negative SJ values signify that the elements are invalid (InE). The average of the 8 SJ values of a hexahedral element was used to describe the quality of the element. The SS metric was measured between 0 and 1, in which 1 signifies a rectangular brick and 0 a degenerate element. The mean values of SS, SJ, and InE for the datasets of 30 patients were used for final comparison.

Patient-specific hexahedral FE mesh models in high (118 × 8×116), medium (78 × 8 × 78), and low (48 × 5 × 48) resolutions were generated by all the three methods. The template FE mesh models used by the hybrid and HMT methods were constructed by applying our eFTP-VP approach on our eFace template model. The template FE mesh models in high, medium, and low resolutions all showed minimal distortion and had a SJ value of around 0.94 and SS value of around 0.96.

The summary of the mesh quality comparison results is shown in Table 2. The results indicated that our eFTD-VP approach-generated hexahedral FE mesh yielded the best mesh quality. Our mesh for all three resolutions contained no InE, SJ value around 0.96, and SS metric around 0.97. The hybrid method showed a diminished mesh quality caused by the deformation of the template to fit the shape of the patient. The hybrid meshes for all three resolutions showed reduced SJ value to around 0.81 and reduced SS metric to around 0.86. Some of the boundary elements were distorted and determined to be invalid. Additionally, from the example mesh in Fig. 7a we can see that the mesh density from outer to inner layer was not uniform. For the HMT method, some elements of the skin and mucosa layers were distorted and rendered invalid, especially elements on the outer and inner layer (see the example mesh in Fig. 7b). Reduced hexahedral mesh quality was seen in low resolution with 254 InE. The quality of HMT-generated high-resolution mesh was further reduced with the presence of 5452 InE. The large number of InE in the HMT method affected the mesh quality. This can be attributed to the not uniformly scaled harmonic field from outer to inner layers, which was affected by the quality of the tetrahedrons.

Table 2.

Comparison with two related methods (30 subjects)

48 × 5 × 48 elements	InE	SJ	SS
HMT method	254	0.885	0.905
Hybrid method	88	0.811	0.858
eFTD-VP method	0	0.952	0.967
78 × 8 × 78 elements	InE	SJ	SS
HMT method	2381	0.825	0.853
Hybrid method	240	0.808	0.859
eFTD-VP method	0	0.958	0.971
118 × 8 × 116 elements	InE	SJ	SS
HMT method	5452	0.807	0.839
Hybrid method	467	0.809	0.861
eFTD-VP method	0	0.956	0.970

Fig. 7.

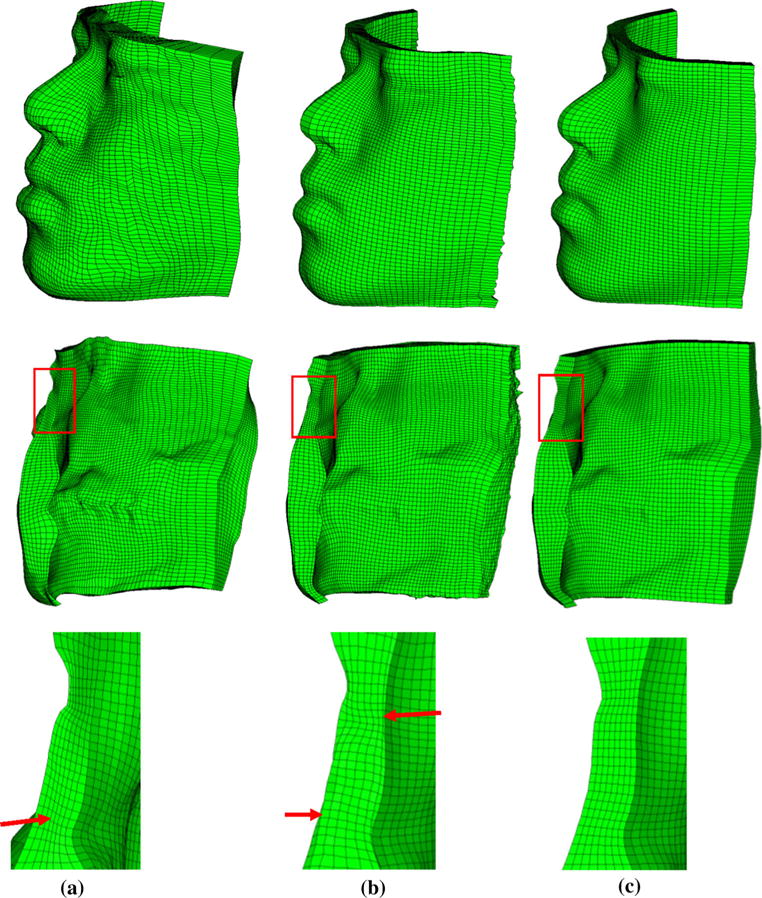
Hexahedral meshes generated by three methods. Top: left view of front face; middle: left view of back face; bottom: Close-up view of regions in red box in middle. Red arrow in a indicates the non-uniform mesh density from outer to inner layer. Red arrow in b indicates the folded elements in outer and inner layers. a Hybrid method, b HMT method, c eFTD-VP method

The computational time of the three methods was similar, and each took around 3 min. The majority of computational time of our eFTD-VP approach was spent on hexahedral mesh generation (around two minutes). The high computational cost of hexahedral mesh generation was caused by the calculation of harmonic fields and determination of muscle elements. Computational cost also increased slightly with increased mesh resolution due to determination of more detailed muscle elements. We believe a significant improvement in speed is possible when the MATLAB code is converted to executable Microsoft Foundation Class C/C++ code. It is expected to improve execution time to within one minute.

4.2 Validation #2: evaluation of the accuracy of internal structure matching

The purpose of this validation was to determine the accuracy of internal anatomical structures (i.e., muscles) between our eFTD-VP generated model and the ground truth model. Four visible human datasets [(NLM Visible Male (NLM-M), NLM Visible Female (NLM-F), Chinese Visible Human 3 (CVH3), and Korea Visible Male (KVM) (Shin et al. 2012)] were used to assess the accuracy of the internal anatomical structures (i.e., muscles). For each visible human dataset, anatomically detailed facial soft tissue models, including skin, mucosa, and individual muscles, were manually segmented and generated. This served as the ground truth during validation. The segmented ground truth muscles, generated muscles from eFace template, and muscle elements in hexahedral models for NLM-M are shown in Fig. 8.

Fig. 8.

Muscles of NLM-M. The name of each muscle is indicated in a. a Segmented ground truth muscles, b generated muscles from eFace template, c low resolution, d medium resolution, e high resolution

Our eFTD-VP generated hexahedral mesh was superimposed to the ground truth model to evaluate the accuracy of internal anatomical structure. Two overlap ratios (measured by recall and precision) were used to measure the difference between the experimental and ground truth models. For the volume of template muscle elements A and the volume of ground truth muscles B, $\mathit{recall}=\frac{A\cap B}{B}$, and $\mathit{precision}=\frac{A\cap B}{A}$. Higher recall and precision values imply a better overlap between the eFTD-VP generated muscles and ground truth muscles.

The accuracy of internal structure matching was evaluated in two ways. Firstly, the overall muscle overlap ratios of our eFTP-VP approach were compared to those of state-of-the-art muscle generation methods that were used for facial soft tissue change prediction. Then, the individual muscle overlap ratios were evaluated by comparing to the midpoint of the test variable (50%).

The methods used for the comparison with our eFTP-VP approach were the hybrid method (Zhang et al. 2016), HMT method (Li et al. 2011), the landmark-based transformation (LbT) method (Lou et al. 2012), landmark-based TPS (L-TPS) method (Kim et al. 2012), affine transformation (Affine) based on landmarks (Hung et al. 2015), and mesh-matching (M-M) method (Chabanas et al. 2003). These methods generated the patient-specific muscles by deforming a template muscle model based on surface, landmark or volume registration. Our digitized skin and skull landmarks in total of 93 were used in the hybrid, Lbt, and Affine methods. The 48 landmarks on the skull were used in the L-TPS method. The M-M method conducted the registration by using the rigid, affine, and local spline registration without landmarks. The muscle overlap ratios for FE mesh in high (118 × 8 × 116), medium (78 × 8 × 78), and low (48 × 5 × 48) resolutions were all calculated for hybrid, HMT and our methods. In contrast, for Lbt, L-TPs, Affine, and M-M methods, the overlap ratios of the deformed muscle geometry volume to the ground truth muscle geometry volume were calculated without dividing into hexahedrons. The comparison is shown in Fig. 9.

Fig. 9.

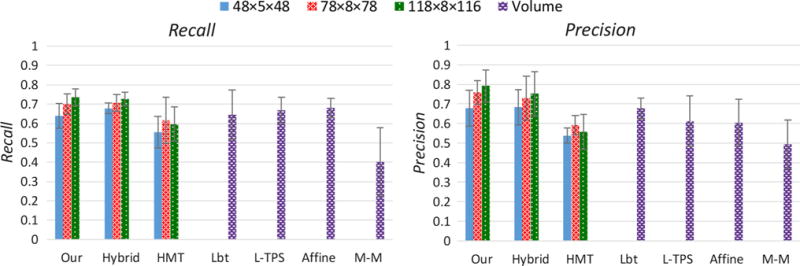
Bar plot of recall and precision values for comparing accuracy of muscle matching by the seven methods: Hybrid, HMT, LbT, L-TPS, Affine, M-M, and our eFTD-VP methods. The recall and precision values in the bar are the average values of the four visible human subjects. The recall and precision values for each visible human subject are calculated by considering all eleven muscles as a unified piece. The error bar describes the standard deviation (SD) of the four visible human subjects. The volume overlap ratio means the overlap between deformed muscle geometry volume and the ground truth muscle geometry volume without dividing into hexahedrons

Compared to state-of-the-art muscle generation methods, our method showed superior muscle matching accuracy. Our eFTD-VP approach achieved recall and precision values as follows: 0.74/0.04 (average/SD) of recall and 0.79/0.08 of precision for high-resolution mesh, 0.70/0.05 of recall and 0.76/0.06 of precision for medium-resolution mesh, and 0.64/0.06 of recall, and 0.68/0.09 of precision for low-resolution mesh. This demonstrated that regardless of mesh resolution, the eFTD-VP generated patient-specific mesh displayed an internal structural accuracy of greater than 60%. Generally, with the increase of mesh resolution the overlap ratios slightly increased. The overlap ratios of hybrid method had similar values with our eFTP-VP approach. This was reasonable as these two methods used the same surface registration. The overlap ratios of the HMT method were distinctly smaller than those of our method for all the three resolutions. This was due to the heavy distortion of elements in the hexahedral mesh transferring. The three methods that generate patient-specific muscles based on landmark registration (Lbt, L-TPs, and Affine) had similar recall values (around 0.65), and they were close to those of our method. This demonstrated the efficiency of use of landmark information in preserving anatomical correspondence. However, the registration based on landmarks only could not generate fine surface fitting. This resulted in poor precision values of the three methods compared with our method. The M-M method had recall of 0.40/0.18 and precision of 0.50/0.12 which were significantly smaller than those of our method. The bad muscle matching of M-M method was resulted from the mesh matching without landmark constraints. The comparison generally concluded that our method preserved the correspondence of internal anatomical structure better than the state-of-the-art methods (HMT, Lbt, L-TPs, Affine, and M-M). The reason is due to the accurate surface registration in our method.

Recall and precision values for each individual muscle of the four visible human subjects in three resolutions are shown in Fig. 10. The overlap of muscle elements to the ground truth model slightly decreased from high resolution to low resolution. This was expected as muscles have more detail in high-resolution models. Among individual muscles, 73% in high resolution, 70% in medium resolution, and 52% in low resolution displayed both overlap ratios (recall and precision) as higher than 50% to the ground truth model.

Fig. 10.

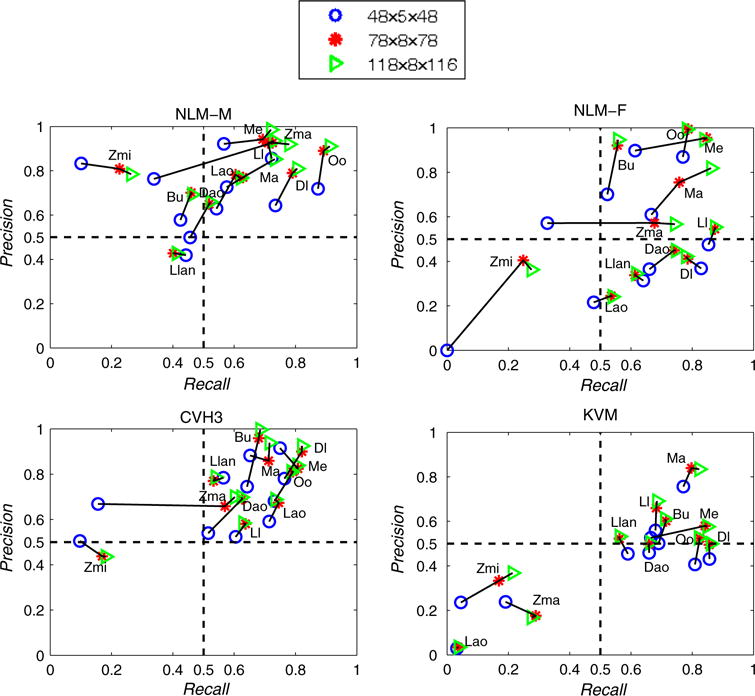
Recall and precision values for each muscle of the four visible human datasets

Only Zma, Zmi, Llan, and Lao muscles were more likely to have less than 50% overlap ratio for both recall and precision. The overlap of these muscles had distinct significant difference between visible humans. The main reason for this statistically significant difference is the varying shape and placement of these muscles among people. This can be seen from the ground truth muscles in Fig. 11. Additionally, mesh resolution also factored into the difference for recall and precision of Zmi and Zma muscles. Decreasing mesh resolution from medium to low led to distinct decrease in recall, while the precision value remained fairly constant. This finding was due to the disappearance of Zmi and Zma muscles in the low-resolution mesh model (see Fig. 8c), while both muscles were visible in the medium-resolution mesh model (see Fig. 8d). The precision of Zmi was relatively larger than its recall because the volume of the eFTD-VP generated Zmi was smaller than the ground truth Zmi. Finally, recall and precision for the Lao muscle varied significantly in KVM compared to NLM-M, NLM-F, and CHV3. This was caused by placement differences of Lao in KVM compared to its placement in NLM-M, NLM-F, and CVH3.

Fig. 11.

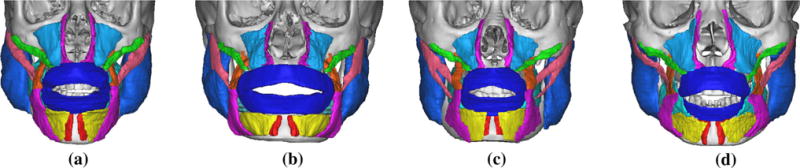
Segmented ground truth muscles for the four visible human datasets. a NLM-M, b NLM-F, c CVH3, d KVM

5 Discussion

This paper presents a novel eFTD-VP framework to generate high-quality patient-specific anatomically detailed facial soft tissue FE mesh. Firstly, in order to efficiently generate the patient-specific anatomically detailed facial soft tissue model (including skin, mucosa, muscles), a hybrid landmark-based morphing and dense surface fitting approach is developed to deform an eFace template to match the shape of the patient. This eFace template deformation method could generate the patient-specific facial soft tissue model with accurate corresponding internal structures (overall overlap of muscles larger than 60%) and accurate surface matching (surface fitting error of 0.2 mm for skin and 0.5 mm for skull) within one minute. Then, high-quality 3D hexahedral mesh is generated for the patient-specific facial soft tissue model based on volumetric parameterization (SJ is bigger than 0.95, SS is bigger than 0.96, and no invalid elements) within two minutes. The resulted patient-specific facial soft tissue FE mesh can be directly used to simulate soft tissue changes following an osteotomy. Furthermore, the patient-specific facial soft tissue FE mesh generated by our method provides the potential for conducting parameter optimization to characterize the mechanical behaviors of the tissue when simulating craniomaxillofacial surgery.

The eFTD-VP approach performs better than both our previous hybrid method and the HMT method in the generation of high-quality hexahedral mesh. The hybrid method utilizes a template hexahedral mesh to fit the shape of the patient, but distortions in the mesh present after shape fitting. The HMT method constructs volumetric parameterization by calculating triple volumetric harmonic fields (i.e., from outer surface to inner, from right to left, and from bottom to top). However, a significant reduction of hexahedral mesh quality is observed, because it is difficult to generate uniform harmonic fields from the outer to inner surfaces for the varying thickness of the soft tissue model and the quality of tetrahedrons. In contrast, our method constructs volumetric parameterization for the facial soft tissue model by calculating only a pair of volumetric harmonic fields (i.e., from right to left and bottom to top) while generating a uniformly scaled harmonic field from the outer to inner dimension. Additionally, our approach generates the patient-specific anatomically detailed facial soft tissue model by deforming a template model instead of manual generation, which saves a lot of time.

Surface of the resulted muscle structure is not as smooth as the real muscle surface because the muscle structure is composed of numbers of hexahedral elements (jagged, especially for low-resolution mesh). It is difficult to remesh muscle element along the real muscle surfaces even for tetrahedral element mesh (Kim et al. 2012). The jagged muscle surface may result in discontinuities of strain in the FEM simulation that can further affect the convergence (Liu et al. 2012). To avoid this problem, material properties of the elements that intersect with the muscle surface can be assigned considering volumetric portion of the muscle in each of the corresponding element (Kim et al. 2012; Warburton and Maddock 2013).

Functional simulation such as active muscle reaction or muscle attachment change is not considered during the development of our method. In our mesh, detailed anatomy of muscle (e.g., skeletal muscle fiber and its orientation) is not reflected because active deformation mechanics such as active contraction of muscle fibers is not considered. There is a previous study that integrates the fiber orientation into the soft tissue simulation for craniomaxillofacial surgery (Kim et al. 2012). Our FE mesh could also be extended for performing active mechanics simulations (e.g., facial expression simulation) by adding the fiber information. The effect of muscle structure integration (tissue geometry and properties) combined with the mesh density will be studied in our future research.

We have noted certain areas that could be improved in the future. These improvements include landmark digitization and the incorporation of variable mesh density. Landmark constraint is necessary and effective in the preservation of anatomical correspondence. However, we recognized the landmark digitization error. In addition, although we selected easily identifiable anatomical landmarks, it still took around 20 minutes to complete landmark digitization. An automatic process for digitizing landmarks may significantly improve both its accuracy and efficiency, e.g., using landmark atlas (Saloa et al. 2015), or shape-based method (Gilani et al. 2015). We are currently working on separate projects to achieve automatic landmark digitization.

The hexahedral mesh generated by our approach shares the same layers and resolution throughout the entire tissue. However, in reality, the thickness of certain tissue sections is greater than that of others. Therefore, more layers may be needed in thicker regions while other regions may only require a few layers. In future studies, we may develop a hexahedral mesh generation method to generate elements with varying mesh density.

6 Conclusions

This paper presents a novel eFTD-VP framework to generate high-quality, patient-specific, anatomically detailed, facial soft tissue FE mesh. First, the structured patient-specific facial soft tissue (including skin, mucosa, and muscles) is efficiently generated by deforming an eFace template model. Then, high-quality hexahedral mesh is constructed by using volumetric parameterization. Users can control the resolution of the hexahedron mesh to best reflect individual need and conduct mesh density sensitivity analysis. Experimental results show high accuracy and high quality in the generation of facial soft tissue FE mesh while preserving the anatomical correspondence. The presented method has clinical significance as it saves time and improves accuracy and quality of subject-specific facial soft tissue FE mesh.