Proton range verification in homogeneous materials through acoustic measurements

Abstract

Clinical proton beam quality assurance (QA) requires a simple and accurate method to measure the proton beam Bragg peak (BP) depth. Protoacoustics, the measurement of the pressure waves emitted by thermal expansion resulting from proton dose deposition, may be used to obtain the depth of the BP in a phantom by measuring the time-of-flight (TOF) of the pressure wave. Rectangular and cylindrical phantoms of different materials (aluminum, lead, and polyethylene) were used for protoacoustic studies. Four different methods for analyzing the protoacoustic signals are compared. Data analysis shows that, for Methods 1 & 2, plastic phantoms have better accuracy than metallic ones because of the lower speed of sound. Method 3 does not require characterizing the speed of sound in the material, but it results in the largest error. Method 4 exhibits minimal error, less than 3 mm (with an uncertainty ≤1.5 mm) for all the materials and geometries. Psuedospectral wave-equation simulations (k-Wave MATLAB toolbox) are used to understand the origin of acoustic reflections within the phantom. The presented simulations and experiments show that protoacoustic measurements may provide a low cost and simple QA procedure for proton beam range verification as long as the proper phantoms and calculation methods are used.

1. Introduction

Proton therapy is an advantageous tool for radiation therapy because of the proton beam’s characteristic Bragg Peak (BP). When protons pass through materials they slow down and the energy deposition increases due to the inverse square relationship between stopping power and velocity. The main advantage of proton therapy is that the dose drops steeply beyond the BP, and, because of this feature, the Planning Target Volume (PTV) can be precisely covered while nearby normal tissue is spared. This sharp dose fall-off feature, however, presents clinical difficulties due to range uncertainty. To avoid overdosing the normal tissue or under-dosing the tumor, a number of possible in vivo proton range verification techniques are being studied (Knopf and Lomax 2013; Knopf 2009; Min, et al. 2006).

Protoacoustics (Albul, et al. 2001; Askaryan 1957; Bychkov, et al. 2008; Hayakawa, et al. 1995; Jones, et al. 2016a; Jones, et al. 2015; Jones, et al. 2014; Sulak, et al. 1979)is a proposed range verification method that measures proton range based on the time-of-flight of acoustic waves emitted due to thermoacoustic conversion of heat to pressure. Protoacoustics is advantageous because it may potentially be a real time monitor. It is simple and lower cost than other methods. It has been demonstrated that the location of the Bragg peak in water can be determined by protoacoustic methods with an accuracy of 1 mm in water (Alsanea, et al. 2015; Assmann, et al. 2015; Jones, et al. 2016a; Jones, et al. 2016b; Parodi and Assmann 2015; Patch, et al. 2016), which is comparable to the PG and PET accuracy reported in literature (Richter, et al. 2016). Previous studies of protoacoustics, however, have all been performed in water tanks with the focus of working towards in vivo range verification, where dose constraints may severely limit accuracy (Jones, et al. 2016a; Jones, et al. 2015; Jones, et al. 2016b). In this study, we investigate the application of protoacoustics as a potential quality assurance (QA) method by measuring the range verification accuracy in various solid materials. Protoacoustic-based QA may be advantageous because of reduced cost, simplicity, and increased information content. Compared to the in vivo attempts, application to QA benefits from higher acceptable doses, homogeneous pre-characterizable materials, and the flexibility to place multiple detectors at known positions on (or in) the phantom surrounding the dose deposition. To understand the QA potential, we measured the proton beam range in rectangular and cylindrically shaped phantoms composed of metal (aluminum and lead) and plastic (polyethylene (PE)). We investigate the following questions: (1) How does the protoacoustic signal amplitude and waveform depend on material and geometry? (2) What method is best suited to process and analyze the acoustic signal? (3) What accuracy can we expect to achieve in determining the proton BP depth in these phantoms? This study can provide further insight into which thermoacoustic material features are of importance for designing a future protoacoustic-based QA device. There are different approaches to obtain the acoustic time-of-flight (TOF) (Assmann, et al. 2015; Jones, et al. 2016b; Parodi and Assmann 2015; Patch, et al. 2016), which involves extensive calibration and calculation. We develop four novel methods for extracting the protoacoustic arrival times from the detected signal and compare their accuracy in determining the proton BP depth in the phantom. Each method has its own phantom material and phantom geometry strengths and limitations.

In section II, we introduce the basic physics of protoacoustics which explains how the proton dose is converted to acoustic pressure in materials. The proton dose was calculated using GEANT4-based TOPAS Monte Carlo (Perl, et al. 2012) and protoacoustic pressure was simulated using k-Wave (Treeby and Cox 2010). These simulations were validated by experimental data. In section III, we compared the four different methods, which were applied to obtain the longitudinal range of the proton beam in different phantoms. The accuracy of our methods are evaluated and discussed. In section IV, we present discussion for future work.

2. Methods

2.1. Acoustic signal detection

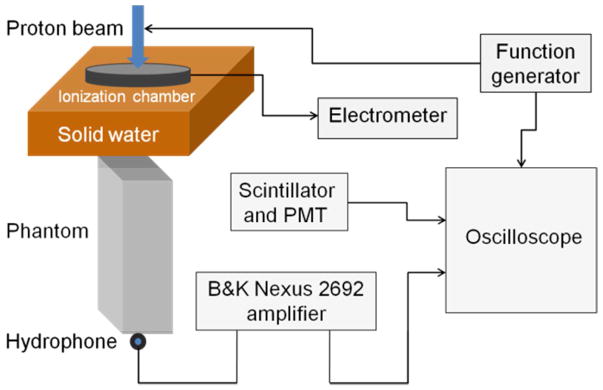
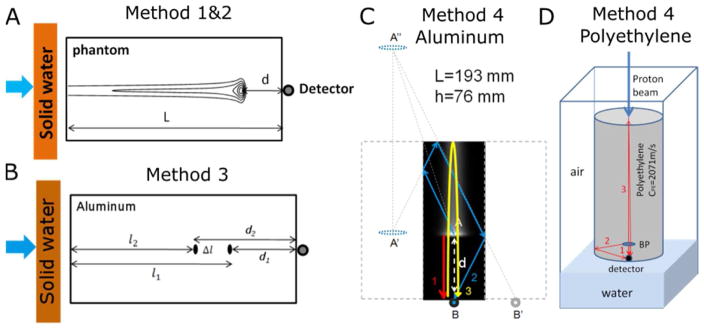
The experimental setup is illustrated in figure 1. The proton beam was produced with a maximum energy of 230MeV using the IBA clinical system at the Hospital of the University of Pennsylvania (Lin, et al. 2014a). The protoacoustic signals were measured by a Brüel & Kjær hydrophone 8105, which was amplified (65dB, x1780 gain) and filtered (10Hz high pass and 100kHz low pass filter) by a Nexus charge amplifier 2692. The hydrophone was mounted on a water tank, and its position was controlled by IBA Dosimetry Control Unit CU500E, Schwarzenbruck (Germany). The short, pulsed proton beam (pulse duration ~15 μs, IBA) was modulated by a function generator (rise time < 1 μs). The time-averaged proton current was measured by using a Bragg peak chamber (PTW T34070, Freiburg, Germany) placed in the beam path upstream of the phantom. The temporal proton beam signal was measured by collecting the prompt gamma photons with a scintillator and PMT. The PMT signal, the trigger signal from the function generator, and the amplified acoustics waves were output to a digital oscilloscope (Agilent DS07104A, Santa Clara, CA). The time-dependent acoustic signal detected by the hydrophone was averaged over 1024 measurements to achieve a stable and precise measurement, although the signal was still discernible from the noise with as low as 64 averages(Jones, et al. 2015). Based on GEANT4 calculations, for 10⁷ incident protons, the dose delivered at the Bragg peak in an aluminum block is 0.412cGy. Therefore, an incident proton beam with an average current of 490nA, which consists of 5.7×10⁷ protons in a pulse, corresponds to 2.36cGy of radiation delivered to the Bragg peak. To collect 64–1024 averages, 1.5 – 24.2Gy were delivered at the BP.

Figure 1.

A Diagram of the experimental setup. The incident 230 MeV proton beam was directed downward from the figure top (the gantry was set as 0^o). The beam passes through the ionization chamber and solid water before reaching the phantom. The Brüel and Kjær 8105 hydrophone was mounted on the control arm of an IBA Blue Phantom water tank. The hydrophone was positioned at the distal surface of the phantom on the beam propagation axis. The distal end of the phantom and the hydrophone were immersed in water for acoustic coupling.

In an infinitely large homogeneous medium, the protoacoustic pressure detected by a hydrophone can be expressed as Eq. (1):

$$\mathrm{P}(\stackrel{\rightharpoonup }{r},t)=\frac{c_s\beta }{4\pi C_p}\frac{\partial }{\partial t}\left[E(t)\otimes \left\{{\int }_0^{2\pi }{\int }_0^{\pi }d{\theta }^{\prime }d{\phi }^{\prime }{|\stackrel{\rightharpoonup }{r}-\stackrel{\rightharpoonup }{r}|}^2\mathit{sin}\theta \frac{E(z,s)}{|\stackrel{\rightharpoonup }{r}-{\stackrel{\rightharpoonup }{r}}^{\prime }|}\right\}\right]$$ (1)

Where c_s is the speed of sound in medium, β is the thermal expansion coefficient, and C_p is the specific heat of the medium. Eq.(1) assumes that the proton beam deposits its energy with a 3D profile E(z, s) where z is along the proton beam’s longitudinal axis and s is on the radial plane relative to the beam axis. The time component of the proton beam pulse is denoted by E(t). r⃑ indicates the position of the hydrophone center and r⃑′ represents the position of each voxel in the phantom. The deposited energy increases the local temperature of the medium, which causes thermal expansion of the medium and the generation of initial pressure. If the excitation proton pulse is infinitely short, the initial pressure can be calculated by Eq.(2).

$$p_{\mathit{source}}(\stackrel{\rightharpoonup }{r})=\mathit{\Gamma }E(z,s)$$ (2)

Where Γ is Grüneisen parameter of materials calculated by $\mathit{\Gamma }=\frac{\beta {c_s}^2}{C_p}$. Although the analytical Eq.(1) is useful for understanding the origin of the protoacoustic signal, it is limited to infinite homogeneous media. To model reflections and attenuation, the k-Wave toolbox is used to obtain the acoustic pressure that reaches the hydrophone following a dose deposition. For k-Wave simulations, p_source was used as an input to simulate the pressure p_i(t) initiated by an instantaneous, infinitely shortproton pulse. To obtain the acoustic pressure waves, p(t), generated by a Gaussian function proton pulse of full-width-half-max (FWHM) of G(t, FWHM), the two terms were convolved:

$$p(t)=p_i(t)\otimes G(t,\mathit{FWHM})$$ (3)

After simulation, peaks in the p(t)were assigned to specific travel paths and reflections based on the TOF.

2.2 Proton dose calculation

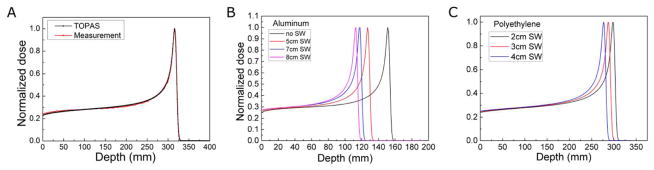
TOPAS was used to calculate the proton dose deposition in the different materials. To ensure that the TOPAS calculations match the clinical dose depositions, reported beam characteristics were used (Lin, et al. 2014a; Lin, et al. 2014b). To verify agreement, the TOPAS calculated dose depositions in water were compared to the dose-depth profile measured in water. The TOPAS calculation agrees with the measurement (figure 2A). The stopping power and proton beam range in metals and plastics obtained through TOPAS calculation agree with the PSTAR database of NIST. Therefore we assume that the proton dose deposition in these homogeneous phantoms is accurately calculated by TOPAS. (TOPAS validation has been presented previously (Lin, et al. 2014b)) The calculated dose distributions (E(z,s)) are used as an input parameter for the k-wave simulation (Eq.(2), figure 2C–F).

Figure 2.

The TOPAS-calculated proton integrated depth dose in water is validated by measured dose in water (A). The TOPAS-calculated integrated depth dose is also shown for aluminum (B) and polyethylene (C) phantoms after energy degradation with variable solid water thicknesses.

2.3. k-Wave acoustic simulation

The temporal acoustic pressure p_i(r⃑,t) generated by the dose distribution was simulated with the k-Wave MATLAB toolbox,(Treeby and Cox 2010) which has been previously validated through agreement between numerical calculations and experimental data collected in a water phantom (Assmann, et al. 2015; Jones, et al. 2015; Jones, et al. 2016b; Jones, et al. 2014). We used the proton dose distribution profile obtained by TOPAS as an input to the k-Wave simulation engine after multiplication by Γ (Eq. (2)). The grid size of the phantom for simulation was 1×1×1 mm³, and the time step was 0.1 μs.

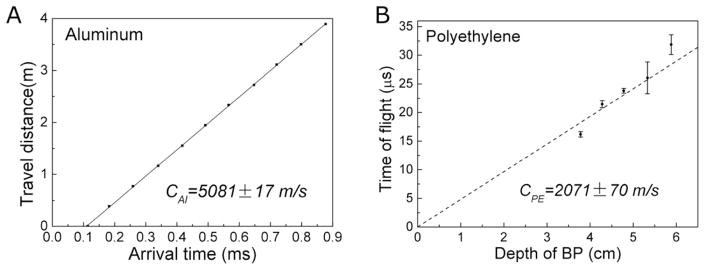
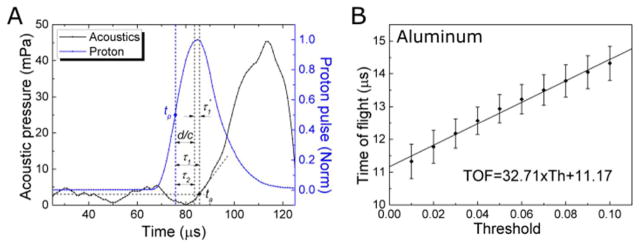
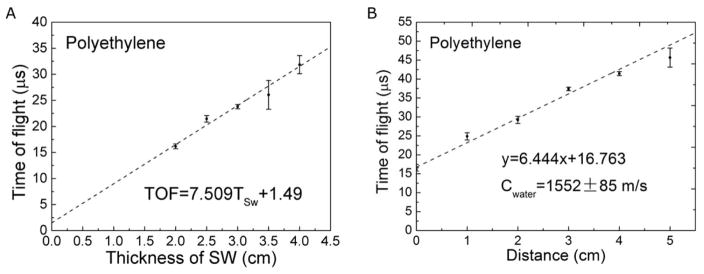
The frequency-dependent speed of sound is crucial to determine the depth of the BP, but the literature reported speeds are generally measured at >1 MHz, much higher than the ~50kHz protoacoustic signals. To properly model the acoustic propagation in k-Wave and to perform accurate conversion from TOF to distance, we experimentally measured the speed of sound of the investigated materials. We used a function generator to produce square wave pulses at a repetition rate of 1kHz and a pulse duration of 20 – 50 μs (the FWHM of our proton beam pulse is ~20 μs). The acoustic transducer’s frequency response is within +/− 14dB over the range from 0.7–10 kHz. The sound speeds were measured using three techniques. The first technique (reflection technique) is applied when acoustic signal reflects between proximal and distal surfaces of the phantom (see figure 3A). The speed of sound is obtained by linearly fitting the acoustic travel distance to its time of arrival. The second technique (shift-Bragg-Peak technique) measures the TOF after shifting the BP to known depths by adding solid water into the proton beam path. The speed of sound is then obtained by linearly fitting the depth of the BP to the TOF (figure 3B,C,D). The third technique (pitch-and-catch technique) measures the TOF of a piezoelectric-generated acoustic wave through a known distance of material. The speed of sound is then calculated by dividing the length of the phantom by the acoustic TOF through the phantom.

Figure 3.

The speed of sound in aluminum was measured with the reflection technique (A). (B) The speed of sound in polyethylene (2071 ± 70 m/s) phantoms were obtained with the shift-Bragg-peak technique by linearly fitting the depth of the BP to TOF (obtained by method 1).

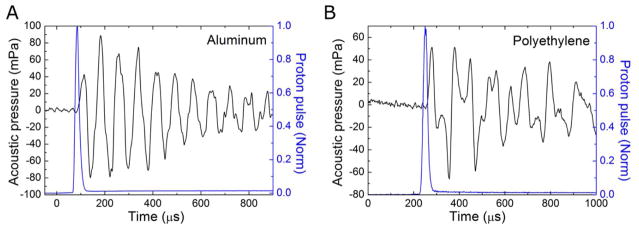
Using the initial pressure p_source(r⃑) and experimentally determined speed of sound, we simulated the acoustic pressure p_i(t) with the k-wave simulation. We then used Eq.(3) to obtain the total acoustic pressure p(t) and compared it with experimental data (see figure 5).

Figure 5.

Experimentally detected protoacoustic signals generated in aluminum (A) and polyethylene (B) phantoms. The normalized proton beam pulse (as measured by the PMT/scintillator) is indicated with the blue line.

2.4. Data analysis methods

We developed four different methods to process and analyze the acoustic pressure waves produced by the proton BP (see figure 4). For the measurements, the hydrophone was placed at the distal surface of the phantom. We define the arrival time (τ) as the time that acoustics travel from the Bragg peak to the detector, is expressed as Eq.(4).

Figure 4.

Illustration of Methods 1- 4 for determining the BP depth. (A) Diagram of method 1&2. (B) Arrival times (τ₁(T1), τ₁(T2)) were measured before and after shifting the depth of the BP by adding solid water into the beam path. The BP is shifted by $\mathrm{\Delta }l=t_w\frac{{\rho }_w}{{\rho }_m}\frac{{\overline{S}}_w}{{\overline{S}}_w}$ . With the help of acoustic simulation, the travel path of acoustic signals inside the phantom can be identified. Hence the difference in the arrival time of acoustic signals can be related to the depth of the BP and the geometry of the rectangular aluminum phantom (C) and the cylindrical polyethylene phantom (D). In the cylindrical case, the second arriving pressure peak is due to reflection off the circular side surface. Although this is depicted with one arrow, the wave is propagated outward in all radial dimensions, reflects off of the outer circular surface, and constructively arrives at the detector.

$$\tau =\frac{d}{c}+S_{\mathit{sys}}+S_{\mathit{det}}+\sigma$$ (4)

Where d is the distance between the BP and the detector, c is the speed of sound in the phantom, S_sys corrects for the asymmetry of the proton dose deposition and the specific feature where the arrival time is measured, S_det offsets a detector-specific delay introduced by the hydrophone. Since our acoustic signal was obtained by the average of 1024 measurements, our signal is expected to be at least one order larger than the thermal and internal electric noise (Ahmad Moiz, et al. 2015). Therefore, σ, is assigned to random acoustic noise and external electric noise from the cyclotron. In order to calculate the distance between the detector and BP d, and measured arrival time, τ, must be measured and corrected with τ′ = S_sys + S_det so that d ≈ (τ − τ′) × c. Multiple arrival time metrics can be used (the protoacoustic wave has multiple peaks and features), but each requires characterizing the accompanying τ′ for accurate calculation of d.

We used four methods for determining τ and its associated τ′. Protoacoustic waves have a characteristic bipolar waveform in which a positive peak precedes a negative peak. In an attempt to measure the earliest arrival of pressure, Method 1 is based on extrapolating the positive peak rise in pressure to zero amplitude. Rather than extrapolating, Method 2 defines τ based on when the pressure wave reaches a threshold value (defined based on experiment at 10% of the maximum achieved pressure). Method 3 does not require characterizing the speed of sound in the material. It instead deduces the depth of the BP by comparing the arrival times before and after shifting the position of the BP in the phantom by a known distance (see Eq.(5)). In Method 4, reflections from multiple phantom surfaces are used to measure the BP depth, but simulations are required to help assign the reflections, and the speed of sound must be known.

Method 1

The arrival time represents the delay between the proton pulse and the arrival of a particular feature of the pressure wave. For all methods, the proton pulse reference time is defined as the midpoint ( $t_p=\frac{1}{2}(t_{10\%}+t_{90\%})$) of the rising part of the proton beam pulse, where the total acoustic pressure to the detector would be approximately maximum according to Eq.(1). For Method 1, the arrival time is the time difference between the acoustic curve t_a and t_p, τ₁ = t_a − t_p (Figure 6A). t_a is extrapolated as the intercept between the pressure baseline (the average pressure preceding the proton pulse) and the line formed by linearly fitting the initial 10% of the acoustic peak amplitude of the linear portion of the first-arriving, rising pressure wave. Assuming the required offset, τ₁′, is constant for different materials, one can obtain the distance from the BP to the distal surface of the phantom through $\frac{d}{c}={\tau }_1-{{\tau }_1}^{\prime }$. The aluminum block measurement with known distance d = 4.2 cm was chosen for calibration, and τ₁′ = 3.05 ± 0.3 μs was empirically determined.

Figure 6.

Depiction of the variables measured for Method 1 and 2. The proton beam pulse (blue) was measured by scintillator/PMT, and the protoacoustic signal was detected with a hydrophone (black) (A). The average of the background acoustic signal is indicated by the horizontal grey line. (B)The rising segment of the acoustic signal is linearly fit to obtain the systematic time delay and threshold value for Methods 1 and 2.

Method 2

Rather than explicitly calibrating a S_det + S_sys, the arrival time can be measured at a relative pressure amplitude that automatically introduces a delay that offsets S_det + S_sys. If we choose the appropriate measurement point, then d/c = τ₂. From figure 7A, one can obtain the linear fit of TOF – Threshold curve shown in Figure 7B, where the intercept on y-axis is τ₂. The threshold is defined as

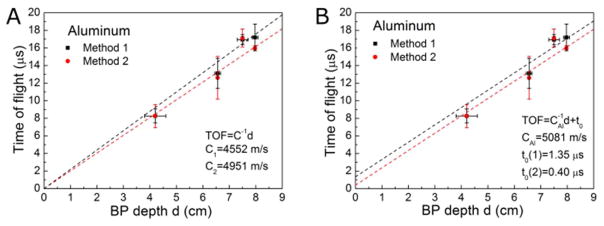
Figure 7.

Comparison of Method 1 and Method 2. (A) The TOF obtained by Method 1 and Method 2 are compared by linearly fitting the TOF to the depth of the BP (the y-intercept was fixed to 0). The inverse of the slopes were compared to the speed of sound in aluminum. (B) Linear fit of the TOF to BP depth BP with a fixed slope, which is the inverse of the speed of sound in aluminum obtained by experiments.

$$\mathit{Threshold}=\frac{A_{th}-A_0}{A_{\mathit{max}}-A_0}$$ (5)

Where A₀ is the background signal to the detector, and A_max is the amplitude of the first acoustic peak. We used the same set of data (protoacoustics in aluminum, without solid water between the nozzle and phantom) as a calibration to find Threshold = 0.105 ± 0.011 (n=10). And we use this threshold value to calculate τ₂(= d/c), which is the second method we used to determine the depth of BP.

Method 3

Because the speed of sound is constant in a homogeneous medium, one can obtain d by comparing the acoustic arrival times before and after introducing a known shift to the BP depth. The scheme is describe in figure 4B, in which solid water (Gammex 457-CTG, Middleton, WI, USA) with thickness Y_m was used to create a BP shift along the beam direction. The distance between the detector and the BP is then obtained through the following equation,

$$d_1=\frac{\mathrm{\Delta }l}{(\frac{\tau (Y_2)}{\tau (Y_1))}-1)}$$ (6)

Where $\mathrm{\Delta }l=Y_m\frac{{\rho }_{sw}}{{\rho }_m}\frac{{\overline{S}}_{sw}}{{\overline{S}}_m}(=l_2-l_1)$. The mass density of solid water and phantom ρ_sw,ρ_m and the mass stopping power S̄_sw, S̄_m, were obtained from the NIST database PSTAR. TOF τ(Y₁) and τ(Y₂) (when the thickness of solid water =Y₁, Y₂, Y₁ < Y₂) were obtained through the first method we introduced in Eq (4) by subtracting τ₁′ = 3.05 μs from the extrapolated pressure peak first arrival time τ₁.

Method 4

The fourth method is based on the geometry of the phantom and the acoustic travel paths between the BP and the detector. As figure 4C, D shows, the first acoustic peak is due to a wave that propagates directly from the BP to the hydrophone. The second peak travels between the distal and proximal surfaces twice before it reaches the detector. The third peak originates from the BP and reflects sequentially off the side surface and proximal surface of the phantom before it reaches the detector. For the aluminum phantom with dimension of 193×76×51 mm³ (L × h × w), the travel distance of the first acoustic wave was l₁=. For the third peak, $l_3=\sqrt{{(2L-d)}^2+{(2h)}^2}$. Therefore, from the differences of arrival time for the first and the second acoustic peak was $\mathrm{\Delta }t=\frac{l_3-l_1}{C}(\mathrm{\Delta }t=t_3-t_1)$, we have:

$$d=\frac{4L^2+4h^2-C^2\mathrm{\Delta }{t}^2}{4L+2C\mathrm{\Delta }t}$$ (7)

For the cylindrical PE (r = 10.44 cm, L = 33.58 cm) phantom, the travel paths for the acoustic waves are different from that in the rectangular aluminum phantom. The second peak is from the acoustic signal reflecting from the side of the phantom (see figure 6D). Therefore its travel distance is $l_2=\sqrt{d^2+h^2}$. From Δt = t₂ − t₁, we have

$$d=\frac{h^2-\mathrm{\Delta }{t}^2{C}^2}{2\mathrm{\Delta }tC}$$ (8)

3. Results

Calibration for systematic time delay and threshold

Materials with a wide range of mass density (ρ_Al =2.7 g/cm³, ρ_Pb =11.35 g/cm³, and ρ_PE =0.92 g/cm³), were tested and studied for the purpose of using protoacoustics for clinic proton beam quality assurance. For rectangular metallic phantoms (aluminum and lead) and cylindrical plastic phantoms (PE), the protoacoustic signal was measured and analyzed.

Compared to the literature reports, the reflection technique resulted in the most accurate measurement of the speed of sound in aluminum:(c_Al = 5081 ± 17 m/s (95% confidence, see figure 3A). In the aluminum phantom, we found the shift-Bragg-peak technique has much larger error than the reflection technique because the very high acoustic propagation speed in aluminum makes the shift in TOF to be too small. Due to echoes in the lead, PP and PE phantoms, the reflection technique was not applicable for characterizing the speed of sound in these materials. For lead, PP and PE, the shift-Bragg-peak technique was used to measure the speed of sounds as c_lead = 2520 ± 336 m/s, c_PE= 2071 ± 70 m/s (see figure 3B, data of lead were not shown). The pitch-and-catch technique was also performed to measure the speed of sound and the results agree with other applied techniques except in the case of lead, (c_lead = 2520 ± 336 m/s) and c_lead = 2119 ± 47 m/s (literature report: c_Al = 5100 m/s, c_lead = 1960 − 2160 m/, c_PE = 1950 − 2400 m/s, see table IV for references). Compared to 2160 m/s reported by literature (Lide 2003), we chose the speed of sound measured by acoustic method (c_lead = 2119 m/s) to calculate the depth of the BP in method 1,2 and 4. The comparison of three techniques are shown in table III. The aluminum phantom was used to calibrate τ₁′ (method 1) and threshold = 10.05% (method2) because it produces the protoacoustic signal with the highest S/N. A characteristic proton pulse and generated protoacoustic wave are shown in figure 6A, where the normalized proton beam can be fitted to a Gaussian function as $G(t,\mathit{FWHM})=\mathit{exp}\left(-\frac{{(t-t_0)}^2}{2{{\sigma }_0}^2}\right)(t_0=81\mu s,{\sigma }_0=5.45\mu s)$. The acoustic arrival time was measured in figure 6A is 11.32 ± 0.32 μs (n=10). From the TOPAS calculation, the distance between the proton BP in aluminum and the distal surface of the phantom is 4.2 cm, which corresponds to the acoustic travel $\text{time}\frac{d}{c}=8.27\mu s$, therefore τ₁′ = S_sys + S_det = 3.05 ± 0.3 μs (mean ± StDev, n=10). For method 2, a threshold of (−10.5 ± 1.1)% was calculated (see figure 6).

TABLE IV.

Thermal acoustic properties for candidate materials.

Materials	Density a (g/cm3)	HU b (±40)	Speed of sound d (m/s)	Cp d (J/kg·K)	β d (1/K ×10−5)	Acoustic impedance (MPa·s/m3)f	Grüneisen parameterg
Water	1.0	0	1481	4184	25.7	1.48	0.13 (Petrova, et al. 2013)
Olive oil	0.91	−112c	1430	1790	70.0	1.93	0.80 (Petrova, et al. 2013)
Paraffin	0.93	−79c	1300	2900	59.0	1.76	0.34
Lexan	1.21	268b	2300	1254	3.70	2.78	0.16
Polyethylene	0.93	−85c	2071	1250	6.67	1.80	0.23 (Engeln, et al. 1985)
Polypropylene	0.92	−90c	2091	1920	4.50	2.34	0.10
Aluminum	2.7	2478b	5081e	921	6.90	17.1	1.94(Harris and Avrami 1972; Prakash and Joshi 1970)
Copper	8.96	2909 ± 228 (Choi, et al. 2010)	3560	390	5.28	41.6	1.72(Harris and Avrami 1972; Huang, et al. 2007)
Brass	8.4	2900 (Choi, et al. 2010)	3480	402	6.09	36.7	1.84
Lead	11.35	2758 ± 539 (Choi, et al. 2010)	2069e	126	8.70	24.6	2.96
Fat	0.95	−70c	1450(Azhari 2010)	2348	9.20	1.38	0.83(Yao, et al. 2014)
Muscle (striate)	1.04	40c	1580(Azhari 2010)	3686	2.80	1.69	0.19
Bones (compact)	1.85	700c	4080(Azhari 2010)	2274	2.70	7.75	1.98

^aPSTAR table (NIST)

^bVarian Eclipse V13.

^cCalculated by linear CT-density curve.

^dwww.engineeringtoolbox.com

^eMeasured by acoustic method at 20° C.

^fAcoustic impedance: α = ρc_s. Other references: (Azhari 2010)

^gGrüneisen parameter was calculated by $\mathit{\Gamma }=\frac{\beta {c_s}^2}{C_p}$. Other references: (Engeln, et al. 1985; Harris and Avrami 1972; Huang, et al. 2007; Petrova, et al. 2013; Prakash and Joshi 1970; Villanueva, et al. 2014; Yao, et al. 2014)

Table III.

Techniques of measuring the propagation speed of acoustic signal in materials. (The values in bold text were used in the BP depth calculations.)

Materials	Reflection (m/s)	Shift-Bragg-peak (m/s)	Pitch-and-catch (m/s)
Aluminum	5081 ± 17	5270 ± 175	5052 ± 130
Lead	−	2520 ± 336	2119 ± 47
PE	−	2091 ± 30	1976 ± 55

Methods 1&2

Methods 1&2 use the calibrated time delay (3.05 μs) and the threshold (−10.5%), respectively, to obtain the BP depth in metal (aluminum and lead) and plastic (PE) phantoms. By adding variable thicknesses of solid water, the BP position was shifted in the phantom. The depths of the BP obtained through TOPAS calculations were compared to the corresponding data calculated by method 1–4. The average error between the results of method 1–4 and TOPAS calculation and the uncertainty (standard error) of each method are listed in table II for the tested phantoms.

Table II.

Comparison of the BP depths obtained by method 1–4: Mean Absolute Error (StDev)

Materials	Method 1 (mm)	Method 2 (mm)	Method 3* (mm)	Method 4 (mm)
Aluminum	0.7(6.4)	2.4(7.1)	0.7	2.2(1.5)
Lead	3.5(1.2)	4.6(1.6)	1.3	2.9(0.7)
PE	4.7(1.7)	3.4(2.8)	2.0	0.2(0.3)

^*Method 3 was applied for only one BP depth.

After calibration in Aluminum, method 1&2 were applied to analyze the acoustic data collected for the lead, and PE phantoms after shifting the depth of the BP in the phantom by adding varying thicknesses of solid water(see table I). There are limitations for methods 1+2. Both method attempt to measure the first arrival time of the pressure wave, which relies on analyzing low amplitude signals. In order to maximize S/N, the base of the phantom and the hydrophone were immersed in water to achieve the best possible acoustic coupling. In order to reduce the uncertainty from a single measurement, multiple measurements can be collected at various hydrophone depths and various shifted BP positions (figure 9). Through this averaging, The TOF error was reduced to less than 1 μs, which corresponds to ~2mm of error in BP range calculation.

TABLE I.

Comparison of protoacoustic-derived BP depths calculated by the four methods.

Materials	Solid water (cm)	TOPAS (cm)	Method 1 (cm)	Method 2 (cm)	Method 3 (cm)	Method 4 (cm)
Al(19.30 cm)	0	4.20	4.20±0.40*	4.20±0.67*	4.18±1.05	----
Al(19.30 cm)	5	6.56	6.67±0.87	6.51±0.52	6.49±1.04	6.67±0.10
Al(19.30 cm)	7	7.50	7.53±0.65	7.93±0.89	----	7.83±0.20
Lead(10.24 cm)	0	4.50	4.68±0.15	4.99±0.27	----	----
Lead(4.90 cm)	8	0.59	0.27±0.05	0.15±0.12	0.36±0.20	0.96±0.0
Lead(4.90 cm)	10	0.94	0.70±0.13	0.63±0.20	0.96±0.19	1.21±0.06
Lead(4.90 cm)	15	1.80	1.32±0.16	1.17±0.12	----	1.56±0.15
PE(33.58 cm)	2	3.78	4.16±0.10	4.28±0.25	3.98±0.18	3.78±0.14
PE(33.58 cm)	4	5.88	6.55±0.09	6.39±0.18	----	5.88±0.11
PE(33.58 cm)	6	7.98	8.34±0.14	8.00±0.36	----	7.92±0.24

^*Measurements used to calibrate τ₁′ and threshold (Method 2)

Figure 9.

By combining multiple measurements at various BP depths (A) and hydrophone-to-phantom distances (B), the Method 1 protoacoustic range verification accuracy was improved. From the linear fit of arrival time to introduced BP shift, the y-intercept gives the acoustic TOF from the BP to the distal surface of the phantom. By plotting the arrival time versus hydrophone to phantom distance, the extrapolated y-intercept gives the acoustic TOF from the BP to the distal surface of the phantom.

Method 3

When the speed of sound in the phantom is unknown, but the proton stopping power of the material is known, method 3 may be used to calculate the depth of the BP. However, method 3 requires measuring a pair of arrival times (τ(Y₁), τ (Y₂) for different BP depths. This known shift is induced by adding different thickness of solid water slabs to the beam path. For example, to find the BP in an aluminum phantom (L = 19.3 cm) without solid water in front of its proximal surface, one needs to obtain the arrival time before and after (τ(Y₁) = 8.27±0.79 μs and τ(Y₂) = 16.30±0.57 μs) placing a thickness of 8 cm solid water in front of the phantom, which gives a shift in BP depth of 3.50±1.11 cm (Eq. (6)). Similarly, one can calculate the depth of the BP with an additional 5 cm solid water by using the arrival time measured with 5 cm solid water inserted, which is 6.49±1.15 cm (see table I:aluminum). The shifted distance by adding 2 cm solid water (from 8 cm to 10 cm solid water) is much smaller than the depth of BP. According to Eq.(6), it results in larger error (larger than 1.0 cm) in calculating the depth of BP. Therefore the depth of BP with 8 cm solid water is not listed in the table. Similarly, method 3 was applied to find the depth of BP in lead with 8 cm and 10 cm solid water, and in PE with 2 cm solid water (table I&II).

Method 4

In method 4 the arrival time of different peaks in the acoustic signal can be assigned to different paths travelled between the BP and the detector (see figure 4C,D). Once these geometry-dependent paths are identified in the phantom, the direct distance between the BP and detector, d, (and therefore the BP depth in the phantom) can be calculated. For rectangular metal phantoms (aluminum and lead), equation (7) was used to calculate the depth of BP. For example, the acoustic signal for aluminum phantom with 5 cm solid water has t₁(T1) = 114 μs, t₂(T2) = 170 μs (for one measurement). We obtained the depth of BP d_exp = 6.80 cm through Eq.(7), close to the TOPAS calculated d_sim = 6.56 cm. For cylindrical plastic phantoms ( PE), equation (8) was used based on travel path/pressure wave peak assignments made with the help of k-Wave acoustic simulations (see figure 4C, D). Method 4 shows the highest accuracy among the four compared methods, with a standard deviation less than 2mm for all measurements (table I). Excessive proton dose deposition caused air bubble formation in the polypropylene (PP) phantom before method 4 data was collected. Therefore, the method was not assessed for the PP case. Post-irradiation CT showed that the method 1–3 data was collected prior to the damage to the phantom.

We have independently measured the speed of sound in the investigated materials. The speed of sound is an important parameter in TOF-based determination of the BP depth because d = c × t. For protoacoustic pressure simulations, additional parameters are required: mass density, specific heat, thermal expansion coefficient, and the Grüneisen parameter. Acoustic impedance and Grüneisen parameter were calculated from these table values (Azhari 2010; Engeln, et al. 1985; Harris and Avrami 1972; Huang, et al. 2007; Petrova, et al. 2013; Prakash and Joshi 1970; Villanueva, et al. 2014; Yao, et al. 2014). Table IV lists parameters collected from experimental data, literature, National Institute of Standard and Technology (NIST) database and the Eclipse treatment planning system. Acoustic impedance is important because it determines the transmission of acoustic power at interfaces, such as between the phantom/water, phantom/coupling gel, or phantom/air - the larger the impedance difference, the lower the transmitted pressure amplitude.

4. Discussion

Characteristic protoacoustic wave forms are shown in figures 5, 6, and 8. The shape of the pressure waves (equation 1) depends on the shape of the dose deposition, shape of the proton pulse, position of the detector and the material speed of sound and geometry. In an infinite water medium, an infinitely short proton pulse generates a bipolar waveform whose leading positive pressure peak arrives at ~ t_p + d/c (when measured by a distal detector). When the rise time of the proton pulse is longer than the acoustic transit time across the BP volume (the BP region in which the proton dose over each voxel is larger than 50% of the maximum dose at the BP), stress confinement is lost, and the waveform is distorted by the proton pulse shape. In a finite medium, reflections complicate the observed waveform due to interference. Due to aluminum’s fast speed of sound, the protoacoustic waves measured in the aluminum phantom are affected by both reflections and loss of stress confinement, and the leading positive peak arrives long after t_p + d/c(figure 6). Method 1 and 2 attempt to measure the arrival time based on the leading edge of the first-arriving pressure wave. Method 4 attempts to take advantage of the reflections in order to extract multiple TOF measurements from a single waveform. In the Al phantoms, echoing interference creates waveforms that appear to be mono-frequency decaying sinusoidal functions (figure 5a). In the lead and PE phantoms, the interference results in less uniform structure.

Figure 8.

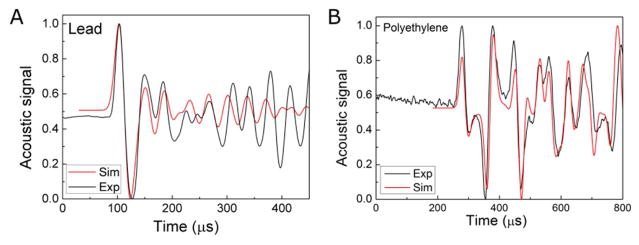
Acoustic k-Wave simulation. Comparison of the simulation to experimental data collected in lead (49×102×202 mm³) (A) and polyethylene (r=104 mm, L=336 mm) (B) phantoms shows that acoustic signal are determined by the geometry and speed of sound in the phantom. (2160 m/s and 11.35 kg/cm³ for lead and 2071 m/s and 0.92 kg/cm³ for polyethylene).

The magnitude of the protoacoustic signal generated in phantoms per deposited energy depends on the thermoacoustic features of the material (grüneisen parameter, which depends on the speed of sound, expansion coefficient, and the specific heat) (Eq.(5)). The pressure amplitude that reaches the detector depends on the distance that the acoustic signal travels from the BP to the detector, the attenuation properties of the material, and the impedance mismatch between the phantom and the detector. From table IV, the Grüneisen parameter of aluminum (1.94) is less than lead (2.96), but based on their relative transmission into water, aluminum (29% amplitude transmission) results in a similar protoacoustic pressure amplitude compared to lead (21% amplitude transmission at the water interface). Because of its higher Grüneisen parameter and interfacial transmission, PE generates a higher amplitude measured protoacoustic signal compared to PP. Among the four tested phantoms, the protoacoustic signal generated in aluminum is the strongest at about 90 mPa (for 5.7×10⁷ protons/pulse). We found that the k-Wave simulated acoustic waves in lead phantom mismatch the experimental data from the 4^th peaks, while the simulation matches the experimental data very well for the polyethylene phantom (figure 8). The reason might be (1) the central axis of the lead phantom is slightly misaligned with the proton beam or (2) the attenuation/dispersion of the acoustic signal is not considered in the simulation. This conjecture needs to be investigated with further measurements and simulations. Here, we are only concerned with the arrival time of the first three peaks for Method 4, and simulation/experiment mismatch does not affect the calculations.

The accuracy of the protoacoustic range verification also depends on the material. Due to the relatively long proton pulse widths generated by the used clinical cyclotron (15 μs), it is difficult to measure changes in arrival time that are less than 1 μs - longer excitation proton pulses translate into longer protoacoustic pressure wave peaks (see the convolution in Eq. (3)). Because d = c × t, the error in time measurements leads to the error in distance. The ~1 μs arrival time resolution limits the ability to resolve changes in BP depth. The larger the sound speed, the worse the achievable spatial resolution. Therefore, phantoms composed of materials with lower speeds of sound are expected to generate more accurate protoacoustic calculated results. Thus, aluminum is not an ideal phantom material because of its large speed of sound, in which an error of 1 μs in time measurements results in an error of 5 mm in BP depth determination. We prefer phantom materials with small relative stopping power (RSP) because our aim is to differentiate the change of proton energy (range) by measuring the shifts in the BP. Therefore plastic phantom material is also a better choice than metal ones - a 10MeV change in energy translates in 2.32 cm shift in PE compared to a 0.4 cm shift in lead. It has to be emphasized that the metal phantom has better durability than PP; we found that in low density PP phantom, air bubbles were created by large doses of proton radiation. It has to be noted that the thermoacoustic properties of metallic materials were investigated for the purpose of proton QA. In proton therapy, metal is to be avoided in the pathway for pencil beam scanning (PBS). We want to investigate applications as a protoacoustic phantom or contrast agents due to their high Grüneisen values. During one data collection session of 5 measurements of ~24.2Gy / 1024 pulses resulted in 121Gy delivery for characterizing one BP depth, which is still significantly less than the dose required to damage plastic scintillators (Pelwan, et al. 2015) but comparable to the dose that modifies Teflon surface patterns (Kitamura, et al. 2013). No degradation to PE was observed in the course of the experiments. This observation has been confirmed by CT images of both phantoms before and after the measurements.

In an attempt to maximize accuracy, maximize signal amplitude, and simplify analysis, only solid phantoms of well-defined geometry were considered for protoacoustic QA methods. Application of protoacoustic techniques to in vivo range verification within patients is complicated by heterogeneity, and further investigations are required to understand the manifestations of these heterogeneities. To determine the proper geometry for the QA phantom using Method 4, one has to consider the following factors: (1) the phantom has to be wide enough so that the acoustic signal reflected at the side surface does not distort the signal travels directly from the BP to the detector. Because it extrapolates to the earliest arriving pressure, however, Method 1 should be immune to this pileup effect. For clinical energies and spot sizes, ~15 μs width Gaussian proton pulses generate >10 μs protoacoustic pressure peaks. To prevent overlap, the BP should be displaced ~10 μs × (2 × c) from any reflective surfaces (aside from the surface separating the phantom from the detector) such that any reflections are delayed from the primary peak by at least 10 μs. (2) The phantom is long enough so that the signals reflecting between the proximal and distal surfaces can be separated from those reflecting at the side of the phantom. (3) The phantom is small enough to be easily moved and aligned. Data analysis shows that the shape (rectangle vs. cylinder) of the phantom does not affect the accuracy of the measurements, but rectangular phantoms are easier to store, move, and align. In summary, a rectangular aluminum phantom can be used to achieve the best accuracy for Method 1, 2 &3, and a PE phantom for Method 4. But the uncertainty for the aluminum phantom is much larger than the lead, PE & PP phantoms because of its much larger speed of sound. It is also found that the error of measurements using Method 1&2 increases significantly when the depth of Bragg peak (d) is more than 8 cm in the aluminum phantom. At large separation between the BP and the hydrophone, the $A~\frac{1}{x^2}$ relationship between pressure amplitude and distance causes a detrimental decrease in signal. In the aluminum case, increasing the distance beyond 8 cm lowers the signal to the point where > 1 cm errors are observed. This is particularly problematic for Methods 1 & 2 because they use low amplitude measurements. Although Method 1&2 are conceptually similar, and they result in similar accuracies (Method 2 is slightly less accurate), both have been included in the presented analysis. Method 1 is conceptually motivated by tracing the signal to its earliest arrival, which is intuitively expected to be the least susceptible to reflection interference. Method 2 is expected to be the most easily implementable technique for automatic electronic analysis, as threshold tracking is easily programmable.

Based on the above discussion, protoacoustic TOF measurements can achieve 0.2 mm depth accuracy in a PE phantom as long as the system is properly calibrated (S_det+S_sys are measured for the chosen method, detector, phantom, and proton pulse). Non-ideal calculation methods and phantoms, however, may result in large errors of up to 8.1 mm (PP, 6.87 cm, Method 2) or large standard deviations of up to 10.4 mm (Al, 6.56 cm, Method 3). To obtain the best S/N for the acoustic signal, 24.2Gy of dose (by averaging 1024 proton pulses) was deposited at the BP. Due to electronic and acoustic noise within the treatment room, 64 averages were required to achieve sufficient signal-to-noise averaging. Looking forward, application of protoacoustics to living, biological tissue will introduce additional biological noise (heartbeat, blood flow, breathing). The <MHz biological noise - which is within the bandwidth of the expected protoacoustic signal – is unknown, and will require further verification. Typical proton range QA procedures compare intensities measured on a 2D array detector after placing different thicknesses of plastic on known positions of the array (Arjomandy, et al. 2008) or through expensive multiple layer ion chambers (Dhanesar, et al. 2013). These can achieve sub-millimeter accuracy with < 1cGy of deposited dose, but they are limited to specific gantry angles and, in the case of the 2D array, to measuring set proton energies (that match the plastic mask). Because the lateral proton beam propagation axis is known, the studies here were focused on calculating the depth of the BP (for a known entrance spot on the phantom). The lateral position uncertainty of the BP spot does not affect the accuracy of the BP depth calculation. For 1mm lateral displacement of the BP spot, the shift of BP depth is less than 1% due to Eq.(7). By placing additional detectors at positions lateral to the pre-BP dose deposition (Jones, et al. 2016b), protoacoustics may be able to achieve simultaneous measurement of the x, y, and z position of the BP. Although the measurements were collected using the output from a clinical cyclotron, the proton pulse output was modified to achieve maximum proton currents and the shortest possible pulse widths. The next generation of proton accelerators, synchrocyclotrons, clinically deliver ~7 μs proton pulses at high currents (W. Kleeven, et al. 2013); pulses that are ideal for protoacoustic wave generation. These shorter, more intense pulses are expected to lead to greater range verification accuracy and pressure wave amplitude, which may allow for single-shot, real-time protoacoustic QA range verification. Although Method 4 took advantage of simulations to assign pressure peaks to specific reflections, there is even more information contained in the full protoacoustic pressure waveform that may be extracted through iterative comparison to acoustic simulations or a library of pre-calculated simulations to determine more features of the dose deposition. For example, the protoacoustic wave shapes depend on the proton beam spot size (Jones, et al. 2014). In the QA environment when the phantom is well characterized and an array of detectors can be used, then 3D imaging may also become possible (Alsanea, et al. 2015; Kellnberger, et al. 2016).

As described above, the best phantom material of those tested is Polyethylene because it has a Grüneisen coefficient ~2× that of water (high initial source pressure), an acoustic impedance relatively close to water (high transmission into water), a low stopping power relative to water (small proton energy changes translate into large changes in penetration depth), and a low speed of sound (small changes in distance translate into larger changes in arrival time). Due to these factors, a high S/N signal was measured and the uncertainty of the protoacoustic-based BP depth measurements were accurate to within 1.5 mm. A list of other possible QA materials and tissues is given in Table IV. Based on this list PE may be the best suited for protoacoustic measurements. Interestingly, for in vivo measurements, fat is expected to have a 3x higher Grüneisen parameter than muscle. Metal has a much higher Grüneisen parameter than tissue. Therefore, metallic fiducial or - if a high enough concentration can be reached - metallic nanoparticles may act as protoacoustic contrast agents. It has been reported that metallic nanoparticles such as gold and iron nanoparticles help to improve the proton absorption in tissue (Kim, et al. 2012; Martínez-Rovira and Prezado 2015). Metallic nanoparticles such as gold and copper sulfide, have been used as contrast agents in the photoacoustic and thermoacoustic tomography (Ku, et al. 2012; Wang, et al. 2004; Zhang, et al. 2009). Although the origin of contrast is different than in photoacoustic applications, metallic nanoparticles may possibly be used as protoacoustic contrast agents in the future, which might help one to detect protoacoustic signals with limited dose deposition in tissue during proton radiotherapy(Sharma, et al. 2015).

This study is aimed to understand the thermoacoustic characters of materials and the protoacoustic wave’s production and propagation in solid phantoms. The methods that we have developed for proton beam range verification is valid for homogeneous phantom with well defined geometry. In patient, the uncertainty in determining the BP position is complicated by the anatomy changes, tissue’s heterogeneity and deformation, which requires extensively investigation in the future. Our colleagues have submitted the manuscript of the simulation study using patient CT in parallel to the same journal, which suggests that the detector should be as close to the BP as possible, and increase the number of detectors can improve the accuracy in determining the BP position.

5. Conclusions

In this paper, we have demonstrated that protoacoustic range verification with less than 2mm accuracy was achieve in a polyethylene phantom. Other phantoms ranging in densities (0.9~11.3 kg/m³) were also tested. Four different methods have been applied to analyze the acoustic signal collected by a hydrophone. We found PE is the best material for the range verification due to its low speed of sound. Method 4 has the highest accuracy of all, which does not depend on the type of phantom material. The S/N and accuracy of our measurements depend on the geometry of the phantom. Our study shows that protoacoustic measurements may potentially provide a low cost (The The price of the protoacoustic apparatus (<$10k) is expected to be an order of magnitude lower than the price of the standard instrument for proton range measurements – the multi-layer ionization chamber (~$100k).) and simple QA method for determining proton beam range when the proper materials and methods are used. Protoacoustics provides a novel, non-invasive method to measure the speed of sound of various materials