Molecular Dynamics Simulations of Stratum Corneum Lipid Mixtures: A Multiscale Perspective

Abstract

The lipid matrix of the stratum corneum (SC) layer of skin is essential for human survival; it acts as a barrier to prevent rapid dehydration while keeping potentially hazardous material outside the body. While the composition of the SC lipid matrix is known, the molecular-level details of its organization are difficult to infer experimentally, hindering the discovery of structure-property relationships. To this end, molecular dynamics simulations, which give molecular-level resolution, have begun to play an increasingly important role in understanding these relationships. However, most simulation studies of SC lipids have focused on preassembled bilayer configurations, which, owing to the slow dynamics of the lipids, may influence the final structure and hence the calculated properties. Self-assembled structures would avoid this dependence on the initial configuration, however, the size and length scales involved make self-assembly impractical to study with atomistic models. Here, we report on the development of coarse-grained models of SC lipids designed to study self-assembly. Building on previous work, we present the interactions between the headgroups of ceramide and free fatty acid developed using the multistate iterative Boltzmann inversion method. Validation of the new interactions is performed with simulations of preassembled bilayers and good agreement between the atomistic and coarse-grained models is found for structural properties. The self-assembly of ceramide-free fatty acid mixtures is investigated and both bilayer and multilayer structures are found to form. This work therefore represents a necessary step in studying SC lipid systems on multiple time and length scales.

Graphical abstract

1. Introduction

Skin plays the essential role in human physiology of preventing water loss and protecting the body form external physical, chemical and biological attack. This barrier function is known to be localized to the stratum corneum (SC), the outermost layer of skin [1]. The SC is composed of dead skin cells surrounded by a dense lamellar-structured lipid matrix containing an approximately equimolar mixture of ceramides (CERs), free fatty acids (FFAs), and cholesterol [2]. This lipid mixture notably lacks phospholipids, which are present in most biological membranes. Since the lipid matrix is the only continuous path through the SC, it is generally recognized that the lipids play an integral role in the barrier properties of skin. Anomalies in lipid composition are known to be associated with impaired barrier function, (see, for example, Refs. [3–6]); however, while many global properties of SC lipid systems can be gleaned from experimental measurements, molecular-level details often remain elusive. Hence, atomistic molecular dynamics simulations have begun to play an important role in examining the molecular-level structure and composition-related changes to membrane structure and properties [7–15], typically focusing on systems based on CER NS (C18 sphingosine base linked to a non-alpha hydroxy acyl chain). Simulation studies have thus far provided considerable insight examining the role of CER acyl chain length [12, 16], the influence of CER headgroup chemistry [11], the influence of mixtures [9, 13, 15–17], and the permeation of small molecules [12, 18, 19]. However, most studies have relied on preassembled bilayer configurations, which may unduly influence the resulting structure and observed properties; the dense, gel phase structures formed by the SC lipids result in very low lipid mobility [14], making them effectively stuck in their initial configurations over the typical simulation timescales considered. The use of bilayer, rather than multilayer structures, may also limit the insight that can be gained, as they restrict the conformations that can be adopted for the two-tailed CERs e.g., hairpin versus extended, which is a controversial topic in the experimental literature [20]. Self-assembled structures, where lipids form the desired structure with minimal external input, would be preferable, but the timescales required to reach equilibrium on what is likely a rough free energy landscape make this approach impractical for atomistic models.

To address these issues, computationally efficient coarse-grained (CG) models can be used. CG models allow the long times and large systems sizes required to observe significant lipid rearrangements, including self-assembly, to be studied [21]. While numerous methods are available for deriving CG force fields [22–25], the structure-based iterative Boltzmann inversion (IBI) [26] method is commonly used. The IBI method iteratively updates pair potentials between successive CG simulations to match target data in the form of site-site radial distribution functions (RDFs), and has been successfully applied to systems ranging from small molecules [27] to lipids [28, 29] and polymers [30–32]. While IBI yields force fields that generally reproduce the target fluid structure with high accuracy, these force fields often fail to reproduce behavior at other state points [27, 31–33], as IBI only provides a means to match the target RDFs and cannot determine if the derived pair potentials accurately represent the underlying energy landscape. This problem is further intensified by the fact that there may be any number of pair potentials that sufficiently reproduce the target RDF [33], and determination of which one is most representative is nontrivial. Hence, the utility of IBI-based force fields may be limited for studying processes that span multiple states, e.g., self-assembly.

In recent work, we developed a multistate extension to IBI (MS IBI) that helps to address the transferability problem of IBI-derived force fields, whereby pair potentials are optimized to match target RDFs at multiple state points simultaneously [33]. This extension effectively adds additional constraints to the optimization process, with the goal of finding a pair potential that simultaneously matches each target RDF, and thus adequately represents the underlying energy landscape. In this communication, we provide an overview of the MS IBI algorithm and summarize prior usage of this methodology to produce CG force fields that are more robust and transferable than single-state methods. We additionally expand on our prior study of SC lipids and present the derivation of the cross-interactions between FFA and CER NS headgroups, and use this force field to investigate the self-assembly of large membranes composed of mixtures of CER and FFA.

1.2. Background: MS IBI

As an extension of the IBI method (single state IBI, or SS IBI), MS IBI updates trial pair potentials based on the deviation between multiple target RDFs and RDFs from running a CG simulation using the trial pair potentials. Instead of a single update term, each state used in the optimization contributes to the update, given by

$$V_{\gamma \beta }^{(i+1)}(r)=V_{\gamma \beta }^{(i)}(r)-N_{\mathit{states}}^{-1}\sum _{\mathit{states}}{\alpha }_s(r)k_B{T}_{s}ln\left[\frac{g_{\gamma \beta ,s}^{AA}(r)}{g_{\gamma \beta ,s}^{(i)}(r)}\right],$$

where $V_{\gamma \beta }^{(i)}(r)$ is the pair potential between bead types γ and β at the i^th iteration, N_states is the number of states used to optimize V_γβ, α_s(r) serves as a damping and weighting function, used to reduce the size of the potential updates and to adjust the “weight” given to each state, T_s is the temperature of state s, k_B is Boltzmann’s constant, $g_{\gamma \beta ,s}^{AA}(r)$ is the target γβ RDF at state s, and $g_{\gamma \beta ,s}^{(i)}(r)$ is the γβ RDF calculated from a simulation of $V_{\gamma \beta }^{(i)}(r)$. In the limit of a single state, MS IBI reduces to the original SS IBI algorithm. Note that alpha is set to a linear function of the separation, with α(0) = α₀, and α(r_cut) = 0; this allows larger updates to occur at short separations, which we found to help reduce structural artifacts in the resulting pair potentials. Additionally, we allow α_s to vary by state, allowing certain states to be given a higher or lower weight, enabling certain behavior or structures to be emphasized [33]. While the goal of MS IBI is to derive a single transferable force field, this cannot necessarily be achieved in all cases, e.g., due to structural rearrangements at the sub-CG bead size scale, similar to how atomistic force fields may lack transferability if the electron density distribution is sufficiently different between states, and for extremely different target states [33]. Thus, adjustment of the relative weights can be used as a means to provide a desired compromise of RDF fitness (e.g., providing a better fit in the RDFs for the state point of most interest).

MS IBI has allowed the development of more robust force fields than the SS IBI approach. For example, using only bulk alkane RDFs, an MS IBI-derived force field was shown to accurately predict the structural properties of both gel and liquid crystalline monolayers, while SS IBI-derived force fields using the same targets failed to accurately capture the behavior of both monolayer states [33]. In other work, MS IBI was used to improve upon an existing CG water force field by using both bulk water and water droplet target states, enabling the resulting CG force field to accurately capture both structural correlations and surface tension [34]; a prior SS IBI-based water model [35] could reproduce structure but not surface tension. In recent work, a force field for CER NS was optimized against both lamellar and bulk fluid target states, finding close agreement with the structural properties of each state and in better agreement with experiment than the MARTINI CER force field [36]. The MS-IBI derived CG force field was also shown to reproducibly self-assemble into ordered membrane structures [37]. MS IBI also allows beads to be made transferable between different molecules by simultaneously using target data from different molecules that share common beads; e.g., the tail beads in FFA and CER NS are identical, and thus optimization of the TAIL-TAIL pair potential included both FFA and CER NS target data. MS IBI has also been used to capture appropriate density-pressure relationships by performing multi-ensemble (e.g., NVT and NPT) optimizations for water and lipids [34, 37].

We have additionally demonstrated coupling of the MS IBI optimizations with a simulated wetting procedure to address a particular shortcoming associated with structure-based force fields; that is, the underlying structure matching procedure cannot differentiate between correlations in the RDFs that result from density and those that result from an underlying attraction, making it difficult to accurately capture hydrophobic interactions. We demonstrated that the hydrophobicity of the lipid tail beads can be corrected by systematically reducing the tail-water attraction such that the contact angle of a water droplet on a monolayer surface composed of lipid tails in a CG simulation matched that from a corresponding atomistic simulation.

The rest of this Communication is organized as follows: the models and methods used to optimize the CER-FFA cross-interactions are detailed in Section 2. In Section 3, the results of the optimizations are presented and the self-assembly of CER-FFA mixtures into lamellar structures explored. Finally, conclusions and a general outlook are briefly discussed in Section 4.

2. Methods and Model

2.1. Simulations

Atomistic simulations used to gather target data were run with the CHARMM36 all-atom force field [38]. Parameters for the CER NS headgroups were taken from our previous work [11]; these have been shown to accurately reproduce the phase behavior of a pure CER NS bilayer. Water, when present, was modeled with TIP3P [39]. Bulk fluid mixtures and bilayers composed of CER NS and FFA were used to gather target data. Two classes of CG simulations were performed: those during the MS IBI optimizations and those using the optimized force field. Simulation- and analysis-specific details can be found in the Supplementary Material.

2.2 Model Description and Force Field Optimization

The coarse-grained mappings for the lipids used in this work are shown in Figure 1 and were defined in a previous publication [37]. Briefly, a 3-to-1 mapping is used, where each CG bead generally represents 3 heavy atoms. A notable exception is the hydroxyl groups in the CER headgroup, which are each mapped to a single bead; this was found to be necessary to capture the in-plane packing of the CER headgroups in a bilayer configuration [37]. Both molecules share identical TAIL beads, which represent 3 successive carbons and their associated hydrogens in the lipid tails. A description of the various terms in the force field can be found in the Supplementary Material.

Figure 1.

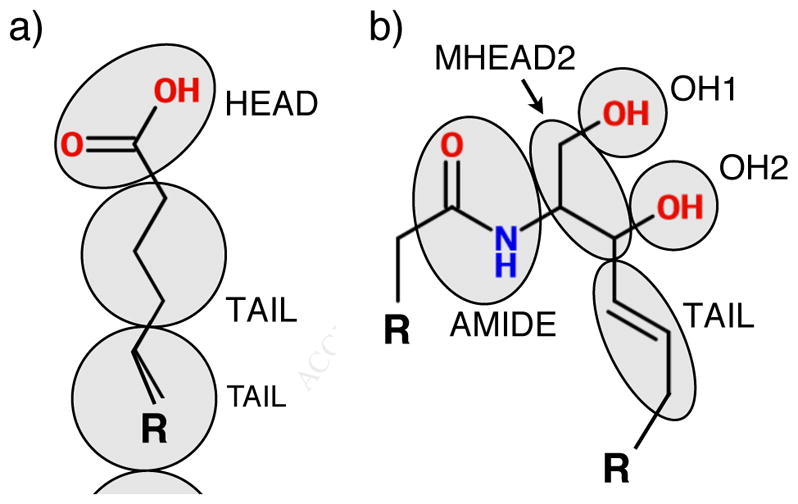
CG mappings for the lipid headgroups considered in this work; a) FFA and b) CER NS. “R” represents a set of TAIL beads bonded in series, with the number of tail beads determined by length of the lipid tails. Note that the CG beads interact through spherically symmetric potentials despite being drawn as ellipses.

The bonded interactions and nonbonded pair potentials for beads on the same type of molecule, along with the lipid-water pair potentials, were optimized with MS IBI and reported in previous work [37]. In this work, we optimize the lipid-cross interactions, i.e., the AMIDE-HEAD, MHEAD2-HEAD, OH1-HEAD, and OH2-HEAD pair potentials, using MS IBI. The states used for these optimizations were the bilayer and bulk fluid states described in the Supplementary Material. In addition to the constant pressure bilayer state, a constant volume bilayer state was included at the same density as the NPT bilayer state. Details pertaining to the optimizations can be found in the Supplementary Material.

3. Results and Discussion

3.1. Force Field Derivation and Validation

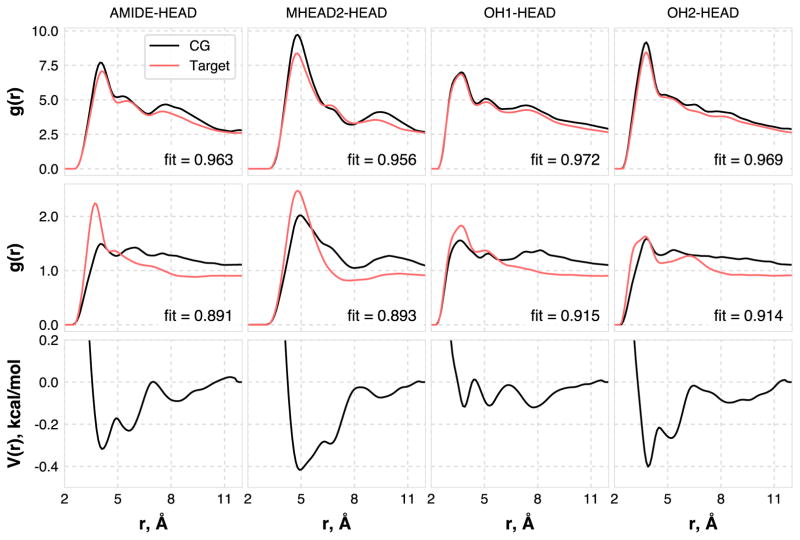
The results of the CER NS-FFA headgroup optimizations are shown in Figure 2 for the NPT states. The target RDFs are reproduced with a high degree of accuracy at the bilayer states, as indicated by the f_fit values > 0.95. The first peak and the general shape of the RDFs are accurately reproduced for each pair, which indicates that the CG model accurately captures the structural ordering of the headgroups within the bilayer plane. The RDFs at the bulk states are also accurately captured, with 0.891 ≤ f_fit ≤ 0.915 for all pairs. The CG model generally underpredicts the height of the first RDF peak slightly and overpredicts the RDF beyond the first peak, which indicates a higher degree of headgroup clustering but a lower degree of ordering in the first solvation shell in the CG model compared to the atomistic one. Note that the AMIDE-HEAD interactions for the bulk show the largest deviation, due to the anisotropic interactions, as seen in prior work [37]. The CG model has slightly longer-ranged ordering than the atomistic, which is a necessary compromise in order to capture the ordering in the bilayer states. The lower degree of RDF matching in the bulk phases is expected, as the bilayer states were given higher weight (via α_s(r)), since they are ultimately of more interest. Despite the lower fitness in the bulk states, the bulk densities calculated via NPT simulations with the CG (0.713 ± 0.003 g/mL) and atomistic models (0.703 ± 0.006 g/mL) compare favorably.

Figure 2.

RDFs and final optimized pair potentials for the pairs considered in this work. Each column corresponds to a single pair, given at the top of the column. The first row shows the target and CG RDFs at the NPT bilayer state, the middle row shows the target and CG RDFs at the NPT bulk fluid state, and the bottom row shows the optimized pair potentials.

The pair potentials were further validated with a 200 ns simulation of the equimolar CER NS C24-FFA C24:0 bilayer to examine structural properties beyond the RDF, which are listed in Table 1. The high nematic order parameter (S₂) shows that both models form bilayers with a high degree of orientational order in the lipid tails. The CG model overpredicts the area per lipid (APL) by ~5%, and is of the same order as the deviation calculated for a pure CER NS C24 bilayer [37]. The atomistic model predicts a higher tilt angle of the lipid tails with respect to the bilayer normal, although the difference is quite small (~7% difference when considering the relevant scale of 0–90°). The bilayer thickness agrees very well with the atomistic model, differing by 1 Å, illustrating the structural accuracy of the model with regard to both the lipid tails and the lipid-water interface. Overall, we find excellent agreement in the structural properties of multicomponent bilayers simulated with the atomistic and CG models.

Table 1.

Comparison of structural properties of equimolar CER NS C24-FFA C24:0 preassembled (PA) and self-assembled (SA) bilayers simulated with the atomistic and CG models. The two numbers listed for the self-assembled systems (CG, SA-X) are for each of the two leaflets, as the asymmetric distribution of lipids between the leaflets, which is listed in the rightmost column, gives rise to different properties of the individual leaflets. Uncertainties represent the standard error in the calculations; for the self-assembled system, the uncertainties are on the same order as the preassembled CG system.

System	S2	APL, Å2	Tilt, deg	Thickness, Å	ntop:nbottom
Atomistic, PA	0.991 ± 0.001	29.2 ± 0.4	13 ± 2	59.7 ± 0.1	-
CG, PA	0.9787 ± 8.7e-4	30.87 ± 0.07	6.3 ± 0.5	60.72 ± 0.02	-
CG, SA-1	0.964/0.975	31.18/30.68	9.6/6.1	60.22 ± 0.01	0.965
CG, SA-2	0.976/0.976	31.36/30.70	6.4/6.2	60.79 ± 0.002	0.978
CG, SA-3	0.975/0.957	30.43/32.37	6.0/11.7	60.04 ± 0.02	1.064

3.2 Self-Assembly into Lamellar Structures

Next, the self-assembly of the CG model into lamellar structures that are completely decorrelated from the initial configuration is examined. In general, bilayer self-assembly occurs in two major steps [40]. First, the lipids aggregate in the water to form separate lipid and aqueous domains; next, the lipids organize themselves such that the hydrophilic headgroups shield the hydrophobic tails from the aqueous phase, thus forming a bilayer structure. In this work, we initialize the lipids in a high temperature, disordered, but phase-separated, configuration, shown in Figure 3a; the systems were set up such that the lipid phase spans the box in the x and y directions, but not along z, to ensure that the lipids can form a 2D periodic structure. From the high temperature state, the system temperature was first reduced to 305 K over 100 ns, followed by an isochoric expansion in the xy plane to 1.7x the APL of the preassembled, equilibrated bilayer. The system was then isochorically compressed in the xy plane to the equilibrium bilayer APL, after which the semi-isotropic barostat was activated, and the simulation continued for another 200 ns at 305 K and 1 atm. This approach of starting from a phase-separated state, followed by expansion and compression, was found in prior work to not affect the self-assembled structures, but rather makes the self-assembly more efficient and reliable, as major structural defects are more rapidly worked out compared to simply running the system at a constant temperature and pressure [37]. Three different bilayer self-assembly simulations were performed and analyzed to show reproducibility, with total compression/expansion times of 200 ns, 400 ns, and 600 ns.

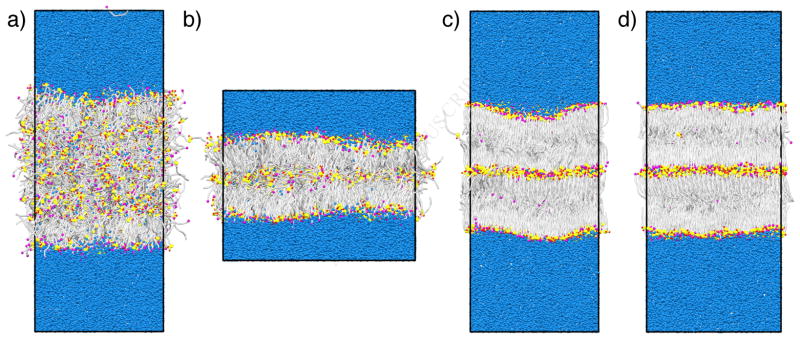
Figure 3.

System snapshots during the bilayer self-assembly process: a) initial, disordered configuration, b) at maximum expansion, c) at the end of the compression phase, and d) after 200 ns of simulation at 305 K and 1 atm. CG beads are colored as follows: blue = water, silver = lipid tails, yellow = AMIDE and MHEAD2 beads, red = OH1 and OH2 beads, and magenta = FFA headgroups.

Stable, well-ordered bilayers formed in each of the three self-assembly simulations. Snapshots of one of the systems during the self-assembly process are shown in Figure 3. Due to the stochastic nature of lipid organization during the cooling phase, the bilayers demonstrate an asymmetric distribution of lipids between the two leaflets and this asymmetry leads to different leaflets having different structural properties. This information is summarized in Table 1 and shows that when a particular leaflet has a lower APL (i.e., more lipids, since the area is taken as the area of the simulation box), the lipid tails in that leaflet are more ordered and demonstrate a smaller tilt angle. In general, the structural properties of the self-assembled bilayers tend to agree well with those of the preassembled bilayer. To examine the APL of the different lipid species individually, a Voronoi tessellation of the lipid positions in the bilayer plane was constructed and APLs of 40 ± 8 Ų for CER NS and 30 ± 8 Ų for FFA obtained. While the APL for FFA is smaller, as expected given it has a single tail, these values seem low for CER and high for FFA, and may be a result of the lipid headgroups being offset in the bilayer normal direction, as observed in previous work [41]. This offset is not captured when the headgroup positions are projected onto the same plane to construct the Voronoi tessellation (see the Supplementary Material for more details).

In the SC, the lipids are organized into repeating lamellar structures (i.e., multilayers), and thus understanding the lipid structure in multilayers is of considerable interest. Here, using the validated CG force fields, simulations of multilayer self-assembly were performed in a similar manner to the bilayer self-assembly simulations, with two changes. First, instead of initially cooling to 305 K from the initial configuration, the system is isochorically compressed in the xy plane to ½ the equilibrium bilayer APL, so that, in principle, two bilayers can fit within the simulation box. This compression was followed by the expansion/compression process used for bilayer self-assembly, except that the temperature was held at 550 K during the expansion, and then lowered to 305 K during the compression. The temperature was kept elevated to give the lipids more energy to reorganize during the expansion. To show reproducibility, three different total expansion/compression times were used: 200 ns, 400 ns, and 600 ns.

Stable multilayer structures formed in each simulation. A representative self-assembly process is shown in Figure 4. Of particular interest in these systems are the fractions of CER molecules that are in hairpin versus extended conformations, as this may have implications for the lamellar arrangements of CERs in the SC [20]. Here, we define an extended conformation as a CER where the angle between the two tails is greater than 90° and a hairpin conformation otherwise. In each of the self-assembled structures, between 23 and 28% of the CERs in the middle layers adopt a hairpin conformation, compared to 15% for pure CER systems [37], suggesting that a mixture of hairpin and extended conformations is favorable. All systems contain a thin layer of water mixed with the headgroups in the middle of the lipid phase, ranging from 0.127 to 0.221 water beads per lipid, corresponding to 0.508 to 0.884 water molecules per lipid, which is consistent with experimental observations of low lipid headgroup hydration in model SC membranes [42, 43].

Figure 4.

Multilayer self-assembly process: a) disordered configuration after resizing to fit two bilayers, b) at maximum expansion, c) the final configuration of the compression phase, and d) final configuration after 200 ns of simulation at 305 K and 1 atm. CG beads colored the same as in Figure 3.

4. Conclusion and Outlook

This work highlights the use of multiscale modeling in studying the SC layer of skin. While atomistic simulations can be used to study properties at the atomistic level, e.g., hydrogen bonding [11], in order to study systems on a larger scale, simplified CG models are needed. We use MS-IBI to derive transferable CG models from atomistic simulations. These CG models can be used to study native lipid structures in the skin through self-assembly, which removes the influence of the initial configurations and hence the structures represent preferred lipid morphologies. As such, skin lipid systems can be computationally studied at multiple levels of resolution to provide a complete picture of how atomic-level features of lipids give rise to mesoscale properties. Information gleaned from these studies will prove useful for a wide range of applications, from strategies for restoring an impaired skin barrier to selectively penetrating the skin barrier, e.g., for transdermal drug delivery [44, 45].

Supplementary Material

1

Figure S1. A typical Voronoi tessellation for a single bilayer leaflet. The location of the lipid headgroup within each cell is given by the point in that cell.

• A coarse-grained force field of stratum corneum lipids is extended to new lipids.

• Interactions between the headgroups of ceramide and free fatty acid are optimized.

• Self-assembly of the lipids into lamellar structures is observed.