Simulated Auditory Nerve Axon Demyelination Alters Sensitivity and Response Timing to Extracellular Stimulation

Abstract

Since cochlear implant function involves direct depolarization of spiral ganglion neurons (SGNs) by applied current, SGN physiological health must be an important factor in cochlear implant (CI) outcomes. This expected relationship has, however, been difficult to confirm in implant recipients. Suggestively, animal studies have demonstrated both acute and progressive SGN ultrastructural changes (notably axon demyelination), even in the absence of soma death, and corresponding altered physiology following sensorineural deafening. Whether such demyelination occurs in humans and how such changes might impact CI function remains unknown. To approach this problem, we incorporated SGN demyelination into a biophysical model of extracellular stimulation of SGN fibers. Our approach enabled exploration of the entire parameter space corresponding to simulated myelin diameter and extent of fiber affected. All simulated fibers were stimulated distally with anodic monophasic, cathodic monophasic, anode-phase-first (AF) biphasic, and cathode-phase-first (CF) biphasic pulses from an extracellular disc electrode and monitored for spikes centrally. Not surprisingly, axon sensitivity generally decreased with demyelination, resulting in elevated thresholds, however, this effect was strongly non-uniform. Fibers with severe demyelination affecting only the most peripheral nodes responded nearly identically to normally myelinated fibers. Additionally, partial demyelination (<50%) yielded only minimal increases in threshold even when the entire fiber was impacted. The temporal effects of demyelination were more unexpected. Both latency and jitter of responses demonstrated resilience to modest changes but exhibited strongly non-monotonic and stimulus-dependent relationships to more profound demyelination. Normal, and modestly demyelinated fibers, were more sensitive to cathodic than anodic monophasic pulses and to CF than AF biphasic pulses, however, when demyelination was more severe these relative sensitivities were reversed. Comparison of threshold crossing between nodal segments demonstrated stimulus-dependent shifts in action potential initiation with different fiber demyelination states. For some demyelination scenarios, both phases of biphasic pulses could initiate action potentials at threshold resulting in bimodal latency and initiation site distributions and dramatically increased jitter. In short, simulated demyelination leads to complex changes in fiber sensitivity and spike timing, mediated by alterations in action potential initiation site and slowed action potential conduction due to non-uniformities in the electrical properties of axons. Such demyelination-induced changes, if present in implantees, would have profound implications for the detection of fine temporal cues but not disrupt cues on the time scale of speech envelopes. These simulation results highlight the importance of exploring the SGN ultrastructural changes caused by a given etiology of hearing loss to more accurately predict cochlear implantation outcomes.

Graphical Abstract

1-Introduction

While the overwhelming majority of cochlear implant recipients with bilateral, post-lingual deafness report at least some improvement in speech recognition and quality of life, there is substantial variability in just how much individual implant recipients benefit from their device (Blamey et al., 1996; Lazard et al., 2012; Orabi et al., 2006). Some individuals achieve near perfect performance on tasks requiring speech recognition in quiet while others receive far less benefit (Poissant et al., 2014). Binaural hearing-dependent tasks, such as localizing sound sources based on interaural timing and level cues, are particularly variable in recipients of bilateral implants, even with optimized delivery of fine temporal structure information, pitch-matching of electrodes, and device synchronization (Kan and Litovsky, 2014; Litovsky et al., 2012). This diversity of CI outcomes is only partially accounted for by pre- and peri-operative factors (Lazard et al., 2012).

Since CI function involves direct depolarization of spiral ganglion neurons (SGNs) by extracellular current, it is presumed that SGN physiological health is an important factor in CI outcomes. Of the epidemiological factors that correlate with outcomes, most predictive pre-operative factors are implicitly related to the neural integrity, including duration and etiology of deafness (Blamey et al., 2012, 1996; Lazard et al., 2012; Rubinstein et al., 1999). This expected relationship has been challenging to directly demonstrate in humans. One of the few studies of post-mortem human temporal bones found significant loss of SGN somata in older individuals, particularly in the basal cochlea; this loss was greater when both inner and outer hair cells were absent, suggesting that progressive SGN loss does occur in humans, particularly those with HL (Zimmermann et al., 1995). A study correlating threshold measures of CI recipients in life with post-mortem SGN counts observed no inter-subject correlation but a significant interaural correlation (Incesulu and Nadol, 1998). Other, less direct, lines of evidence also support the hypothesis that SGN integrity is critical to outcomes. Patients with SGN sparing, non-syndromic etiologies of deafness have significantly better outcomes than those with either genetic lesions impacting SGNs or infectious etiologies known to cause nerve damage (Shearer et al., 2017). Collectively, these findings suggest that SGN function is critical to CI functionality but that gross measures that reflect only the presence of SGNs may not provide sufficient detail into their functional status and capture only part of clinical variance.

Limited human and animal studies have demonstrated both acute and progressive SGN ultrastructural changes, notably axon demyelination, even in the absence of soma death, and corresponding altered physiology following sensorineural deafening. Loss of myelination within the peripheral process precedes that of the central process, and ultimately degeneration of these processes and cell death in both humans and cats (Hardie and Shepherd, 1999; Leake and Hradek, 1988; Shepherd and Javel, 1999). More recently, Tagoe et al. (2014) noted a reduction in myelin lamellae number and a downward shift in the distribution of myelin thickness following deafening via acoustic over-exposure in rats. Collectively, these studies indicate the structural integrity of SGNs, particularly myelin insulation of internodal segments, is damaged following deafening; and the time course, while not fully characterized, suggests progressive processes. Thus far, due to technical constraints, no studies exploring the relationship between SGN myelination and behavioral measures of hearing have been performed in humans. There are, however, case reports of febrile deafness in patients with autoimmune demyelinating disorders in which elevated core body temperature produced temporary hearing impairment, highlighting the important interaction of myelination and auditory nerve function (Cianfrone et al., 2006).

Comparison of electrophysiological responses to extracellular stimulation in acutely and long term deafened animals suggests that substantial changes in neural function do occur, but they are highly dependent on the details of experimental design. Some groups found increases in both auditory evoked brain stem and SGN single unit response thresholds with increasing pre-procedure duration of deafness in rats and cats (Shepherd et al., 2004; Shepherd and Javel, 1997) while another group observed the opposite relationship in Guinea Pigs (Sly et al., 2007). Single unit recordings from Shepherd et al.’s 2004 rat experiments show substantial variability of response latency and jitter between individual fibers but no significant effect of deafness duration, while those in Sly et al.’s 2007 Guinea Pig study exhibited decreasing response latency with duration of deafness. These results highlight the complex and potentially diverse changes in fiber electrophysiological properties after deafening and the need for a theoretical framework with which to ground an understanding of these changes.

Computational models of the CI electrode-neuron interface have the potential to create a mechanistic link between the anatomical and electrophysiological neural changes observed in animal models of HL. Ultimately, such an approach may help explain CI performance variance in human implant recipients. Previously, many studies of myelination and current spread have used analytical models to assess how subthreshold currents spread through fibers (Basser, 2004; Koles and Rasminsky, 1972; Rushton, 1951). While these analytical models can shed light on electrotonic effects, they cannot make any predictions about the suprathreshold behavior of fibers and do not account for the stochastic behavior of neurons introduced by small populations of ion channels; stochasticity that is critical to the dynamic range of populations of neurons (Chow and White, 1996; Imennov and Rubinstein, 2009; White et al., 2000). More recently, empirically derived point-process models have been used to explore neural response to extracellular stimulation. These models are generally able to replicate the electrophysiological behavior of single neurons recorded in animal models and can encode amplitude-modulation information (Goldwyn et al., 2012, 2010). More recently a similar model was extended to simulate both central and peripheral action-potential initiation, facilitating recapitulation of differential responses to opposite polarity monophasic stimuli as observed in cat neurons by Shepherd and Javel in 1999 (Joshi et al., 2017). However, the empirical nature of these models makes interpretation of individual parameters challenging, thus, it is difficult to make predictions regarding how parameters might be changed in different pathological states. Moreover, there currently exist no data exploring chronaxie or rheobase within chronically deafened animals with which to construct such phenomenological models.

In contrast, biophysical models, while more computationally intensive and harder to design, have parameters explicitly related to the physical and electrical properties of the neurons they attempt to simulate. As such, it is possible to predict how reduced internodal myelination would manifest in the model. Previous studies have explored the effect of peripheral process degeneration using this approach and observed shifts in site of action potential generation (Briaire and Frijns, 2006; Rattay et al., 2001b). This model was selected for the following experiments because it is one of the simplest in which interactions between the spatial spread of current and inhomogeneities in the myelination of axons can be explored. In the present study, we first explored how different stimulus waveforms initiate responses in different locations in a sound level-dependent manner even in normal fibers. We then explored the effect of fiber internode myelination by systematically varying severity and distribution of myelin loss. The response properties of these different simulated fibers provide insight into the biophysical sources of changes observed in recordings from animal models of long-term sensorineural HL and shed light on psychophysical phenomena in human CI users. They may also constrain the types of variability in psychophysical outcomes that would be expected with such neural pathology.

2-Methods

2-1 Segmented Cable Model with Stochastic Channel Behavior

The biophysical model used in this study represents the peripheral and central axons of Type 1 SGNs as a single segmented cable, as previously described (Imennov and Rubinstein, 2009; Mino et al., 2004; O’Brien and Rubinstein, 2016). Briefly, the membrane potential within each segment during stimulation by an extracellular electrode is described by a partial differential equation (Eq. 1) relating axial current to capacitive, leak, applied, and ionic currents according to Kirchoff’s law (illustrated in Fig 1A):

$$\frac{-h^2}{R_a(x)}\frac{d^2{V}_m(x,t)}{{dx}^2}=C_m(x)\frac{d{V}_m(x,t)}{dx}-\frac{V_m(x,t)}{R_m(x)}+\frac{h^2}{R_a(x)}\frac{d^2{V}_{\mathit{ext}}(x,t)}{{dx}^2}+I_{\mathit{ion}}(x,t)$$ (1)

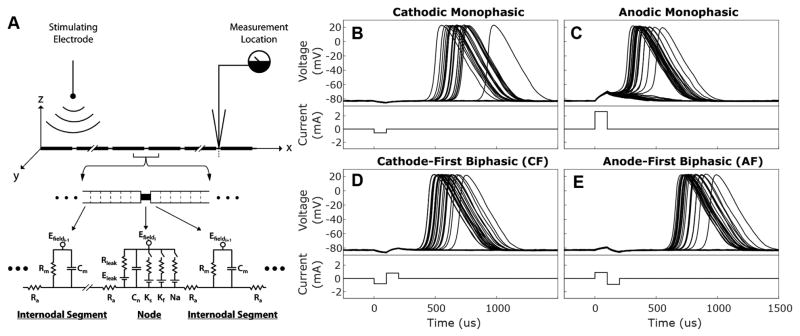
Figure 1. Responses of biophysical, modeled neurons to monophasic and biphasic stimuli.

(A) Wiring diagram illustrates auditory nerve fibers modeled as segmented wires via a core-conductor approach. Each segment is characterized by its membrane resistance (R_leak), membrane capacitance (C_m), and axial resistance (R_a). Internodes are divided into 9 adjacent segments which have dynamics governed solely by passive. Node of Ranvier segments have additional voltage dependent elements for sodium channels (Na), fast potassium channels (K_f), and slow potassium channels (K_s); each of which are defined by channel density, channel conductance, ionic reversal potential, and the number of channels within the open state. Electrodynamics within each segment are expressed by relating axial, membrane leak, membrane capacitive, and ionic currents using Kirchoff’s law (see Eq. 1). A stimulating electrode placed 3 mm from fiber over 10 node of Ranvier segment provides a field potential (E_field) that varies with distance from the electrode. Fibers are 36 nodes long, the approximate number of nodes between the feline auditory periphery and cochlear nucleus, and most recordings are taken from node 32. Reprinted with permission from Imennov and Rubinstein, 2009. (B–E) Responses recorded from node 32 of 36 of normally myelinated fibers (Rel. Myelination = 1) to 50 presentations of the 4 stimuli waveform types described. For each waveform type, current amplitude was selected to produce an action potential response probability of 0.50. Cathodic (B) and anodic (C) monophasic stimuli and responses are depicted in the top panels while cathode-first (D) and anode-first (E) biphasic stimuli and responses are depicted in the bottom panels.

Behavior of each of these currents is dictated by biophysical parameters, originally derived from anatomical and physiological data from model organism, principally feline, auditory nerves. Individual parameters were then allowed to vary within 10% of empirical values until simulated relative spread, spike latency, jitter, chronaxie, relative refractory period, and conduction velocity were within 10% of values recorded from felines in response to intracochlear electrical stimulation. The present study uses identical parameters to those used in Imennov and Rubinstein, 2009 except for the explicit changes described in Sections 2-2 and 2-3.

Each fiber consisted of 36 nodes, with intervening internodes, the approximate number existing between the auditory periphery and cochlear nucleus of felines. Within the segmented cable model, myelinated internodal regions were divided into nine segments each of which possessed electrodynamics described completely by passive axial, leak, and capacitive currents. The biophysical parameters governing the behavior of a standard internodal segment are listed in Table 1. Internodal segment length, plasma membrane caliber, and axonal resistance remained constant for all described experiments while myelin thickness, membrane capacitance, and membrane resistance were experimentally manipulated as described in Section 2-2.

Table I.

Morphological and Electrophysiological Parameters

	Value	Ref		Value	Ref
Node of Ranvier:			Internode:
Length	1 μm	(Berthold, 1978)	Total Number	36
Caliber	0.75 μm	(Liberman and Oliver, 1984)	Segments per internode	9
Capacitance, cm	20.5 fF/mm2	(Tasaki, 1955)	Length/Diameter Ratio	92:1	(Arnesen and Osen, 1978)
Resistance, rm	8.31 kΩ*mm2	(Schwarz et al., 1995)			(Basser, 2004)
		(Brismar, 1981)	Length	230 μm
Axonal Resistance, ra	733 Ω*mm	(McIntyre et al., 2002)	Axon Caliber	1.5 μm	(Liberman and Oliver, 1984)
		(Frijns, 1994)	Myelin Thickness	1 μm
External Resistance	25 kΩ*mm	(Rubinstein, 1993)	Axon/Fiber Ratio	0.6	(Arnesen and Osen, 1978)
Resting Potential	−84 mV	(Schwarz et al., 1995)			(Basser, 2004)
Threshold Potential	50 mV		Resistance, rmmy	1.254 GΩ*mm	(Tasaki, 1955)
Time Step	1 μs		Baseline Capacitance, cmmy	145 zF/mm	(Tasaki, 1955)

In contrast, nodes of Ranvier were represented as single segments possessing both passive elements and stochastic, voltage dependent ionic currents. The parameters governing nodal segment behavior were held constant at the values in Table 1. The behavior of stochastic, voltage-dependent ion channels within nodal segments was modeled using a Markov jump process (Gillespie, 1977; Mino et al., 2004; Mino and Grill, 2002). Total ionic current was defined as the sum of sodium, slow potassium, and fast potassium currents. This procedure enabled computationally efficient simulation of channel dynamics within each segment while maintaining an accurate representation of their stochastic behavior (White et al., 2000).

Simultaneous solution of numerical approximations of the system of differential equations described by Eq. 1, with the relevant ionic currents and applied field induced currents (described in section 2-3), by an implicit Crank-Nicholson scheme yields the potential within each segment of the model fibers for each time step of the simulation (Mino et al., 2004). A time step of 1 μs was used for all simulations. Simulations were performed using custom-built C code, using a MatLab wrapper for managing input parameters and analyzing output data.

2-2 Exploration of Demyelination Parameter Space

To adapt the model to simulate pathological alterations in SGN axons, we implemented a modified version of the core-conductor model of myelinated axons (Basser, 2004; Koles and Rasminsky, 1972). The core-model treats myelinated axons as a single-layer of resistive-capacitive medium separating resistive compartments. The membrane capacitance and resistance across internodal segments can then be described by Eqs. 2 and 3, respectively:

$$\frac{C_{my}}{L}=\frac{2\pi {\kappa }_{my}{\epsilon }_0}{ln(D/d)}$$ (2)

$$\frac{R_{my}}{L}-\frac{\rho }{2\pi L}ln(D/d)$$ (3)

Where κ_my is the dielectric constant of myelin, ρ is the resistivity of myelin, ε₀ is the permittivity of free space, D is the myelin sheath outer diameter, d is the plasma membrane diameter, and L is the length of the internode. From these relationships, the core-conductor model predicts a decrease in the internode membrane space constant and a fixed time constant with decreasing myelin thickness.

A shortcoming of this model is that membrane resistance approaches 0 and capacitance ∞ in the limit of complete myelin loss. We addressed this asymptotic behavior by incorporating the internodal plasma membrane resistance and capacitance in series with the myelin sheath’s, creating a core-dual conductor model. Since the specific resistance of lipid bilayer without ion channels embedded in it is of a similar order to that of myelinated axon (10⁶–10⁸ ohm*cm² and 4.45*10⁸ ohm*cm², respectively), we chose to fix resistance as we decreased myelin width (Imennov and Rubinstein, 2009; Montal and Mueller, 1972). Assuming the plasma membrane dielectric constant remains consistent between nodal and internodal segments, the plasma membrane capacitance of the internode can be estimated using the nodal value divided by the constriction factor. The total internodal capacitance can then be calculated by adding the plasma membrane and myelin contributions in series:

$$\frac{1}{C_{\mathit{internode}}}=\frac{1}{C_{my}}+\frac{1}{C_{m,\mathit{internode}}}=\frac{log(D/d)}{log(1/0.6)C_{my,\mathit{normal}}}+\frac{C_{\mathit{constric}}}{C_{m,\mathit{node}}}$$ (4)

This procedure for varying membrane capacitance while freezing membrane resistance to simulate changes in myelin width produces similar capacitance values to the simple core-conductor model for most values of D but preserves finite capacitance in the limit of no myelination (Fig 2C). Fixing the resistance leads to substantial differences in predicted resistance between the models at extreme amounts of demyelination as well. A consequence of these changes is that this model predicts a constant, static space constant for demyelinated fibers but a monotonic increase in time constant with reduced myelin thickness.

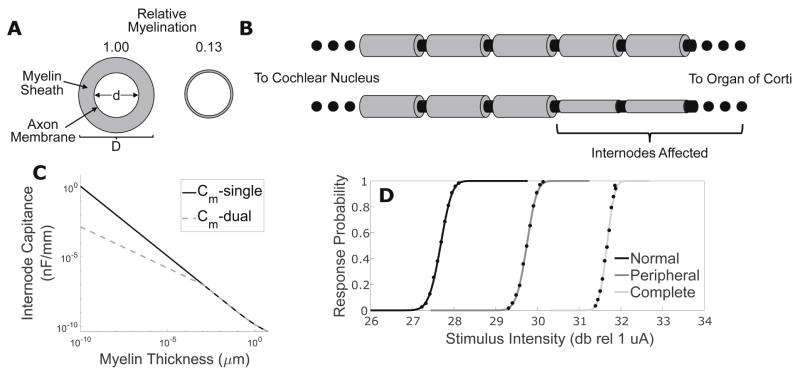
Figure 2. Demyelination shifts input-output functions of fibers.

Using our approach to calculate internodal membrane capacitance presented (Eq. 8) it is possible to modify a single model peripheral axons’ membrane capacitance to represent any gradation of demyelination (A). This procedure can be applied to any subset of internodes, enabling simulation of anything from peripheral to complete demyelination (B). (C) Internodal specific capacitance calculated by dual conductor (solid black) and single conductor (dashed grey) models is plotted as a function of myelin thickness for a 1.5 μm caliber fiber. (D) Input-output functions illustrating response probability plotted as a function of monophasic cathodic stimulus current pulse intensity are presented for normal, peripherally demyelinated (95% reduction in myelin width impacting first 10 internodes), and centrally demyelinated (95% reduction in myelin thickness impacting first 28 internodes) fibers.

Using this novel approach to calculate internodal membrane capacitance and resistance we modified a single model peripheral axon’s membrane capacitance to represent many gradations of demyelination, diagrammed in Fig 2A. This procedure can be applied to any subset of internodes, enabling us to simulate anything from partial, solely peripheral demyelination to complete demyelination of the entire fiber, see Fig 2B.

2-3 Application of Extracellular Currents

Simulated SGN axons were stimulated by an extracellular disk electrode as derived previously by Rubinstein and used in previous versions of this model (Imennov and Rubinstein, 2009; Mino et al., 2004; O’Brien et al., 2016; Rubinstein, 1988). Briefly, by assuming that injected current propagates through an isoresistive medium, the applied potential difference between adjacent segments can be expressed as a function of the injected current and the segment-electrode distance. The field potentials along the fiber can then be calculated for each time step during stimulation for a selected current waveform. In the present study, fibers were presented with one of 4 different stimulation waveforms following a delay of 1 ms. Initial experiments were performed with simple monophasic 100 μs pulses of either cathodic or anodic polarity, as used in Miller et al. 1999, to facilitate ease of interpretation (waveforms illustrated in Fig 1B & C, lower panels) (Miller et al., 1999). Subsequently, charge balanced, biphasic pulses with either anodic (AF) or cathodic (CF) phase first (Fig 1D & E, lower panels, respectively, no inter-phase gap, and 100 μs/phase duration were used for their relevance to the stimulation paradigm used in CIs and for comparison to recordings from animal models of SNHL (Galvin and Fu, 2009; Shannon, 1992; Shepherd et al., 2004; Shepherd and Javel, 1999). Following stimulus presentation, simulations were continued for 4 ms to enable monitoring of fiber-potential evolution. For each stimulus waveform, amplitudes were selected to produce the desired response probabilities for a block of simulations.

2-4 Stimulus Selection and Analysis

For each fiber-stimulus waveform pair, an iterative process was used to identify the current-pulse amplitudes required to produce action potentials with a range of response probabilities. We first identified the stimulus amplitudes between which a fiber’s response probability varied between 0 and 1 using coarse sampling of currents between 0.5 mA and 150 mA using 25 Monte Carlo simulations per fiber-intensity pairing. After identifying this initial range, we linearly sampled the current-amplitude space between these two stimulus intensities using blocks of 500 Monte Carlo simulations per pairing. The amplitude range tested was refined until the resulting stimulus input/response probability output curve could be fit with a cumulative normal distribution function (CDF) using least-squares fitting. We define the stimulus intensity at a response probability of 50%, the CDF mean (μ), as threshold. Relative spread (RS), a measure of dynamic range, was defined as the CDF variance (σ) divided by its mean. The CDF defined threshold and RS were used to further refine the range of stimulation intensities and the 500 block simulations repeated until sampling between threshold − 2*RS and threshold + 2*RS resulted in no substantial trial to trial variation in calculated threshold or RS.

For each fiber-stimulus pair, the latency between stimulus onset and threshold crossing at the recording node (node 32) was calculated for each trial generating an action potential. From this distribution of latencies, the mean latency and jitter (latency standard deviation) were calculated for each stimulus amplitude. The described simulation enables recording of potentials within each segment of the fiber. By identifying the segment in which the membrane potential first crosses threshold, the node of Ranvier responsible for action potential generation was found for each trial. From the resulting distribution of initiation sites, the mean initiation site and variance in initiation location were calculated.

The latency of response arrival at the recording node was decomposed into initiation and conduction delay components. Initiation delay is defined as the time interval between stimulus onset and the first action potential arising within a fiber node, termed the initiation node. Conduction delay is defined the time interval between the first action potential initiation and action potential arrival at the predefined recording node. From these quantities, the mean conduction velocity of action potentials between the initiation and recording nodes can be determined via Eq. 5:

$$\langle V_{\mathit{conduction}}\rangle =\frac{d_{\mathit{internodal}}\ast (N_{\mathit{Rec}}-N_{\mathit{Ini}})}{(t_{\mathit{Rec}}-t_{\mathit{Ini}})}$$ (5)

2-5 Simulating interaural timing difference (ITD) Artifacts Induced by Asymmetric Demyelination

To explore potential ramifications of demyelination on fine temporal cue encoding, we simulated the ITD distributions produced by delivery of biphasic pulses to different fibers, which in this case represent the populations of neurons nearest corresponding electrodes in ‘left’ and ‘right’ simulated cochlea. For each case, normal fibers were used in the left cochlea while those of the right were variably demyelinated. AF biphasic pulses, intensity matched by response probability, were then delivered simultaneously bilaterally. The distribution of ITDs produced by repeatedly subtracting a randomly selected right fiber latency from one from the left over 1000 trials is presented.

3-Results

3-1 Different Passive Responses to Opposing Polarity Currents Drive Stimulus-Dependent Variation in Fiber Sensitivity

To better understand how CI stimulation is encoded by SGNs we first explored the response patterns of normal fibers to different stimulus waveforms. Membrane potential responses of normally myelinated fibers (myelin thickness = 1 μm) to cathodic monophasic, anodic monophasic, CF biphasic, and AF biphasic stimuli are illustrated in Figure 1B–E, upper panels. For each waveform type, current amplitude was selected to produce an action potential firing efficiency of 0.50. Note responses to all four stimulus types exhibit a passive, deterministic-appearing behavior at the recording site that is hyperpolarizing for cathodic polarity pulses and depolarizing for anodic ones. Viewed as a function of distance from the electrode (data not shown), these passive responses consist of depolarization and hyperpolarization of the fiber immediately underlying the electrode, for cathodic and anodic pulses respectively, with an opposing shift in membrane potential along the more central axon. This predominantly passive response is followed probabilistically by an action potential of variable, but stimulus dependent, latency. Other trials exhibit no membrane potential change during this latter period, indicating response failure.

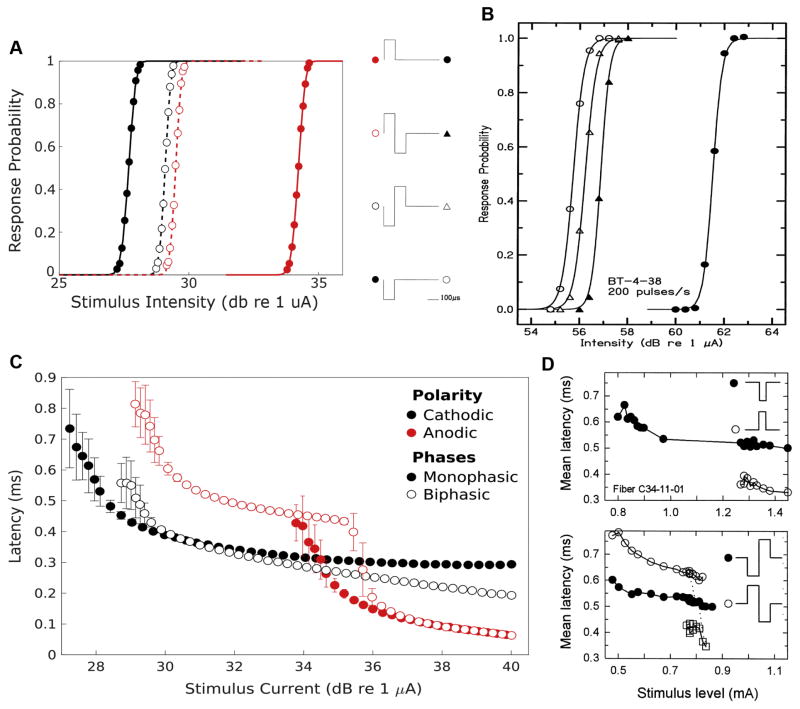
To more thoroughly characterize the interaction between stimulus-waveform, intensity, and fiber responses; Figure 3A contains plots of the response probabilities of normal fibers as functions of current intensity for the four stimuli. The stimulus intensity necessary to produce a given response probability is substantially lower for cathodic than anodic monophasic stimuli (Thresh_Cathodic = 27.68 and Thresh_Anodic= 34.23 dB re 1 μA). Biphasic stimuli generated input-output functions falling between these extremes but substantially closer to the cathodic monophasic curve (Thresh_CF = 29.09 and Thresh_AF = 29.50 dB). This reflects the fact that the depolarizing center of the cathodic phase of biphasic pulses initiates action potentials in the periphery (data not shown). The biphasic stimuli result in thresholds elevated with respect to the cathodic monophasic stimulus due to the hyperpolarizing effects of the adjacent anodic phase; an effect modestly more prominent with the AF biphasic stimulus type. Input-output functions to the monophasic pulses possessed similar RSs (RS_cathodic = 0.0506 vs Rs_anodic=0.0499) while those to biphasic pulses exhibited substantially lower values (RS_CF = RS_AF = 0.0402). This modest decrease in dynamic range for the biphasic pulses reflects the requirement that the depolarizing stimulus be sufficiently large to overcome the antecedent or subsequent hyperpolarizing phase. These simulation observations qualitatively resemble the input/output functions produced from recordings of spiral ganglion central axons in response to intracochlear electrical stimulation by Shepherd and Javel in 1999 (Fig 3B). Although Shepherd and Javel used a bipolar electrode configuration for these recordings and the present simulations use a monopolar configuration, at the single fiber level the qualitative similarity in relative threshold sensitivity is notable.

Figure 3. Normal fiber input-output curves and latencies vary with stimulus waveform.

(A) response probability, averaged over 500 Monte Carlo trials, of normal simulated fibers to varying current intensities of cathodic monophasic, anodic monophasic, cathode-first biphasic, and anode-first biphasic stimuli (markers). These response profiles are fit with a CDF (lines). (B) Input/output functions using similar stimuli produced from recordings from spiral ganglion central axons in response to intracochlear electrical stimulation by Shepherd and Javel in 1999 for comparison (reprinted with permission). (C) Mean latency between stimulus onset and action potential arrival at node 32 is plotted as a function of stimulus current for each of the 4 stimulus waveforms applied to normally myelinated fibers (n = 500 monte carlos). Error bars represent jitter, the variance of the latency distribution. Solid markers and lines correspond to monophasic stimuli while empty markers and dashed lines correspond to biphasic stimuli. Black markers and lines indicate waveforms with cathode leading phases while red ones indicate anodic leading phases. (D) Latency-intensity functions for responses to monopolar stimuli recorded from cats by Miller and Colleagues. Monophasic pulses (top panel) were 39 μs in duration while biphasic stimuli (bottom panel) were 100 μs/phase with no interphase gap. Cathodic monophasic and CF stimuli plotted as filled markers while anodic monophasic and AF plotted as open markers. AF latencies separated into long (open circles) and short (open squares) populations. Adapted, with permission, from Miller et al., 1999.

3-2 Suprathreshold Initiation Site Shifts Lead to Decreases in AF Stimulus Induced Response Latencies

The different distributions of passive responses also lead to variations in action potential initiation site that drive stimulus specific response timing characteristics. Latency between stimulus onset and central action potential arrival is plotted as a function of current magnitude for each of the stimuli applied to normal fibers in Figure 3C. For all stimulus waveforms, fiber response latency and jitter initially decrease with increasing stimulus intensity. Each stimulus waveform produces responses with characteristic mean latency at threshold. Responses to solely anodic stimuli exhibit the shortest latency at threshold (0.3607 ms) due to central action potential initiation. Cathodic stimuli produce responses with substantially longer latency (0.6336 ms), resulting from peripheral initiation and conduction delay. Biphasic pulses also initiate action potentials at this node closest to the electrode but are subject to pulse sequence-dependent effects. CF biphasic pulses produce responses with a shorter latency (0.5230 ms) compared to monophasic cathodic pulses owing to the more intense current at threshold required to initiate action potentials before the onset of the hyperpolarizing phase. In contrast, AF biphasic stimuli produce responses delayed by 199 μs (0.7535 ms) relative to monophasic cathodic stimuli due to the combined effect of the first phase duration and the requirement to overcome the consequent hyperpolarization.

Latencies of responses also vary with stimulus type at intensities above threshold. Response latencies to cathodic and anodic monophasic stimuli decay with growing current intensity until they asymptote to minima, (approximately 290 and 60 μs respectively). Biphasic stimuli induced response latencies exhibit more complex behavior. Initially they decay at a similar rate to cathodic monophasic stimuli, however, instead of approaching an asymptote, the latter demonstrate polarity order-dependent behavior. Increasing CF biphasic pulse currents produces a near linear reduction in latency due to the anodic polarity pulse facilitating conduction of the peripherally generated stimulus. In contrast, latencies to AF biphasic stimuli initially approach a local minimum before exhibiting an abrupt and dramatic decrease in latency near the threshold for anodic monophasic stimuli. Additional increases in current intensity result in another exponential decay phase that parallels that of anodic monophasic responses. This pattern of latency changes is produced by an abrupt transition from peripheral AP initiation by the cathodic phase to central initiation by the preceding anodic phase.

These simulated latency findings exhibit marked similarity to the latency-stimulus functions recorded from cats in response to monopolar stimulation by Miller et al. (Fig 3D) (Miller et al., 1999). Responses to monophasic stimuli (top panel) exhibit lower latency, albeit with higher threshold, to anodic stimuli. Latencies for both monophasic stimuli initially decrease with increasing stimulus intensity but ultimately approach asymptotic values; asymptotic anodic monophasic latencies are ~200 μs shorter than those for cathodic monophasic stimuli. Response latencies to biphasic stimuli (lower panel, different fiber) instead exhibit either a gradual decline, for CF stimuli, or gradual decay punctuated by an abrupt shift to shorter latency, for AF stimuli. As with the simulation results, responses to AF stimuli with intensities in this transition region exhibit bimodal latency distributions (separately plotted in Fig 3D, bottom panel).

3-3 Moderate Demyelination Negligibly Impacts Thresholds and Only Modestly Alters Timing

Input-output functions illustrating response probability plotted as a function of monophasic cathodic stimulus current pulse intensity are presented in Fig 2D for normal, peripherally demyelinated (95% reduction in myelin width impacting first 10 internodes), and centrally demyelinated (95% reduction in myelin thickness impacting first 30 internodes). Peripheral demyelination results in an elevated threshold (29.75 dB) relative to the normal fiber (27.68 dB) with a reduced relative spread (0.045 vs 0.051). Demyelination extended to involve the central internodes of the fiber causes a further increment in threshold (31.67 dB) and decrement in dynamic range (RS = 0.034).

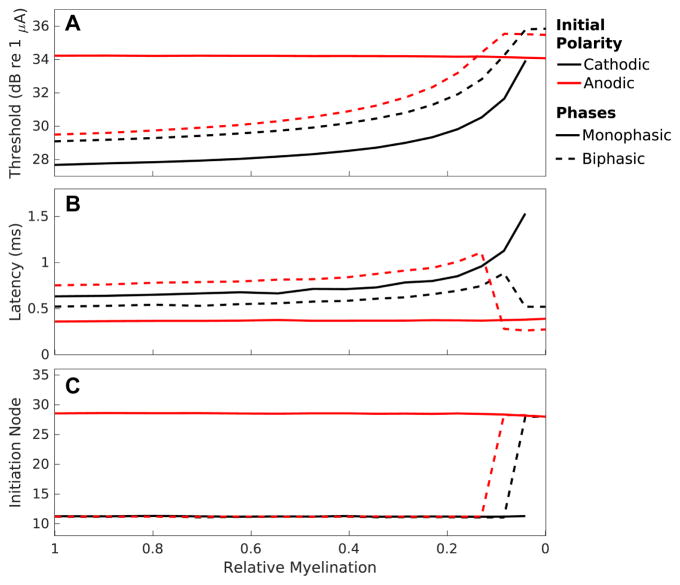
To explore the impact of demyelination in finer detail; Figure 4 presents thresholds (A), mean latencies at threshold (B), and mean initiation sites at threshold (C) to cathodic and anodic monophasic stimuli and CF and AF biphasic stimuli as a function of myelin thickness for peripheral demyelination affecting the first 16 internodes. Modest amounts of demyelination, <~50% reduction in myelin width, produce only minute changes in threshold (<0.5 dB in all cases) and modest changes in latency (64 μs and 113 μs for peripheral and central, respectively) for the cathodic stimulus type. Anodic stimulus-induced response thresholds and latencies do not change at all in the case of peripheral demyelination; however, centrally demyelinated fibers exhibit modest changes in threshold (0.31 dB) and latency (46 μs) with <50% reduction in myelin thickness to this stimulus type. With these modest amounts of demyelination, initiation site means and variances for the different stimulus types remain constant. Cathodic monophasic and biphasic stimuli all initiate APs at a mean location of about node 11 while anodic monophasic stimuli initiate action potentials centered around node 28.

Figure 4. Peripheral demyelination alters fiber sensitivity, response timing, and initiation site.

Response properties to cathodic (solid black) and anodic (solid red) monophasic stimuli and cathode-first (dashed black) and anode-first (dashed red) biphasic stimuli are presented as a function of myelin thickness for demyelination affecting the first 16 internodes. (A) Thresholds (mean of CDF fit to input-output function) plotted in units of decibels relative to 1 μA. (B) Mean latencies at threshold with error representing jitter. (C) Mean initiation sites at threshold with error represent initiation site variance. Myelin thickness is plotted on the abscissa, with normal myelination corresponding to a thickness of 1 μm, on the left, and complete demyelination to 0 μm, on the right. Each data point derived from 500 Monte Carlo simulations with a set of fiber-stimulus pairings.

3-4 Severe Peripheral Demyelination Alters Response Properties to Cathodic, but not Anodic, Monophasic Stimuli

More severe peripheral demyelination leads to profound changes in sensitivity to cathodic monophasic stimuli (Fig 4A). A 96% reduction in myelin thickness produces an approximately 6.27 dB threshold increase while complete loss leads to failure of the fiber to conduct action potentials. This increase in threshold is accompanied by a concomitant decrease in dynamic range with RS reduced to 50% of normal. Even with this extreme level of peripheral demyelination anodic thresholds and RS remain unperturbed.

Severe peripheral demyelination also dramatically altered response timing to cathodic but not anodic monophasic responses (Fig 4B). Cathodic response latency increased exponentially with reduced myelin thickness up to a loss of 96%. Again, in the absence of myelin fibers cannot initiate or propagate action potentials. Response jitter decreases for the changes in myelin thickness producing exponential increases in latency. In contrast, anodic monophasic stimuli induced response latency and jitter remain nearly constant over the entire range of myelin thicknesses for peripheral loss. The mean site of action potential initiation, at threshold, for cathodic and anodic monophasic pulses remained constant (Fig 4C), except for parameter pairings where cathodic stimuli failed to produce responses.

3-5 Response Properties to Biphasic Pulses Exhibit Discontinuous Non-Monotonic Changes with Severe Peripheral Demyelination

While at least 13% of myelin remains, response thresholds and latencies to the 2 biphasic waveforms (black and red dashed traces) nearly parallel those to cathodic alone (Fig 4A&B). Initial thresholds and latencies exhibit the relatively small translations due to the waveform-dependent effects presented in section 3-1. As with cathodic monophasic stimuli, response threshold increases, and RS decreases, in a monotonic fashion for these biphasic stimuli with peripheral demyelination until myelin loss becomes severe (<13% remaining). This relationship ultimately results in substantially elevated thresholds, with increases of 5–6 dB between thresholds for normally myelinated fibers and those demyelinated by 90%. With still more extreme peripheral demyelination, thresholds for CF and AF stimuli plateau. These plateaued thresholds parallel the near constant thresholds of fibers to anodic monophasic stimuli. While normal fibers are more sensitive to CF than AF stimuli, this relationship becomes inverted for fibers with sever myelin loss resulting in greater relative sensitivity to AF stimuli.

Mean latencies of responses to these biphasic pulses increase approximately exponentially with decreasing myelin thickness up to this limit as well (Fig 4B). With more severe demyelination (>87% reduction in myelin thickness) responses to biphasic pulses exhibit abrupt non-monotonic changes, deviating significantly from the patterns observed with cathodic monophasic stimuli. Plateauing of biphasic response thresholds in the setting of peripheral demyelination is accompanied by dramatic decreases in mean response latencies. CF stimuli response latencies increase with severity of peripheral demyelination from a baseline of 0.52 ms to a maximum of 0.85 ms with 92% demyelination. With >92% myelin loss, this latency abruptly drops back to 0.51 ms. Likewise, AF response latency is 0.75 ms at baseline, increases to a maximum value of 1.11 ms with 87% demyelination, and then abruptly drops to 0.28 ms with 92% or greater myelin loss. The low latencies of these heavily affected fibers are similar to the constant latency exhibited by responses to anodic monophasic pulses, even when peripheral myelin is absent. These observed non-monotonicities in response latencies to biphasic pulses as demyelination becomes more severe are driven, principally, by changes in the site of action potential initiation (data not shown). Both cathode-first and anode-first stimuli abruptly transition from initiating action potentials peripherally to centrally with severe loss of myelin.

3-6 Both Initiation and Conduction Delay Change in Demyelinated Fibers

With demyelination affecting 12–20 nodes, AF pulses produce responses that increase in mean latency of responses at threshold as loss of myelin becomes more severe, up to the abrupt transition to central initiation with extreme myelin thinning. This increase in latency reflects both a modest increase in the conduction delay along the fiber (Fig 5a), reflecting a modest reduction in conduction velocity (Fig 5b), and a more substantial and variable delay in initiation. The abrupt transition to central initiation corresponds with a dramatic decrease in conduction delay, due to both a reduction in the distance action potentials need to travel and increased conduction velocity due to the broad nature of the depolarizing surround facilitating conduction. The high variability in conduction velocity at these extreme values results from rounding errors introduced in the small interval between initiation and recording due to the discrete time steps of the simulation.

Figure 5. Initiation and conduction delays both contribute to latency changes.

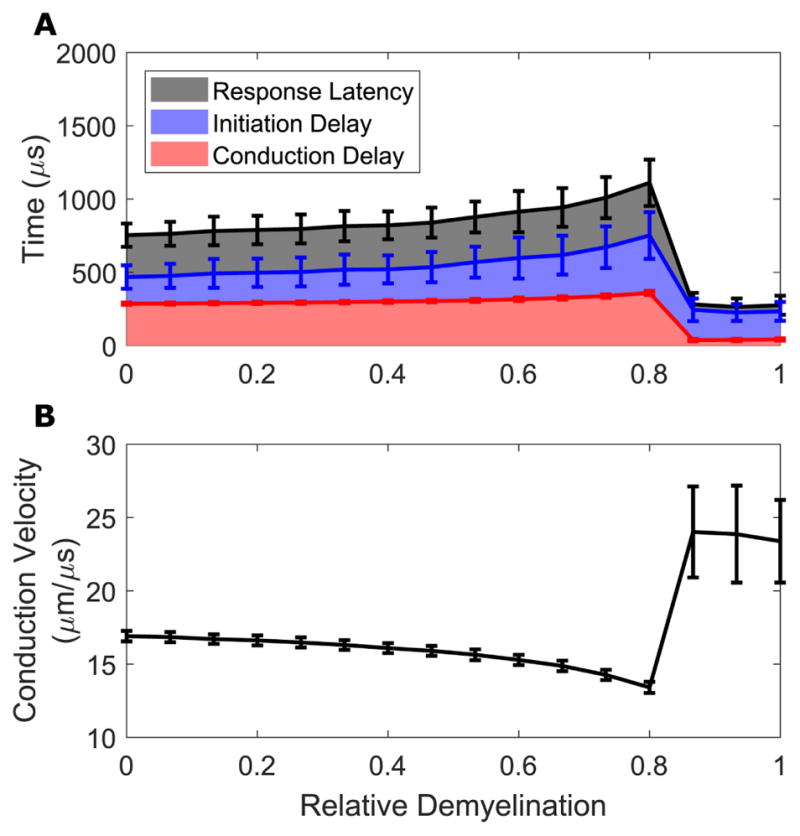
Response mean delays (A) and conduction velocity (B) are presented for responses to AF stimuli as a function of relative demyelination severity affecting the peripheral-most 16 nodes. (A) Latencies represent the elapsed simulation time between stimulus onset and recording node AP arrival (black); initiation delays that between stimulus onset and first AP threshold crossing at any node (blue), and conduction delays that between initiation time and recording node AP arrival (red). (B) Mean conduction velocity during conduction delay. Error bars represent standard deviations.

3-7 Thresholds are Robust to Demyelination

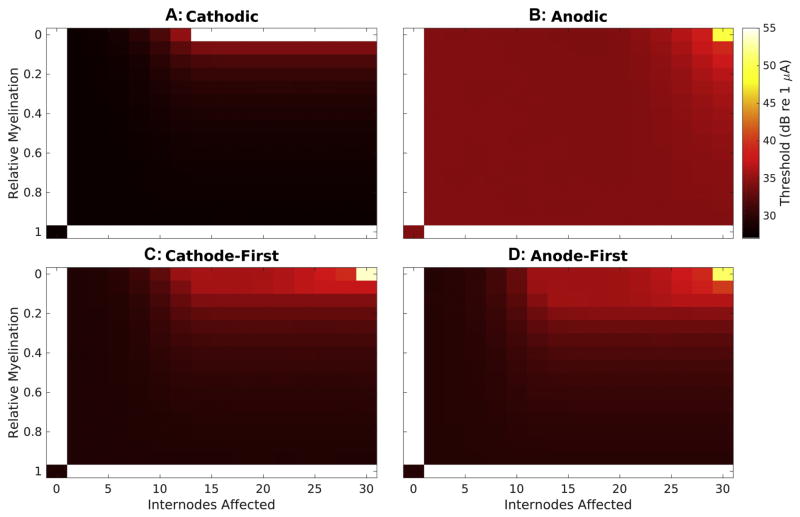
Visualizing the entire parameter space created by varying myelin width and the number of internodes affected provides additional insight into the impact of demyelination on response properties. Response thresholds, plotted in Fig 6, generally demonstrate a surprising robustness to the demyelination procedure but become dramatically elevated with extreme demyelination. Cathodic, CF, and AF waveforms (A,B,&C, respectively) produce responses with thresholds of 27.68, 29.09, and 29.49 dB in normal fibers, respectively. With demyelination affecting less than 10 internodes these thresholds change by less than 5 dB regardless of degree of myelin thinning. Conversely, when myelin thickness is at least 50% of normal, thresholds for these stimulus types change by less than 4 dB regardless of the number of internodes affected. Threshold changes for these stimuli types only become functionally important with greater than ~70% loss of myelin involving at least the 10 most peripheral internodes. While the baseline threshold for anodic monophasic stimuli (B) is substantially higher than for the other stimuli types (34.22dB), modified fiber thresholds show even greater robustness, only exhibiting elevation of at least 5 dB with greater than 90% demyelination of the entire fiber.

Figure 6. Thresholds vary with both severity of demyelination and stimulus waveform.

Threshold (color-mapping) is presented over the entire variable space created by the parameters of myelin thickness (ordinate) and number of internodes affected (abscissa) for each stimulus tested. Thresholds for monophasic stimuli are presented in the top two panels, cathodic in (A) and anodic in (B), while those for biphasic stimuli are presented below, cathode-first in (C) and anode-first in (D). Response thresholds for normal fibers are presented in the bottom left corner for each waveform. Myelin thickness decreases moving up the ordinate and number of internodes affected (beginning peripherally) increases along the abscissa, resulting in maximal demyelination in the top right.

3-8 Varying the Number of Internodes Demyelinated Alters Threshold, Dynamic Range, and Response Latency in Polarity-Dependent Manner

When demyelination impacts more than the 10 most peripheral nodes of a fiber, cathodic stimuli produce responses that increase in threshold (Fig 6A) and decrease in dynamic range (data not shown) with decreasing myelin thickness. The magnitude of this effect becomes more dramatic as additional internodes are involved until with 14 or more affected the relationship becomes that described in section 3-4 for 16 internodes affected. A complete absence of myelin involving at least the first 14 internodes prevents action potentials at the recording node due to initiation and conduction block. These increasing thresholds coincide with decreases in dynamic range (data not shown).

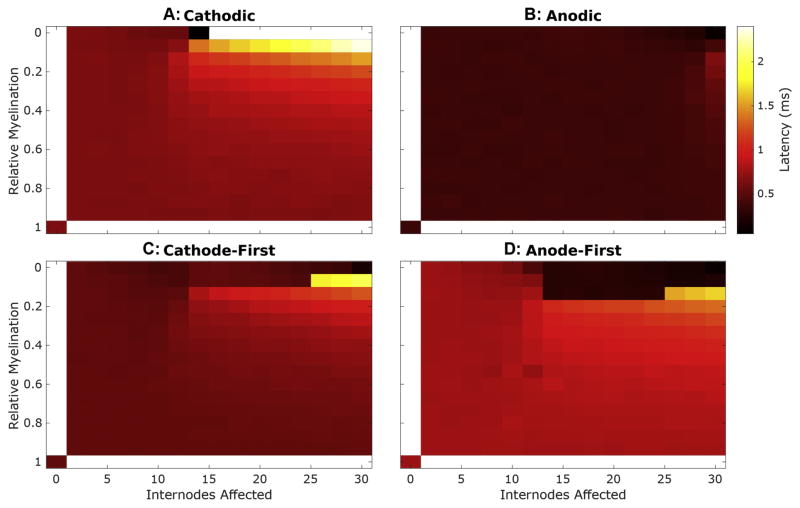
Mean latencies of responses to cathodic monophasic stimuli, at threshold, (Fig 7A) demonstrate substantially greater sensitivity to this demyelination procedure. While demyelination affecting less than the 10 most peripheral internodes generally has little effect on mean latency regardless of severity, once demyelination involves more than 10 internodes, latency increases in a manner proportional to the number of internodes affected and exponentially related to the decrease in myelin thickness.

Figure 7. Response latencies varies with both severity of demyelination and stimulus waveform.

Mean response latency, at threshold, is plotted as described in Fig 5.

Unlike in the case presented in 3-4, responses to anodic monophasic stimuli can be impacted by broad demyelination provided it impacts more than the most peripheral 20 internodes. Generally, the pattern of threshold (Fig 6B) and latency (Fig 7B) changes seen in fibers with varying myelin thickness applied to the entire fiber in response to anodic stimuli parallels the changes observed with peripheral demyelination and cathodic monophasic stimuli. At the extreme of complete fiber involvement, as myelin thickness decreased responses to anodic stimuli exhibited monotonic increases in threshold, ultimately resulting in a 15.09 dB threshold change, and 70% reduction in relative spread. Response latency first increases modestly with loss of myelin, up to 96% reduction, but then decreases to near 0 ms as the site of initiation shifts to the recording site.

Despite these observed changes in response latencies, mean initiation sites for monophasic stimuli change only in the most extreme limit of myelin loss. Cathodic monophasic pulses initiate action potentials almost exclusively at the peripheral site underlying the electrode with only a modest shift to more central nodes in regions of the parameter space adjacent to where conduction failure begins. Anodic monophasic pulses, in contrast, produce responses exclusively at more central locations with a shift even further centrally with complete demyelination.

3-9 Non-Monotonicities in Biphasic Response Properties are Consistent Across a Broad Range of Extent of Demyelination

Whereas response thresholds and latencies to cathodic monophasic stimuli increase exponentially with decreasing myelin thickness affecting at least 14 internodes until failure of action potential generation occurs, those to biphasic stimuli initially follow similar exponential trajectories but then exhibit dramatic non-monotonicities. The relative myelination corresponding to this transition differs with polarity order; this transition generally occurs for CF and AF stimuli with relative myelinations of 0.08 and 0.13 respectively. Thresholds in this region are of the same order, but slightly larger than, the corresponding thresholds for anodic monophasic stimuli. With this transition, the relative sensitivity of fibers to CF and AF pulses is inverted, with AF producing lower thresholds. The dynamic ranges of responses to biphasic stimuli follow those for cathodic monophasic, except for the lower baseline RS described previously, prior to the inflection point. With more severe myelin loss, response dynamic ranges to these pulse types abruptly increase to near that for normal fibers. More central demyelination involvement results in further decreases in the RSs of responses to biphasic stimuli, following a similar pattern to those for anodic monophasic stimuli in this regime.

As with monophasic pulses, demyelination affecting less than the 10 most peripheral internodes has inconsequential impact on mean latency regardless of severity for biphasic stimuli. With loss affecting 12 or more internodes, coincident with the changes in threshold and dynamic range, mean response latencies to biphasic stimuli initially increase as relative myelination decreases up to the mentioned inflection regions. With more pronounced myelin thinning, mean latencies to biphasic pulses precipitously drop to values comparable to those produced by monophasic anodic stimuli. The net effect is that biphasic response latencies exhibit abrupt transitions between extremely high and low latency with modest change in applied demyelination for some regions in the parameter space explored.

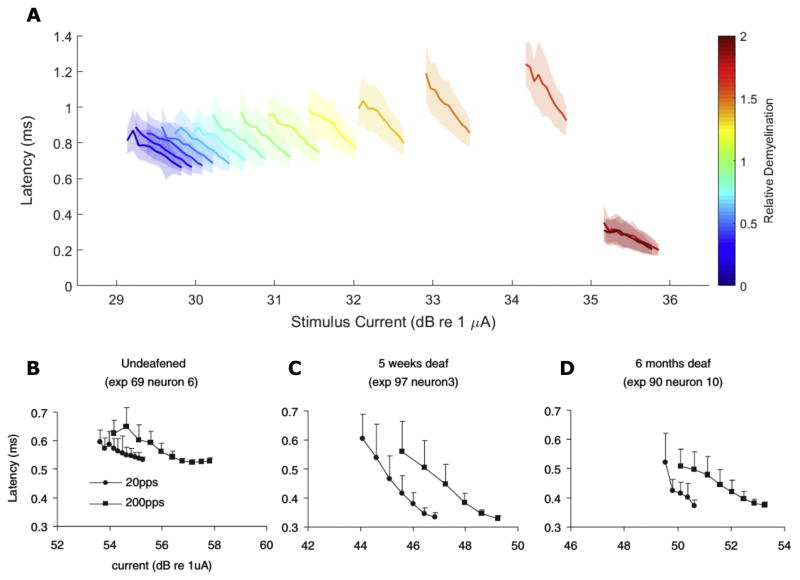
Demyelination changes the slope of latency-intensity curves in addition to the threshold magnitude (Fig 8A). The slope of these functions becomes steeper with loss of myelin thickness until myelin thickness loss that produces an abrupt drop in latency for biphasic pulses in the setting of peripheral myelin loss. Thereafter, the slope of these functions returns to approximately that of normally myelinated fibers. This pattern of latency-intensity slope changes is consistent with the findings of Sly and colleagues from single unit recordings from SGN central axons in guinea pigs; they observed a steeper response latency-stimulus intensity slope in an animal deafened for 5 weeks prior to implantation (C) when compared to an acutely deafened control (B). A chronically (6 mo.) deafened animal’s responses (D) exhibited shallow slopes, similar to the control animal’s, at 200 pulses-per-second (pps) but a slope similar to the 5-week deafened animal at 20 pps.

Figure 8. Response Latency-Stimulus Intensity Function Slopes Change with relative myelination.

(A) Mean response latencies (solid lines) ± jitter are plotted for fibers with different degrees of relative demyelination (colormapping) as a function of stimulus current. (B–D) Mean latency ± jitter of single fiber responses recorded from guinea pigs deafened either acutely (B), 5-weeks (C), or 6-months (D) prior to implantation by Sly and colleagues. Cathode-first biphasic pulses were 50 μs/phase with a 10 μs interphase gap using a monopolar electrode configuration. Circles and squares represent pulses delivered at 20 and 200 pps, respectively. Adapted, with permission, from Sly et al., 2007.

These abrupt non-monotonicities in response properties to biphasic pulses are driven largely by a shift in initiation sites (data not shown). Mean site of action potential generation for these stimuli depend on the precise combination of myelin thickness and number of internodes affected. For most of the variable space, these action potentials are initiated at the periphery, immediately under the stimulating electrode. Beyond the inflection region, fibers abruptly become more sensitive to action potential initiation at more central nodes.

3-10 Specific Patterns of Demyelination Lead to Pronounced Increases in Jitter and, in specific cases, Bimodal Latency Distributions

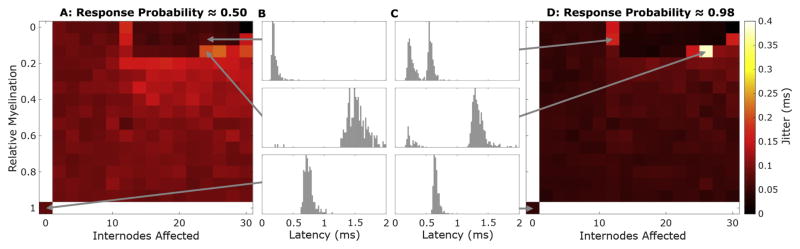
Response jitter at threshold increases across most of the demyelination variable space, for cathodic, CF, or AF stimuli (Fig 9A, AF shown). Fibers with dramatic myelin loss that have not quite reached the inflection region show substantially elevated spread of latencies (Fig 9B compare middle to bottom, normal). Jitter then abruptly declines for fibers activated by biphasic pulses when demyelination becomes severe enough in the periphery to shift response initiation centrally (Fig 9, top).

Figure 9. Response jitter elevated by slowed electrodynamics and multiple initiation sites.

Jitter, standard deviation of response latencies, is plotted over the variable space described in Fig 5 for AF biphasic stimuli at threshold (A) and suprathreshold (D). (B) and (D) show histograms of response latencies for the indicated fiber-stimulus pairings with a window of 0–2 ms post-simulus and a bin width of 40 μs.

Supra-threshold response jitters (Fig 9D) are generally much lower due to both more consistent sites of initiation and closer to deterministic ion channel dynamics. However, fibers with specific combinations of demyelination parameters activated by biphasic pulses, in the presented case AF, show profoundly elevated jitter. Histograms of response latencies for these conditions (Fig 9C, middle and top) show bimodal distributions in contrast to the unimodal distributions for normal fibers (Fig 9C, bottom).

4-Discussion

4-1 Healthy Fiber Response Thresholds and Latencies Differ Between Stimulus Waveforms

To better understand how CI stimulation is encoded within the primary neurons of the auditory pathway, and the impact of pathology upon this encoding, several groups have performed single unit recordings from SGN axons as they enter the brain stem of cats. Shepherd and Javel’s 1999 study found the polarity of stimuli could lead to variations in threshold and latency of neural responses indicating these different phases may activate neurons in different locations (Shepherd and Javel, 1999). Similarly, Miller et al.’s finding of bimodal latency of responses to monophasic CI stimulation suggests the presence of multiple potential sites of activation even within a single fiber and in response to a single stimulus polarity (Miller et al., 1999). Such variations in site of activation have the potential to profoundly alter encoding of timing cues, however, the biophysical factors mediating which initiation site a stimulation paradigm activates are not well understood. The present work suggests these stimulus waveform-dependent dynamics may be explained by the antisymmetric electrotonic effects that anodic and cathodic currents have upon membranes and the subsequent variation in sites of action potential initiation. This effect interacts with cochlea and fiber structure to produce the complex interactions observed in electrophysiologic recordings.

4-2 Simulations Provide Insight into Complexity Observed in Animal Models of Hearing Loss

These simulation results provide a novel perspective from which to consider conflicting electrophysiological findings observed in animal models following deafening. Studies of single unit responses to intracochlear CF biphasic electrical stimulation have observed both increases and decreases in threshold with duration of deafness (Shepherd et al., 2004; Sly et al., 2007). In contrast, our simulations show consistent increases in response threshold for single fibers as demyelination becomes more severe though this effect is modest except in the most extreme cases. A number of scenarios might reconcile these disparate findings. For instance, demyelination may generally promote higher thresholds in individual fibers but asymmetric degeneration, impacting primarily smaller high threshold fibers, complicates this trend. In at least some hearing loss settings such asymmetries have been observed and are thought to interfere with population level coding of stimulus intensity (Furman et al., 2013; Kujawa and Liberman, 2009). Another possibility is that changes to the electrical structure of the cochlea following hair cell loss might alter tissue impedance, ultimately lowering neural thresholds despite loss of neural insulation. Finally, while both studies explored the impact of duration of deafness on single unit responses to stimulation, they used different animal models (rats and guinea pigs in the 2004 and 2007 studies, respectively). It’s likely that there exist significant differences in the progression of cochlear pathology in these different species.

Timing properties of SGNs in these studies exhibit similarly complex relations to duration of deafness. Latency of single unit responses showed no significant change with progressive deafness in the 2004 study, however, the 2007 one found a progressive decrease with duration of deafness, consistent with our findings (Shepherd et al., 2004; Sly et al., 2007). Interpretation of this data is challenging both due to variations in the details of deafening and because the experimental approach precludes the possibility of determining where a recorded unit lies in the cochlea relative to the electrode. The latter effect may lead to different patterns of SGN activation than occur in human implantees and cause results to be sensitive to the details of single unit selection. Our findings suggest that depending on the specific progression of demyelination within a fiber, both increases and decreases in latency at threshold may be possible. As such, depending on the precise details of the mechanism and duration of deafness, different distributions of demyelination severity might exist within animals leading to large between fiber variability.

Our results suggest opportunities for developing a better understanding of the relation between structural and electrophysiological dynamics following deafening in animal models. We observed dramatic changes in the relative sensitivity of fibers to different pulse polarities with severe demyelination. We believe that comparing input-output functions of responses to AF and CF biphasic stimuli for animals with varying durations of deafness would provide insight into how myelination was changing. We predict that duration of deafness will correlate with the average ratio of CF to AF thresholds due to the peripheral processes of fibers becoming more difficult to depolarize. Additionally, when this ratio nears 1, fibers will be particularly likely to possess multiple action potential initiation foci resulting in a greater frequency of bimodal latency distributions. The incidence of such bimodality would then be expected to decrease as demyelination, and/or peripheral process degeneration, progressed still further to involve nearly all fibers.

In addition to altering single fiber properties, pathological perturbations of SGNs are expected to alter population signal encoding. Based on our preliminary single fiber results, we predict demyelination will generally not alter populations’ sensitivities substantially but that heterogeneity in the amount of demyelination across a population may lead to profound dispersion in spike times and loss of temporal fine structure information. While this an area of great interest, implementing heterogenous demyelination within a population will require careful grounding in histopathological data to achieve reasonable representations of pathology across populations.

4-3 Only Extreme Demyelination Shifted Thresholds Sufficiently to Promote Current Spread and Pathological Recruitment

The simulations in the present study suggest that thinning of the myelin sheath surrounding SGNs may alter how they are excited by extracellular stimulation. Decreased myelin thickness that affects more than just the most peripheral nodes, lead to increased thresholds particularly in scenarios where fibers are depolarized by cathodic polarity pulses. The magnitude of this change, however, was exponentially related to the diameter of remaining myelin leading to relatively modest changes of little practical significance until demyelination becomes more severe than is consistent with the histopathological literature. In the extreme case of complete loss of myelin, we observed the absence of action potentials due to failed conduction of responses to monophasic cathodic stimuli. Response thresholds to anodic phases exhibited complete resistance to peripheral demyelination and only exhibited substantial change with broadly distributed near complete loss of myelin. These threshold changes suggest, in the extreme, that demyelination might require elevated current amplitudes generating increased spread of excitation within the cochlea and greater channel interaction; however, fiber thresholds are overall remarkably robust to this myelination perturbation. Additionally, demyelination generally resulted in a decrease in the dynamic range of fibers, suggesting they begin behaving more deterministically. Such a reduction in dynamic range would interfere with the detection of loudness cues and could promote pathological recruitment. Overall these effects generally occurred only at remarkably extreme amounts of demyelination consistent with the clinical observation that the vast majority of CI recipients receive at least some benefit in speech recognition in quiet from their device.

4-4 Demyelination Induced Timing Changes Would Alter Binaural Timing cues

Efforts to deliver fine temporal information potentially critical to temporal pitch coding and certainly to interaural time differences rely on precise neural responses to individual pulses from a cochlear implant. As such, pathology-induced latency changes in responses to single pulses are expected to set limits on the quality of such information that can be delivered. Since even with relatively modest perturbations of myelin, timing of stimulus-induced action potentials changed in ways that could have dramatic behavioral impact. Although phonetically relevant temporal information in speech is unlikely to occur in a window shorter than ~ 20 ms (Rosen, 1992; Saberi and Perrott, 1999), the binaural system utilizes interaural differences on the order of tens of microseconds (Bernstein and Trahiotis, 2015; Zwislocki and Feldman, 1956). Our demyelination simulations predict latency changes of an order relevant to the latter but not the former.

With demyelination involving at least the most peripheral 10 nodes, latency of action potentials initiated by cathodic polarity pulses increased with both the extent of fiber affected and severity of myelin thinning due to reduced conduction velocity along demyelinated axons. For instance, a 77% reduction in myelin involving the first half of a fiber resulted in a mean latency delay of 175 μs for responses to monophasic cathodic pulses which, if paired with healthy fibers contralaterally, would introduce an interaural timing difference artifact, leading to an error on the order of 20–30° in perceived sound source location (Nordlund, 1962). More severe demyelination introduces even larger errors; severe demyelination (87%) impacting at least 16 nodes of a fiber stimulated by monophasic cathodic stimuli yields delays of greater than 300 μs, nearly half the maximum possible ITD for humans. In contrast, anodic-phase induced responses exhibited almost no change in latency unless severe demyelination was applied to nearly the entire fiber.

The different relationships between fiber response properties and myelination state for opposite polarity pulses has a dramatic implication for biphasic pulses. Both CF and AF biphasic stimuli produce responses with thresholds and latencies like cathodic monophasic stimuli in normal fibers, those with demyelination affecting fewer than the first 10 nodes, and those with broad demyelination but retaining at least 15% of their myelin. In fibers with demyelination of greater severity and broader distribution, response properties become more like those to anodic monophasic stimuli. This behavior is due to abrupt changes in site of action potential initiation when demyelination impacts the region of fiber normally depolarized by cathodic polarity pulses but spares the central portion of fibers activated by anodic ones. This shift in relative phase sensitivity profoundly alters the timing of responses.

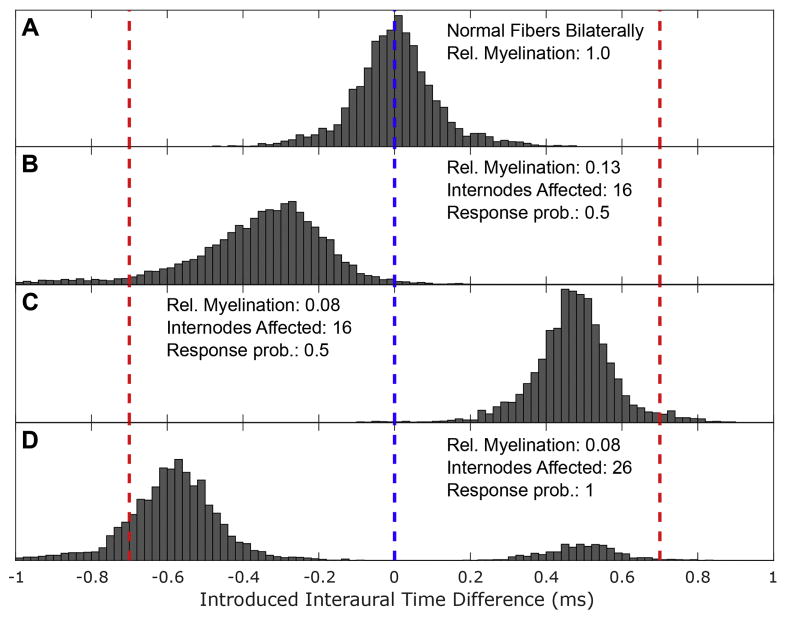
Normal hearing listeners have been shown to make lateralization judgements using ITDs extremely rapidly and to weight the onset ITD of pulse train stimuli particularly strongly (Brown and Stecker, 2010; Freyman, 1997; Klein-Hennig et al., 2011). Providing implantees access to these cues will, therefore, require faithful encoding of timing of single pulses. To illustrate the potential magnitude of the latency variability observed in our simulations on fine temporal structure coding, expected onset ITDs between cochlear nucleus arrival times of coincidentally delivered AF biphasic pulses are plotted for different degrees of myelination asymmetry in Fig 10. AF biphasic pulses were selected since modern implants typically use biphasic pulses and latency effects were more pronounced with AF pulses (though they were still present and substantial with CF pulses). While fibers with 87% demyelination impacting the first 16 internodes stimulated by AF biphasic pulses exhibit a mean latency that lags that of normal fibers by 350 μs, similarly affected fibers with slightly greater, 92%, demyelination respond with mean latency leading normal fibers by 470 μs; a net difference of 820 μs, significantly greater than the maximal physiological ITD (compare Fig 10A,B,&C). If a fiber population contained fibers with both such demyelination states a single biphasic stimulus would produce population activity with a large degree of temporal distortion.

Figure 10. Asymmetric demyelination introduces interaural timing difference artifacts.

Histograms of pathology induced interaural time difference artifacts were constructed by repeatedly subtracting latencies sampled from the ‘right’ fiber’s distribution from that of the ‘left’ to anode-first biphasic pulses presented concurrently to both sides. Here the induced interaural timing difference is presented on the abscissa and frequency of these outcomes is plotted on the ordinate. This procedure presumes a situation where the electrodes stimulating both sides are synchronized and that they have independent, but ideal, mappings. For each panel, the left fiber was kept normally myelinated and the myelination state of the ‘right’ was varied: (A) normal fiber, (B) fiber with first 16 internodes 87% demyelinated, (C) fiber with first 16 internodes 92% demyelinated, and (D) fiber with 26 internodes 92% demyelinated. For (A–C), stimulating pulses were delivered at threshold for both sides while for (D) the stimuli used produced a response probability of 0.98 on their respective side. For each fiber pairing, 10,000 random samplings were taken from the distributions of response latencies.

In addition to these dramatic between fiber response latency differences, we observed elevated response jitter and bimodal latency distributions, depicted in Figure 9C&D, for some fibers, resulting from stochastic activation of both peripheral and central sites. While only captured for fibers with specific parameter pairs in this work, we intuit there must be some stimulus intensity for each fiber that leads to comparable sensitivity to both phases of biphasic pulses. Figure 10D illustrates how a fiber with bimodal latency distributions could stochastically provide opposing ITD cues. In this scenario, it would be impossible for downstream elements of the auditory pathway to decode the spike timing of single SGNs to ascertain the true relative phases of binaural acoustic stimuli, even if there exists plasticity in the circuit. These elevations in between and within fiber jitter may lead to interaural decorrelation, which is the measurement underlying the framework of a many of theories of binaural hearing (Bernstein and Trahiotis, 2017).

While the observed timing deficiencies are large enough to affect ITDs, they are not likely to affect speech discrimination in quiet since the relevant timing properties occur on a scale at least an order of magnitude larger. However, since normal spatial hearing is dominated by perception of fine-structure ITD cues (Wightman and Kistler, 1992) and perceived spatial separation of speech and noise facilitate improved speech intelligibility (Freyman et al., 1999; Hawley et al., 2004), poor transmission of ITD cues will have serious, detrimental effects to hearing speech in everyday (i.e. noisy) environments. As poor speech perception in noise is the chief complaint of most people with hearing loss, there is a potentially important connection to be made between the physiological impact of demyelination and behavioral performance in certain tasks.

4-5 Human Psychophysical Predictions

Studies comparing thresholds between CF and AF biphasic stimuli within humans have revealed no statistically significant average difference between these two pulse types (Macherey et al., 2006). However, recent work has found that individual patients tend to exhibit a clear sensitivity difference, that can vary between electrode, but that these variations tend to average out between patients (Macherey et al., 2017). Moreover, this group found that all patients exhibited lower maximum comfortable levels with anodic polarity dominated waveforms. The present study suggests that the variability in relative sensitivity between these different pulses may be partially due to differences in the myelination state of SGNs near the electrode in question. As such, we predict that in a large cohort there should exist a correlation between average CA/AC threshold ratio and duration of deafness. Moreover, our simulations predict such changes in relative sensitivity should coincide with alterations in the fidelity of response timing. We anticipate that when the CA/AC threshold ratio is greater than 1.0, detection of ITDs should be superior with AF pulses. Additionally, when thresholds to CF pulses are lower ITD detection is predicted to be better at lower stimulus strengths, below the onset of bimodal latency distributions.

4-6 Neuron Structure and Channel Distribution Simplifications May Mask Additional Complexity

In the present simulations, the stimulating electrode was placed over node 10 to avoid terminal effects in the numerical solutions. Rattay and colleagues observed initiation sites substantially more peripheral to those found in the present study but this previous work positioned electrodes nearest the peripheral-most nodes (Rattay et al., 2001b). The more central positioning of the electrode in the present study is likely why the more lateral excitation site is substantially more central than that observed by Rattay et al.

The presented model does not explicitly treat the cell body as a unique structure, distinguish between peripheral and central axons segments, or account for heterogeneity in the distribution of ion channels between nodal segments. Other simulations have incorporated such structural asymmetries and found they may alter model behavior, however, due to a paucity of electrophysiological, structural, and expression studies involving the cell body such simulations introduce additional poorly constrained parameters (Frijns et al., 2000; Rattay et al., 2001a). Additionally, while excitatory channels are present at each node of Ranvier to support saltatory conduction, particularly dense Nav1.6 expression has been observed in the nodes immediately adjacent to the cell body (heminode and initial segment) and in fiber terminals adjacent to hair cells (Hossain et al., 2005); this excitatory channel distribution may also critically contribute to the site of cochlear implant action potential generation. Exploring the impact of these other structural elements is critical but simulating them effectively will require more constraining morphometric and histopathological data.

The model used in the present study was constructed and tuned such that it produced responses with similar characteristics to feline ANFs in the absence of explicit modeling of a soma or asymmetries in peripheral and central axons (Imennov and Rubinstein, 2009). To a rough approximation, the contributions of these structural elements are, therefore, implicitly incorporated into the tuned parameters. The simulated latency difference between peripherally and centrally initiated events by AF pulses in normally myelinated fibers are of the same order of those recorded by Miller et al. (compare Fig 3C & D) suggesting this spatial variability in excitation is preserved despite the use of implicit soma incorporation and axonal homogeneity (Miller et al., 1999). Nevertheless, the variability in initiation site observed should be viewed as related to electrical distance, impedance, rather than true distance. The presence of a cell body, particularly if its myelination state is subject to change, would introduce a large capacitive load and create larger potential gradients with axial distance than predicted in the current study. While the peripheral and central initiation sites are relatively farther apart in our study than in studies leveraging cell bodies, incorporating the high capacitive load of a discrete soma would reduce this distance and likely bring our findings in line with previous studies. Such changes in relative distance between initiation sites would be consistent with Finley, Wilson, and White’s comparison of models with and without soma (Finley et al., 1990).

We opted to constrain our parameter space to demyelination within a simple core-conductor model to simplify interpretation and limit speculation regarding model parameters. Importantly, we anticipate the substantial latency difference due to the difference in the conduction delay between initiation sites would be qualitatively preserved in this setting since while the distance may be shorter the cell body would introduce a high capacitive load, particularly if its myelination state changes.

4-7 Myelin Loss Induced Changes in Adaptation and/or Refractoriness May Alter Responses to Pulse Trains

While the temporal fidelity of responses to individual pulses is critical for conveying fine temporal structure, modern cochlear implants use relatively high pulse rates to optimize speech reception. The response properties of single neurons, and populations, with different myelination states to faithfully to paired pulses, pulse trains, and more speech-relevant stimuli are, therefore, of great interest. The present model does not exhibit physiological relevant adaptation so responses to such high-rate stimuli will need to be interpreted with care. The addition of non-homogenously distributed additional cation channels to a cell-body-containing model has also been shown to produce a source of adaptation that could be incorporated into a segmented model in the future (Boulet and Bruce, 2017; Negm and Bruce, 2014).

4-8 Other Pathological Changes May Further Alter Neural Responses

This work used a highly simplified model of neural stimulation by extracellular currents and modified only two anatomical parameters: myelin thickness and extent of demyelination. Even considering only these two parameters, more complex relations than those presented here could be used to introduce loss of myelin. We believe the results of the present study are likely robust to such details since the relationships between fiber responses and myelin thickness were relatively insensitive to the exact number of internodes affected. The transitions in site of action potential observed were dramatic so small amounts of within internode variability in the demyelination are unlikely to impact them significantly.

Elements other than internode myelin diameter have been observed to change following deafening, including: increases in node length and diameter, paranode diameter, and juxtaparanode length; and decreases in paranode length and juxtaparanode (Tagoe et al., 2014). Whether changes in internode length occur as well remains unexplored. Moreover, whether such changes occur independently or in concert, due to some common dis-regulation remains unknown. Focal axonal swelling incorporated into auditory nerve fiber models was previously observed to alter conduction velocity even in the absence of internodal myelination loss suggesting the possibility of complex interplay between these structural changes (Kolaric et al., 2013). Work in deafened Guinea Pigs has also observed sub myelin vacuolization due to retraction of neural axoplasm in the absence of significant myelin loss on a shorter timescale than the myelin thinning observed in cats and humans, suggesting at least some species-specific pathological progression (Wise et al., 2017). In addition to changes in the geometry of SGNs, it is possible that their electrical properties might be altered by compensatory or pathological changes in the expression or distribution of ion channels. Such changes have been observed following monocular deprivation in the visual system (Craner et al., 2003). In the setting of the cochlea such changes could dramatically alter action potential initiation and/or propagation.

In addition to these neuron simplifications, we employed a simplified electrical model of the cochlea. The details of the electrical structure of the cochlea will certainly impact where action potentials are initiated. Others have simulated the effects of predicted cochlear electrical structure and found it can dramatically shape where modeled nerves are most easily excited (Briaire and Frijns, 2006, 2000; Rattay et al., 2001a; van Gendt et al., 2016). Implementing parameter exploration, as performed here, within a multi-compartment model of the cochlea might further improve predictions about where CIs might depolarize SGNs in different functional states. Unfortunately, little is known about these electrical properties to constrain such complex cochlear models and assumptions must be made at some level, thus we opted for a simple model for clarity. Exploring how pathological changes in the electrical properties of the cochlea, such as altered impedance due to tissue fibrosis, impact neural response timing is another valuable avenue of research.

5-Conclusions

Collectively, these observations provide some insight into how a dysfunctional periphery may differentially impact encoding of stimulus elements critical to different kinds of tasks. Fibers maintained the ability to produce at least some responses to charge-balanced pulses, like those used in modern implants, even with profound demyelination. Only in the event of demyelination more severe than previously observed in cellular imaging studies would we expect sufficiently elevated thresholds to lead to increased spread of excitation and greater channel interaction. Moreover, while we did not look at longer-term adaptation or refractory effects, the latencies we observed are likely too small to dramatically alter recognition of critical elements of speech in quiet (with relevant features generally lasting >20 ms). In contrast, fine temporal coding, including the phase locking needed to detect ITDs, was dramatically altered even by relatively modest perturbations of myelin. Extrapolating these effects out to populations of neurons, we anticipate that non-uniform changes in ultrastructure will lead to dispersion of the population timing signals which would further degrade implantees ability to utilize fine temporal cues but generally preserve thresholds and modulation detection. This predicted sensitivity parallels clinical observations where most implant recipients experience at least some, and usually substantial, improvement in their ability to recognize speech in quiet but few can perform well when tasks involve detecting speech in noise or ITD-based sound localization.

Highlights.

• Simulated spiral ganglion neurons with variable internodal demyelination.

• Only extreme demyelination meaningfully altered response thresholds.

• Response latency and jitter differed dramatically with myelination and stimulus.

• Bimodal latency distributions observed for some demyelinated neurons.

• This would potentially degrade fine temporal structure but spare thresholds.

Abbreviations

SGN

spiral ganglion neuron

AF

anodic-first

CF

cathodic-first

CI

Cochlear Implant

HL

Hearing Loss

eCAP

electrically-evoked compound action potential