Abstract
To correct eye motion artifacts in en face optical coherence tomography angiography (OCT-A) images, a Lissajous scanning method with subsequent software-based motion correction is proposed. The standard Lissajous scanning pattern is modified to be compatible with OCT-A and a corresponding motion correction algorithm is designed. The effectiveness of our method was demonstrated by comparing en face OCT-A images with and without motion correction. The method was further validated by comparing motion-corrected images with scanning laser ophthalmoscopy images, and the repeatability of the method was evaluated using a checkerboard image. A motion-corrected en face OCT-A image from a blinking case is presented to demonstrate the ability of the method to deal with eye blinking. Results show that the method can produce accurate motion-free en face OCT-A images of the posterior segment of the eye in vivo.
OCIS codes: (170.4500) Optical coherence tomography, (170.4470) Ophthalmology, (170.3880) Medical and biological imaging, (100.0100) Image processing
1. Introduction
Imaging of ocular circulation is of major importance not only for ophthalmic diagnosis but also for the study of eye diseases such as glaucoma, diabetic retinopathy, and age-related macular degeneration [1, 2]. The most commonly used angiography methods include fluorescein angiography (FA) [1] and indocyanine green angiography (ICGA) [2]. However, these angiography methods are invasive and require dye injection into the human body, which can occasionally have adverse effects [3–6].
In recent years, optical coherence tomography (OCT) has become a popular noninvasive imaging method in ophthalmic applications [7, 8]. As an extension of OCT, en face OCT angiography (OCT-A) [9–13] provides vasculature images noninvasively and can be used to partially replace conventional invasive angiography. However, OCT-A measurements take several seconds and are thus vulnerable to the effects of eye motion. Any eye motion corrupts the en face OCT-A imaging process to produce structural gaps and distortions, which appear as motion artifacts. The most straightforward approach that can be used to correct these artifacts is to add hardware to monitor and compensate for eye motion [14–17]. However, any additional hardware may increase both the cost and the complexity of the system. Another approach is to use a redundant scanning pattern in conjunction with image post-processing [18–22].
In our previous research, we developed a Lissajous scanning optical coherence tomography method [22, 23]. In this method, the probe beam scans the retina using a Lissajous pattern. The trajectory of the Lissajous scan frequently overlaps. This property of the Lissajous scan is considered to have the following advantages for motion correction. First, eye motion estimation is considered to be more robust because it is based on registration of short segments that overlap each other in multiple regions. Next, the motion correction success rate will be improved. This improvement is based on the flexibility of the registration order. Finally, even if some data must be discarded, blank sections are unlikely to appear in the image. If some strips cannot be registered because of large-scale distortion or blinking, these strips can be discarded. Additionally, the sinusoidal scanning pattern used for each mechanical beam scanner is suitable for high-speed scanning. The characteristic properties of Lissajous scanning were used to develop a post-processing method that corrects the eye motion artifacts. However, the method was not compatible with OCT-A imaging. This is because the Lissajous scan is not suitable to be applied to multiple scans repeated at the same location within a short time period.
In this paper, we present a new Lissajous scanning pattern that is compatible with OCT-A imaging, and also present a motion correction algorithm that has been tailored for this scanning pattern. A motion-free OCT-A method based on this modified Lissajous scan pattern is demonstrated. To demonstrate the effectiveness of the proposed method, we compared en face Lissajous OCT-A images with and without motion correction. To validate the ability of the proposed method to retrieve true retinal vasculature, an en face Lissajous OCT-A image is compared with a scanning laser ophthalmoscopy (SLO) image, which is regarded as an appropriate reference standard. Additionally, to evaluate the repeatability of motion artifact correction, a checkerboard image was created using two Lissajous OCT-A images that were acquired from two independent measurements of the same subject. To demonstrate the clinical utility of the proposed method, slab-projection OCT-A images of three retinal plexuses and the motion-corrected Lissajous OCT-A image acquired from a blinking case are presented.
2. Method
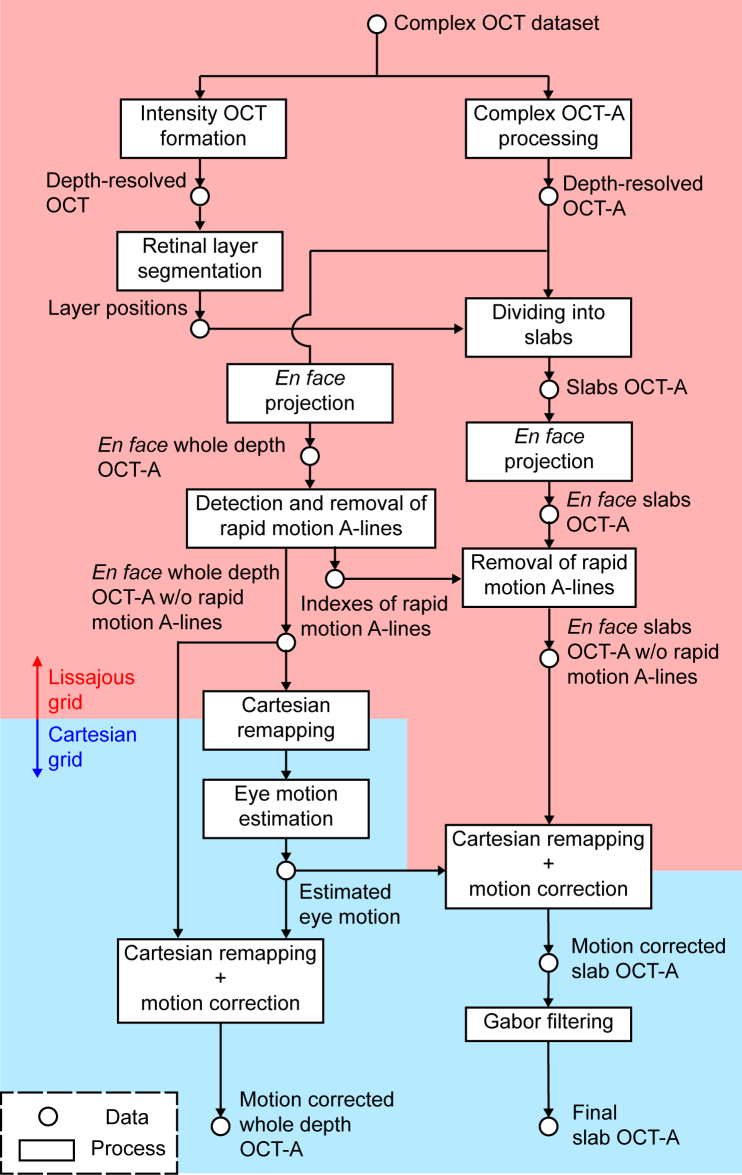
The OCT data are acquired using the modified Lissajous trajectory. After OCT-A processing, a motion estimation algorithm is then applied. Then, motion-corrected en face OCT-A images are obtained by transforming the Lissajous data into a Cartesian grid. An overview of the motion-correction process is shown in Fig. 1 . Step-by-step descriptions of the OCT system, the modified Lissajous scan, and the signal processing are given in the following. The notations used in the following sections are listed in Appendix A.
Fig. 1.
Process diagram of OCT-A image reconstruction from Lissajous-scanned OCT signal. The boxes and circular nodes represent the processes and the data, respectively. In the red region, the OCT and OCT-A data are represented by the acquisition time sequence, i.e., the data along the original Lissajous scan trajectory. In contrast, in the blue region, these data are presented as remapped data on a Cartesian grid.
2.1. System
We used a 1-µm Jones-matrix OCT (JM-OCT) to collect the data. JM-OCT is polarization sensitive, however, only the intensity information is used in this study. The system has a depth resolution of 6.2 µm in tissue and an A-line rate of 100,000 A-lines/s. The probe power on the cornea is 1.4 mW. The system details are described in the literature [24, 25]. The macula and optic nerve head (ONH) of healthy human subjects were measured. The study protocol adhered to the tenets of the Declaration of Helsinki, and was approved by the institutional review board of the University of Tsukuba.
2.2. Modified Lissajous scanning pattern
In our previous research, we used a standard Lissajous scan to obtain a motion-free OCT intensity volume [22]. The probe beam scanning trajectory in the laboratory coordinate system is described as follows:
| (1) |
| (2) |
where x and y are the orthogonal lateral positions of the probe beam, and Tx and Ty are the periods of the x- and y-scans, respectively. From Ref. [26], the ratio of the coordinate periods is defined as Ty/Tx = 2N/(2N – 1), where the parameter N represents the number of y-scan cycles that are used to fill the scan area. Although it has been successfully applied in structural OCT imaging, the method is not compatible with OCT-A. We have therefore modified the scanning pattern as follows.
OCT-A measurements require the OCT probe to scan the same location multiple times with appropriate time separation. However, each cycle of x(t) and y(t) fails to form a closed scanning pattern because Tx ≠ Ty. Specifically, the start and end point positions for each of the cycles are not the same. If we repeat these cycles multiple times, this discontinuity then leads to mechanical ringing of the scanner and finally causes decorrelation in the acquired OCT signals. To mitigate this effect, we add a time margin between each scan cycle and its subsequent repeat cycle. Each scan is delimited by the x-scan period Tx, as indicated by the green curve in Fig. 2 . The margin is then filled using a smooth trajectory with limited low acceleration (red curve). Hereafter, we call this set of scan cycles such as traces the green trajectory a “repeat-cycle-set.”
Fig. 2.
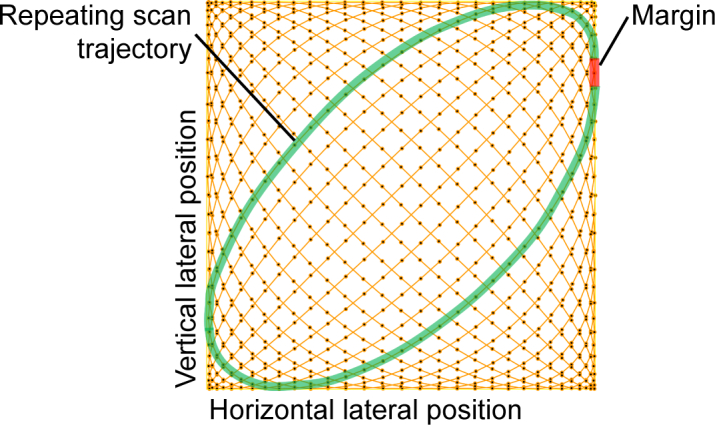
Example set of repeating scans in the modified Lissajous scanning pattern. The probe beam scans the green trajectory multiple times and the scan set is called the “repeat-cycle-set.” The red line indicates the trajectory that connects the repeating cycles, and is called the “margin.”
This modified scanning pattern is then described as
| (3) |
| (4) |
where the t parameters in Eqs. (1) and (2) are replaced by χx and χy, respectively, which are both functions of the time t and are defined as
| (5) |
| (6) |
where Tc is the time lag between the repeated scans at the same location and ΔT is the time margin between adjacent repeated cycles. Tc and ΔT are related in that Tc = Tx + ΔT. n is the index of a repeat-cycle-set that is given by
| (7) |
k = m + Mn is the total number of cycles that were counted from the beginning of the Lissajous scan and is related to t as follows:
| (8) |
M is the number of repeated cycles included a repeat-cycle-set, while m is the repeated cycle count determined by k − Mn.
The profiles of the phases of the cosine functions 2πχx(t)/Tx and 2πχy(t)/Ty are shown in Fig. 3 . At the margin between the repeats (i.e., the red regions), χx has a small flat region located between the repeats at which the x-scan stops. The phase of x′(t) is a multiple of 2π at the margin and is thus in the zero-slope (flat) region of the cosine function. This ensures that the resulting x-scan is smooth.
Fig. 3.

Temporal profiles of the phase of the modified Lissajous scanning pattern, where the number of repeats (M) is 4. Red regions indicate the scan margin.
Similar to our previous work [22], the x-scan period is set to be a multiple of the A-line period TA as Tx = LxTA, where Lx is the number of A-lines within a single x-scan period. To scan the same location, the time margin ΔT must be a multiple of the acquisition period as follows:
| (9) |
where δ is an arbitrary integer. A practical example of the selection of δ is described in the second last paragraph of this section. The time margin should be also close to the difference between the periods of the x- and y-scans, i.e., ΔT ≈ Ty − Tx = Tx/(2N − 1) This is necessary to avoid abrupt changes in scanning location in the y-scan.
Acquisition of the A-lines is performed during the modified Lissajous scan described above with an acquisition rate of 1/TA. However, because the acquisition process was not performed during the time margin, the duty cycle is MLx/[M(Lx + δ) – δ].
The location of the i-th A-line (i = 0, 1, 2, ⋯) is then given by
| (10) |
| (11) |
where
| (12) |
| (13) |
By substituting i = l + Lx(m + M · n) into these equations, where l = 0, 1, 2, ⋯, Lx − 1, the location of the i-th line can be expressed using the indexes of (l, m, n) as
| (14) |
| (15) |
It is evident that both and have the same value for each of the repeats, i.e., for any value of m. Therefore, the line acquisitions are performed at the same laboratory coordinate positions for the repeats.
We set the same Lissajous scanning parameter that was used in our previous study, i.e., N = Lx/4 (see Eq. (8) of Ref. [22]). Therefore, the difference between the periods of the x- and y-scans is Ty − Tx = 2TA/(1 − 2/Lx). For large Lx, this difference between periods is approximately two A-line periods. We therefore set the time margin to be the time required to scan two A-lines, i.e., δ ≡ 2. The discrepancy between the set time margin 2TA and the ideal time margin Ty − Tx is 4TA/(Lx − 2). Here, the maximum spatial gap in the y-scanning pattern becomes . Because Lx usually has a value of several hundreds, the maximum spatial gap is approximately . In this study, this gap is less than 1 µm and thus does not cause mechanical ringing. The duty cycle in the configuration presented here is 99.86% (M=2, δ=2, and Lx=724).
2.3. Motion-corrected OCT-A
2.3.1. OCT-A processing
Eye motion is detected and corrected using an en face OCT-A image. In our study, the OCT-A signal is obtained by computing the complex decorrelation among multiple repeated scans using Makita’s noise correction. The details of this OCT-A process are described in Ref. [10], so we simply summarize the essential aspects of the computation process here. To compute the temporal correlation for this OCT-A process, we first express a pair of OCT signals as a vertical vector gn as follows:
| (16) |
where g(l, n, z, m, p) is the complex OCT signal at the z-th pixel along the depth of the i-th acquisition line (the l-th line of the m-th repeated cycle in the n-th repeat-cycle-set) of the p-th polarization channel of the JM-OCT. From Section 4.2 of Ref. [10], the correlation signal for OCT-A rn(Tc; l, z) with time lag Tc is computed using gn(Tc; l, z, m, p). We first substitute g(τ; x, z, f, p) into Eq. (30) of Ref. [10] and then compute Eq.(34). The value of this equation (which is in the notation of Ref. [10]) is the noise-corrected correlation, which is denoted by rn(Tc; l, z) in this paper.
An en face OCT-A image is then used for the subsequent motion estimation and correction processes. For this purpose, an en face OCT-A image was created from a whole volumetric OCT-A in the manner described in Section 5.2 of Ref. [10]. In short, the en face OCT-A signal is given by
| (17) |
where
2.3.2. Pre-processing
Rapid eye motion can lead to decorrelation artifacts and structural discontinuities in en face OCT-A images. To discard the repeat-cycle-sets that exhibit these artifacts, we detect the repeat-cycle-sets that are dominated by high OCT-A signals (high decorrelation) and/or show low structural correlation with successive sets.
These high-decorrelation repeat-cycle-sets are detected using the mean OCT-A value for each repeat-cycle-set, given by , where n is the index of the repeat-cycle-set. The mean OCT-A value for the entire volume, , is also computed. If the mean OCT-A value for a repeat-cycle-set is greater than 1.2 times the mean for the entire volume, i.e., if , then the repeat-cycle-set is considered to be suffering from rapid eye motion, and is discarded.
The cross-correlation values of the en face OCT-A between the adjacent repeat-cycle-sets are calculated as , where cor is the correlation operation. If the cross-correlation value between adjacent repeat-cycle-sets is less than 0.8 times the mean value of the all cross-correlation values, i.e., if , then the repeat-cycle-set is considered to have low structural correlation and is discarded.
Figure 4 shows an example of en face OCT-A images before [Fig. 4(a)] and after [Fig. 4(b)] artifact removal. The vertical and horizontal directions in these images are used as the indexes of the repeat-cycle-set and the A-line in the repeat-cycle-set, respectively. While several horizontal white (highly decorrelated) lines are visible in Fig. 4(a), these lines can be removed using the method described above. In Fig. 4(b), these discarded lines are shown in black.
Fig. 4.
Example of OCT-A map (a) before and (b) after rapid eye motion artifact removal. The vertical and horizontal directions in the images represent the indexes of the repeat-cycle-set and the A-line in the repeat-cycle-set, respectively.
After the artifacts caused by rapid eye motion are discarded, we divide the en face OCT-A image into strips using two rules. The first rule is that each strip must be free from rapid eye motion. The second rule is that the maximum acquisition time for each strip is set to be 0.2 s. Therefore, the en face projection is divided into strips that consist of continuous sets after the discarded sets have been removed. Strips that are longer than 0.2 s are then further divided. The resulting strips are then used to detect and correct the motion artifacts that are caused by eye motion, and this process will be described in the next section (Section 2.3.3).
2.3.3. Motion estimation
We performed lateral motion estimation, which was previously described in Section 2.2.2 of Ref. [22]. In the first step of our motion estimation process, the strips that were created in the previous section (Section 2.3.2) were remapped into a Cartesian grid with Lx/2 × Lx/2 grid points. The strips are then sorted in size from large to small. The strips are then registered sequentially to a reference en face image. At the beginning of this sequence, the reference image is the strip itself. Therefore, the registration process is not performed in practice. For the second strip, the reference image is the first strip. The registered strip is then merged with the reference strip and this merged image is used as the new reference for the next registration process. This registration sequence is iterated several times.
The motion correction process is identical to that which was described in Ref. [22], but with two exceptions. The first exception is that the method presented here uses the en face OCT-A signal, while the previous method used the en face OCT intensity. The second exception is that the resulting motion-corrected OCT-A is then evaluated using the method in the following, while it was blindly accepted in the previous method. Here, if there are more than 2Lx blank grid points to which no OCT-A value has been assigned, the motion estimation result is discarded. In this case, a subordinate strip is then selected as the initial reference strip and the lateral registration process is redone.
In the second step, a single strip is divided into four quadrants. Each of these quadrants is then registered to a reference image that is formed by all strips other than the target strip. After iteration of the registration process, the quantity of motion is obtained for each acquisition point. This lateral motion estimation process is described in more detail in Section 2.2.2 of Ref. [22].
Finally, the OCT-A signals are re-transformed into the Cartesian grid. The re-transformation process takes the estimated motion into account to cancel out the motion artifacts. A motion-corrected en face OCT-A image is then obtained.
2.4. Image formation
2.4.1. Slab en face OCT-A formation
The OCT intensity volume, I(l, d, n), is obtained using the sensitivity-enhanced scattering OCT method (Eq. (30), Section 3.8 of Ref. [24]), which combines a set of the scans from a repeat-cycle-set with phase correction. The retinal layers were identified from this intensity volume using the Iowa Reference Algorithms (Retinal Image Analysis Lab, Iowa Institute for Biomedical Imaging, Iowa City, IA) [27–29]. The segmentation process used here was then applied to the cross-sectional intensity image of each of the repeat-cycle-sets.
After layer segmentation, the en face OCT-A signal for each A-scan at a target layer is obtained by selecting the minimum correlation coefficient along the depth within the target layer. Motion-corrected slab en face OCT-A images are then obtained by correcting the motion using the quantities of motion that were estimated in Section 2.3.3.
2.4.2. Image enhancement using Gabor filter
A Gabor filter is used to suppress noise and enhance the visibility of the retinal vascular network [30].
We used the real part of the Gabor filter. The kernel is formulated as follows [20]:
| (18) |
where
| (19) |
| (20) |
Here, x and y are the lateral spatial coordinates, while the other parameters determine the size (σx and σy) and the direction of the kernel (θ).
We set σx = σy = σ and the kernel size (s) to be 6 × σ. Because we only detect vessels across the kernel’s center, f is set as follows so that each kernel contains only a single cosine period:
| (21) |
The Gabor kernels thus become
| (22) |
To filter the en face image, we convolved the image with the Gabor kernels that have several directions (θ) and a range of kernel sizes (s) that are based on the visible retinal vessel sizes. The final filtered image E′ (x, y) is formed based on the maximum between filter outputs as follows:
| (23) |
where E(x, y) is the original en face OCT-A image. The function returns the maximum value of f(x) from any values of x.
2.4.3. Color-coded multiple plexus imaging
To show multiple vascular plexuses within a single image, we integrate the images of these plexuses in a manner similar to that of the volume rendering process and assign different colors to the different images. For the volume rendering procedure, we assume that each ray is only either reflected or transmitted. Then, the reflection coefficient (r) and the transparency (α) have the following relationship:
| (24) |
The percentage of reflection (R) from each vascular plexus can then be calculated as follows
| (25) |
where j is the index of a slab (plexus) and j = 1 is the shallowest slab.
For the volume rendered image formation, an en face OCT-A projection of a slab after background subtraction and min-max scaling is used as rj as follows:
| (26) |
where Bj is the background of the image that was estimated using the rolling-ball method [31]. Subsequently, different colors are assigned to each retinal vascular plexus and a single image is then created using the maximum red-green-blue (RGB) values from the three images at each pixel point.
| (27) |
where Cj is the color (RGB) vector assigned to the j-th slab.
2.5. Scanning protocols
Transverse areas of 2 mm × 2 mm (Ax = Ay = 1 mm), 3 mm × 3 mm (Ax = Ay = 1.5 mm), and 6 mm × 6 mm (Ax = Ay = 3 mm) on the posterior segment of the eyes were scanned using the modified Lissajous scanning pattern that was described in Section 2. A single repeat-cycle-set consists of two repeated cycles (M = 2). Data are acquired during a single cycle of the modified Lissajous scan that consists of 362 repeat-cycle-sets × 2 repeats × 724 A-scans (Lx = 724), and the acquisition takes 5.25 s. The time lag between the repeated cycles, Tc, is approximately 7.26 ms. The maximum separations between the adjacent trajectories are approximately 12.3 µm, 18.4 µm, and 36.8 µm for the 2 × 2, 3 × 3, and 6 × 6 mm2 scanning areas, respectively.
3. Results
3.1. Motion correction
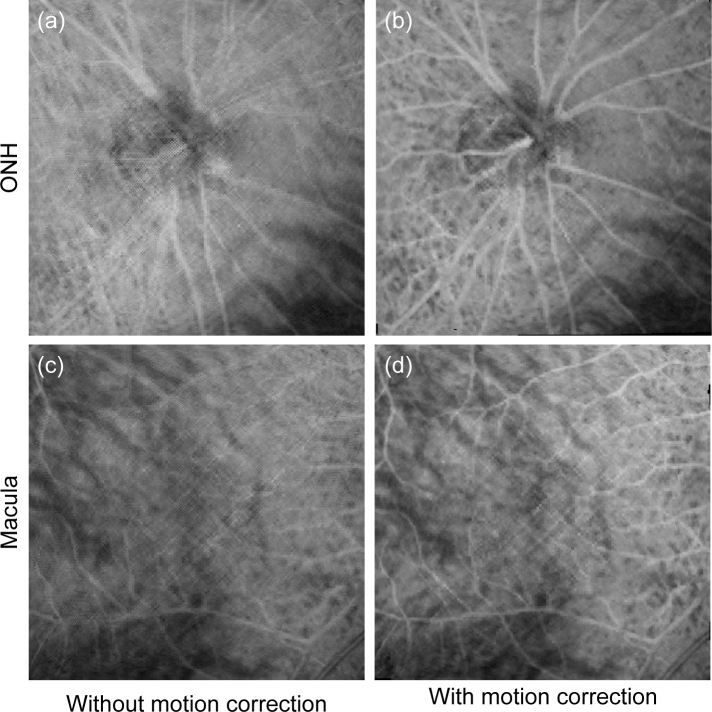
Figure 5 shows the whole depth en face OCT-A images without [Figs. 5(a) and (c)] and with [Figs. 5(b) and (d)] motion correction. Figures 5(a) and (b) show the ONH and Figs. 5(c) and (d) show the macula. It is evident from these figures that the blurring and the ghost vessels that are caused by sample motion are clearly resolved in the images with motion correction.
Fig. 5.
Whole depth en face OCT-A images of (a), (b) the optic nerve head and (c), (d) the macula. (a) and (c) show images without motion correction, while (b) and (d) show the images with motion correction.
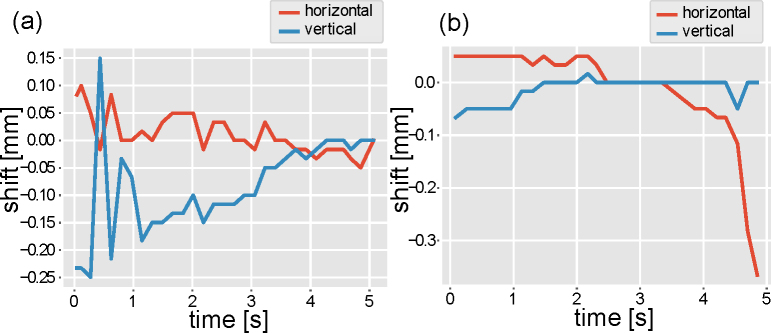
The estimated lateral shifts at the first step of the motion estimation (Section 2.3.3) is shown in Fig. 6 . Figures 6(a) and 6(b) correspond to the ONH scan [Figs. 5(a) and 5(b)] and the macular scan [Figs. 5(c) and 5(d)], respectively. Note that rapid eye motion which corrupted OCT-A imaging is not shown in these plots, because it has not been estimated in our method (Section 2.3.2). It shows that there are several fast motions and slow drifts. It is noteworthy that these slow drifts and few fast motions do not blur but warp raster images [see Fig. 13(a)]. On the other hand, the Lissajous image is blurred by these motions. It is because our volumetric Lissajous scan samples the same region of the eye multiple times.
Fig. 6.
Estimated lateral shifts with first motion estimation step. (a) Estimated motion in ONH imaging [Figs. 5(a) and 5(b)]. (b) Estimated motion in macular imaging [Figs. 5(c) and 5(d)].
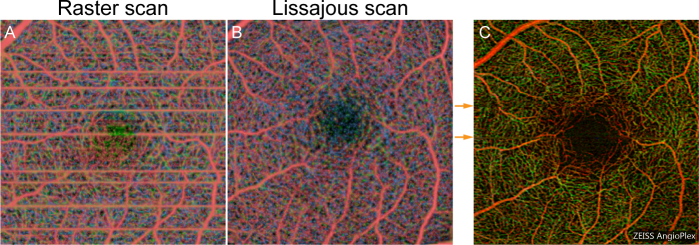
Fig. 13.
Color-coded slab en face OCT-A images with (a) raster scan and (b) modified Lissajous scan with motion correction. In both cases, the macular region scanned over an area of 3 × 3 mm2. The same location was scanned by Cirrus HD-OCT Model 5000 (Carl Zeiss). The color-coded AngioPlex image is shown in (c).
In Fig. 5(d), it appears that dot-like artifacts have occurred. These artifacts appear to have occurred along part of the Lissajous scan’s trajectory. This artifact may therefore be caused by residual decorrelation noise. For example, if only some of the A-lines in a repeat-cycle-set show high decorrelation, this particular set may not be eliminated by the algorithm that was described in section 2.3.2. Therefore, it seems that A-lines that show high decorrelation noise are included in the final image, and that artifacts such those as shown in Fig. 5(d) are considered to have occurred.
The typical processing times are approximately 240 s for lateral motion estimation and 8 s for motion correction (remapping) of a single en face OCT-A image. The processing time was studied using an Intel Core i7-6820HK CPU operating at 2.70 GHz with 16.0 GBytes of RAM, and the processing program was written in Python 2.7.13 (64-bit).
3.2. Validation of motion correction
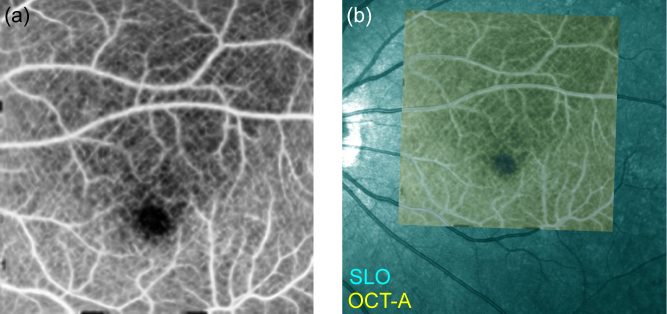
The motion correction of the en face OCT-A image was validated using a comparison with an SLO image (Spectralis HRA+Blue Peak, Heidelberg Engineering Inc., Heidelberg, Germany). The SLO image can be used as a motion-free reference standard because of its short measurement time. The motion-corrected en face OCT-A image (internal limiting membrane (ILM) to outer plexiform layer (OPL) slab) is manually registered with the SLO image as shown in Fig. 7 , in which the SLO and OCT-A images are displayed in cyan and yellow, respectively. The resulting images show good agreement between the OCT-A and SLO images.
Fig. 7.
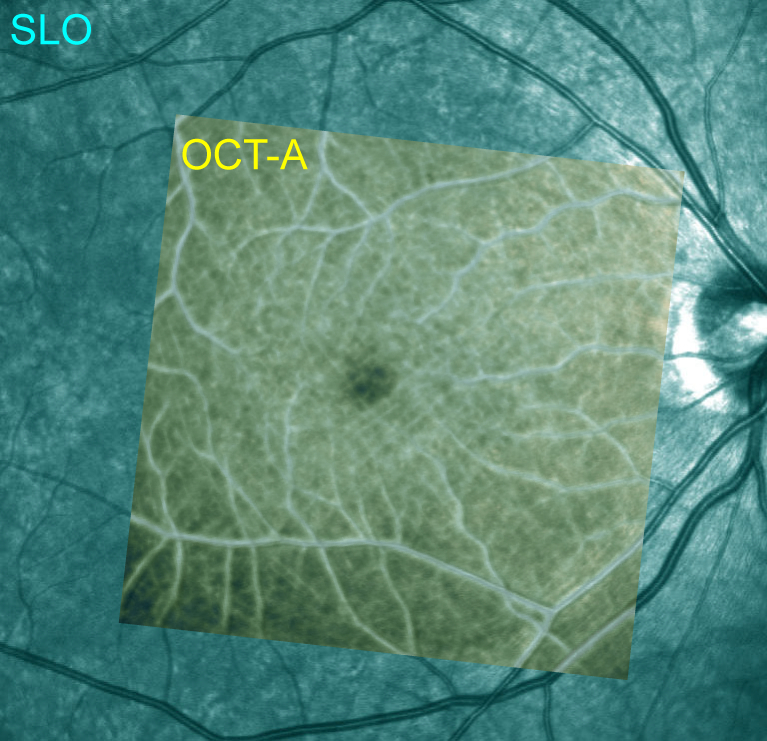
En face OCT-A image (yellow) overlaid on a scanning laser ophthalmoscope (SLO) image (cyan). Because the SLO image is regarded as a motion-free reference standard, this image demonstrates that our method provides a sufficient motion correction capability.
For quantitative analysis, SLO images and corresponding en face OCT images were compared. Because SLO image shows not only vasculature but also static scattering structures, the OCT image rather than OCT-A was used for this comparison. For three eyes, en face OCT-A images were registered with the corresponding SLO images. Then, the root-mean-square (RMS) errors between the en face OCT and the SLO were computed. Before calculating the RMS errors, the images have been normalized to have zero mean and unit variance. It was found that the mean RMS error decreased from 1.62 to 1.60 after the motion correction. The reductions of the RMS errors were computed for each eye. The mean reduction is 0.0257 ± 0.0102 (mean ± standard deviation). The motion correction improved the agreement with the SLO.
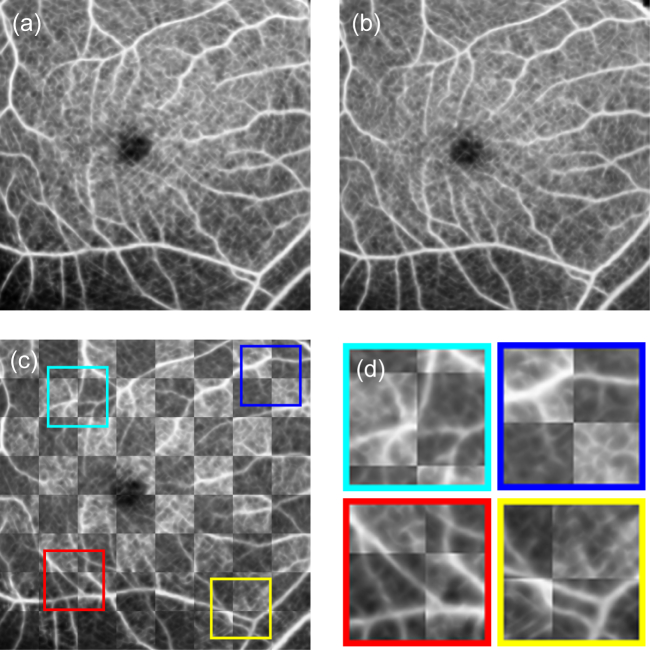
The motion correction repeatability was also evaluated by forming a checkerboard image from two motion-corrected en face OCT-A images (ILM to OPL slab), as shown in Fig. 8 . Figures 8(a) and 8(b) are both motion-corrected macular images of the same eye. Figure 8(c) shows a checkerboard image that was created from Figs. 8(a) and 8(b), and Fig. 8(d) shows magnified images of the regions that are indicated by the colored boxes in Fig. 8(c). To create the checkerboard image, the two motion-corrected en face OCT-A images were rigidly and manually registered and were then combined to form the checkerboard image. The brighter squares that are shown in Figs. 8(c) and 8(d) are from Fig. 8(a), while the darker squares are from Fig. 8(b). The checkerboard image shows the good connectivity of the blood vessels at the boundaries of these squares. This indicates the good repeatability of the motion correction method.
Fig. 8.
(c) Checkerboard image created from the two motion-corrected en face images that were shown in (a) and (b), where the brighter squares are from (a) and the darker squares are from (b). (d) shows a set of magnified images of (c), in which the colored boxes indicate the magnified region.
3.3. Imaging of three retinal vascular plexuses
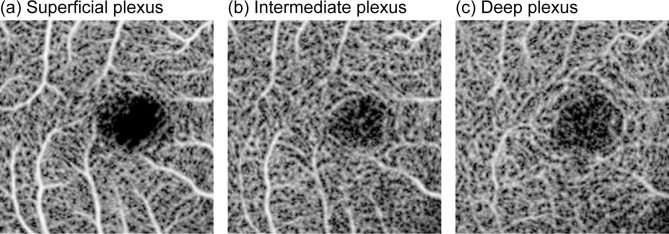
Figure 9 shows three slab OCT-A images. Figure 9(a) shows the superficial plexus, which ranges from the ILM to 24.8 µm above the boundary between the inner plexiform layer (IPL) and the inner nuclear layer (INL). Figure 9(b) shows the intermediate capillary plexus, which is in the ± 24.8 µm range around the IPL-INL boundary. Figure 9(c) shows the deep capillary plexus, which ranges from 24.8 µm below the IPL-INL boundary to the OPL-Henle’s fiber layer (HFL) boundary. While projection artifacts do exist in the images, the fine vascular networks are visualized.
Fig. 9.
En face OCT-A images of three retinal vascular plexuses. (a) Superficial plexus; from the ILM to 24.8 µm above the IPL-INL boundary. (b) Intermediate plexus; ±24.8 µm around the IPL-INL boundary. (c) Deep plexus; from 24.8 µm below the IPL-INL boundary to the OPL-HFL boundary.
In the color-coded multiple plexus image [Fig. 10(d) ], we used three different colors (red, green, and blue) for the superficial [Fig. 10(a)], intermediate [Fig. 10(b)], and deep plexuses [Fig. 10(c)], respectively. The projection artifacts are not prominent when this visualization method is used and the vessel connectivity among the three plexuses can then be seen.
Fig. 10.

(a)–(c) show slab OCT-A images at different depths and correspond to Figs. 9(a)–(c), respectively. These images are color-coded and are then combined as shown in (d).
3.4. Motion correction for the blinking case
One of the advantages of the Lissajous OCT-A is its immunity to blinking. As same as standard Lissajous OCT [22], one Lissajous OCT-A scan cycle consists of four quadrants, and the retinal area is scanned sequentially four times. Even if a blink disturbs one of these quadrants to produce a blank region, the other quadrants fill the blank region.
Figure 11 shows OCT [Fig. 11(a)] and OCT-A [Fig. 11(b)] images of an example case that includes a blink before Cartesian remapping. The vertical and horizontal directions in the images represent the indexes of the repeat-cycle-set and the A-line in that repeat-cycle-set, respectively. The blink appears as a black horizontal line region in the OCT image (indicated by red arrows) and a white (highly decorrelated) region in the OCT-A image. This region is thus discarded at the same time as the rapid motion artifacts, as shown in 11(c).
Fig. 11.
Examples of non-Cartesian remapped OCT (a) and OCT-A (b). The blink appears as the dark horizontal line in the OCT image and as the white (highly decorrelated) line in the OCT-A image. The blink region is removed from the OCT-A image at the same time as the rapid motion artifacts (c).
After motion correction, Cartesian remapping, and Gabor filtering, the blink is no longer obvious as shown in the ILM-OPL slab OCT-A image [Fig. 12(a) ]. Despite the partial information deficit, this deficit was filled and the motion was corrected perfectly as demonstrated by the perfect co-registration of the resulting image with the SLO image [Fig. 12(b)].
Fig. 12.
(a) Motion-corrected en face OCT-A image in blinking case. (b) Comparison with corresponding SLO image.
4. Discussion
Several OCT-A devices scan the retina using a raster scanning pattern. Here, OCT-A images based on a raster scanning pattern and the Lissajous scanning pattern are compared. We used the raster scan protocol with the 300 × 300 transversal sampling points with four repetitions of the B-scan. Color-coded slab en face OCT-A images of the same three retinal plexuses that were shown in Section 3.3 are shown in Fig. 13(a) and (b) . Both of raster-scan and Lissajous-scan images were obtained using the same JM-OCT system over a 3 × 3 mm2 area at the macula of the same subject. The data acquisition process took 5.14 s with the raster scan (70 % duty cycle). The time lag between the repeated B-scans is approximately 4.28 ms. In the Lissajous scan case (Section 2.5), the acquisition time is 5.25 s (99.86 % duty cycle). The Lissajous OCT-A image shows the retinal capillary vessels well, while the raster-scan OCT-A image is disturbed by several motion artifacts.
The main disadvantage of the Lissajous scan may be that the density of the A-scan is not uniform in the scanned region. The spatial sampling step at the center of the scan region will be larger than that of the raster scan if the data are acquired at similar scanning times and over similar scanning ranges. In the configuration used for Fig. 13(b), the maximum distance between adjacent trajectories at the center of the scanning area is 18.4 µm, while the constant sampling step of the raster scan protocol is 10 µm. This will probably contribute to a reduction in contrast at the center. This disadvantage is believed to have been alleviated by scanning of the positions on the retina that are slightly displaced because of eye motion. However, longer measurement duration or multiple measurements may overcome this drawback. Since the Lissajous OCT-A has immunity to blinking, long-time measurement can be easily performed. Beside this, employing high speed light sources [32] or spectral splitting method [33] may improve the imaging quality of Lissajous OCT-A by increasing sampling density.
We used a commercial OCT-A device (Cirrus HD-OCT Model 5000 with Angioplex, Carl Zeiss) [34] for further comparison. The scanning mode of 3 × 3 mm2 was used. There are 245 × 245 sampling points and the B-scan is repeated at the same scanning location four times. The axial and transversal resolutions are 5 µm and 15 µm, respectively. The color-coded OCT-A image provided by Cirrus HD-OCT Model 5000 is shown in Fig. 13(c). Because different devices and signal and image processing were used, it is hard to compare imaging quality directly. However, the commercial device provides high-contrast capillary image. One reason of that is probably the lower resolutions of JM-OCT compared with those of the commercial OCT device. The shorter wavelength of the commercial device (840 nm of center wavelength) provides higher spatial resolutions. Other significant factor of imaging quality is number of repetitions. It is two times in Lissajous OCT-A while four times in the image of commercial device. Because vasculature contrast is similar between Fig. 13(a) and (b), the lower contrast than the commercial device [Fig. 13(c)] would not due to Lissajous scan but due to the difference in the OCT hardware and subsidiary image processing. In addition, the OCT-A image obtained with Cirrus HD-OCT Model 5000 [Fig. 13(c)] exhibits residual motion artifacts (discontinuity along horizontal direction indicated by orange arrows) even an active (hardware) eye tracking is used [34]. On the other hand, apparent motion artifacts are not evident in the case of Lissajous OCT-A [Fig. 13(b)]. Hence, the application of the presented Lissajous scan and the motion correction algorithm to commercial devices will further improve OCT-A imaging quality.
5. Conclusion
We have demonstrated motion-free en face OCT-A imaging using a specialized Lissajous scan. A standard Lissajous scanning pattern was modified for compatibility with OCT-A measurements. A motion correction algorithm, which was tailored for the modified Lissajous scan, was designed to obtain motion-corrected en face OCT-A images. By validating both the motion correction ability and its repeatability, we conclude that this motion-free en face OCT-A method can provide accurate motion-free en face OCT-A images of the posterior segment of the eye in vivo.
Acknowledgments
The research and project administrative work of Tomomi Nagasaka from the University of Tsukuba is gratefully acknowledged. We thank David MacDonald, MSc, from Edanz Group (www.edanzediting.com/ac) for editing a draft of this manuscript. We also thank Deepa Kasarago, PhD, for her help in editing the manuscript.
Appendix A. List of symbols
The descriptions of the symbols used in Section 2 are listed in Table 1
Table 1. Descriptions of symbols.
| Symbols | Descriptions |
|---|---|
| l | Index of axial line (A-line) in a repeated cycle (0, 1, ⋯, Lx − 1). |
| Lx | Number of A-lines in a repeated cycle. |
| m | Count of repeated cycles in a repeat-cycle-set (0, 1, ⋯, M − 1). |
| M | Number of repeated cycles in a repeat-cycle-set. |
| n | Index of repeat-cycle-set. |
| k | Total count of repeat-cycle-set (= m + M · n), which is counted from the beginning of the whole scan trajectory. |
| i | Index of A-line in ascending order of acquisition time (= l + Lx · k). |
| z | Index of pixel in an A-line. |
| p | Index of polarization channel. |
| δ | Number of A-lines during the margin between repeated cycles. |
|
| |
| x(t), y(t) | Standard Lissajous trajectory parameterized usin t. |
| t | Time. |
| Ax, Ay | Amplitudes of x- and y-scanning patterns, respectively. |
| Tx, Ty | Periods of x- and y-scanning patterns, respectively. |
| x′(t), y′ (t) | Modified Lissajous trajectory for OCT-A. |
| χx(t), χy(t) | Temporal functions used to modify the Lissajous pattern. |
| χx,i, χy,i | Discrete values of χ when the i-th A-line is acquired. |
| ΔT | Duration of the margin between repeated cycles. |
| Tc | Time lag between repeated scans at the same location. |
| TA | Period of A-lines. |
|
| |
| g | Complex OCT signal. |
| g n | Pair of OCT signals used to compute OCT-A at the n-th repeat-cycle-set. |
| rn | Temporal correlation coefficient of OCT data for OCT-A at the n-th repeat-cycle-set. |
| El,n | En face OCT-A data at the l-th A-line of the n-th repeat-cycle-set. |
| ρn | Cross-correlation coefficient between en face OCT-A of adjacent repeat-cycle-sets. |
.
Funding
Japan Society for the Promotion of Science (JSPS) (KAKENHI 15K13371); Ministry of Education, Culture, Sports, Science and Technology (MEXT) through Local Innovation Ecosystem Development Program; Korea Evaluation Institute of Industrial Technology.
Disclosures
YC, YJH: Topcon (F), Tomey Corporation (F), Nidek (F), KAO (F). SM, YY Topcon (F), Tomey Corporation (F, P), Nidek (F, P), KAO. YJH is currently employed by Koh Young Technology.
References and links
- 1.Novotny H. R., Alvis D. L., “A Method of Photographing Fluorescence in Circulating Blood in the Human Retina,” Circulation 24(1), 82–86 (1961). 10.1161/01.CIR.24.1.82 [DOI] [PubMed] [Google Scholar]
- 2.Owens S. L., “Indocyanine green angiography,” Br. J. Ophthalmol. 80(3), 263–266 (1996). 10.1136/bjo.80.3.263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lira R. P. C., Oliveira C. L. d. A., Marques M. V. R. B., Silva A. R., Pessoa C. d. C., “Adverse reactions of fluorescein angiography: a prospective study,” Arq. Bras. Oftalmol. 70(4), 615–618 (2007). 10.1590/S0004-27492007000400011 [DOI] [PubMed] [Google Scholar]
- 4.Karhunen U., Raitta C., Kala R., “Adverse reactions to fluorescein angiography,” Acta Ophthalmol. (Copenh.) 64(3), 282–286 (1986). 10.1111/j.1755-3768.1986.tb06919.x [DOI] [PubMed] [Google Scholar]
- 5.Hope-Ross M., Yannuzzi L. A., Gragoudas E. S., Guyer D. R., Slakter J. S., Sorenson J. A., Krupsky S., Orlock D. A., Puliafito C. A., “Adverse Reactions due to Indocyanine Green,” Ophthalmology 101(3), 529–533 (1994). 10.1016/S0161-6420(94)31303-0 [DOI] [PubMed] [Google Scholar]
- 6.Benya R., Quintana J., Brundage B., “Adverse reactions to indocyanine green: A case report and a review of the literature,” Cathet. Cardiovasc. Diagn. 17(4), 231–233 (1989). 10.1002/ccd.1810170410 [DOI] [PubMed] [Google Scholar]
- 7.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., Et A., “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Drexler W., Fujimoto J. G., Optical Coherence Tomography: Technology and Applications (Springer Science & Business Media, 2008). 10.1007/978-3-540-77550-8 [DOI] [Google Scholar]
- 9.Makita S., Hong Y., Yamanari M., Yatagai T., Yasuno Y., “Optical coherence angiography,” Opt. Express 14(17), 7821–7840 (2006). 10.1364/OE.14.007821 [DOI] [PubMed] [Google Scholar]
- 10.Makita S., Kurokawa K., Hong Y.-J., Miura M., Yasuno Y., “Noise-immune complex correlation for optical coherence angiography based on standard and Jones matrix optical coherence tomography,” Biomed. Opt. Express 7(4), 1525–1548 (2016). 10.1364/BOE.7.001525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jia Y., Tan O., Tokayer J., Potsaid B., Wang Y., Liu J. J., Kraus M. F., Subhash H., Fujimoto J. G., Hornegger J., Huang D., “Split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Opt. Express 20(4), 4710–4725 (2012). 10.1364/OE.20.004710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liu G., Chou L., Jia W., Qi W., Choi B., Chen Z., “Intensity-based modified Doppler variance algorithm: application to phase instable and phase stable optical coherence tomography systems,” Opt. Express 19(12), 11429–11440 (2011). 10.1364/OE.19.011429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liu G., Qi W., Yu L., Chen Z., “Real-time bulk-motion-correction free Doppler variance optical coherence tomography for choroidal capillary vasculature imaging,” Opt. Express 19(4), 3657–3666 (2011). 10.1364/OE.19.003657 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hammer D. X., Ferguson R. D., Iftimia N. V., Ustun T., Wollstein G., Ishikawa H., Gabriele M. L., Dilworth W. D., Kagemann L., Schuman J. S., “Advanced scanning methods with tracking optical coherence tomography,” Opt. Express 13(20), 7937–7947 (2005). 10.1364/OPEX.13.007937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pircher M., Baumann B., Götzinger E., Sattmann H., Hitzenberger C. K., “Simultaneous SLO/OCT imaging of the human retina with axial eye motion correction,” Opt. Express 15(25), 16922–16932 (2007). 10.1364/OE.15.016922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vienola K. V., Braaf B., Sheehy C. K., Yang Q., Tiruveedhula P., Arathorn D. W., Boer J. F. d., Roorda A., “Real-time eye motion compensation for OCT imaging with tracking SLO,” Biomed. Opt. Express 3(11), 2950–2963 (2012). 10.1364/BOE.3.002950 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ferguson R. D., Hammer D. X., Paunescu L. A., Beaton S., Schuman J. S., “Tracking optical coherence tomography,” Opt. Lett. 29(18), 2139–2141 (2004). 10.1364/OL.29.002139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kraus M. F., Potsaid B., Mayer M. A., Bock R., Baumann B., Liu J. J., Hornegger J., Fujimoto J. G., “Motion correction in optical coherence tomography volumes on a per A-scan basis using orthogonal scan patterns,” Biomed. Opt. Express 3(6), 1182–1199 (2012). 10.1364/BOE.3.001182 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kraus M. F., Liu J. J., Schottenhamml J., Chen C.-L., Budai A., Branchini L., Ko T., Ishikawa H., Wollstein G., Schuman J., Duker J. S., Fujimoto J. G., Hornegger J., “Quantitative 3d-OCT motion correction with tilt and illumination correction, robust similarity measure and regularization,” Biomed. Opt. Express 5(8), 2591–2613 (2014). 10.1364/BOE.5.002591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hendargo H. C., Estrada R., Chiu S. J., Tomasi C., Farsiu S., Izatt J. A., “Automated non-rigid registration and mosaicing for robust imaging of distinct retinal capillary beds using speckle variance optical coherence tomography,” Biomed. Opt. Express 4(6), 803–821 (2013). 10.1364/BOE.4.000803 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zang P., Liu G., Zhang M., Dongye C., Wang J., Pechauer A. D., Hwang T. S., Wilson D. J., Huang D., Li D., Jia Y., “Automated motion correction using parallel-strip registration for wide-field en face OCT angiogram,” Biomed. Opt. Express 7(7), 2823–2836 (2016). 10.1364/BOE.7.002823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen Y., Hong Y.-J., Makita S., Yasuno Y., “Three-dimensional eye motion correction by Lissajous scan optical coherence tomography,” Biomed. Opt. Express 8(3), 1783–1802 (2017). 10.1364/BOE.8.001783 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hong Y.-J., Chen Y., Li E., Miura M., Makita S., Yasuno Y., “Eye motion corrected OCT imaging with Lissajous scan pattern,” Proceedings of SPIE 9693, 96930 (2016). 10.1117/12.2212227 [DOI] [Google Scholar]
- 24.Ju M. J., Hong Y.-J., Makita S., Lim Y., Kurokawa K., Duan L., Miura M., Tang S., Yasuno Y., “Advanced multi-contrast Jones matrix optical coherence tomography for Doppler and polarization sensitive imaging,” Opt. Express 21(16), 19412–19436 (2013). 10.1364/OE.21.019412 [DOI] [PubMed] [Google Scholar]
- 25.Sugiyama S., Hong Y.-J., Kasaragod D., Makita S., Uematsu S., Ikuno Y., Miura M., Yasuno Y., “Birefringence imaging of posterior eye by multi-functional Jones matrix optical coherence tomography,” Biomed. Opt. Express 6(12), 4951–4974 (2015). 10.1364/BOE.6.004951 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bazaei A., Yong Y. K., Moheimani S. O. R., “High-speed Lissajous-scan atomic force microscopy: Scan pattern planning and control design issues,” Rev. Sci. Instrum. 83(6), 063701 (2012). 10.1063/1.4725525 [DOI] [PubMed] [Google Scholar]
- 27.Li K., Wu X., Chen D. Z., Sonka M., “Optimal Surface Segmentation in Volumetric Images-A Graph-Theoretic Approach,” IEEE Trans. Pattern Anal. Mach. Intell. 28(1), 119–134 (2006). 10.1109/TPAMI.2006.19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Garvin M. K., Abramoff M. D., Wu X., Russell S. R., Burns T. L., Sonka M., “Automated 3-D Intraretinal Layer Segmentation of Macular Spectral-Domain Optical Coherence Tomography Images,” IEEE Trans. Med. Imaging 28(9), 1436–1447 (2009). 10.1109/TMI.2009.2016958 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chen X., Niemeijer M., Zhang L., Lee K., Abramoff M. D., Sonka M., “Segmentation Three-Dimensional of Abnormalities Fluid-Associated in OCT RetinalThree-Dimensional Segmentation of Fluid-Associated Abnormalities in Retinal OCT: Probability Constrained Graph-Search-Graph-Cut,” IEEE Trans. Med. Imaging 31(8), 1521–1531 (2012). 10.1109/TMI.2012.2191302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Estrada R., Tomasi C., Cabrera M. T., Wallace D. K., Freedman S. F., Farsiu S., “Enhanced video indirect ophthalmoscopy (VIO) via robust mosaicing,” Biomed. Opt. Express 2(10), 2871–2887 (2011). 10.1364/BOE.2.002871 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sternberg S. R., “Biomedical Image Processing,” Computer 16(1), 22–34 (1983). 10.1109/MC.1983.1654163 [DOI] [Google Scholar]
- 32.Klein T., Wieser W., Reznicek L., Neubauer A., Kampik A., Huber R., “Multi-MHz retinal OCT,” Biomed. Opt. Express 4(10), 1890–1908 (2013). 10.1364/BOE.4.001890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ginner L., Blatter C., Fechtig D., Schmoll T., Gröschl M., Leitgeb R. A., “Wide-Field OCT Angiography at 400 KHz Utilizing Spectral Splitting,” Photonics 1(4), 369–379 (2014). 10.3390/photonics1040369 [DOI] [Google Scholar]
- 34.Rosenfeld P. J., Durbin M. K., Roisman L., Zheng F., Miller A., Robbins G., Schaal K. B., Gregori G., “ZEISS Angioplex™Spectral Domain Optical Coherence Tomography Angiography: Technical Aspects,” in “OCT angiography in retinal and macular diseases,”, vol. 56 of Developments in Ophthalmology Bandello F., Souied E., Querques G., eds. (S. Karger AG, 2016), pp. 18–29. . 10.1159/000442773 [DOI] [PubMed] [Google Scholar]