Impact of errors in experimental parameters on reconstructed breast images using diffuse optical tomography

Abstract

Near-infrared diffuse optical tomography (NIR-DOT) is an emerging technology that offers hemoglobin based, functional imaging tumor biomarkers for breast cancer management. The most promising clinical translation opportunities are in the differential diagnosis of malignant vs. benign lesions, and in early response assessment and guidance for neoadjuvant chemotherapy. Accurate quantification of the tissue oxy- and deoxy-hemoglobin concentration across the field of view, as well as repeatability during longitudinal imaging in the context of therapy guidance, are essential for the successful translation of NIR-DOT to clinical practice. The ill-posed and ill-condition nature of the DOT inverse problem makes this technique particularly susceptible to model errors that may occur, for example, when the experimental conditions do not fully match the assumptions built into the image reconstruction process. To evaluate the susceptibility of DOT images to experimental errors that might be encountered in practice for a parallel-plate NIR-DOT system, we simulated 7 different types of errors, each with a range of magnitudes. We generated simulated data by using digital breast phantoms derived from five actual mammograms of healthy female volunteers, to which we added a 1-cm tumor. After applying each of the experimental error types and magnitudes to the simulated measurements, we reconstructed optical images with and without structural prior guidance and assessed the overall error in the total hemoglobin concentrations (HbT) and in the HbT contrast between the lesion and surrounding area vs. the best-case scenarios. It is found that slight in-plane probe misalignment and plate rotation did not result in large quantification errors. However, any out-of-plane probe tilting could result in significant deterioration in lesion contrast. Among the error types investigated in this work, optical images were the least likely to be impacted by breast shape inaccuracies but suffered the largest deterioration due to cross-talk between signal channels. However, errors in optical images could be effectively controlled when experimental parameters were properly estimated during data acquisition and accounted for in the image processing procedure. Finally, optical images recovered using structural priors were, in general, less susceptible to experimental errors; however, lesion contrasts were more sensitive to errors when tumor locations were used as a priori info. Findings in this simulation study can provide guidelines for system design and operation in optical breast imaging studies.

1. Introduction

Near-infrared diffuse optical tomography (NIR-DOT) is emerging as a useful imaging tool for breast cancer management [1–6]. In particular, optical imaging has been demonstrated to offer early sensitivity to tissue changes predictive of therapy outcome in patients undergoing neoadjuvant chemotherapy [7–14]. However, DOT image reconstructions suffer from ill-posedness that makes the technology intrinsically sensitive to measurement noise and model errors [15,16]. In addition to the consistency over the field of view needed to distinguish lesions from the normal breast tissue background for diagnosis, therapy monitoring requires longitudinal imaging of the same patient several times before and during the course of the treatment while maintaining quantitative accuracy of the optical image reconstructions such that direct comparisons of absolute hemoglobin concentrations or other relevant tissue properties can be made. Factors relating to patient positioning repeatability, variation in optode coupling and breast shape, as well as accuracy in generating the finite element mesh used for reconstruction can negatively impact the sensitivity of optical tissue monitoring. Therefore, methods that are designed to define and ensure quantification accuracy, precision, and reproducibility, especially over the long time frame of therapy monitoring studies, are essential for the clinical translation of NIR-DOT [17].

The goal of this paper is to evaluate the impact of several error sources on the accuracy of quantitative optical images and hence provide guidance for system design and operation in the context of optical breast imaging studies. To this end, we considered a parallel-plate transmission imaging geometry similar to our combined optical/x-ray mammography instrumentation [18]. We used breast structural and compositional maps derived from Philips MicroDose dual-energy mammographic measurements on five healthy female volunteers chosen to sample a variety of breast sizes and densities. To these we added a tumor region and generated simulated continuous-wave and frequency domain diffuse optical tomography measurements using our in-house finite element diffusion approximation solver – Redbird [19]. We then applied simulated experimental errors to the data and used it to reconstruct hemoglobin concentration maps to estimate the impact of the errors with respect to overall quantification accuracy and with respect to tumor to background contrast.

In the following sections, we first elaborate the creation of digital breast phantoms. We then describe the simulation of realistic optical measurements and reconstruction methods. Next, the methods of introducing various experimental errors are explained and the metrics used to quantify the influence of these errors to the recovered optical images are described. We present and discuss the outcomes of this systematic simulation study in the Results and Discussion sections, respectively, and summarize our key findings in the Conclusions section.

2. Methods

2.1 Digital breast phantoms

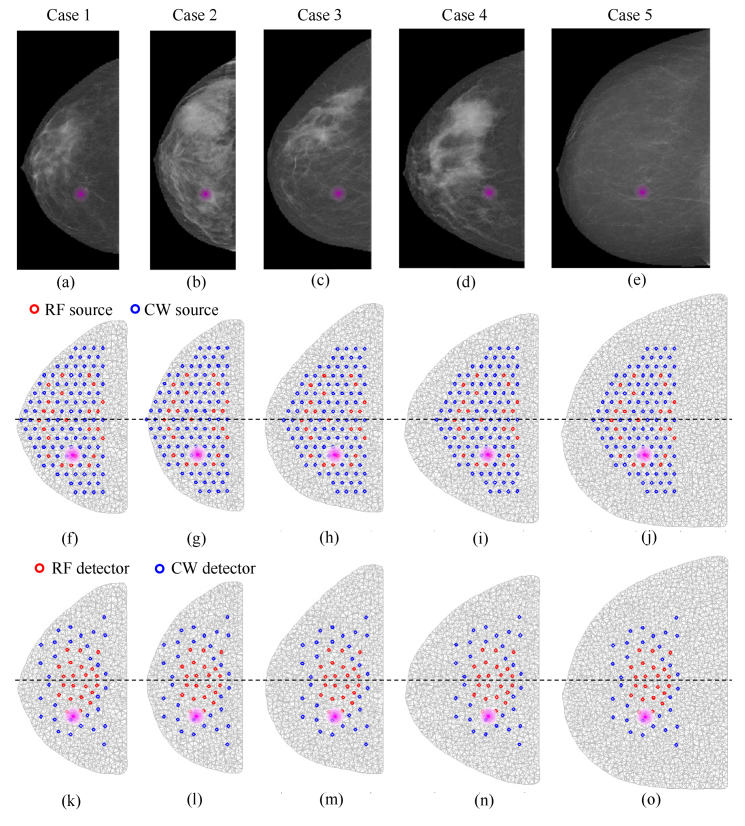
Using a similar approach to the one described previously in-detail in making DigiBreast [20,21], an open-source complex digital breast phantom with three-dimensional (3D) tissue compositions, we constructed 5 digital breast phantoms on which we tested the influence of experimental errors on the quality of recovered optical images. Each 3D breast phantom was generated from the breast tissue composition and thickness maps of a healthy volunteer measured by a Philips MicroDose SI system using dual-energy photon-counting technology [22–24]. The breast tissue composition measurement provides us with a two-dimensional (2D) fibroglandular tissue volume fraction map, referred to as C_f, with a pixel resolution of 500 µm × 500 µm. We first down-sampled the 2D fibroglandular map to a pixel size of 1 by 1 mm, and then expanded it into a 3D structure by stacking repeated 1-mm slices to the measured subject breast thickness. This cylindrical quasi-3D profile was subsequently converted to a curved 3D breast shape by shrinking the outline of non-midplane slices using a mask whose curvature was derived from the measured breast thickness map. Finally, we added a 2-cm wide, full-height slab to the 3D volume towards the chest-wall to minimize the optical modeling errors caused by chest-wall truncation [25]. This extended region was excluded from the error calculations of recovered optical properties described in Section 2.4.

As shown in Table 1, the resulting 5 digital breast phantoms have a range of densities (25.7 ± 18.1%, mean ± std) and thicknesses (47.46 ± 11.57 mm) that are representative for cases usually seen in the clinic. For each 3D phantom profile, a pair of tetrahedral meshes, a finer one for solving the optical forward problem and a coarser one for the inversion, were generated using a MATLAB-based meshing toolbox – iso2mesh [25]. Meshing parameters were set to ensure that the median inter-node distances for all five cases were consistent regardless of breast size. Thus, larger breasts, such as Case 5, yielded a significantly larger number of nodes than smaller ones. Nevertheless, the median inter-node distances were maintained at 4.71 ± 0.08 mm and 6.09 ± 0.03 mm for forward and reconstruction meshes, respectively.

Table 1. Statistics of five digital breast phantoms and their corresponding meshes and forward models.

		Case 1	Case 2	Case 3	Case 4	Case 5
Breast thickness (mm)		29.67	43.76	49.89	54.02	59.98
Area of breast in CC view (cm2)		163.48	142.29	199.06	230.22	358.56
Breast density (%)		24.2	54.1	15.1	28.8	6.4
Number of nodes	Forward	14,490	17,067	23,714	27,904	43,421
	Recon.	4,732	5,894	8,334	10,076	15,955
Max SNR of 690 nm data (dB)		64.1	54.4	52.5	49.6	47.5
Src-Det separation limit (cm)		8.6	10.8	11.7	12.1	12.9

To define the simulated tissue physiological and optical properties, namely oxy-hemoglobin concentration (HbO), deoxy-hemoglobin (HbR), and the reduced scattering coefficients (µ_s') at 690 and 830 nm on the finite-element phantom, we first interpolated the aforementioned volume fraction map of fibroglandular tissue, C_f, to the fine forward mesh. The volume fraction of adipose tissue C_a was then defined as C_a = 1 - C_f, at each node location r. One of the primary goals of this study is to investigate how experimental errors translate into mischaracterization of breast tumors using DOT. To this end, we created tumor-bearing digital breast phantoms by adding a tumor profile C_t centered at the middle slice on each of the above normal breast phantoms consisting of only adipose and fibroglandular tissues. The lesion has volume fraction profile of a Gaussian sphere with an effective diameter of 10 mm defined as the full-width half-maximum (FWHM). Accordingly, we scaled both C_a and C_f by (1 - C_t) to ensure that the total volume fractions add to 1 at all nodes. Finally, optical properties µ at each forward node r were calculated by multiplying tissue volume fractions with their reference optical properties using Eq. (1):

$$\mathbf{\mu }\left(\mathbf{r}\right)=C_f\left(\mathbf{r}\right)\times {\mathbf{\mu }}_f\times \left[1–C_t\left(\mathbf{r}\right)\right]+\left[1–C_f\left(\mathbf{r}\right)\right]\times {\mathbf{\mu }}_a\times \left[1–C_t\left(\mathbf{r}\right)\right]+C_t\left(\mathbf{r}\right)\times {\mathbf{\mu }}_t,$$ (1)

where, µ_f, µ_a, and µ_t denote the set of optical properties (absorption and scattering) of the fibroglandular, adipose tissues and tumor, respectively, as shown in Table 2. The reference properties of adipose and fibroglandular tissues were derived from a large (N = 189) clinical study of diffuse optical breast imaging reported in [5]. To ensure the lesion is differentiable from surrounding tissues in all cases tested, we chose a contrast of total hemoglobin concentration (HbT = HbO + HbR) and reduced scattering coefficients (µ_s') between tumor and fibroglandular tissue of 2.10 and 1.37, respectively, and between tumor and adipose tissue of 2.86 and 1.49, respectively. Based on our previous study [21], with these lesion-to-normal tissue contrasts optical properties of the tumor could be reasonably well recovered regardless of tumor vicinities, i.e., whether the tumor resides within adipose or fibroglandular tissues, even in reconstructions that apply no structural priors as guidance. In addition, to further limit the potentially confounding effect caused by variation in tumor locations, as shown in Fig. 1 , the lesion centroid was chosen to be at the same location relative to optodes in all five cases, ensuring comparable source and detector coverage. We assumed a uniform refractive index of n = 1.37, lipid concentration of 58%, and water concentration of 23% throughout all five breast phantoms. Scattering was represented as µ_s'(λ) = S_a×λ^{- Sp}, where S_a is the scattering amplitude and S_p is the scattering power.

Table 2. Reference optical properties for various breast tissue types.

	HbO (µM)	HbR (µM)	HbT (µM)	µs' (cm−1)
				at 690 nm	at 830 nm
Adipose (µa)	13.84	4.81	18.65	8.51	7.13
Fibroglandular (µf)	18.96	6.47	25.43	9.25	7.75
Tumor (µt)	40.90	12.46	53.36	12.65	10.65

Fig. 1.

(a-e) 2D mammographic cranio-caudal (CC) views of five healthy volunteers whose clinical scans taken by Philips MicroDose SI system were used to generate the digital breast phantoms in this study. Cross-sectional views of 3D reconstruction mesh overlaid with optical (f-j) sources and (k-o) detectors for all five cases. Shadowed magenta areas around central magenta dots indicate the defined lesion regions and lesion centroids.

2.2 Optical measurements simulation and image reconstruction

We used a diffusion-equation-based forward model [16] to simulate optical measurements at 690 and 830 nm under the ideal scenario, i.e., with no experimental error, as well as under various practical scenarios where instrumentation-related errors were introduced. The in-house finite-element solver, Redbird [19], was used to numerically solve the diffuse equation on the forward mesh with a parallel-plate transmission configuration of optical source and detector locations as in our 2nd-generation tomographic optical breast imaging (TOBI2) system [18].

As shown in the second row of Fig. 1, the source plate contains 96 continuous-wave (CW) sources and 24 radio-frequency (RF) sources shared by both wavelengths. On the detector plate, shown in the third row of Fig. 1, 32 CW and 22 RF detectors are used for both wavelengths. For each forward simulation, shot-noise (n₁ = A₁ × U × $\sqrt{\left|{\Phi }_0(s,d)\right|}$) and electronic noise (n₂ = max(|Φ₀|) × A₂ × U) were also added to the model output fluence Φ₀(s,d) to simulate realistic measurement noise, where U is a random variable in the standard normal distribution. The maximum amplitudes of shot-noise and electric noise were set to A₁ = 10⁻⁵ mm⁻¹ and A₂ = 10⁻⁵, respectively, according to the worst-case scenario of our instrument as reported in [18], assuming a unit source intensity. The resulting noise floor was used to objectively determine the separation limit for each case (shown in Table 1) that was later used to select measurements in reconstruction.

Image reconstructions were done in two steps. First, a spectrally constrained fit was performed for the overall average tissue properties from a preset initial guess of HbO, HbR, scattering amplitude and scattering power. Results of this bulk property fitting step were then used as the starting point for the image reconstruction step that focuses on recovering spatial variations. Image reconstructions were obtained using a nonlinear, spectrally constrained inversion of the diffuse approximation using a Tikhonov-regularized Gauss-Newton method performed on the coarser mesh for 10 iterations using Redbird. We only included measurements from source-detector (SD) pairs that were within the predetermined maximum limits described above. Since varying the preset initial guesses had resulted in only minimal changes of the fitted bulk optical properties in the first step of image reconstruction, in this study, we used the same preset initial guesses for all phantom cases, error types and levels. The preset values are 14.1 µM for HbO, 4.1 µM for HbR, 0.2 cm⁻¹ for S_a, and 0.92 for S_p.

Our group and others have demonstrated that DOT reconstruction guided by structural prior information derived from imaging modalities such as mammography, ultrasound, and magnetic resonance imaging (MRI) can result in significantly improved resolution in optical images and more accurate characterization of breast tumors [21, 26–31]. Therefore, in this study, we generated structural priors for each phantom from their x-ray images using our previously described dual-Gaussian segmentation algorithm [21], and tested the susceptibility to experimental errors of three approaches: 1) reconstruction with no structural priors, 2) reconstruction with structural priors of normal tissues only, i.e., two-composition-priors composed of only adipose and fibroglandular tissue types, and 3) reconstruction with structural priors of both normal tissues and lesion (three-composition-prior), with the tumor location and size assumed known a priori, e.g., as would be the case for chemotherapy monitoring studies or for differential diagnosis of breast lesions.

2.3 Scenarios of experimental errors

Before introducing any errors, optical images were reconstructed based on the accurate probe geometry, true breast shape, and ideal signal collection. Results from this best-case scenario served as a benchmark to gauge the extent to which experimental errors deteriorate the recovered optical images. Then, three categories of experimental errors were introduced, namely, plate positioning errors, breast shape inaccuracy, and signal contamination during DOT data acquisition. In each error scenario, we considered several degrees of severity. Forward modeling was then performed to obtain error-bearing optical measurement data. Finally, image reconstructions were performed using baseline assumptions on error-bearing DOT, as would be the case when experimental errors are not known/considered at the time of image reconstructions. We also took our study one step further by reconstructing images from error-bearing DOT data using modified/corrected parameters to mimic the case where experimental errors are quantified and included in the light transport model. In the following subsections, we elaborate the methods we used to implement each error scenario.

2.3.1 Plate positioning errors

Plate positioning errors, such as translational offset, i.e., shift between source and detector probes, rotational misalignment, and tilt of a plate as usually seen in the parallel-plate settings, violate assumptions of the probe geometry. Inaccurate source and detector locations lead to misinterpretation of light attenuation along the path between a source and detector pair, and in turn, result in deviations of estimated optical properties from their true values.

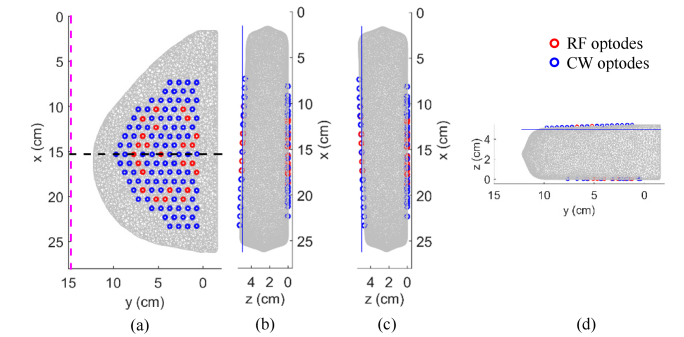
To mimic the translational offset error, we shifted all optodes on the source plate along the x-axis by decreasing the x-coordinates of all sources, by 0.2, 0.5, 1 and 2 mm, respectively. For in-plane rotational misalignment, we rotated all sources counter-clockwise around the origin by 0.1, 0.25, 0.5, 0.75, 1, and 2 degrees. We also tilted the source probe out-of-plane around two axes as shown in Fig. 2 . The tilt about the black sagittal axis represents a left-to-right (L-R) tilt, and the tilt about the magenta lateral axis represent a nipple-to-chest wall (N-C) tilt. We tilted the source probe by ± 0.5, ± 1, ± 1.5, ± 2, ± 3, ± 4, ± 5-degree angles around the sagittal axis to evaluate the influence of tilt direction on the recovery of tumor contrasts. When tilt was introduced around the lateral axis, however, only positive angles of 0.5, 1, 1.5, 2, 3, 4, 5 degrees were applied since the nipple end is always more compressed than the breast tissue near the chest wall in real-life cases. In all tilt modifications, forward and reconstruction meshes were also modified accordingly to ensure contact between modified source optodes and the top of breast phantom.

Fig. 2.

Schematic drawings of source probe modification to simulate the tilt experimental error scenario. Case 3 is used as a representative example. (a) Forward mesh overlaid with source optodes. Black and magenta dashed lines represent the sagittal and lateral axes around which tilting modifications are performed. x-z plane views from the chest wall of modified meshes and optodes with (b) −2° and (c) 2° tilt, respectively, about the sagittal axis, i.e., in the L-R direction. (d) y-z plane view of the modified mesh and probe with 2° tilt about the lateral axis, i.e., in the N-C direction. Blue solid lines in (b-d) represent the unmodified plate surface.

2.3.2 Breast shape inaccuracy

Geometric accuracy of the finite-element meshes used for DOT image reconstruction depends heavily on precise knowledge of the breast shape. For multi-modal imaging systems, such as our optical-DBT device, such information can be acquired from co-registered clinical scans. However, in stand-alone optical systems or in applications like longitudinal therapy monitoring studies using DOT only, breast shape frequently needs to be estimated, for example, from cameras/profilometers, previous clinical images, etc. Moreover, when imaged under compression, breast tissue may experience gradual relaxation that might result in a slight expansion in breast contour and change in breast thickness.

In this study, we tested two types of breast shape errors. For breast expansion errors, we grew the forward mesh, and thus shifted the nodal optical property locations outwards from the center of the chest wall by 0.5, 1, 2, 5, and 10% while keeping the optode coordinates constant. For breast thickness errors, we increased phantom thickness, i.e., raised z-coordinates of forward nodes from the bottom, by 0.5, 1, 2, 5, and 10%. Accordingly, we adjusted the z-coordinates of all sources to ensure contact with the breast surface.

2.3.3 Signal contamination during data acquisition

We modified results of the forward model in the best-case scenarios to create error cases where NIR light collected at a certain detector location is contaminated by light piping effects (leading to emission beyond the individual fiber locations) or cross-talk between detection channels. If the fluence transmitted from source i to detector j is defined as ${\Phi }_{s_i{d}_j}$, the modified fluence ${\Phi }_{s_i{d}_j}^{\text{'}}$ detected at detector j with contributions from other interfering source-detector (SD) pairs can be defined as:

$$\begin{array}{l}{\Phi }_{s_i{d}_j}^{\text{'}}=\left(1-\epsilon \right)\cdot {\Phi }_{s_i{d}_j}+{\displaystyle {\sum }_{\begin{array}{l}k=1\\ k\ne i\end{array}}^n{w}_{s_k{d}_j}\cdot {\Phi }_{s_k{d}_j}},\\ \hfill {\displaystyle {\sum }_{\begin{array}{l}k=1\\ k\ne i\end{array}}^n{w}_{s_k{d}_j}=\epsilon },\hfill \end{array}$$ (2)

where, n is the total number of sources, $w_{s_k{d}_j}$ is the weight function of each interfering SD pair s_kd_j, which adds up to ε for all contributing pairs. We chose ε levels of 0.1, 0.5, 1, 2, and 5‰ for this study. To simulate cross-talk, we assumed equal chances of signal leakage across channels. Therefore, the weight function can be defined simply as:

$$w_{s_k{d}_j}=\epsilon /(n-1),$$ (3)

In the case of light piping, however, we assumed sources that are located closer to source i have larger contributions. Therefore, the weight function used for the light piping scenario is:

$$w_{s_k{d}_j}=\epsilon \cdot \frac{1}{{\Vert r_{s_i}-r_{s_k}\Vert }^2}/{\displaystyle {\sum }_{\begin{array}{l}k=1\\ k\ne i\end{array}}^n\frac{1}{{\Vert r_{s_i}-r_{s_k}\Vert }^2}}.$$ (4)

where, $\Vert r_{s_i}-r_{s_k}\Vert$ is the Euclidean distance between source i and k. As shown in Eq. (4), the weight function is inversely proportional to the square of the distance between the source in question and others.

2.4 Quantification of the accuracy of reconstructed optical images

To quantify the overall accuracy of reconstructed optical images, optical properties assigned on the fine forward mesh were interpolated onto the coarse reconstruction mesh. Then, the root-mean-square errors (RMSEs) between the assigned and recovered nodal HbT were calculated. HbT RMSEs were used to compare degrees of overall image deterioration among different types and various levels of experimental errors. Of note, while we report sample reconstructions of scattering maps, we have focused our analysis on the recovery of HbT.

To quantify the accuracy of recovered lesion properties as well as lesion contrast, we defined a 1-cm diameter sphere around the lesion centroid as the lesion region-of-interest (ROI), or Ω_t. The surrounding normal tissue ROI, Ω_n, was defined as a spheroid of 4-cm diameter in the x-y plane and 3-cm in z centered at the lesion centroid with a 3-cm diameter spherical void space to separate it from Ω_t. Note that the 2-cm extended chest wall region and surface regions within 5 mm from each plate were excluded in Ω_t and Ω_n. We interpolated the nodal optical properties on the reconstruction mesh into a 1 mm×1 mm×1 mm 3D grid. HbTt and HbTn, mean values of HbT on the grid in tumor and normal tissue ROIs, respectively, were calculated. Then, the ratio of HbTt to HbTn was defined as lesion contrast (R). The shapes and dimensions of Ω_t and Ω_n were chosen to allow us to maintain consistent ROIs and commensurate numbers of optical property values on the 3D grid in all five cases.

3. Results

3.1 Comparisons of the best-case scenarios between five breast phantom cases

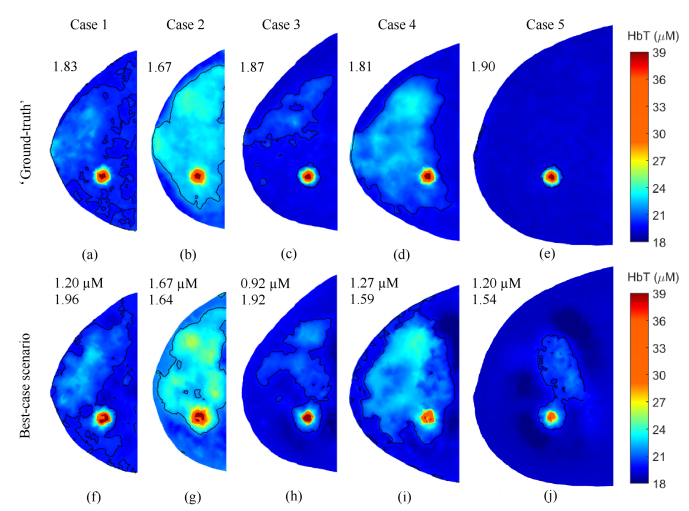
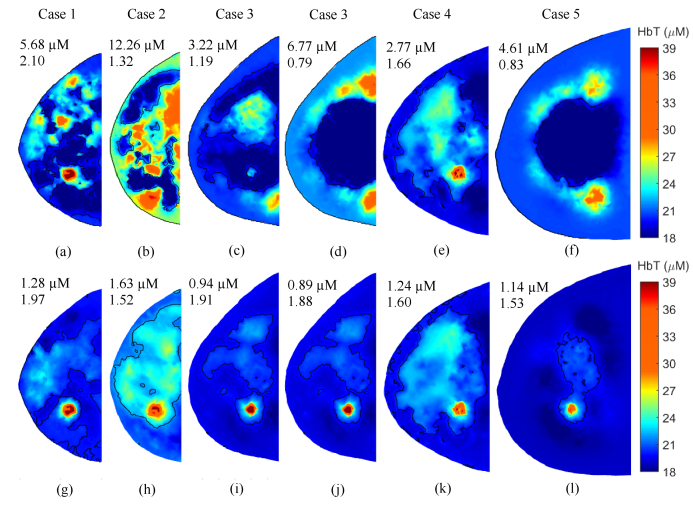
Under the best-case scenarios with no experimental errors added, we recovered the HbT images for all five breast phantoms using no structural prior, two-composition-prior, and three-composition-prior approaches. Figure 3 shows the ‘ground-truth’ reference HbT images, i.e., those calculated directly from the input optical properties used to generate the raw optical data, and reconstructed HbT images guided by three-composition-prior. The other two methods yielded similar images (not shown), but with limited accuracy within breast regions outside the optode coverage area and with underestimation of lesion HbT as seen in Table 3, which summarizes the RMSEs, lesion HbT values (HbTt) and lesion contrasts (R) under the best-case scenarios for all five cases using three reconstruction methods.

Fig. 3.

(a-e) ‘Ground-truth’ reference HbT images, and (f-j) HbT images recovered using three-composition-prior under the best-case scenarios for all five cases. Black contour lines mark out regions where HbT > 20 µM in all cases except Case 2, the densest case, where HbT > 22 µM were used to draw the contour line. RMSE of HbT and tumor contrast R are shown in the upper left corner of each plot (R only for ground truth). All images are extracted from the z-slice that crosses the lesion center.

Table 3. Reconstruction statistics of the best-case scenarios for each breast phantom case.

		Case 1	Case 2	Case 3	Case 4	Case 5
RMSE of HbT (µM)	no prior	1.32	1.99	1.19	1.53	1.28
	2-comp. prior	1.19	1.72	1.07	1.32	1.27
	3-comp. prior	1.20	1.67	0.92	1.27	1.20
HbT in the lesion ROI, HbTt (µM)	ground truth	37.10	38.18	36.72	37.47	36.62
	no prior	31.50	30.41	25.25	26.06	23.12
	2-comp. prior	31.69	30.16	25.10	26.09	23.06
	3-comp. prior	38.70	37.86	38.54	33.78	30.67
Lesion contrast, R	ground truth	1.83	1.67	1.87	1.81	1.90
	no prior	1.60	1.31	1.24	1.21	1.15
	2-comp. prior	1.60	1.29	1.23	1.21	1.14
	3-comp. prior	1.96	1.64	1.92	1.59	1.54

3.2 Impacts of error types and severities on recovered tumor contrasts

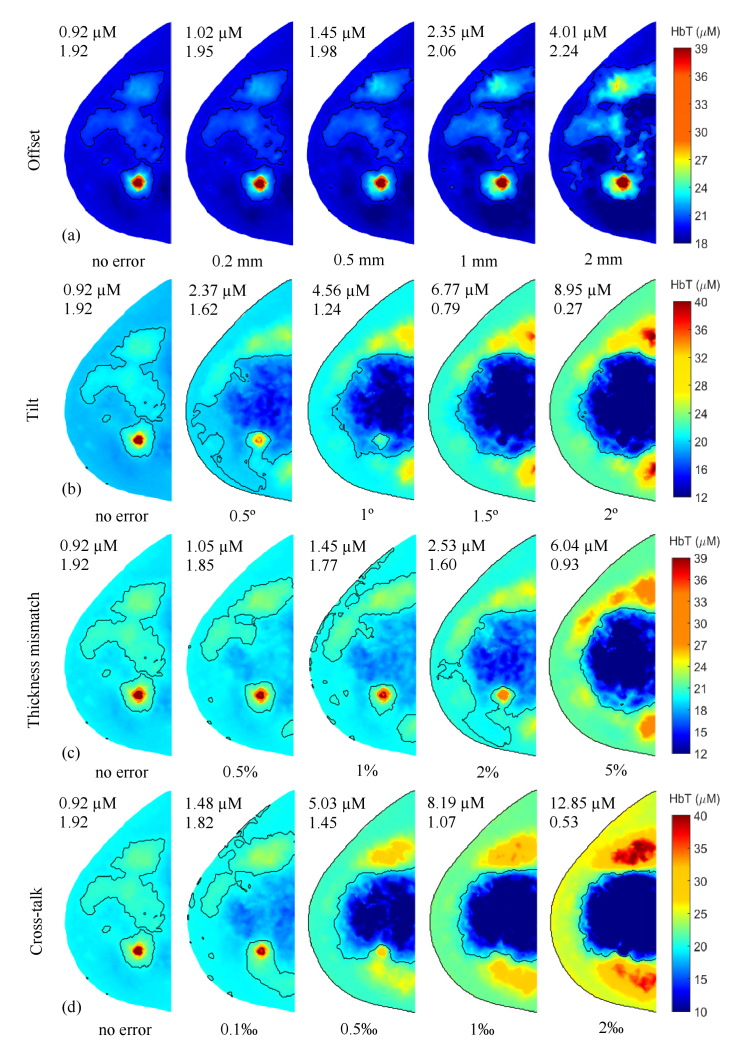
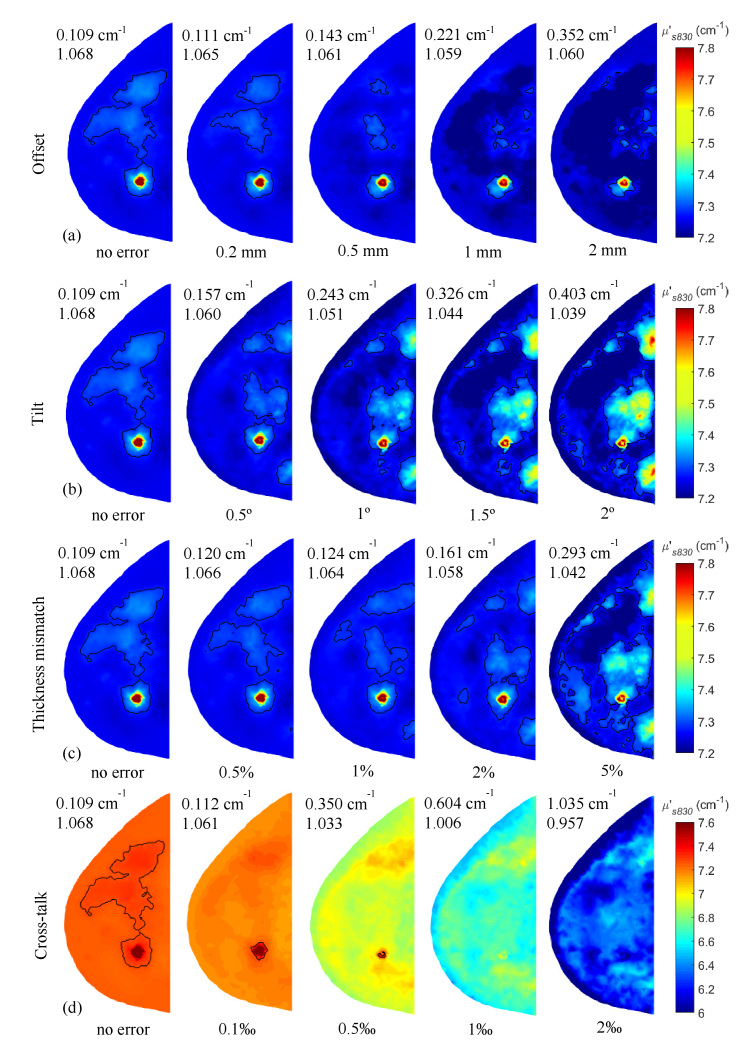
Due to space limitations, in Fig. 4 , we showcase the recovered three-composition-prior guided HbT images only for Case 3, under four representative and commonly seen experimental errors, namely, translational offset along the x-axis, source plate N-C tilt, breast thickness mismatch, and cross-talk between signal channels. The unmodified best-case-scenario images are plotted on the far left in each row alongside error-bearing results at four error-severity levels with the color map adjusted to suit for each error type. Figure 5 demonstrates simultaneously reconstructed reduced scattering coefficients at the 830-nm wavelength (µ_s'₈₃₀) for the same error types and levels as shown in Fig. 4. Similar trends in µ_s'₆₉₀ images are expected since µ_s' at 690 nm and 830 nm are calculated from the same amplitude and power components of a power law fit obtained from the Redbird reconstruction of reduced scattering.

Fig. 4.

HbT images recovered using three-composition-prior for Case 3 under four experimental errors. Rows from top to bottom represent error types of (a) translational offset along the x-axis, (b) source plate N-C tilt, (c) breast thickness mismatch, and (d) cross-talk between signal channels. All images are extracted from the z-slice that crosses the lesion center. RMSE of HbT and recovered tumor contrast R are shown in the upper left corner of each plot. Black contour lines mark out regions where HbT > 20 µM.

Fig. 5.

Images of reduced scattering coefficients at 830 nm (µ_s'₈₃₀) recovered using three-composition-prior for Case 3 under the same four experimental errors as shown in Fig. 4. Rows from top to bottom represent error types of (a) translational offset along the x-axis, (b) source plate N-C tilt, (c) breast thickness mismatch, and (d) cross-talk between signal channels. All images are extracted from the z-slice that crosses the lesion center. Black contour lines circle out regions where µ_s'₈₃₀ > 7.28 cm⁻¹ to help visualize progressive changes caused by experimental errors. RMSE of µ_s'₈₃₀ and recovered tumor contrast in µ_s'₈₃₀ are shown in the upper left corner of each plot.

3.3 Tolerance to experimental errors

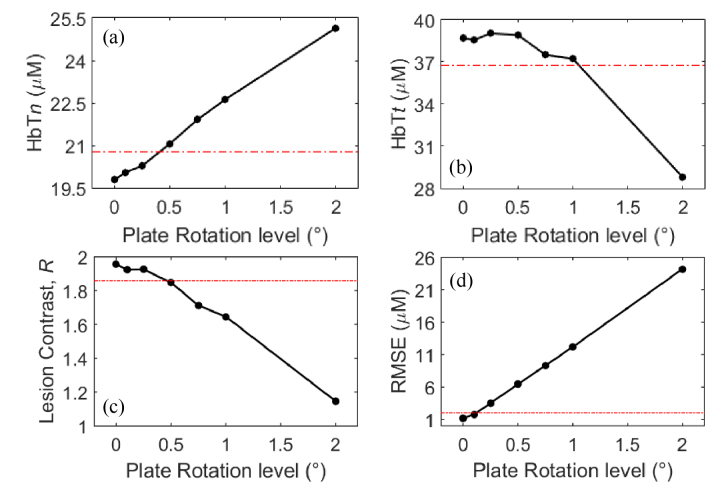
To enable direct comparisons of the influence of experimental errors on all phantom cases using various reconstruction methods, two metrics were introduced to determine the tolerance of recovered optical properties to errors, i.e., the maximum extent of each experimental error at which reconstructed optical images still yield acceptable quality/accuracy. To derive these metrics, we first calculated the overall RMSE, HbTn, HbTt, and R at all severity levels simulated for each error type. It was observed that RMSEs increase monotonically with increasing levels of error, as shown in Fig. 6(d) . To characterize the influence of experimental errors on the overall image quality, tolerance determined by the first metric is defined to be the level at which RMSE equals to 2 µM.

Fig. 6.

Scatter plots of (a) mean HbT in surrounding normal tissue area, HbTn, (b) mean HbT in the lesion ROI, HbTt, (c) lesion contrast, R, and (d) overall RMSE of HbT, versus source plate rotation levels in Case 1. Red dot-dashed lines in (a-c) represents thresholds that equal to 5% deviation from the best-case scenario values (rotation level = 0), and that in (d) represents RMSE = 2 µM.

The second metric was chosen to characterize the influence of experimental errors only within the lesion region and its surrounding area. To this end, tolerance determined by the second metric is defined to be the level at which any value of HbTn, HbTt, or R first deviates 5% from the best-case scenario values. The reason to include absolute HbT values in determining the tumor ROI-specific metric is to ensure lesion contrast R is evaluated on a valid basis. In some error types, e.g. source plate L-R tilt, HbTn and HbTt change in the same direction in progressively deteriorating optical images, which could lead to falsely acceptable contrast values. In the sample case in Fig. 6, the tolerance determined by RMSE metric is 0.12°, and that determined by tumor metric by taking the minimum tolerance among Fig. 6(a)-6(c) is 0.47°. The same approach has been applied to all error types in all phantom cases. Tolerances determined by both metrics in three-composition-prior, two-composition-prior and no-prior guided image reconstructions are summarized in Tables 4–6.

Table 4. Tolerance of HbT images recovered using three-composition-prior guided reconstruction to various experimental errors in all phantom cases.

(a) Metric 1: Overall RMSE ≤ 2 µM
	Case 1	Case 2	Case 3	Case 4	Case 5	Mean	std
Breast thickness (mm)	29.67	43.76	49.89	54.02	59.98	47.46	11.57
Area of breast (cm2)	163.48	142.29	199.06	230.22	358.56	218.72	85.10
Breast density (%)	24.2	54.1	15.1	28.8	6.4	25.7	18.1
Offset in x-direction (mm)	0.26	0.31	0.80	0.86	1.03	0.65	0.35
Source plate rotation (°)	0.12	0.16	0.35	0.34	0.43	0.28	0.13
Source plate L-R tilt (–°)	−0.53	−0.53	−1.18	−1.16	−1.28	-0.94	0.37
Source plate L-R tilt ( + °)	0.56	0.41	1.03	1.19	1.46	0.93	0.44
Source plate N-C tilt (°)	0.13	0.09	0.37	0.44	0.64	0.33	0.23
Breast expansion (%)	0.55	0.62	1.57	1.41	1.78	1.19	0.56
Thickness increase (%)	1.25	0.85	1.51	1.55	2.01	1.43	0.43
Cross-talk (‰)	0.12	0.05	0.16	0.17	0.26	0.15	0.08
Light piping (‰)	0.54	0.40	0.98	1.09	1.88	0.98	0.58
(b) Metric 2: R, HbTt, or HbTn change ≤ 5%
	Case 1	Case 2	Case 3	Case 4	Case 5	Mean	std
Offset in x-direction (mm)	0.65	1.24	0.68	1.69	0.78	1.01	0.45
Source plate rotation (°)	0.47	0.69	1.17	1.24	1.18	0.95	0.35
Source plate L-R tilt (–°)	−0.48	−0.38	−0.30	−0.35	−0.43	-0.39	0.07
Source plate L-R tilt ( + °)	0.49	0.39	0.34	0.37	0.47	0.41	0.06
Source plate N-C tilt (°)	0.19	0.25	0.16	0.26	0.23	0.22	0.04
Breast expansion (%)	1.51	4.26	1.50	1.78	4.13	2.64	1.43
Thickness increase (%)	1.28	0.78	0.48	0.92	0.71	0.83	0.30
Cross-talk (‰)	0.38	0.14	0.07	0.07	0.19	0.17	0.13
Light piping (‰)	0.58	0.42	0.48	0.37	0.87	0.54	0.20

Table 6. Tolerance of HbT images recovered without using structural priors to various experimental errors in all phantom cases.

(a) Metric 1: Overall RMSE ≤ 2 µM
	Case 1	Case 2	Case 3	Case 4	Case 5	Mean	std
Offset in x-direction (mm)	0.25	0.01	0.73	0.71	0.98	0.54	0.39
Source plate rotation (°)	0.11	0.01	0.31	0.27	0.40	0.22	0.16
Source plate L-R tilt (–°)	−0.49	−0.02	−1.16	−0.97	−1.30	-0.79	0.53
Source plate L-R tilt ( + °)	0.56	0.01	1.02	1.02	1.55	0.83	0.58
Source plate N-C tilt (°)	0.11	0.00	0.29	0.28	0.60	0.26	0.23
Breast expansion (%)	0.50	0.02	1.30	1.13	1.66	0.92	0.66
Thickness increase (%)	1.09	0.04	1.28	1.21	1.87	1.10	0.66
Cross-talk (‰)	0.10	0.00	0.13	0.13	0.24	0.12	0.09
Light piping (‰)	0.41	0.11	0.80	0.84	1.71	0.77	0.60
(b) Metric 2: R, HbTt, or HbTn change ≤ 5%
	Case 1	Case 2	Case 3	Case 4	Case 5	Mean	std
Offset in x-direction (mm)	0.77	1.81	1.14	1.79	1.28	1.36	0.44
Source plate rotation (°)	0.38	0.79	1.47	1.72	1.38	1.15	0.55
Source plate L-R tilt (–°)	−0.80	−0.60	−0.57	−0.64	−0.61	-0.64	0.09
Source plate L-R tilt ( + °)	0.88	0.63	0.59	0.68	0.63	0.68	0.12
Source plate N-C tilt (°)	0.51	0.41	0.40	0.42	0.46	0.44	0.05
Breast expansion (%)	4.97	4.19	>10.00*	>10.00*	>10.00*	4.58**	0.55**
Thickness increase (%)	3.36	1.76	1.49	1.39	1.41	1.88	0.84
Cross-talk (‰)	0.32	0.72	0.29	0.19	0.44	0.39	0.20
Light piping (‰)	0.96	1.94	1.16	0.85	1.77	1.34	0.49

^*:Tolerance values are beyond the maximal tested experimental error levels.

^**:Statistics are determined by excluding tolerance values marked by *.

3.4 Regain optical image accuracy by acknowledging experimental errors

Among the three error-type categories, plate positioning errors and breast shape inaccuracies can be taken into consideration during the optical image reconstruction process given the level of errors can be properly estimated during data acquisitions through improved instrumentation and procedures once their presence is suspected. In the top row of Fig. 7 , recovered HbT images with levels of experimental errors well above the tolerance levels in Table 4 are shown for various cases and error types. In the bottom row, HbT images reconstructed from the same error-bearing raw data but with experimental errors acknowledged by using either corrected optode locations or reconstruction meshes with corrected breast shapes are shown. In all cases and error types, HbT RMSEs have been significantly reduced to ± 0.08 µM of their corresponding best-case scenario values in Table 3. Lesion contrasts are also successfully restored to ± 0.04 of best-case scenario values except for the densest Case 2, where R is 0.12 lower than its best-case scenario value of 1.64.

Fig. 7.

Recovered three-composition-prior guided HbT images with (bottom row) and without (top row) accounting for plate positioning errors or breast shape inaccuracies. (a,g) 1 mm translational x-axis offset error in Case 1; (b,h) 2° source plate rotation error in Case 2; (c,i) −2° source plate L-R tilt in Case 3; (d,j) 1.5° source plate N-C tilt in Case 3; (e,k) 5% breast shape expansion in Case 4; (f,l) 5% breast thickness mismatch in Case 5. Colormap is set to be the same as the best-case scenario images shown in Fig. 3 for easy comparison. RMSE of HbT and R are shown in the upper left corner of each plot.

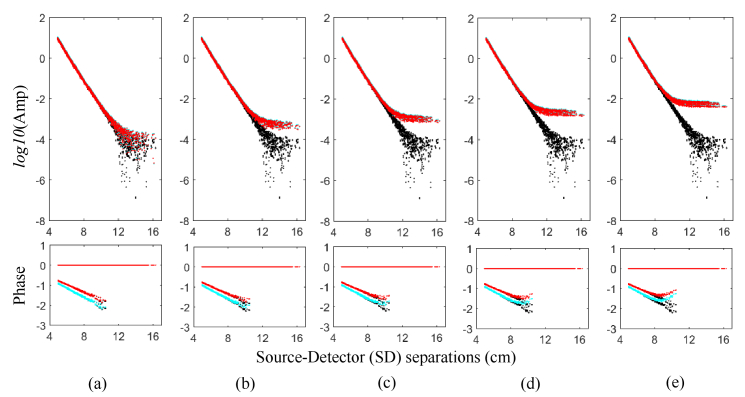
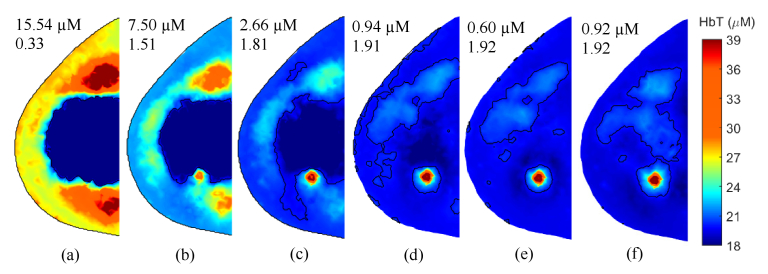
The level of signal contamination caused by cross-talk or light piping, while possible to measure during system characterization, is difficult to correct during image reconstruction. Nevertheless, deterioration of image quality due to such errors can be reasonably managed by pruning the raw measurements used to solve the inverse problem. In this study, the source-detector (SD) separation limits listed in Table 1, i.e., the maximum allowed separation of a SD measurement pair to be included as input for reconstruction, were determined at the SD distance where measured signal hit the noise floor in the best-case scenario. These SD separation limits were kept the same in selecting raw data used for all error cases. However, as shown in Fig. 8 , increasing levels of error result in gradually higher contamination to the raw data. As a result, measurements included in the image reconstruction, e.g., those with SD separations less than 11.7 cm in Case 3, contain considerable contribution from cross-talk, leading to erroneous recovered optical images. Simply by lowering the SD separation limit, the number of significantly contaminated raw measurements used in reconstruction can be reduced. Figure 9 shows HbT images for Case 3 with 5‰ signal cross-talk contamination recovered using various SD separation limit settings.

Fig. 8.

Raw data of Case 3 with (a) 0.1‰, (b) 0.5‰, (c) 1‰, (d) 2‰, and (e) 5‰ contamination by cross-talk overlaid with unmodified raw data. Black dots: unmodified raw data; Cyan dots: error-bearing raw data at 690 nm; Red dots: error-bearing raw data at 830 nm.

Fig. 9.

Reconstructed HbT images of Case 3 guided by three-composition-priors with 5‰ cross-talk contamination in raw data and SD separation limit settings of (a) 11 cm, (b) 10 cm, (c) 9 cm, (d) 8 cm, and (e) 7 cm. (f) The best-case scenario HbT image for comparison.

4. Discussion

From HbT images reconstructed using the three-composition-prior approach in the best-case scenario shown in Fig. 3, the 10-mm diameter lesion is distinguishable from surrounding tissues in all five cases. However, the absolute HbT values, as well as lesion contrasts, clearly decrease with increasing breast thickness. Also, as evidenced in Table 3, when comparing cases with similar thicknesses but dramatically different breast densities, e.g., Case 2 vs. Case 3, the denser case (Case 2) tends to bear more inaccuracy as quantified by RMSE. This indicates that generally it is more difficult to obtain high quality optical images in dense breasts, largely due to lower levels of detected signals caused by stronger tissue absorption.

Moreover, lesion contrasts are also generally lower in denser breasts, making cancer detection in dense breasts more challenging. Nevertheless, by using more advanced image reconstruction methods, especially those with tissue structural guidance, RMSE can be significantly reduced. Lesion contrasts can also be greatly enhanced when concordant lesion centroids are provided as in three-composition-prior guided cases. These observations are consistent with those from other groups [30–32], as well as our own previous studies [21,28].

We simulated 7 commonly encountered experimental errors in a parallel-plate transmission optical breast imaging setting using levels of severity based on our experience with clinical imaging of breast cancer patients and healthy volunteers. Using Case 3 as a representative case, in Figs. 4 and 5, we demonstrated the influence of several typical errors on the recovered HbT images, and the patterns of changes with progressive severity levels. Positioning errors with no influence on the breast shape, such as source plate translational offset shown in Fig. 4(a) and rotation (not shown), tend to have a fairly small impact. Lesion contrasts are largely preserved with a mild progression of erroneous recovery of optical properties with increasing severity levels. In Fig. 4(c), when the phantom thicknesses used to generate simulated optical measurements are slightly bigger than that for reconstruction, absolute HbT values for both the lesion and surrounding normal tissue ROIs decrease systematically with progressive error levels. In the simultaneously recovered reduced scattering coefficient images shown in Fig. 5(c), µ_s'₈₃₀ complement HbT images in the central near-chest wall region, where deviation from the best-case scenario case progresses much faster than the rest of the breast, resulting in increasing tissue attenuations with increasing breast thicknesses as expected. The error type in Fig. 4(b), i.e., source plate N-C tilt, when compared to Figs. 4(a) and 4(c), involves both optodes and breast shape inaccuracy; therefore, leads to faster image deterioration. Moreover, comparing to Figs. 4(c) and 5(c), regions that are closer to the chest wall, i.e., further away from the lateral axis, bear more errors than those near the nipple. Obviously, in error types like tilt, where the influence of experimental errors on the recovered optical properties vary spatially (also evident in Fig. 7(c)), the recovery of lesion contrast is highly dependent on the location of the tumor. In our case, the lesion resides fairly close to the chest wall in Case 3. Therefore, recovered lesion contrast fades away much faster in Fig. 4(b) than in Fig. 4(c), where the influence of breast thickness mismatch is relatively uniform within the entire breast. In the last error type shown in Figs. 4(d) and 5(d), cross-talk between signal channels can cause rather dramatic impacts on both HbT and µ_s'₈₃₀ images that lead to significant quantification errors. As shown later in Fig. 8, the introduction of cross-talk has severely altered the raw data used for optical image reconstruction. It is likely that the bent-up signals toward the longer source-detector separations have led to an underestimation of the overall tissue attenuation, resulting in a set of extremely off-the-chart reduced scattering coefficients images. In the most severe level in Fig. 4(d), high HbT values along the breast contour indicate an overestimate of bulk absorption coefficients as an attempt to counteract the underestimation of scattering in Fig. 5(d).

To generalize our findings on how recovered optical images, and HbT images in particular, respond to various experimental errors, we used two methods illustrated in Fig. 6 to derive quantitative tolerance values. By doing so, we were able to compare tolerances to experimental errors between breast phantom cases, as well as between different error types. Tolerances determined by RMSEs are characteristic to the overall impact of experimental errors on reconstructed optical images, whereas those determined by percentage changes of HbTt, HbTn, and R focus on the capability of successful reconstruction of lesion contrast. In determining lesion-focused tolerances, we also consider the percentage changes of absolute HbT values in the lesion and surrounding normal tissues. This is because in some error types where HbTt deviates in the same direction as HbTn, such as the one shown in Fig. 7(c), changes of R can significantly lag behind changes of absolute HbT values. The selections of the 2 μM threshold for RMSE and 5% change threshold for lesion contrast (R) and HbTs within ROIs are necessarily somewhat subjective; however, the choices are based on the following: (1) Once RMSEs are above 2 μM, recovered optical images appear to deviate far from their respective best-case scenario images and therefore no longer represent reasonably accurate distributions of tissue constituents within the breasts. (2) In order to use HbT as an effective imaging biomarker for the early prediction of neoadjuvant chemotherapy outcome, HbT RMSE errors cannot exceed the difference in changes of HbT between responders and non-responders. From various NIR-DOT therapy monitoring studies [7,9,11], responders have seen 10-30% further decrease of HbT (approximately 4-30 μM due to a wide range of reported baseline HbT) at 1 week to 1 month into therapy vs. non-responders. A threshold that is half the minimum expected effect size is chosen in this study to ensure real-life measurements would have enough power to differentiate responders from non-responders.

Tolerances determined in optical image reconstructions using the three-composition-prior guided approach by the RMSE and tumor metrics are tabulated in Tables 4(a) and 4(b), respectively. There are some similar characteristics shared by both tables. First, in all phantom cases but one, recovered HbT images bear the least tolerance to cross-talk compared to other error types. Unsurprisingly, the mean tolerances for cross-talk error are also the smallest in both tables, indicating cross-talk among signal channels is the most deleterious to optical images and its impact is strong and pervasive in both the entire breast and the specific lesion ROI. Moreover, as expected, source plate L-R tilt shows similar tolerances regardless of tilt directions, i.e., either positive or negative tilts. Finally, compared to the other two error categories, breast shape inaccuracies caused by breast expansion and thickness mismatch tend to only have a localized impact near the boundary on recovered optical properties. Thickness mismatch is the least prone to cause overall RMSE, evidenced by the largest tolerances in all five cases in Table 4(a), and similarly for breast expansion error in Table 4(b). This result suggests that moderate changes of breast shape as seen in compression-induced dynamic DOT or small inaccuracies in plate distance measurements are unlikely to impose serious errors in the reconstructed optical images.

In Table 4(a), some interesting patterns are present among different breast phantom cases. First, the largest tolerances in all error types are observed in Case 5, which is the thickest and least dense phantom case. Second, for all error types except source plate rotation and breast expansion, the smallest tolerances are observed in Case 2, which is the densest phantom case. This is likely due to the challenging nature of optical properties reconstruction in dense breast, where even in the best-case scenario RMSE is 1.67 µM, already close to the 2 µM threshold. Lastly, when Case 2 is excluded, tolerances for each error type increase with increasing phantom thicknesses. By contrast, these patterns are absent in Table 4(b), where tolerances determined by tumor metric are not correlated with either thickness or density.

When comparing tolerances between Tables 4(a) and 4(b), in nearly all phantom cases, positioning errors that influence only the relative positions between optodes and phantom breasts, such as translational offset, source plate in-plane rotation, and breast expansion, have more stringent tolerances determined by overall RMSEs than those determined by lesion characteristics. In Table 4(b), mean tolerances among all phantom cases of these three error types rank the last three places amongst all simulated error types, suggesting they are the least likely to impact the lesion contrast. By contrast, positioning errors that have heterogeneous impact on different parts of the breast phantom, such as tilt of source plate regardless of tilting axis and directions, tend to yield more stringent tolerances determined by lesion characteristics than by overall RMSEs. In Table 4(b), mean tolerances of the three plate tilt error types also take top ranks as expected. It is important to mention here that for these experimental error types, tolerances listed in Table 4(b) are also subjective to the lesion location. It is expected that the tolerances of tilt error types to be smaller when lesions are located further away from the tilt axis. This study is limited to the fixed lesion locations relative to the layouts of optical sources and detectors to enable fair comparisons across all five phantom cases. However, we tested the above location-dependency hypothesis by tilting the source plate about another lateral axis that was much closer to the lesion. As expected, the resulting tolerances (not shown) were significantly larger than those tabulated in Table 4(b).

The same tolerance metrics for HbT images recovered using two-composition-prior guided and no-prior guided approaches are shown in Table 5 and Table 6, respectively. Tolerances determined by RMSEs in no-prior guided reconstructions are generally smaller than those with prior guidance. The same tolerances in two-composition-prior reconstructions are close to, but slightly smaller than, those in three-composition-prior results in all error types and cases. However, for tolerances determined by lesion characteristics, the opposite trend is observed. Tolerances in the three-composition-prior approach are much smaller than those in the other two reconstruction methods. Tolerances in two-composition-prior guided reconstructions resemble, but are generally larger than, those without prior guidance. These observations suggest that by using prior-guided image reconstruction approaches, the overall accuracy of recovered optical images can be improved, therefore resulting in less stringent tolerances determined by RMSEs. Meanwhile, these prior-guided methods, especially the one with a lesion prior, are also more sensitive to errors in the raw data, probably due to the disagreement between assumed tissue spatial distributions and optical data.

Table 5. Tolerance of HbT images recovered using two-composition-prior guided reconstruction to various experimental errors in all phantom cases.

(a) Metric 1: Overall RMSE ≤ 2 µM
	Case 1	Case 2	Case 3	Case 4	Case 5	Mean	std
Offset in x-direction (mm)	0.26	0.28	0.77	0.84	0.99	0.63	0.34
Source plate rotation (°)	0.12	0.14	0.33	0.33	0.41	0.27	0.13
Source plate L-R tilt (–°)	−0.52	−0.49	−1.14	−1.13	−1.25	-0.91	0.37
Source plate L-R tilt ( + °)	0.58	0.36	1.00	1.17	1.41	0.90	0.43
Source plate N-C tilt (°)	0.13	0.08	0.34	0.42	0.63	0.32	0.22
Breast expansion (%)	0.55	0.57	1.45	1.37	1.68	1.12	0.53
Thickness increase (%)	1.22	0.78	1.43	1.51	1.98	1.38	0.44
Cross-talk (‰)	0.12	0.04	0.15	0.16	0.25	0.14	0.08
Light piping (‰)	0.52	0.35	0.92	1.07	1.84	0.94	0.58
(b) Metric 2: R, HbTt, or HbTn change ≤ 5%
	Case 1	Case 2	Case 3	Case 4	Case 5	Mean	std
Offset in x-direction (mm)	0.90	1.75	1.27	1.76	1.22	1.38	0.37
Source plate rotation (°)	0.42	0.79	1.56	1.56	1.34	1.13	0.51
Source plate L-R tilt (–°)	−0.77	−0.66	−0.65	−0.65	−0.64	-0.67	0.05
Source plate L-R tilt ( + °)	0.70	0.69	0.67	0.69	0.67	0.68	0.01
Source plate N-C tilt (°)	0.64	0.39	0.37	0.39	0.44	0.45	0.11
Breast expansion (%)	3.91	4.16	1.91	>10.00*	>10.00*	3.33**	1.23**
Thickness increase (%)	3.56	1.72	1.36	1.33	1.36	1.87	0.96
Cross-talk (‰)	0.70	0.42	0.23	0.17	0.36	0.38	0.21
Light piping (‰)	0.98	1.12	0.98	0.80	1.56	1.09	0.29

In Figs. 7-9, we demonstrated how reconstructed image accuracy and lesion contrast can be recovered by accounting for the encountered experimental errors. As shown in Fig. 7, even when the levels of positioning errors in the simulated measurement data are well above the tolerances shown in Table 4, reconstructed HbT images are quite comparable to the best-case scenario ones. In real measurements, although the exact levels of errors cannot always be accurately gauged and more than one type of error may present at the same time, they usually can be well compensated for by using extra pre-processing steps, such as alignment checks, tilt correction, image transformation and registration [29,33,34]. However, signal contaminations caused by cross-talk and light piping are less well controlled (and in fact sometimes unavoidable due to instrumental limitations) and therefore must be accounted for indirectly. Nevertheless, as shown in Fig. 9, by including raw data selected by limiting the maximum SD separation, recovered HbT images are able to regain accuracy, demonstrating, undoubtedly, the crucial role of clean raw data with minimal noise and contamination in the quality of reconstructed optical images. This result suggests that criteria that are capable of effectively excluding noisy and erroneous raw measurements are needed in DOT image reconstruction.

There are limitations in this simulation study. First, we used a parallel-plate geometry, which is only one of the possible design choices for breast DOT. However, the parallel-plate design has been used by several other standalone and multi-modal imaging systems [3,5,35,36]. One reason for using this design is that the optical images can be easily registered with mammographic images, the most prevalent tool for the diagnosis of breast cancer, to facilitate more straightforward interpretation. Also, the parallel-plate design offers a simple compression scheme to introduce external pressure onto the breast to obtain dynamic tumor contrast from the time courses of optical images [37]. Nevertheless, we hope this work offers an informative estimation of the amount of deviations in recovered tissue properties from the real values for at least one typical optical breast imaging approach. It would be equally important in other experimental settings to compensate for errors that are similar to the ones investigated in this study to obtain reliable optical images. Another limitation of this study is that we focused mainly on HbT images, especially in developing tolerance metrics shown in Fig. 6 and Table 4. Although other optical biomarkers, e.g., tissue oxygenation (StO₂ = HbO /HbT) and scattering (µ_s'), have been investigated, HbT is by far the best established and most widely accepted one [38]. Moreover, µ_s' and HbT images are often correlated because red blood cells, the carrier of the dominant optical absorber, i.e., hemoglobin, are also a major source of endogenous scattering in human breast tissues in the NIR spectral range [39]. Lastly, we studied the impact of experimental errors using a unifocal lesion with one level of contrast and a fixed centroid in the z direction. In the clinic, multifocal and multicentric lesions exist, but rare, representing approximately 6-8% of all breast cancer cases [40]. The unifocal tumor profile, though not comprehensive, is more representative for breast cancer cases usually encountered in clinical studies using optical imaging. To provide a fair comparison across all phantom cases, we also fixed all tumors in the same xy-plane location and a z-location equidistant between the source and detector plates. However, we observed increasing quantification errors, especially in tumor characteristics, for lesions located closer to the surface of the breast (results not shown). This is mostly because parallel-plate transmission DOT typically suffers more significant reconstruction artifacts near the source and detector planes. Nevertheless, tolerances determined by RMSE metric were insensitive to tumor z-location, and those determined by tumor metric generally followed the same patterns as described earlier. With respect to the chosen lesion contrast, although malignant and benign lesions have different levels of optical contrasts, we anticipate the impact of experimental errors on recovered optical images are not driven primarily by the level of contrast. Therefore, key findings of our study are not expected to be compromised by using different tumor contrasts. A thorough investigation could be of future interest.

Despite these limitations, this work presents a systematic simulation study to investigate the impact of some commonly encountered experimental errors in NIR optical imaging. The results of this work can provide a useful basis for quantitative estimations of the reliability of recovered optical images. Our results can be of value during the optical system development for novel designs to ensure that potential experimental errors are below the tolerance levels determined in this work. Finally, as demonstrated in this work, proactive pre-processing of raw optical measurements and the prior-guided image reconstruction approach is effective in reducing the impact of experimental errors on optical images.

5. Conclusions

We performed a simulation study on five digital breast phantoms for estimating the impact of various experimental errors on reconstructing optical properties represented by HbT and tumor characteristics. While slight in-plane probe misalignment and plate rotation did not result in large quantification errors, out-of-plane probe tilting that is not accounted for can result in significant deterioration in lesion contrast. Among all error types investigated in this work, optical images are the least likely to be impacted by breast shape inaccuracies, but suffer from the most deterioration by the cross-talk between signal channels. However, errors in optical images can be effectively controlled when experimental errors are properly estimated and accounted for in image processing procedure. Finally, optical images recovered using structural priors were in general less susceptible to experimental errors; however, lesion contrasts were more sensitive to errors when tumor locations were used as a priori info. These results can offer guidance in designing robust optical imaging systems, help us identify the sources of error in reconstructed DOT images and provide us with a set of guidelines to determine the reliability of optical images, which is essential for adopting DOT in differential diagnosis of malignant vs. benign lesions and in longitudinal clinical studies to monitor the effectiveness of breast cancer treatment therapy.

Funding

NIH (NIBIB) R00EB011889 (SAC), NIH (NCI) R01CA142575 (BD, QF, SAC), NIH (NCI) R01CA187595 (BD, QF, SAC), R01CA204443 (QF, SAC), MLSC Cooperative Grant (BD, ML, QF).

Disclosures

The authors declare that there are no conflicts of interest related to this article.