Background field removal using a region adaptive kernel for quantitative susceptibility mapping of human brain

Abstract

Background field removal is an important MR phase preprocessing step for quantitative susceptibility mapping (QSM). It separates the local field induced by tissue magnetic susceptibility sources from the background field generated by sources outside a region of interest, e.g. brain, such as air-tissue interface. In the vicinity of air-tissue boundary, e.g. skull and paranasal sinuses, where large susceptibility variations exist, present background field removal methods are usually insufficient and these regions often need to be excluded by brain mask erosion at the expense of losing information of local field and thus susceptibility measures in these regions. In this paper, we propose an extension to the variable-kernel sophisticated harmonic artifact reduction for phase data (V-SHARP) background field removal method using a region adaptive kernel (R-SHARP), in which a scalable spherical Gaussian kernel (SGK) is employed with its kernel radius and weights adjustable according to an energy “functional” reflecting the magnitude of field variation. Such an energy functional is defined in terms of a contour and two fitting functions incorporating regularization terms, from which a curve evolution model in level set formation is derived for energy minimization. We utilize it to detect regions of with a large field gradient caused by strong susceptibility variation. In such regions, the SGK will have a small radius and high weight at the sphere center in a manner adaptive to the voxel energy of the field perturbation. Using the proposed method, the background field generated from external sources can be effectively removed to get a more accurate estimation of the local field and thus of the QSM dipole inversion to map local tissue susceptibility sources. Numerical simulation, phantom and in vivo human brain data demonstrate improved performance of R-SHARP compared to V-SHARP and RESHARP (regularization enabled SHARP) methods, even when the whole paranasal sinus regions are preserved in the brain mask. Shadow artifacts due to strong susceptibility variations in the derived QSM maps could also be largely eliminated using the R-SHARP method, leading to more accurate QSM reconstruction.

1. Introduction

Tissue magnetic susceptibility is an intrinsic tissue property that is known to be closely related to its concentration of iron, myelin and calcification [1,2]. Several neurodegenerative disorders, such as Alzheimer’s disease, Parkinson’s disease, and Huntington’s disease have been found to be associated with increased brain iron accumulations [2–5]. If tissue susceptibility changes, such as those induced by local brain iron deposition or myelin loss [6], can be estimated accurately, they may serve as a potential biomarker for clinical diagnosis of these diseases. Recent developments in quantitative susceptibility mapping (QSM) have made it possible to obtain high-resolution susceptibility maps [7] by solving the field to source inverse problem using MR phase commonly acquired using a gradient echo (GRE) sequence, which is a sensitive measure of magnetic susceptibility induced field perturbation [8–13]. However, the field perturbation inside certain volume of interest (VOI), e.g. inside the brain, is composed both of local fields generated from local tissue susceptibility sources and an overwhelming background field generated from sources outside the VOI, usually from the static magnetic field or the air-tissue interface, where large susceptibility variations exist [9,14,15]. The background field extends deeply into the VOI and needs to be correctly removed to get an accurate estimation of the local field, which is used in the QSM dipole inversion to map local tissue susceptibility sources. Any residual background field will propagate into the following susceptibility reconstruction, leading to errors or artifacts in the final QSM maps. This is especially problematic over regions with large susceptibility gradients, e.g. the outer cortical regions and paranasal sinus regions.

Several background field removal methods have been proposed and great progress has been achieved in recent years [8,10,16–22]. The projection onto dipole field (PDF) method [16] exploits dipole field functions to estimate the background field on the assumption that background field and local field are orthogonal in the VOI. In the Laplacian-based methods [17], e.g. the sophisticated harmonic artifact reduction for phase data (SHARP) method [8], the background field is removed using a spherical mean value (SMV) function according to its harmonic features [23,24]. In the original SHARP method, a constant radius was used in the SMV convolution kernel and fairly large erosion has to be used in the brain tissue mask. In the improved variable-kernel (V-SHARP) method a varying SMV kernel size is used to balance between preserving the VOI boundary and reducing the phase error [9]. Another improved SHARP method known as RESHARP uses Tikhonov regularization at the deconvolution stage and can be extended with variable kernel [18,21]. Yet an SMV with equal weights does not perform well in estimating the local field for voxels with high field gradients [19,25]. The Laplacian boundary value (LBV) method was proposed to remove the background field by solving the boundary value problems of Laplace’s or Poisson’s equation to retain data near the boundary [20]. However, in most studies, brain regions around the paranasal sinuses are usually excluded due to insufficient background field removal [2,16,18]. Very recently, the total field inversion method was developed to combine background field removal and susceptibility dipole inversion into a single framework [26]. Although the reconstruction quality is comparable to the two-step QSM reconstruction methods, the algorithm implementation needs additional calculation of a ${\mathrm{T}}_2^{\ast }$ map, which won’t be available in single echo acquisition.

In this paper, we propose an improved V-SHARP background field removal method by constructing a region adaptive spherical Gaussian kernel (SGK), which can achieve more accurate local field estimation as well as preserve the tissue structures around the skull and air-filled sinuses. The SGK in this region-adaptive-kernel SHARP (R-SHARP) approach is designed as a scalable 3D Gaussian kernel whose kernel weights are adaptive to the energy functional of the field map. Around the air-tissue boundary or over strong field variation areas, the SGK will have large kernel weights at the sphere center, while the surrounding weights reduce to zero rapidly. Using such an adaptive SGK, field biases resulting from sources outside the VOI can be effectively suppressed, leading to less residual error in the estimated local field map. In addition, residual background fields around regions of large susceptibility variations usually yield significant shadow artifacts in QSM reconstruction. Therefore, susceptibility maps reconstructed with different local field estimations were used to further evaluate the background field removal performance. For single-orientation QSM, we used our recently developed Structural Feature based Collaborative Reconstruction (SFCR) method [9] and compared the results to the gold standard multiple orientation COSMOS method [27,28].

2. Methods

In this section, after giving a brief review of background field removal methods based on the Laplacian equation, we introduce the theory of fitting energy functionals and our proposed background field removal method. For reference, a functional is a function from a vector space into its underlying field of scalars.

2.1. Laplacian equation based background field removal

For a static magnetic field B₀ in z-direction, the induced field perturbation can be represented as the convolution of a unit magnetic dipole with the susceptibility distribution [29], which is formulated as

$$B^{\mathrm{\Delta }}=\frac{1}{4\pi }|B_0|{\displaystyle \int \chi ({\mathit{r}}^{\prime })d(\mathit{r}-{\mathit{r}}^{\prime })d^3{\mathit{r}}^{\prime }}$$ (1)

where B^Δ = B(r) − |B₀| denotes the z-component of the perturbed magnetic field, and r is the dipole vector. The unit dipole is defined as d(r) = (3 cos² θ − 1)/|r|³, with θ denoting the angle between B₀ and r. The perturbation field B^Δ in the VOI can be decomposed into the contributions of the local field B_loc and the background field B_bkg [18,20] as

$$B^{\mathrm{\Delta }}=B_{\mathit{loc}}+B_{\mathit{bkg}}$$ (2)

Since B_loc is induced by sources inside the VOI, it is not harmonic throughout the VOI. However, B_bkg results from sources outside the VOI and is harmonic throughout the entire VOI and satisfies the Laplacian equation, i.e. ΔB_bkg = 0, with the 3D Laplacian operator $\mathrm{\Delta }={\partial }_x^2+{\partial }_y^2+{\partial }_z^2$ . Using this assumption, B_loc can be obtained by solving the partial differential equation ΔB^Δ = ΔB_loc with appropri ate boundary conditions [20]. In addition, using the harmonic mean value theorem from the SHARP method [7], we can introduce an interim variable B_inter as

$$B_{\mathit{inter}}=B^{\mathrm{\Delta }}-\rho \otimes B^{\mathrm{\Delta }}=B_{\mathit{loc}}-\rho \otimes B_{\mathit{loc}}$$ (3)

where ρ is a nonnegative, radially symmetric, normalized convolution kernel and the symbol ⊗ denotes the 3D convolution operator. Rewriting Eq. (3) with the Dirac function, we have B_inter = (δ − ρ) ⊗ B_loc, which then leads to

$$B_{\mathit{loc}}=(\delta -\mathrm{\rho }){\otimes }^{-1}{B}_{\mathit{inter}}$$ (4)

Note here that B_loc can be estimated by deconvolution (⊗⁻¹) in Fourier space. One limitation of the original SHARP method is that reliable estimation of B_inter requires several imaging voxels around the brain to be eroded depending on the radius of the spherical mean value filtering kernel, and brain areas around skull and sinus air are usually removed [24]. In addition, for voxels located close to air-tissue boundaries, extra brain mask erosion may be needed to compensate for the large field gradients. Any residual background field that is not sufficiently removed may lead to strong shadow artifacts in the subsequent susceptibility map reconstruction. However, according to the mean value theorem of harmonic functions, the B_loc can be preserved under convolution transform with any nonnegative, radially symmetric, normalized (total integral equals one) function. Therefore, we propose to use a scalable SGK adaptive to a certain voxel energy functional reflecting magnitude of field variation for more accurate estimation of the local field with better preservation of the brain areas around the air-tissue interface.

2.2. Fitting the energy functional into a level set formulation

In order to overcome the difficulties caused by intensity inhomogeneities in image segmentation, Li et al. proposed a region-based active contour model that draws upon intensity information in local regions at a controllable scale [30–32]. A data fitting energy is defined in terms of a contour plus two fitting functions that locally approximate the image intensities on the two sides of the contour. This energy is then incorporated into a variational level set formulation with a level set regularization term, from which a curve evolution equation is derived for energy minimization. Due to a kernel function in the data fitting term, intensity information in local regions is extracted to guide the motion of the contour, which thereby enables the model to cope with intensity inhomogeneity. This method was originally proposed for segmentation of images with intensity inhomogeneity, so we here use it to extract the field inhomogeneity information arising from variations in object susceptibility.

Considering the topological changes, the energy functional is converted to a level set formulation using the level set function Ψ, taking positive and negative values outside and inside the closed contour L corresponding to the image subdomains R₁ and R₂, respectively. The optimal fitting functions are two weighted intensity averages of local intensities on the two sides of the contour, dominated by image intensities in the neighborhood of x.

$$f_i(\mathit{x})=\frac{K_s(\mathit{x})\ast [M_i(\mathrm{\Psi })I(\mathit{x})]}{K_s(\mathit{x})\ast M_i(\mathrm{\Psi })},i=1,2$$ (5)

where I(x) is the unwrapped phase image. The size of the Gaussian kernel $K_s(\mathit{x})=\frac{1}{{(2\pi )}^{1/2}s}\exp (-|\mathit{x}{|}^2/2s^2)$ is proportional to the scale parameter s. Its region-scalability is due to a scale parameter, which allows the use of intensity information in regions at a controllable scale, from small neighborhoods to the entire domain. The operators M₁(Ψ) = H(Ψ) and M₂(Ψ) = 1 − H(Ψ) relate to the Heaviside function H(Ψ), which is approximated by a smooth function as $H(\mathrm{\Psi })=\frac{1}{2}\left(1+\frac{2}{\pi }\mathit{arctan}\left(\frac{\mathrm{\Psi }}{\epsilon }\right)\right)$.

The energy functional, also called the region-scalable fitting (RSF) energy, is defined in terms of a contour and two fitting functions that locally approximate the image intensities on the two sides of the contour

$$E_{\mathit{RSF}}(\mathrm{\Psi },f_1(\mathit{x}),f_2(\mathit{x}))={\displaystyle \sum _{i=1}^2{\alpha }_i{\displaystyle {\int }_{R_i}{K}_s(\mathit{x}-\mathit{y})|I(\mathit{y})-f_i(\mathit{x}){|}^2{M}_i(\mathrm{\Psi }(\mathit{y}))d\mathit{y}}}$$ (6)

where α_i is positive constant, and R_i the image subdomain. The Gaussian kernel K_s(x − y) is inversely proportional to the coordinate distance between pixels y and x with a scale parameter s, set to be s = 5 [27]. This energy is then incorporated into a variational level set formulation with a level set regularization term. Thus, the energy functional at point x is expressed as

$$E_{\mathit{RSF}}^{\ast }=\mathit{argmi}{n}_{\mathrm{\Psi }}{E}_{\mathit{RSF}}(\mathrm{\Psi },f_1(\mathit{x}),f_2(\mathit{x}))+\nu L(\mathrm{\Psi }(\mathit{x}))+\mu P(\mathrm{\Psi }(\mathit{x}))$$ (7)

The level set regularization term $L(\mathrm{\Psi })={\displaystyle {\int }_{R_1}|\nabla H(\mathrm{\Psi }(\mathit{x},\mathit{y}))|d\mathit{x}d\mathit{y}}$ is introduced to smooth the contour by penalizing its length, where ∇ is the gradient operator. The other term $P(\mathrm{\Psi })=\frac{1}{2}{\displaystyle \int {\left(|\nabla \mathrm{\Psi }(\mathit{x})|-1\right)}^{2}d\mathit{x}}$ is to preserve the regularity of the level set function from a signed distance function.

To minimize this energy functional with respect to the level set function, the standard gradient descent method is used by solving the gradient flow equation with evolution step t as follows

$$\frac{\partial \mathrm{\Psi }}{\partial t}=-\delta {\displaystyle \sum _{i=1,2}{\alpha }_i}{\displaystyle \int K_s(\mathit{x}-\mathit{y})|I(\mathit{y})-f_i(\mathit{x}){|}^{2}dy+\upsilon \delta di\nu \left(\frac{\nabla \mathrm{\Psi }}{|\nabla \mathrm{\Psi }|}\right)}+\mu \left({\nabla }^2\mathrm{\Psi }-di\nu \left(\frac{\nabla \mathrm{\Psi }}{|\nabla \mathrm{\Psi }|}\right)\right)$$ (8)

where υ and μ are regularization parameters, and div represents divergence operator. The Dirac function Δ is equal to the derivative of H(Ψ). The evolution step t and scale parameter s are empirically set as 0.1 and 5.0, respectively. Given a center point x, the fitting energy can be minimized when the contour L is exactly on the object boundary and the fitting values f₁ and f₂ optimally approximate the local image intensity in the normalized phase image in R₁ and R₂. At that time, the level set values are relevant to the energy functional E_RSF as stated in Eqs. (6) and (8), proportional to the field inhomogeneous degrees. This allows us to distinguish tissue susceptibility variations and to exploit them to design a region adaptive SGK for background field removal. Since the sign of level set just represents outside and inside the closed contour L but does not reflect the definite values, we hereafter take the absolute value of Ψ as shown in Fig. 1 rendered in colormap.

Fig. 1.

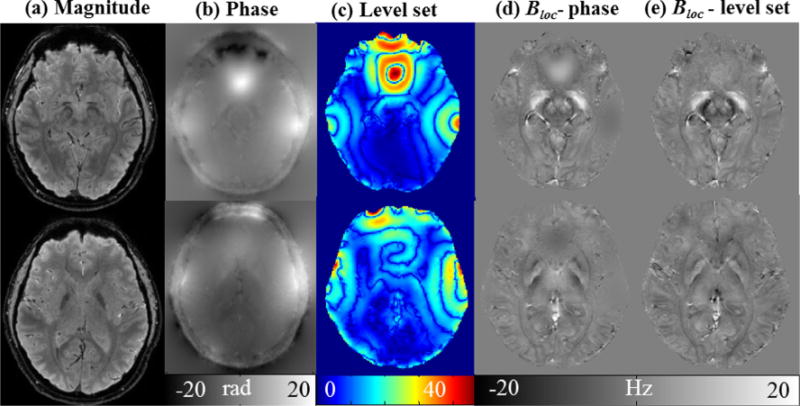
Comparison of anatomical structures in different images. (a) Magnitude images, (b) unwrapped phase images, (c) level set value of (b), (d) local field estimated with R-SHARP using phase directly, (e) local field estimated with R-SHARP using level set values.

2.3. Background field removal using R-SHARP

At the air-tissue boundaries, the background field variation is much larger than the local field variation, which may cause inaccurate local field estimation and often an eroded brain mask has to be used during the background field removal. We aim to improve the local field estimation in these regions by adopting a SGK of smaller spatial scale. Our proposed background field removal method is based on a scalable SGK that is a nonnegative and radially symmetric function. For any voxel (X,Y,Z), the kernel scale is defined related to the energy functional of the phase image as

$${\rho }_{\mathit{SGK}}(x,y,z)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{x^2+y^2+z^2}{2{\sigma }^2}\right)$$ (9)

where (x,y,z) denotes the point coordinate in the kernel function. The scale parameter σ is inversely proportional to the voxel value in the level set function Ψ obtained by Eq. (8)

$$\sigma (X,Y,Z)=r{\mathrm{\Psi }}_0(Z)/C\mathrm{\Psi }(X,Y,Z)$$ (10)

where r is the kernel radius initialized to be 6 voxels, and the radius will decrease to 1 voxel as the voxel approaching to the brain skull boundary to protect the tissue integrity, i.e. the kernel radius is assigned to be 1 for the voxels right on the boundaries. The level set mean of the Zth slice is calculated by ${\mathrm{\Psi }}_0(Z)=\frac{1}{NM}{\displaystyle {\sum }_{X=1}^N{\displaystyle {\sum }_{Y=1}^M\mathrm{\Psi }(X,Y,Z)}}$, with the slice resolution N × M. The parameter C is an adjustment constant to control the relationship between the ratio Ψ₀(Z)/Ψ(X, Y, Z) and the scale parameter σ. Since C is inversely proportional to σ, a decreasing C will make the exponential function decay more sensitive to ratio Ψ₀(Z)/Ψ(X, Y, Z). We determined C using the parameter sweeping in the range of 0.6–2.2 as shown in the Results section.

As seen from Eqs. (9) and (10), the adaptive voxel-wise convolution kernel SGK is a function of level set Ψ(X, Y, Z). Since the level set value directly reflects the field inhomogeneity, their Ψ(X, Y, Z) over regions of large susceptibility variation must be larger than the slice mean. Around air-tissue interfaces, the background field is usually much larger than the background field in other brain area. Therefore, the convolution sphere kernel should have a small radius and extremely high center weight that is adaptive to the field inhomogeneous degree. However, for those voxels with a level set function value less than the slice mean Ψ₀(Z), using the SMV kernel gives comparable performance to using the SGK. Considering the computation efficiency, we use the SMV kernel for those voxels in order to save computational time.

Then, the data domain is divided into a field inhomogeneous and a homogeneous subdomain as Ω₁ and Ω₂. Hence, our proposed background field removal algorithm becomes

$$B_{\mathit{inter}}^{\mathrm{\Delta }}(X,Y,Z)=\{\begin{array}{cc}(\delta -{\rho }_{\mathit{SGK}})\otimes B_{\mathit{loc}}(X,Y,Z),& (X,Y,Z)\in {\mathrm{\Omega }}_1=\{\mathrm{\Psi }(X,Y,Z)>{\mathrm{\Psi }}_0(Z)\}\\ (\delta -{\rho }_{\mathit{SMV}})\otimes B_{\mathit{loc}}(X,Y,Z),& (X,Y,Z)\in {\mathrm{\Omega }}_2=\{\mathrm{\Psi }(X,Y,Z)\le {\mathrm{\Psi }}_0(Z)\}\end{array}$$ (11)

The local field can then be calculated by $B_{\mathit{loc}}=(\delta -\rho ){\otimes }^{-1}{B}_{\mathit{inter}}^{\mathrm{\Delta }}$ in Fourier space. We explored the energy functional in the level set formulation to partition the phase data into different subdomains according to the field inhomogeneity. In the regions of large susceptibility variation, such as tissues around the skull and paranasal sinuses, the background field is commonly one or two orders larger than the local field [20]. Our proposed scalable kernel is capable to adjust the kernel radius into a small size, while the kernel weights focus on the sphere center with adjacent weights approaching zero rapidly. Thus, compared to the equal weight SMV kernel as used in SHARP, RESHARP or V-SHARP methods, R-SHARP can have better performance on suppressing the overwhelming background field close to the air-tissue boundary, which can further help reduce shadow artifacts in the subsequence QSM reconstruction.

As for our proposed ρ_SGK, it depends on the relationship between the ratio Ψ₀(Z)/Ψ(X, Y, Z). We can observe in Fig. 1 that the unwrapped phase has lower contrast than the corresponding map of level set function. If the unwrapped phase is directly used as the measure of field inhomogeneity in the background field removal, the adaptive SGK is not able to preserve the local fields over regions of the paranasal sinuses and VOI boundary as shown in Fig. 1d. However, their values of level set function are accumulated to higher levels compared to their phase values, which facilitates us to detect out regions with large susceptibility variations. Another property is that there are significantly clear level grades in the level set function map, which is important in adjusting the kernel weights for different voxels. Therefore, level set processing is actually needed and using the unwrapped phase data itself as a measure of inhomogeneity is not sufficient. We implemented the algorithm as following:

Algorithm Implementation
(1)	Initialize the closed contour L and the parameters α1, α2, υ, μ, δ and Ks in Eq. (8);
(2)	Calculate the level set function Ψ satisfying Eq. (8) for each slice of the unwrapped phase data;
(3)	Create a binary brain mask;
(4)	Initialize the SMV kernel, ρSMV;
(5)	Divide the phase data in the brain mask into two sub-domains Ω1 and Ω2 as in Eq. (11);
(6)	Calculate the adaptive SGKs for the voxels in subdomain Ω1 using Eq. (9);
(7)	Apply SGK to Ω1 and SMV to Ω2 as in Eq. (11);
(8)	Obtain Bloc in Fourier domain, with $B_{\mathit{loc}}=F^{-1}({(F(\delta -\rho ))}^{-1}F(B_{\mathit{inter}}^{\mathrm{\Delta }}))$.

3. Experiments

In the experiments, the local field estimated by R-SHARP is compared to that from V-SHARP [9] and RESHARP [18] with numerical simulation, phantom simulation and in vivo human brain MRI data. To further verify the background field removal performance, we adopted the estimated local field to reconstruct the susceptibility map with the recently developed SFCR method [9], utilizing COSMOS as the standard (calculated from local field estimated by R-SHARP) [27]. Root Mean Square Error (RMSE) and Mean Structure Similarity Index (MSSIM) were chosen to evaluate the accuracy of the susceptibility mapping results. All implementations were carried out in Matlab 2013a, on a personal desktop with Intel (R) CoreTM i7-4790 CPU, 8 GB RAM.

3.1. Numerical simulation

We constructed a numerical simulation model of size 128 × 128 × 64 (Fig. 2), composed of a large ellipsoid and four small spheroids to mimic human brain tissues, i.e. Caudate Nucleus (CN), Globus Pallidus (GP), vein and paranasal sinuses, whose susceptibilities were assigned to be 0 ppm, 0.05 ppm, 0.1 ppm, 0.3 ppm and 9.4 ppm [16]. Gaussian noise was added and the signal to noise ratio (SNR) of the magnitude image was set to be 40. The total field was generated by Eq. (1) in k-space [8], which can be separated into the local field and the background field as shown in Fig. 2. A binary mask was created to take the spheroid of 9.4 ppm and imaging background regions out of the VOI. The level set parameters for R-SHARP were determined to be α₁ = 1, α₂ = 1000, μ = 0.5, ν = 0.65, s = 5, which were empirically tested for a level set function that can well separate the inhomogeneous regions of large field gradients from the homogenous field. The adjustment constant C was chosen to be 1.8 as demonstrated in the Results section. The truncated singular value decomposition (TSVD) threshold was 0.05, which was determined by varying the value over a scale of 0.01 to 0.08 and visually inspecting the resulting local field [8]. The SMV kernel used in RESHARP method was extended to varied radii, and its regularization parameter λ was optimized to be 0.05 employing the parameter sweeping method combined with visual inspection, thereby gaining artifacts suppression without inducing apparent contrast loss [18]. The kernel radius varied from 6 to 1 for all the three methods in comparison. The total computing times were 21.1 s and 8.84 s for V-SHARP and RESHARP, respectively, and about 90.5 s for R-SHARP, in which the energy computation took about 51.5 s. For the susceptibility reconstruction, the SFCR parameters were λ₁ = 50, λ₂ = 2, γ₁ = 500 and γ₂ = 1.

Fig. 2.

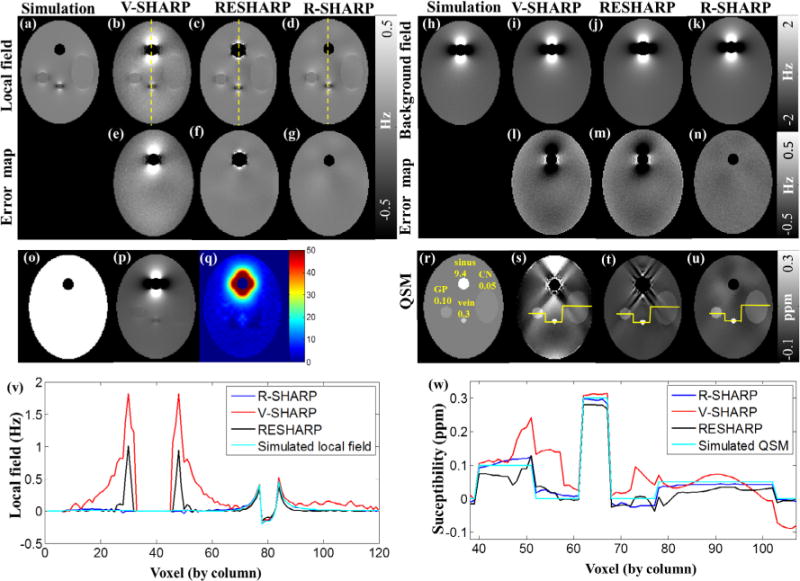
Numerical simulations. (a–g) Local fields of the simulation target input, V-SHARP, RESHARP and R-SHARP and their error maps, (h–n) background fields of the simulation target input, V-SHARP, RESHARP and R-SHARP and their error maps, (o) simulated binary mask, (q) level set function of phase image (p), which is the summation of (a) and (h), (r–u) QSMs derived from the simulated local field (r), V-SHARP(s), RESHARP (t) and R-SHARP (u), (v) local field profiles of the dashed yellow lines in (b–d), (w) susceptibility profiles of the yellow lines in (s–u). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.2. Phantom experiment

A cylindrical water phantom with two vials filled with Gd solution was constructed to gain the total field, and the background field scan was done by scanning the same phantom without the two vials. Phantom data were acquired at the F. M. Kirby Research Center in Kennedy Krieger Institute and Johns Hopkins University, using a multi-echo GRE pulse sequence on a 3.0 T scanner Philips Medical System using 32-channel head coil with field of view 120 × 120 × 120 mm³, voxel size 0.94 × 0.94 × 1.5 mm³, flip angle = 10°, TE/ΔTE/TR = 3/3/35 ms, 10 echoes. The raw phase map was estimated by using Laplacian based phase unwrapping and linear fitting over echo times [33]. The local field used as the gold standard was calculated from the difference between the two scans with and without the Gd vials. We compared R-SHARP method with V-SHARP and modified RESHARP of varied radii, and their parameters were optimized in the similar way to that of the numerical simulation. The TSVD was determined as 0.12 for V-SHARP and R-SHARP, while the regularization parameter λ for RESHARP was 0.004 as illustrated in the results section. The kernel radii were varied from 6 to 1 voxels for all methods. The parameters used for R-SHARP were determined as α₁ = α₂ = 1, μ = 0.5, ν = 0.65, s = 5 and the C value was 1.8. The total computing times were 28.9 s, 18.4 s and 225.7 s for V-SHARP, RESHARP and R-SHARP, respectively.

3.3. In vivo human brain data

The in vivo human brain data were acquired on a healthy male volunteer at the F. M. Kirby Research Center in Kennedy Krieger Institute and Johns Hopkins University, approved by the local Institutional Review Board. The study was performed on a 7T Philips Healthcare MRI scanner equipped with a 32-channel head coil (Novamedical). A three dimensional multi-echo GRE sequence was applied and the imaging parameters include TR = 45 ms, TE1 = 2 ms, ΔTE = 2 ms, 8 echoes. The imaging matrix size was 224 × 224 × 110 with a FOV of 220 mm × 220 mm × 110 mm. The scanning duration for each acquisition was 5:15 min [33]. The volunteer was scanned with the head placed in four different positions, i.e. supine position, tilted to the right shoulder, tilted to the left shoulder and tilted to backwards. The tilting angle for each position varied from 5 to 22 degrees from the main field B₀ axis. The first echo magnitude data acquired at the three tilted positions were coregistered to the first echo magnitude data of the supine position by rigid body linear transformation utilizing the FSL FLIRT tool [34,35]. The coregistration transformation matrix was obtained and applied to the data at every echo time to gain the coregistered magnitude and phase images. Then a Laplacian-based algorithm of phase unwrapping was applied to the coregistrated phase data for unwrapping. The linear fitting of the phase data over echo times was used to estimate the initial phase to preclude voxels with unreliable measurement [8,15,33]. The FSL BET tool was utilized to generate the brain mask using the magnitude image of the supine position with paranasal sinuses preserved in the mask. The susceptibility maps reconstructed by COSMOS were calculated with relative convergence tolerance of 10⁻⁵ using LSQR algorithm.

The parameters used for R-SHARP were determined as α₁ = α₂ = 1, μ = 0.5, ν = 0.65, s = 5, and C = 1.8. The TSVD was 0.12 that was varied from 0.01 to 0.12 in steps of 0.01 along with visual inspection on the resulting local field [8]. The RESHARP was extended to varied kernel radii and the optimal regularization parameter λ was selected as 0.005. The kernel radius varied from 6 to 1 for all the three methods. The total computation times were 90.6 s and 91.7 s for V-SHARP and RESHARP, respectively, and 323.4 s for R-SHARP, of which the energy computation took about 53.4 s. The parameters of SFCR were set to be λ₁ = 50, λ₂ = 2, γ₁ = 1200 and γ₂ = 1. In recent work, the regions of paranasal sinuses have been mostly excluded from QSM by the brain mask, in order to suppress the strong susceptibility artifacts around the air-tissue interface. However, some useful information in its neighborhood may also be precluded. If we can preserve these regions, additional brain tissue information would become available. Thus, we verified our proposed method on the phase data without erosion of the paranasal sinuses.

4. Results

4.1. Numerical simulation

Fig. 2 shows the results of numerical simulations using R-SHARP, RESHARP and V-SHARP. The spheroid of 9.4 ppm is designed to simulate the air-tissue interface over the paranasal sinuses in the human brain, which is excluded from the VOI in the subsequent data processing by the binary mask in Fig. 2o. Taking the advantage of the energy functional, we could detect inhomogeneous fields caused by sharp susceptibility changes, in which local regions over the ellipsoid of 9.4 ppm present high energy in the level set function in Fig. 2q. It can be seen from Fig. 2a–g that the local field obtained by the R-SHARP method is more accurate than that of the V-SHARP and RESHARP, while the V-SHARP and RESHARP results exhibit noticeable residual background fields around the ellipsoid of 9.4 ppm. More details can be seen in the error maps as compared to the true local field and their local field profiles along the dashed yellow lines in Fig. 2v. Similar comparisons can be seen in the estimated background fields for the three methods in Fig. 2h–n.

Susceptibility maps calculated from the local fields estimated by V-SHARP, RESHARP and R-SHARP methods are given in Fig. 2s–u, with profile comparisons shown in Fig. 2w. We see that the susceptibility maps from the V-SHARP and RESHARP methods have severe streaking and shadow artifacts, while the QSM map corresponding to R-SHARP can better recover the structures and their susceptibility values. Table 1 quantitatively evaluates the background field removal of the three methods by comparing susceptibility values of the three spheroids. The susceptibility values derived from R-SHARP are closer to the target simulation data than those from RESHARP and V-SHARP, and have smaller standard deviations. Moreover, the RMSE values of the selected slice are 0.070, 0.174 and 0.011, while the MSSIMs are 0.611, 0.781 and 0.926 for V-SHARP, RESHARP and R-SHARP methods, respectively.

Table 1.

Mean susceptibility values (ppm) of the structures corresponding to the two background field removal methods, in comparison to the target simulated susceptibilities.

Simulation target	V-SHARP	RESHARP	R-SHARP
0.05	0.035 ± 0.025	0.042 ± 0.024	0.041 ± 0.009
0.10	0.139 ± 0.042	0.154 ± 0.043	0.107 ± 0.010
0.30	0.304 ± 0.005	0.308 ± 0.003	0.298 ± 0.007

Note: susceptibility values are in the format of mean ± standard deviation.

In the R-SHARP method, it is necessary to predetermine the optimal value of constant C in Eq. (9), so we tested C in the range of 0.6–2.2 with step 0.2 through the susceptibility reconstruction. In Fig. 3, the accuracy of MSSIM and RMSE is inversely proportional to the C values, tending to be steady with the increasing of C. Meanwhile, streaking artifacts around the simulated sinuses are better suppressed with greater values of C, as pointed by the yellow arrows. However, the accuracy of the susceptibility values of the regions is best at C = 1.8. Hence, we set C to be 1.8 in the simulation experiment.

Fig. 3.

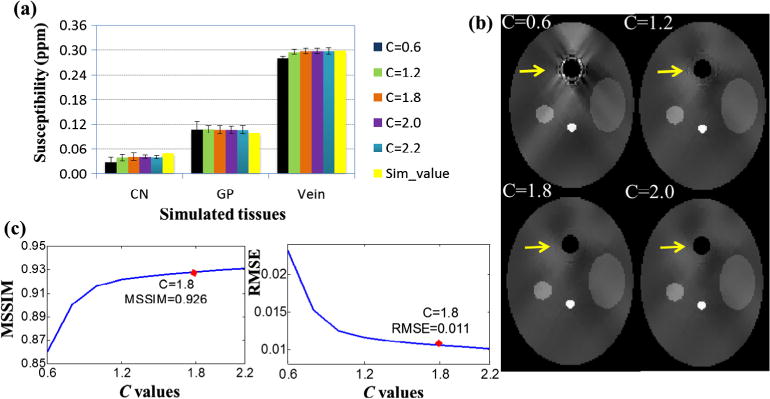
Selection of the optimal C value for adaptive SGK with respect to the susceptibility reconstruction using the simulation data. (a) The mean susceptibilities of simulated tissues for different C values, (b) susceptibility maps corresponding to different C values, (c) MSSIM and RMSE with respect to C values.

4.2. Phantom experiment

Fig. 4 shows the corresponding background fields and local fields calculated from the three methods, whose sums are equal to the known total fields. The error maps denote the difference between the calculated local fields to the “gold standard” local field. In the local field map obtained by V-SHARP, there are obvious shadow artifacts around the air-solution interface above the yellow dashed lines in Fig. 4 and noticeable residual error on the phantom boundary. Compared to V-SHARP, we find that the RESHARP method have good performance on removing background field with less error in the error map, but the strong susceptibility variations still affect its estimation accuracy. However, no obvious artifacts can be observed over the air-solution interface in the local field obtained from R-SHARP method, meanwhile the field values in other regions are closest to the “gold standard” local field map. Due to the strong susceptibility variation between the air and the Gd solution, the local field shows severe artifacts over the air-solution interface in the “gold standard” local field, which makes the local field before 25th slice suspect and excluded from the whole 3D volume in the RMSE accuracy evaluation. The RMSE values are 2.674, 2.167 and 2.155 for V-SHARP, RESHARP and R-SHARP, respectively. Among the three methods, R-SHARP presents the best performance on both the common background field removal and the susceptibility artifacts elimination.

Fig. 4.

Results of phantom experiments. (a) The “gold standard” background field (left) and local field (right) of the Gd phantom, (b) background fields, local fields and error maps of local fields estimated by the three methods.

In Fig. 5, the major parameters TSVD, λ and C used in V-SHARP, RESHARP and R-SHARP are optimized by parameter sweeping method, with the estimated local fields for visual perception. The TSVD values were varied from 0.01 to 0.12 in steps of 0.01, and 0.12 was selected for V-SHARP and R-SHARP as shown in Fig. 5a. The regularization parameter λ for RESHARP was chosen to be 0.004, where the RMSE value was minimal. As for the C value of R-SHARP, it was tested in the range of 0.1 to 2.0 with step 0.1 in Fig. 5c. The RMSE value slightly decreases from 2.18 to 2.15 with an increasing C. We set the global optimum as C = 1.8 when the susceptibility artifacts are almost removed from the field map.

Fig. 5.

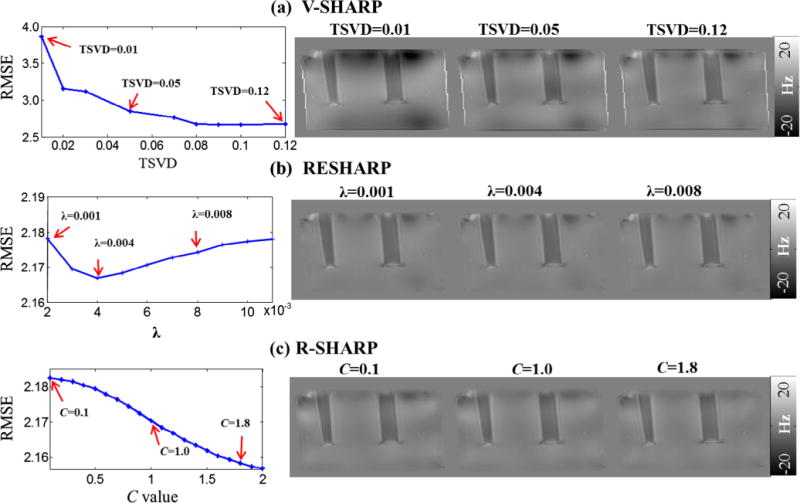
Parameter optimizations for the three methods using parameter sweeping method and corresponding field maps with different values of TSVD (a), regularization parameter λ (b) and adjustment constant C (c).

4.3. In vivo human brain data

As we have discussed the selection of C-value in the numerical simulation and phantom experiment, both turn out to be the best choice of 1.8. Hence, parameter C is also determined to be 1.8 for in vivo human brain. The results of background field removal by R-SHARP, RESHARP and V-SHARP without excluding the brain tissues around the paranasal sinuses are shown in Fig. 6. As shown in Fig. 6a–c, the residual background field in the regions of large susceptibility variations is less using the R-SHARP method. As marked by the yellow rectangles in the three views, we see that the impact of sinuses is so strong that V-SHARP cannot remove the background field completely leading to serious shadow artifacts in the susceptibility maps. In the axial view, no discernible brain tissues can be observed as pointed out by the yellow arrows in Fig. 6e. Although the RESHARP method performs better over the sinuses region than V-SHARP as shown in Fig. 6b, some errors still remain in the estimated local field and cause shadow artifacts in the susceptibility map in Fig. 6f. However, the strong background fields induced by sinuses can be better suppressed by R-SHARP and the fine structures hidden by the artifacts can be better recovered in the corresponding QSM images. In Fig. 6d, the profiles across SN and RN suggest that the results of the R-SHARP method are more accurate than those calculated with the V-SHARP and RESHARP methods using COSMOS as the reference. The RMSE values of the selected slice (23rd slice) in axial views are 0.017, 0.015 and 0.011 for the V-SHARP, RESHARP and R-SHARP methods, respectively. The MSSIM is 0.861 for the R-SHARP and 0.813, 0.775 for V-SHARP and RESHARP. Table 2 shows the mean susceptibility values of red nucleus (RN), substantia nigra (SN), caudate nucleus (CN), Globus Pallidus (GP) and Putamen (PU), in which susceptibility values calculated using R-SHARP are closest to those estimated from COSMOS in the three methods.

Fig. 6.

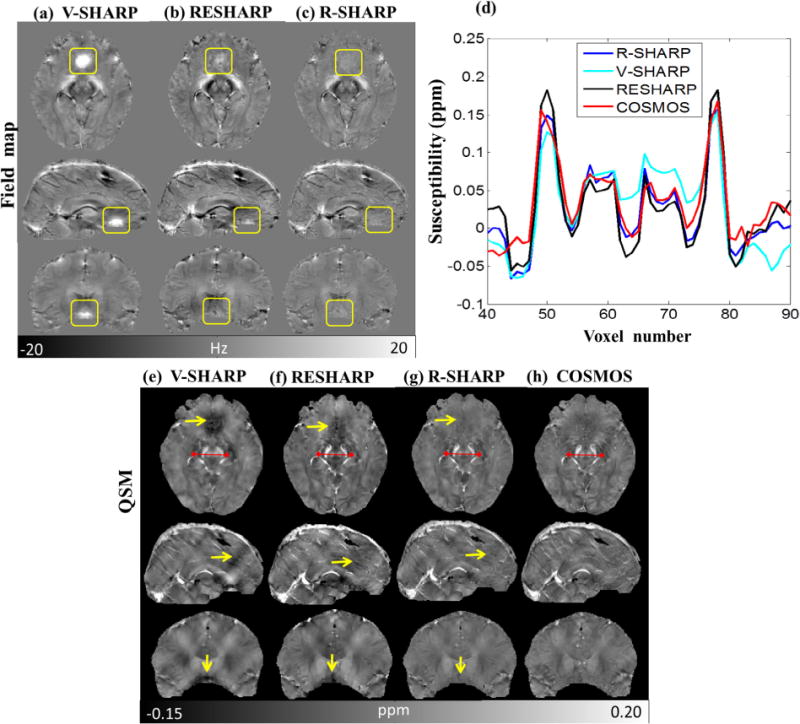
Results of background field removal without excluding the brain tissues around paranasal sinuses. (a–c) Background field removal of the three views by V-SHARP, RESHARP and R-SHARP (axial view, 23rd slice; sagittal view, 112th slice; coronal view, 85th slice), (d) profiles of the red lines in (e–h), (e–g) susceptibility reconstruction results with background field removed by the three methods, (h) COSMOS susceptibility maps. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 2.

Susceptibility estimation without excluding the brain tissue around sinuses (ppm).

Tissue	V-SHARP	RESHARP	R-SHARP	COSMOS
CN	0.042 ± 0.022	0.049 ± 0.017	0.033 ± 0.010	0.028 ± 0.012
GP	0.140 ± 0.040	0.208 ± 0.042	0.145 ± 0.030	0.144 ± 0.028
PU	0.032 ± 0.026	0.052 ± 0.024	0.027 ± 0.016	0.026 ± 0.017
SN	0.148 ± 0.031	0.186 ± 0.042	0.173 ± 0.036	0.182 ± 0.035
RN	0.091 ± 0.022	0.056 ± 0.023	0.068 ± 0.021	0.076 ± 0.021

Note: The results are mean value ± standard deviation.

5. Discussion

Experiments of numerical simulation, phantom and in vivo human demonstrated the feasibility of our proposed method R-SHARP for background field removal. It is shown that R-SHARP outperforms V-SHARP and RESHARP, especially in areas close to the air-tissue interface. The field map is separated into two subdomain as Ω₁ and Ω₂, which background fields are removed with SGK and SMV respectively. Over strong field variation regions, the background field is usually much larger than other brain areas, which is effectively suppressed using an adaptive kernel. Since the level set value directly reflects the field inhomogeneity degree, this allows us to exploit them to design region adaptive kernels. However, for those voxels with small level set values, we use the SMV kernel considering the computation efficiency. Adaptive spherical Gaussian kernels (SGK) were designed voxel-wise according to the energy value of level set function and adopted when such an energy function is larger than a threshold. By adjusting the radius and weights of the SGK, we can better recover the local field in those problematic areas around the sinuses or on the air-tissue interface commonly, which otherwise would need to be masked out to avoid convoluting strong background fields.

The level set function can dynamically drive the active contour evolution based on the voxels energy distribution on both sides of the contour, until the active contour stops at interfaces of the inhomogeneous regions in the phase map. For any voxel, the SGK scale parameter σ is inversely proportional to the level set function Ψ of the phase image. Around the air-tissue boundary, the SGK will have large kernel weights at the sphere center, while the surrounding weights reduce to zero rapidly, leading to less residual error in the estimated local field. If the unwrapped phase data is directly used as the measure of field inhomogeneity in Eq. (10), the adaptive SGK is not able to preserve the local field while remove the background field effectively as shown in Fig. 1, so the unwrapped phase is not suitable to design the adaptive convolution kernel in our method. Therefore, we employ the level set function of the unwrapped phase, but not the unwrapped phase directly.

In level set function, the regularization parameter μ is independent of phase map and it is empirically chosen to be 0.5. As for the regularization parameter υ, we need to generate multiple contours to distinguish different levels of susceptibility variations, where small value of υ is proper. The local fitting functions based on kernel K_s are two weighted averages on the two sides of the contour, dominated by image intensities in the neighborhood of x. We empirically determine s to be 5.0 after a series of experimental tests. The coefficients α₁ and α₂ are the weights of the two local fitting functions that represent the fitting energy outside and inside the contour, in which the intensity information in local regions is extracted to guide the contour motion. In the experiment, the level set contours are initialized using an rectangle in the image center, where the regions of strong susceptibility variations are outside the initial contours. For the in vivo human brain data, the intensity levels of the energy function inside and outside the initial contour are 5 and 17, while 0.4 and 8 for the simulation data. Since the tissue structure in the numerical simulation data is not as complex as the in vivo human brain data, the energy function level inside the initial contour of the simulation data is much smaller than the human brain data. Hence, we assigned α₁ = α₂ = 1 in the phantom and in vivo human brain experiments, but for the numerical simulation data, to overcome the energy distribution unbalance on the two sides of the contour, it is necessary to use larger weight α₂ for the inside of the contour. Actually, setting α₂ = 10 or 100 can also achieve equivalent results on background field removal, at the expense of more iterations than α₂ = 1000. Our method need more running time on the level set function computation, maybe an automatic initialization of the level set contour can further improve the computation efficiency, but it is beyond the scope of this paper.

Solving Eq. (11) may be accomplished by utilizing the well-known mean value property of harmonic functions, the theorem of which states that a harmonic function B_loc is preserved under convolution transform with any nonnegative, radially symmetric, normalized (total integral equals one) function. The mean value property thus enables the elimination of any information from the external magnetic field perturbations in B^Δ [6]. Although both the kernels of SMV and SGK satisfy these properties, SMVs of equal weights and a constant radius do not consider the amplitude of the background field. In traditional Laplacian-based methods, tissues around the paranasal sinuses are excluded from the VOI to satisfy the harmonic theorem. If these regions are taken into account to define a new VOI, the V-SHARP method with SMV performs poorly for background field removal. Normally in those areas the background field is one or two orders of magnitude greater than the local field and dominates the measured total field. From Eqs. (3) and (11), when the center weight of a normalized SGK is assigned, the adjacent weights decay rapidly to near-zero values and greater components can be subtracted from the total field at the calculated voxel. Thus less residual phase error remains. On the boundary voxel, the kernel radius is shrunk to 1 in the three methods. In this case, thanks to the adaptive weights in the R-SHARP, the whole kernel weights almost focus on the center of the SGK, but the SMV used in the V-SHARP and RESHARP have equal weights for all voxels in the kernel. Therefore, our method can preserve the integrity of brain tissues by avoiding convolution with the invalid signal outside the VOI, while one voxel width of boundary information may be discarded in V-SHARP and RESHARP methods.

As we know, the performance of the SHARP and V-SHARP methods can be regarded as a high-pass filter on the background-corrected phase images in k-space [3,22,25]. However, the background field may contain high frequency components [16] that fail to be removed by these methods. The parameters of SGK are adjusted to obtain a suitable bandwidth to filter the background field while preserving the local field. The parameter C in Eq. (9) determines the Gaussian standard deviation of susceptibility reconstruction (in Fig. 3). The susceptibility artifacts around the region of simulated sinuses are reduced and the reconstructed susceptibility values are closer to the ground truth, as the value of C increases (Fig. 3b). According to Eq. (9), when a greater value of C is selected, smaller Gaussian standard deviation can be obtained in the spatial domain, which corresponds to a wider spectrum range in k-space. The background field with higher frequency components in the vicinity of sinuses can be better filtered out. Hence, an optimal C value was determined by making a trade-off between the artifact levels and the susceptibility reconstruction accuracy. For in vivo human brain, the R-SHARP method effectively suppressed the strong background field caused by the paranasal sinuses without excluding the adjacent brain tissues and thus prevented the need for eroding anatomical structures. In all experiments on numerical simulation, phantom and in vivo human data, the C values ranging from 1.6 to 2.0 were suitable to obtain comparable results, and then the optimum was determined as 1.8 for three kinds of data in the paper for consistence.

Sun proposed RESHARP method by adding Tikhonov regularization to SHARP, which chose a radius of 5 voxels as the optimal kernel size considering both the result fidelity and integrity. For fair comparison, we extended RESHARP by employing a varying kernel size scheme in the same way as V-SHARP and R-SHARP. As we know, the regularization parameter in RESHARP is related to the difference values between the total fields and estimated local fields. However, when the processed data involves regions with large susceptibility variations, such as tissues around the paranasal sinuses, larger λ value should be selected to suppress the artifacts, which may cause over-smoothing the local field in other regions. The regularization parameter λ controls the weights between data term and regularization term, which is a constant value but not an adaptive parameter in RESHARP. We think using an adjustable parameter λ or adding a weighting matrix to B_loc, which enable to reflect the field inhomogeneity, will improve its background field removal performance. As for our method, since the level set value directly reflects the field inhomogeneity degree, this allows us to exploit them to design region adaptive kernels.

To further verify the background field removal performance, susceptibility maps were reconstructed by a modified SFCR method without using the fidelity masks in the reconstruction algorithm [9] to objectively assess the artifact suppression performance of R-SHARP, RESHARP and V-SHARP methods. When the tissues around the sinuses are included, serious shadow artifacts caused by large susceptibility variations are significantly better suppressed by the R-SHARP method than by V-SHARP and RESHARP methods. The reason is that the R-SHARP method avoids the residual phase error propagating into the susceptibility mapping. As a consequence, more accurate susceptibility reconstruction can be achieved. The application of QSM is a popular research topic at present, in human organs of brain, liver, kidney, heart, knee joint [36] and so on. For instance, for the heart and kidney, the air-tissue interfaces generate a large susceptibility and bone-soft tissue interfaces have large susceptibility variations for the knee joint, especially for the small cartilage regions. Our proposed R-SHARP method has potential to better address these problems in future QSM applications.

6. Conclusion

In this paper, we proposed a new background field removal method using region adaptive kernel (R-SHARP) based on a fitting energy functional. Simulations and in vivo human data demonstrated that our method has good performance with respect to suppressing the susceptibility artifacts caused by large susceptibility variations, such as in boundary regions close to brain skull, paranasal sinuses and venous vessels. This can should benefit more accurate QSM mapping and facilitate its further application in the clinic.